2013-2014(上)数学论文
2013-2014学年高一数学上学期期末考试试题及答案(新人教A版 第89套)

宜昌市部分示范高中教学协作体2013年秋季期末考试高 一 数 学 试 题考试时间:120分钟 试卷满分:150分 注意事项:1.答卷前,考生务必将自己的相关信息填写在规定的位置,并检查所持试卷是否有破损和印刷等问题。
若试卷有问题请立即向监考教师请求更换。
2.答题答在答题卡上对应的答题区域内,答在试题卷、草稿纸上的无效。
3.考生必须保持答题卡的整洁。
考试结束后,请将答题卡上交。
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={}x y x lg =,B={}022≤-+x x x ,则=B A ( )A .)0,1[-B .]1,0(C .]1,0[D .]1,2[-2.已知集合}01|{2=-=x x A ,则下列式子表示正确的有( ) ①A ∈1 ②A ∈-}1{ ③A ⊆φ ④A ⊆-}1,1{A .1个B .2个C .3个D .4个3、设2:f x x →是集合M 到集合N 的映射, 若N={1,2}, 则M 不可能是 ( )A 、{-1}B 、{C 、{-D 、 4、已知函数xx f 1)(=,则1)1(+-=x f y 的单调递减区间为( ) A 、[0,1) B 、(-∞,0) C 、}1|{≠x x D 、(-∞,1)和(1,+∞) 5、偶函数()f x 与奇函数()g x 的定义域均为[4,4]-,()f x 在[4,0]-,()g x 在[0,4]上的图象如图,则不等式()()0f x g x ⋅<的解集为( )A 、[2,4]B 、(4,2)(2,4)--C 、(2,0)(2,4)- D 、(2,0)(0,2)-6.已知函数)(1)62sin(2)(R x x x f ∈-+=π则)(x f 在区间[0,2π]上的最大值与最小值分别是( )A. 1, -2 B .2 , -1 C. 1, -1 D.2, -2 7..函数)(x f y =的图象向右平移6π个单位后与函数)22cos(π-=x y 的图象重合.则)(x f y =的解析式是( )A.)32cos()(π-=x x f B. )62cos()(π+=x x fC. )62cos()(π-=x x f D. )32cos()(π+=x x f8.设02x π≤≤,sin cos x x =-,则( ) A.0x π≤≤ B.744x ππ≤≤C.544x ππ≤≤D.322x ππ≤≤ 9.若)2sin(3)(ϕ+=x x f +a ,对任意实数x 都有),3()3(x f x f -=+ππ且4)3(-=πf ,则实数a 的值等于( )A .-1B .-7或-1C .7或1D .7或-710.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y =f (x )(实线表示),另一种是平均价格曲线y =g(x )(虚线表示)(如f (2)=3是指开始买卖后两个小时的即时价格为3元g(2)=3表示2个小时内的平均价格为3元),下图给出四个图象:其中可能正确的图象序号是 。
2013-2014第一学期论文

一年级识字、写字教学是语文教学的一项重要任务。
新课标在识字、写字方面,实行“认写分开”、“多认少写”,提出“会认、会写”两种要求,这对培养学生的阅读能力以及获取信息的能力都有重要意义。
但是,低年级学生在掌握字形方面是难点,如何突破这个难点呢?下面我来谈谈我的几点看法:一、教学生在自学中掌握汉字的构字规律过去的教学一般是老师教,学生学,学生处于被动地位。
新课程充分体现了让学生自学,用多种方法思考、记忆、分析字形的思想,培养学生自主识字能力,放手让学生自己思考,自己发现问题,想办法解决问题。
这样不仅激发了学生识字的兴趣,对字形的记忆也会更加扎实牢固,还可以从中摸索体会汉字的构字规律。
在一年级的识字教学中我是这样做的:先引导学生观察情境图,让他们产生读书的欲望,在反复朗读中掌握生字读音、认识字形。
接着我就问学生:“今天我们要学习这几个生字,看谁最聪明?自己动脑筋想出最好的记忆方法,请你告诉大家。
”这样一问,同学们兴趣盎然,马上就开始在大脑中寻找答案,提出了许多不同的记忆方法:“熟字加笔画”、“形近字对比”、“同音字”、“熟字去偏旁”、“拆部件”、“减笔画”……如学习“天”字,有的说“大”字加一横就是天;有的说“人”字加两横就是天;有的说“夫”字不出头就是天。
学习“园”字时,有的说是在“元”字外面加上围墙“口”就是“园”,从而明白“校园、公园”是有围墙的,以区别“元、园”的用法。
学习“爱”字,学生把它拆成“、冖、友”,我配上儿歌“爪字头,秃宝盖,小朋友,真可爱”。
这样学生很快就记住了生字。
二、在轻松愉快的学习中突破字形难点刚刚入学的孩子年龄小,注意力不集中,易于疲劳。
《新课标》提出:培养学生对汉字以及汉字学习的态度和情感,有主动识字的愿望,初步感受汉字的形体美。
所以,教学时要采用多种方式方法,激发学生兴趣,让他们在兴趣盎然中边玩边学。
这样,在充分调动学生无意注意的同时也促使其有意注意的发展。
并且老师要为解决困难创设情境,以促使学生思维灵活、有创造性地发展。
2013-2014学年新人教版五年级(上)期中数学检测卷e(一)

2013-2014学年新人教版五年级(上)期中数学检测卷E(一)一、打开知识窗,轻松填一填.(每空1分,共18分)1.(2分)0.52×2.4的积是_________位小数;9.6÷0.24的商的最高位是_________位.2.(2分)如果185×87=16095,那么18.5×8.7=_________,160.95÷0.87=_________.3.(2分)一件商品降价a元后是128元,原价是_________.当a=32时,原价就是_________元.4.(1分)在5.6、5.666、5.、5.中,最大的数是_________.5.(4分)在横线里填上“>”“<”或“=”.1.4_________ 1.793÷1.01_________7933.02÷0.1_________ 3.02×100.31×1.01_________0.31.6.(2分)5÷6的商用循环小数表示是_________,保留两位小数是_________.7.(2分)小明今年x岁,爸爸今年的年龄是小明的3倍,爸爸今年有_________岁,小明和爸爸今年一共_________岁.8.(3分)从_________面看到,从_________面看到,从_________面看到(填“正”“上”或“左”).二、激活分辨力,准确辨一辨.(每题1分,共5分)9.(1分)0.999×1.23的积大于0.999小于1.23._________.10.(1分)与x2相等的式子是2x._________.(判断对错)11.(1分)x=0.6是方程9x﹣3x=4.2的解._________.(判断对错)12.(1分)(2010•建华区)无限小数一定是循环小数._________.(判断对错)13.(1分)这三个图形从侧面看的形状是相同的._________.(判断对错)三、点击选择框,认真选一选.(每题2分,共10分)四、走进计算园.(29分)20.(6分)用竖式计算.8.45×3.9(结果保留一位小数)36÷9.9(商用循环小数表示)21.(12分)计算下面各题,能简算的要简算.12.5×16×0.54.8÷0.16÷0.348.7﹣32.76÷8.40.57×102.22.(6分)解方程.6x﹣7.8=10.925×2.5+5x=36.五、实践操作,我会做.(9分)23.(3分)看一看,连一连.24.(6分)画出下面立体图形从正面、左面和上面看到的形状.六、关注生活,灵活运用.(29分)25.(5分)水果店购进了13吨水果,要用小货车把这些水果运回水果店,每次最多能运送1.9吨.这辆小货车至少要运送多少次?26.(6分)妈妈买了两种商品.罐头15瓶,每瓶4.5元;蛋糕10千克,花了58.5元钱.妈妈带了100元钱,够用吗?27.(6分)如图是小东家的客厅和厨房的平面图.(1)用字母表示小东家的客厅比厨房的面积大多少平方米?(2)当b=6.5时,小东家的客厅比厨房的面积大多少平方米?28.(6分)张叔叔买了3箱苹果和2箱梨,每箱水果的价钱都相同,一共用了198元,每箱水果多少元钱?(用方程解)29.(6分)猎豹追捕猎物时的速度大约是一名优秀短跑运动员百米赛跑时速度的3倍,大约比这名运动员每秒多跑20m.这名运动员每秒大约跑多少米?猎豹呢?七、附加题(共1小题,满分0分)30.王老师给品学兼优的学生发奖品.如果每人发2本日记本,则多出13本日记本;如果每人发3本日记本,则少5本日记本.获奖的学生有多少人?2013-2014学年新人教版五年级(上)期中数学检测卷E(一)参考答案与试题解析一、打开知识窗,轻松填一填.(每空1分,共18分)1.(2分)0.52×2.4的积是三位小数;9.6÷0.24的商的最高位是十位.2.(2分)如果185×87=16095,那么18.5×8.7=160.95,160.95÷0.87=185.3.(2分)一件商品降价a元后是128元,原价是128+a.当a=32时,原价就是160元.4.(1分)在5.6、5.666、5.、5.中,最大的数是 5..=5.666< 5...5.(4分)在横线里填上“>”“<”或“=”.1.4> 1.793÷1.01<7933.02÷0.1= 3.02×100.31×1.01>0.31.>6.(2分)5÷6的商用循环小数表示是0.8,保留两位小数是0.83.=0.8≈,7.(2分)小明今年x岁,爸爸今年的年龄是小明的3倍,爸爸今年有3x岁,小明和爸爸今年一共4x岁.8.(3分)从正面看到,从左面看到,从上面看到(填“正”“上”或“左”).根据题干分析可得:正面看到左面看到上面看到二、激活分辨力,准确辨一辨.(每题1分,共5分)9.(1分)0.999×1.23的积大于0.999小于1.23.√.10.(1分)与x2相等的式子是2x.×.(判断对错)11.(1分)x=0.6是方程9x﹣3x=4.2的解.×.(判断对错)12.(1分)(2010•建华区)无限小数一定是循环小数.×.(判断对错)13.(1分)这三个图形从侧面看的形状是相同的.√.(判断对错)三、点击选择框,认真选一选.(每题2分,共10分)四、走进计算园.(29分)20.(6分)用竖式计算.8.45×3.9(结果保留一位小数)36÷9.9(商用循环小数表示)9.9=3.;21.(12分)计算下面各题,能简算的要简算.12.5×16×0.54.8÷0.16÷0.348.7﹣32.76÷8.40.57×102.22.(6分)解方程.6x﹣7.8=10.925×2.5+5x=36.五、实践操作,我会做.(9分)23.(3分)看一看,连一连.24.(6分)画出下面立体图形从正面、左面和上面看到的形状.六、关注生活,灵活运用.(29分)25.(5分)水果店购进了13吨水果,要用小货车把这些水果运回水果店,每次最多能运送1.9吨.这辆小货车至少要运送多少次?26.(6分)妈妈买了两种商品.罐头15瓶,每瓶4.5元;蛋糕10千克,花了58.5元钱.妈妈带了100元钱,够用吗?27.(6分)如图是小东家的客厅和厨房的平面图.(1)用字母表示小东家的客厅比厨房的面积大多少平方米?(2)当b=6.5时,小东家的客厅比厨房的面积大多少平方米?28.(6分)张叔叔买了3箱苹果和2箱梨,每箱水果的价钱都相同,一共用了198元,每箱水果多少元钱?(用方程解)29.(6分)猎豹追捕猎物时的速度大约是一名优秀短跑运动员百米赛跑时速度的3倍,大约比这名运动员每秒多跑20m.这名运动员每秒大约跑多少米?猎豹呢?七、附加题(共1小题,满分0分)30.王老师给品学兼优的学生发奖品.如果每人发2本日记本,则多出13本日记本;如果每人发3本日记本,则少5本日记本.获奖的学生有多少人?参与本试卷答题和审题的老师有:冯凯;林清涛;齐敬孝;似水年华;姜运堂;彭京坡;晶优;nywhr;吴涛;zcb101;陆庆峰;languiren(排名不分先后)菁优网2014年7月15日。
2013-2014学年上学期期末考试(含答案)八年级数学

八年级(上)数学期末测试题第1卷(选择题)一、选择题(本题20小题,每小题3分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,并把答题卡上对应题目的正确答案标号涂黑)1.下列各组数中不能作为直角三角形的三条边长的是( )A.6,8,10B.9,12, 15C.1.5,2,3D.7,24, 252.一三,27t,等,o,0.23 2233 2233 2233…中,有理数的个数是( ) A.l B.2 C.3 D.43.下列扑克牌中,绕着某一点旋转1800后可以与原来的完全重合的是( )4.点P(-5,6)关于原点对称的点的坐标是( )A.(-5, -6)B.(5,6)C.(6,.5)D.(5,.6)5.估算24的算术平方根在( )A.2和3之间B.3和4之间C.4和5之间D.5和6之间中,一次函数的有( )A.4个B.3个C.2个D.l个7.为了筹备班级初中毕业联欢会,班长对全班同学爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )A.平均数 B.力口权平均数 C.中位数 D.众数8.-次函数y= -x-l不经过的象限是( )A.t第一象限 B.第二象限 C.第三象限 D.第四象限A. 20 B.15 C.10 D.510.w边形ABCD中,AC、BD相交于点D,能判别这个四边形是正方形的条件是( )11.点彳的坐标为(6,3),D为原点,将OA绕点0按顺时针方向旋转90度得到OA1,则点A1的坐标为 ( )么.(3.-6) B.(-3,6) C.(一3,.6) D.(3,6)12.下列说法正确的有____个.( )①有两个底角相等的梯形是等腰梯形②有两边相等的梯形是等腰梯形③有两条对角线相等的梯形是等腰梯形④等腰梯形上下底中点连线把梯形分成面积相等的两部分A.l个 B.2个 C.3个 n 4个13.如果直线y=3x+6 y=2x-4交点坐标为(a,b),的解( )14.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输为 15,那么与实际平均数的差为( )A.3B..3C.j 0.5D.3.515.把一张正方形纸片按如图所示的方法对折两次后剪去两个角,那么打开以后的形状是( )么.六边形 B.八边形 C.十二边形D.十六边形16.如图,在四边形ABCD中,动点P从点A开始沿A→_B→C→D的路径匀速前进到D为止。
2014数学中国国际赛论文参考模版分解

数学建模国际赛承诺书我们仔细阅读了第三届“认证杯”数学中国数学建模国际赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们允许数学中国网站()公布论文,以供网友之间学习交流,数学中国网站以非商业目的的论文交流不需要提前取得我们的同意。
我们的参赛队号为:1402我们选择的题目是: B参赛队员(签名) :队员1:队员2:队员3:参赛队教练员(签名):无数学建模国际赛编号专用页参赛队伍的参赛队号:(请各个参赛队提前填写好):1402 竞赛统一编号(由竞赛组委会送至评委团前编号):竞赛评阅编号(由竞赛评委团评阅前进行编号):TITLE Abstract:Key words:Contents1. Introduction (3)1.1 Why does toll way collects toll? (3)1.2 Toll modes (3)1.3 Toll collection methods (3)1.4 Annoyance in toll plazas (3)1.5 The origin of the toll way problem (3)1.6 Queuing theory (4)2. The Description of Problem (5)2.1 How do we approximate the whole course of ? (5)2.2 How do we define the optimal configuration? (5)2.2.1 From the perspective of (5)2.2.2 From the perspective of the (6)2.2.3 Compromise (6)2.3 Overall optimization and local optimization (6)2.4 The differences in weights and sizes of (7)2.5 What if there is no data available? (7)3. Models (7)3.1 Basic Model (7)3.1.1 Symbols and Definitions (7)3.1.2 Assumptions (8)3.1.3 The Foundation of Model (9)3.1.4 Solution and Result (11)3.1.5 Analysis of the Result (11)3.1.6 Strength and Weakness (13)3.2 Improved Model (14)3.2.1 Extra Symbols (14)3.2.2 Additional Assumptions (14)3.2.3 The Foundation of Model (14)3.2.4 Solution and Result (15)3.2.5 Analysis of the Result (18)3.2.6 Strength and Weakness (19)4. Conclusions (19)4.1 Conclusions of the problem (19)4.2 Methods used in our models (19)4.3 Application of our models (19)5. Future Work (19)5.1 Another model (19)5.2 Another layout of (23)5.3 The newly- adopted methods (23)6.References (23)7.Appendix (23)Programs and codes (24)I. IntroductionIn order to indicate the origin of problems, the following background is worth mentioning.1.11.21.31.41.51.6II. The Description of the Problem2.1 How do we approximate the whole course of ?●●●●2.2 How do we define the optimal configuration?1) From the perspective of :2) From the perspective of the :3) Compromise:2.3 The local optimization and the overall optimization●●●Virtually:2.4 The differences in weights and sizes of2.5 What if there is no data available?III. Models3.1 Basic Model3.1.1 Terms, Definitions and SymbolsThe signs and definitions are mostly generated from queuing theory.●●●●●3.1.2 Assumptions●●●●●3.1.3 The Foundation of Model1) The utility function●The cost of :●The loss of :●The weight of each aspect:●Compromise:2) The integer programmingAccording to theory, we can calculate the statistical properties as follows.3)The overall optimization and the local optimization●The overall optimization:●The local optimization:●The optimal number of :3.1.4 Solution and Result1) The solution of the integer programming:2) Results:3.1.5 Analysis of the Result●Local optimization and overall optimization:●Sensitivity: The result is quite sensitive to the change of the threeparameters●Trend:●Comparison:3.1.6 Strength and Weakness●Strength: In despite of this, the model has proved that . Moreover, wehave drawn some useful conclusions about . The model is fit for, such as●Weakness: This model just applies to . As we have stated, .That’sjust what we should do in the improved model.3.2 Improved Model3.2.1 Extra SymbolsSigns and definitions indicated above are still valid. Here are some extra signs and definitions.●●●●3.2.2 Additional Assumptions●●●Assumptions concerning the process are the same as the Basic Model.3.2.3 The Foundation of Model1) How do we determine the optimal number?As we have concluded from the Basic Model,3.2.4 Solution and Result1) Simulation algorithmBased on the analysis above, we design our simulation arithmetic as follows.●Step1:●Step2:●Step3:●Step4:●Step5:●Step6:●Step7:●Step8:●Step9:2) Flow chartThe figure below is the flow chart of the simulation.3) Solution3.2.5 Analysis of the Result3.2.6 Strength and Weakness●Strength: The Improved Model aims to make up for the neglect of .The result seems to declare that this model is more reasonable than the Basic Model and much more effective than the existing design.●Weakness: . Thus the model is still an approximate on a large scale. Thishas doomed to limit the applications of it.IV. Conclusions4.1 Conclusions of the problem●●●4.2 Methods used in our models●●●4.3 Applications of our models●●●V. Future Work5.1 Another model5.1.1The limitations of queuing theory 5.1.25.1.35.1.41)●●●●2)●●●3)●●●4)5.2 Another layout ofTeam # 1402 Page 11 of 11 5.3 The newly- adopted charging methodsVI. References[1][2][3][4]VII. Appendix。
2013-2014八年级上学期数学教学总结

2013—2014学年度上学期期末考试质量分析
暨教学工作总结
第一部分:基本情况
教师姓名:陈自先任教班级:132 任教科目:数学填表日期2014.2.23 1、个人主要承担的各班教学工作情况:
2、个人主要承担的各班教学各分数段情况
第二部分:期末试题分析
第三部分:考情分析
以本班学生为样本容量,统计分析各学生各知识点的得失分
第四部分:所教班级学生答题情况分析及教学反思
填表要求:
1、每位教师填表前必须认真分析期末考试情况,包括试卷情况和学生答题情况。
2、分析清楚情况后,要认真进行教学反思,找出以往教学中的经验和存在的不足,认真思考今后如何改进自己的教学工作。
3、“期末试题分析”部分的表格若与本学科试卷题号结构不符,由教师自己修改表格
4、填写后的表格,教研组和教务处必须认真一一审核,分析不认真细致者返回重填。
2013-2014学年高一数学上学期第一次阶段考试试题及答案(新人教A版 第88套)
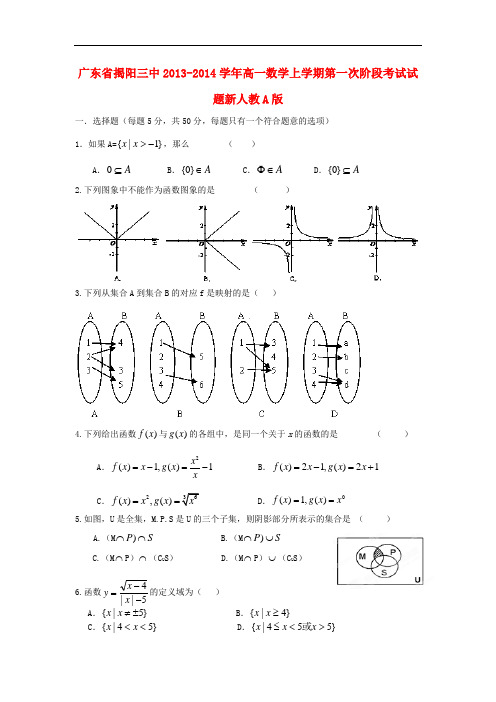
广东省揭阳三中2013-2014学年高一数学上学期第一次阶段考试试题新人教A 版一.选择题(每题5分,共50分,每题只有一个符合题意的选项) 1.如果A=}1|{->x x ,那么 ( )A .A ⊆0B .A ∈}0{C .A ∈ΦD .A ⊆}0{2.下列图象中不能作为函数图象的是 ( )3.下列从集合A 到集合B 的对应f 是映射的是( )4.下列给出函数()f x 与()g x 的各组中,是同一个关于x 的函数的是 ( )A .2()1,()1x f x x g x x=-=- B .()21,()21f x x g x x =-=+C .2(),()f x x g x ==.0()1,()f x g x x ==5.如图,U 是全集,M.P.S 是U 的三个子集,则阴影部分所表示的集合是 ( )A.(M S P ⋂⋂)B.(M S P ⋃⋂)C.(M ⋂P )⋂(C U S )D.(M ⋂P )⋃(C U S ) 6.函数5||4--=x x y 的定义域为( )A .}5|{±≠x xB .}4|{≥x xC .}54|{<<x xD .}554|{><≤x x x 或7.已知⎩⎨⎧>+-≤+=)1(32)1(1)(2x x x x x f ,则=)]2([f f ( )A .5B .-1C .-7D .28.若集合}|{},21|{a x x B x x A ≤=<<=,且Φ≠B A ,则实数a 的集合( )A .}2|{<a aB . }1|{≥a aC .}1|{>a aD .}21|{≤≤a a 9.设偶函数f(x)的定义域为R ,当x [0,)∈+∞时f(x)是增函数,则f(-2), f(π), f(-3)的大小关系是( )A. f(π)>f(-3)>f(-2)B. f(π)>f(-2)>f(-3) C .f(π)<f(-3)<f(-2) D. f(π)<f(-2)<f(-3)10.已知函数)1(52)(2>+-=a ax x x f ,若)(x f 的定义域和值域均是[]a ,1,则实数a 的值为( )A .5B .-2C .-5D .2 二. 填空题(每题5分,共20分)11.已知集合{}12|),(-==x y y x A ,}3|),{(+==x y y x B 则AB =12.已知函数)(x f 满足关系式52)2(+=+x x f ,则=)3(f _________13.设奇函数f(x)的定义域为]5,5[-.若当]5,0[∈x 时, f(x)的图象如右图, 则不等式f(x)<0的解集是14.已知定义在)1,1(-上的奇函数)(x f ,在定义域上为减函数,且,0)21()1(>-+-a f a f 则实数a 的取值范围是三.解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)。
2013年论文数学

公式是鱼,思想是渔——渗透在多边形面积计算中的转化思想人教版五(上)多边形面积这一单元包括平行四边形的面积、三角形的面积、梯形的面积和组合图形的面积四块内容。
教材是根据图形面积之间的内在联系安排教学内容的。
这些图形的面积计算又以长方形面积计算为基础,以图形内在联系为线索,以变换为途径,以未知向已知转化为基本方法开展教学,在这一单元的教学中,我始终感到转化思想是多边形面积计算的关键!单纯地叫学生背诵记忆面积公式意义不大,有失偏颇。
下面我来谈下我在多边形面积公式的推导教学中集中体现了两种具体的转化思想:等积变换和倍积变换。
多边形面积计算以经历探究面积公式为主导,辅以实际意义的理解和把握,实践面积的计算,促进能力的提高。
在平行四边形面积教学中,先借助数方格(单位面积度量)的方法,得到平行四边形的面积;再引导学生通过割补法将平行四边形转化为已学的长方形,推导出平行四边形的面积计算公式。
通过割补演示,学生明白了“原来”的平行四边形变成“现在”的长方形,图形转化了,面积没变。
像这样的等积变换的转化思想在课本的好多习题中都有体现。
从而也反证了等积变换的转化思想是这部分内容的重点!授人以鱼,不如授之以渔。
对于三角形面积计算的教学,要求学生将三角形转化为已学过的图形来推导面积计算公式。
教材呈现的是两个完全一样的三角形拼成一个平行四边形,体现的是倍积变换思想,而这种转换思想教材是第一次出现。
有了前面的探究经验,在进行梯形面积教学时,要求学生综合运用学过的方法自己推导出面积计算公式。
我认为用两个完全一样的梯形可以拼成平行四边形的转换思想学生更容易推导。
可以说,每一种图形教材都没有给出推导的过程和公式,让学生通过多种途径探索,自己发现规律,自己得出结论,从而给教师和学生留有较大的创造空间。
等积变换是几何学习中重要的思想方法,也是数学推导与证明的一种重要手段。
例如,我们计算中的递等式计算、解方程时实际上体现了等值变换的一种思想。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论文:数学课堂教学的几点反思作者:寇国威单位:铁岭市清河区聂家满族乡学校数学课堂教学的几点反思铁岭市清河区聂家中学寇国威“学然后知不足教然后知困。
知不足然后能自反也,知困,然后能自强也”。
在当前轰轰烈烈的课改中,如何培养学生的反思习惯和加强反思教师自己的教学行为,是笔者今天和教育同仁共同探讨的话题。
本文主要阐述了对初中数学教学的反思。
一、数学课堂教学中的基本理念的反思数学课堂教学是数学活动的教学,是师生之间、学生之间交往互动与共同发展的过程。
数学课堂教学,要紧密联系学生的生活实际,从学生的生活经验和已有知识出发,创设生动有趣的情境,引导学生开展观察、操作、猜想、推理、交流等活动,使学生通过数学活动,掌握基本的数学知识和技能,初步学会从数学的角度去观察事物、思考问题,激发学习数学的兴趣。
学生是数学教学的主体,教师是学生数学活动的组织者、引导者与合作者。
教师要正确地认识学生个体差异,因材施教,使每个学生都在原有的基础上得到充分的发展;要关注学生的学习过程,不仅要关注学生观察、分析、自学、表达、操作、与人合作等一般能力的发展,以及运算、空间观念、统计、解决问题等数学能力的发展,更要关注学生在情感、态度与价值观等方面的健康和谐的发展;不仅要关注课堂教学的结果,更要关注课堂教学的过程。
数学课堂教学是教师依据数学课程标准的理念与基本要求,在全面驾驭教科书的知识体系、知识结构和编写意图的基础上,根据学生的具体情况,对教学内容进行再创造的过程。
数学课堂教学是数学教师的教学技能、教学能力、业务水平、文化修养、教育观点、师德和思想素质的综合表现。
二、数学课堂教学中的基本意识的反思1.整体意识一节课是一个整体,一门学科是一个整体,各门学科又构成了一个整体教学内容,学生良好的精神品格的培养,学习能力的培养和提高,决不是某一门学科单独所能完成的。
教师要淡化学科的个性,强化各门学科的共性,注意各门学科之间的相互渗透和沟通。
就一门学科而言,要在课堂中培养学生的全面素质,也必须着眼于整体,有整体意识。
在教学目标的制定和把握上必须跳出认知技能的框框,注重目标的整体性和全面性。
2.主体意识“主体性教育”是素质教育的核心。
当今世界许多国家教育改革的趋势是在教育教学过程中,不仅要承认和尊重学生的主体地位,更要注意发展学生的主体性。
但实际的课堂教学又如何呢?尽管许多教师在理性上承认:学生是课堂的主人,是学习的主体。
但在实际的课堂教学中,学生的主体地位总是有意无意地被忽视。
使得培养出来的学生缺乏一种内在的精神,在自主性上,不能根据需要主动地发展自我;在主动性上,缺乏主动参与、大胆竞争、勇于表现的意识和能力;在创造性上,不善于独立思考,缺乏分析问题和解决问题的能力。
可见,课堂教学必须倡导鲜明的主体意识,让教师充分认识到:课堂是学生学习知识的场所,而不仅仅是自己施展才华的舞台;要重视学生获取知识的过程和获取知识的能力的培养。
不能满足于自己讲得舒服,讲得痛快,而要关注在40分钟里学生的变化和发展。
3.创新意识创新意识是指教师的创新的欲望和信念,其核心是自我批判的意识,不受固有思维模式的束缚,勇于立新。
创造性的设计教学,目的是为了更有效地达成教学目标,使教学过程更加优化,提高课堂教学效率。
而从数学课堂教学现状来看,尽管许多教师有较强的敬业精神和钻研精神,但无论在教学的模式还是在教学方法上都是“继承多于创造”,也很少有自己的教学风格。
课堂教学设计中的创新主要包括:(1)教学内容组织的创新。
例如,对教材内容的解构与重组;对概念、命题赋予不同的现实模型或不同的数学模型;对例题、习题的改造与扩充等,均是在原有基础上的创新。
(2)教学模式构建的创新。
根据不同的教学内容合理地选择教学模式,更注意综合一些教学模式,创建一些新的教学模式。
(3)教学组织形式的创新。
(4)教育技术的创新。
主要是多媒体的合理组合,课件编制更富创意等。
4.反思意识反思是立足于自我之外的批判地考察自己的行动及情境的能力。
反思意识是教师自觉产生对自己的活动目的、活动计划、活动策略、活动过程及活动评价的反思欲望和信念。
反思不是单纯的事后行为,还包括事前和过程中的反思。
首先,要对教学目的进行反思。
数学知识的建构、数学技能的形成、数学能力的发展、数学思想方法的渗透、数学知识产生的过程体验等,都是数学教学的目的。
因此,在教学设计中要认真分析教学内容,确定多个教学目的,有的是主要目的,有的是次要目的;有的是直接目的,有的是间接目的,设计时要统筹把握。
其次,要对教学程序第二设计及教学策略的选择进行反思。
反思知识展示的顺序是否合理;选择的教学策略是否恰当;例题与习题的搭配是否符合教学目的的要求;采用的媒体是否真正发挥辅助教学的目的;为什么要这样设计教学程序;为什么要选择这样的教学策略等等。
第三,教学实施后的反思。
主要是对教学效果评价的反思,如何改进教学设计的反思。
三、数学课堂教学中的策略方法的反思(一)重学习环境,让学生参与数学通过创设良好的人际关系和学习氛围激励学生学习潜能的释放,努力提高学生的参与质量。
和谐的师生关系便于发挥学生学习的主动性、积极性。
现代教育家认为,要使学生积极、主动地探索求知,必须在民主、平等、友好合作的师生关系基础上,创设愉悦和谐的学习气氛。
因此,教师只有以自身的积极进取、朴实大度、学识渊博、讲课生动有趣、教态自然大方、态度认真、治学严谨、和蔼可亲、不偏不倚等一系列行为在学生中树立起较高威信,才能有较大的感召力,才会唤起学生感情上的共鸣,以真诚友爱和关怀的态度与学生平等交往,对他们尊重、理解和信任,才能激发他们的上进心,主动地参与学习活动。
教师应鼓励学生大胆地提出自己的见解,即使有时学生说得不准确、不完整,也要让他们把话说完,保护学生的积极性。
交往沟通、求知进取、和谐愉快的学习氛围为学生提供了充分发展个性的机会,教师只有善于协调好师生的双边活动,才能让大多数学生都有发表见解的机会。
例如,在讨论课上教师精心设计好讨论题,进行有理有据的指导,学生之间进行讨论研究。
这样学生在生动活泼、民主和谐的群体学习环境中既独立思考又相互启发,在共同完成认知的过程中加强思维表达、分析问题和解决问题能力的发展,逐步提高学生参与学习活动的质量。
要提供合作学习的机会。
合作学习是21世纪学生学习的一种重要方式之一,它是在教师主导作用下,群体研讨,协作交流的一种学习方式,它能有效地改善学习环境,扩大参与面,提高参与度。
在学习过程中,学生在与同学共同操作、互相讨论、交流中促进学习进步和智力发展。
通过合作,有利于引导学生用不同的方式探讨和思考问题,培养其参与意识、创造意识,产生创新思维。
(二)、重问题情境,让学生亲近数学。
人的思维过程始于问题情境。
问题情境具有情感上的吸引力,能使学生产生学习的兴趣,激发其求知欲与好奇心。
因此,在数学教学中,教师要精心创设问题情境,激起学生对新知学习的热情,拉近学生与新知的距离,为学生的学习作好充分的心理准备,让学生亲近数学。
可以有以下几种方法:1、创设动画情境:学生对于形象的动画卡片、投景、实物或生动的语言描述非常感兴趣,他们的思维也就容易被启迪、开发、激活。
对创设的问题情境产生可持续的动机,这种直观是一种催化剂,给学生的学习活动带来一定的生活色彩。
不仅对创设情境产生表象,更重要的是增强了学生的学习策略意识的培养,必将促使学生积极思维。
2、创设生活情境:数学来源于生活,让学生感受到数学就在他们的周围。
因此,从学生已有的生活经验出发,创设生活中的情境,强化感性认识,从而达到学生对数学的理解。
3、创设故事情境:学生都很喜欢听故事,而且可以从故事中得到更多的数学启示。
4、创设挑战性情境:根据教学内容,创设新奇的,具有神秘色彩的情境,能有效的激趣、导疑、质疑、解疑,培养学生的创新意识。
5、创设游戏情境:学生集中注意的时间较短,稳定性差,分配注意的能力较差,教师可创设游戏情境,让学生在游戏的活动中不知不觉地进行学习,以延长有意注意的时间及增强学习效果。
6、创设发现情境:培养学生创新意识,并不是都让学生去发明创造,更重要的是让学生去独立思考去发现,这种发现本身就是创造。
7、创设实践情境:学生的第一发展水平和第二发展水平之间存在着差异。
教师应走在学生发展的前面,创造“最近发展区”。
注意适时、适度创设实践情境,培养学生的创新意识和实践能力。
一个生动有趣、富有挑战性和实际意义的问题情境,可以巧妙地引发学生的认知冲突,使得学生对新知识满怀无比强烈的求知欲。
(三)、重动手操作,让学生体验数学。
马芯兰老师曾经说过:“儿童的智慧在他的指尖上。
”现代教学论也认为:要让学生动手做科学,而不是用耳朵听科学。
的确,思维往往是从人的动作开始的,切断了活动与思维的联系,思维就不能得到发展。
而动手实践则最易于激发学生的思维和想象。
在教学活动中,教师要十分关注学生的直接经验,让学生在一系列的亲身体验中发现新知识、理解新知识和掌握新知识,让学生如同“在游泳中学会游泳”一样,“在做数学中学习数学”,发展思维能力。
例如教学立体图形这一节课时,由于它接近于实际生活。
在了解学生已掌握的知识基础上,可以让他们自己总结、交流他们对立体图形的感受、自己动手制作熟悉的立体图形,并根据自己的想像利用丰富图形构造生活实景。
这样避免了教师一味地讲解,学生一味地记忆。
课堂气氛非常活跃,学生在轻松的学习氛围中掌握了知识。
又如在进行轴对称图形和轴对称的教学时,可以组织这样的活动:⑴组织一次对称面具制作比赛。
用卡片,纸板,甚至三合板来制作。
要学生制作对称图案的面具,并进行比赛,参加的学生一定会在笑声中感到创造的乐趣。
⑵收集有对称图案的昆虫、动物的照片,进行展览。
⑶教师课始借助一幅学生非常熟悉而又滑稽的大头娃娃的头像,通过“眼睛的不对称,让学生想办法使其变成对称”这样一个过程,使学生在游戏中初步感知“轴对称图形”,这样的过程做到了“寓知识于游戏,化抽象为形象,变空洞为具体”,使学生的学习具有形象性、趣味性。
通过动手操作使数学知识不再那么抽象,理解数学也不再那么空洞。
教师这样将数学教学设计成看得见,摸得着的物化活动,让学生对十分抽象的知识获得了相当清晰的认识和理解,而且,这样通过动手操作后获得的体验是无比深刻的。
(四)、重自主探索,让学生“再创造”数学。
关于“再创造”,荷兰著名数学教育家H.Freudenthal是这样解释的:“将数学作为一种活动来进行解释和分析,建立在这一基础上的教学方法,我称之为再创造方法。
”也就是说,数学知识应由学生本人在数学活动中去发现或创造出来,而不是由教师“灌”给学生。
学生学习数学的过程应该是学生自身的探索、发现与创造的过程,而不是被动的接受过程。
因此,当学生对某种感兴趣的事物产生疑问并急于了解其中的奥秘时,教师不能简单地把自己知道的知识直接传授给学生,令他们得到暂时的满足,而应该充分相信学生的认知潜能,鼓励学生自主探索,积极从事观察、实验、猜测、推理、交流等数学活动,去大胆地“再创造”数学。
