高中数学专题专练15 平行垂直关系的证明
2020届高考数学专题十五平行垂直的证明精准培优专练文

培优点十五 平行垂直的证明例1:如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,点E 在PC 上,3PC PE =,3PD =.(1)证明:CD ∥平面ABE ;(2)若M 是BC 中点,点N 在PD 上,MN ∥平面ABE ,求线段PN 的长. 【答案】(1)证明见解析;(2)2PN =.【解析】(1)∵底面ABCD 是平行四边形,∴CD AB ∥, ∵CD ⊄平面ABE ,AB ⊂平面ABE ,∴CD ∥平面ABE .(2)∵MN ∥平面ABE ,设过MN 且与平面ABE 平行的平面与PC 交与点F ,与AD 交于点G ,则MF BE ∥,MG AB ∥, 又ABCD 是平行四边形,CD AB ∥,∴MG CD ∥,∴CD ∥平面MFNG ,∴CD FN ∥,∵M 是BC 中点,∴F 是CE 中点,∵3PC PE =,∴23PF PC =,一、平行的证明∴223PN PD==.例2:如图,在直三棱柱111ABC A B C-中,1BC BB=,12BAC BCA ABC∠=∠=∠,点E是1A B与1AB的交点,点D在线段AC上,1B C∥平面1A BD.(1)求证:1BD A C⊥;(2)求证:1AB⊥平面1A BC.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)证明:连结ED,二、垂直的证明∵平面1AB C 平面1A BD ED =,1B C ∥平面1A BD ,∴1B C ED ∥.∵E 为1AB 中点,∴D 为AC 中点,∵12BAC BCA ABC ∠=∠=∠,∴AB BC =,∴BD AC ⊥. 由1A A ⊥平面ABC ,BD ⊂平面ABC ,得1A A BD ⊥.由1A A 、AC 是平面11A ACC 内的两条相交直线,得BD ⊥平面11A ACC ,因为1AC ⊂平面11A ACC ,故1BD A C ⊥. (2)由(1)及条件知AB BC =,AB BC ⊥,∵1BB ⊥平面ABC ,BC ⊂平面ABC ,∴1BC BB ⊥. ∵1ABBB B =,AB ,1BB ⊂平面11ABB A ,∴BC ⊥平面11ABB A .∵1AB ⊂平面11ABB A ,∴1BC AB ⊥,∵1BB BC =,∴1BB AB =,∴四边形11ABB A 是正方形,∴11AB A B ⊥, ∵1BCA B B =,BC ,1A B ⊂平面1A BC ,∴1AB ⊥平面1A BC .一、选择题对点增分集训1.设α,β表示两个不同平面,m 表示一条直线,下列命题正确的是()A .若m α∥,αβ∥,则m β∥B .若m α∥,m β∥,则αβ∥C .若m α⊥,αβ⊥,则m β∥D .若m α⊥,m β⊥,则αβ∥【答案】D【解析】A 选项,可能m 在平面β内,故错误;B 选项,如果m 平行α与β交线,而该两平面相交,故错误;C 选项,m 可能在平面β内,故错误;D 选项,满足平面平行判定条件,故D 正确.2.如图,三棱柱111ABC A B C -中,侧棱1AA ⊥底面111A B C ,底面三角形111A B C 是正三角形,E 是BC 中点,则下列叙述正确的是()A .1CC 与1B E 是异面直线B .AC ⊥平面11ABB AC .AE ,11B C 为异面直线,且11AE B C ⊥D .11AC ∥平面1ABE 【答案】C【解析】A 不正确,因为1CC 与1B E 在同一侧面中,故不是异面直线;B 不正确,由题意知,上底面ABC 是一个正三角形,故不可能存在AC ⊥平面11ABB A ;C 正确,因为AE ,11B C 为在两个平行平面中且不平行的两条直线,故它们是异面直线, 因为E 是BC 中点,所以AE BC ⊥, 又11BC B C ∥,所以11AE B C ⊥;D 不正确,因为11A C 所在的底面与平面1ABE 相交,将平面延伸可知11A C 与交线有公共点, 故11AC ∥平面1AB E 不正确;故选C .3.已知正方体1111ABCD A B C D -中,E ,F ,G 分别是1BB ,1DD ,11A B 的中点,则下列说法错误的是()A .1B D ∥平面11A FC B .CE ∥平面11A FC C .CE ∥平面11A FCD .AE ∥平面11A FC【答案】C【解析】作出图形如图所示,O 为底面对角线的交点,观察可知,1B D FO ∥,1CE A F ∥,1AE C F ∥,FO ⊂平面11A FC ,1A F ⊂平面11A FC ,1C F ⊂平面11A FC ,所以选项A ,B ,D 正确;因为1GE A B ∥,所以GE 与平面11A FC 相交,所以选项C 错误,故选C .4.如图,在正四面体P ABC -中,D ,E ,F 分别是AB ,BC ,CA 的中点,下面四个结论不成立的是()A .BC ∥平面PDFB .DF ⊥平面PAEC .平面PDF ⊥平面PAED .平面PDE ⊥平面ABC【答案】D【解析】因为BC DF ∥,BC ⊄平面PDF ,DF ⊂平面PDF , 所以BC ∥平面PDF ,A 正确;易证BC ⊥平面PAE ,BC DF ∥,所以DF ⊥平面PAE ,所以结论B ,C 都正确; 点P 在平面ABC 内的射影为ABC △的中心,不在中位线DE 上,故D 错误. 5.若平面α∥平面β,点A ,C α∈,B ,D β∈,则AC BD ∥的充要条件是()A .AB CD ∥ B .AD CB ⊥C .AB 与CD 相交D .直线AB 与直线CD 共面【答案】D【解析】∵平面α∥平面β,要使直线AC ∥直线BD , 则直线AC 与直线BD 是共面直线,∴A ,B ,C ,D 四点必须共面,即直线AB 与直线CD 共面.6.如图,在四棱锥P ABCD -中,PAB △与PBC △都是正三角形,平面PAB ⊥平面PBC ,AC BD ⊥,则下列结论不一定成立的是()A .PB AC ⊥ B .PD ⊥平面ABCD C .AC PD ⊥D .平面PBD ⊥平面ABCD【答案】B【解析】取PB 的中点为O ,连接AO ,CO .∵PAB △与PBC △都是正三角形,∴AO PB ⊥,CO PB ⊥. 又∵AOCO O =,∴PB ⊥平面AOC ,∴PB AC ⊥,故A 不符合题意.∵PB AC ⊥,AC BD ⊥,且PB BD B =,∴AC ⊥平面PBD ,∴AC PD ⊥,故C 不符合题意.∵AC ⊥平面PBD ,AC ⊂平面ABCD ,∴平面PBD ⊥平面ABCD ,故D 不符合题意.∴故选B .二、填空题7.在正四棱柱1111ABCD A B C D -中,O 为底面ABCD 的中心,P 是1DD 的中点,Q 在1CC 上,若存在实数λ使得1CQ CC λ=时,平面1D BQ ∥平面PAO ,则λ=.【答案】12【解析】当Q 为1CC 的中点,即112CQ CC =时,平面1D BQ ∥平面PAO . 理由如下:∵Q 为1CC 的中点,P 为1DD 的中点,所以QB PA ∥.因为P ,O 分别为1DD ,DB 的中点,所以1D B PO ∥, ∴1D B ∥平面PAO ,QB ∥平面PAO , 又1D BQB B =,所以平面1D BQ ∥平面PAO .8.如图,AB 为圆O 的直径,PA 垂直于圆O 所在的平面,C 为圆O 上异于A ,B 的一点,PA AB =,F 为PB 的中点,AE PC ⊥,则下列说法错误的是.(1)平面PAC ⊥平面PBC (2)平面AEF ⊥平面PBC (3)平面AEF ⊥平面PAC(4)平面AEF ⊥平面PAB【答案】(3)【解析】因为PA 垂直于圆O 所在的平面,所以PA BC ⊥, 因为AB 为圆O 的直径,所以BC AC ⊥, 因为PAAC A =,所以BC ⊥平面PAC ,又BC ⊂平面PBC ,所以平面PAC ⊥平面PBC ,故(1)正确; 由平面PAC ⊥平面PBC ,及AE PC ⊥,根据面面垂直的性质定理,即可得到AE ⊥平面PBC ,因为AE ⊂平面AEF ,所以平面AEF ⊥平面PBC ,故(2)正确; 由PA AB =,F 为PB 的中点,得到AF PB ⊥, 又由AE ⊥平面PBC ,得到AE PB ⊥,AEAF A =,∴PB ⊥平面AEF ,进而得到平面AEF ⊥平面PAB ,故(4)正确;若平面AEF ⊥平面PAC ,而EF AE ⊥,可以得到EF ⊥平面PAC ,则EF PC ⊥, 而EF PB ⊥,则PB PC ∥,与PB PC P =矛盾,故(3)不正确.三、解答题9.如图,在直三棱柱111ABC A B C -中,已知AC BC ⊥,设1AB 的中点为D ,11B C BC E =,1BC CC =,求证:(1)DE ∥平面11AAC C ; (2)1BC ⊥平面1AB C .【答案】(1)证明见解析;(2)证明见解析. 【解析】(1)依题意四边形11BB C C 为正方形,11B C BC E =,所以E 为1B C 的中点,又D 为1AB 的中点,因此DE AC ∥.又因为DE ⊄平面11AAC C ,AC ⊂平面11AAC C ,所以DE ∥平面11AAC C . (2)因为棱柱111ABC A B C -为直三棱柱,所以1CC ⊥底面ABC , 因为AC ⊂平面ABC ,所以1AC CC ⊥,又因为AC BC ⊥,1CC ⊂平面11BB C C ,BC ⊂平面11BB C C ,1CC BC C =,所以AC ⊥平面11BB C C .因为1B C ⊂平面11BB C C ,所以1BC AC ⊥.因为1BC CC =,所以矩形11BB C C 是正方形,因此11BC B C ⊥.因为AC ,1B C ⊂平面1B AC ,1ACB C C =,所以1BC ⊥平面1AB C .10.如图,在直三棱柱111ABC A B C -中,点D ,E 分别是BC ,11B C 的中点,且AB AC =.求证:(1)BE ∥平面1AC D ;(2)平面1ADC ⊥平面11BCC B .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)∵在直三棱柱111ABC A B C -中,点D ,E 分别是边BC ,11B C 中点,∴1EC BD ∥,1EC BD =,∴四边形1BDC E 是平行四边形,∴1BE DC ∥,∵BE ⊄平面1AC D ,1DC ⊂平面1AC D ,∴BE ∥平面1AC D .(2)∵在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,∴1AD BB ⊥,∵点D 是边BC 中点,且AB AC =,∴AD BC ⊥,∵1BC BB B =,AD ⊥平面11BCC B .∵AD ⊂平面1ADC ,∴平面1ADC ⊥平面11BCC B .11.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,点E 在棱PC 上(异于点P ,C ),平面ABE 与棱PD 交于点F .(1)求证:AB EF ∥;(2)若AF EF ⊥,求证:平面PAD ⊥平面ABCD .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)因为四边形ABCD 是矩形,所以AB CD ∥.又AB ⊄平面PDC ,CD ⊂平面PDC ,所以AB ∥平面PDC ,又因为AB ⊂平面ABE ,平面ABE平面PDC EF =,所以AB EF ∥.(2)因为四边形ABCD 是矩形,所以AB AD ⊥.因为AF EF ⊥,AB EF ∥,所以AB AF ⊥,又AB AD ⊥,由点E 在棱PC 上(异于点C ),所以点F 异于点D ,∵AF AD A =,AF ,AD ⊂平面PAD ,所以AB ⊥平面PAD ,又AB ⊂平面ABCD ,所以平面PAD ⊥平面ABCD .12.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AB CD ∥,2CD AB =,AB AD ⊥,E ,F 分别是CD 和PC 的中点.(1)证明:AB PD ⊥;(2)证明:平面BEF ∥平面PAD .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)证明:∵PA ⊥平面ABCD ,AB ⊂平面ABCD ,∴AB PA ⊥,又∵AB AD ⊥,PA AD A =,∴AB ⊥平面PAD ,∵PD ⊂平面PAD ,∴AB PD ⊥.(2)∵2CD AB =,E 为CD 的中点,∴AB DE =,又AB DE ∥,∴四边形ABED 为平行四边形,∴AD BE ∥,∵E ,F 分别是CD 和PC 的中点,∴EF PD ∥, ∵EF BE E =,PD AD D =,∴平面BEF ∥平面PAD .。
立体几何中平行与垂直证明方法归纳

c c ∥∥b a ba ∥⇒本文档系统总结归纳了立体几何中平行与垂直证明方法,特别适合于高三总复习时对学生构建知识网络、探求解题思路、归纳梳理解题方法。
是一份不可多得的好资料。
一、“平行关系”常见证明方法(一)直线与直线平行的证明1) 利用某些平面图形的特性:如平行四边形的对边互相平行 2) 利用三角形中位线性质3) 利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
4)利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
5) 利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.6) 利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
abαβba a =⋂⊂βαβα∥ba ∥⇒b a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒αab7) 利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
8) 利用定义:在同一个平面内且两条直线没有公共点(二)直线与平面平行的证明1) 利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
2) 利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
3) 利用定义:直线在平面外,且直线与平面没有公共点(三)平面与平面平行的证明常见证明方法:1) 利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
αbaβαaβαα∥⊂a β∥a ⇒ααββ////∩⊂⊂b a P b a b a =αβ//⇒αβbaPb∥a b a αα⊂⊄α∥a ⇒2)利用某些空间几何体的特性:如正方体的上下底面互相平行等3)利用定义:两个平面没有公共点二、“垂直关系”常见证明方法(一)直线与直线垂直的证明1)利用某些平面图形的特性:如直角三角形的两条直角边互相垂直等。
高中数学专项提升——立体几何中平行与垂直证明
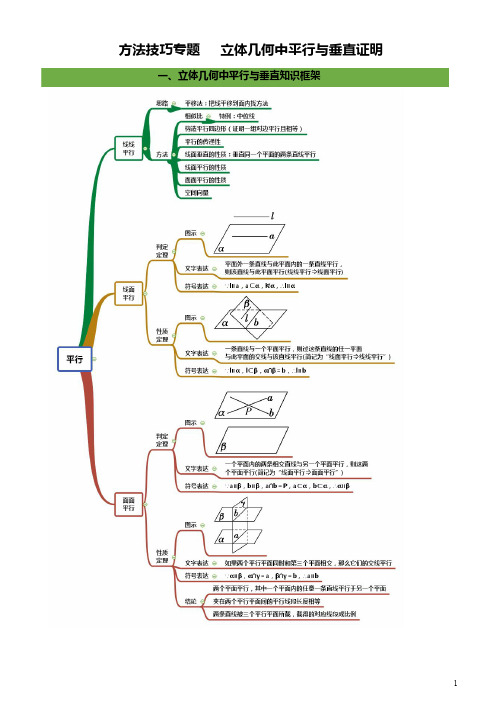
方法技巧专题立体几何中平行与垂直证明一、立体几何中平行与垂直知识框架cc∥∥b a ba ∥⇒二、立体几何中的向量方法【一】“平行关系”常见证明方法1.1直线与直线平行的证明1.1.1利用某些平面图形的特性:如平行四边形的对边互相平行等1.1.2利用三角形中位线性质1.1.3利用空间平行线的传递性(即公理4):平行于同一条直线的两条直线互相平行。
1.1.4利用直线与平面平行的性质定理:如果一条直线与一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
1.1.5利用平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.1.1.6利用直线与平面垂直的性质定理:垂直于同一个平面的两条直线互相平行。
1.1.7利用平面内直线与直线垂直的性质:在同一个平面内,垂直于同一条直线的两条直线互相平行。
1.1.8利用定义:在同一个平面内且两条直线没有公共点1.2直线与平面平行的证明1.2.1利用直线与平面平行的判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
αbaabαβb a b a ////⇒⎪⎭⎪⎬⎫==γβγαβα βα⊥⊥b a ba ∥⇒b∥a b a αα⊂⊄α∥a ⇒αab1.2.2利用平面与平面平行的性质推论:两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
βαaβαα∥⊂a β∥a ⇒1.2.3利用定义:直线在平面外,且直线与平面没有公共点1.3平面与平面平行的证明1.3.1利用平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
ααββ////∩⊂⊂ba Pb a b a =αβ//⇒αβbaP1.3.2利用某些空间几何体的特性:如正方体的上下底面互相平行等1.3.3利用定义:两个平面没有公共点1.例题【例1】如图,已知菱形ABCD ,其边长为2,60BAD ∠=,ABD ∆绕着BD 顺时针旋转120得到PBD∆,M 是PC 的中点.(1)求证://PA 平面MBD ;(2)求直线AD 与平面PBD 所成角的正弦值.证明(1)连结AC 交BD 于点O ,连结OM在菱形ABCD 中,O 为AC 中点, M 为PC 的中点∴OM 为∆APC 的中位线,∴OM ∥AP---------------(利用1.1.2中位线性质)又 OM ⊂面MBD ,且PA ⊄面MBD∴//PA 平面MBD----------------(利用1.2.1直线与平面平行的判定定理)【例2】已知四棱锥P-ABCD ,底面ABCD 是60=∠A 、边长为a 的菱形,又ABCD PD 底⊥,且PD=CD ,点M 、N 分别是棱AD 、PC 的中点.证明:DN//平面PMB 。
高中数学证明直线与平面垂直的方法

高中数学证明直线与平面垂直的方法高中数学中,证明直线与平面垂直是一个重要而基础的概念。
垂直关系在几何学中占有核心地位,因为它决定了物体的形状、大小和位置。
证明直线与平面垂直不仅需要运用基础的几何知识,还需要严谨的逻辑推理。
下面将详细介绍证明直线与平面垂直的几种方法。
方法一:定义法根据直线与平面垂直的定义,如果直线与平面内的任意一条直线都垂直,则这条直线与这个平面垂直。
在实际证明中,我们通常需要选择平面内的一条特殊直线(如平面的法线或已知与直线垂直的直线)来进行证明。
方法二:向量法向量法是证明直线与平面垂直的一种常用方法。
首先,我们需要确定直线和平面的向量表示。
如果直线的方向向量与平面的法向量平行(即它们的外积为零),则直线与平面垂直。
这种方法需要一定的向量知识和运算能力。
方法三:几何性质法通过利用几何图形的性质来证明直线与平面垂直也是一种常见方法。
例如,如果一条直线同时垂直于一个平面的两条相交直线,那么这条直线与这个平面垂直。
这种方法依赖于对几何图形的深入理解和灵活运用。
方法四:反证法反证法是一种常用的逻辑推理方法,也可以用于证明直线与平面垂直。
假设直线与平面不垂直,然后根据已知条件和几何性质推导出矛盾,从而证明原假设不成立,即直线与平面垂直。
这种方法需要较强的逻辑推理能力。
方法五:综合法综合法是将以上几种方法综合运用,根据具体情况选择合适的方法进行证明。
在实际应用中,我们可能需要结合定义法、向量法、几何性质法和反证法等多种方法来完成证明。
注意事项在证明直线与平面垂直时,需要注意以下几点:理解定义:首先要清楚直线与平面垂直的定义,这是进行证明的基础。
选择适当的方法:根据题目的具体条件和已知信息,选择最合适的方法进行证明。
逻辑推理:在证明过程中,要保持清晰的逻辑思路,每一步都要有充分的理由和依据。
严谨性:几何证明需要严谨的态度和精确的表达,不能随意跳过关键步骤或忽略重要细节。
通过以上方法的学习和实践,我们可以更好地理解和掌握直线与平面垂直的概念,提高我们的几何证明能力和逻辑推理能力。
高中数学证明直线与平面垂直的方法

高中数学证明直线与平面垂直的方法全文共四篇示例,供读者参考第一篇示例:高中数学是学生学习生活中不可或缺的一部分,其中数学证明是需要花费一定时间和精力的部分,而证明直线与平面垂直的方法也是一项重要的内容。
在数学中,我们经常需要判断直线与平面是否垂直,这个问题在几何学中是非常重要的,因为垂直关系直接影响到几何图形的性质和性质。
在这篇文章中,我将介绍一些关于证明直线与平面垂直的方法,希望能帮助大家更好地理解这一概念。
我们需要了解什么是直线和平面。
直线是由无限多个点连在一起形成的一条直线,而平面是由无限多个点连在一起形成的一个平面。
在空间中,直线和平面是两种不同的几何对象,它们之间有很多不同的性质和关系。
在数学中,我们通常用直线上的一点和平面上的一个点来判断直线和平面之间的关系。
证明直线与平面垂直的方法有很多种,其中比较常用的方法包括投影法、距离法和点法。
下面我们将分别介绍这三种方法。
首先是投影法。
在数学中,我们常常利用几何图形之间的投影关系来判断它们之间的垂直关系。
对于一条直线和一个平面,我们可以利用它们的投影关系来判断它们是否垂直。
具体来说,我们可以在直线上选取一个点,然后在该点处作出直线在平面上的垂直投影,如果这个投影与平面是垂直的,那么我们就可以得出直线与平面垂直的结论。
其次是距离法。
距离法是另一种常用的证明直线与平面垂直的方法。
在这种方法中,我们需要计算直线上某一点到平面的距离,然后再计算这个点在平面上的垂直投影点到平面的距离,如果这两个距离相等,那么我们就可以得出直线与平面垂直的结论。
证明直线与平面垂直的方法有很多种,投影法、距离法和点法是比较常用的方法。
通过学习这些方法,我们可以更好地理解直线与平面之间的垂直关系,提高数学证明的能力。
希望这篇文章能够帮助大家更好地理解和掌握这一重要的数学概念。
第二篇示例:高中数学证明直线与平面垂直的方法在高中数学学习中,我们经常会遇到需要证明直线与平面垂直的问题。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)
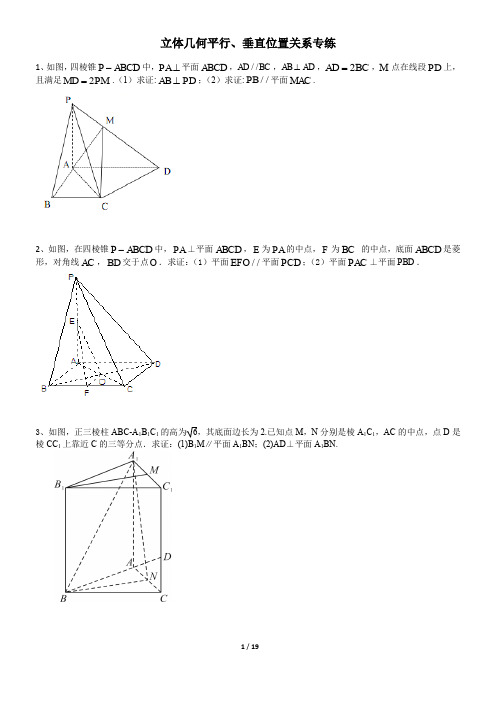
立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高中数学立体几何平行、垂直位置关系证明题专项练习(带答案)

立体几何平行、垂直位置关系专练1、如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .2、如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD .3、如图,正三棱柱ABC-A 1B 1C 1的高为6,其底面边长为2.已知点M ,N 分别是棱A 1C 1,AC 的中点,点D 是棱CC 1上靠近C 的三等分点.求证:(1)B 1M ∥平面A 1BN ;(2)AD ⊥平面A 1BN.4、如图,等边三角形ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;(2)在边AC上找一点N,使CD∥平面BEN.5、如图,矩形ABCD所在平面与三角形ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE 的中点.求证:(1)MN∥平面BEC;(2)AH⊥CE.6、如图,在三棱台ABCDEF中,CF⊥平面DEF,AB⊥BC.(1)设平面ACE∩平面DEF=a,求证:DF∥a;(2)若EF=CF=2BC,试问在线段BE上是否存在点G,使得平面DFG⊥平面CDE?若存在请确定点G的位置;若不存在,请说明理由.7、在三棱锥S ABC -中,平面SAB ⊥平面SBC ,AB BC ⊥,AS AB =,过A 作AF SB ⊥,垂足为F ,点E ,G 分别是棱SA ,SC 的中点.(1)求证:平面EFG ∥平面ABC .(2)求证:BC SA ⊥.8、如图,在直三棱柱111ABC A B C -中,AB BC ⊥,点D 为棱1C C 的中点,1AC 与1A D 交于点E ,1BC 与1B D 交于点F ,连结EF .求证:(1)//AB EF ;(2)平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A 1B 1∥平面DEC 1;(2)BE ⊥C 1E .点,平面PAB ⊥底面ABCD ,90PAB ∠= .求证:(1)//PB 平面AEC ;(2)平面PAC ⊥平面ABCD .11、2.(2020·江苏省镇江高三二模)如图,三棱锥P ABC -中,点D ,E 分别为AB ,BC 的中点,且平面PDE ⊥平面ABC .()1求证://AC 平面PDE ;()2若2PD AC ==,PE =PBC ⊥平面ABC .12、(2020·江苏省建湖高级中学高三月考)如图,在四面体ABCD 中,,90AD BD ABC =∠= ,点,E F 分别为棱,AB AC 上的点,点G 为棱AD 的中点,且平面//EFG 平面BCD .(1)求证:12EF BC =;(2)求证:平面EFD ⊥平面ABC .点,PA ⊥平面ABCD .(1)求证://PB 平面AEC ;(2)若四边形ABCD 是矩形且PA AD =,求证:AE ⊥平面PCD .14、(2020·江苏省高三二模)如图,在三棱柱111ABC A B C -中,侧面11ABB A ⊥底面ABC ,AB AC ⊥,E ,F 分别是棱AB ,BC 的中点.求证:(1)11AC ∥平面1B EF ;(2)1AC B E ⊥.15、(2020·江苏省连云港高三)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,平面PAD ⊥平面ABCD ,PA PD ⊥,PA PD =,E 、F 分别为AD 、PB 的中点.(Ⅰ)求证:PE BC ⊥;(Ⅱ)求证:平面PAB ⊥平面PCD ;(Ⅲ)求证://EF 平面PCD .16、(2020·江苏省苏州高三)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别为BC ,AC 的中点,AB =BC .求证:(1)A1B 1∥平面DEC 1;(2)BE ⊥C 1E .17、(2020·江苏省通州高三)如图,在三棱柱111ABC A B C -中,侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点.(1)求证: 平面ABE ⊥平面11B BCC ;(2)求证:1C F ∥平面ABE ;18、(2020·江苏省高三三模)如图,三棱柱111ABC A B C -中,1BC B C =,O 为四边形11ACC A 对角线交点,F 为棱1BB 的中点,且AF ⊥平面11BCC B .(1)证明://OF 平面ABC ;(2)证明:四边形11ACC A 为矩形.参考答案1.如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,//AD BC ,AB AD ⊥,2AD BC =,M 点在线段PD 上,且满足2MD PM =.(1)求证:AB PD ⊥;(2)求证://PB 平面MAC .【解析】(1)∵四棱锥P ABCD -中,PA ⊥平面ABCD ,AB 平面ABCD , ∴AB PA ⊥,又AB AD ⊥,,PA AD ⊂平面PAD ,PA AD A ⋂=, ∴AB ⊥面PAD .PD ⊂面PAD ,∴AB PD ⊥. (2)连结BD AC O ⋂=,连结MO , ∵//AD BC ,2AD BC =,2DO BO ∴=,∵在PBD ∆中,2DM MP =,2DO BO =∴//PB MO , 又PB ⊄面MAC ,MO ⊂面MAC ,∴//PB 面MAC .2.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,E 为PA 的中点,F 为BC 的中点,底面ABCD 是菱形,对角线AC ,BD 交于点O .求证:(1)平面//EFO 平面PCD ;(2)平面PAC ⊥平面PBD . 【详解】(1)因为在ΔPAC 中,E 为PA 的中点,O 为AC 的中点, 所以//EO PC又EO ⊄平面PCD ,PC ⊂平面PCD , 所以//EO 平面PCD同理可证,//FO 平面PCD ,又EO FO O = ,EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD .(2)因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥因为底面ABCD 是菱形,所以AC BD ⊥,又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。
高三数学复习:立体几何的平行与垂直证明

高三数学复习——立体几何中的平行与垂直的证明一、平面的基本性质公理1:公理2:推论1:推论2:推论3:公理3:二、空间中直线与直线的位置关系平行:相交:异面:三、平行问题1.直线与平面平行的判定与性质2.平行问题的转化关系:四、垂直问题(一)、直线与平面垂直1.直线和平面垂直的定义:直线l与平面α内的都垂直,就说直线l与平面α互相垂直.2.直线与平面垂直的判定定理及推论①直线垂直于平面,则垂直于平面内任意直线.②垂直于同一个平面的两条直线平行.③垂直于同一条直线的两平面平行.(二)、平面与平面垂直1.平面与平面垂直的判定定理2.平面与平面垂直的性质定理类型一、平行与垂直例1、如图,已知三棱锥中,为中点,为中点,且△为正三角形。
(Ⅰ)求证:∥平面;(Ⅱ)求证:平面平面; (Ⅲ)若,,求三棱锥的体积。
例2. 如图,已知三棱柱111ABC A B C -中,1AA ⊥底面ABC ,2AC BC ==,14AA =,AB =M ,N 分别是棱1CC ,AB 中点.CA 1B 1C 1M(Ⅰ)求证:CN ⊥平面11ABB A ; (Ⅱ)求证://CN 平面1AMB ; (Ⅲ)求三棱锥1B AMN -的体积.【变式1】. 如图,三棱柱111C B A ABC -中,侧棱1AA ⊥平面ABC ,ABC ∆为等腰直角三角形,ο90=∠BAC ,且1AA AB =,F E D ,,分别是BC CC A B ,,11的中点。
(1)求证://DE 平面ABC ; (2)求证:⊥F B 1平面AEF ;(3)设AB a =,求三棱锥D AEF -的体积。
二、线面平行与垂直的性质例3、如图4,在四棱锥中,平面平面,,是等边三角形,已知,. (1)求证:平面; (2)求三棱锥的体积.例4、如图,四棱锥P —ABCD 中,⊥PD 平面ABCD ,底面ABCD 为正方形,BC=PD=2,E 为PC 的中点,.31CB CG =(I )求证:PC BC ⊥; (II )求三棱锥C —DEG 的体积;(III )AD 边上是否存在一点M ,使得//PA 平面MEG 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
十五 平行垂直关系的证明1.平行关系的证明例1:如图,E ,F ,G ,H 分别是正方体1111ABCD A B C D -的棱BC ,1CC ,11C D ,1AA 的中点. 求证:(1)EG ∥平面11BB D D ; (2)平面BDF ∥平面11B D H .【答案】(1)见解析;(2)见解析.【解析】证明(1)如图,取11B D 的中点O ,连接GO ,OB ,因为1112OG B C BE ∥∥,所以BE OG ∥,所以四边形BEGO 为平行四边形,故OB EG ∥, 因为OB ⊂平面11BB D D ,EG ⊄平面11BB D D ,所以EG ∥平面11BB D D . (2)由题意可知11BD B D ∥.连接HB ,1D F ,因为1BH D F ∥,所以四边形1HBFD 是平行四边形,故1HD BF ∥ 又1111=B D HD D I ,=BD BF B I ,所以平面BDF ∥平面11B D H .2.垂直关系的证明例2:如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面ABC ,M 为棱AC 的中点.=AB BC ,=2AC ,1AA(1)求证:1B C ∥平面1A BM ; (2)求证:1AC ⊥平面1A BM ;(3)在棱1BB 上是否存在点N ,使得平面1AC N ⊥平面11AA C C ?如果存在,求此时1BNBB 的值;如果不存在,请说明理由.【答案】(1)见解析;(2)见解析;(3)存在,12. 【解析】(1)证明:连接1AB 与1A B ,两线交于点O ,连接OM .在1B AC △中,∵M ,O 分别为AC ,1AB 的中点,∴1OM B C ∥, 又∵OM ⊂平面1A BM ,1B C ⊄平面1A BM ,∴1B C ∥平面1A BM . (2)证明:∵侧棱1AA ⊥底面ABC ,BM ⊂平面ABC ,∴1AA BM ⊥, 又∵M 为棱AC 的中点,=AB BC ,∴BM AC ⊥. ∵1=AA AC A ,1AA ,AC ⊂平面11ACC A ,∴BM ⊥平面11ACC A ,∴1BM AC ⊥∵=2AC ,∴=1AM.又∵1AA ,∴在1Rt ACC △和1Rt A AM △中,11tan tan AC C A MA ∠==∴11AC C A MA ∠∠=,即111190AC C C AC A MA C AC ∠+∠=∠+∠=︒,∴11A M AC ⊥ ∵1BMA M M =,BM ,1A M ⊂平面1A BM ,∴1AC ⊥平面1A BM .(3)解:当点N 为1BB 的中点,即112BN BB =时,平面1AC N ⊥平面11AA C C证明如下:设1AC 的中点为D ,连接DM ,DN ,∵D ,M 分别为1AC ,AC 的中点,∴1DM CC ∥,且112DM CC =.又∵N 为1BB 的中点,∴DM BN ∥,且DM BN =,∴四边形BNDM 为平行四边形,∴BM DN ∥,∵BM ⊥平面11ACC A ,∴DN ⊥平面11AA C C .又∵DN ⊂平面1AC N , ∴平面1AC N ⊥平面11AA C C .一、单选题1.平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是1m 和1n ,给出下列四个命题:①11m n m n ⊥⇒⊥;②11m n m n ⊥⇒⊥;③1m 与1n 相交m ⇒与n 相交或重合;④1m 与1n 平行m ⇒与n 平行或重合;其中不正确的命题个数是( ) A .1 B .2C .3D .4【答案】D【解析】结合题意逐一分析所给的四个说法,在如图所示的正方体1111ABCD A B C D -中:对点增分集训对于说法①:若取平面α为ABCD ,1m ,1n 分别为AC ,BD ,m n ,分别为11A C BD ,, 满足11m n ⊥,但是不满足m n ⊥,该说法错误;对于说法②:若取平面α为11ADD A ,1m ,1n 分别为111A D AD ,,m n ,分别为111A C BD ,,满足m n ⊥,但是不满足11m n ⊥,该说法错误;对于说法③:若取平面α为ABCD ,1m ,1n 分别为AC BD ,,m n ,分别为11AC BD ,,满足1m 与1n 相交,但是m 与n 异面,该说法错误;对于说法④:若取平面α为11ADD A ,1m 、1n 分别为11A D AD ,,m 、n 分别为11A C BC ,,满足1m 与1n 平行,但是m 与n 异面,该说法错误;综上可得:不正确的命题个数是4.本题选择D 选项. 2.已知m 、n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是( ) A .若l m ⊥,l n ⊥,且m n α⊂,,则l α⊥B .若平面α内有不共线的三点到平面β的距离相等,则αβ∥C .若m α⊥,m n ⊥,则n α∥D .若m n ∥,n α⊥,则m α⊥ 【答案】D【解析】对于选项A ,若l m ⊥,l n ⊥,且m n α⊂,,则l 不一定垂直平面α,∵m 有可能和n 平行, ∴该选项错误;对于选项B ,若平面α内有不共线的三点到平面β的距离相等,则α、β可能相交或平行,∴该选项错误;对于选项C ,若m m n α⊥⊥,,则n 有可能在平面α内,∴该选项错误;对于选项D ,由于两平行线中有一条垂直平面α,则另一条也垂直平面α,∴该选项正确,故答案为D .3.给出下列四种说法:①若平面αβ∥,直线a b αβ⊂⊂,,则a b ∥; ②若直线a b ∥,直线a α∥,直线b β∥,则αβ∥; ③若平面αβ∥,直线a α⊂,则a β∥;④若直线a α∥,a β∥,则αβ∥.其中正确说法的个数为( ) A .4个 B .3个C .2个D .1个【答案】D【解析】若平面αβ∥,直线a b αβ⊂⊂,,则a b ,可异面;若直线a b ∥,直线a α∥,直线b β∥,则αβ,可相交,此时a b ,平行两平面的交线; 若直线a α∥,a β∥,则αβ,可相交,此时a b ,平行两平面的交线; 若平面αβ∥,直线a α⊂,则a β与无交点,即a β∥;故选D .4.已知m 、n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的有( )(1)m α⊂,n α⊂,m β∥,n βαβ⇒∥∥ (2)n m ∥,n m αα⊥⇒⊥(3)αβ∥,m α⊂,n m n β⊂⇒∥(4)m α⊥,m n n α⊥⇒∥ A .0个 B .1个C .2个D .3【答案】B【解析】由m α⊂,n α⊂,m β∥,n β∥,若a b ,相交,则可得αβ∥,若a b ∥,则α与β可能平行也可能相交,故(1)错误;若m n ∥,n α⊥根据线面垂直的第二判定定理可得m α⊥,故(2)正确; 若αβ∥,m α⊂,n β⊂,则m n ∥或m n ,异面,故(3)错误; 若m α⊥,m n ⊥,则n α∥或n α⊂,故(4)错误;故选B .5.如图,在正方体1111ABCD A B C D -中,M N P ,,分别是1111C D BC A D ,,的中点,则下列命题正确的是( )A .MN AP ∥B .1MN BD ∥C .11MN BBD D ∥平面 D .MN BDP ∥平面【答案】C【解析】A :MN 和AP 是异面直线,故选项不正确; B :MN 和1BD 是异面直线,故选项不正确;C :记AC BD O =I .∵正方体1111ABCD A B C D -中,M N ,分别11C D BC ,是的中点,∴1ON D M CD ∥∥,112ON D M CD ==,∴1MNOD 为平行四边形,∴1MN OD ∥,∵MN ⊄平面1BD D ,1OD ⊂平面1BD D ,∴MN ∥平面1BD D .D :由C 知11MN BB D D ∥平面,而面11BB D D 和面BDP 相交,故选项不正确;故选C . 6.已知m n ,是两条不同的直线,αβ,是两个不同的平面,则下列命题正确的是( ) A .若αβ,垂直于同一平面,则αβ与平行 B .若m n ,平行于同一平面,则m n 与平行C .若αβ,不平行,则在α内不存在与β平行的直线D .若m n ,不平行,则m n 与不可能垂直于同一平面 【答案】D【解析】垂直于同一平面的两平面相交或平行,A 不正确; 平行于同一平面的两直线可相交、平行或异面,B 不正确;平面不平行即相交,在一个平面内平行两平面交线的直线与另一平面平行,C 不正确; D 为直线与平面垂直性质定理的逆否命题,故D 正确.故选D .7.已知m n ,是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题:①若m m αβ⊥⊥,,则αβ∥; ②若αγβγ⊥⊥,,则αβ∥; ③若m n m n αβ⊂⊂,,∥,则αβ∥;④若m n ,是异面直线,m m n n αββα⊂⊂,∥,,∥,则αβ∥.其中真命题是( ) A .①和② B .①和③C .③和④D .①和④【答案】D【解析】逐一考查所给的命题:①由线面垂直的性质定理可得若m m αβ⊥⊥,,则αβ∥,命题正确;②如图所示的正方体1111ABCD A B C D -中,取平面αβγ,,分别为平面1111ABB A ADD A ABCD ,,,满足αγβγ⊥⊥,,但是不满足αβ∥,命题错误;③如图所示的正方体1111ABCD A B C D -中,取平面αβ,分别为平面1111ABB A ADD A ,, 直线m n ,分别为11BB DD ,,满足m n m n αβ⊂⊂,,∥,但是不满足αβ∥,命题错误;④若m n ,是异面直线,m m n n αββα⊂⊂,∥,,∥,由面面平行的性质定理易知αβ∥,命题正确;综上可得,真命题是①和④,本题选择D 选项.8.如图,正方体的棱长为1,线段11A C 上有两个动点E F ,,且2EF =;则下列结论错误的是( ).A .BD CE ⊥B .EF ABCD ∥平面C .三棱锥E FBC -的体积为定值D .BEF △的面积与CEF △的面积相等【答案】D【解析】在正方体1111ABCD A B C D -中,BD ⊥平面11A ACC , 而CE ⊂平面11A ACC ,故BD CE ⊥,故A 正确.又11A C ∥平面ABCD ,因此EF ∥平面ABCD ,故B 正确.当EF 变化时,三角形CEF 的面积不变,点B 到平面CEF 的距离就是B 到平面11A CCC 的距离,它是一个定值,故三棱锥E FBC -的体积为定值(此时可看成三棱锥B CEF -的体积),故C 正确.在正方体中,点B 到EF C 到EF 的距离为1,D 是错误的,故选D . 9.如图所示,AB 是圆O 的直径,VA 垂直于圆O 所在的平面,点C 是圆周上不同于A B ,的任意一点,M N ,分别为VA VC ,的中点,则下列结论正确的是( )A .MN AB ∥ B .MN 与BC 所成的角为45︒ C .OC ⊥平面VACD .平面VAC ⊥平面VBC【答案】D【解析】对于A 项,MN 与AB 异面,故A 项错;对于B 项,可证BC ⊥平面VAC ,故BC MN ⊥,∴所成的角为90︒,因此B 项错; 对于C 项,OC 与AC 不垂直,∴OC 不可能垂直平面VAC ,故C 项错; 对于D 项,由于BC AC ⊥,VA ⊥平面ABC ,BC ⊂平面ABC ,∴VA BC ⊥,∵=AC VA A I ,∴BC ⊥平面VAC ,BC ⊂平面VBC ,∴平面VAC ⊥平面VBC ,故选D . 10.如图,在三棱柱111ABC A B C -中,侧棱1AA ⊥底面111A B C ,底面三角形111A B C 是正三角形,E 是BC 中点,则下列叙述正确的是( )A .1CC 与1B E 是异面直线B .AC ⊥平面11ABB A C .AE ,11B C 为异面直线且11AE B C ⊥D .11A C ∥平面1AB E【答案】C【解析】对于A 项,1CC 与1B E 在同一个侧面中,故不是异面直线,∴A 错;对于B 项,由题意知,上底面是一个正三角形,故AC ⊥平面11ABB A 不可能,∴B 错; 对于C 项,∵AE ,11B C 为在两个平行平面中且不平行的两条直线,故它们是异面直线,∴C 正确;对于D 项,∵11A C 所在的平面与平面1AB E 相交,且11A C 与交线有公共点,故11A C ∥平面1AB E 不正确,∴D 项不正确;故选C .11.设E F ,分别是正方体1111ABCD A B C D -的棱DC 上两点,且21AB EF ==,,给出下列四个命题:①三棱锥11D B EF -的体积为定值;②异面直线11D B 与EF 所成的角为45︒;③11D B ⊥平面1B EF ;④直线11D B 与平面1B EF 所成的角为60︒.其中正确的命题为( )A .①②B .②③C .①②④D .①④【答案】A【解析】由题意得,如图所示,①中,三棱锥的体积的为11111111112223323D B EF B D EF D EF V V S B C EF --==⨯⋅=⨯⨯⨯⨯=△,∴体积为定值;②中,在正方体中,11EF C D ∥,∴异面直线11D B 与EF 所成的角就是直线11D B 与11C D 所成的角,即11145B D C ∠=︒,∴这正确的;③中,由②可知,直线11D B 与EF 不垂直,∴11D B ⊥面1B EF 不成立,∴是错误的; ④中,根据斜线与平面所成的角,可知11D B 与平面1B EF 所成的角,即为11145B D C ∠=︒,∴不正确.12.如下图,梯形ABCD 中,AD BC ∥,145AD AB AD AB BCD ==⊥∠=︒,,,将ABD △沿对角线BD 折起.设折起后点A 的位置为A ',并且平面A BD '⊥平面BCD .给出下面四个命题:①A D BC '⊥;②三棱锥A BCD '-;③CD ⊥平面A BD '; ④平面A BC '⊥平面A DC '.其中正确命题的序号是( )A .①②B .③④C .①③D .②④【答案】B【解析】①∵90BAD AD AB ∠=︒=,,∴45ADB ABD ∠=∠=︒, ∵45AD BC BCD ∠=︒∥,,∴BD DC ⊥,∵平面A BD '⊥平面BCD ,且平面A BD 'I 平面BCD BD =,∴CD ⊥平面A BD ', ∵A D '⊂平面A BD ',∴CD A D ⊥',故A D BC '⊥不成立,故①错误;②棱锥A BCD '-的体积为113226⋅=③由①知CD ⊥平面A BD ',故③正确;④由①知CD ⊥平面A BD ',又∵A B '⊂平面A BD ',∴CD A B ⊥',又A B A D '⊥',且A D '、CD ⊂平面A DC ',A D CD D '=,∴A B '⊥平面A DC ',又A B '⊂平面A BC ',∴平面A BC '⊥平面A DC ',故④正确.故选B .二、填空题13.设m n ,是两条不同的直线,αβ,是两个不同的平面,则下列命题正确的是________.(填序号)①若m α∥,n α∥,则m n ∥;②若m α∥,m β∥,则αβ∥;③若m n ∥,m α⊥,则n α⊥;④若m α∥,αβ⊥,则m β⊥.【答案】③【解析】m α∥,n α∥,则m n ∥,m 与n 可能相交也可能异面,∴①不正确; m α∥,m β∥,则αβ∥,还有α与β可能相交,∴②不正确;m n ∥,m α⊥,则n α⊥,满足直线与平面垂直的性质定理,故③正确;m α∥,αβ⊥,则m β⊥,也可能m β∥,也可能m A β=,∴④不正确;故答案为③.14.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论①AB EF ⊥;②AB 与CM 所成的角为60︒;③EF 与MN 是异面直线;④MN CD ∥. 以上四个命题中,正确命题的序号是_________.【答案】①③【解析】把正方体的平面展开图还原成原来的正方体,如图:则AB EF ⊥,EF 与MN 异面,AB CM MN CD ⊥∥,,只有①③正确.故答案为①③.15.若四面体ABCD 的三组对棱分别相等,即AB CD AC BD AD BC ===,,,给出下列结论:①四面体ABCD 每组对棱相互垂直;②四面体ABCD 每个面的面积相等;③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大90︒而小于180︒;④连接四面体ABCD 每组对棱中点的线段相互垂直平分.其中正确结论的序号是__________.(写出所有正确结论的序号)【答案】②④【解析】①将四面体ABCD 的三组对棱分别看作平行六面体的对角线,由于三组对棱分别相等,∴平行六面体为长方体.由于长方体的各面不一定为正方形,∴同一面上的面对角线不一定垂直,从而每组对棱不一定相互垂直.①错误;②四面体ABCD 的每个面是全等的三角形,面积是相等的.②正确;③由②,四面体ABCD 的每个面是全等的三角形,从四面体ABCD 每个顶点出发的三条棱两两夹角能够等量代换为同一个三角形内的三个内角,它们之和为180︒.③错误;④连接四面体ABCD 每组对棱中点构成菱形,线段互垂直平分④正确,故答案为②④.16.如图,一张矩形白纸ABCD ,10AB =,AD =E F ,分别为AD BC ,的中点,现分别将ABE △,CDF △沿BE DF ,折起,且A C 、在平面BFDE 同侧,下列命题正确的是____________(写出所有正确命题的序号).①当平面ABE ∥平面CDF 时,AC ∥平面BFDE②当平面ABE ∥平面CDF 时,AE CD ∥③当A C 、重合于点P 时,PG PD ⊥④当A C 、重合于点P 时,三棱锥P DEF -的外接球的表面积为150π【答案】①④【解析】在ABE △中,tan ABE ∠=,在ACD △中,tan CAD ∠=, ∴ABE DAC ∠=∠,由题意,将ABE CDF △,△沿BE DF ,折起,且A C ,在平面BEDF 同侧,此时A C G H ,,,四点在同一平面内,平面ABE I 平面AGHC AG =,平面CDF I 平面AGHC CH =,当平面ABE ∥平面CDF 时,得到AG CH ∥,显然AG CH =,∴四边形AGHC 是平行四边形,∴AC GH ∥,进而得到AC ∥平面BFDE ,∴①正确的;由于折叠后,直线AE 与直线CD 为异面直线,∴AE 与CD 不平行,∴②错误的;折叠后,可得PG =10PD =,其中10GD =,222PG PD GD +≠, ∴PG 和PD 不垂直,∴③不正确;当,A C 重合于点P 时,在三棱锥P DEF -中,EFD △和FCD △均为直角三角形,∴DF 为外接球的直径,即2DF R ==,则三棱锥P DEF -的外接球的表面积为2244150R π=π⨯=π⎝⎭,∴④是正确, 综上正确命题的序号为①④.三、解答题17.如图,四棱锥P ABCD -中,22AB AD BC ===,BC AD ∥,AB AD ⊥,PBD △为正三角形.且PA =(1)证明:平面PAB ⊥平面PBC ;(2)若点P 到底面ABCD 的距离为2,E 是线段PD 上一点,且PB ∥平面ACE ,求四面体A CDE -的体积.【答案】(1)见解析;(2)89.【解析】(1)证明:∵AB AD ⊥,且2AB AD ==,∴BD =,又PBD △为正三角形,∴PB PD BD ===,又∵2AB =,PA =AB PB ⊥, 又∵AB AD ⊥,BC AD ∥,∴AB BC ⊥,PBBC B =,∴AB ⊥平面PBC ,又∵AB ⊆平面PAB ,∴平面PAB ⊥平面PBC .(2)如图,连接BD ,AC 交于点O ,∵BC AD ∥,且2AD BC =,∴2OD OB =,连接OE ,∵PB ∥平面ACE ,∴PB OE ∥,则2DE PE =,由(1)点P 到平面ABCD 的距离为2,∴点E 到平面ABCD 的距离为24233h =⨯=, ∴111482233239A CDE E ACD ACD V V S h --⎛⎫==⋅=⨯⨯⨯⨯= ⎪⎝⎭△, 即四面体A CDE -的体积为89. 18.如图,四边形ABCD 为正方形,EA ⊥平面ABCD ,EF AB ∥,4AB =,2AE =,1EF =.(1)求证:BC AF ⊥;(2)若点M 在线段AC 上,且满足14CM CA =,求证:EM ∥平面FBC ; (3)求证:AF ⊥平面EBC .【答案】(1)见解析;(2)见解析;(3)见解析.【解析】(1)∵EF AB ∥,∴EF 与AB 确定平面EABF ,∵EA ⊥平面ABCD ,∴EA BC ⊥.由已知得AB BC ⊥且=EA AB A I , ∴BC ⊥平面EABF .又AF ⊂平面EABF ,∴BC AF ⊥.(2)过M 作MN BC ⊥,垂足为N ,连接FN ,则MN AB ∥. 又14CM AC =,∴MN AB =.又EF AB ∥且14EF AB =,∴EF MN ∥且EF MN =,∴四边形EFNM 为平行四边形,∴EM FN ∥. 又FN ⊂平面FBC ,EM ⊄平面FBC ,∴EM ∥平面FBC .(3)由(1)可知,AF BC ⊥.在四边形ABFE 中,4AB =,2AE =,1EF =,90BAE AEF ∠=∠=︒, ∴1tan tan 2EBA FAE ∠=∠=,则EBA FAE ∠=∠. 设AF BE P =I ,∵90PAE PAB ∠+∠=︒,故90PBA PAB ∠+∠=︒,则90APB ∠=︒,即EB AF ⊥.又∵EB BC BI,∴AF⊥平面EBC.=。
