第二章 自动控制原理答案
自动控制理论第二章习题答案
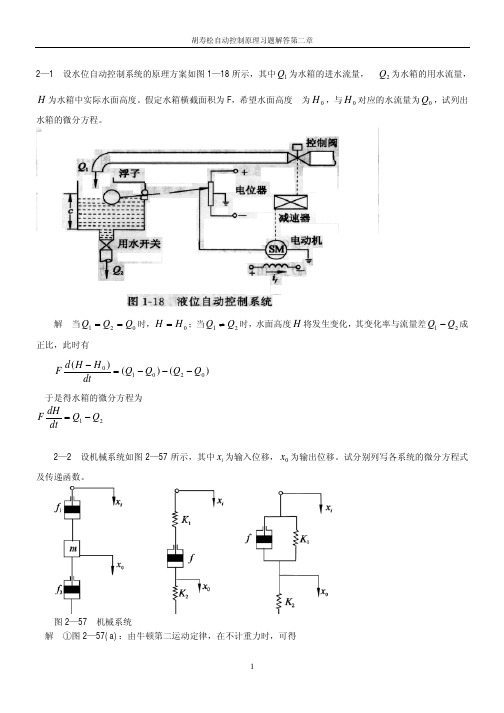
式中 K 为比例常数, P 为阀门前后的压差。若流量 Q 与压差 P 在其平衡点 (Q0 , P0 ) 附近作微小变化,试导出线性化
方程。 解:
设正常工作点为 A,这时 Q0 = K P0
在该点附近用泰勒级数展开近似为:
y
=
f
(
x0
)
+
df (x) dx
x0
(
x
−
x0
)
即 Q − Q0 = K1 (P − P0 )
其中 K1
= dQ dP P=P0
=
1K 2
1 P0
2-7 设弹簧特性由下式描述:
F = 12.65 y1.1
其中,是弹簧力;是变形位移。若弹簧在变形位移附近作微小变化,试推导的线性化方程。 解:
设正常工作点为 A,这时 F0
=
12.65
y1.1 0
在该点附近用泰勒级数展开近似为:
2-3 试证明图2-58(a)的电网络与(b)的机械系统有相同的数学模型。
2
胡寿松自动控制原理习题解答第二章
图 2-58 电网络与机械系统
1
解:(a):利用运算阻抗法得: Z1
=
R1
//
1 C1s
=
R1 C1s
R1
+
1 C1s
=
R1 = R1 R1C1s + 1 T1s + 1
Z2
=
R2
+
1 C2s
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
自动控制原理第二章习题解答
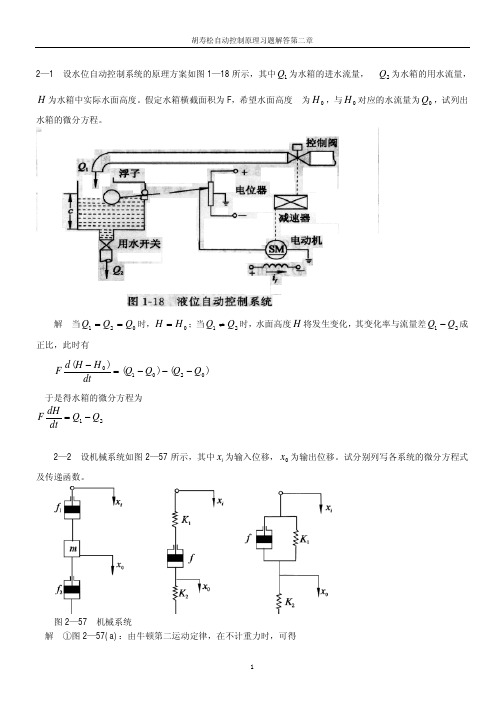
Z1 + Z2
R1 T1s +
1
+
1 C2
s
(T2
s
+
1)
R1C2 s + (T1s + 1)(T2 s + 1)
(b)以 K1 和 f1 之间取辅助点 A,并设 A 点位移为 x ,方向朝下;根据力的平衡原则,可列出如下原始方程:
K 2 (xi − x0 ) + f 2 (x&i − x&0 ) = f1 (x&0 − x&) (1)
+
C1C2
R
d 2u0 dt 2
整理得:
C1C2
R
d 2u0 dt 2
+
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
+ ui R
+
2C1
dui dt
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) 2x&(t) + x(t) = t;
所以:
f1 f2 s2 + ( f1 + f2 )s +1
X 0 (s) =
f1 f2s2 + ( f1K2 + K1 f2 )s + K1K2
= K1K2
K 1
K2
X i (s) f1 f2s2 + ( f1K2 + K1 f1 + K1 f2 )s + K1K2
f1 f2 s2 + ( f1 + f2 )s +1+ f1
自动控制原理第二章习题答案详解
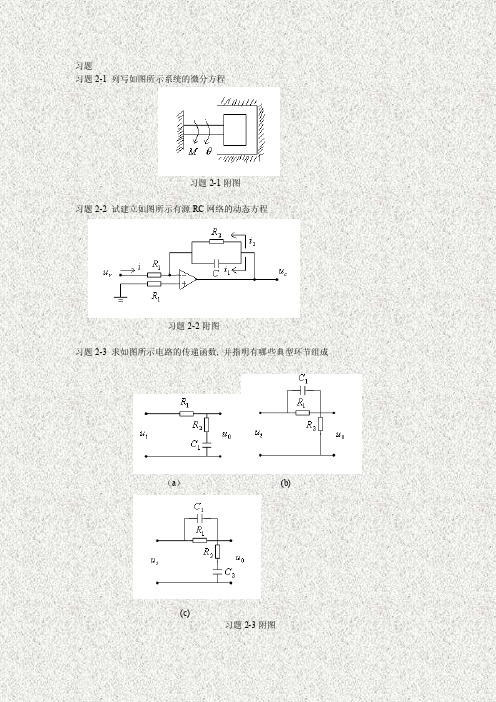
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成(a)(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图(a)图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。
),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。
习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。
图(a )图(b)习题2-8附图习题2-9 求如下各图的传递函数(a)(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图(a )(b)(c)(d)习题2-10附图习题答案习题2-1答案:解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案:解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案: 解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节,惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节,惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节,二阶振荡环节组成。
自动控制原理 第2章习题解答

第2章 控制系统的数学模型习题及解答2-1 已知质量-弹簧系统如题2-1图所示,图中标明了质量和弹簧的弹性系数。
当外力F (t )作用时,系统产生运动,如果在不计摩擦的情况下,以质量m 2的位移y (t )为输出,外力F (t )为输入,试列写系统的运动方程。
解: 设 质量m 1的位移量为x (t ),根据牛顿第二定律有y k y x k dt yd m 21222-)(−= ①)(1221y x k F dtxd m −−= ②①式可以写作y k k x k dtyd m )(211222+−= ③由①式也可以得到y k dtyd m y x k 22221)(+=− ④③式两端同时求二阶导数,可得2221221442)(dty d k k dt x d k dt yd m +−= ⑤将②、③式代入⑤式中,整理可得F m k y m k k dty d m k m k m m dt y d m 1112122122121442)(=−++++ 2-2 求题2-2图中由质量-弹簧-阻尼器组成的机械系统,建立系统的运动方程。
其中,x (t )为基底相对于惯性空间的位移,y (t )为质量相对于惯性空间的位移。
z (t )= y (t )- x (t )为基底和质量之间的相对位移,z (t )由记录得到, x (t )和z (t )分别为输入量和输出量。
解:应用牛顿第二定律可得dtt dz f kz dt y d m )(22−−= 将z (t )= y (t )- x (t )代入上式,整理可得2222dtx d m kz dt dz f dt z d m −=++题2-2图题2-1图解:(a )引入中间变量u c (t)表示电容器两端的电压。
根据基尔霍夫电流定律有o c c u R u R dt du C2111=+ 根据基尔霍夫电压定律有o i c u u u −=联立消去中间变量,可得描述输入量u i (t )和输出量u o (t )之间关系的微分方程为i i o o u R dt du C u R R R R dt du C121211+=++ (b )引入回路电流i (t )和电容器两端的电压u c (t)作为中间变量,根据基尔霍夫电压定律有i o u u i R =+1 另有电容元件的元件约束关系方程dtdu Ci c =和i R u u o c 2−=联立求解,消去中间变量可得i i o o u R dt du C u R R R R dt du C121211+=++(c )设电容器C 2两端的电压为u c 2(t),根据基尔霍夫电流定律有dtduC u u R dt u u d C c o i o i 2211)(1)(=−+− ①求导可得22221221)(1)(dtu d C dt u u d R dt u u d C c o i o i =−+− ② 另有输出支路电压方程o c c u u dtdu C R =+2222 等式两边求导有dtdu dt du dt u d C R oc c =+222222 ③将①、②代入③式,整理可得i ii ooo u C R dt du C R C R C R dt u d C R u C R dt du C R C R C R C R dt u d C R 2121221121221212122112121122+++=++++2-4 试求题2-4图所示有源RC 电路的微分方程,其中u i (t )为输入量,u o (t )为输出量。
自动控制原理课后习题答案第二章

解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
自动控制原理第2章课后习题及解答
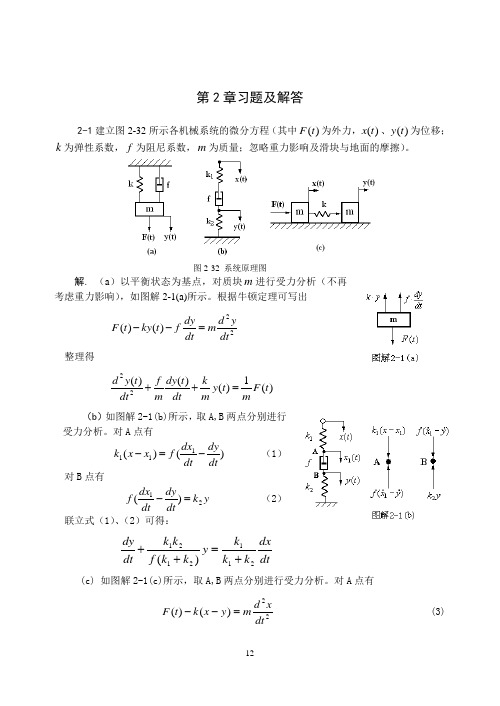
2-3 证明图 2-34 (a) 所示的力学系统和图 2-34 (b) 所示的电路系统是相似系统 (即 有相同形式的数学模型) 。
图 2-34 系统原理图
解 (a) 取A、B两点分别进行受力分析,如图解2-3(a)所示。对A点有
−y ) = f1 ( y −y 1 ) k 2 ( x − y) + f 2 ( x
比较两系统的传递函数,如果设 R1 = 1 k1 , R2 = 1 k 2 , C1 = f 1 , C 2 = f 2 ,则两系统 的传递函数相同,所以两系统是相似的。 2-4 如图 2-35 所示,二极管是一个非线性元件,其电流 id 和电压 ud 之间的关系为
= id 10−14 ( e 0.026 − 1) ,假设电路在工作点 u(0) = 2.39V , i= (0) 2.19 × 10−3 A 处做微小变
(c) 由图解 2-2(c)可写出
Ur ( = s ) R1 [ I1 ( s ) + I 2 ( s )] + ( Ls + R2 ) I 2 ( s ) 1 I 1 ( s ) = ( Ls + R2 ) I 2 ( s ) Cs U c ( s ) = R2 I 2 ( s )
(6) (7) (8)
F (t ) − k ( x − y ) = m
d 2x dt 2
(3)
- 12 -
对 B 点有
k ( x − y) = m
d2y dt 2
(4)
联立式(3) 、 (4)消去中间变量 x 可得
d 4 y 2K d 2 y K + = F (t ) dt 4 m dt 2 m 2
2-2 应用复数阻抗方法求图 2-33 所示各无源网络的传递函数。
自控原理习题解答(第二章)

[答2 ( 31 ) 1 ) ] (t) x(t) (t) Tx T sx(s) x (s) 1 1 1 T x (s) 1 T s 1 s T 1 t 1 T 1 1 T x ( t ) L x (s) L e 1 s T T
答2 4(c)
e y (s) e x (s) C2 1 1 I(s) R 1 R2 C1s C 2s R 2 C 1 C 2 s 2 C 1s 1 R 2 C1 C 2 s C1 2 (R1 R 2 )C1C 2 s C 2 s C1s (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 s C1 (R1 R 2 )C1C 2 s C 2 C1 (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 C1 s K d Td s C 2 C1 C 2 C1 K (R1 R 2 )C1C 2 s (R1 R 2 )C1C 2 s Td s 1 T s 1 1 1 C 2 C1 C 2 C1 为实际微分环节 惯性环节 1 I(s) (R 2 ) C 2s
X(s) G1 G1 H3 H2 H1
-
Y(s) G2
G3
G4 X(s)
G1
-
-
G2 H3
-
Y(s) G3 G4
-
H2
G4 H3
1 2e 2t e t cos 3t 3s2 2s 8 8 A s 1 2 s(s 2)(s 2s 4) s 0 2 4 3s2 2s 8 B (s 2) 2 2 s(s 2)(s 2s 4) s 2
第2章-自动控制原理习题答案
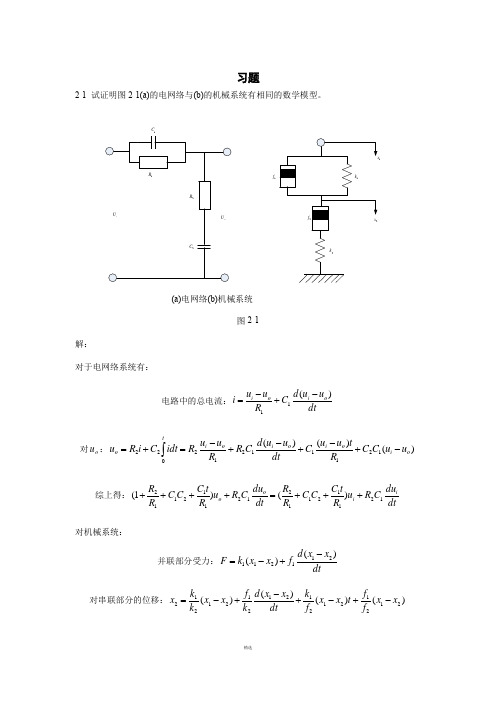
习题2-1 试证明图2-1(a)的电网络与(b)的机械系统有相同的数学模型。
1C 1f 1(a)电网络(b)机械系统图2-1解:对于电网络系统有:电路中的总电流:dtu u d C R u u i o i o i )(11-+-=对o u :)()()(1211121222o i o i o i o i to u u C C R t u u C dt u u d C R R u u R idt C i R u -+-+-+-=+=⎰综上得:dtdu C R u R tC C C R R dt du C R u R t C C C R R i i o o 1211211212112112)()1(+++=++++对机械系统:并联部分受力:dtx x d f x x k F )()(211211-+-= 对串联部分的位移:)()()()(21212121212121212x x f f t x x f k dt x x d k f x x k k x -+-+-+-=整理得:dtdx k f x f f t f k k k dt dx k f x f f t f k k k 12122121212211212121)()1(+++=++++所以,两系统具有相同的数学模型2-5求图2-2中RC 电路和运算放大器的传递函数c ()/()i U s U s 。
1R1R(a) RC 电路 (b) RC 电路1R(c) RC 电路 (d) 运算放大器图2-2解:21212)()()R sCR R R R s u s u a r c ++=οο1)()()()()()()3122112322121121211231212112++++++++=S R C R C R C S R R C C R R C C SR C R C S R R C C R R C C s u s u b rc οο2121212)()()()R R S CR CR R R CS R s u s u c r c +++=οο21212112)()()()S LCR R R S CR R LR R LS s u s u d r c ++++=οο2-6求图2-3所示系统的传递函数C(s)/D(s)和E(s)/D(s)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图2.68 习题2.1图解:(a)11r c u u i R -=,2()r c C u u i -= ,122c u i i R +=,12122121212c c r r R R R R R Cu u Cu u R R R R R R +=++++(b)11()r c C uu i -= ,121r u u i R -=,1221i i C u+= ,121c u i R u =+, 121211122112121121()()c c c r r r R R C C uR C R C R C u u R R C C u R C R C u u ++++=+++ (c)11r cu u i R -=,112()r C u u i -=,1122u i i R +=,1121c u i dt u C =+⎰, 121212222112122221()()c c c r r r R R C C uR C R C R C u u R R C C u R C R C u u ++++=+++ 2.2 试证明图 2.69(a)所示电路与图 2.69(b)所示的机械系统具有相同的微分方程。
图2.69(b)中X r (t )为输入,X c (t )为输出,均是位移量。
(a) (b)图2.69 习题2.2图解:(a)11r cu u i R -=,12()r c C uu i -= ,12i i i +=,221c u idt iR C =+⎰, 121211122212121122()()c c c r r r R R C C uR C R C R C u u R R C C u R C R C u u ++++=+++ (b)2121()c B xx K x -= ,1121()()()r c r c c B x x K x x B x x -+-=- , 121221212121211212()()c c c r r r B B B B B B B B Bx x x x x x K K K K K K K K K ++++=+++(a) (b) (c)图2.70 习题2.3图解:(a)12c r r u u Cu R R +=- ,221c r r R u R Cu u R =-- (b)12c r c u u CuR R =-- ,221c c r RR Cu u u R +=- (c)2111r r c u uu R dt R C R =--⎰,12c r r R CuR Cu u =-- 2.4 某弹簧的力-位移特性曲线如图2.71所示。
在仅存有小扰动的情况下,当工作点分别为x 0 =-1.2、0、2.5时,试计算弹簧在工作点附近的弹性系数。
图2.71 习题2.4图解:设力f 与位移x 的关系为f=g (x )。
取增量方程:()x dg x f x dx∆=∆, x 0 =-1.2、0、2.5()x dg x dx为工作点处的弹性系数,分别从曲线中量出为30201660,20,80.512=== 2.5 设某系统的传递函数为G (s ),在初始条件为零时,施加输入测试信号r (t )= t (t ≥0),测得其输出响应为c (t )=1+sin t +2 e -2t (t ≥0),试确定该系统的G (s )。
解:21)(ss R =,22111)(2++++=s s s s C ,222533)(23234++++++=s s s s s s s s G2.6 系统的微分方程组如下:)(d )(d )( , )(d )(d )()()()( , )()()(d )(d )( , )()()(54435553422311121t c tt c T t x K t x K t t x t c K t x t x t x t x K t x t x K tt x t x t c t r t x +==--==+=-=τ其中τ,K 1,K 2,K 3,K 4,K 5,T 均为正常数。
试建立系统r (t )对c (t )的结构图。
解:2.7 系统的微分方程组如下:t t c tt c t x K t nNN K t x t x x tt x Tt x t x t x t x K t x t n t c t r t x d )(d d )(d )( , )()()(d )(d , )()()()()( , )()()()(225022453452311211+=-==-==+-=其中K 0,K 1,K 2,T 均为正常数。
试建立系统结构图。
解:2.8 图2.72是一个模拟调节器的电路图。
试写出输入与输出之间的微分方程,并建立该调节器的结构图。
图2.72 习题2.8图解:(a)11r cu u i R -=,)(11211dt du C R u i +-=,312R u i =,⎰-=dt i C u 2221,542R u R u c -=, r c c c u u u R R CR R R uR C C R R R -=-+ 5224315214312.9 图2.73是一个转速控制系统,输入量是电压u a ,输出量是负载的转速ω,试写出其输入输出间的微分方程,并画出系统的结构图。
图2.73 习题2.9图解:(a)ωe a aa a a K dt di L R i u ++=,a i d i K M =,ωωB dtd J M d +=, a ee i a a a e i e i a u K K K B R B L J R K K K K J L 1)1()(1=++++ωωω2.10 某机械系统如图2.74所示。
质量为m 、半径为R 的均质圆筒与弹簧和阻尼器相连(通过轴心),假定圆筒在倾角为α的斜面上滚动(无滑动),试求出其运动方程和结构图。
图2.74 习题2.10图2.11 试化简图2.75中各系统结构图,并求传递函数C (s )/R (s )。
(a) (b)(c)图2.75 习题2.11图解:(a) 1222132211)(H G H G G G G G G s G +++=(b)211121211)1()(H H H G H H G G s G +++=(c)14321443232133243211)(H G G G G H G G H G G G H G G G G G G s G -+++=2.12 已知系统结构如图2.76所示,试将其转换成信号流图,并求出C (s )/R (s )。
(a) (b)图2.76 习题2.12图解:(a) 21212211211)(H H G G H G H G G G s G +++=(b) 2211211)(H G H G G G s G ++=2.13 系统的信号流图如图2.77所示,试用梅逊公式求C (s )/R (s )。
(a) (b)图2.77 习题2.13图解:(a) Ks s s Ks G 5.05.35.0)(23+++=(b)2142124513211212465143211)1()(H H G G G H G G G G G G H G G H G G G G G G G G s G ++++++++=2.14 试梅逊公式求图2.78所示结构图的传递函数C (s )/R (s )。
(a)(b)图2.78 习题2.14图解:(a) 3212521211241)(G G G H G G H G G H G G s G ++-+=(b)21212121312)(G G G G G G G G s G -++-+=2.15 已知系统结构图如图2.79所示,试写出系统在输入R (s )及扰动N (s )同时作用下输出C (s )的表达式。
图2.79 习题2.15图解:HG G G G G H G G G s N H G G G G G G G H G s R H G G G G G s C 3213122124314212231211)()]1(1[)()]1([)(+++++++++++=2.16 系统的结构如图2.80所示。
(1)求传递函数C 1(s )/R 1(s ),C 2(s )/R 1(s ),C 1(s )/R 2(s ),C 2(s )/R 2(s );(2)求传递函数阵G (s ),其中,C (s )=G (s )R (s ), C (s )=⎥⎦⎤⎢⎣⎡)()(21s C s C ,R (s )=⎥⎦⎤⎢⎣⎡)()(21s R s R 。
图2.80 习题2.16图解: (1))(1)1()()(1187513252532111s G G G G H G H G H G G G G s R s C =-+++=)(1)()(218751325765112s G G G G H G H G G G G G s R s C =-++=)(1)()(128751325954321s G G G G H G H G G G G G s R s C =-++=)(11)()(2287513251365422s G G G G H G H G H G G G G s R s C =-+++=)((2) ⎥⎦⎤⎢⎣⎡=)()()()()(22211211s G s G s G s G s G2.17 已知系统结构图如图2.81所示。
(1)试求传递函数C (s )/R (s )和C (s )/N (s );(2)若要消除干扰对输出的影响,即C (s )/N (s )=0,试问应如何选取G 0(s )。
图2.81 习题2.17图解: (1))1()()(321321++=Ts s K K K K K K s R s C )1()()()(321430321++-=Ts s K K K sK K s G K K K s N s C (2)2140)(K K sK s G =。
