自动控制原理(第三版)第二章答案华南理工出版社彭康拥陈来好

合集下载

自动控制原理习题及答案(冯巧玲)

第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dtyd m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有 )()(111dtdydt dx f x x k -=- （1）对B 点有 y k dtdydt dx f 21)(=- （2）联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （3） 2)()(R s Uc s I =（4）联立式（3）、（4），可解得：CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++ 2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

自动控制原理第二章习题课答案

第二章习题课
(2-8)
2-8 设有一个初始条件为零的系统，系统的输入、输出曲线如图，求G(s)。
δ (t)
c(t)
T
解: t
δ (t)
c(t)
T
K 0
K 0
t
-TS K K K c(t)= T t- T (t-T) C(s)= Ts2 (1-e ) C(s)=G(S)
第二章习题课
(2-９)
2-9 若系统在单位阶跃输入作用时，已知初始条件为零的条件下系统的输出响应，求系统的传递函数和脉冲响应。 -t 1 -2t R ( s )= c(t)=1-e +e r(t)=I(t) s 2+4s+2) (s 1 1 1 解: C(s)= s - s+2 + s+1 = s(s+1)(s+2) 2+4s+2) ( s G(S)=C(s)/R(s) = (s+1)(s+2)
第二章习题课
(2-1b)
2-1(b) 试建立图所示电路的动态微分方程。 duc CL d2uo duo du L ic= = +C o L 2 R 1 uL= dt R2 dt dt R2 dt ＋＋ 2 uo C CL d uoR2 duo uo u u + +C i1= i o i2= R ui=u1+uo 2 dt － R2 R2 dt － 2 输入量为ui，输出量为uo。 duc d(ui-uo) u1=i1R1 ic=C dt = dt diL uo u =L L dt iL=i2= i1=iL+ic R2
2-11(b) 求系统的传递函数
G3(s) R(s)

自动控制原理谢克明第三版部分习题答案

《自动控制原理（第3版）》部分习题答案第2章C2-1(a)21211()(1)()()(1)R sL R Cs G s R sL R Cs R ++=+++C2-221114232233342526()()(1)(1)()()()()()()()()()()()()()m a a a a a e ma a L a a a a e mffRG s K R R G s R Cs K T s R G s K c s G s U s JL s L f JR s fR c c L s R s G s M s JL s L f JR s fR c c U s G s K s =-=-=-+=-+=-Ω==++++-+Ω==++++==Ω123412346512346()()()()()()1()()()()()()()()1()()()()()r L G s G s G s G s s U s G s G s G s G s G s G s s M s G s G s G s G s G s Ω=+Ω=+C2-4(a)3123123()()()R LsG s R R R Ls R R R =++++C2-4(b)323123()()()R LsG s R R Ls R R R =+++C2-5321122211212311(1)(1)(),(),(),()()1a b c d R Cs R Cs R C s R C s RG s RCs G s G s G s R CsR C sR R R Cs ++++=-=-=-=-++C2-6 12314512123214342123312341232233344()()()()()()()1()()()()()()()()()()()()()()()()()()()()1()()()()()()()()()()a b G s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s G s G s G s G s G s H s G s G s H s G s G s H s +=++++++=+++-12341()()()()()G s G s G s G s H sC2-7 13241761113241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ 283261213241762851324()()()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s+=+++++ 24132852213241762851324()()[1()()]()()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++17413152113241762851324()()()[1()()]()()()()1()()()()()()()()()()()()()()G s G s G s G s G s G s G s C s R s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++=+++++ C2-812341123243123312312()()()()()1()()()()()()()()()()()()()()()()G s G s G s G s G s G s H s G s G s H s G s H s G s G s G s H s G s G s G s H s H s +=+++++C2-912345214561111452145145124561112322()()()[1()()()]()()()()()()()1()()()()()()()()()()()()()()()()[1()()]()()(()()()G s G s G s G s G s H s G s G s G s G s C s s R s G s H s G s G s H s G s G s G s G s G s G s H s H s G s G s G s G s H s G s G s G C s s R s --Φ==+-+-++Φ==4511452145145121122)()()1()()()()()()()()()()()()()()()()()()s G s G s G s H s G s G s H s G s G s G s G s G s G s H s H s C s s R s s R s +-+-=Φ+Φ C2-1013453564256313421356253431342535643535123561434523345624()()[1()()]()[1()()]()()1()()()()()()()()()a G s G G G s G H s G G H s G G G s G H s G G H s G G G G s G G G G s G H s G G H s G H s G G H s G G s G G H H s G G G H H s G G G H H s G G G G H H s =++++++-+++++++++12353241212131223123()()()()()[1()]()[1()()2()()]()1()()2()()()()2()()()b G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s G s ++++++=+++++第3章C3-1 221()TsTsK e Tse G s Ts ----=C3-2 220.910()1110ss s s s ++Φ=++ C3-3105050()10.283sin(545)()1 1.4sin(545)t t tc t e e t c t et ---=--+=-+精近C3-422*0.23()(0.5)2*0.23()0.50.23G s s s s s s =+Φ=++C3-51212T T bK T T ε+<<C3-6 阶跃信号作用下稳态误差为零，要求n m a b =加速度信号作用下稳态误差为零，要求1122,,n m n m n m a b a b a b ----=== C3-7 21()(1)c sG s K T s =+C3-8 24()(46)G s s s s =++C3-9 250()(1225)G s s s s =++C3-100.243τ=C3-11 (1)06,(2)303,(4)010/3K K K <<<<<<结构不稳（）C3-12 (1)015,(2)0.72 6.24K K <<<< C3-13(1)(2)34系统稳定系统不稳定，有两个右根，（）系统稳定（）系统不稳定，有三个右根C3-14 3,5K ω== C3-1533231()()1()()()()()n r G s G s G s H s G s G s G s =-+=第4章C4-1 图略图略C4-2 (1)图略图略(2) 2233()24x y ++=C4-3 (1)图略图略(2) 0.40.5K << C4-4 分会点和渐近线分会点和渐近线123-6+)(2)(18)=0,,=,42,22a a a a a d d d a πδϕ±---+==±（ 12320,2a d d d ====-(1)(1)当当时，图略图略123180,6a d d d ====-(2)(2)当当时，图略图略 120,0a a d σ<=>(3)(3)当当0<时，图略图略1180,0a a d δ<=<(4)(4)当当2<时，图略图略12318,,0a a d d d δ><(5)(5)当当时，三个不同实数分会点，图略图略C4-5(1) 图略,原系统不稳定; (2)增加零点且选择合适位置,可是系统稳定,零点05z <<C4-6图略,系统稳定34K > C4-7 (1) 图略图略(2)当0.8629.14K <<,系统为欠阻尼状态,且 1.87K =阻尼比最小,系统地闭环极点为3 2.8j -±(3)试探求得试探求得 2,4 2.8K j =-±闭环极点, 1.06,0.75~1P s M t ==C4-8 (1)等效开环传递函数为: (1)()(2)K s G s s s --=+正反馈系统根轨迹, 图略图略 (2)系统稳定02K << (3) 2,2K ω==C4-9等效开环传递函数为: 22()===10)(44)(4410)KaK G s K a s s s K s s s ''++++等（,图略图略C4-10(1) 图略图略 (2) 64,12K ω== (3)1,20.5,13s j ζ==-±C4-11(1) 图略图略 (2) 不在根轨迹上; (3) ()1cos 4c t t =-C4-12等效开环传递函数为: 322()=(4416)(4)(4)KKG s s s s s s s s =+++++等,K=8时试探求特征根.第5章C5-1(1)C5-1(2)C5-1(3)C5-1(4)C5-200000(1)()0.83sin(30 4.76)(2)()0.83sin( 4.76) 1.64cos(2459.46)c t t c t t t =+-=----C5-3当12T T <,系统稳定系统稳定当12T T >,系统不稳定. C5-4 2100()10100G s s s =++C5-5(a) 0110(1)300(),4111(1)(1)510s G s s s γ+==++ (b) 00.1(),2581(1)50s G s s γ==+ (c) 032(),141(1)2G s s s γ==+ (d) 025(), 1.66(1001)(0.11)G s s s s γ==-++(e) 020.5(21)(),36.8(0.51)s G s s s γ+==+(f) 0231.62(),9.860.010.0981G s s s γ==++C5-6 (1) K=1(2)K=25(3)K=2.56(或精确求K=3.1) C5-7()()()a g i 稳定，稳定，(b)(b)(b)不稳定，不稳定，不稳定，(c)(c)(c)稳定，稳定，稳定，(d)(d)(d)稳定，稳定，稳定，(e)(e)(e)不稳定，不稳定，(f)(f)稳定，稳定，不稳定，不稳定，(h)(h)(h)不稳定，不稳定，不稳定，不稳定，(j)(j)(j)不稳定，不稳定，C5-8 102510000K K <<<和 C5-9（1）（2）闭环系统稳定；）闭环系统稳定；（3）078.5,g K γ==∞（4）K 增大10倍，对数幅值上升，但相频特性不变，系统的快速性提高，平稳性降低，系统地抗干扰性降低。

自动控制原理习题2（含答案）

第二章习题及答案2-1试建立题2-1图所示各系统的微分方程[其中外力)(t F ，位移)(tx 和电压)(t u r为输入量；位移)(t y 和电压)(t u c为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。

根据牛顿定理可写出22)()(dt yd m dt dy f t ky t F =--整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++—（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。

对A 点有)()(111dtdydtdxf x x k -=-（1）对B 点有y k dtdydt dx f 21)(=-（2）联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++(c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs Rs U c r ++=（3）`2)()(Rs Uc s I =（4）联立式（3）、（4），可解得：），可解得： Cs R R R R Cs R R s U s U r c 212112)1()()(+++= 微分方程为: r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1（d ）可写出）可写出[]Cs s I s I s I R s U c R R r 1)()()()(++= （5）)()(1)(s RI s RI Css I c R c -= （6）[]Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c |微分方程为微分方程为 rr r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。

自动控制理论第三版课后答案

由和知系统有一串联纯滞后环节。系统的开环传递函数为
由解得。可确定系统的传递函数为
5-12系统的开环传递函数为
系统稳定的增益范围。
第六章
6-1 (a) ，超前网络的伯德图如图A-6-1所示。
图A-6-1题6-1超前网络伯德图
(b) ，滞后网络的伯德图如图A-6-2所示。
图A-6-2题6-1滞后网络伯德图
图A-3-1二阶系统极点在s平面上的分布区域
3-6系统在单位斜坡输入下的稳态误差为
加入比例—微分环节后
可见取，可使
3-7
3-8
3-9按照条件（2）可写出系统的特征方程
将上式与比较，可得系统的开环传递函数
根据条件（1），可得
解得，于是由系统的开环传递函数为
3-10
，过阻尼系统，无超调。
3-11（1）当a= 0时，。
（3）当时，系统处于临界阻尼状态，此时系统有二重闭环极点。
4-9主根轨迹如图A-4-9所示。系统稳定的值范围是。
图A-4-9题4-9系统主根轨迹
4-10 主根轨迹分离点；与虚轴交点，临界值。主根轨迹如图A-4-10所示。
图A-4-10题4-10系统主根轨迹
4-11（1）的根轨迹如图A-4-11所示。
图A-4-4题4-3系统常规根轨迹
（2）
分离点为；常规根轨迹如图A-4-4（b）所示。从根轨迹图看，加了零点后，无论取何值，系统都是稳定的。
4-4系统的根轨迹族如图A-4-6所示。
图A-4-6题4-4系统的根轨迹族
4-5系统的根轨迹族如图A-4-7所示。
图A-4-7题4-5系统的根轨迹族
4-7系统特征方程为
5-3

自动控制原理第二章习题答案详解

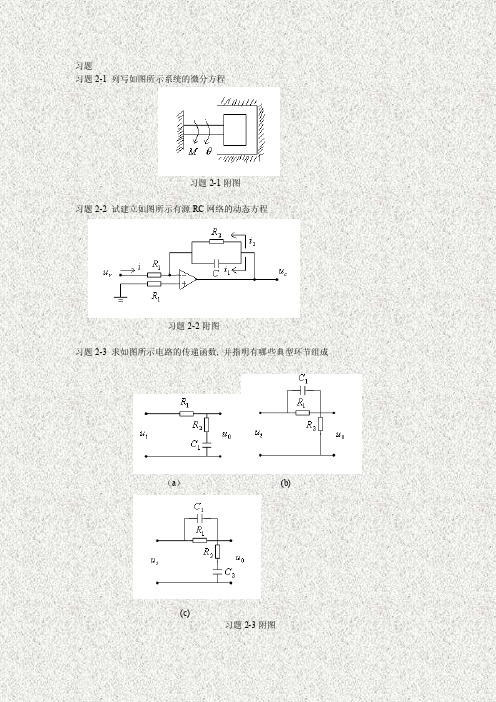
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成（a）(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图（a）图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。

),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。

习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。

图（a ）图（b）习题2-8附图习题2-9 求如下各图的传递函数（a）(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图（a ）(b)(c)(d)习题2-10附图习题答案习题2-1答案：解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案：解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案：解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节，惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节，惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节，二阶振荡环节组成。

自动控制原理第二章到第七章课后习题答案

自动控制原理第二章到第七章课后习题答案第二章2-1试求下图所示电路的微分方程和传递函数。

解：（a ）根据电路定律，列写出方程组：001Li R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰消除中间变量可得微分方程：20002i d u du L L C u u dt R dt⋅⋅+⋅+=对上式两边取拉氏变换得：2000()()()()i LL C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ （b ）根据电路定律，列写出方程组：12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程：121012i R R Ru u idt R R C+=-⎰ 对上式两边取拉氏变换得：2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++传递函数为0212()1()()1i U s R CsG s U s R Cs R Cs+==++2-3求下图所示运算放大器构成的电路的传递函数。

解：（a ）由图（a ），利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+（b ）由图（b ），利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C s R C s++++==-=-+2-5试简化下图中各系统结构图，并求传递函数()()C s R s 。

2-6试求下图所示系统的传递函数11()()C s R s ，21()()C s R s ，12()()C s R s 及22()()C s R s 。

自动控制理论机械工业出版社课后习题答案夏德岑_第三版 PDF可打印

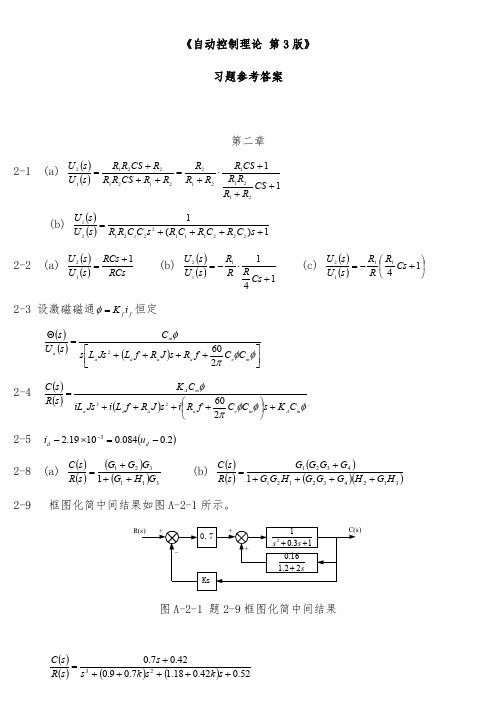
, t 0
比较上述两种情况，可见有 z 1 零点时，单位脉冲响应的振幅较无零点时小，而且产生相移，相移角为 arctg
1 2 n 。 1 n
2．单位阶跃响应 (a) 无零点时
ct 1
2 n t 1 2 t arctg 1 e sin n 1 2
G( s) 2a ss (2 a) s (2 2a)
2
根据条件（1），可得
Kv 1 2a 0.5 esr 2 2a
解得 a 1 ，于是由系统的开环传递函数为
G( s) 2 ss 3s 4
2
3-10
1M 2M
3t
s
p p
46.6%, t s 7.99s2%, ( n 2.12rad / s, 0.24) 16.3%, t s 8s2%, ( n 1rad / s, 0.5)
C m s 60 U a s s La Js 2 La f Ra J s Ra f C eC m 2
2-4
C s Rs
K A C m 60 iL a Js 3 iL a f Ra J s 2 i Ra f C eC m s K A C m 2
C 2 lim
s 0
d2 2(0.1s 2 s 10) 20(0.2s 1) 2 s lim 0 e s 0 ds 2 (0.1s 2 s 10) 3
(1)
s (t ) r (t ) R0 ，此时有 rs (t ) R0 , r r (t ) 0 ，于是稳态误差级数为 s esr t C0 rs (t ) 0 ， t 0

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

G3
G4 1 G 4H 4

G 2 G 3 G 4(1 G 1H 1 ) (1 G 1H 1 )(1 G 2 H 2 )(1 G 4 H 4 ) G 1G 2 G 3 G 4 H 0
自动控制原理第二章习题分析2-9(3)
则C(s) C R( s ) R(s ) R(s ) N 1( s ) N 2( s )
U o s U i s

Zo
Zi 1 R 5 R 2 // C1s
1 // R4 C s 2
自动控制原理第二章习题分析
2 2(a) f1( f1 dxi dt dt dx o dt ) k 1( x i x o ) f2 dx o dt dx o dt k 2xo
dxi
k 1 x i ( f1 f2 )
(k1 k 2 )x o
( f1 s k 1 ) X i( s ) [ ( f1 f2 ) s ( k 1 k 2 ) ] X o( s ) f1s k 1 X i( s ) ( f1 f2 ) s k 1 k 2 X 0( s )
2
R 2 Cs 1
Uo Ur Uc Ur

Zo Zr
R 1 CLs
2
R1 R 2 C L s R1 R 2 Uo R2
Ls R 2

Uc Uo Uo Ur

R2
Ls R 2 U r
R 1 CLs
2
R1 R 2 C L s R1 R 2
G3 G3

G 1G 2 G 3 G 4 (1 G 1H 1 )(1 G 2 H 2 )(1 G 4 H 4 ) G 1G 2 G 3 G 4 H 0
自动控制原理第二章习题分析2-9(2)
自动控制原理第二章习题分析2-9(2)
G2 令R(s) N 2(s) 0,则 C N1 (s) N 1(s) 1 1 G 2H 2 G2 1 G 2H 2 G3 G4 1 G 4H 4 H0 G1 1 G 1H 1
u i a R 3 ,i a u ua R1 R2 R1
R1
ua R1 R2
ua Ra R3
当满足R u
R R 2 R 3时, 即 1 a R3 c eR 3 Ra R3
R1 R2
时:
c eω Ra R3
ω;
U(s) Ω(s)
c eR 1 R1 R2
2
G s
Z s X s
ms
ms
2
2
fs k
自动控制原理第二章习题分析2-3
Zo 1 Cs // Ls R 2 Ls R 2 LCs
2
2
R 2 Cs 1
Z r R1 Z o
R 1 LCs
R 1 R 2 Cs Ls R 1 R 2 LCs
自动控制原理第二章习题分析2-8(a)
G2 G1 U o(s) U i(s) 1 G2 1 G1 1 G2 G 3G 4 1 G 3G 4H 2 G3G 4 G 3G 4 1 G 3G 4H 2 G 3G 4 H1 1 G 3G 4H 2 G 4 H1 1 G 3G 4H 2 G 4
自动控制原理第二章习题分析2-9(1)
自动控制原理第二章习题分析2-9(1)
G1 令N 1(s) N 2(s) 0,则 C R(s) R(s) 1 G1 G2 G2 G4 1 G 4H 4 G4 1 G 4H 4 H0
1 G 1H 1 1 G 2 H 2 1 G 1H 1 1 G 2 H 2
G2
G 1G 2 G 3 G 4 1 G 3 G 4 H 2 G 2 G 3 H 1 G 1G 2 G 3 G 4
自动控制原理第二章习题分析2-8(b)
自动控制原理第二章习题分析2-8(b)
C(s) R(s) G1 G4 1 G1 G4 G 2G 3 1 G 2 G 3(H 2 H 1 /G 3 ) G 2G 3 G 1G 2 G 3 1 G 2 H 1 G 1G 2 H 1 G 2 G 3 H 2 H1 1 G 2 G 3(H 2 H 1/G 3 ) G 3

- G 3 G 4(1 G 1H 1 )(1 G 2 H 2 ) (1 G 1H 1 )(1 G 2 H 2 )(1 G 4 H 4 ) G 1G 2 G 3 G 4 H 0
自动控制原理第二章习题分析2-10
自动控制原理第二章习题分析2-10
局部闭环Φ (s)
'
Ω d(s) U Δ(s)
2

R 1R 2 C 1C 2 s R 1C 1 R 1C 2 R 2 C 2 s 1
2
( b ) Z i R1 G s U o s U i s
1 C1s
R2
1 C2s
; Z o R2
1 C2s
Zo Zi
R1 R 2 C 1C 2 s C 1 C 2
(b).
C(s) R(s)

G1 G2 1 (G 1 源自 G 2 )(G G1 G23
G4 )
1 G 1G 3 G 2 G 3 G 1G 4 G 2 G 4
自动控制原理第二章习题分析2-14©(d)
自动控制原理第二章习题分析2-14©(d)
R 2 C 1C 2 s C 1
自动控制原理第二章习题分析
(c).Z
2
R 2 // U o (s) Ui ( s )
1 C 2s Z2 Z1
,Z 1 R 1 R2 1
G(s)
R 1 (R 2 C 2 s 1)
1 // R4 C s 2 1 // R4 C s 2
4
K3
Ku K3 Ku
s K4 s
K3 T1 s 1
2
K 1 1 s 1 K 2 2 s 1 s
T1 s 1 T m s 1 T1 s 1 T m s 1 K5
1 2 s 1 2 s 1
B s
3 2
B s T1 s T1 T m K 2 K 3 K 4 2 T m s 1 K 2 K 3 K 4 2 K 2 K 3 K 4 T m K 1 K 2 K 3 K 5 K u 1 2 s K 2 K 3 K 4 K 1 K 2 K 3 K 5 K u 1 K 1 K 2 K 3 K 5 K u 2 s K 1 K 2 K 3 K 5 K u
自动控制原理第二章习题分析
2 1.求U o(s)/U i(s). (a).Z
2
R2 U o(s) U i(s)
1 C 2s
,Z 1 R 1 // Z2
1 C 1s

R 1 1 C 1s R 1 1 C 1s

R1 R 1C 1s 1
G(s)
Z1 Z 2
(R 1C 1s 1)(R 2 C 2 s 1) (R 1C 1s 1)(R 2 C 2 s 1) R 1C 2 s R 1R 2 C 1C 2 s R 1C 1 R 2 C 2 s 1
自动控制原理第二章习题分析2-2(b)
2 2(b) dz t m kz t f 2 dt dt z t y t x t
2
d y t
ms Y s KZ s fsZ s Z s Y s X s
C N 1 s) ( N 1( s ) C N 2( s ) N 2( s )
自动控制原理第二章习题分析2-9(3)
G4 1 G 4H 4 H0 G1 G2 1 G 1H 1 1 G 2 H 2
令R(s) N 1(s) 0,则
C N 2(s) N 2(s)
- G3 1 G3 G4 1 G 4H 4
2
s U a s
扰动输入前为负号
自动控制原理第二章习题分析2-8(a)
方法 1 : G4 前分支点C 后移至方法 2 : 综合点A后移至G2 后然后与综合点B互换; 方法 3 : 综合点B前移至G2 前然后与综合点A互换; 方法 4 : 套用公式( 2 8 2 ) 。面, D点面,
K1
Ts 1 K 2 K 3 K 4 is Ts 1 K 2 K 3 K 4 is
1 K1
自动控制原理第二章习题分析2-11
s U i s
K 1 1 s 1 K 2 2 s 1 1 s K 2 2 s 1 s K 1K 2 K 3K u
2

k 2 k 3 k 4 s k 1 k 2 k 3 k 4
自动控制原理第二章习题分析2-5
2 5 : e c eω, u u u u ua R1 R2 R 1 ,u a c eω i a(R a R 3 ) u a c eω Ra R3 u a c eω Ra R3 R3 R3 c eω Ra R3 R3 Ra R3 ua R1 R2 c eR 3 Ra R3 R1 ua Ra R3 R1 0
( d ) Z i R1 1 Z o R 3 R 5 R 2 // C1s U i s Zi

1 R 5 R 2 // C1s U o s Zo