初一数学上册计算题天天练(强烈推荐)37
人教版初一数学上册400道计算题及练习题之欧阳语创编

初一数学上册计算题(400道题)时间:2021.03.01 创作:欧阳语(1)= (2)= (3) = (4) = (5)= (6)=(7)= (8) = (9)= (10)=(11)(12)(13)(14)(15)(16)(17)(18)(19)(20);(21);(22);(23);(24);(25);(26).(27)(28)(29)(30)(31)(32)(33)(34)(35)(36)(37)(38)如果,求的值(39)已知与互为相反数,求的值。
(40)(41)(42)(43)(44)(45)(46)(47)(48)(49)(50)100(51)(52)(53)(54)(55)(56)(57)(58)(59)若,,求a + b的值.(60)已知│a+1│与│b-2│互为相反数,求a-b的值.(61)(-12)÷4×(-6)÷2; ;(62)(62)(63);(64);(64);(67);(68)(-5)×(-7)-5×(-6)(69).(72)(73);(75);(76)(-5)×(-8)×0×(-10)×(-15);(77)(-3)×(-4)×(-5)+(-5)×(-7)(78)(-0.1)×(-1)×(-100)-0.•01×(1000).(79)2×(-1)×(-)×(-);(80)- + --)×(-20);(81)(-3)×(-0.12)×(-2)×33;(82)(- + -)×(-36).(83)-×(12-2-0.6)(84)(+)×|-|×2×(-5);(85)(-1)×3(-)×(-1)(86)(87)(-2)×(-)= (88)0×(-13.52)= (89)(-1)×a =(90)(-3.25)×(+)=(91)(-185.8)×(-36)×0×(-25)=(92)(93)(94)(-)×0.125×(-2)×(-8);97)(98)(-0.25)×0.5×(-4)×4;(99)(-4)×(-18.36)×2.5;(100)(-)×(-18)+(-)×(-3)×2;(101)(-47.65)×2+(-37.15)×(-2)+10.5×(-7).(102)[(-2)×(-4)+(-5)]×[-3-(-2)×(-3)].(103)(104)(105)(106)(107)(-23)+7+(-152)+65 (108)|+(-)|(109)(-)+|―|(112)38+(-22)+(+62)+(-78)(113)(-8)+(-10)+2+(-1)(114)(-)+0+(+)+(-)+(-)(115)(-8)+47+18+(-27)(116)(-5)+21+(-95)+29 (117)(-8.25)+8.25+(-0.25)+(-5.75)+(-7.5)(118) 6+(-7)+(9)+2 (119)72+65+(-105)+(-28)(120)(-23)+|-63|+|-37|+(-77)(121)19+(-195)+47 (122)(+18)+(-32)+(-16)+(+26)(122)(-3)-5(123)(-0.8)+(-1.2)+(-0.6)+(-2.4)(124)(-8)+(-3)+2+(-)+12(125)5+(-5)+4+(-)(126)(-6.37)+(-3)+6.37+2.75(127)(-12.5)-(-7.5) (128)(-26)―(-12)―12―18(129)―1―(-)―(+) (130)(-20)-(+5)-(-5)-(-12)(131)(-23)―(-59)―(-3.5) (132)|-32|―(-12)―72―(-5)(133)(-)―(-)―(134)(+)―(-)―(-)―(135)(-)―3―(-3.2)―7 (136)(+)―(-)―(137)(+6.1)―(-4.3)―(-2.1)―5.1 (138)(-)―(-1)―(-1)―(+1.75)(139)(-3)―(-2)―(-1)―(-1.75) (140)-8-5+4-3(141)-4++(-)―(142)0.5+(-)-(-2.75)+(143)(+4.3)-(-4)+(-2.3)-(+4)(144)(-0.5)-(-3)+6.75-5(145)(-9)×(146)(-)×(-0.26)(147)(-2)×31×(-0.5)(148)×(-5)+×(-13)(149)(-4)×(-10)×0.5×(-3)(150)(-)××(-1.8)(151)(-0.25)×(-)×4×(-7)(152)(-)×(-)×(-)(153)(-8)×4×(-)×(-0.75)(154)4×(-96)×(-0.25)×(155)(-1+)×56(156)(――)×36 (157)(-36)×(+-)(158)(-)×(8--0.4)(159)(-66)×〔1-(-)+(-)〕(160)25×-(-25)×+25×(161)(+-+)×72(162)×(2-)×(-)×(-) (163)18÷(-3)(164)(-24)÷6(165)(-57)÷(-3)(166)(-)÷(167)(-42)÷(-6)(168)(+)÷(-)(169)(-)÷9 (170)0.25÷(-)(171)-36÷(-1)÷(-)(172)(-1)÷(-4)÷(173)3÷(-)×(-) (174)0÷[(-3)×(-7)](175)-3÷(-)(176)(-24)÷(-6)(177) 2÷(5-18)×(178)1÷(-3)×(-)(179)-×(-)÷(-)(180)(-)÷(-)(181)(-+)÷(-)(182)-3.5 ×(-0.5)×÷(183)-1÷(-1)×1×(-7)(184)×(--)÷(185)÷(-2)-×-÷4(186)0.8×+4.8×(-)-2.2÷+0.8×(187)2÷(-)×÷(-5)(188)(-)×(-15×4)(189)(-2.4)(190)[15-(1÷1+3]÷(-1)(191)×(-5)÷(-)×5(192)-(-+-)÷(-)(193)-13×-0.34×+×(-13)-×0.34(194) 8-(-25)÷(-5)(195)(-13)×(-134)××(-)(196)(-4)-(-5)+(-4)-3(197)(-16-50+3)÷(-2)(198)(-0.5)-(-3)+6.75-5(199)178-87.21+43+53-12.79(200)(-6)×(-4)+(-32)÷(-8)-3 (201)--(-)+|-1|(202)(-9)×(-4)+ (-60)÷12 (203)[(-)-1+]÷(-)(204)-|-3|÷10-(-15)×(205)-1×(-)÷2(206)(2-3+1)÷(-1)×(-7)(207)-×(8-2-0.04)(208)-2×( 209)--(210)-(211)-2×(212)÷(213)×(214)+(215)××(216)×-(217)++(218)-×-(219)+(220)0-÷3×(221)×÷(222)-×-÷(223)×(-+1) ×0 (224)6+×(225)-10+8÷-4×3 (226)--(227)-(1-0.5)×(228)××(229)4×+6 (230)×××(231)-+2×+(-6)÷(232)÷(-8)-×(-)(233)×()×(234)-2[-3×]÷(235)÷9÷(236)36×(237)-{}(238)-+(1-0.5)××[2×](239)-4×+(240)--+×÷(241)(-5.3)-(+4.8)+(-3.2)-(-2.5);(242)(243)-10+8÷(-2)2-3×(-4)-15;(244)-14-(1-0.5)××[2-(-3)2].(245)(246)(247)(248)(249)(250)(251)(252)(253); (254)(x+1)-3(x-1)=1-3x; (255)(x-2)-2(4x-1)=3(1-x).(256)(257);(258)(259)(260)(261)(262)(263)(264)(265)(266)(267)(268)(269)(270)(271)(272)(273)(274)(275)(276)(277)错误!未找到引用源。
初一上册的有理数计算题。

初一上册的有理数计算题。
初一上册的有理数计算题包括以下几种类型:
1.加法:同号的两数相加,并把绝对值相加,取相同的符号;异号且绝对值不
相等的两数相加,进行抵消后,取绝对值较大的数的符号;互为相反数的两个数相加,结果为零;任何有理数与零相加,仍得这个数。
2.减法:减去一个数相当于加上这个数的相反数。
3.乘法:两数相乘同号得正,异号得负,然后将两数的绝对值相乘,得出结果;
任何数与0相乘,结果都得0。
4.除法:除以一个不等于0的数,等于乘以这个数的倒数;两数相除,同号得
正,异号得负;0除以任何一个不等于0的数,得数都是0。
下面是一些具体的初一上册的有理数计算题示例:
1. 2 + 3 - 4 × 5 ÷ 6
2.( - 3) + ( - 2) - ( - 5)× ( - 6) ÷ ( - 12)
3.-4 + 2×(-3) -6÷0.25
4.(-5)÷[1.85-(2-1.75)×7]
5.18÷{1-[0.4+ (1-0.4)]×0.4}
6.1÷(-2/3)×7
7.-3-[4-(4-3.5×2)]×[-2+(-3)]
8.8+(-1/4)-5-(-0.25)
9.99×26
10.(3.5-7.75-4.25)÷1.1
请注意,这些题仅供参考,可以结合实际的教材内容进行选择。
人教版初一数学上册计算题(400道题)
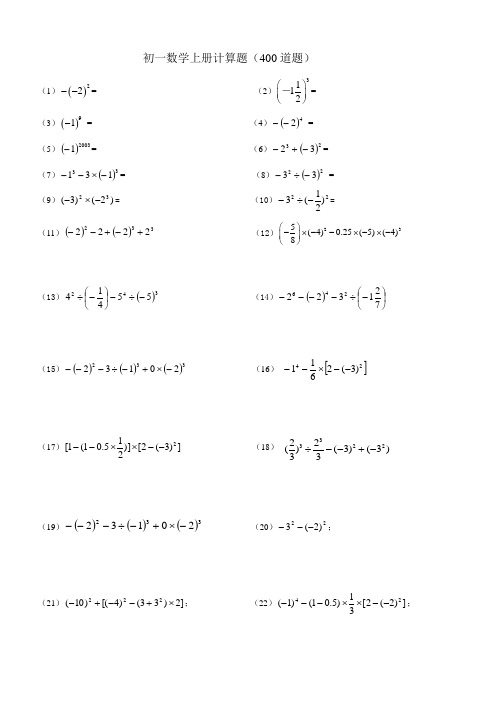
初一数学上册计算题(400道题)(1)()22--= (2)3112⎛⎫⎪⎝⎭-=(3)()91- = (4)()42-- =(5)()20031-= (6)()2332-+-=(7)()33131-⨯--= (8)()2233-÷- =(9))2()3(32-⨯-= (10)22)21(3-÷-=(11)()()3322222+-+-- (12)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(13)()34255414-÷-⎪⎭⎫ ⎝⎛-÷ (14)()⎪⎭⎫ ⎝⎛-÷----721322246(15)()()()33220132-⨯+-÷--- (16) []24)3(2611--⨯--(17)])3(2[)]215.01(1[2--⨯⨯-- (18)(19)()()()33220132-⨯+-÷--- (20)22)2(3---;(21)]2)33()4[()10(222⨯+--+-; (22)])2(2[31)5.01()1(24--⨯⨯---;332222()(3)(3)33÷--+-(23)94)211(42415.0322⨯-----+-; (24)20022003)2()2(-+-;(25))2()3(]2)4[(3)2(223-÷--+-⨯--; (26)200420094)25.0(⨯-.(27)()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ (28)()()----⨯-221410222(29)()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. (30)()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.(31) (32)(56)(79)---(33)(3)(9)(8)(5)-⨯---⨯- (34)3515()26÷-+(35)5231591736342--+- (36)()()22431)4(2-+-⨯---(37)411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--(38)如果0)2(12=-++b a ,求20112010()-3ab a b a a ++-()的值(39)已知|1|a +与|4|b -互为相反数,求b a 的值。
人教版初一数学上册有理数的计算题天天练3

-4.5 ,-2.25 ,8 ,4.5 ,8二、-11的绝对值是( ),-3.8的相反数是( )。
三、-16的绝对值是( ),7.2的相反数是( ),-5.5的倒数是( )。
四、|42.5|=( ),(-1)4=( )。
五、计算。
2 1(-—)-(-—)+(-6) 3×[(-4)3÷(-1)]7 73 1 1—+(-—)+(-—)17-(-26)-9-(-15)4 6 51(-0.8)×—×(-9) (-1)3+52(-1)101861 1 1(-—)÷(-—-—)×0 8-[(-4)3+(-3]9 4 9(—-—)+(-—) 14+(-26)+9-(-16)8 2 89 1(—+—)×(-70) (-4)4+52(-1)17258 8(-7)+(-16) 6×(-10) -11.5+(-8)1 1(-—)×(-—) -12+[5+(-15+8)] (-5)2+125 4-40+10+(-17)-(-21) 8.6-(-5.4)-(-4.5)+4.22 1 134 9 (—-—)+(—+—) 8.3-(-—)-(-4.9)-—5 7 4 7 5 5-4 ,-4.25 ,3 ,-3 ,-2二、3.5的绝对值是( ),6.9的相反数是( )。
三、-22的绝对值是( ),4的相反数是( ),6的倒数是( )。
四、|28|=( ),(-2)4=( )。
五、计算。
2 6(-—)-(-—)+(-9) 25+[(-3)3×(-5)]7 76 1 6—-(-—)+(-—)3+(-13)+10-(-10)7 6 51(-0.1)×—×(-200) (-4)3+23(-1)124491 1 1(-—)÷(-—+—)×0 10+[(-1)2-(-4]9 9 8(—+—)÷(-—) 10-(-25)+9+(-17)6 2 71 1(—+—)×(-10) (-3)2-33(-1)15626 6(-8)÷(-19) 1÷(-7) 2+(-11)1 1(-—)-(-—) -2+[-4+(-17-6)] (-5)2-426 330+13-(-6)+(-21) 3.5+(-9)-(-1.7)+42 1 1 1 6 7 (—-—)-(—-—) 7.4+(-—)-(-1.5)-—9 6 7 5 5 5-3 ,-1 ,5 ,3.5 ,-7二、20.5的绝对值是( ),-6.6的相反数是( )。
七年级上册数学计算题专练

七年级上册数学计算题专练一、有理数运算类。
1. 计算:(-3)+5 - (-2)- 解析:- 根据有理数加减法法则,减去一个数等于加上这个数的相反数。
- 所以(-3)+5 - (-2)=(-3)+5 + 2。
- 先计算(-3)+5 = 2,再计算2+2 = 4。
2. 计算:-2×(-3)÷(1)/(2)- 解析:- 根据有理数乘除法法则,先算乘法-2×(-3)=6。
- 再算除法6÷(1)/(2)=6×2 = 12。
3. 计算:(-2)^3+(-3)×[(-4)^2 - 2]- 解析:- 先计算指数运算,(-2)^3=-8,(-4)^2 = 16。
- 然后计算括号内的式子(-4)^2-2 = 16 - 2=14。
- 接着计算乘法-3×14=-42。
- 最后计算加法-8+(-42)=-8 - 42=-50。
二、整式加减类。
4. 化简:3a + 2b-5a - b- 解析:- 合并同类项,对于a的同类项3a-5a=(3 - 5)a=-2a。
- 对于b的同类项2b - b=(2 - 1)b = b。
- 所以化简结果为-2a + b。
5. 计算:(2x^2 - 3x + 1)-(3x^2 - 5x - 2)- 解析:- 去括号,得到2x^2-3x + 1-3x^2 + 5x+2。
- 合并同类项,2x^2-3x^2=(2 - 3)x^2=-x^2,-3x+5x=( - 3+5)x = 2x,1 + 2=3。
- 所以结果为-x^2+2x + 3。
三、一元一次方程类。
6. 解方程:2x+3 = 5x - 1- 解析:- 移项,将含x的项移到一边,常数项移到另一边,得到2x-5x=-1 - 3。
- 合并同类项-3x=-4。
- 系数化为1,x=(4)/(3)。
7. 解方程:(x+1)/(2)-(2x - 1)/(3)=1- 解析:- 先去分母,等式两边同时乘以6,得到3(x + 1)-2(2x - 1)=6。
人教版初一数学上册计算题(400道题)
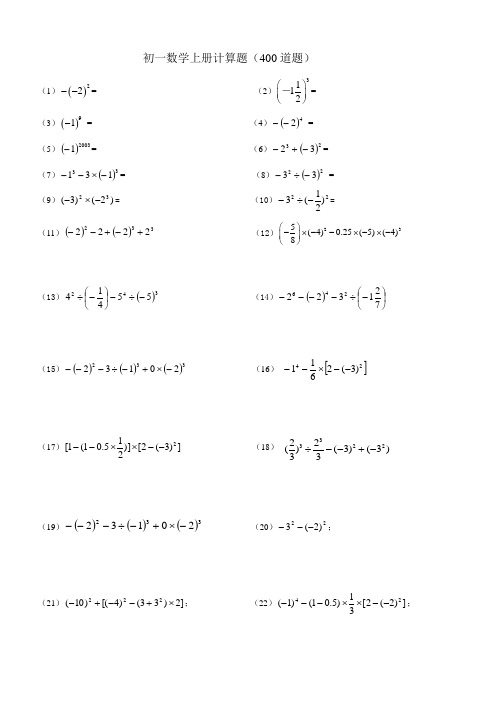
初一数学上册计算题(400道题)(1)()22--= (2)3112⎛⎫⎪⎝⎭-=(3)()91- = (4)()42-- =(5)()20031-= (6)()2332-+-=(7)()33131-⨯--= (8)()2233-÷- =(9))2()3(32-⨯-= (10)22)21(3-÷-=(11)()()3322222+-+-- (12)235(4)0.25(5)(4)8⎛⎫-⨯--⨯-⨯- ⎪⎝⎭(13)()34255414-÷-⎪⎭⎫ ⎝⎛-÷ (14)()⎪⎭⎫ ⎝⎛-÷----721322246(15)()()()33220132-⨯+-÷--- (16) []24)3(2611--⨯--(17)])3(2[)]215.01(1[2--⨯⨯-- (18)(19)()()()33220132-⨯+-÷--- (20)22)2(3---;(21)]2)33()4[()10(222⨯+--+-; (22)])2(2[31)5.01()1(24--⨯⨯---;332222()(3)(3)33÷--+-(23)94)211(42415.0322⨯-----+-; (24)20022003)2()2(-+-;(25))2()3(]2)4[(3)2(223-÷--+-⨯--; (26)200420094)25.0(⨯-.(27)()0252423132.⨯--÷-⎛⎝ ⎫⎭⎪+⎡⎣⎢⎢⎤⎦⎥⎥ (28)()()----⨯-221410222(29)()()()-⨯÷-+-⎛⎝ ⎫⎭⎪⨯-÷-3120313312232325.. (30)()()()-⎛⎝ ⎫⎭⎪⨯-⨯-⨯-212052832.(31) (32)(56)(79)---(33)(3)(9)(8)(5)-⨯---⨯- (34)3515()26÷-+(35)5231591736342--+- (36)()()22431)4(2-+-⨯---(37)411)8()54()4()125.0(25⨯-⨯-⨯-⨯-⨯33182(4)8-÷--(38)如果0)2(12=-++b a ,求20112010()-3ab a b a a ++-()的值(39)已知|1|a +与|4|b -互为相反数,求b a 的值。
七年级数学上册综合算式专项练习题多项式的加减法运算

七年级数学上册综合算式专项练习题多项式的加减法运算数学是一门需要思考和解决问题的学科,而多项式的加减法运算是数学中一个基础且重要的概念。
加减法运算是我们在日常生活中最常见的运算之一,掌握多项式的加减法运算方法对我们的数学学习和解决实际问题都非常有帮助。
本文将为大家介绍七年级数学上册综合算式专项练习题——多项式的加减法运算。
一、多项式的加法运算多项式的加法运算是指对两个或多个多项式进行相加的操作。
在进行多项式的加法运算时,需要考虑同类项的合并,即将同类项的系数相加,而同类项的组成要素包括变量和指数。
例如,我们有两个多项式:3x² + 2x + 5 和 2x² + 4x + 1,要求将它们相加。
首先,我们可以按照同类项进行合并,即将同类项的系数相加。
合并后的多项式为 (3x² + 2x + 5) + (2x² + 4x + 1) = 5x² + 6x + 6。
在实际的加法运算中,可能会涉及到更多的多项式。
同样的原则,我们需要将所有的同类项进行合并,合并后得到的多项式即为最终的结果。
二、多项式的减法运算多项式的减法运算是指对两个多项式进行相减的操作。
在进行多项式的减法运算时,需要考虑同类项的合并,即将同类项的系数相减,而同类项的组成要素包括变量和指数。
例如,我们有两个多项式:5x² + 3x + 7 和 2x² + x + 3,要求将它们相减。
同样地,首先,我们可以按照同类项进行合并,即将同类项的系数相减。
合并后的多项式为 (5x² + 3x + 7) - (2x² + x + 3) = 3x² + 2x + 4。
同样地,在实际的减法运算中,可能会涉及到更多的多项式。
我们需要将所有的同类项进行合并,合并后得到的多项式即为最终的结果。
三、综合算式专项练习题为了巩固多项式的加减法运算,我们来做一些综合算式专项练习题。
七年级数学上册综合算式专项练习题平均数的计算练习

七年级数学上册综合算式专项练习题平均数的计算练习本文旨在为七年级数学上册的综合算式专项练习题提供平均数的计算练习。
以下是一系列练习题,可以帮助学生巩固平均数的概念,并提供一些实际应用的练习。
练习题一:一家餐馆连续7天的日销售额(单位:元)分别为1200,1500,800,1300,1000,1100,900。
求这7天的平均日销售额。
解答:将这7天的日销售额相加:1200 + 1500 + 800 + 1300 + 1000 + 1100 + 900 = 6900。
然后将总销售额除以天数:6900 ÷ 7 = 985.71(保留两位小数)。
所以这7天的平均日销售额为985.71元。
练习题二:某班级的学生身高(单位:厘米)如下:150,155,158,160,165,168,170,175,178,180。
求这些学生的平均身高。
解答:将这些学生的身高相加:150 + 155 + 158 + 160 + 165 + 168 + 170 + 175 + 178 + 180 = 1599。
然后将总身高除以学生人数:1599 ÷10 = 159.9(保留一位小数)。
所以这些学生的平均身高为159.9厘米。
练习题三:某商品在1月~10月的每月销量(单位:件)如下:100,150,80,120,90,110,130,70,95,105。
求这10个月的平均月销量。
解答:将这10个月的销量相加:100 + 150 + 80 + 120 + 90 + 110 + 130 +70 + 95 + 105 = 1050。
然后将总销量除以月数:1050 ÷ 10 = 105。
所以这10个月的平均月销量为105件。
练习题四:某家庭的每月用电量(单位:千瓦时)如下:200,150,180,220,250,190,210。
求这7个月的平均月用电量。
解答:将这7个月的用电量相加:200 + 150 + 180 + 220 + 250 + 190 + 210= 1400。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、在数轴上将下列各数表示出来。
2
1—, -3.5 ,0 , 6.4
5
2、写出下列各数的相反数。
1
—, -2 ,11 ,-0.1
6
3、写出下列各数的绝对值。
4
-3—, 1.2 ,-4 ,-0.48
7
4、比较下列各组数的大小。
(1)-20与0 (2)-4.75与0.5 (3)|-8.8|与|1.2|
1 2
(4)-—与-—(5)10与-|-10| (6)|-25.6|与|-7.3|
7 5
5、计算。
1 11
3-—+—10×(-17)-5×(-17)
3 15
1 9 1
(---)×-(-150)÷6×(-15)
3 8 6
6 7 4
-(—+—+—)×126 1×[20-(-1)3]
7 6 3
6、合并同类项。
5a+(9a-2) 4a+(9a+4d)-(7d+a)
9(8m-10)-4m 1-(9m-8)-(2m+5)
5(ab-7a)+(5a+2b) 6(abc-5a)+9(6a+5abc)
9(xy+7z)+(-xy+5z) -7(pq-pr)-(8pq+pr)
7、解方程。
7 x 1
—x+—=—0.9x+0.7=5.5-8.2x
9 8 3
2 1
—+8x=3+—x 7(x-8)+8(x+2)=16
7 3
1 2
—(5x+6)=—x-8 9x+3(7+x)=-1
2 5
y+2 y+3
——=9-—— 3.5x-7.5(x-9)=20
2 6
1 2
—(4-4x)=—(3x-1) 5(8x-2)=16
8 7
1、在数轴上将下列各数表示出来。
2
-2—, -4 ,0 , 5.6
5
2、写出下列各数的相反数。
1
—, 18.5 ,-12 ,8.4
4
3、写出下列各数的绝对值。
1
9—, 4.45 ,3 ,-0.64
7
4、比较下列各组数的大小。
(1)-15与6 (2)-3.5与1 (3)|-3.9|与|3.8|
1 2
(4)-—与-—(5)14与-|-3| (6)|-4.3|与|-2.9|
4 7
5、计算。
1 1
6-—+—9×(-8)+30×(-8)
6 15
9 1 7
(---)÷-(-66)÷18×(-27)
8 7 8
5 3 1
-(—-—-—)×168 5×[9+(-5)3]
6 4 7
6、合并同类项。
-5b+(7b+9) b-(7b+4p)+(4p+4b)
-4(6a-2)+2a 2+(7y-6)-(8y+4)
9(-ab+3a)-(7a-6b) 19(abc+9a)+6(9a+5abc)
3(xy+8z)+(-xy+9z) -4(pq+pr)+(7pq+pr)
7、解方程。
5 x 1
—x+—=—0.4x+0.3=4.6+0.7x
9 2 6
4 1
—-6x=9+—x 5(x+5)+5(x+7)=19
3 9
1 4
—(7x+6)=—x+3 8x-9(7-x)=-5
9 5
y+1 y-1
——=1-—— 3.5x+5.5(x+4)=15
2 6
1 2
—(5+4x)=—(5x+1) 9(4x+3)=20
5 5
1、在数轴上将下列各数表示出来。
3
-5—, -4.5 ,0 , 1.6
5
2、写出下列各数的相反数。
1
—, -15 ,-13 ,2
7
3、写出下列各数的绝对值。
4
-7—, 2.15 ,7 ,-0.32
7
4、比较下列各组数的大小。
(1)-10与0 (2)-4与-0.75 (3)|-6.8|与|0|
1 2
(4)-—与-—(5)-15与-|-10| (6)|-77.8|与|-3.8|
7 3
5、计算。
7 1
2-—+—21×(-8)-19×(-8)
6 18
1 3 1
(-+-)×-(-162)÷14÷(-27)
3 4 5
4 5 6
-(—-—-—)×126 1×[18-(-4)2]
3 6 7
6、合并同类项。
-2y+(2y+7) y+(6y+3c)-(4c-y)
4(9m-3)+6m 1+(5m-3)-(4m-4)
5(ab+6a)-(3a+4b) 19(abc+2a)+3(5a+7abc)
9(xy+2z)-(-xy+9z) -3(pq+pr)+(5pq-pr)
7、解方程。
5 x 1
—x-—=—0.6x-0.7=0.5+0.1x
9 4 3
2 1
—-3x=4+—x 6(x+3)+2(x+6)=16
7 6
1 4
—(5x+8)=—x-6 8x+9(17+x)=-8
6 5
y+2 y-3
——=5+—— 4.5x+9.5(x-3)=45
2 5
1 2
—(2+3x)=—(5x-4) 5(8x+2)=8
9 5
1、在数轴上将下列各数表示出来。
3
-4—, 2.5 ,0 ,-1.6
5
2、写出下列各数的相反数。
1
—, -3 ,13 ,1.1
3
3、写出下列各数的绝对值。
1
-1—, 1.3 ,-3 ,-0.8
9
4、比较下列各组数的大小。
(1)-12与4 (2)-5与0.5 (3)|-4.5|与|1.2|
1 2
(4)-—与-—(5)3与-|-10| (6)|-9.6|与|-2.3|
8 3
5、计算。
5 7
1-—-—27×(-20)-21×(-20)
3 12
5 1 7
(-+-)×-(-150)÷16÷(-3)
4 4 6
6 1 1
-(—-—-—)×90 6×[1-(-5)3]
5 3 6
6、合并同类项。
-6a-(3a+3) a-(3a-4c)+(3c-a)
7(3a+6)+2a 10+(5n-5)+(7n+6)
2(ab+8a)+(3a+7b) 2(abc+2a)-5(8a-2abc)
5(xy-3z)-(-xy-8z) -6(pq-pr)-(7pq+pr)
7、解方程。
5 x 1
—x-—=—0.7x+0.9=8.1-2.6x
3 4 9
4 1
—+7x=7+—x 6(x+9)-6(x+1)=8
7 3
1 3
—(2x+1)=—x-6 8x-2(19+x)=-7
6 5
y+2 y+1
——=2-——0.5x-7(x-2)=20
4 5
1 2
—(2+2x)=—(2x-5) 9(2x-1)=7
2 3
1、在数轴上将下列各数表示出来。
1
-1—, -1 ,0 , 6.4
5
2、写出下列各数的相反数。
1
-—, 4.5 ,1 ,2.6
7
3、写出下列各数的绝对值。
4
-3—, -2.65 ,-1 , 0.64
9
4、比较下列各组数的大小。
(1)-9与5 (2)-2.5与-2 (3)|-9|与|2|
1 2
(4)-—与-—(5)-7与-|-3| (6)|-83.7|与|-4.6|
6 5
5、计算。
5 7
6-—-—7×(-20)-3×(-20)
3 18
1 9 9
(-+-)÷-(-168)÷14÷(-6)
8 8 8
2 1 4
-(—+—+—)×54 8×[3-(-1)2]
3 6 3
6、合并同类项。
-7y-(2y-1) 7y-(9y-3s)-(7s+y)
2(2t-6)+2t 7+(2x+1)+(2x+9)
7(ab-3a)+(7a-3b) 7(abc+5a)-6(6a+8abc)
7(xy+9z)+(-xy-3z) -8(pq+pr)+(2pq+pr)
7、解方程。
5 x 1
—x-—=—0.3x+0.1=9.2+7.3x
3 2 3
2 1
—+6x=8+—x 2(x+6)-4(x+7)=8
7 3
1 3
—(6x-2)=—x+8 2x-5(4-x)=-9
5 5
y+3 y+3
——=1+—— 3.5x+4(x-1)=5
3 5
1 2
—(2+3x)=—(4x+5) 9(7x-9)=15
9 7。
