人教版【高中数学】选修2-1第三章空间向量的基本定理讲义
新人教A版高中数学选修2-1第三章《空间向量与立体几何》知识点汇总及解题方法总计

第三章 空间向量与立体几何单元小结[核心速填]1.空间向量的有关定理和推论(1)共线向量定理:对空间任意两个向量a ,b (b ≠0),a ∥b 的充要条件是存在实数λ,使得a =λb .(2)共线向量定理的推论:若OA →,OB →不共线,则P ,A ,B 三点共线的充要条件是OP →=λOA →+μOB →,且λ+μ=1.(3)共面向量定理:如果两个向量a ,b 不共线,那么向量p 与向量a ,b 共面的充要条件是存在惟一的有序实数对(x ,y ),使得p =x a +y b .(4)共面向量定理的推论:已知空间任意一点O 和不共线的三点A ,B ,C ,则P ,A ,B ,C 四点共面的充要条件是OP →=xOA →+yOB →+zOC →(其中x +y +z =1).(5)空间向量基本定理:如果三个向量a ,b ,c 不共面,那么对空间任一向量p ,存在有序实数组{x ,y ,z },使得p =x a +y b +z c ,其中{a ,b ,c }叫做空间的一个基底.2.空间向量运算的坐标表示设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3). (1)a +b =(a 1+b 1,a 2+b 2,a 3+b 3),a -b =(a 1-b 1,a 2-b 2,a 3-b 3),λa =(λa 1,λa 2,λa 3),a ·b =a 1b 1+a 2b 2+a 3b 3.(2)重要结论:a ∥b ⇔a =λb ⇔a 1=λb 1,a 2=λb 2,a 3=λb 3(λ∈R ); a ⊥b ⇔a ·b =0⇔a 1b 1+a 2b 2+a 3b 3=0.3.模、夹角和距离公式(1)设a =(a 1,a 2,a 3),b =(b 1,b 2,b 3),则①|a |=a ·a②cos 〈a ,b 〉=a ·b |a ||b |=(2)设A (a 1,b 1,c 1),B (a 2,b 2,c 2),则d AB =|AB →|4.空间向量的结论与线面位置关系的对应关系(1)设直线l 的方向向量是u =(a 1,b 1,c 1),平面α的法向量v =(a 2,b 2,c 2), 则l ∥α⇔u ⊥v ⇔u ·v =0⇔a 1a 2+b 1b 2+c 1c 2=0,l ⊥α⇔u ∥v ⇔u =k v ⇔(a 1,b 1,c 1)=k (a 2,b 2,c 2)⇔a 1=ka 2,b 1=kb 2,c 1=kc 2(k ∈R ).(2)设直线l ,m 的方向向量分别为a ,b ,平面α,β的法向量分别为u ,v ,则l ∥m ⇔a ∥b ⇔a =k b ,k ∈R ; l ⊥m ⇔a ⊥b ⇔a ·b =0; l ∥α⇔a ⊥u ⇔a ·u =0; l ⊥α⇔a ∥u ⇔a =k u ,k ∈R ;α∥β⇔u ∥v ⇔u =k v ,k ∈R ; α⊥β⇔u ⊥v ⇔u ·v =0. 5.空间向量与空间角的关系(1)设异面直线l 1,l 2的方向向量分别为m 1,m 2,则l 1与l 2的夹角θ满足cos θ=|cos 〈m 1,m 2〉|.(2)设直线l 的方向向量和平面α的法向量分别为m ,n ,则直线l 与平面α的夹角θ满足sin θ=|cos 〈m ,n 〉|.(3)求二面角的大小:(ⅰ)如图31①,AB ,CD 是二面角αl β的两个半平面α,β内与棱l 垂直的直线,则二面角的大小θ=〈AB →,CD →〉.图31(ⅱ)如图31②③,n 1,n 2分别是二面角αl β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos 〈n 1,n 2〉或-cos 〈n 1,n 2〉.[体系构建][题型探究]类型一、空间向量的基本概念及运算例1、如图32,在四棱锥S ABCD 中,底面ABCD 是边长为1的正方形,S 到A 、B 、C 、D 的距离都等于2.给出以下结论:图32①SA →+SB →+SC →+SD →=0; ②SA →+SB →-SC →-SD →=0; ③SA →-SB →+SC →-SD →=0; ④SA →·SB →=SC →·SD →; ⑤SA →·SC →=0.其中正确结论的序号是________. 【答案】 ③④【解析】容易推出SA →-SB →+SC →-SD →=BA →+DC →=0,所以③正确;又因为底面ABCD 是边长为1的正方形,SA =SB =SC =SD =2,所以SA →·SB →=2·2·cos∠ASB ,SC →·SD →=2·2·cos ∠CSD ,而∠ASB =∠CSD ,于是SA →·SB →=SC →·SD →,因此④正确,其余三个都不正确,故正确结论的序号是③④.[规律方法] 1.空间向量的线性运算包括加、减及数乘运算,选定空间不共面的三个向量作为基向量,并用它们表示出目标向量,这是用向量法解决立体几何问题的基本要求,解题时可结合已知和所求,根据图形,利用向量运算法则表示所需向量.2.空间向量的数量积(1)空间向量的数量积的定义表达式a ·b =|a |·|b |·cos 〈a ,b 〉及其变式cos 〈a ,b 〉=a ·b|a | ·|b |是两个重要公式. (2)空间向量的数量积的其他变式是解决立体几何问题的重要公式,如a 2=|a |2,a 在b 上的投影a ·b|b |=|a |·cos θ等.[跟踪训练]1.如图33,已知ABCD A ′B ′C ′D ′是平行六面体.设M 是底面ABCD 的中心,N 是侧面BCC ′B ′对角线BC ′上的34分点,设MN →=αAB →+βAD→+γAA ′→,则α+β+γ=________.图33【答案】32[连接BD ,则M 为BD 的中点,MN →=MB →+BN →=12DB →+34BC ′→=12(DA →+AB →)+34(BC →+CC ′→)=12(-AD →+AB →)+34(AD →+AA ′→)=12AB →+14AD →+34AA ′→.∴α=12,β=14,γ=34.∴α+β+γ=32.]类型二、空间向量的坐标运算例2、(1)已知a =(2,3,-4),b =(-4,-3,-2),b =12x -2a ,则x =( )A .(0,3,-6)B .(0,6,-20)C .(0,6,-6)D .(6,6,-6)(2)已知向量a =(x,1,2),b =(1,y ,-2),c =(3,1,z ),a ∥b ,b ⊥C . ①求向量a ,b ,c ;②求a +c 与b +c 所成角的余弦值.【答案】(1)B [由b =12x -2a 得x =4a +2b ,又4a +2b =4(2,3,-4)+2(-4,-3,-2)=(0,6,-20), 所以x =(0,6,-20).](2)①∵向量a =(x,1,2),b =(1,y ,-2),c =(3,1,z ),且a ∥b ,b ⊥c ,∴⎩⎪⎨⎪⎧x 1=1y =2-23+y -2z =0,解得⎩⎪⎨⎪⎧x =-1,y =-1,z =1,∴向量a =(-1,1,2),b =(1,-1,-2),c =(3,1,1). ②∵a +c =(2,2,3),b +c =(4,0,-1), ∴(a +c )·(b +c )=2×4+2×0+3×(-1)=5,|a +c |=22+22+32=17,|b +c |=42+02+(-1)2=17, ∴a +c 与b +c 所成角的余弦值为(a +c )·(b +c )|a +c ||b +c |=517.[规律方法] 熟记空间向量的坐标运算公式 设a =(x 1,y 1,z 1),b =(x 2,y 2,z 2), (1)加减运算:a ±b =(x 1±x 2,y 1±y 2,z 1±z 2). (2)数量积运算:a ·b =x 1x 2+y 1y 2+z 1z 2. (3)向量夹角:cos 〈a ,b 〉=x 1x 2+y 1y 2+z 1z 2x 21+y 21+z 21x 22+y 22+z 22. (4)向量长度:设M 1(x 1,y 1,z 1),M 2(x 2,y 2,z 2),则|M 1M 2→|=(x 1-x 2)2+(y 1-y 2)2+(z 1-z 2)2. 提醒:在利用坐标运算公式时注意先对向量式子进行化简再运算. [跟踪训练]2.在空间直角坐标系中,已知点A (1,-2,11),B (4,2,3),C (6,-1,4),则△ABC 一定是( )A .等腰三角形B .等边三角形C .直角三角形D .等腰直角三角形【答案】C [∵AB →=(3,4,-8),AC →=(5,1,-7),BC →=(2,-3,1),∴|AB →|=32+42+(-8)2=89,|AC →|=52+12+(-7)2=75,|BC →|=22+(-3)2+1=14,∴|AC →|2+|BC →|2=|AB →|2,∴△ABC 一定为直角三角形.]类型三、利用空间向量证明平行、垂直问题例3、 在四棱锥P ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA =AD =CD =2AB =2,M 为PC 的中点.(1)求证:BM ∥平面PAD ;(2)平面PAD 内是否存在一点N ,使MN ⊥平面PBD ?若存在,确定N 的位置;若不存在,说明理由.[思路探究] (1)证明向量BM →垂直于平面PAD 的一个法向量即可;(2)假设存在点N ,设出其坐标,利用MN →⊥BD →,MN →⊥PB →,列方程求其坐标即可. 【答案】以A 为原点,以AB ,AD ,AP 分别为x 轴、y 轴、z 轴建立空间直角坐标系如图所示,则B (1,0,0),D (0,2,0),P (0,0,2),C (2,2,0),M (1,1,1),(1)证明:∵BM →=(0,1,1),平面PAD 的一个法向量为n =(1,0,0), ∴BM →·n =0,即BM →⊥n ,又BM ⊄平面PAD ,∴BM ∥平面PAD . (2)BD →=(-1,2,0),PB →=(1,0,-2), 假设平面PAD 内存在一点N ,使MN ⊥平面PBD . 设N (0,y ,z ),则MN →=(-1,y -1,z -1), 从而MN ⊥BD ,MN ⊥PB , ∴⎩⎪⎨⎪⎧MN →·BD →=0,MN →·PB →=0,即⎩⎪⎨⎪⎧1+2(y -1)=0,-1-2(z -1)=0,∴⎩⎪⎨⎪⎧y =12,z =12,∴N ⎝ ⎛⎭⎪⎫0,12,12,∴在平面PAD 内存在一点N ⎝ ⎛⎭⎪⎫0,12,12,使MN ⊥平面PBD .[规律方法]利用空间向量证明空间中的位置关系(1)线线平行:证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2)线线垂直:证明两条直线垂直,只需证明两直线的方向向量垂直. (3)线面平行:①证明直线的方向向量与平面的法向量垂直;②证明可在平面内找到一个向量与直线的方向向量是共线向量;③利用共面向量定理,即证明直线的方向向量可用平面内两不共线向量线性表示.(4)线面垂直:①证明直线的方向向量与平面的法向量平行;②利用线面垂直的判定定理转化为线线垂直问题.(5)面面平行:①证明两个平面的法向量平行(即是共线向量);②转化为线面平行、线线平行问题.(6)面面垂直:①证明两个平面的法向量互相垂直;②转化为线面垂直、线线垂直问题.[跟踪训练]3.如图34,长方体ABCDA1B1C1D1中,点M,N分别在BB1,DD1上,且AM⊥A1B,AN⊥A1D.图34(1)求证:A1C⊥平面AMN.(2)当AB=2,AD=2,A1A=3时,问在线段AA1上是否存在一点P使得C1P∥平面AMN,若存在,试确定P的位置.【答案】(1)证明:因为CB⊥平面AA1B1B,AM⊂平面AA1B1B,所以CB⊥AM,又因为AM⊥A1B,A1B∩CB=B,所以AM⊥平面A1BC,所以A1C⊥AM,同理可证A1C⊥AN,又AM∩AN=A,所以A1C⊥平面AMN.(2)以C 为原点,CD 所在直线为x 轴,CB 所在直线为y 轴,CC 1所在直线为z 轴,建立空间直角坐标系,因为AB =2,AD =2,A 1A =3,所以C (0,0,0),A 1(2,2,3),C 1(0,0,3),CA 1→=(2,2,3), 由(1)知CA 1⊥平面AMN ,故平面AMN 的一个法向量为CA 1→=(2,2,3).设线段AA 1上存在一点P (2,2,t ),使得C 1P ∥平面AMN ,则C 1P →=(2,2,t -3), 因为C 1P ∥平面AMN ,所以C 1P →·CA 1→=4+4+3t -9=0, 解得t =13.所以P ⎝⎛⎭⎪⎫2,2,13, 所以线段AA 1上存在一点P ⎝ ⎛⎭⎪⎫2,2,13,使得C 1P ∥平面AMN .类型四、利用空间向量求空间角例4、如图35,在等腰直角三角形ABC 中,∠A =90°,BC =6,D ,E 分别是AC ,AB 上的点,CD =BE =2,O 为BC 的中点.将△ADE 沿DE 折起,得到如图(2)所示的四棱锥A ′BCDE ,其中A ′O = 3.(1) (2)图35(1)证明:A ′O ⊥平面BCDE ;(2)求二面角A ′CD B 的平面角的余弦值.[思路探究] (1)利用勾股定理可证A ′O ⊥OD ,A ′O ⊥OE ,从而证得A ′O ⊥平面BCDE ;(2)用“三垂线”法作二面角的平面角后求解或用向量法求两个平面的法向量的夹角.【答案】(1)证明:由题意,得OC =3,AC =32,AD =2 2. 如图,连接OD ,OE ,在△OCD 中,由余弦定理,得OD =OC 2+CD 2-2OC ·CD cos 45°= 5.由翻折不变性,知A ′D =22,所以A ′O 2+OD 2=A ′D 2,所以A ′O ⊥OD . 同理可证A ′O ⊥OE .又因为OD ∩OE =O ,所以A ′O ⊥平面BCDE .(2)如图,过点O 作OH ⊥CD 交CD 的延长线于点H ,连接A ′H .因为A ′O ⊥平面BCDE ,OH ⊥CD , 所以A ′H ⊥CD .所以∠A ′HO 为二面角A ′CD B 的平面角. 结合图(1)可知,H 为AC 的中点,故OH =322,从而A ′H =OH 2+A ′O 2=302. 所以cos ∠A ′HO =OH A ′H =155. 所以二面角A ′CD B 的平面角的余弦值为155. [规律方法] 用向量法求空间角的注意点(1)异面直线所成角:两异面直线所成角的范围为0°<θ≤90°,需找到两异面直线的方向向量,借助方向向量所成角求解.(2)直线与平面所成的角:要求直线a 与平面α所成的角θ,先求这个平面α的法向量n 与直线a 的方向向量a 夹角的余弦cos 〈n ,a 〉,易知θ=〈n ,a 〉-π2或者π2-〈n ,a 〉.(3)二面角:如图36,有两个平面α与β,分别作这两个平面的法向量n 1与n 2,则平面α与β所成的角跟法向量n 1与n 2所成的角相等或互补,所以首先应判断二面角是锐角还是钝角.图36[跟踪训练]4.在如图37所示的圆台中,AC 是下底面圆O 的直径,EF 是上底面圆O ′的直径,FB是圆台的一条母线.图37(1)已知G ,H 分别为EC ,FB 的中点,求证:GH ∥平面ABC . (2)已知EF =FB =12AC =23,AB =BC ,求二面角F BC A 的余弦值.【答案】 (1)证明:设CF 的中点为I ,连接GI ,HI .在△CEF 中,因为点G ,I 分别是CE ,CF 的中点, 所以GI ∥EF .又EF ∥OB ,所以GI ∥OB .在△CFB 中,因为H ,I 分别是FB ,CF 的中点, 所以HI ∥BC .又HI ∩GI =I ,BC ∩OB =B , 所以平面GHI ∥平面ABC . 因为GH ⊂平面GHI , 所以GH ∥平面ABC .(2)连接OO ′,则OO ′⊥平面ABC .又AB =BC ,且AC 是圆O 的直径, 所以BO ⊥AC .以O 为坐标原点,建立如图所示的空间直角坐标系. 由题意得B (0,23,0),C (-23,0,0). 过点F 作FM ⊥OB 于点M , 所以FM =FB 2-BM 2=3, 可得F (0,3,3).11 故BC →=(-23,-23,0),BF →=(0,-3,3). 设m =(x ,y ,z )是平面BCF 的法向量.由⎩⎪⎨⎪⎧m ·BC →=0,m ·BF →=0可得⎩⎨⎧ -23x -23y =0,-3y +3z =0.可得平面BCF 的一个法向量m =⎝ ⎛⎭⎪⎫-1,1,33.因为平面ABC 的一个法向量n =(0,0,1), 所以cos 〈m ,n 〉=m ·n|m |·|n |=77,所以二面角F BC A 的余弦值为77.。
(人教版)高中数学选修2-1课件:第3章空间向量与立体几何3.1.1

①(A→B+B→C)+C→C1=A→C+C→C1=A→C1; ②(A→A1+A→1D1)+D→1C1=A→D1+D→1C1=A→C1; ③(A→B+B→B1)+B→1C1=A→B1+B→1C1=A→C1; ④(A→A1+A→1B1)+B→1C1=A→B1+B→1C1=A→C1. 所以 4 个式子的运算结果都是A→C1. 答案: 4
• (3)注意零向量的书写,必须是0这种情势. • (4)两个向量不能比较大小.
空间向量的加减法与运算律
空间向 量的加 减法
类似平面向量,定义空间向量的加、减法运算 (如图):
O→B =O→A +A→B =_a_+__b___; C→A =O→A -O→C =_a_-__b___
加法运 (1)交换律:a+b=b+a;
◎在长方体 ABCD-A1B1C1D1 中,化简D→A-D→B+B→1C-
B→1B+A→1B1-A→1B. 【错解】 D→A-D→B+B→1C-B→1B+A→1B1-A→1B
=A→B+C→B+B→1B=D→C+D→A+B→1B=D→B+D→1D=D→1B.
【错因】 对向量减法的三角形法则理解、记忆错误,
中,老师从学校大门口回到住地方产生的总位 移就是三个位移的合成(如右图所示),它们是
不在同一平面内的位移,如何刻画这样的位移 呢?
• [问题1] • [提示1] • [问题2] 吗?
• [提示2]
老师的位移是空间向量吗? 是. 空间向量的加法与平面向量类似
类似.
空间向量
定义
长度 几何表 示法
在空间,把具有大___小__和_方__向__的量叫做空间向量 向量的_大__小__叫做向量的长度或_模__
6分
(3)在线段 CC1 上取中点 M,则有C→M=12C→C1, 则有:A→B+A→D+12C→C1=A→B+B→C+C→M=A→M. 9 分 (4)由(2)知13(A→B+A→D+A→A1)=13A→C1,在线段 AC1 上取点 G,使得 AG=13AC1,即:13(A→B+A→D+A→A1)=A→G. 12 分
人教版选修21第三章空间向量的线性运算讲义

人教版选修21第三章空间向量的线性运算讲义课堂协作探求重点难点打破知识点一空间向童的概念在学习空间向量的槪念时,要对比平面向疑的有关概念停止了解记忆.(1)向量:具有大小和方向的量叫做向量.(2)相等向量:同向且等长的有向线段表示同一向虽或相等的向量.(3)零向量:终点与终点重合的向虽叫做零向量,记为0. (4)向量的长度:表示向量a的有向线段的长度叫做向量的长度或模,记作a|. (5)基线:有向线段所在的直线叫做向量的基线.(6)共线向量:假设空间一些向量的基线相互平行或重合,那么这些向虽叫做共线向量或平行向量,如a平行于b,记作a〃b.留意:①共线向量(或平行向量)是指向量的基线相互平行或重合,平行向量的基线能够重合,共线向量的基线能够不重合•②共线向量(或平行向量)的方向能够同向,也能够反向. 如下右图a〃b〃c〃d.知识点二空间向量的加法、减法和数乘向量运算我们可把平而向量的线性运算法那么,推行到空间,用来定义空间向量的加法、减法和数乘向量运算.(1)平而向量求和的三角形法那么战争行四边形法那么,对空间向量也异样成立.(2)平而向量求和的多边形法那么, 对空间向量也异样成立•如上右图而二鬲+入瓦+B\B + BC + CG +GD・这也就是说,表示相加向量的有向线段依次首尾相接,构成的折线从首到尾的向量就是这些相加向量的和为了便于记忆,常把这个和向量叫做"封口向量"(3)空间向量的加法和数乘向量运算与平而向量一样,满足如下运算律:①加法交流律:a+b二b+a:②加法结合律:(a+b)+c=a+(b+c);③分配律:(X +u) a= X a+ua; A. (a+b) = X a+ X b. (4)两个结论:①有限个向量求和,交流相加向量的顺序英和不变;②三个不共而的向量的和等于以这三个向量为邻边的平行六面体的对角线所表示的向量.说明1.关于空间恣意两个非零向疑a、b,当它们的基线不在任何同一个平而内(两基线异而),那么总可以经过平移,把它们移到同一平而内,这说明恣意两个向量都可以经过平移,转化为平而向量.2.向量数乘的运算除了满足分配律及结合律外,还有以下些性质:(1)假定aHO, X :a二X -a, 么入丄=入 n;(2)假定X HO, X a:二X a:,那么a t=a:;(3) A. ;a+ X :a+…+ 入迢二(X i+ X 2+••• X c) a;(4) A. ai+ X a:+•••+ X 比二入(ai+a:+"・+a』.典型例题剖析题型1 空间向量的有关概念【例1】回答以下效果:(1)单位向量一定相等?(2)终点不同,但方向相反且模相等的几个向量是不是相等的向量?(3)相等的非零向量,假圧终点不同,那么终点一泄不同,这一判别正确吗?(4)空间恣意两个非零向量都可以平移到同一平而内?解析应用向屋的有关概念停止判别.答案(1)不一定.单位向量是指模为1,方向却是不确泄的,所以单位向量不左相等.两个非零向量相等必需具有两个条件:一是模相等,二是方向相反•两个条件缺一不可.(2)是.对照向呈相等必需具有的两个条件,这两个条件中,并没有对相应的有向线段的终点加任何限制因此看来,表示相等向量的有向线段的终点是很自在的,相等向疑的终点位置具有恣意性.(3)正确.由于在终点不同的情形下,假设终点相反,那么这些向量就不平行,即这些向量的方向就不相反,这与向量相等的左义相矛盾.(4)正确.在空间任取一点,过此点引两个与非零向疑相等的向量,而这两个向疑所在的直线相交于此点,两条相交直线确左一个平而,所以两个非零向量可以平移到同一平而内.规律总结此题共4个小题,解答每一小题都需对所学的知识有一个准确、片而的了解. 掌握好概念及相美的基础知识,是学好数学的重要基础.【变式训练1】回答以下效果:(1)模为0的向量是零向量?(2)方向相反的两个单位向量互为反向量?(3)终点相反且模相等的向虽终点在同一圆周上?(4)a-a=O?答案⑴正确;⑵正确;⑶不正确;(应该是在同一球而上)⑷不正确.(应该为a-【例2】如以下图,在长、宽、高区分为AB二3, AD二2, AA产1长方体ABCD — AbCD的八个顶点的两点为始点和终点的向量中,(1)写出一切的单位向量:(2)写出与丽相等的一切向量:(3)写出与而相反的一切向虽:;A B(4)写出模为、S的一切向疑.解析运用单位向量、相等的向量、相反向量、向量的模的概念及长方体的性质解•即在空间我们将向量对应线段的长度称为该向量的模;将模为1的向量称为单位向量;将模相等且方向相反的向量称为相等的向量;将模相等而方向相反的向量称为相反向量.在长方体ABCD-A:B:C:Di 中,由于长、宽、高区分为AB 二3, AD 二2, AA F I, AB1=VP+? = ^.答案⑴单位向量共有:两,乔,丽,丽,cq,电,场,书这八个:⑵与AB相等的向量共有,DC ,万石,兀瓦式这三个:⑶与而相反的一切向量共有:丽,CB,雨,丽这四个;⑷模为、S 的向疑共有:丽,8不A Bj, AC 9 CA.BD.DB, CD,, D,C, nq, qn, ^c,, qX,孫,万同这十六个.错因剖析对向量的相关概念了解不透,思索效果不细心、不片面,招致答案中出现漏解状况如⑴中易漏掉乔,丽,qc,万0这四个解:(3)中漏掉丽这个解等.【变式训练2] 如右图,在棱长为1的正三棱柱ABC-AbC:六个顶点的两点为始点和终点的向量中,(1)单位向量共有多少个?(2)写出与眉相等的一切向量;⑶写出与AC相反的一切向量:(4)写出模为、氏的一切向量.答案⑴18个;⑵兀瓦:(3)乙5,丽;⑷由于皆J A^+B氏=JL所以满足要求的向量共有:両,乔,丽,两,AQ , C/, AC, CA l, BC|, C,B, B、C, CB,这十二个题型2 空间向量的线性运算【例3】如右图,在长方体ABCD-AbCD中,以下各式中运算结果为而的是()(1)(应-鬲)-廳:(2)(BC+BX)-D^ :(3)(A5-AB)-5^;⑷(孫-币)+网.A. (1) (2)B. (2) (3)C. (3) (4)D. (1) (4)解析在停止减法运算时,可将减去一个向量转化为加上这个向量的相反向量,而在停止加法运算时,首先思索这两个向量在哪个平而内,然后与平面向量求和一样,运用向量运算圧律、平行四边形法那么、三角形法那么及多边形法那么来求解.答案⑴(应一乔)-A斤二应+两+应二施+丽 + 应二两:(2)(而-而)-丙二而+ 书二而+ 西-2西二3£>;-2西 H丽;因此(1) (2)两式的运算结果为向量西,而(3) (4)运算的结果不为BD^故应选择A.规律总结在对向量停止加、减法运算时,一泄要运用其运算法那么及运算左律来简化, 特别要留意的是将某些向量停止平移,将其转化到同一平而中去求解,另外,此题是一个选择题,因此,在汁算岀(1) (2)两式结果后,就已失掉选项,故(3) (4)两式不用计算,这样可提高解题速度,表达 ''小题"小解或巧解的特点【变式训练3] 在平行六而体ABCD-AbCD中,化简BB^ AB-DA等于 ( )A.AC; B・ GA, C. BD、 D. DB、答案丽+而-丽二西+帀+而二疋+疋二疋,应选择A.【例4】如右图,平行六而体ABCD-A' B‘ C' D r,点M是棱AA'的中点,点G在对角线A' C上且CG:GA‘ =2:1,设而二心而二b,左二c, 试用向M a, b, c 表示CA9CA f f CM, CG解析要想用a, b, c表示出所给向呈,只需结合图形,充沛运用空间向量加、减法的运算律及平行四边形法那么或多边形法那么即可.(1)由平行四边形法那么,得CA=CB + CD=a+b,(2)由平行四边形或三角形法那么,得CA^CA+CC^(a+b) +c二a+b+c:・• - —• ・• ・・’• ・• 1 ・•(3)同上,得CM =CA +A/W =CB + CD+- CC =a+b+ 一c:2 2⑷由⑵,得碌捋弓(*)•答案(1)鬲二a+b:(2)CA f =a+b+c:(3)CM =a+b+ 丄c;2z― 2 “(4)CG -— (a+b+c).3规律总结在用向量表示未知向量的时分,要留意寻求两者之间的关系,通常可将未知向量停1上一系列的转化,将英转化到与向量在同一四边形(更多的是平行四边形)或三角形中, 从而可以树立与未知之间的关系式。
高中数学选修2-1第3章3-1空间向量及其运算课件

上一节课,我们把平面向量的有关概念及加减运算扩展
到了空间.
加法 减法 运算
运 算 律
平面向量 加法:三角形法则或 平行四边形法则 减法:三角形法则 加法交换律
ab ba 加法结合律:
(a b) c a (b c)
空间向量
加法:三角形法则或 平行四边形法则 减法:三角形法则
加法交换律 a b b a 加法结合律
OG kOC,OH kOD. 由于四形ABCD是平行四形,所以 AC AB AD . 因此
EG OG OE kOC kOA=k AC
k( AB AD) k(OB OA OD OA)
OF OE OH OE EF EH 由向量共面的充要件知E ,F,G ,H 四共面.
(3)在正方体 ABCD - A中1B,1C1必D1有
. AC = A1C1
(4)若空间向量 m,n满,p足
,m = n,n = p
则 m . p
(5)空间中任意两个单位向量必相等.
其中不正确命题的个数是( C)
A.1 B.2 C.3 D.4
数学 选修2-1
2.给出以下几种说法:
①若| a |=| b |,则a , b 的长度相同,方
a+b=b+a (2)加法结合律
(a + b) + c = a + (b + c)
数学 选修2-1
证明加法交换律:
C
a
B
o
a
A
因为 OA = CB = a, AB = OC = b,
所以 a + b = b + a.
数学 选修2-1
证明加法结合律: O
a
A
C
高中数学人教B版选修2-1第三章《3.1.2 空间向量的基本定理》优质课公开课教案教师资格证面试试讲教案

高中数学人教B版选修2-1第三章《3.1.2 空间向量的基本定理》优质课公开课教案教师资格证面试试讲教案
1教学目标
1.知识与技能
通过本节学习理解向量共线的条件,共面向量定理和空间向量基本定理.
能够判定空间向量是否共面.
了解基向量、基底的概念、空间任意三个不共面的向量都可构成空间的一个基底.
2.过程与方法
通过对空间向量基本定理的学习,让学生体验数学定理的产生、形成过程,体验定理所蕴含的数学思想.
3.情感态度与价值观
事物之间可以相互转化,渗透由特殊到一般的思想,通过对空间向量基本定理的运用,增强学生的应用意识.
2学情分析
立体几何的学习主要在于培养空间抽象能力的基础上,发展学生的逻辑思维能力和空间想象能力。
立体几何是中学数学的一个难点,学生普遍反映“几何比代数难学”。
但很多学好这部分的同学,又觉得这部分很简单。
立体几何中抓住向量这个重要工具
如点到直线的距离,抓住直线的方向向量;找二面角的平面角而不是二面角,二面角的平面角等于二面角的大小.具体你可以,比如先求平面的法向量,那么两个平面的法向量的夹角的大小就是二面角的大小。
求角先定平面角、三角形去解决,正余弦定理、三角定义常用,若是余弦值为负值,异面、线面取锐角。
对距离可归纳为:距离多是垂线段,放到三角形中去计算,经常用正余弦定理、勾股定理,若是垂线难做出,用等积等高来转换。
不断总结,才能不断高。
3重点难点
重点:共线向量定理、共面向量定理和空间向量分解定理.
难点:空间向量分解定理.。
数学:第三章《空间向量与立体几何》教案(人教版选修2-1)
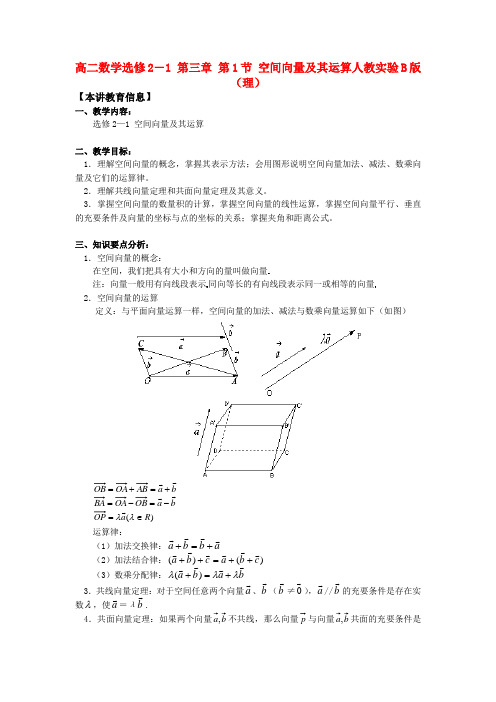
高二数学选修2-1 第三章 第1节 空间向量及其运算人教实验B 版(理)【本讲教育信息】一、教学内容:选修2—1 空间向量及其运算二、教学目标:1.理解空间向量的概念,掌握其表示方法;会用图形说明空间向量加法、减法、数乘向量及它们的运算律。
2.理解共线向量定理和共面向量定理及其意义。
3.掌握空间向量的数量积的计算,掌握空间向量的线性运算,掌握空间向量平行、垂直的充要条件及向量的坐标与点的坐标的关系;掌握夹角和距离公式。
三、知识要点分析: 1.空间向量的概念:在空间,我们把具有大小和方向的量叫做向量注:向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量2.空间向量的运算定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下(如图)b a AB OA OB+=+=b a-=-=)(R a OP ∈=λλ运算律:(1)加法交换律:a b b a+=+(2)加法结合律:)()(c b a c b a++=++(3)数乘分配律:b a b aλλλ+=+)(3.共线向量定理:对于空间任意两个向量a 、b (b ≠0 ),a //b的充要条件是存在实数λ,使a=λb .4.共面向量定理:如果两个向量b a ,不共线,那么向量p 与向量b a ,共面的充要条件是存在有序实数组),(y x ,使得b y a x p +=。
5.空间向量基本定理:如果三个向量c ,b ,a 不共面,那么对空间任一向量p ,存在唯一的有序实数组(x ,y ,z ),使c z b y a x p ++= 6.夹角定义:b a ,是空间两个非零向量,过空间任意一点O ,作b OB a OA ==,,则AOB ∠叫做向量a 与向量b 的夹角,记作><b a , 规定:π>≤≤<b a ,0特别地,如果0,>=<b a ,那么a 与b 同向;如果π>=<b a ,,那么a 与b 反向;如果90b ,a >=<,那么a 与b 垂直,记作b a ⊥。
高中数学新人教B版选修2-1课件:第三章空间向量与立体几何3.1.2空间向量的基本定理

(5)对空间任一点 O,若 = + + , 则P,A,B,C 四点
共面的充要条件是 x+y+z=1.
典例透析
题型一
题型二
题型三
空间向量的共线共面概念
【例1】 下列命题正确的是(
)
A.若a与b共线,b与c共线,则a与c共线
B.向量a,b,c共面即它们所在的直线共面
这三个向量就不是共面向量.
知识梳理
(3)共面向量定理.
如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:
存在唯一的一对实数x,y,使c=xa+yb.
(4)三个向量共面,又称这三个向量线性相关.
名师点拨1.a∥α是指a的基线在平面α内或平行于平面α.
2.共面向量是指这些向量的基线平行于同一平面或在同一平面
的有序实数组x,y,z,使p=xa+yb+zc.这时不共面的三个向量a,b,c叫
做空间的一个基底,记作{a,b,c}.
【做一做3】已知空间的一个基底{a,b,c},m=a+b,n=a-b,则a,b,c
中能与m,n构成空间的一个基底的是
.
答案:c
名师点拨1.用空间三个不共面的已知向量组{a,b,c}可以线性表
1
2 1
1
1
1
1
= + - + + (-) = + + .
2
3 2
2
6
3
3
典例透析
题型一
题型二
题型三
反思要求某向量m在给定基底{a,b,c}下的分解式,就是要找到一组
有序实数x,y,z,使m=xa+yb+zc.一般是寻找一个包含目标向量的封
高中数学 第三章 空间向量与立体几何 3.1.2 空间向量的基本定理讲义 新人教B版选修2-1

【解析】 M→N=M→A+A→A1+A→1N =-13A→C+A→A1+23A→1D =-13(A→B+A→D)+A→A1+23(A→D-A→A1) =-13(a+b)+c+23(b-c) =-13a+13b+13c. 【答案】 -13a+13b+13c
4.从空间一点P引出三条射线PA,PB,PC,在PA,PB,PC上分别取P→Q=
∴1c,c+a不共面. ∴{a+b,b+c,c+a}可以作为空间的一个基底.
判断给出的某一向量组能否作为基底,关键是要判断它们是否共面,如果从 正面难以入手,可用反证法或利用一些常见的几何图形进行判断.
[再练一题] 2.已知{e1,e2,e3}是空间的一个基底,且 O→A =e1+2e2-e3, O→B = -3e1+ e2+2e3,O→C=e1+e2-e3,试判断{O→A,O→B,O→C}能否作为空间的一个基底? 【解】 假设O→A,O→B,O→C共面,由向量共面的充要条件知存在实数x,y使 O→A=xO→B+yO→C成立. ∴e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3) =(-3x+y)e1+(x+y)e2+(2x-y)e3. ∵{e1,e2,e3}是空间的一个基底,
1.空间的任意三个向量a,b,3a-2b,它们一定是( )
A.共线向量
B.共面向量
C.不共面向量
D.既不共线也不共面向量
【答案】 B
2.对于空间任意一点O和不共线的三点A,B,C,有6 O→P = O→A +2 O→B + 3O→C,则( )
A.四点O,A,B,C必共面 B.四点P,A,B,C必共面 C.四点O,P,B,C必共面 D.五点O,P,A,B,C必共面 【答案】 B
基底的判断
若{a,b,c}是空间的一个基底,试判断{a+b,b+c,c+a}能否作 为该空间的一个基底.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例(二)——精析精练课堂合作研究重点难点突破知识点一 共线向量定理(1)定理内容:对空间两个向量()0,≠b b a ,b a //的充要条件是存在唯一的实数x , 使xb a =。
此定理可以分解为以下两个命题;①若()0//≠b b a ,则存在唯一实数x ,使xb a =。
②存在实数x ,使()0≠=b xb a ,则b a //。
(2)在定理中为什么要规定0≠b 呢?当0=b 时,若0=a ,则b a //,也存在实数x 使xb a =;但若0≠a ,我们知道零向量和任一非零向量共线,但不存在实数x ,使xb a =,因此在定理中规定了0≠b 。
若将定理写成xa b b a =⇔//,则应规定0≠a 。
说明:①在xb a =功中,对于确定的x 和b ,xb a =功表示空间与b 平行或共线且长度为xb 的所有向量;②利用共线向量定理可以证明两线平行,或三点共线。
知识点二 共面向量定理(1)共面向量已知向量a ,作a =,如果的基线平行于平面a ,记作α//a (右图),通常我们把平行于同一平面的向量,叫做共面向量。
说明:①α//a 是指a 的基线在平面α内或平行平面α。
②共面向量是指这些向量的基线平行或在同一平面内,共面向量的基线可能相交、平行或异面。
我们已知,对空间任意两个向量,它们总是共面的,但空间任意三个向量就不一定共面了。
例如,在下图中的长方体,向量AB 、、AD ,无论怎样平移都不能使它们在同一平面内。
(2)共面向量定理共面向量定理:如果两个向量a 、b 不共线,则向量c 与向量a 、b 共面的充要条件是,存在唯一的一对实数y x ,,使yb xac +=。
说明:①在证明充要条件问题时,要证明两个方面即充分性和必要性。
②共面向量的充要条件给出了平面的向量表示,说明任意一个平面可以由两个不共线的平面向量表示出来,它既是判断三个向量是否共面的依据,又是已知共面条件的另一种形式,可以借此已知共面条件化为向量式,以便我们的向量运算。
③利用共面向量定理可证明点线共面、线面平行等。
三个向量共面,又称做三个向量线性相关。
反之,如果三个向量不共面,则称做三个向量线性无关。
知识点三 空间向量分解定理(1)空间向量分解定理:如果三个向量a 、b 、c 不共面,那么对空间任一向量p ,存在一个唯一的有序实数组x ,y ,z ,使xc yb xa p ++=。
(2)如果三个向量a 、b 、c 是三个不共面的向量,则a 、b 、c 的线性组合zc yb xa ++能生成所有的空间向量,这时a 、b 、c 叫做空间的一个基底,记作{}c b a ,,,其中a 、b 、c 都叫做基向量。
(3)空间向量基本定理说明:①用空间三个不共面的已知和向量组{}c b a ,,可以线性表示出空间任意一个向量,而且表示的结果是唯一的。
②空间任意三个不共面的向量都可以作为空间向量的一个基底。
③由于0可看做是与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含它们都不是0。
要明确:一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念。
典型例题分析题型1 概念问题【例1】 设b a x +=,c b y +=,a c z +=,且{}c b a ,,是空间的个基底,给出下列向量组:①{}x b a ,,,②{}y b a ,,,③,{}z y x ,,,④{}y x a ,,,⑤{}c b z y x ++,,。
其中可以作为空间基底的向量组有 ( )A.1个B.2个C.3个D.4个解析 正确理解向量的基底与基向量。
答案 如图所示,设c b a ===,,1,则z y x ===,,1,1AC c b a =++,由A 、1B 、C 、D 1D 四点不共面,可知x 、y 、z 也不共面,同理可知a 、b 、c和x 、y 、z 、c b a ++也不共面。
∴选D.方法指导 能否作为空间的基底,即是判断给出的向量组中的三个向量是否共面。
充分利用一些常见的几何体,如:正方体、长方体、平行六面体、四面体等可以帮助我们进行直观判断,即模型法的应用。
【变式训练1】 设a 、b 、c 是三个不共面向量,现从①b a +,②b a -,③c a +,④c b +,⑤c b a -+中选出一个使其与a 、b 构成空间向量的一个基底,则可以选择的向量为 。
【答案】 ③④⑤。
题型2 共线向量定理的应用【例2】 已知空间三个不共面的向量p n m ,,,若p n m a 423--=,()p yn m x b 21+++=,且b a //,求实数y x ,的值。
解析 解决向量共线问题的依据是应用共线向量的充要条件,即()R a b ∈=λλ,且λ是唯一确定的实数及0≠a 。
答案 因为b a //,所以()R a b ∈=λλ,即()p n m p yn m x λλλ42321--=+++。
由于向量p n m ,,不共面,所以⎪⎩⎪⎨⎧+==-=-,13,2,24x y λλλ 解之,得⎪⎩⎪⎨⎧=-=,1,25y x 故实数y x ,的值分别为1,25-。
规律总结 待定系数法也可以用来解决空间向量中的有关问题。
在解决本题的过程中有两个关键:一是运用共线向量的充要条件得到相应的关系式;二是根据空间向量定理的推论得到关于y x ,,λ的方程组。
【变式训练2】 已知空间三个非零向量a 、b 、c 满足c b a c b a 5,3=-=+,判断向量a 与b 是否平行。
答案 因为⎩⎨⎧=-=+cb ac b a 53 ②① 所以2②①+得:c a 4=,2②①-得:c b -=,所以b a 4-=,故由共线向量充要条件得:b a //。
【变式训练3】 已知向量a 、b ,且b a b a b a 27,65,2-=+-=+=,则一定共线的三点是 ( )A.A 、B 、DB.A 、B 、CC.B 、C 、DD.A 、C 、D答案 AB b a b a b a BD CD BC 2422765=+=-++-==+。
所以AB BD //,所以A 、B 、D 三点共线。
∴选A.题型3 共面向量定理及应用【例3】 已知A ,B ,C 三点不共线,对平面ABC 外一点O ,确定下列各条件中的点P 是否与点A ,B ,C 一定共面,(1)525152++=;(2)OC OB OA OP --=22。
解析 由共面向量定理知,要证明P ,A ,B ,C 四点共面,只要证明存在有序实数对()y x ,使得y x +=。
答案 (1)共面。
OC OB OA OP 525152++= , ()()52515251525153+=-+-=++-=-∴,即5251+=. 主不共线,,,∴共面且具有公共点A ,从而P ,A ,B ,C 四点共面。
(2)不共面。
如果P 与A ,B ,C 共面,则存在唯一的实数对()y x ,,使得y x +=,对平面ABC 外一点O ,有()()y x -+-=-,即()y x y x ++--=1,与原式比较得⎪⎩⎪⎨⎧-=-==--,1,2,21y x y x ,此方程组无解,故A ,B ,C ,P 四点不共面。
规律总结 判断四点共面,除了本题中的解题方法外,还可以用其变形,即:空间一点P 位于平面ABC 内的充分必要条件是存在有序实数对()y x ,,使得对空间任一定点O ,有y x ++=;或若四点P ,A ,B ,C 共面,则对空间任一定点O ,有 ()1=++++=z y x z y x 。
【变式训练4】 若321,,e e e 是三个不共面的向量,试问向量32123e e e a ++=,3213e e e b ++-=,32142e e e c --=是否共面,并说明理由。
答案 令()()()042323321321321=--+++-+++e e e z e e e y e e e x ,亦即,()()()043223321=--+-+++-e z y x e z y x e z y x ,因为321,,e e e 是三个不共面的向量,所以⎪⎩⎪⎨⎧=-+=-+=+-,043,02,023z y x z y x z y x ,解得⎪⎩⎪⎨⎧==-=,5,7,1z y x从而c b a c b a ,,,57+=三个向量共面。
【例4】 求证:三向量21212132,23,e e c e e b e e a +=-=+=共面;若nc mb a +=,试求实数n m ,的值。
解析 要证明三个向量21212132,23,e e c e e b e e a +=-=+=共面,可以利用向量共面定理的推论,证明存在三个不全为零的实数γμλ,,,使得0=++c b a γμλ即可。
答案()()()()()2212121321233223e e e e e e e e c b a γμλγμλγμλγμλ+-+++=++-++=++如果γμλ,,,适合方程组⎩⎨⎧=+-=++,032,023γμλγμλ那么就能使0=++c b a γμλ,而显然上述方程组有无数组解⎪⎩⎪⎨⎧==-=,5,,13t t t γμλ,其中R t ∈。
于是有0513=++-tc tb ta ,所以,c b a ,,三向量共面,并且可得c b a 135131+=。
故所求的实数135,131==m 。
规律总结 事实上,对于任意两非零向量21,e e ,则2111e e a μλ+=,2212e e b μλ+=,()R e e c ∈+=3213212313,,,,,μμμλλλμλ总是共面的。
从本题的解法中不难发现,其解题方法是一箭双雕,即在证明c b a ,,三向量共面同时,只要对结论稍作变形就得到了m 与n 的值。
另外,面对解题过程中关于γμλ,,的方程组有数组解的情况,若不能利用其中的一组解,或者是获得λμ与λγ的值,就不能就得所求的m 与n 的值。
【变式训练5】 已知c b a ,,是三个不共面向量,若c b a ,,的起点相同,则当实数t 为何值时,tc b a ,,及()c b a ++41的终点共面? 答案 由于tc b a ,,及()c b a ++41的终点共面,所以等价于a tc a b --,及()a c b a -++41共面,于是,设 ()()()041=⎥⎦⎤⎢⎣⎡-+++-+-a c b a a tc a b γβα, 所以04443=⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛---c y b a γβγαγβα.故有方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=---,04,04,043γβγαγβαy 有解, (1)+(2)得:γβ21=,由(3)得:γβt 41-=,所以2141=t ,即21=t . 题型4 空间向量分解定理及应用【例5】 如右图所示,平行六面体C B A O OABD ''''-,且a =,c OO b OC ==,,用c b a ,,表示如下向量:(1)OB 、B O '、AC ;(2)GH (G 、H 分别是侧面C C B B ''和C B A O ''''的中心)。
