3-5-9保守力与非保守力
合集下载
大学物理 第三章 动量守恒定律和能量守恒定律 3-5 保守力与非保守力
①引力势能 引力势能
m' m m' m 引力的功 引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能： 点势能： 且令E 设B点为无限远 即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关，只决定于初末位置。 功与路径无关，只决定于初末位置。 第三章 动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力 势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章 动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下 从该点到势能零点保守力所作的功
第三章 动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力 势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功 引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能 引力势能
m' m Ep = −G r
弹性势能 弹性势能
弹力的功 弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2
m' m m' m 引力的功 引力的功 WAB = −(−G r ) − (−G r ) B A
A点势能： 点势能： 且令E 设B点为无限远 即rB=∞ 且令 PB=0 点为无限远
m' m WAB = −G rA
= − ( E pB − E pA ) = E pA
功与路径无关，只决定于初末位置。 功与路径无关，只决定于初末位置。 第三章 动量守恒和能量守恒
4
} ⇒ dW
物理学
第五版
3-5 保守力与非保守力 势能 -
F
dW
O
x1
x2
dx
x2 x
W = ∫ Fdx = ∫
x1
x2
x1
1 2 1 2 − kxdx = −( kx2 − kx1 ) 2 2
5
第三章 动量守恒和能量守恒
W p → p0 = −( Ep0 − Ep ) = −∆Ep
E p ( x, y, z) =
∫
E p0 = 0
( x, y,z )
F ⋅ dr
任意一点的势能等于在保守力作用下 从该点到势能零点保守力所作的功
第三章 动量守恒和能量守恒 10
物理学
第五版
3-5 保守力与非保守力 势能 -
W AB = − ( E pB − E pA ) = − ∆ E P
引力的功 引力的功
m' m m' m WAB = −(−G ) − (−G ) rB rA
引力势能 引力势能
m' m Ep = −G r
弹性势能 弹性势能
弹力的功 弹力的功
W AB 1 1 2 2 = − ( kx B − kx A ) 2 2
大学物理-保守力与非保守力
第三章 动量守恒和能量守恒
4/12
物理学
第五版
3-5 保守力与非保守力 势能 2 保守力作功的数学表达式
∫
(The mathematical expression of work by the conservative force)
ACB
F ⋅ dr = ∫
F ⋅ dr =
ADB
F ⋅ dr
∫
BDA
m 从 A 到 B 的过程中 作功： 的过程中F作功 作功：
A mθ m'm W = ∫ F ⋅ dr = ∫ − G 2 er ⋅ dr dr r A r rA e r dr er ⋅ dr = er ⋅ dr cos θ = dr r + dr
B
rB m'm B W = ∫ − G 2 dr rA r 1 1 m'm W = Gm′m( − ) W = −G dr = 0 2 rB rA l r
Elastic potential energy
m' m Ep = −G r
1 E p = kx 2 2
6/12
第三章 动量守恒和能量守恒
物理学
第五版
3-5 保守力与非保守力 势能 物体在地球表面附近距地面高为y时 具有的引力 物体在地球表面附近距地面高为 时,具有的引力 势能称为重力势能 重力势能(Gravity potenial) Ep = −mgy 重力势能 保守力的功(Work of conservative force) 保守力的功
第三章 动量守恒和能量守恒
z = 0, Ep = 0
11/12
物理学
第五版
本章目录
选择进入下一节： 选择进入下一节：
4/12
物理学
第五版
3-5 保守力与非保守力 势能 2 保守力作功的数学表达式
∫
(The mathematical expression of work by the conservative force)
ACB
F ⋅ dr = ∫
F ⋅ dr =
ADB
F ⋅ dr
∫
BDA
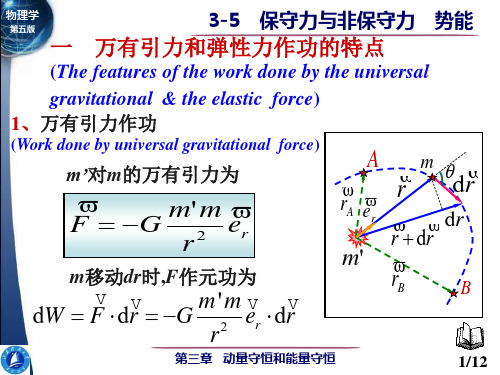
m 从 A 到 B 的过程中 作功： 的过程中F作功 作功：
A mθ m'm W = ∫ F ⋅ dr = ∫ − G 2 er ⋅ dr dr r A r rA e r dr er ⋅ dr = er ⋅ dr cos θ = dr r + dr
B
rB m'm B W = ∫ − G 2 dr rA r 1 1 m'm W = Gm′m( − ) W = −G dr = 0 2 rB rA l r
Elastic potential energy
m' m Ep = −G r
1 E p = kx 2 2
6/12
第三章 动量守恒和能量守恒
物理学
第五版
3-5 保守力与非保守力 势能 物体在地球表面附近距地面高为y时 具有的引力 物体在地球表面附近距地面高为 时,具有的引力 势能称为重力势能 重力势能(Gravity potenial) Ep = −mgy 重力势能 保守力的功(Work of conservative force) 保守力的功
第三章 动量守恒和能量守恒
z = 0, Ep = 0
11/12
物理学
第五版
本章目录
选择进入下一节： 选择进入下一节：
3-4-6 动能定理,保守力与非保守力,功能原理 机械能守恒定律
o
W Fcos d s
os 1
ds
s2
s
3
(3) 功是一个过程量，与路径有关。
(4) 合力的功，等于各分力的功的代数和。
F F i F j F k x y z d r d x i d y j d z k B B W F d r （ F d x F d y F d z ） x y z
21
3-6 功能原理 机械能守恒定律
一 质点系的动能定理
对第 i个质点，有
W W E E k i k i 0
ex i in i
m1
ex F i
外力功 内力功
m2
in m i F i
对质点系，有
i ex i i in i i k i k i 0 k k 0 i ex in
W W E E E E
8
1 2 1 2 W m v m v E E 2 1 k 2 k 1 2 2
合外力对质点所作的功，等于质点动能 的增量 ——质点的动能定理
注意
功是过程量，动能是状态量；
功和动能依赖于惯性系的选取， 但对不同惯性系动能定理形式相同。
9
例 2 一质量为1.0 kg 的小球系
在长为1.0 m 细绳下端，绳的上
势能具有相对性，势能大小与势能零点 的选取有关。 势能是属于系统的。 势能差与势能零点的选取无关。
20
3-5 保守力与非保守力
势能
四 势能曲线
E z p mg
1 2 Ep kx 2
m 'm E G p r
Ep
Ep
Ep
O
x
O
z
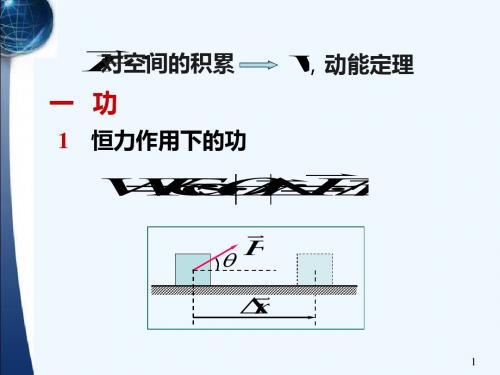
W Fcos d s
os 1
ds
s2
s
3
(3) 功是一个过程量，与路径有关。
(4) 合力的功，等于各分力的功的代数和。
F F i F j F k x y z d r d x i d y j d z k B B W F d r （ F d x F d y F d z ） x y z
21
3-6 功能原理 机械能守恒定律
一 质点系的动能定理
对第 i个质点，有
W W E E k i k i 0
ex i in i
m1
ex F i
外力功 内力功
m2
in m i F i
对质点系，有
i ex i i in i i k i k i 0 k k 0 i ex in
W W E E E E
8
1 2 1 2 W m v m v E E 2 1 k 2 k 1 2 2
合外力对质点所作的功，等于质点动能 的增量 ——质点的动能定理
注意
功是过程量，动能是状态量；
功和动能依赖于惯性系的选取， 但对不同惯性系动能定理形式相同。
9
例 2 一质量为1.0 kg 的小球系
在长为1.0 m 细绳下端，绳的上
势能具有相对性，势能大小与势能零点 的选取有关。 势能是属于系统的。 势能差与势能零点的选取无关。
20
3-5 保守力与非保守力
势能
四 势能曲线
E z p mg
1 2 Ep kx 2
m 'm E G p r
Ep
Ep
Ep
O
x
O
z
3-5 保守力和非保守力
F dr
ADB
F dr
F dr
ADB
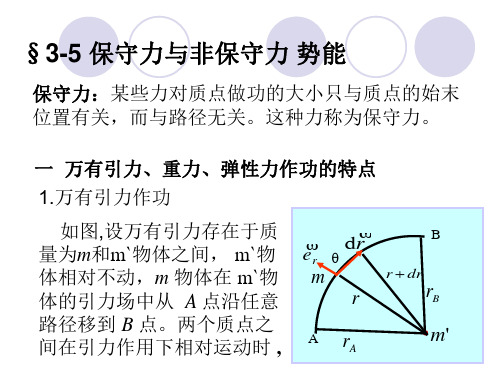
W F dr
L
ACB
F dr 0
物体沿闭合路径运动一周时，保守力做功为零
W F dr 0
L
三 势能 E p 1.定义：
设保守力 F 将质点 m 由a→b，保守力的功： b Wab F dr EPa EPb ～势能 E P a
④系统具有势能的条件是物体之间的相互作用力必 须是保守力，而对非保守力系统谈论势能，则没有 任何意义。 如：摩擦力为非保守力，不存在什么摩擦势能。
§3-6 功能原理
机械能守恒定律
动能定理适合于单个物体，也可将其推广到多个 物体组成的系统，成为系统的功能原理。 一、质点系的动能定理 设系统由n个物体（质点）组成，作用于各个质点 的力所作的功分别为：
Mm 1 EP＝ r －G r 2 dr GMm r
F m r
M
o
③弹性势能
Wab
xb
xa
1 2 1 2 kxdx ( kxb kxa ) EP 2 2
弹性势能以弹簧原长为零势能点。
1 1 2 E P kxdx (0 kx ) kx 2 x 2 2 势能曲线对照表(势能随位置变化的曲线～势能曲线)
重力势能曲线
弹性势能曲线
万有引力势能曲线
WCin ( EPi EPi0 )
i 1 i 1
n
n
质点系的动能定理：
W Wnc ( Eki EPi ) ( Eki0 EPi0 )
ex in i 1 i 1 i 1 i 1
保守力-势能
A保＋A非保
A 外 A 保 A 非 保 E K 2 E K 1
A 保 F 保 • d r E P 0 E P E p
A 外 A 非 ( E 保 K E P ) ( E K 0 E P 0 )
机械能E
A 外 A 非 保 E 2E 1
外力和系统非保守内力对系统做功之和等于系统机械 能的增量------功能原理定理
为研究系统，系统的机械能是否守恒?
解：（1）以小球为研究系统
外力：重力、弹性力；内力：无。
小 球 的 (动 机能 械） 能不
守 v0 h恒
2.以小球+地球+弹簧为研究系统 外力：无；内力：重力、弹性力；
是保守力 系统机械能守恒
例题1 质量为m的小球，如图所示，系在绳的一端，另
一端固定在O点，绳长为l 。若将小球以水平速度v 0 从 A点抛出，使小球在竖直平面内绕一周。求证：v 0 必须
A F d r 0
典型的保守力： 重力、万有引力、弹性力 与保守力相反的是非保守力
典型的非保守力： 摩擦力
1、重力的功
m在重力作用下由a运动到b，取地面为坐标原点.
A Ga bm g d r
b ( m ) k ( d g i x d j d yk )
zb (mg)dz a za
Z
mg azmg b z
•万有引力、重力、弹性力
i1
i1
i1
作功的特点
•质点系的功能原理
A 外 力 ＋ A 非 保 守 内 力 ＝ E－ E0
•机械能守恒定律
n
n
n
n
E ki Ep＝ i E k0i Ep0i
i0
i0
i0
i0
保守力和非保守力-PPT课件
A
rA
r
rB
m
m'
B
4
( 2)
弹性力作功
设原长为坐标原点, 物体在F’外,位移： x ' F外 F
o
x
P
xபைடு நூலகம்
F d x kx i dx i kx 弹力： F kx i dW
1 2 1 2 ( kx k1 x ) W k x d x 2 dW x 1 2 2
mgy
Gm E g 2 RE
E
m y
Ep 0
取： E 0 有： E mgy p ,R E p ,R y
RE
)
15
重力势能： E mgy ( 取地面为零势点 p
谢谢大家！
16
1
一
万有引力和弹性力作功的特点
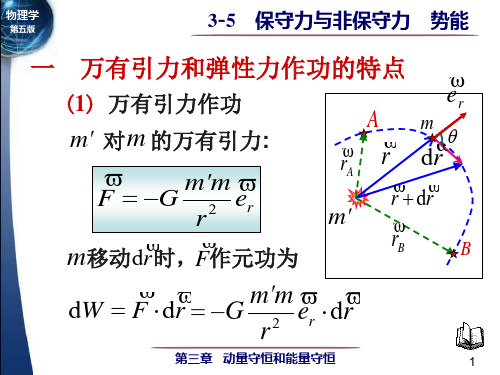
(1) 万有引力作功
m ' 对m 的万有引力为
m 'm F G 2 e r r
r时，F m 移动d 作元功为
A
r d r
r r
m
er
m'
B
m 'm G 2 e r d W F d r r d
r
2
m 'm d W F d r G 2 e r r d r
11
注意: 势能是状态的函数 E E ( x ,y ,z ) p p 是坐标的函数 势能具有相对性，与势能零点的选取有关.
通常取地面为重力势能的零点；取无穷远处为引力势 能的零点；取平衡位置处为弹性势能的零点。这样这 三种势能分别为：
重力势能： E p mgy
m m 引力势 E 能 G： p r 1 2 弹性势 E 能 ： kx p 2 注意：如果另选势能零点，则势能的值就不能 用上式来计算了。
保守力与非保守力_势能
积分可得
y 16t
y1 16m t1 1s
y2 32m t2 2s
2 1
A Fx dx Fy dy 320t 3dt 1200 J
二 万有引力、重力、弹性力作功的特点
m 的位置矢量为 r 以m ' 为参考系， m' 对 m 的万有引力为
m' m F G 2 er r
B mg
R
H
小车在最高点不脱离轨道的临界 条件是：N = 0 ，则
2 vB mg m v B gR R
根据机械能守恒定律：
1 1 5 v B gR 2 mgH mg 2 R mv B H 2R R R 2 2 2
* 四 宇宙速度
牛顿的《自然哲学的数学原理》插图，抛体的运轨 迹取决于抛体的初速度
vx
0
dv 3tdt
0
2 3
t
dv a dt
vx 1.5t
2
2
dx vxdt 1.5t dt
W Fdx 9t dt 36.0 (J)
0
例3
v v v 2 v 4t i 16 j
质量为10kg 的质点，在外力作用下做平面曲线运动，速度为 ,开始时质点位于坐标原点。
W kx dx 0
1 2 1 2 W ( kxB kxA ) 2 2
三
保守力和非保守力
保守力： 力所作的功与路径无关，仅决定于相 互作用质点的始末相对位置 . 引力功 重力功
m' m m' m W (G ) (G ) rB rA
弹力功
F dr
大学物理(一)教学大纲
《大学物理（一）》课程教学大纲一、课程名称1.中文名称大学物理（一）2.英文名称 University Physics (I)3.课程号 WL310011二、学时总学时54学时其中：授课54学时实验0学时三、考核方式考试四、适用专业应用型非物理各专业五、课程简介（200字以内）本课程系统地阐述了物理学中“力学”和“热学”的基本概念、基本理论和基本方法。
“力学”包括质点运动学、牛顿定律、动量守恒定律和能量守恒定律、刚体转动、振动、波动、相对论等；“热学”包括气体动理论和热力学基础等。
六、本门课程在教学计划中的地位、作用和任务物理学是探讨人类直接接触世界、时间、空间、以及时空中的物质结构和物质运动规律的科学,物理学着重研究世界中最普遍、最基本的运动形式及规律。
因此,它是自然科学和工程技术的基础,也是人类思想方法、世界观建立的基础。
在高等工科院校中,物理是一门重要的必修基础课,是一门建立正确的科学思想和科学方法论的基础课。
它的教学目的和任务是: 使学生对物理学的基本概念、基本原理和基本规律有较全面系统的认识，了解各种运动形式之间的联系,以及物理学的近现代发展和成就。
使学生在运算能力、抽象思维能力和对世界的认识能力等方面受到初步的训练；熟悉研究物理学的基本思想和基本方法；培养学生分析问题和解决问题的能力。
使学生在学习物理学知识的同时,逐步建立正确的思想方法和研究方法,充分发挥本课程在培养学生辩证唯物主义世界观方面的作用,进行科学素质教育。
大学物理课的教学宗旨不仅是为后续专业课打好基础，而且也是使学生建立正确的科学思想和方法论的一门基础课。
作为处在当今科学、社会高速发展阶段的大学生，应了解科学的进展，具备科学的思想和方法。
学生通过物理学的学习可以培养自己判断、推理、归纳的逻辑思维能力；细致、敏锐、准确的观察能力、想象创造力和运用其他学科知识处理、解决实际问题的能力等。
这些能力正是人们在自然界和社会中生存与发展必不可少的基本素质。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
物理学
第五版
3-5
保守力与非保守力
势能
一
万有引力重力和弹性力作功的特点
(1) 万有引力作功
m' 对m 的万有引力为
m' m F G 2 er r
m 移动dr 时，F作元功为
A
rA e
m'
r
r
rB
m
dr
dr r dr
B
m' m dW F dr G 2 er dr r
W
R
Rh
F dr
r
R
Mm o G dr 2 Rh r R dr 1 1 GMm GMm 2 Rh r R Rh GMm h R ( R h)
R
(2) 重力作功
重力mg 在曲线路径 M1M2 上的功为
z
M1
②
m ①
G O
M2
A
M2
M 1 1
Fz dz （ mg）dz
Z1 1
Z2
mg（z1 z2）
y
x
重力所作的功等于重力的大小乘以质点起始位置与末了 位置的高度差。 结论 (1)重力的功只与始、末位置有关，而与质点所行经的路 径无关。 (2)质点上升时，重力作负功；质点下降时，重力作正功。
物理学
第五版
物理学
第五版
3-5
保守力与非保守力
势能
( 4)
摩擦力作功
v
M2
摩擦力 F 在这个过程中所作的功为
A
M2
M1 L
F cos ds
M1
F
F mg
A mgs
结论
摩擦力方向始终与质点相对运动方向相反
摩擦力的功，不仅与始、末位置有关，而且与质点所行经 的路径有关 。
第三章 动量守恒和能量守恒 10
M
1. 重力势能 重力势能以地面为零势能点
E p (mg )dz mgz
z
0
O x
G
y
M 0 ( x0 , y0 , z0 )
2. 弹性势能 弹性势能以弹簧原长为零势能点 O F 0 1 2
E p (kx) dx kx x 2
x
3. 万有引力势能 引力势能以无穷远为零势能点。 等势面
例 一轻弹簧的劲度系数为k =100N/m，用手推一质量 m =0.1 kg 的物体把弹簧压缩到离平衡位置为x1=0.02m处, 如图所 示。放手后，物体沿水平面移动到x2=0.1m而停止。 求 物体与水平面间的滑动摩擦系数。
解 放手后，物体运动到 x 1 处和弹簧分离。在整个程中，
1 2 kx1 弹簧弹性力作功 2 摩擦力作功 mgx2
第三章 动量守恒和能量守恒 4
物理学
第五版
3-5
保守力与非保守力
势能
m从A到B的过程中 F作功：
B m'm W F dr G 2 er dr A m A r dr r rA e er dr er dr cos dr r
3-5
保守力与非保守力
势能
( 3)
弹性力作功
F
' F
P
o
弹性力 F kxi
x
x
dW kx dx
W Fdx
x1
x2
x2
x1
1 2 1 2 kxdx ( kx 2 kx1 ) 2 2
8
第三章 动量守恒和能量守恒
物理学
第五版
3-5
x2 x2
保守力与非保守力
m'm W G 2 dr rA r
rB
m'
dr r dr
rB
B
1 1 W Gmm( ) rB rA
第三章 动量守恒和能量守恒 5
例1、一陨石从距地面高为h处由静止开始落向地 面，忽略空气阻力，求陨石下落过程中，万有引 力的功是多少？ a 解：取地心为原点，引力与矢径方 h F b 向相反
l
C
D
B
质点沿任意闭合路径运动一周时，保守 力对它所作的功为零． 非保守力：力所作的功与路径有关． （例如摩擦力）
第三章 动量守恒和能量守恒 13
三
势能
质点在保守力场中某点的势能，在量值上等于质点 从M点移动至零势能点M0 的过程中保守力 F 所作的功。 M0 z E p F dr M ( x, y , z )
m 'm m 'm 引力的功 W (G ) (G ) rB rA 1 2 1 2 弹力的功 W ( kxB kx A ) 2 2
第三章 动量守恒和能量守恒 12
物理学
第五版
3-5
保守力与非保守力
势能
F d r F d r A ACB ADB l F dr ACB F dr BDA F dr W F dr 0
根据动能定理有
x1 x2
1 2 kx1 mgx2 0 0 2 kx12 100 0.022 0.20 2mgx2 2 0.1 9.8 0.1
物理学
第五版
3-5
保守力与非保守力
势能
二
保守力与非保守力 保守力作功的数学表达式
保守力所作的功与路径无关，仅决定 于始、末位置．
势能
W Fdx kxdx
x1 x1
F
dW
1 2 1 2 ( kx 2 kx1 ) 2 2
O
x1
dx
x2 x
结论 (1) 弹性力的功只与始、末位置有关，而与质点所行
经的路径无关。 (2) 弹簧的变形减小时，弹性力作正功；弹簧的变 形增大时，弹性力作负功。
第三章 动量守恒和能量守恒 9
复
•冲量 •动量定理 •质点系的动量定理 •动量守恒定律 •功与功率
习
t2 I ＝ Fdt
t1
I
I＝P－P0
i 1
F dt＝ P
n P＝ mi vi 恒 矢 量
dW F dS
B
dW P＝ dt
W
A
B F dr F cos ds
A
第五次课 保守力与非保守力
★
势能
★
机械能守恒定律
质点系的动能定理
质点系的功能原理
★
完全弹性碰撞 完全非弹性碰撞
基本要求
1.功的计算，熟练计算变力的功，理解 保守力做功的特征；
2.质点、质点系的动能；
3.熟练使用动能定理或功能原理解题， 注意内力的功可以改变质点系的总动能； 4.熟练使用机械能守恒定律解题，对综 合性问题要能划分阶段，分别选用恰当 的力学定理或守恒定律求解。