保守力势能
运动的守恒定律之保守力的势能和力

5.0295b (a / b)2/ 6.9
当x→∞时,有F→ 0。 8.9 9.9a 6b
令dF/dx = 0,可得
x10.9 2
x24 0
解得x2 = (8.9×9.9a/6b)1/6.9 = 1.47616(a/b)1/6.9。 这是引力。
作用力的 极值为
8.9a 2b
F (x2 )
[解析]在势能公式中,第一项是斥力势能,第二项是引力势能。
当势能为零时,V(x0) = 0,可得 解得x0 = (a/b)1/6.9。
a x8.9
0
b x02
0
当x→∞时, 也有V→ 0。
离子间的相互 F dV 8.9a 2b
作用力为
dx x9.9 x3
其中,第一项是斥 力,第二项是引力。
8.9a x9.91Biblioteka 2b x13
0
解得x1 = (8.9a/2b)1/6.9 = 1.2416(a/b)1/6.9。 x1处的势能为
V (x1)
a x8.9
1
b x12
( a / b 1) b
x6.9 1
x12
(2 8.9
1)( 2 )2/6.9 8.9
(a
/
b b)2/ 6.9
两离子之间的斥 力、引力和合力 随距离的变化规 律与斥力势能、 引力势能和总势 能随距离的变化 规律类似。
总势能存在极小值。
当x = x0时,两个离子 之间的总势能为零; 当x = 1.242x0时,两个离子之 间的总势能最小,为-0.503V0, 相互作用力为零;
当x = 1.476x0时,两个离子之间 的引力最大,为-0.4334F0。
势能函数与保守力的关系

势能函数与保守力的关系势能函数与保守力的关系势能函数和保守力是两个重要的物理概念,它们之间有着密切的关系。
势能函数描述了物体所处的位置的势能大小,而保守力则是指一类物理力,其做功与物体所经过的路径无关。
在本文中,我们将探讨势能函数与保守力之间的关系。
首先,我们需要了解什么是势能函数。
如果一个物体在场中的位置发生了变化,那么它的势能也会发生变化。
在一定条件下,物体的势能与位置之间存在一种确定的数学关系,这种关系就是势能函数。
在物理中,势能函数常常用U(x)来表示,其中X是物体的位置。
其次,我们需要明白什么是保守力。
保守力是指其做功与路径无关的力,也就是说,无论物体经历了怎样的路径,保守力所做的功都是相同的。
在物理中,保守力常常被描述为一类势力,它们的势能变化与位置之间存在确定的数学关系。
接着,我们来看一下势能函数与保守力之间的关系。
势能函数与保守力之间存在着一种紧密的联系,也就是说,如果一个力是保守力,那么它所描述的势能函数一定存在。
反之亦然,如果一个势能函数存在,那么它所描述的力一定是保守力。
这是因为在物理中,只有保守力才能描述为一类势力,保守力的存在必然导致势能函数的存在。
同样的,势能函数的存在也必然说明描述这种情形的力是保守力。
此外,我们还需要了解,保守力的势能函数在很多方面都是唯一的。
也就是说,对于一个特定的保守力,存在着唯一一个势能函数可以描述它,并且这个势能函数的形式是确定的。
这是由保守力的基本特性所决定的。
总结一下,势能函数与保守力之间存在着密切的关系。
保守力可以描述为一类势力,保守力的存在必然导致势能函数的存在。
同样的,势能函数的存在也必然说明所描述的力是保守力。
在大多数情况下,保守力的势能函数都是唯一的,这是由保守力的基本特性所决定的。
深入了解势能函数与保守力之间的关系有助于我们更好地理解物理学的基本概念,进一步提高我们的学术水平。
浅议物理学中的保守力和势能

浅议物理学中的保守力和势能【摘要】保守力和势能在物理学中扮演着重要的角色。
保守力是指不依赖路径的力,其所做的功与路径无关。
势能则是对保守力的一种描述,是可用于确定力学系统状态的函数。
保守力和势能之间存在着密切的关系,一般通过势能函数来确定。
根据保守力和势能的关系,我们可以推导出机械能守恒定律,即在只受保守力的情况下,力学系统的机械能保持不变。
保守力和非保守力的区别在于是否可以用势能来描述。
保守力和势能的重要性体现在它们对力学系统的描述和分析中起到了关键作用,而在物理学中也有着广泛的应用。
为了更深入地理解和探索保守力和势能,未来的研究方向可能会集中在更复杂系统下的运用和拓展。
【关键词】保守力、势能、物理学、性质、关系、确定、守恒定律、区别、重要性、应用、未来研究方向。
1. 引言1.1 保守力的基本概念保守力是物理学中一个非常重要的概念,它在描述物体运动和相互作用过程中起着至关重要的作用。
保守力是一种在物体运动中所做的功与路径无关的力,即对于沿着任意闭合路径作功的保守力,总是零。
这意味着保守力对物体的位移所做的功只依赖于起点和终点,而与具体路径无关。
保守力的基本概念包括以下几个要点:1. 保守力与势能的关系:保守力可以用势能来描述和计算。
势能是对物体在某个力场中位置所储存的能量,而保守力则是通过势能的梯度来定义和推导的。
具体来说,对于一个保守力F,其对应的势能函数为U,满足F = -∇U。
这里的负号表示力是势能的负梯度方向,即力的方向指向势能减小的方向。
2. 势能的引入:为了便于描述和计算保守力对物体的作用,我们引入了势能这一概念。
势能可以是位置的函数,也可以是速度和其他物理量的函数。
通过引入势能,我们可以将关于保守力的问题转化为寻找势能函数和利用势能函数进行计算的问题。
保守力的基本概念包括了与势能的关系和势能的引入。
这些概念在物理学中有着广泛的应用和重要性,对于解决各种运动和相互作用问题都起着至关重要的作用。
大学物理-保守力和势能

e rdr dr co srdr
Wa bG r2M d rm GM (r1 a m r1 b)
But if M~m, what is the work?
Example: 质量为M、m的两球原来相距为a,在万有引力作
用下逐渐靠近至相距为b,求在此过程中引力所作的功。
When only gravitation does work:
(1) Near the earth’s surface 质点高度变化不大:
12m2vmgz常数
(2) High above the earth’s surface 质点高度变化很大:
1 2m2vmg2/R r常数
When only elastic force does work: 弹性力场:
m
m
体作质功心G 占系主里m mm要,M M 内 地(力位1a的。b1)功与质量成r1反0比Mm 。m 对a,小r1' 质M 量m 物mb
引力的功只m与M物1体1系统的初始和最终相对位置 有W 关2,G 与路M m 径无M关(a。b)
W 1W 2Gm(a 1M b 1)W W1/W2m/M
Case study 2: Work done by elastic forces
Work done by a conservative force 保守力的功:
(1) Reversible, “work” can be stored in a “BANK”;
(2) Independent of the path of the body;
(3) Zero work for closed path.
ba acbW0 elastriccefo dko wo
保守力和势能
一对力所作的总功的只取决于两质点的相对运动;
一对力做功的代数和与参考系的选择无关;
5
什么条件下, 一对内力做功为零?
v
m
M
f
s s
C
f
v
N
C
N
Af Af 0
作用点无相对位移
AN AN 0
相互作用力与相对位移垂直
6
功的大小与参照系有关
功的单位为焦耳 功率(power) 功率:单位时间内力对物体所作的功 平均功率
yb ya
W mgdy mg( yb ya ) mg( ya yb )
重力是保守力。重力的功等于重力势能增量 的负值。重力势能以地面为零势能点。
y dy a p o
12
dr dx
W mg( yb ya ) =-EP 为势能增量
dr
b
EP mgdy mg(0 y) mgy
P
C
y
R
.
o
m
F
解:
F F0 xi F0 yj
r
x
0
dr dxi dyj
2R
r xi yj
2 A F d r F0 x d x F0 y d y 2F0 R
0 0
8
练习2 如图 M =2kg , k =200N m , s = 0.2m , g ≈ 10ms
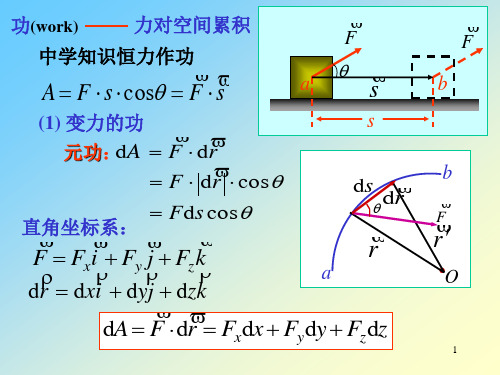
功(work)
力对空间累积
中学知识恒力作功
F
a
F
A F s cos F s
s
s
ds
dr
2.3保守力和势能

• 一般来说,功是一个过程量,不但与初始位置和终止位置 有关,还与物体的具体运动路径有关。
• 但是,自然界中还存在一类力,它所做功的大小只由物体 的始末位置决定,而与路径无关,这种力称为保守力。
2.3 保守力和势能
一 保守力与耗散力 万有引力: F
AACB
B
GMmr r3
Mo
ra
rb
F
ACB
F dr
GMm r dr 3 r ACB
r
dr
C
rb
ra
GMm dr 2 r
A
极坐标系
r rer r dr rdr
GMm GMm rb ra
dr drer e rd
B 质点沿ADB从A到B点,引力作功为:
rb
F dr
AADB
C为任意常数
B
GMm C 万有引力势能 E p r
• 势能的分类:势能按作用性质的不同,可分为引力势能、弹性势能 、重力势能和电势能等。 • 势能零点:在描述势能大小时选择的一个参考点
•
r 设空间 o
r 点为势能零点,则空间任意一点 的势能为: r0 E p E p r E p r0 Ar r0 F dr
2.3 保守力和势能
例 讨论重力做功特点。设质量为m的物体从a点沿任一曲 线acb移动到b点,计算在这一过程中重力做的功。若从a 点沿adb移动到b点呢? 解 在acb路径上的元位移 dr 中,重力做的元功为
dA mg dr
2.3 保守力和势能
mg mgk ,dr dxi dzk
∴两种情况下势能差是完全一样的。
保守力与非保守力及势能

§3.6 保守力与非保守力、势能
3. 三种势能函数:
(1) 重力势能:
y y
E p ( y ) F重 d r
(0)
( mg ) ˆ j dy ˆ j
y
( y) 0
o
Ep( y )
mg
E p ( y ) mgy
即:势能零点正上方重力 势能为正,下方为负。
E p ( y ) mgy
m?????epr?f引?drf引mrrorep?0??mm????g2er?drerrreprmmepr?gorrmmepr?gr即
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
§3.6 保守力与非保守力、势能
·1 ·
Chapter 3.力,其势能函数为何不同?它们
有何内在关系? 3. 若选地表为万有引力势能零点,则 引力势能表达式如何?
?
( The end ) ·7 ·
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
归纳:
1.重力势能: E p ( y ) mgy
1 2 2. 弹性势能: E p ( x ) kx 2
Ep( y )
1 E p ( x ) kx 2 2
o
x
·5 ·
Chapter 3. 守恒定律
§3.6 保守力与非保守力、势能
(3) 万有引力势能:
M
F引 m
E p ( r ) F引 d r
(r )
( )
o
r
Ep( ) 0
Mm ˆ r dr e ˆr ( G 2 )e r r
2. 势能函数选取应遵从的原则:
质点在保守力场中的势能

dEp dx
y,z
E p x
同一可得:
Fy
E p y
,
Fz
E p z
于是:
F
Fxi
Fy j
Fzk
i
E p z
j
E
p
z
k
E
p
z
i
z
j
z
k
z
E
p
r
Ek
1 mv2 2
k 2r
F
(2) Er
r
kr0 r2
dr
r
k r2
dr
k r
质点在保守力场中 的势能
一、质点在保守力场中的势能
A重 (mgy2 mgy1)
A弹
( 1 2
k x2 2
1 2
kx12 )
A引
[(G
Mm ) r2
(G
Mm r1
)]
保守力作功可以表示为由质点的位置决定的某种
潜在能量(势能)的减少。
b
a F dr Epa Epb
E p
四、势能曲线
Ep
o
r
Ep
o
y
重力势能曲线
Ep 引力势能曲线
o
x
弹性势能曲线
例1、一质量为m 的质点在指向圆心的平方反比 力 F=-k/r2 的作用下作半径为 r 的圆周运动,求 (1)此质点的动能。(2)如取距圆心无穷远 处为势能零点,求它的势能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m' m E p G r
Ep
Ep
Ep
O
x
O
z
O
x
弹性势能曲线 引力势能曲线
重力势能曲线
z 0, Ep 0 x 0, Ep 0
3-5 保守力与非保守力
r , Ep 0
上页
下页
首页
目录
物理学
第五版
Ep mgz
1 2 Ep kx 2
2.25
4y x 6
2
1
O
3 X
A2
x2 , y2
x1 , y1
( Fx dx Fy dy )
y2 y1
2 ydx 4dy
x1
x2
做 功 与 路 径 有 关
94 1 ( x 6)dx 4dy 21.25 J 2 2 1 3
3-5 保守力与非保守力
第五版
( 2)
弹性力作功
F
' F
P
o
弹性力 F kxi
WAB Fdx
xA xB xB xA
x
x
dW kx dx
1 2 1 2 kxdx ( kx B kx A ) 2 2
3-5 保守力与非保守力
上页
下页
首页
目录
物理学
第五版
二
保守力与非保守力 保守力作功的数学表达式
2
2. 质点的运动轨道为直线 4 y x 6
Y x2 4 y
2.25
4y x 6
2
1
O
3 X
上页 下页 首页 目录
3-5 保守力与非保守力
物理学
第五版
A F dr
A
B
Fx dx Fy dy Fz dz
b a
Y x2 4 y
2.25
1
2
保守力:某些力对质点做功的大小只与质 点的始末位置有关,而与路径无关。这种 力称为保守力。
m 'm m 'm ) (G ) 引力的功 Wab (G rb ra
弹力的功 Wab
1 2 1 2 ( kx b kx a ) 2 2
3-5 保守力与非保守力
上页
下页
m 'm m 'm Wab (G ) (G ) rb ra
若选势 能零点
重力势能 引力势能
弹性势能
3-5 保守力与非保守力
上页
下页 返回 首页 退出 目录
物理学
第五版
保守力的功 W (Ep2 Ep1 ) EP 注意: 保守力作正功,势能减少.
势能是状态的函数 Ep Ep ( x, y, z)
势能具有相对性,势能大小与势能零 点的选取有关,但势能差与势能零点 选取无关.
势能是属于系统的.
3-5 保守力与非保守力
上页
下页
首页
目录
物理学
第五版
已知势能函数,可以计算保守力 由 W ( E E ) E p2 p1 p (1) d W d Ep
对一维运动,当物体在保守力F的作用下 沿ox轴发生位移dx时,保守力所做的功为
dr r dr
B
m' m dW F dr G 2 er dr r
3-5 保守力与非保守力
上页 下页 首页 目录
物理学
第五版
m从A到B的过程中 F 作功: B m'm WAB F dr G 2 er dr A r
4y x 6
A1
x2 , y2
x1 , y1 x2
( Fx dx Fy dy )
y2 y1
O
3 X
2 ydx 4dy
x1
94 x2 dx 4dy 10.8 J 2 2 1 3
3-5 保守力与非保守力
上页
下页
首页
目录
物理学
第五版
Y x2 4 y
上页
下页
首页
目录
物理学
第五版
三
势能
与物体的位置相联系的系统能量称为势 能,常用Ep表示。 保守力的功是势能变化的量度:
物体在保守力场中a、b两点的势能Epa、 Epb 之差等于质点由a点移动到b点过程中保守 力做的功Wab:
3-5 保守力与非保守力
上页
下页 返回 首页 退出 目录
物理学
第五版
如:
物理学
第五版
3-5 保守力 势能
3-5 保守力与非保守力
上页
下页
结束放映 首页 目录
理学
第五版
一 万有引力和弹性力作功的特点
(1) 万有引力作功
m' 对m 的万有引力为
m' m F G 2 er r
m 移动dr 时,F作元功为
A
rA e
m'
r
r
rB
m
dr
3-5 保守力与非保守力
上页 下页 首页 目录
物理学
第五版
例1 :试证明重力是保守力
m在重力作用下由a运动到b,取地面为坐标原点.
Aab mg dr
a b
b
(mg )k (dxi dyj dzk ) a zb Z mgdz
za
dr
mgza mgzb
初态量 末态量 可见,重力是保守力。 X
a
O
b
mg
Y
3-5 保守力与非保守力
上页
下页
首页
目录
物理学
第五版
例2 作用在质点上的力为 F 2 yi 4 j ( N ) 在下列情况下求质点从 x1 2(m) 处运动到 x2 3(m )处该力作的功:
1. 质点的运动轨道为抛物线 x 4 y
d W F cos d x Fx d x (2) d Ep 由(1)(2)两式得: Fx dx 结论: 保守力沿某坐标轴的分量等于势能对 此坐标的导数的负值。
3-5 保守力与非保守力
上页 下页 返回 首页 退出 目录
物理学
第五版
四
势能曲线
Ep mgz
1 2 Ep kx 2
A
rA e
m'
r
er dr er dr cos dr
WAB m'm G 2 dr rA r
rB
r
rB
m
dr
dr r dr
B
WAB
1 1 Gmm( ) rB rA
3-5 保守力与非保守力
上页
下页
首页
目录
物理学
首页
目录
物理学
第五版
l
ACB
F dr
ACB
ADB
F dr
A
F dr
F dr
F dr
C
BDA
W F dr 0
l
D B
上式表明:质点沿任意闭合路径运动一周时, 保守力对它所作的功为零. 非保守力:力所作的功与路径有关。 (例如摩擦力)
