第二章_勾股定理与平方根复习课件
平方根ppt课件

平方根的历史背景
平方根的早期发展
在古代文明中,人们已经意识到某些数的平方的值。例如,古埃及人和古巴比 伦人已经知道π和√2的近似值。随着数学的发展,人们对平方根的认识逐渐深 入。
电容
在计算电容时,需要使用平方根来 计算电容器容纳电荷的能力。
在日常生活中的应用
建筑测量
在建筑测量中,需要使用平方根 来计算建筑物的面积和体积。
土地测量
在土地测量中,需要使用平方根 来计算土地的面积和周长。
商业交易
在商业交易中,需要使用平方根 来计算商品的价格和利润。
05
平方根的注意事项
Chapter
平方根函数的奇偶性
平方根函数的值域
函数$y = sqrt{x}$的值域为所有非负 实数。
函数$y = sqrt{x}$是非奇非偶函数, 因为对于所有的x值,都有$sqrt{-x} neq sqrt{x}$。
平方根的几何性质
平方根与数轴的关系
在数轴上,一个数的平方根表示该数距离原点的距离。例如,4位 于2的右边,因为2是4的平方根。
平方根的除法性质
如果a和b都是正数,那么 $frac{sqrt{a}}{sqrt{b}} = sqrt{frac{a}{b}}$。
平方根的加法性质
如果a和b都是正数,那么 $sqrt{a} + sqrt{b}$不一 定等于$sqrt{a + b}$。
平方根的函数性质
平方根函数的单调性
对于函数$y = sqrt{x}$,当x的值从 负无穷增加到正无穷时,y的值也从负 无穷增加到正无穷,因此该函数是单 调递增的。
勾股定理与平方根复习

第 1 页 共 3 页第二章勾股定理与平方根 ( 教案)班级 姓名 学号学习目标:1回顾勾股定理及其逆定理,利用勾股定理解决生活中的实际问题2平方根及立方根,能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数,会进行实数的有关计算 学习难点:勾股定理及其应用,平方根及立方根教学过程:一、知识要点1、勾股定理:在一个直角三角形中,两直角边的平方和等于斜边的平方。
2、勾股定理的应用:在一个直角三角形中,知道其中的任意两边都可以求第三边。
①c2=a2+b2;②a2=c2-b2;③b2=c2-a2。
3、直角三角形的识别(勾股定理的逆定理):如果三角形的三边长a 、b 、c 满足a2+b2 =c2,那么这个三角形是直角三角形。
(这是判定一个三角形是直角三角形的又一种方法)4、平方根的定义:一般地,如果一个数的平方等于a ,那么这个数叫做a 的平方根。
也称二次方根,也就是说,如果x2=a ,那么x 就叫做a 的平方根。
5、平方根的性质:①一个正数有两个平方根,它们互为相反数;②0的平方根是0,记作0 ;③负数没有平方根。
6、开平方的定义:求一个数a 的平方根的运算,叫做开平方。
7、算术平方根的定义:正数a 有2个平方根,其中正数a 的正的平方根,也叫做a 的算术平方根。
公式:( a )2=a (a ≥0),a2 =a (a ≥0) , a2 =-a(a ≤0)。
8、立方根的定义:一般地,如果一个数的立方等于a ,这个数就叫做a 的立方根,也称为三次方根;也就是说,如果x3=a ,那么x 叫做a 的立方根,数a 的立方根记作3a 读作“三次根号a ”。
9、开立方的定义:求一个数的立方根的运算,叫做开立方。
开立方和立方互为逆算。
10、立方根的性质:正数有一个正的立方根,负数有一个负的立方根,0的立方根0。
二、课堂小练习 1、16 的平方根________,64 的立方根_______。
勾股定理、方根专题知识点整理
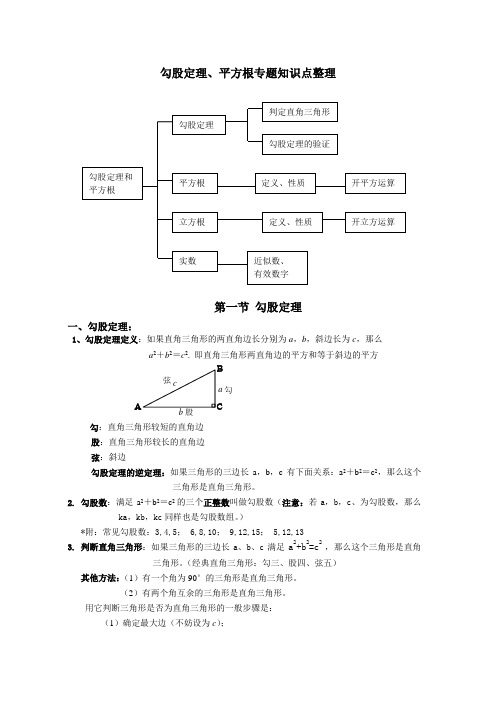
勾股定理、平方根专题知识点整理第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
勾股定理与平方根的数学知识点

勾股定理与平方根的数学知识点一、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
我国古代把直角三角形中,较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦。
结论为:勾三股四弦五a2+b2=c21、如果三角形的三边长a、b、c满足a+b=c,那么这个三角形是直角三角形。
2、满足a+b=c的3个正整数a、b、c称为勾股数。
(例如,3、4、5是一组勾股数)。
利用勾股数可以构造直角三角形。
二、平方根1、定义一般地,如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根。
也就是说,如果x2=a,那么x就叫做a的平方根。
2、一个正数有2个平方根,它们互为相反数;0只有一个平方根,它是0本身;负数没有平方根。
3、求一个数a的平方根的运算,叫做开平方。
4、正数a有两个平方根,其中正的平方根,也叫做a的算术平方根。
例如:4的平方根是2,其中2叫做4的算术平方根,记作=2;2的平方根是其中2的算术平方根。
0只有一个平方根,0的平方根也叫做0的算术平方根,即三、立方根1、定义一般地,如果一个数的立方等于a,那么这个数叫做a的立方根,也称为三次方根。
也就是说,如果x=a,那么x就叫做a的立方根,数a的立方根记作,读作三次根号a。
2、求一个数a的立方根的运算,叫做开立方。
3、正数的立方根是正数,负数的立方根是负数,0的立方根是0。
四、实数1、无限不循环小数称为无理数。
2、有理数和无理数统称为实数。
3、每一个实数都可以用数轴上的一个点来表示,反之,数轴上的每一个点都表示一个实数,实数与数轴上的点是一一对应的。
五、近似数与有效数字1、例如,本册数学课本约有100千字,这里100是一个近似似数。
2、对一个近似数,从左边第一个不是0的数字起,到末位数字止,所有的数字都称为这个近似数的有效数字。
初二数学勾股定理知识点勾股定理在任何一个直角三角形(Rt△)中(等腰直角三角形也算在内),两条直角边的长度的平方和等于斜边长度的平方,这就叫做勾股定理。
人教版八年级下册数学《勾股定理》说课教学复习课件(第2课时)

A.2和3之间
B.3和4之间
C.4和5之间
D.5和6之间
课堂练习
3.如图,网格中的小正方形边长均为1,△ABC的三个顶点均在格点上,
8 13
则AB边上的高为_______.
13
4.长为 26的线段是直角边长为正整数 5 , 1
边.
的直角三角形的斜
课堂练习
∵AB= A′B′ , BC= B′C′ ,
∴AC²= A′C′ ²,
∴AC= A′C′ .
在△ABC和△ A′B′C′中,
∵∠C=∠C′ , AC= A′C′ , BC= B′C′,
∴△ABC≌△ A′B′C′.
B′
探究
数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示
的点吗?
分析引导:(1)你能画出长为 2的线段吗?怎么画?说说你的画法.
比较,只要_______________,
01
情景引入
一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板
能否从门框内通过?为什么?
解:连接DB,
在Rt△ABC中,根据勾股定理,得
AC2=AB2+BC2=12+22=5.
AC= 5≈2.24>2.2.
所以木板能从门框内通过.
01
情景引入
杯高AB=12cm,杯底直径BC=5cm;
Rt△ABC中,AB=12cm,BC=5cm;
由勾股定理得:AC=
2 + 2 =13cm
故吸管的长度最少要:13+4.6=17.6cm.
02
练一练
2.如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.
2024年新人教版九年级数学上册全册精彩课件.

2024年新人教版九年级数学上册全册精彩课件.一、教学内容1. 第一章:二次函数1.1 二次函数的概念与性质1.2 二次函数的图像与方程1.3 二次函数的应用2. 第二章:勾股定理与平方根2.1 勾股定理2.2 平方根2.3 勾股定理与平方根的应用3. 第三章:概率初步3.1 随机事件与概率3.2 概率的计算3.3 概率的应用二、教学目标1. 掌握二次函数、勾股定理、平方根和概率的基本概念与性质。
2. 学会运用二次函数、勾股定理、平方根和概率解决实际问题。
3. 培养学生的逻辑思维能力和数学应用能力。
三、教学难点与重点1. 教学难点:二次函数的性质、勾股定理的证明、概率的计算。
2. 教学重点:二次函数的应用、平方根的计算、概率的实际应用。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:练习本、草稿纸、计算器。
五、教学过程1. 实践情景引入:通过生活中的实例,引出二次函数、勾股定理、平方根和概率的概念。
2. 例题讲解:详细讲解教材中的例题,引导学生理解和掌握知识点。
3. 随堂练习:针对每个知识点,设计相应的练习题,让学生及时巩固所学内容。
六、板书设计1. 用大号字体书写课题名称,如“二次函数的应用”。
2. 内容:列出本节课的主要知识点,用不同颜色粉笔标出重点和难点。
七、作业设计1. 作业题目:第一章:求给定二次函数的最大值、最小值,并画出图像。
第二章:证明给定三角形的勾股定理,并计算其面积。
第三章:计算给定概率问题,如掷骰子、抽签等。
答案:见附件。
八、课后反思及拓展延伸2. 拓展延伸:布置一些拓展性的练习题,如研究二次函数的性质、探索勾股定理的推广等,激发学生的兴趣和求知欲。
通过本课件的教学,希望学生能掌握九年级数学上册的核心知识点,提高数学素养和应用能力,为今后的学习打下坚实基础。
重点和难点解析1. 教学内容的详细性与针对性2. 教学目标的具体性与实用性3. 教学难点与重点的识别与处理4. 教学过程中的实践情景引入与随堂练习设计5. 板书设计的清晰性与结构性6. 作业设计的层次性与拓展性7. 课后反思与拓展延伸的实际操作一、教学内容的详细性与针对性教学内容的选择应紧密结合教材章节,确保覆盖所有核心知识点。
(完整版)勾股定理知识点+对应类型
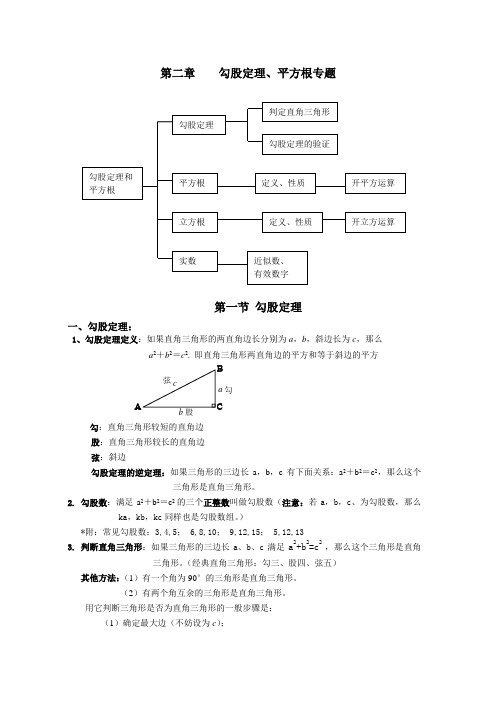
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
勾股定理复习课件

h
1.如图,已知长方体的长、宽、高分 别为4cm、3cm、12cm,求BD’的长。
解:连结BD,在直角三角形 ABD中,根据勾股定理 A’
BD AB AD 4 3 5
2 2 2 2 2 2
D’ B’
C’
BD 5
在直角三角形D’ BD 中,根 据勾股定理
BD'2 DD '2 BD 2 12 2 52 13 2 BD' 13(cm)。
4.若一个三角形某两边的平方和不等于第三边的平 方,则这个三角形一定不是直角三角形( ).
选择: 直角三角形的两条直角边长为a,b, 斜边上的高为h,则下列各式中总能成立 的是 ( D )
A. ab=h
2
B. a +b =2h
2
2
2
1 1 1 C. + = a b h
1 1 1 D. 2 + 2 = 2 a b h
4.互逆命题与互逆定理的概念
无理数在数轴上的表示
在数轴上表示 13 , 17 , 5,20
4.勾股定理及其逆定理的应用
①勾股定理可以解决直角三角形当中一些
与边有关的问题(直角边、斜边、斜边上
的高、面积等)
②勾股定理的逆定理可以判断一个三角形
是否是直角三角形(此时先找到最长边,再
看看两较短边的平方和是否等于长边的平
本章知识框图:
实际问题
(直角三角形边长计算)
互逆 定理
由形到数
勾股定理
实际问题 (判定直角三角形)
由数到形
勾股定理 的逆定理
题设
勾股定理 在Rt△ABC 中,∠C=900
勾股定理的逆定理 在△ABC 中, 三边 a,b,c满足a2+b2=c2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、典型错误
初 中 数 学
八 上
1.
4 的算术平方根是
2
。
2.一个直角三角形,一条边长为3,另一
条边长为4,则第三边的长为 5 或 3.在
,
7。
中无理数有
2 1 22 3 3 、 、 73、 1. 、-0. 16、 3、 、 0.8 2 4 27 7 2 3
2
4
0.8 。
万 4. 1.78 106 精确到______位. 5. 若 x 2 4 ,则 x =_______. 2
初 中 数 学
八 上
初中数学八年级
上册
第二章复习
一、本章知识结构
初 中 数 学
八 上
勾股定理
勾股定理 与平方根
勾股定理
平方根
逆定理
应用
平方根
立方根
实数
近似数与 有效数字
二、重要概念剖析
初 中 数 学
八 上
概 念 相同点
平方根
算术平方根 都是开方运算
立方根
不同点
负数不能 负数没有算术 任何数都能 开平方 平方根 开立方 正数的平方根 非负数的算 任何数的立 有两个它们 术平方根只 方根都只有 互为相反数 有一个 一个 平方根等于 算术平方根 立方根等于 本身的数只 等于本身的 本身的数有 有一个,为 数有两个, 三个, 0 0、1 0、1、-1
练习1:如图,点阵中以相邻4个点为顶 点的小正方形面积为1,计算
初 中 数 学
八 上
(1)△ABC的面积;
(2) △ABC的周长.
初 中 数 学
八 上
如图,折叠长方形的一边,使点D落在BC 边上的点F处,若AB=8,AD=10. (1)你能说出图中哪些线段的长? (2)能求出EC的长吗?
提示:
在Rt△EFC中,
∠C=90°
A
10
D 8-x
∵EC2+FC2=EF2
∴X2+42=(8-X)2
8
10 8-x 6
E x C
∴x=3 即 EC=3
B
F
4
初 中 数 学
八 上
◆如图,在⊿ABC中,AB=15,AC=17,AD是边 BC上的中线,AD=4.求⊿ABC的面积.
A
C
D E
B
◆如图,在的正方形网格中,每个小正方形的边 长都为1.请在所给网格中按下列要求画出图形.
初 中 数 学
八 上
如图,由5个小正方形组成的十字形 纸板,现在要把它剪开,使剪成的若 干块能够拼成一个大正方形. (1)如果剪4刀,应如何剪拼?
(2) 少剪几刀,也能拼成一个大正方形吗?
初 中 数 学
八 上
② ③
① ①
② ③
初 中 数 学
八 上
例3.如图,以△ABC的三边为直径向 外作半圆,且S1+S3=S2,试判断△ABC 的形状?
初 中 数 学
八 上
⑴从点A出发的一条线段AB,使它的另一 个端点落在格点(即小正方形的顶点)上, 且长度为 ;8
A
.
◆如图,在的正方形网格中,每个小正方形的边 长都为1.请在所给网格中按下列要求画出图形.
初 中 数 学
八 上
⑵以⑴中的AB为边的一个等腰△ABC,使点 C在格点上,且另两边的长都是无理数.
6. 比较大小: 3 3 < 2
四、例题讲解
D
八 上
提示:先证△ABC为直角三角形,利用△ABC 面积的两种算法来解决
1 1 S ABC AC BC AB CD 2 2
∟
初 中 数 学
例1、△ABC中,AB=5,BC=3,AC=4,求 AB边上的高CD。 C A B
初 中 数 学
A
. .B
■在数轴上找出表示
3的点.
初 中 数 学
八 上
2 -2 3 -1
· · · ·· ··
┒ 0 1 2 3
初 中 数 学
八 上
你还有什么疑问吗? 请提出来相方形。
A · ·C·C1 3
B·
·C2
·C4
·C5
初 中 数 学
八 上
变式:你能将五个连续的小正方形分 割后拼接成一个大正方形吗?
初 中 数 学
八 上
小贴士:
1.网格型问题一般先采用勾股定理 进行相关计算,再画出相应的图形
2.图形拼接问题的原则是拼接前后 的两个图形总面积不变。
S1
S3 S2
例4. 如图,有一圆柱形食品盒,它的高为
初 中 数 学
八 上
16cm,底面直径为
24
的一只蚂蚁想吃到盒内对面上底面B处的食物,
它至少需要爬行多少路程?
cm,在盒内下底面A处
B ·
D
16
12
B
· A
C
A
小贴士:
初 中 数 学
八 上
1.解决实际问题,应该读懂题意,画 出相关示意图,建立数学模型,将实 际问题转化为数学问题来解决。 2.几何的应用题,也要根据题意,写 清楚相关的理由和过程,原则是先几 何,后代数,先写出表达式,再带入 数字。
八 上
变式、△ABC中, BC=4,AC=3,AB=6, 求△ABC的面积。
C
B
D
∟
A
初 中 数 学
八 上
小贴士:
1.△ABC不是直角三角形时,需添加 辅助线(一般为作高)构造直角三角 形。
2.设未知数,利用勾股定理列方程来 解决问题,是本章的一个重要的解题 方法。
初 中 数 学
八 上
例2.如图,正方形网格中的每个小正方形边 长都是1,点A是其中的一个点。 (1)请在网格中最左边的边线上找一点B, 使线段 AB = 5 (2)在网格点上标出所有以AB为一边的等腰 三角形ABC的第三个顶点C。
