第二章 勾股定理与平方根 基础知识复习讲义(2)
第二章_勾股定理与平方根复习课件

三、典型错误
初 中 数 学
八 上
1.
4 的算术平方根是
2
。
2.一个直角三角形,一条边长为3,另一
条边长为4,则第三边的长为 5 或 3.在
,
7。
中无理数有
2 1 22 3 3 、 、 73、 1. 、-0. 16、 3、 、 0.8 2 4 27 7 2 3
2
4
0.8 。
万 4. 1.78 106 精确到______位. 5. 若 x 2 4 ,则 x =_______. 2
初 中 数 学
八 上
初中数学八年级
上册
第二章复习
一、本章知识结构
初 中 数 学
八 上
勾股定理
勾股定理 与平方根
勾股定理
平方根
逆定理
应用
平方根
立方根
实数
近似数与 有效数字
二、重要概念剖析
初 中 数 学
八 上
概 念 相同点
平方根
算术平方根 都是开方运算
立方根
不同点
负数不能 负数没有算术 任何数都能 开平方 平方根 开立方 正数的平方根 非负数的算 任何数的立 有两个它们 术平方根只 方根都只有 互为相反数 有一个 一个 平方根等于 算术平方根 立方根等于 本身的数只 等于本身的 本身的数有 有一个,为 数有两个, 三个, 0 0、1 0、1、-1
练习1:如图,点阵中以相邻4个点为顶 点的小正方形面积为1,计算
初 中 数 学
八 上
(1)△ABC的面积;
(2) △ABC的周长.
初 中 数 学
八 上
如图,折叠长方形的一边,使点D落在BC 边上的点F处,若AB=8,AD=10. (1)你能说出图中哪些线段的长? (2)能求出EC的长吗?
勾股定理平方根专题知识点整理
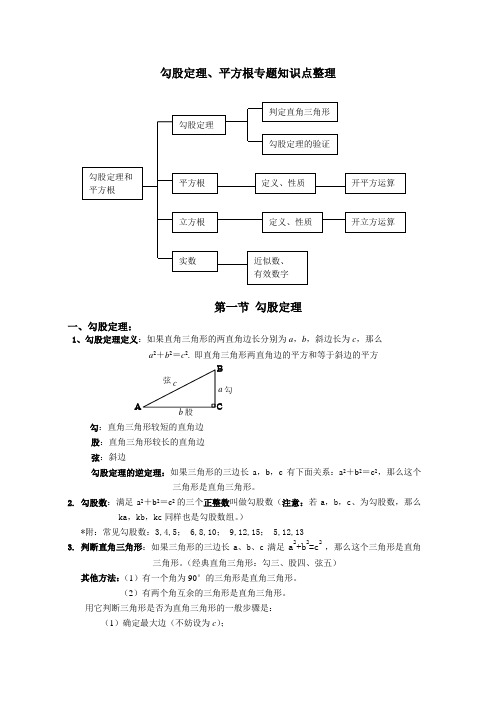
勾股定理、平方根专题知识点整理第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
小结和思考二

第二章勾股定理与平方根复习(二)主备人:徐红石 审核:席美丽 时间:2009年10月21日一、教学目标:1.灵活应用平方根、立方根、实数相关知识解决问题,提高学生用所学的知识探索、分析、解决问题的能力。
2.培养学生用数学的思维方式去观察思考、分析解决实际问题,增强学生的应用意识。
二、知识结构:ìïïïïïíïïïïïî üïïïïïýïïïïïþ 三、基础练习:1.4的算术平方根是( )A 2B ±2 C ±22.和数轴上的点一一对应的是( )A 整数B 无理数C 实数D 有理数3.在所给的数据:22,31,π,0.5 7,0.585885888588885…(相邻两个5之间的8的个数逐次增加1个),无理数的个数有( )A 2个B 3个C 4个D 5个4.下列整数最接近 )A 4B 5C 6D 75.下列说法错误的个数是( )①循环小数都是有理数 ②9π是分数 ③无理数是无限小数 ④实数包括有理数和无理数的平方根是2±2A 1个B 2个C 3个D 4个6. 下列说法中正确的有( )①2±都是8x ,③81的立方根是3,④283=--A 1个B 2个C 3个D 4个7. 若21a =,则a= ,若38a =-,则a = ,若∣x ∣=2,则x= 。
8. 算术平方根等于本身的数是 ;立方根等于本身的数是 ;9.若一个正数的算术平方根为a ,那么比这个正数大1的正数的平方根是 。
10.绝对值小于13的整数有: ,这些数的和是 .11.求下列各式中的x :(1)|x |=25; (2)(x+2) 2=16; (3)2(x -2) 3=54.平方根定义---性质---和平方的关系---平方根等于本身的数 立方根定义---性质---和立方的关系---立方根等于本身的数 开方运算---结果---和乘方的关系 无理数 实数---分类 有效数字四、例题选讲:(复习题1、2、3、4、、5)例1.填空:①|π-3.14|=;|2-1.42|=.②3-2的相反数;的相反数是310.③数轴上表示-3.14的点在表示-π的点的边(填左、右);④表示-6的点到原点距离是.例2.选择:①如果m20是一个正整数,那么正整数m的最小值是()A 2B 0C 1D 5②若是x-6的立方根,则()A x<6B x=6C x≥6D x为一切实数=0,求2n-m-3的值。
勾股定理、方根专题知识点整理
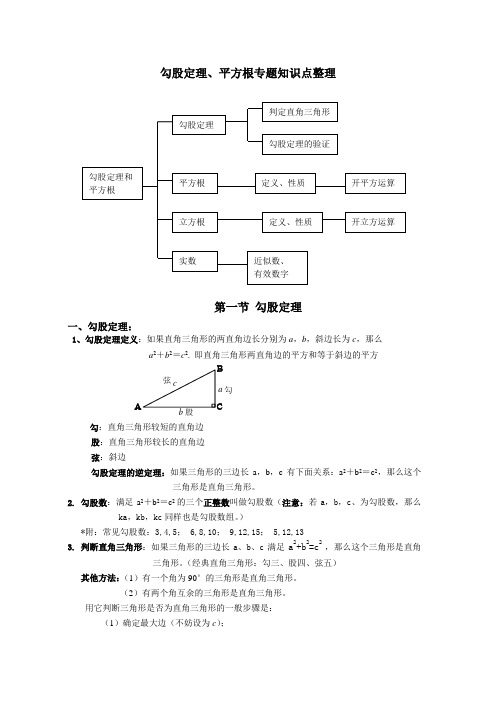
勾股定理、平方根专题知识点整理第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
苏教版数学八年级上册知识点总结

苏教版《数学》(八年级上册)知识点总结第一章 轴对称图形第二章 勾股定理与平方根一.勾股定理1、勾股定理直角三角形两直角边a ,b的平方和等于斜边c 的平方,即222c b a =+ 2、勾股定理的逆定理如果三角形的三边长a,b,c 有关系222c b a =+,那么这个三角形是直角三角形。
3、勾股数:满足222c b a =+的三个正整数,称为勾股数。
二、实数的概念及分类1、实数的分类ﻩ正有理数有理数 零 有限小数和无限循环小数 实数 负有理数正无理数无理数 无限不循环小数 负无理数2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有四类:(1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等; (3)有特定结构的数,如0.1010010001…等; (4)某些三角函数值,如s in 60o 等三、平方根、算数平方根和立方根1、算术平方根:一般地,如果一个正数x 的平方等于a,即x 2=a,那么这个正数x 就叫做a 的算术平方根。
特别地,0的算术平方根是0。
表示方法:记作“a ”,读作根号a。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数x的平方等于a,即x 2=a,那么这个数x就叫做a 的平方根(或二次方根)。
表示方法:正数a的平方根记做“a ±”,读作“正、负根号a ”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
开平方:求一个数a 的平方根的运算,叫做开平方。
0≥a注意a 的双重非负性:a ≥03、立方根一般地,如果一个数x 的立方等于a ,即x 3=a 那么这个数x 就叫做a 的立方根(或三次方根)。
表示方法:记作3a性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意:33a a -=-,这说明三次根号内的负号可以移到根号外面。
(完整版)勾股定理知识点+对应类型
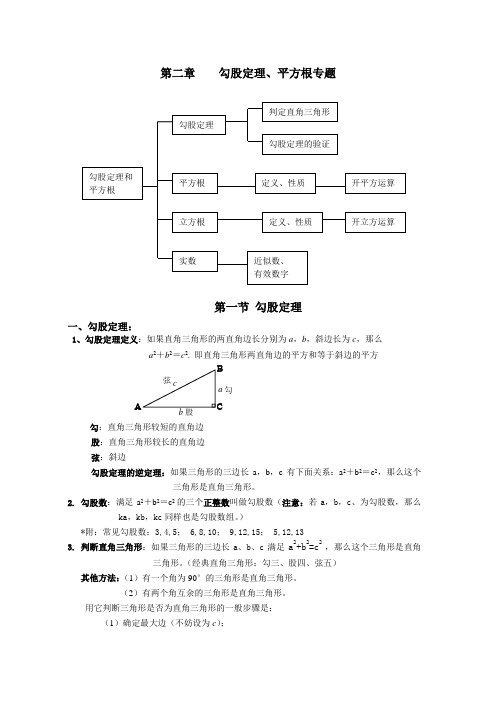
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c 2=a 2+b 2,则△ABC 是以∠C 为直角的三角形; 若a 2+b 2<c 2,则此三角形为钝角三角形(其中c 为最大边); 若a 2+b 2>c 2,则此三角形为锐角三角形(其中c 为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n 的线段二、平方根:(11——19的平方)1、平方根定义:如果一个数的平方等于a ,那么这个数就叫做a 的平方根。
第二章 勾股定理与平方根复习讲义

第二章勾股定理与平方根复习讲义要点回顾【知识点1】勾股定理内容:符号语言:1、在Rt△ABC中,a,b,c分别是三条边,∠C=90°,已知,a b则c=;已知,a c则b=。
2、在Rt△ABC中,a,b,c分别是三条边,∠B =90°,已知a=6,b=10,则c= 。
【知识点2】勾股定理的逆定理:符号语言:回忆常见的勾股数:1、下列各组数中,不能作为直角三角形三边长度的是()A.72425a b c===B. 1.52 2.5a b c===C.111345a b c===D.15817a b c===2、判断a、b、c是否是勾股数。
(1)a=7,b=24,c=25 (2)a=5,b=13,c=12 (3)a=4,b=5,c=6 ⑷ a=0.5,b=0.3,c=0.4【知识点 3】勾股定理与逆定理的应用1、三角形的三边长为ab c b a 2)(22+=+,则这个三角形是 。
2、已知a 、b 、c 为三个正整数,如果a +b +c =12,那么以a 、b 、c 为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形.以上符合条件的正确结论是___.3、在△ABC 中, AB=15,AD=12,BD=9,AC=13,求△ABC 的周长和面积。
【知识点 4】 勾股定理与方程的综合运用 〖基础回顾〗1、 AC =6c m ,BC =8c m ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗?2、 在长方形纸片ABCD 中,AD =4cm ,AB =10cm ,按如图方式 折叠,使点B 与点D 重合,折痕为EF ,求DE.CBADE【知识点5】利用割补法求面积如图,大正方形网格是由16个边长为1的小正方形组成,求图中阴影部分的面积和边长。
【知识点6】勾股定理数学图形内的应用〖基础回顾〗1、已知等腰三角形的一条腰长是5,底边长是6,求它底边上的高。
期中复习(2)

A EBCDFC ′期中复习(2)——勾股定理与平方根制卷:卞文辉 审核:张传美班级: 姓名: 学号:一、知识梳理1.勾股定理:直角三角形两直角边的平方和等于 的平方.即在Rt △ABC 中,∠C =90°,则 .勾股定理逆定理:如果三角形的三边长a 、b 、c 满足222a b c +=,那么这个三角形是 .2.如果一个数的平方等于a ,那么这个数叫做a 的 . 也称为 .即如果2x a =,那么 就叫做a 的平方根.记作 ,读作 .一个正数a 有 个平方根,它们互为 ,其中正的平方根,也叫做a 的 ;0有 个平方根,它是 ;负数 平方根. 3. 如果一个数的立方等于a ,这个数就叫做a 的 .也称为 .即如果3x a =,那么 叫做a 的立方根.记作 ,读作 .任何数都有立方根,正数的立方根是 ,负数的立方根是 ,0的立方根是 . 4. 称为无理数. 和无理数统称为 . 5.用四舍五入法取近似数时,四舍五入到哪一位,就说这个数精确到哪一位.对一个近似数,从 数字起,到 为止,所有的数字都称为这个近似数的 .如:0.010597......0.01060≈,就是精确到 位,有效数字 位,分别是 . 二、课前练习1.如图,图中的字母S 所代表的正方形的面积为 . 2.在矩形纸片ABCD 中,AD =4 cm , AB =10 cm , 按如图方式折叠,使点B 与点D 重合,折痕为EF , 则DE = cm .32 ; 3π- 0.24.当m时,m时,有意义. 5.计算: (42120++--= ;(2)312523832-+--= . 6.据统计,2009年十 · 一期间,连云港市某风景区接待中外游客8674人次,将这个数字精确到百位为 ,此时有效数字分别为 . 7.求下列各式中的x 的值.(1)()310+x =-343 (2)()2336-x = 49S50808.已知一个正数a 的平方根为2m -3和3m -22,则m = ;a = . 9.将下列各数填入相应的集合内:227, -..65.1 , 3.14 , 13,0π-- ,-0.1010010001,0.2020020002… (每两个2之间多一个0),3216-,23- …①有理数集合{ … } ②无理数集合{ … } ③负实数集合{ … } 10.如图,在ΔABC 中,∠BAC =90°,AB =15,AC =20,AD ⊥BC ,垂足为D . (1)求BC 的长;(2)求AD 的长.三、典型例题例1.如图,正方形ABCD 的边长为3,E 在BC 上,且BE =2,P 是BD 上的动点,则PE +PC的最小值为 .例2.在一个长为2米,宽为1米的矩形草地上,如图堆放着一根长方体的木块,它的棱长EF 和场地宽AD 平行且相等,木块的主视图是边长为0.2米的正方形,一只蚂蚁从点A 处,到达C 处需要走的得最短路程是 米.例3.如图1是单位为1的方格图.(1)请把方格图中的带阴影的图形适当剪开,重新拼成正方形;(画出分割线与拼成正方形的草图)(2)所拼成正方形的边长为多少?周长为多少?(3)利用这个事实,在图2的数轴上画出表示-5的点.(要求保留画图痕迹)DE PC B A BCDA图1图2---DCBAEF例4.已知a 、bb =0,解关于x 的方程()122-=++a b x a .例5.先填写下表,观察后再回答问题.(1)被开方数a 规律,请写出它的移动规律.(20.041 4.1=,你能求a 出的值吗?b 37.42≈,你能求出b 的值吗?(保留3个有效数字)(3x 的大小.(直接写出结果)例6.为美化环境,计划在某小区内用30平方米的草皮铺设一块其中一边长为10米的等腰三角形绿地,请你求出这个等腰三角形绿地的另两边长.(结果保留根号)答案:设△ABC 为面积为30m 2的等腰三角形,且AB =10m ,过C 作CH ⊥AB 于点H . (1)如图1,AC =10.0m ,BC =40 (2)如图2,AC =BC =61 (3)如图3,BC =10,AC =36010A C B H (图1) 55CH(图2)1010CAB H(图3)-3 4321 0-1 -2 DC B O ADCBA四.随堂练习 1.判断:(1)()10102-=- ( ) (2)2= ( )(3)无理数一定是无限小数 ( ) (4)两个无理数的和一定是无理数 ( ) (5)数轴上的点与实数一一对应( ) (6)任何实数不是有理数就是无理数( ) 2.81的平方根为 ;-216的立方根为 ;9的算术平方根为 ;的相反数是 ; 289开平方得 ; 计算:2= .3.(1)已知某直角三角形的两边为3,4,则第三边长等于 . (2)若直角三角形斜边上的高和中线分别是5 cm ,6 cm ,则它的面积是 . 4.如图,若数轴上的点A ,B ,C ,D 表示数-2,1,2,3,则表示74-的点P 应在( ) A 线段AB 上 B 线段BC 上 C 线段CD 上 D 线段OB 上5.如图,AD ⊥BC ,垂足为D ,如果CD =1,AD =2,BD =4,试判断ΔABC 的形状,并说明理由.6.已知Rt △ABC 的周长为3,∠ACB =90°,中线CD =1.5,求这个三角形的面积.DCBA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 勾股定理与平方根 基础知识复习讲义(2)
要点回顾
【知识点 1】 平方根概念:
算术平方根:
〖基础回顾〗
1.求下列各数的平方根和算术平方根(先表示,再化简)
36 42 1452-1442 16
2.求下列各式中x 的值. 0252=-x 81)1(42=+x 6442
=x 09822
=-x
【知识点 2】 平方根意义:
〖基础回顾〗
计算:
914414449⋅ 494 8116- 416
13+-
【知识点 3】立方根概念:
立方根的意义: 〖基础回顾〗
1.求各数的立方根(先表示,再化简) 125 (-8)
2 - 64
2.计算
⑴ 327
102
- (2)3271-- (3)336418-∙
3.求下列各式的x.
⑴x 3-216=0 ⑵8x 3+1=0 ⑶(x+5)3=64
【知识点 4】 无理数概念:
常见无理数有:
〖基础回顾〗
1.在实数3
1,38-,3.14,π,2-,39中属于有理数有 ; 属于无理数的有 .
2.下列说法正确的是( ).
A.无限小数都是无理数
B.带根号的数都是无理数
C.无理数是无限小数
D.无理数是开方开不尽的数
【知识点 5】 实数概念及分类 实数:
〖基础回顾〗 1.与数轴上的点一一对应的数是 。
2. 数轴上表示6-的点到原点的距离是 。
点M 在数轴上与原点相距5个单位,则点M 表示的实数为 。
3. 227.2540.317
π-- 1.232232223222 有理数集合:{ …}
无理数集合:{ …}
正实数集合:{ …}
负实数集合:{ …}
4
.在数轴上画出表示
实数
正无理数
负无理数
【知识点 5】 在实数范围内,无理数与有理数意义相同
〖基础回顾〗
1.21-的相反数是 ;绝对值是 .
2. -8-
3. 的倒数是 ,绝对值是 ,相反数是 。
的算术平方根为 。
【知识点 6】 近似数与有效数字
有效数字 。
了解精度的意义
〖基础回顾〗
1.用四舍五入法求30449的近似值,要求保留三个有效数字,结果是( )
A.3.045×104
B.30400 C3.05×104 D3.04×104
2.近似数0.003020的有效数字个数为( )
A.2
B.3
C.4
D.5
3.2.4万的原数是 .
4.近似数0.4062精确到 ,有 个有效数字。
5.5.47×105
精确到 位,有 个有效数字。
6.近似数1.69万精确到 位,有 个有效数字,有效数字是 .
7.小明的体重约为51.51千克,如果精确到10千克,其结果为 千克;如果精确到1千克,其结果为 千克;如果精确到0.1千克,其结果为 千克.
课堂检测
1.下列各数没有平方根的是( )
A .18
B .3)3(-
C .2)1(-
D .11.1
2.144的平方根是( ).
A .12±
B .12
C 12-
D .12±
3.有下列四个说法:①1的算术平方根是1,②81的立方根是±2
1,③-27没有立方根,④互为相反数的两数的立方根互为相反数,其中正确的是( )
A .①②
B .①③
C .①④
D .②④
4.我国最厂长的河流长江的全长约为6300千米,用科学记数法表示为( ).
A.63×102千米 A.6.3×102千米 C.6.3×103千米 D.6.3×104千米
5. 如图,以数轴的单位长线段为边作一正方形,以数轴的原点为圆心,
正方形对角线长为半径画弧,交数轴正半轴于点A ,
则点A 表示的数是( ). A.211 B.1.4 C.3 D. 2
6.49的平方根是 ,36的算术平方根是 ,8-的立方根是 。
的倒数是 ,的倒数的相反数是 。
8.π
22753
9.,则它的面积为 。
10. 若|x -3|+(y +3
3)2=0,则(x ·y )2005= 。
112值大约在哪两整数之间 。
12.设m 是5的整数部分,n 是5的小数部分,试求m -n 的值。
13.计算
2810x -= 24640x -= 32160x -= 3(5)64x +=
14.化简:计算:64273+- 102-
)5(522133-+-+⋅ππ。
