初一数学最新课件-64因式分解的简单应用浙教版002 精
七年级下浙教版6.4因式分解的简单应用3课件

(1) (4 x − 9) ÷ (3 − 2 x)
2
(2) ( xy − 2 x y + x y ) ÷ ( x − 1)
2 3
(1) (2)
(a
2
− 4) ÷ ( a + 2)
2
[(a − b) + 2(b − a)] ÷ (a − b)
先请同学们思考、讨论以下问题: 先请同学们思考、讨论以下问题: 1.如果 A×5 =0,那么A的值 . × ,那么 的值
2分钟 分钟
计算: 计算:
(16 − x ) ÷ (4 + x ) ÷ ( x − 2)
4 2
为三角形的三边, 已知 a、b、c为三角形的三边,试判断 大于零?小于零?等于零? a2 -2ab+b2-c2大于零?小于零?等于零?
3分钟 分钟
解:
a2
-2ab+b2-cc)(a=(a-b+c)(a-b-c) a、 ∵ a、b、c为三角形的三边 a+ a﹤ ∴ a + c ﹥b a ﹤b + c a∴ a - b + c ﹥0 a - b - c ﹤0 即:(a-b+c)(a-b-c) ﹤0 (a-b+c)(a小于零。 因此 a2 -2ab+b2-c2小于零。
因式分解的几种方法
一“提”、二“套” (1)提取公因式法:ma + mb 提取公因式法: (2)公式法: 公式法: 应用平方差公式: 应用平方差公式:
= m(a + b )
a 2 − b 2 = (a + b )(a − b )
2
应用完全平方公式: 应用完全平方公式: a
± 2ab + b = (a ± b )
因式分解的简单应用 PPT课件 2 浙教版

•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。
探索新知
( 2 ) 4 x 2 9 3 2 x
解: 原式 2 x 3 2 x 3 2 x 3
2x3
2x3
因式分解
两个多项式相除
(未知)
换元
单项式的除法 (已知)
运用因式分解进行多项式除
梳理知识 法的步骤:1、因式分解
练习1.计算:
挑战自我
( 3) x2x22
温馨提示
当方程两边有公因式时, 切忌两边同时除以公因式, 仍应按一般步骤解.
开动脑筋,试试吧!
例3 解下列方程:
(1) 3x3 48x (2) x3 4x 0
综合与应用
( 1 )若 a b c 0 ,求 ( a 2 b 2 ) ( a c c b ) 的 值
,
x2
3.
梳理知识 练习2.解下列方程:
用因式分解解方程的步骤: ( 1) x22x0
1、移项,使方程右边变形为零;
2、等式左边因式分解; ( 2) 4x2x12
3、转化为一元一次方程.
8765432198765432101987654320 8765432198765432101987654320
6.4因式分解的简单应用1

0
将方程的左边分解因式,得
则 x 0, 或 2 x 1 0
原方程的根是
3 x 1 x 3 0
则3 x 1 0, 或 x 3 0
x1 0,
x2
1 2
.
原方程的根是
只含有一个未知数的方程的解也叫做根。
x1
1 3
,
x2 3.
2 3
2
2
(4)
xy 2 x y x y xy x 1
思考: 怎样计算
2 2 2 a b -8 a b 4 a - b
一、运用因式分解进行多项式除法.
例1 计算:
(1)
解:
2 ab
2
8 a b 4 a b
2 2
(2)
4 x
2
2
9 3 2 x
当方程的根多于一个时,常用带足标的字母表示,如 x1 , x2 等
练习2.解下列方程: (1) 用因式分解解方程的步骤: (2)
x 2x 0
2
4 x x 1
2
2
1、移项,使方程右边变形为零;
2、等式左边因式分解;
(3)
x 2 x 2
2
温馨提示 当方程两边有公因 式时,切忌两边同时除 以公因式,仍应按一般 步骤解.
开动脑筋,试试吧!
因式分解是进行代数运算的常用工具之
一,灵活、合理地应用因式分解可帮助我们 解决很多数学问题. 1、运用因式分解进行简单的多项式除法. 2、运用因式分解解简单的方程. 若 A B 0, 则 A0 或
B 0 .
2 x 3
2022年浙教初中数学七下《 因式分解》PPT课件

3、一个多项式分解因式的结果
是 (b32)2 (b3),那么这个多项式
是:
。
4、若 x2axb能分解为 (x6)(x7),
试求 a , b 的值。
5、已知 1 x2 5 x1有一个因式
为
(1
x
6
1)
6
,则另一个因式
2
是:
。
6、一个多项式若能因式分解成两个因式
的积,则这个多项式被其中任一个因式除,
解 (2)x 2(y 1) 1 y (3)2 x 2 2 x 1 2 ( 4 )( x y ) 5 ( y x ) 3 ( 5 )( x 2 3 x ) 2 ( 3 x 1 ) 2
(6)(x2y2)24x2y2
( 7 ) 9 ( a b ) 2 1 ( a 2 2 b 2 ) 4 ( a b ) 2
19980
(5) 1999
2
1997
2
14、若 ab7,ba3 ,
求 a2 b2
7
15、若ab1 , a b 2,求
1a3ba2b21ab3
2
2
2x y 12 16、不解方程组 x 2 y 11
求 (2xy)3 (2xy)2(x 3y)
的值。
17、若 (N200)32 98765432
22 (10 ) 4 q (1 p ) 2 n 1 2 ( p 1) 2 n (11 )ax ay bx by
运用公式法进行分解的多项式的特点:
(1)运用平方差公式分解的多项式是二 项式,这两项必须是平方式,且这两项 的符号相反。
(2)运用完全平方公式分解的多项式是 三项式,且符合首平方,尾平方,首尾 两倍中间放的特点,其中首尾两项的符 号必须相同,中间项的符号正负均可。
浙教版数学七年级下册因式分解课件

因式分解与整式乘法的关系 整式乘法
m(a+b+c)=ma+mb+mc
因式分解
因式分解和整式乘法是互逆关系
正确认识因式分解 (1)因式分解的对象必须是一个多项式. (2)因式分解的结果必须是几个整式的积的情势. 一般有两种情势:①单项式×多项式;②多项式×多项式. (3)因式分解是一个恒等变形.
对于(x+1)(x+2)=x2+3x+2是 整式乘法 ; 对于16-x2=(4+x)(4-x)是 因式分解 . (填“整式乘法”或“因式分解”)
因式分解与整式乘法是互逆变形,可以用整式的乘法算出结 果,再利用对应系数相等,求出未知系数的值.
因式分解的
因
概念
式
分
解
与整式乘法 的区分
因式分解的 简单应用
1.已知(x+1)(x-1)=x2-1,则将x2-1进行因式分解的结果
是 (x+1)(x-1)
.
2.[202X·瑞安期末] 下列各式从左到右的变形中,是因式分解
因式分解和整式的乘法有互逆关系,因此可以用整式的乘 法运算,来检验因式分解
例1 检验下列因式分解是否正确: (1) x²y-xy=xy (x-y) (2) 2x²-1=(2x+1)(2x-1) (3) x²+3x+2=(x+1)(x+2)
检验因式分解是否正确,只要看等式右边几个整式相乘的积 与左边的多项式是否相等。
第四章 因式分解
4.1 因式分解
1. 3×3×4=36 整数的乘法
2. 2×7×8=112 整数的乘法
36=3×3×4 因数分解
112=2×7×8 因数分解
因式分解课件 浙教版(PPT)4-2
(3)#43;1=x(x-3)+1
(4)因式分解与整式乘法是互逆的
(5).( x4 1) (x2 1)( x2 1)
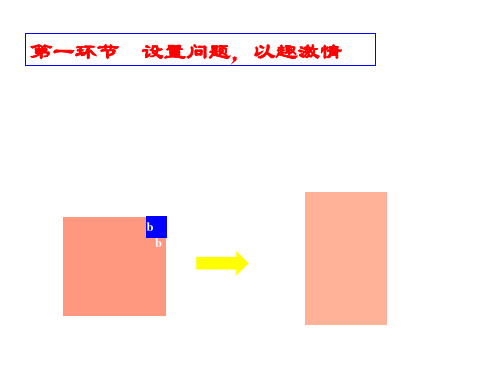
第一环节 设置问题,以趣激情
手工课上,老师给南韩兵同学发下一张如左图形状的纸 张,要求他在恰好不浪费纸张的前提下剪拼成右图形状的 长方形,作为一幅精美剪纸的衬底,请问你能帮助南韩兵 同学解决这个问题吗?能给出数学解释吗?
b b
a
a
类食用的频率也高得多;而野菜则多半未经过人类驯化,几乎均为野生种,人类也较不常食用。 水果 水果 水果 水果是指可以生食,多汁液,有酸味或甜味 的果实,像苹果、橙、葡萄、草莓、香蕉及柠檬、蓝莓等。但在植物学的定义上,也有一些不是水果的果实,例如玉米粒、小麦粒及番茄。 香料 香料,又名 辛香料或香辛料,是一些; 万和城:/ ;干的植物的种子、果实、根、树皮做成的调味料的总称,例如胡椒、丁香、肉桂等。它们 主要是被用于为食物增加香味,而不是提供营养。 用于香料的植物有的还可用于医药、宗教、化妆、香氛、或食用。香料很少单独使用,大部分以数种数十 种成分调和构成。有时,香料也指制造香味用的材料。 油料作物 人们做饭时使用的烹调油是从一些油脂含量很高的油料作物的果实或种子中提炼出来的。常
见的油料作物主要有油棕、花生、大豆、芝麻、油菜、向日葵等。花生豆类以及一些干果的仁都是很好的油料。我国种植较广泛的油料作物有花生、大豆、 油菜等。 糖料作物 糖料作物——甘蔗 糖料作物——甘蔗 用于制糖的作物称为糖料作物。糖料作物主要有两种:一是甘蔗,它是一种高高的绿色的茎;一是 甜菜,它是一种长在地下的好大的根。人们榨取他们的汁液,把汁液收集起来转化为糖的结晶。在我国,北方一般以甜菜为原料制糖,南方则常以甘蔗为原 料制糖。 原料价值 酸角树 酸角树(张) 木材被用在建筑、家具、纸张、乐器和运动用具上头。布料通常是由棉花、亚麻或其原料为纤维素的合成纤维,如嫘 萦和醋酸根。来自植物的可再生燃料包括柴、泥炭和其他生质燃料。炭和石油是来自植物的化石燃料。来自植物的药物包括阿司匹灵、紫杉醇、吗啡、奎宁、 利血平、秋水仙素、毛地黄和长春新碱等。植物中存在于上百种药草如银杏、紫锥花、解热菊和贯叶连翘等。来自植物的农药包括尼古丁、鱼藤酮、番木鳖 碱和除虫菊精等。来自植物的毒品包括鸦片、古柯碱和大麻等。来自植物的毒药包括蓖麻毒素、毒参和箭毒等。植物是许多天然产品如纤维、香精油、染料、 颜料、蜡、丹宁、乳胶、树脂、松香、生物碱、琥珀和软木的原料。源自于植物的产品包括肥皂、油漆、洗发精、香油、化妆品、松节油、橡胶、亮光漆、 润滑油、亚麻油地毡、塑胶、墨水、口香糖和麻绳等。植物亦为大量有机化合物的工业合成中,基本化合物的主要来源。 观赏价值 各种观赏植物 各种观赏 植物(张) 成千的植物物种被种植用来美化环境、提供绿荫、调整温度、降低风速、减少噪音、提供隐私和防止水土流失。人们会在室内放置切花、干燥花和
初一数学最新课件-64因式分解的简单应用浙教版002 精品

整式除法
计算:
12a3b3c 6ab2 2a2bc
am bm m a b
a2 4 a 2
a 2a 2a 2
a2
二、运用因式分解进行多项式除法.
例2 计算:
(1) 2ab2 8a2b 4a b
(2) 4x2 9 3 2x
பைடு நூலகம்
填空:
(1)(ab2 a2b) (a b) ab
(6)a2 4ab 4b2 (a 2b)2
提取公因式法 应用平方差公式 应用完全平方公式
想若一A想×:如B=果0已,知则(A和B中)×至(少有一)=个0 ,为那零么,这两个 括即号A内=应0,填或入怎B=样0的数或代数式才能够满足条件呢?
若A试×B一=0试,:下你面能两运个结用论上对面吗?的结论 (1)A和解B同方时程都(为2零x+,1即)(A3=0x,-2且)B==00吗?
(2) x2 2xy y2 x y x y
试一试
你能在括号内填入适当的代数式,使 等式成立吗?
(x 7)
综合与应用
计算:(16 x4 ) (4 x2 ) (x 2)
开动脑筋,试试吧!
因式分解是进行代数运算的常用工具之 一,灵活、合理地应用因式分解可帮助我们 解决很多数学问题.
1、运用因式分解进行简单的多项式除法.
2、运用因式分解解简单的方程.
若 A B 0, 则 A 0 或 B 0 .
综合与应用
(1) 若a b c 0, 求(a2 b2 ) (ac cb)的值
(2) 求满足等式 a2 b2 29 的正整数解
义务教育课程标准实验教科书 浙江版《数学》七年级下册
6.4 因式分解的简单应用
宜山一中
将下列各式因式分解:
浙教版七年级下册数学因式分解的简单应用导学案PPT课件教案课堂教学实录

浙教版七年级下册数学《因式分解的简单应用》导学案PPT课件教案课堂教学实录浙教版七年级下册数学《因式分解的简单应用》导学案PPT课件教案课堂教学实录第6.4因式分解的简单应用翁洋一中何菊莉背景材料:因式分解是初中数学中的一个重点内容,也是一项重要的大体技术和基础知识,更是一种数学的变形方式,在尔后的学习中有着重要的作用。
因此,除单纯的因式分解问题外,因式分解在解某些数学问题中有着普遍的作用,因式分解在三角形中的应用,因式分解能够用来证明代数问题,用于代数式的求值,用于求不定方程,用于解应用题解决有关复杂数值的计算,本节课的例题因式分解在数学题中的简单应用。
教材分析:本节课是本章的最后一节,是学生学习因式分解初步应用,第一要使学生体会到因式分解在数学中应用,第二给学生提供更多机遇体验主动学习和探讨的“进程”与“经历”,使多数学里拥有必然问题解决的体会。
教学目标:一、在整除的情形下,会应用因式分解,进行多项式相除。
二、会应用因式分解解简单的一元二次方程。
3、体验数学问题中的矛盾转化思想。
4、培育观看和动手能力,自主探讨与合作交流能力。
教学重点:学会应用因式分解进行多项式除法和解简单一元二次方程。
教学难点:应用因式分解解简单的一元二次方程。
设计理念:依照本节课的内容特点,要紧采纳师生合作控讨式课堂教学方式,以教师为主导,学生为主体,动手实践训练为主线,创新思维为核心,态度情感能力为目标,引导学生自主探讨,动手实践,合作交流。
注重使学生经办观看、操作、推理等探讨进程。
这种教学理念,反映了时期精神,有利于提高学生的数学素养,能有效地激发学生的思维踊跃性,学生在学习进程中调动各类感官,进行观看与抽象、操作与试探、自主与交流等,进而改良学生的学习方式。
教学进程:一、创设情境,温习提问一、将正式各式因式分解(1)(a+b)2-10(a+b)+25 (2)-xy+2x2y+x3y(3)2 a2b-8a2b (4)4x2-9[四位同窗到黑板上演板,本课时用温习“练习引入”也不失为一种好方式,既先温习因式分解的提取分因式和公式法,又为下面解决多项式除法运算作铺垫]教师订正提出问题:如何计算(2 a2b-8a2b)÷(4a -b)二、导入新课,探讨新知(先让学生试探上面所提出的问题,教师从旁启发)师:若是显现竖式计算,教师能够给予确信;可能显现(2 a2b-8a2b)÷(4a-b)= ab-8a2追问学生怎么得来的,运算的依据是什么?如此暴露学生的思维,让学生自己发觉错误的地方;观看2 a2b-8a2b=2 ab(b-4a),其中一个因式正好是除式4a-b的相反数,若是用“换元”思想,咱们就能够够把问题转化为单项式除以单项式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B0 .
综合与应用
(1) 若a b c 0, 求(a b ) (ac cb)的值
2 2
(2) 求满足等式 a b 29 的正整数解
2 2
2
应用完全平方公式
(6)a 4ab 4b (a 2b)2
2 2
若 A× B=0,则( A和B中至少有一个为零, 想一想 :如果已知 ) ×( )=0 ,那么这两个 即A=0,或B=0 括号内应填入怎样的数或代数式才能够满足条件呢?
:你能运用上面的结论 若A试零,即 A=0,且B=0吗? 解方程 (2x+1)(3x-2)=0 (2)A和B中至少有一个为零,即A=0,或B=0
综合与应用
计算: (16 x ) (4 x ) ( x 2)
4 2
开动脑筋,试试吧!
因式分解是进行代数运算的常用工具之
一,灵活、合理地应用因式分解可帮助我们 解决很多数学问题. 1、运用因式分解进行简单的多项式除法. 2、运用因式分解解简单的方程. 若 A B 0, 则 A0 或
计算:
am bm m a b 2 a 4 a 2 a 2 a 2 a 2
a2
12a b c 6ab 2a bc
3 3 2
2
二、运用因式分解进行多项式除法.
(1) 2ab 8a b 4a b
2 2
例2 计算:
(2) 4 x 9 3 2 x
2
填空:
(1)(ab a b) (a b)
2 2
2 2
ab
(2) x 2 xy y x y x y
试一试
你能在括号内填入适当的代数式,使 等式成立吗?
( x 7)
(2x+1)(3x-2)=0 则2x+1=0或3x-2=0 1 2 解得原方程的解是 根 x1 , x2
2
3
一、运用因式分解解方程.
解下列方程: (1) x
2
2x 0
x2 (2)
温 馨 提 示
x 2
2
当方程两边有公因式时,切忌两边同
时除以公因式,仍应按一般步骤解
整式除法
义务教育课程标准实验教科书
浙江版《数学》七年级下册
6.4 因式分解的简单应用
宜山一中
将下列各式因式分解:
3 n (n 1) (1)n n
4
3
提取公因式法 应用平方差公式
(2) ax bx x(ax b) (3) x 2 9 ( x 3)( x 3) (4)4s 2 9 2s 3 2s 3 2 2 (5) x 2 xy y ( x y)2
