复习卷1
人教版四年级上册数学书复习题1-9单元

1.一(个)、十、百、千、万......亿都是()。
2.在用数字表示数的时候,这些计数单位间要按照一定的顺序排列起来,他们所占的位置叫做()。
3.你能填出数位顺序表吗?试一试。
(1)从个位起,第()位是万位,第()位是亿位。
(2)万位的右边一位是()位,左边一位是()。
4.读出下面各数308000读作()24690000读作()40500000读作()54621读作()6400000读作()10030040 读作()5.含有两级的数怎么读?(1)先读()级,再读()级;(2)万级的数,要按照()的读法来读,再在后面加上一个()字;(3)每级末尾不管有几个0,都(),其他数位上有一个0或连续几个0,都()。
1.你能写出下列数吗?二十三万零一百八十四写作()十万二千三百四十五写作()三百零二万六千写作()二千零四十万零七百写作()2.含有两级的数怎么写?(1)先写()级,再写()级;(2)哪个数位上一个单位也没有,就在那个数位上写()。
3.写出下列各数三百二十六万七千五百写作(),四万零九十写作()九千零二十万零三百写作(),一百万写作()4.写出横线上数字表示的含义32086 ()93787 ()107398 ()69 0250()5.照样子,说一说47578,表示4个万,7578个一。
280064,表示28个万,64个一。
498909,表示();2700006,表示();55523870,表示();1.写出下面横线上的数。
(1)正常人的心脏一年大约要跳四千二百万次。
()(2)地球赤道周长四千零七万五千七百米。
()(3)有一头蓝鲸重十二万五千千克,相当于23头大象的体重。
()(4)光的传播速度大约是每秒二十九万九千八百千米。
()(5)蜻蜓的眼睛是由二万多只小眼睛组成的。
()2.写出下面各数三百六十万二千写作(),五十四万零三百七十写作()六万八千九百二十写作(),四千六百四十一万写作()十万零五写作(),一千零五十万零三十写作()3.你能用不同的方式表示下面的数吗?例:440000,这个数由四十万和四万组成,440000=400000+40000。
2023年部编版一年级语文下册期末复习试卷 (1)

2023年部编版一年级语文下册期末复习试卷一、把加点字的音节补充完整。
(8分)gu sh j l 广.场 身.体 据.说 铃.声 uì ú uàn ú 嘴.巴 浮.萍 锻.炼 成熟. 二、看拼音,写词语。
(10分)chī shuǐ cǎo fáng gē ge chuáng qián gēn zhefàng shēng ài xīn zhǎo rén pá shān yǐ hòu三、根据查字典的知识填空。
(10分)四、组词。
(12分)东( ) 住( ) 远( ) 冬( ) 往( ) 运( ) 请( ) 从( ) 讲( ) 清( ) 以( ) 进( ) 五、按要求完成句子练习。
(10分) 1.读一读,给句子加上标点。
(2分) 能见到小伙伴,我多么开心呀别的孩子也像我一样,这么想吗2.把句子补充完整。
(6分)(1)小花狗在(2)要是 ,我就(3)我多想3.你要去书店借书,可不知道怎么走,李明知道,你可以这样问他:“”(2分)六、背诵填空。
(13分)1.夜来( ) ( ) ( ),花落知多少。
2.床前明月光,疑是( ) ( )霜。
3.和风对( ) ( ),朝霞对( ) ( )。
4.玉不琢,不成器,人不( ),不知( )。
5.敏而好学,不耻( ) ( )。
七、读一读,完成作业。
(12分)1.“和大人一起读”,你读了吗?请判断下面说法的对错,对的打“✔”,错的打“×”。
(4分)(1) 《胖乎乎的小手》中,全家人都喜欢兰兰胖乎乎的小手,因为这双手帮他们做了好多事情呢!( )(2)儿歌《妞妞赶牛》中,牛牛饿了,妞妞就牵着牛,去吃河边嫩嫩的柳叶。
( )(3) 《狐狸和乌鸦》中,狐狸说乌鸦的羽毛漂亮,是真心夸它长得美。
( )(4) 《三只白鹤》中,第二只白鹤把大鱼埋在了柳树旁边。
( )八、我爱阅读。
七年级下册数学期末复习试卷(一附答案
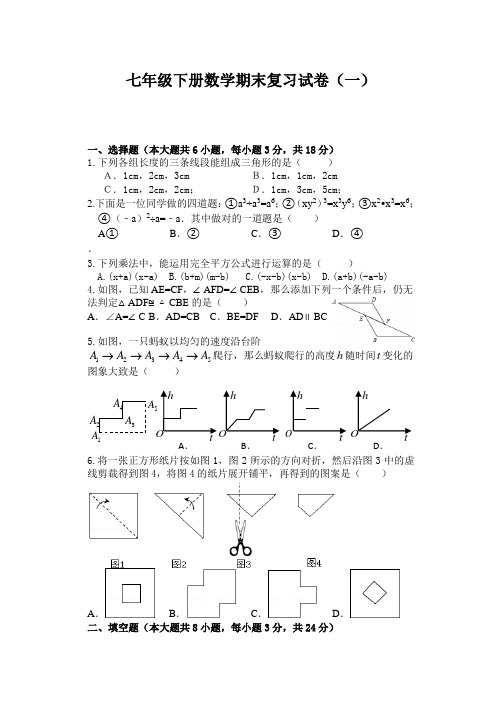
七年级下册数学期末复习试卷(一)一、选择题(本大题共6小题,每小题3分,共18分) 1.下列各组长度的三条线段能组成三角形的是( ) A.1cm ,2cm ,3cm B.1cm ,1cm ,2cm C.1cm ,2cm ,2cm ; D.1cm ,3cm ,5cm ;2.下面是一位同学做的四道题:①a 3+a 3=a 6;②(xy 2)3=x 3y 6;③x 2•x 3=x 6;2A.(x+a)(x-a)B.(b+m)(m-b)C.(-x-b)(x-b)D.(a+b)(-a-b) 4.如图,已知AE=CF ,∠AFD=∠CEB ,那么添加下列一个条件后,仍无法判定△ADF ≌△CBE 的是( )A .∠A=∠CB .AD=CBC .BE=DFD .AD ∥BC5.如图,一只蚂蚁以均匀的速度沿台阶12345A A AA A →→→→爬行,那么蚂蚁爬行的高度h 随时间t 变化的图象大致是( )6.将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图4,将图4的纸片展开铺平,再得到的图案是( )A .B .C .D .二、填空题(本大题共8小题,每小题3分,共24分)1A 2A 3A 4A 5A A .B .C .D .7.计算21()2--= _______8.如图有4个冬季运动会的会标,其中不是轴对称图形的有______个9.已知等腰三角形的一边长为4,另一边长为8,则这个等腰三角形的周长为___________. 10.已知:2211,63a b a b -=-=,则22a b +=_______ 11.如图,是我们生活中经常接触的小刀,刀柄外形是一个直角梯形(挖去一小半圆),刀片上、下是平行的,转动刀片时会形成∠1、∠2,则∠1+∠2=_______. 12.如图所示,∠E=∠F=90°,∠B=∠C ,AE=AF .给出下列结论:①∠1=∠2;②BE=CF ;③△ACN ≌△ABM ;④CD=DN .其中正确的结论是 .(将你认为正确的结论的序号都填上)第11题图 第12题图 第13题图13.如图是叠放在一起的两张长方形卡片,图中有∠1、∠2、∠3,则其中一定相等的是_____14.如果a 2+b 2+2c 2+2ac-2bc=0,那么2015a b+的值为三、(本大题共4小题,每小题6分,共24分) 15.已知:2x ﹣y=2,求:〔(x 2+y 2)﹣(x ﹣y )2+2y (x ﹣y )〕÷4y 的值.16.若2(1)()a a a b --- =4,求222a b ab +-的值17.已知:如图,AB ∥CD ,∠ABE=∠DCF ,说明∠E=∠F 的理由.18.如图,把宽为2cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,若△PFH的周长为10cm,求长方形ABCD的面积.四、(本大题共3小题,每小题8分,共24分)19.将一副直角三角尺BAC和BDE如图放置,其中∠BCA=30°,∠BED=45°,(1)若∠BFD=75°,判断AC与BE的位置关系,并说明理由;(2)连接EC,如果AC∥BE,AB∥EC,求∠CED的度数.20.投掷一枚普通的正方体骰子24次.(1)你认为下列四种说法中正确的为(填序号);①出现1点的概率等于出现3点的概率;②投掷24次,2点一定会出现4次;③投掷前默念几次“出现4点”,投掷结果出现4点的可能性就会加大;④若只连续投掷6次,出现的点数之和不可能等于37.(2)求出现奇数的概率;(3)出现6点大约有多少次?21.如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,(1)若∠DAE=50°,求∠BAC的度数;(2)若△ADE的周长为19cm,求BC的长.五、(本大题共2小题,每小题9分,共18分)22.小明的父亲在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图像回答下列问题:(1)降价前他每千克西瓜出售的价格是多少?(2)随后他按每千克下降0.5元将剩余的西瓜售完,这时他手中的钱(含备用的钱)是450元,问他一共批发了多少千克的西瓜?(3)小明的父亲这次一共赚了多少钱?23.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D 不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.(1)当∠BDA=115°时,∠BAD=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)当DC等于多少时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.六、(本大题共1小题,共12分)24.如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)①找出图1中的一对全等三角形并说明理由;②写出图1中线段DE、AD、BE满足的数量关系;(不必说明理由)(2)当直线MN绕点C旋转到图2的位置时, 探究线段DE、AD、BE之间的数量关系并说明理由;(3)当直线MN绕点C旋转到图3的位置时,问DE、AD、BE之间又具有怎样的数量关系?直接写出这个数量关系(不必说明理由).七年级下册综合复习试卷(一)参考答案1~6. CBDBBB 7.4 8.3 9.20 10.1 11.90°12.①②③13.∠2=∠314.1 15. 1.16.8 17.略18.解:∵把宽为2cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,∴BF=PF,PH=CH,∵△PFH的周长为10cm,∴PF+FH+HC=BC=10cm,∴长方形ABCD的面积为:2×10=20(cm 2),19. (1)AC∥BE,理由略(2)45°.20. (1)①④(2)12(3)421. (1)∠BAC=115°;(2)BC=19cm.22(1)3.5元(2)120千克,(3)450﹣120×1.8﹣50=184元,②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,24. 解:(1)①△ADC≌△CEB.理由如下::∵∠ACB=90°,∠ADC=90°,∠BEC=90°∴∠ACD+∠DAC=90°,∠ACD+∠BCE=90°,∴∠DAC=∠BCE,在△ADC与△BEC中,,∴△ADC≌△BEC(AAS);②DE=CE+CD=AD+BE.理由如下:由①知,△ADC≌△BEC,∴AD=CE,BE=CD,∵DE=CE+CD,∴DE=AD+BE;(2)∵AD⊥MN于D,BE⊥MN于E.∴∠ADC=∠BEC=∠ACB=90°,∴∠CAD+∠ACD=90°,∠ACD+∠BCE=90°.∴∠CAD=∠BCE.在△ADC和△CEB中,∴△ADC≌△CEB.∴CE=AD,CD=BE.∴DE=CE﹣CD=AD﹣BE.(3)同(2),易证△ADC≌△CEB.∴AD=CE,BE=CD∵CE=CD﹣ED∴AD=BE﹣ED,即ED=BE﹣AD;当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE﹣AD(或AD=BE﹣DE,BE=AD+DE等).。
NPDP复习测试卷1 部分习题解析

●NPDP复习测试卷1 部分习题解析●第一章:●58、大多数使用投资组合管理流程的公司都承认造成整体组合失败的主要原因在于?●A.过少的支持型项目●B.过多的突破性项目●C.可用资源不足以支持过多的项目●D.过多的平台型项目和过少的衍生型项目●58、●【答案】C●【难度】一般●【考点】第二章资源配置P54●【解析】资源配置。
新产品开发的成功率受限于以下因素:同时段内进行的项目太多、项目计划糟糕、●执行能力差、优先级不清晰、缺乏完善的辅助支持●66、以下哪项是组合管理中自下而上战略方法的特征?●A.将战略包括于对每个项目的评价标准中●B.生成单一的项目列表,并在过程中对项目优先级进行排序●C.确保多个项目类型的支出达到理想比例●D.以上全不正确●66、●【答案】A●【难度】一般●【考点】第二章确保产品组合与战略匹配的方法P45●【解析】自下而上的方法不考虑项目的优先级,所以B 不正确,书上原话:“不刻意追求在项目组合中达●成某种意义的平衡”,所以C 不正确。
●70、关于组合管理,下列哪些说法是正确的?I 组合管理是决策过程II 持续审核与更新是组合管理过程的独特点III 组合管理在高度动态的环境中应对未来事件IV 组合管理关键作用在于管理稀缺和有限资源●A.I、II●B.I、II、III●C.II、III、IV●D.I、II、III、IV●70、●【答案】D●【难度】一般●【考点】第二章组合管理的特征P42●【解析】组合管理的特征:处于动态环境中的决策过程、持续不断地审查、项目处于不同的完成阶段、●涉及未来事件、无法确保成功、提高整个项目或产品成功的可能性、管理有限的资源、依照组织的整体●战略分配资源。
●75、在商业术语上,重点舞台可被定义为?●A.目标市场(竞争地点)●B.关键技术和营销方法(如何竞争)●C.竞争对手的优势和劣势●D.以上所有选项●75、●【答案】D●【难度】一般●【考点】第三章产品创新章程P89●【解析】重点舞台:目标市场、关键技术和营销方法(如何竞争)、支持项目成功的关键技术和市场规模、●竞争对手的优势和劣势(其他表演者)●79、公司董事会在创新流程治理中主要起到什么重要作用?●A.确保选择了最好的开发项目●B.验证新产品开发流程满足公司需求●C.检查高优先级产品特办列表最具产品附加值●D.确保预算分配与项目进度相一致●79、●【答案】B●【难度】一般●【考点】第三章产品流程治理P86●【解析】董事会提出流程的要求和验收是否满足。
高中数学-高二期末复习卷(1)

高二期末复习卷一、单选题1.已知()f x '是()f x 的导函数,()f x '的图象如图所示,则()f x 的图象只可能是()A.B.C.D.2.“m>2”是“方程22212x ym m +=+表示焦点在x 轴上的椭圆”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知等差数列{}n a 的前n 项和为n S ,且2121S =,则616a a +的值为()A .1B .2C .3D .44.若直线l :12y x m =-+与曲线C :21164x x y +=有两个公共点,则实数m 的取值范围为()A.()(0,- B.(0,C .()()2,00,2-⋃D .()0,25.已知()f x 在0x x =处可导,则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于()A .()0f x 'B .()0f x C .()20f x '⎡⎤⎣⎦D .()()002f x f x '6.有关数据显示,2015年我国快递行业产生的包装垃圾约为400万吨.有专家预测,如果不采取措施,快递行业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从()年(填年份)开始,快递行业产生的包装垃圾超过4000万吨.(参考数据:lg 20.3010,lg 30.4771≈≈)A .2019B .2020C .2021D .20227.数列{}n a 满足154a =,211n n n a a a +=-+,*n ∈N ,则122022111a a a +++ 的整数部分是()A .1B .2C .3D .48.已知抛物线22(0)y px p =>)的焦点为F ,过F 且倾斜角为π4的直线l 与抛物线相交于A ,B 两点,12AB =,过A ,B 两点分别作抛物线的切线,交于点Q .则下列四个命题中正确的个数是()个.①QA QB ⊥;②若M (1,1),P 是抛物线上一动点,则||||PM PF +的最小值为52;③AOB (O为坐标原点)的面积为;④(,0)2PM -,则tan AMB ∠=A .1B .2C .3D .4二、多选题9.下列说法正确的是()A .已知函数3()2f x x x =+,则该函数在区间[]1,3上的平均变化率为30B .已知11(,)A x y ,22(,)B x y 在函数()y f x =图象上,若函数()f x 从1x 到2x则曲线()y f x =的割线AB 的倾斜角为3πC .已知直线运动的汽车速度V 与时间t 的关系是221V t =-,则2t =时瞬时加速度为7D .已知函数()f x x =,则(9.05) 3.008f ≈10.在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中,O 为棱1A A 上一点,且111,4A O A A P Q =、分别为线段1111B D A D 、上的动点,M 为底面ABCD 的中心,N 为线段AQ 的中点,则下列命题正确的是()A .CN 与QM 共面B .三棱锥A DMN -的体积为43C .PQ QO +的最小值为322D .当11113D Q D A = 时,过,,A Q M 三点的平面截正四棱柱所得截面的周长为()82103+11.数列{}n a 满足1a a =,2131n n n a a a +=--,则下列说法正确的是()A .若1a ≠且2a ≠,数列{}n a 单调递减B .若存在无数个自然数n ,使得1n n a a +=,则1a =C .当2a >或1a <时,{}n a 的最小值不存在D .当3a =时,121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦12.设F 是抛物线2:4C y x =的焦点,直线:1l x ty =+与抛物线C 交于,A B 两点,O 为坐标原点,则下列结论正确的是()A .||4AB ≥B .OA OB ⋅可能大于0C .P 为抛物线上异于A 、B 的点,直线l 与准线交于点T ,当0,t A >为第一象限的点时,若APB α∠=,PF 平分APB ∠,则π2APT +∠=αD .若在抛物线上存在唯一一点Q (异于,)A B ,使得QA QB ⊥则3t =±三、填空题13.若()f x 为可导函数,且()()0121lim 14x f x f x→--=-,则过曲线()y f x =上点()()1,1f 处的切线斜率为______.14.对于数列{}n a ,若1,n n a a +是关于x 的方程2103n n x c x -+=的两个根,且12a =,则数列{}n c 所有项的和为________.15.法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆,这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=,过C 上的动点M 作Γ的两条切线,分别与C 交于P ,Q 两点,直线PQ 交Γ于A ,B 两点,则下列说法,正确的有______.①椭圆Γ的离心率为22②MPQ 面积的最大值为232a③M 到Γ的左焦点的距离的最小值为()22a-④若动点D 在Γ上,将直线DA ,DB 的斜率分别记为1k ,2k ,则1212k k =-16.已知数列{}n a 的通项公式为4152nn n a +⎛⎫=-⋅ ⎪⎝⎭,设数列{}n a 的最大项和最小项分别为,M N ,则M N +=______.四、解答题17.已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12.(1)求椭圆C 的标准方程;(2)过椭圆C 右焦点且倾斜角为135︒的直线l 交椭圆C 于M 、N 两点,求MN 的值.18.已知双曲线2222:1(0,0)x y C a b a b -=>>,四点12346,,4,,4,333M M M M ⎛⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭中恰有三点在C 上.(1)求C 的方程;(2)过点(3,0)的直线l 交C 于P ,Q 两点,过点P 作直线1x =的垂线,垂足为A .证明:直线AQ 过定点.19.如图1,在等腰直角三角形ABC 中,4AC BC ==,D 是AC 的中点,E 是AB 上一点,且DE AB ⊥.将ADE V 沿着DE 折起,形成四棱锥-P BCDE ,其中点A 对应的点为点P ,如图2.(1)在图2中,在线段PB 上是否存在一点F ,使得CF ∥平面PDE ?若存在,请求出PFPB的值,并说明理由;若不存在,请说明理由;(2)在图2中,平面PBE 与平面PCD 所成的锐二面角的大小为3π,求四棱锥-P BCDE 的体积.20.在①11a =,525S =;②35a =,917a =;③416S =,864S =这三个条件中任选一个补充在下面的横线上并解答.已知等差数列{}n a 满足________.(1)求数列{}n a 的通项公式;(2)求数列{3}n n a ⋅的前n 项和.n T (如果选择多个条件分别解答,按第一个解答计分)21.在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“Z 拓展”.如数列1,2第1次“Z 拓展”后得到数列1,3,2,第2次“Z 拓展”后得到数列1,4,3,5,2.设数列a 、b 、c 经过第n 次“Z 拓展”后所得数列的项数记为n P ,所有项的和记为n S .(1)求1P 、2P ;(2)若2023n P ≥,求n 的最小值;(3)是否存在实数a 、b 、c ,使得数列{}n S 为等比数列?若存在,求a 、b 、c 满足的条件;若不存在,说明理由.21.记数列{}n a 的前n 项和为111,2,34n n n n S a S S a ++=+=-.(1)求{}n a 的通项公式;(2)设2log n n n b a a =,记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立,求实数t 的取值范围.22.已知抛物线的顶点为原点,焦点F 在x轴的正半轴,F 到直线20x +=的距离为54.点()2,2N ,不过点N 的直线l 与抛物线交于两点,A B ,且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程(2)求证:直线AB 过定点,并求该定点坐标.高二期末复习卷(答案)一、单选题1.已知()f x '是()f x 的导函数,()f x '的图象如图所示,则()f x 的图象只可能是()2.“m>2”是“方程22212x y m m +=+表示焦点在x 轴上的椭圆”的()A .充分不必要条件B .必要不充分条件3.已知等差数列{}n a 的前n 项和为n S ,且2121S =,则616a a +的值为()A .1B .2C .3D .4【答案】B【分析】根据等差数列前n 项和公式以及等差数列的性质,可得2121S =与616a a +的关系式,即可求得结果.4.若直线l :12y x m =-+与曲线C :21164x x y +=有两个公共点,则实数m 的取值范围为()A .()(0,-B .(0,2,00,2-⋃0,2如图可知,当直线l 介于直线12y x =-和与曲线C 有两个公共点.设1l 的方程为012y x m =-+,()00m >,则有联立220116412x yy x m⎧+=⎪⎪⎨⎪=-+⎪⎩,消去x 并整理得2y 由()2200Δ4840m m =--=,解得022m =故m 的取值范围为()0,22.故选:B .5.已知()f x 在0x x =处可导,则()()02200lim x x f x f x x x →-⎡⎤⎡⎤⎣⎦⎣⎦-等于()A .()0f x 'B .()0f x C .()20f x '⎡⎤⎣⎦D .()()002f x f x '业产生的包装垃圾年平均增长率将达到50%.由此可知,如果不采取有效措施,则从()年(填年份)开始,快递行业产生的包装垃圾超过4000万吨.(参考数据:lg 20.3010,lg 30.4771≈≈)7.数列{}n a 满足154a =,211n n n a a a +=-+,*n ∈N ,则122022111a a a +++ 的整数部分是()8.已知抛物线22(0)y px p =>)的焦点为F ,过F 且倾斜角为π4的直线l 与抛物线相交于A ,B 两点,12AB =,过A ,B 两点分别作抛物线的切线,交于点Q .则下列四个命题中正确的个数是()个.①QA QB ⊥;②若M (1,1),P 是抛物线上一动点,则||||PM PF +的最小值为52;③AOB (O 为坐标原点)的面积为;④(,0)2PM -,则tan AMB ∠=二、多选题9.下列说法正确的是()A .已知函数3()2f x x x =+,则该函数在区间[]1,3上的平均变化率为30B .已知11(,)A x y ,22(,)B x y 在函数()y f x =图象上,若函数()f x 从1x 到2x 则曲线()y f x =的割线AB 的倾斜角为3πC V 与时间t 的关系是221V t =-,则2t =时瞬时加速度为7D .已知函数()f x =,则(9.05) 3.008f ≈【答案】BD10.在底面边长为2、高为4的正四棱柱1111ABCD A B C D -中,O 为棱1A A 上一点,且11,4A O A A P Q =、分别为线段1111B D A D 、上的动点,M 为底面ABCD 的中心,N 为线段AQ 的中点,则下列命题正确的是()A .CN 与QM 共面B .三棱锥A DMN -的体积为43C .PQ QO +的最小值为2D .当11113D Q D A = 时,过,,A Q M 三点的平面截正四棱柱所得截面的周长为83对于C ,如图2,展开平面点P ,交11A D 与点Q ,则此时对于D ,如图3,取11113D H D C =uuuu r uuuu r共面,即过,,A Q M 三点的正四棱柱的截面为梯形,且12233QH AC ==,所以平面截正四棱柱所得截面的周长为故选:ACD.11.数列{}n a 满足1a a =,1n n n +=--,则下列说法正确的是()A .若1a ≠且2a ≠,数列{}n a 单调递减B .若存在无数个自然数n ,使得1n n a a +=,则1a =C .当2a >或1a <时,{}n a 的最小值不存在D .当3a =时,121111,12222n a a a ⎛⎤++⋅⋅⋅⋅⋅⋅+∈ ⎥---⎝⎦【答案】ACD【分析】A 选项,根据()2110n n n a a a +=--<-求出1n a ≠,再由21311n n n a a a +=--≠求出2n a ≠,从而得到1a ≠且2a ≠,数列{}n a 单调递减,A 正确;B 选项,可举出反例;与抛物线C 交于两点,O 为坐标原点,则下列结论正确的是()A .||4AB ≥B .OA OB ⋅可能大于0C .P 为抛物线上异于A 、B 的点,直线l 与准线交于点T ,当0,t A >为第一象限的点时,若APB α∠=,PF 平分APB ∠,则π2APT +∠=α对于D 选项,因QA QB ⊥,则Q 为以因()()1122,,A x y B x y ,,1222y y t +=,212212x xt +=+,2AB 则以AB 为直径的圆的方程为(22x t -将其与2:4C y x =联立,消去x 化简得:注意到()4228166448y t y ty +---4y =()()2244412yty yty =--++,由题可得,联立方程有2440y ty --=,其判别式恒大于0,则24120y ty ++=的判别式216t -故选:ACD【点睛】关键点点睛:本题为直线与抛物线综合题为常用手段;对于C 选项,在抛物线中有很多的等量关系与成比例的关系分解因式处理.三、填空题13.若()f x 为可导函数,且()()121lim14x f x f x→--=-,则过曲线()y f x =上点()()1,1f 处的切线斜率为14.对于数列n a ,若1,n n a a +是关于x 的方程203n n x c x -+=的两个根,且12a =,则数列{}n c 所有项的和为________.【答案】92##4.5种情况进行分类讨论,利用分组和法来求得n T ,进而可利用极限求得“数列所有项的和”.15.法国数学家加斯帕•蒙日被称为“画法几何创始人”、“微分几何之父”.他发现与椭圆相切的两条互相垂直的切线的交点的轨迹是以该椭圆中心为圆心的圆,这个圆称为该椭圆的蒙日圆.若椭圆()2222:10x y a b a bΓ+=>>的蒙日圆为2223:2C x y a +=,过C 上的动点M 作Γ的两条切线,分别与C 交于P ,Q 两点,直线PQ 交Γ于A ,B 两点,则下列说法,正确的有______.①椭圆Γ②MPQ 面积的最大值为232a③M到Γ的左焦点的距离的最小值为(2a④若动点D 在Γ上,将直线DA ,DB 的斜率分别记为1k ,2k ,则1212k k =-16.已知数列{}n a 的通项公式为52n n a +⎛⎫=-⋅ ⎪⎝⎭,设数列{}n a 的最大项和最小项分别为,M N ,则四、解答题17.已知椭圆()2222:10x y C a b a b+=>>的四个顶点构成的四边形的面积为12.18.已知双曲线2222:1(0,0)x yC a ba b-=>>,四点12346,,4,,3M M M M⎛⎛⎛-⎝⎭⎝⎭⎝⎭中恰有三点在C上.(1)求C的方程;将ADEV沿着DE折起,形成四棱锥-P BCDE,其中点A对应的点为点P,如图2.(1)在图2中,在线段PB 上是否存在一点F ,使得CF ∥平面PDE ?若存在,请求出PFPB的值,并说明理由;若不存在,请说明理由;(2)在图2中,平面PBE 与平面PCD 所成的锐二面角的大小为3π,求四棱锥-P BCDE 的体积.3PB 理由如下:过点C 作CH ED ⊥,垂足为H ,在PE 上取一点M ,使得13PM PE =,连接因为13PM PE =,13PF PB =,所以FM 建立空间直角坐标系,设PEB θ∠=,则()2,0,0D -,()22,2,0C -,(P 则()2,2,0DC =- ,(2,2cos DP = 设平面PCD 的法向量为(),,m x y z =,则220,22cos 2sin m DC x y m DP x y θθ⎧⋅=-+=⎪⎨⋅=+⋅+⎪⎩取sin x θ=,则sin y θ=,cos z θ=-所以()sin ,sin ,cos 1m θθθ=--,,948153线上并解答.已知等差数列{}n a满足________.(1)求数列{}n a的通项公式;(2)求数列{3}na⋅的前n项和.n Tn一次“Z拓展”.如数列1,2第1次“Z拓展”后得到数列1,3,2,第2次“Z拓展”后得到数列1,4,3,5,2.设数列a、b、c经过第n次“Z拓展”后所得数列的项数记为n P,所有项的和记为n S.(1)求1P 、2P ;(2)若2023n P ≥,求n 的最小值;(3)是否存在实数a 、b 、c ,使得数列{}n S 为等比数列?若存在,求a 、b 、c 满足的条件;若不存在,说明n 项和为111n n n n ++(1)求{}n a 的通项公式;(2)设2log n n n b a a =,记{}n b 的前n 项和为n T .若2(1)2n t n T -+≤对于2n ≥且*N n ∈恒成立,求实数t 的取值范围.【答案】(1)2nn a =(2)8t ≤【分析】(1)利用n a 与n S 的关系证得数列{}n a 是等比数列,从而求得2n n a =;22.已知抛物线的顶点为原点,焦点F 在x 轴的正半轴,F 到直线20x +=的距离为4.点2,2N ,不过点N 的直线l 与抛物线交于两点,A B ,且2NA NB k k +=-.(1)求抛物线方程及抛物线的准线方程。
水二中2020七(上)期末复习作业卷(一)复习卷(一) 答案

湖水二中2020-2021七(上)期末复习卷一、选择题(每小题3分,共30分)1.四个有理数-2、1、0、-1,其中最小的是( ) A .1 B .0 C .-1 D .-2 【答案】D.2.下列关于单项式-253xy 的说法中,正确的是( )A .系数是-25,次数是4B .系数是-25,次数是3C .系数是-5,次数是4D .系数是-5,次数是3【答案】A.3.多项式x 3+x 2+x +1的次数是( )A .3B .4C .5D .6【答案】A .4.下列式子中,是一元一次方程的是( )A .5x -3B .x 2-8=x +7C .1+2x =50D . x -y =4 【答案】C.5.如图,将直角三角形绕其斜边旋转一周,得到的几何体为( )【答案】D.6.下面等式成立的是( ) A . 83.5°=83°5' B . 37°12'36"=37.48° C . 24°24'=24. 4° D . 41.25°=41°25' 【答案】C .7.长方形一边的长等于3a +2b ,另一边比它长a -b ,则这个长方形的周长是( )A .14a +6bB .7a +3bC .10a +10bD .12a +8b 【答案】A .8.几个人共同种一批树苗,如果每人种5棵,则剩下3棵树苗未种;如果每人种6棵,则缺4棵树苗.若设参与种树的人数为x 人,则下面所列方程中正确的是( )A .5x +3=6x +4B .5x +3=6x -4C .5x -3=6x -4D .5x -3=6x +4 【答案】B .9.在数轴上有理数a 、b 、c 得点如图所示,若ac <0,a +b <0,则( )A .b +c <0B .⎪b ⎪<⎪c ⎪C .⎪a ⎪>⎪b ⎪D .abc <0 【答案】C .10.如图,将长方形ABCD 分割成1个灰色长方形与148个面积相等的小正方形.若灰色长方形的长与宽之比为5∶3,则AD ∶AB 的值为( ) A .5∶3 B .17∶15 C .47∶29 D .23∶14二、填空题(每小题3分,共18分)11.某市2016年元旦最低气温为—2℃,最高气温为8℃,这一天最高气温比最低气温高_______℃. 【答案】10.12.据统计,全国每年被浪费的食物总量可养活约350 000 000人.用科学记数法表示为______. 【答案】3.5×108.13.已知∠1=32°5′,∠1与∠2互余,则∠2=___________. 【答案】57°55′.14.若关于x 的方程2x -1=3与3103a x--=的解相同,则a 的值是 .15.如图,延长线段AB 到C ,使BC =12AB ,D 为AC 的中点,DC =2,则AB 的长为________.【答案】83.16.对于一个大于1的正整数n 进行如下操作:①将n 拆分为两个正整数a 、b 的和,并计算乘积a×b ;②对于正整数a 、b 分别重复此操作,得到另外两个乘积;③重复上述过程,直至不能再拆分为止(即拆分到正整数1). 当n =6时,所有的乘积的和为_________,当n =100时,所有的乘积的和为_________.三、解答题(共8小题,共72分) 17.(8分)计算:(1) (-1)10×2+(-2)3÷4; (2) 2m -3(2m +3n)+4(n -m).18.(8分)先化简,再求值:2x 2-5x +4-(2x 2-6x ) ,其中x =-3 .19.(8分)解方程:(1) 2x +3=6-4x ; (2) x -24=1-4-3x6.20. (8分)如图,已知∠AOB =56°,∠AOC =10° ,OD 平分∠BOC,求∠BOD 的度数.21.(8分)A 、B 两种型号机器生产同一种产品,已知7台A 型机器一天生产的产品装满8箱后还剩2个,5台B 型机器一天生产的产品装满6箱后还剩8个,每天A 型机器比每台B 型机器一天少生产2个产品,求每箱装多少个产品?22.(本题10分)已知:如图,点C 为线段AB 的中点,点E 为线段AB 上的点,点D 为AE 的中点.(1) 若线段AB =a ,CE =b ,|a -15|+(b -4.5)2=0,求a 、b ; (2) 在(1)的条件下,求线段DE ;(3) 若AB =15,AD =2BE ,求线段CE ;23.(10分)把线段AB 延长到D ,使BD =32AB ,再延长线段BA 到C ,使CA =AB .(1) 请补充图形并求出CD 是AB 的几倍?(2) 补充完后的图中共有几条线段?若图中所有线段长度和为46,求线段AB 的长度; (3) 若AB =6cm ,点E 、F 分别是线段AC 、CD 的中点,(若固定线段CD 不动)当线段AB 以2cm /秒的速度向右运动t 秒时,是否存在点F 是线段BE 的中点.若存在,请求出t 的值;若不存在,请说明理由.DABOCA B24. (12分)已知∠AOC=m°,∠BOC=n°,且m、n满足|21n-40|+(2m-80)2=0.(1)如图1,求∠AOC、∠BOC的度数;(2)如图2,若OM平分∠AOC,ON在∠BOC内部,分∠BOC为1∶3的两部分,请画出ON,并求∠MON的度数;(3)如图3,过点O作射线OD,若2∠AOD=3∠BOD,求∠BOD的大小.学海迷津:数学学习十大方法AB C图1OMAB C图2AB图3O1、配方法所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。
期末联考复习试卷(一) - 打印

中外历史纲要下复习试卷一、选择题:共16小题,每小题3分,共48分。
在每小题给出的四个选项中,只有一项符合题目要求。
1.“古风时代初期的希腊雕刻,与埃及的雕刻风格几乎完全一致;埃及人的测地学,被希腊人发展为几何学;两河流域的神话曾传入希腊,影响了早期希腊的创世以及世代更替的神话;至于天文、历法、货币和计量单位,希腊对西亚的借用更明显。
”这说明()A.古代文明具有多元特征B.早期文明之间存在交流C.欧亚非大陆间联系紧密D.古希腊文明具有先进性2.伊斯兰文化是信奉伊斯兰教的阿拉伯、波斯、突厥等民族共同创造的文化,它立足自身文化传统,在吸收东西方文化的基础上创造了独特的阿拉伯文化,是西方古典文明和现代文明之间的重要纽带。
据此可知伊斯兰文化()A.使世界由分散孤立走向整体B.促进了阿拉伯帝国经济的繁荣C.推动了人类文明进程的发展D.为欧洲文艺复兴运动提供条件3.奇穆文化(约公元1000年到1461年)分布在特鲁吉罗(秘鲁)南北的沿海谷地,崇拜月神“夕”,印加人尊奉的太阳神仅居次要地位。
但是,1200年以后,太阳神作为主神崇拜的地位在这些地区逐渐被确立。
这一变化缘于()A.玛雅文化的兴盛B.阿兹特克文明的传播C.印加帝国的扩张D.自然崇拜现象的流行4.下表为16世纪和17世纪亚洲香料(丁香和胡椒)在西欧的出售价与其收购价的比值(单位:倍)时间丁香胡椒16世纪73—18413—1617世纪67—9注:16比,17世纪的数据主要来源于印尼香料的采购价及其在荷兰的出售价对比。
A.贵金属不断涌入引发价格革命B.三角贸易降低了商品交易成本C.全球航路的开辟引发商业革命D.机器大规模运用降低生产成本5.1492年哥伦布首次航行到美洲大陆,这是世纪性大规模航海,也是旧大陆与新大陆之间联系的开始。
这种生态学上的变革,称之为“哥伦布大交换”。
以下植物品种来自美洲的有()①葡萄②花生③南瓜④燕麦A.①②B.①④C.②③D.③④6.据统计:丹麦于1792年通过政府法令废除了奴隶贸易;美国国会从1794年到1802年通过法律禁止美国公民和船只参与奴隶贸易;自1814年起,英国政府与几乎所有海上大国都缔结了禁止奴隶贸易的双边条约。
苏教版2022-2023扬州市育才小学五年级数学下册期末复习试卷(一)及答案

五年级数学下册期末复习试卷(一)一 、选择题。
1. 一根绳被剪成两段,第一段长52米,第二段占全长的52。
比较两段的长度,发现( )。
A.第一段长 B.第二段长 C.一样长 D.无法判断2. 把 27 的分子加上10,要使分数的大小不变,分母应加上( )。
A.10B. 42C. 35 D .283. 一个五位数万位上是最小的质数,十位上是最小的合数,其余各个数位上数字相同,这个五位数一定是( )。
A.2的倍数B.3的倍数C.5的倍数D.无法判断4. 小军、小明两人读同一篇文章,小军用51小时,小明用了61小时,( )读得快。
A.小军 B.小明 C.一样快 D.无法判断5. 分母是8的最简真分数有( )个。
A .2B .3C .4D .76.学校合唱社团,每组5人或每组8人都多1人,学校合唱社团最少有( )。
A .81 人B .41人C .40 人D .39人7. 右图中,正方形的面积是10平方厘米,圆的面积是( )。
A .2.5π平方厘米B .4π 平方厘米C .5π平方厘米D .6.25π平方厘米8. 古希腊人认为:如果一个数恰好等于它的所有因数(本身除外)相加之和,那么这个数就是“完美数”。
下面各数中,是“完美数”的是( )。
A.14B.28C.35D.519.要反映一个人一天的体温变化情况,应绘制( )。
A.复式统计表B.单式统计表C.条形统计图D.折线统计图10. 如右图,小红从甲地到乙地有两条路线可走,走哪一条路线近一些?( )。
A. 走①号路线近B. 走②号路线近C.一样近D.无法确定二、填空题。
1.( )÷20=)(15=53=15)(=( )(此空填小数)。
2. 一个数最大因数与最小倍数的和是36,把这个数分解质因数,是( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学(理)综合卷(一)
命题人:史磊 审题人:李向华 时间:2016.12.1
一、选择题:本大题共12小题。
每小题5分,共60分.在每小题给出的四个选项中。
(1)设集合
}23{<<-∈=m Z m M ,
}
31{≤≤-∈=n Z n N ,则=⋂N M
A .}1,0{ B. }1,0,1{- C. }2,1,0{ D }2,1,0,1{- (2)设a ,b ∈R 且b ≠0,若复数3
bi)(a +是实数,则
A . 2
2
3a b = B. 2
2
3b a = C. 2
2
9a b = D.2
2
9b a = (3)函数x x
x f -=
1
)(的图像关于 A . y 轴对称 B.直线y=-x C.坐标原点对称 D.直线y=x
(4)若)1,(1
-∈e x ,x ln =a ,x ln 2=b ,x 3
ln =c ,则
A .c b a << B. b a c << C. c a b << D. a c b <<
(5)设变量x,y 满足约束条件:2
,22,
-≥≤+≥x y x x y 则y x z 3-=的最小值为:
A .-2 B.-4 C. -6 D.-8
(6)从20名男同学,10名女同学中任选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的概率为
A .
299 B. 2910 C. 2919 D. 29
20 (7)(
)(
)
4
611x x +-
的展开式中x 的系数是
A .-4 B.-3 C.3 D.4
(8)若动直线a x =与函数x x f sin )(=和x x g cos )(=的图像分别交于M 、N 两点,则MN 的最大值为
A .1 B. 2 C.
3 D.2
(9)设1>a ,则双曲线1)
1(2
2
22=++a y a x 的离心率e 的取值范围是 A .)2,2( B. )5,2( C. )5,2( D. )5,2(
(10)已知正四棱锥S-ABCD 的侧棱长与底面边长都相等,E 是SB 的中点,则AE 、SD 所成的角的余弦值为 A .
31 B. 32 C. 33 D. 3
2
(11)等腰三角形两腰所在直线的方程分别为02=-+y x 和047=--y x ,原点在等腰三角形的底边上,则底边所在直线的斜率为 A .3 B. 2 C. 31-
D. 2
1
- (12)已知球的半径为2,相互垂直的两个平面分别截球面得两个圆.若两圆的公共弦长为2,则
两圆的圆心距等于
A .1 B. 2 C. 3 D. 2
二、填空题:本大题共4小题。
每小题5分.共20分.把答案填在题中横线上. (13)设向量a=(1,2),b=(2,3).若向量λa+b 与向量c=(4,-7)共线,则λ= . (14)设曲线ax
e y =在点(0,1)处的切线与直线012=++y x 垂直,则a= .
(15)已知F 为抛物线C :x y 42
=的焦点,过F 且斜率为1的直线交C 于A 、B 两点.设FB FA >.
则FA 与FB 的比值等于 .
(16)平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行.类似地,写出
空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件① ; 充要条件② . (写出你认为正确的两个充要条件)
三、解答题:本大题共6小题,70分.解答应写出文字说明、证明过程和演算步骤. (17)(本小题满分10分) 在△ABC 中,135cos -=B ,54
cos =C . (Ⅰ)求A sin 的值; (Ⅱ)求△ABC 的面积2
33
=
ABC
S
,求BC 的长.
(18)(本大题满分12分)
购买某种保险,每个投保人每年度向保险公司交纳保费a 元,若投保人在购买保险的一年度内出险,则可以获得10000元的赔偿金.假定在一年度内有10000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10000元的概率为4
10999
.01-.
(Ⅰ)求一投保人在一年度内出险的概率p ;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元).
(19)( 本大题满分12分)
如图,正四棱柱1111D C B A -ABCD 中,421==AB AA ,点E 在上且EC E C 31=. (Ⅰ)证明:⊥C A 1平面BED ; (Ⅱ)求二面角B -DE -A 1的大小.
(20) (本大题满分12分)
设数列}{n a 的前n 项和为n S .已知a a =1,n
n n S a 31+=+,*N n ∈. (Ⅰ)设n
n n S b 3-=,求数列}{n b 的通项公式;
(Ⅱ) 若n n a a ≥+1,*N n ∈,求a 的取值范围.
(21) (本大题满分12分)
设椭圆中心在坐标原点,A(2,0)、B(0,1)是它的两个顶点,直线)0(>=k kx y 与AB 相交于点D ,与椭圆相较于E 、F 两点.
(Ⅰ)若 DF ED 6=,求k 的值; 求四边形AEBF 面积的最大值.
(22) (本大题满分12分) 设函数x
x
x f cos 2sin )(+=
.
(Ⅰ)求)(x f 的单调期间;
(Ⅱ)如果对任何0≥x ,都有ax x f ≤)(,求a 的取值范围.。
