绳杆端速度分解模型问题的分析含答案
2020年高考物理考点练习4.2 绳端速度分解问题(解析版)

2020年高考物理100考点最新模拟题千题精练第四部分 曲线运动 专题4.2绳端速度分解一.选择题1. (2019安徽江淮十校联考)如图所示,重物M 沿竖直杆下滑,并通过 一根不可伸长的细绳带动小车沿水平面向右运动。
若当滑轮右侧的绳与竖直方向成β角,且重物下滑的速率为v 时 ,滑轮左侧的绳 与水平方向成α角,则小车的速度为( )A .sin sin v βα B .sin cos v βα C .cos sin v βα D .cos cos v βα【参考答案】.D【名师解析】设小车的速度为v 车,沿细绳方向的分速度为v 3=v 车cos α,重物M 速度沿细绳方向的分速度v 1=v cos β。
由于细绳不可伸长,小车和重物沿细绳方向的速度相等,即v 车cos α= v cos β,解得v 车=cos cos v βα,选项D 正确,2(2018洛阳联考)如图所示,长为L 的轻直棒一端可绕固定轴O 转动,另一端固定一质量为m 的小球,小球搁在水平升降台上,升降平台以速度v 匀速上升,下列说法正确的是 ( )A .小球做匀速圆周运动B .当棒与竖直方向的夹角为α时,小球的速度为vL cos αC .棒的角速度逐渐增大D .当棒与竖直方向的夹角为α时,棒的角速度为vL sin α【参考答案】D【名师解析】棒与平台接触点(即小球)的运动可视为竖直向上的匀速运动和沿平台向左的运动的合成.小球的实际运动即合运动方向是垂直于棒指向左上方,如图所示.设棒的角速度为ω,则合速度v 实=ωL ,沿竖直向上方向上的速度分量等于v ,即ωL sin α=v ,所以ω=vL sin α,小球速度为v 实=ωL =vsin α,由此可知棒(小球)的角速度随棒与竖直方向的夹角α的增大而减小,小球做角速度越来越小的变速圆周运动.选项ABC 错误D 正确。
3.(2018湖南师大附中月考)如图所示,A 、B 两球分别套在两光滑的水平直杆上,两球通过一轻绳绕过一定滑轮相连,现在A 球以速度v 向左匀速移动,某时刻连接两球的轻绳与水平方向的夹角分别为α、β,下列说法正确的是( )A .此时B 球的速度为cos αcos βvB .此时B 球的速度为sin αsin βvC .在β增大到90°的过程中,B 球做匀速运动D .在β增大到90°的过程中,B 球做加速运动 【参考答案】.AD【名师解析】由于两球沿绳方向的速度大小相等,因此v cos α=v B cos β,解得v B =vcos αcos β,A 项正确,B 项错误;在β增大到90°的过程中,α在减小,因此B 球的速度在增大,B 球在做加速运动,C 项错误,D 项正确.4.如图所示,一辆货车利用跨过光滑定滑轮的轻质缆绳提升一箱货物,已知货箱的质量为m0,货物的质量为m,货车以速度v向左做匀速直线运动,在将货物提升到图示的位置时,下列说法正确的是()A.货箱向上运动的速度大于vB.缆绳中的拉力F T等于(m0+m)gC.货箱向上运动的速度等于v cosθD.货物对货箱底部的压力等于mg【参考答案】 C【名师解析】将货车的速度进行正交分解,如图所示。
绳、杆、光线末端速度的分解问题
六、图3、图4中绳一端做匀速直 线运动,另一端也匀速吗?
练习:如图,在不计滑轮摩擦 和绳子质量的条件下,当小车 匀速向右运动时,物体A的受 力情况是 ( ) A.绳的拉力大于A的重力 B.绳的拉力等于A的重力 c.绳的拉力小于A的重力 D.拉力先大于重力,后变 为小于重力
v/
v
图3
七、若放在墙角的均匀直杆A端靠在
习题练习
v/
v M m 图 3
图4
习题练习
v/
v α M
m
图 3
图4
五、如果绳两端速度分析与绳都不 在一条直线上,两端的速度如何联系?
若A车以速度v1向右匀速 运动,当绳与水平面的夹角分 别为α和β时,B车的速度V2是 多少?
小车在以恒定速度V1前进的 过程中,小球始终没有离开球 面;求当绳子与小球速度方向 夹角为β时小球的速度V2
九、跨过同一高度处的定滑轮的细线连接着质 量相同的物体A和B,A套在光滑水平杆上,定滑轮 离水平杆的高度为h,开始时让连着A的细线与水 平杆的夹角θ1 = 53°,由静止释放B,你能通过A、 B两端速度关系结合物体受力情况分析清两个物体 做什么样的运动吗?(一个物体速度最大,另一个 物体速度也最大吗?)你会求A获得的最大速度吗?
h
)530
B
A
1、不可伸长的绳或杆尽管各点的速度可能不
同,但各点沿绳或杆方向的速度相同。
2、当绳或杆末端运动方向与绳、杆不在一条 直线上时,把该断速度分解 (绳子拉长或缩短 ) 分 沿绳方向 解 垂直于绳方向(以滑轮支点为圆心的圆周 到 运动)
3、这类问题除了会分析两端速度关系外,还 要善于结合力分析过程,以后还要会用过程规律求 解。
竖直墙上,B端放在水平地面,当滑到图 示位置时,B点速度为v,你会求A点速度 吗?(α为已知)
绳(杆)端速度分解模型问题的分析(含答案)

绳(杆)端速度分解模型一、基础知识1、模型特点沿绳(或杆)方向的速度分量大小相等.2、思路与方法3(1)(2)二、练习1m,忽略答案解析(1)0绳以定滑轮为圆心的摆动,它不改变绳长.即速度v分解为沿绳方向和垂直绳方向的分速度,如图所示,v cosθ=v0,v=.拉力F产生竖直向上拉物体和水平向右拉物体的效果,其水平分量为F cosθ,加速度a=.2、如图所示,一人站在岸上,利用绳和定滑轮拉船靠岸,在某一时刻绳的速度为v,绳AO段与水平面的夹角为θ,OB段与水平面的夹角为α.不计摩擦和轮的质量,则此时小船的速度多大?解析小船的运动引起了绳子的收缩以及绳子绕定滑轮转动的效果,所以将小船的运动分解到绳子收缩的方向和垂直于绳子的方向,分解如图所示,则由图可知v A=.答案3、如图所示,在水平地面上做匀速直线运动的小车,,物体所ABCD答案解析变大,物体做加速4、穿在光滑的竖直杆上,当以速度v0θ)A.v0C.v0答案解析由运动的合成与分解可知,物体A参与两个分运动:一个是沿着与它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动.而物体A实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A的合运动,它们之间的关系如图所示.由几何关系可得v=,所以D项正确.5、如图,人沿平直的河岸以速度v行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行.当绳与河岸的夹角为α时,船的速率为()A.v sinα B.C.v cosα D.答案 C解析如图所示,把人的速度沿绳和垂直绳的方向分解,由几何知识有v船=v cosα,所以C正确,A、B、D错误.6、A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上,现物体A以v1的速度向右匀速运动,当绳被拉成与水平面夹角分别为α、β时,如图所示.物体B的运动速度v B为(绳始终有拉力A.C.v答案解析v绳B由于所以。
(3) 绳杆末端速度分解
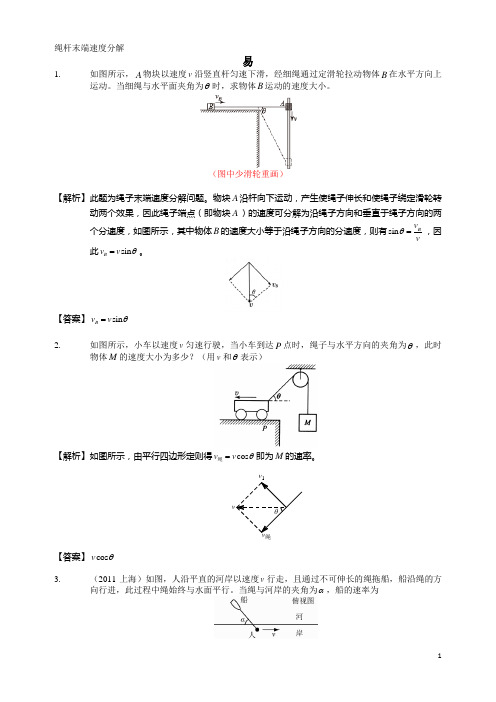
绳杆末端速度分解易1.如图所示,A 物块以速度v 沿竖直杆匀速下滑,经细绳通过定滑轮拉动物体B 在水平方向上运动。
当细绳与水平面夹角为θ时,求物体B 运动的速度大小。
(图中少滑轮重画)【解析】 此题为绳子末端速度分解问题。
物块A 沿杆向下运动,产生使绳子伸长和使绳子绕定滑轮转动两个效果,因此绳子端点(即物块A )的速度可分解为沿绳子方向和垂直于绳子方向的两个分速度,如图所示,其中物体B 的速度大小等于沿绳子方向的分速度,则有sin B vvθ=,因此sin B v v θ=。
【答案】 sin B v v θ=2.如图所示,小车以速度v 匀速行驶,当小车到达P 点时,绳子与水平方向的夹角为θ,此时物体M 的速度大小为多少?(用v 和θ表示)【解析】 如图所示,由平行四边形定则得cos v v θ=绳即为M 的速率。
【答案】 cos v θ 3. (2011上海)如图,人沿平直的河岸以速度v 行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行。
当绳与河岸的夹角为α,船的速率为v 绳A .sin v αB .sin vα C .cos v αD .cos v α【答案】 C中4.在水平面上有A 、B 两物体,通过一根跨过滑轮的不可伸长的轻绳相连接,现A 物体以A v 的速度向右匀速运动,当绳被拉成与水平面夹角分别为α、β时(如图所示),B 物体的运动速度B v 为(绳始终有拉力)A .sin /sin A v αβB .cos /sin A v αβC .sin /cos A v αβD .cos /cos A v αβ【解析】 将A 和B 的速度分别分解为沿着绳的速度1A v 、1B v 和垂直于绳的速度2A v 、2B v ,则1cos A A v v α=,1cos B B v v β=,因为轻绳不可伸长,所以沿着绳方向速度大小相等,即11A B v v =,有cos /cos B A v v αβ=。
模型10绳杆关联运动模型(解析版)-备战2021年高考物理模型专题突破

10绳杆关联运动模型1.(2020·辉县市第二高级中学高一月考)如图所示,AB 杆以恒定角速度ω绕A 点转动,并带动套在光滑水平杆OC 上的质量为M 的小环运动,运动开始时,AB 杆在竖直位置,则小环M 的速度将( )A .逐渐增大B .先减小后增大C .先增大后减小D .逐渐减小【答案】A 【详解】设经过时间t ,OAB t ω∠=,则AM 的长度为cos h t ω,则AB 杆上M 点绕A 点的线速度cos hv tωω=⋅.将小环M 的速度沿AB 杆方向和垂直于AB 杆方向分解,垂直于AB 杆上分速度等于M 点绕A 点的线速度v ,则小环M 的速度2cos cos v hv t tωωω==',随着时间的延长,则小环的速度的大小不断变大.故A 正确,BCD 错误. 故选A .2.(2020·浙江高一专题练习)如图所示,套在细杆上的小环沿杆匀速下滑,其在水平方向和竖直方向的分运动分别是( )A .匀速运动,匀速运动B .匀加速运动,匀加速运动C .匀速运动,匀加速运动D .匀加速运动,匀速运动【答案】A 【详解】小环沿杆匀速下滑,说明小环的合力为零,所以小环在水平方向所受合力为零,竖直方向的合力也为零,即小环在水平方向和竖直方向都做匀速直线运动,故A 正确.3.(2020·四川眉山市·高一期中)如图所示,人用轻绳通过定滑轮拉穿在光滑竖直杆上的物块A ,人以速度v 0向左匀速拉绳,某一时刻,绳与竖直杆的夹角为θ,与水平面的夹角为α,此时物块A 的速度v 1为A .10sin cos v v αθ=B .01sin sin v v αθ=C .10cos cos v v αθ=D .01cos cos v v αθ=【答案】D 【解析】对人进行速度分解,如图所示:可知:'0cos v v α=对物块A 进行速度分解,如图所示,则可知:'1cos v v v cos cos αθθ==,故选项D 正确,选项ABC 错误. 点睛:解决本题的关键会对速度进行分解,要正确找到合运动与分运动,注意两个物体沿着绳子方向的分速度相等.4.(2020·湖南娄底市·娄底一中)两根光滑的杆互相垂直地固定竖直平面内.上面分别穿有一个小球.小球a 、b 间用一细直棒相连如图.释放后两球都开始滑动.当细直棒与竖直杆夹角为α时,两小球实际速度大小之比v a ∶v b 等于A .sin α∶1B .cos α∶1C .tan α∶1D .cot α∶1【答案】C 【详解】速度的合成与分解,可知,将两球的速度分解,如图所示,则有:a v v cos α=杆 ,而b v v sin α=杆,那么两小球实际速度之比 v a :v b =sin α:cos α=tan α:1故C 正确,ABD 错误. 故选C .5.(2020·运城市景胜中学高一期末)如图所示,小球a 、b 用一细直棒相连,a 球置于水平地面,b 球靠在竖直墙面上,释放后b 球沿竖直墙面下滑,当滑至细直棒与水平面成θ角时,两小球的速度大小之比为( )A .absin v v θ= B .ab cos v v θ= C .ab tan v v θ= D .abcot v v θ= 【答案】C 【详解】如图所示,将a 球速度分解成沿着杆与垂直于杆方向,同时b 球速度也是分解成沿着杆与垂直于杆两方向。
高中物理运动的合成与分解之绳杆模型专题

绳(杆)端速度分解模型1.模型特点沿绳(杆)方向的速度分量大小相等. 2.思路与方法合速度→绳(杆)拉物体的实际运动速度v分速度→⎩⎪⎨⎪⎧其一:沿绳(杆)的速度v 1其二:与绳(杆)垂直的分速度v 2方法:v 1与v 2的合成遵循平行四边形定则. 3.解题的原则把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量,根据沿绳(杆)方向的分速度大小相等求解.常见的模型如图7所示.关联体:通过绳子、轻杆或者其他之间联系的两个相互作用的物体 【核心方法点拨】(1)如果物体是通过杆或者绳子关联,由于高中研究的绳都是不可伸长的,杆都是不可伸长和压缩的,即绳或杆的长度不会改变,所以解题的原则是:把物体的实际速度分解为垂直于绳(或杆)和平行于绳(或杆)的两个分量,根据沿绳(杆)方向的分速度大小相同求解.(2)若两物体是通过接触面接触的,则将物体的实际速度沿平行与垂直接触面方向进行分解,在垂直接触面方向上速度相等题型一 通过轻绳关联1.(2021·安徽·定远县育才学校高一阶段练习)如图所示,物体A 和B 的质量均为m ,分别与跨过定滑轮的轻绳连接(不计绳与滑轮、滑轮与轴之间的摩擦)。
现用水平变力F 拉着物体A 沿水平方向向右做匀速直线运动。
则下列说法中正确的是( )A .物体B 做匀速直线运动 B .物体B 做加速直线运动C .绳子对物体B 的拉力等于mgD .绳子对物体B 的拉力小于mg2.(2021·河南·濮阳南乐一高高二开学考试)如图所示,已知m A =3m B ,C 为内壁光滑、半径为R 的半圆形轨道,D 为定滑轮,开始时A 、B 均处于静止状态,释放后,A 沿圆弧轨道下滑,若已知A 球下滑到最低点时的速度为v ,则此时B 的速度为( )A vB .12v C v D .2v3.(2022·广东高州·高一期末)如图所示绳子通过固定在天花板上的定滑轮,左端与套在固定竖直杆上的物体A 连接,右端与放在水平面上的物体B 相连,到达如图所示位置时,绳与水平面的夹角分别为夹角为37︒、53︒,两物体的速率分别为A v 、B v ,且此时20m /s 3+=A B v v ,3sin 375︒=、4cos375︒=,则A v 的大小为( )A .10m/s 3 B .4m/s 3C .2m/sD .4m/s4.(多选)(2022·山东·威海市教育教学研究中心高一期末)如图所示,不可伸长的轻绳绕过光滑定滑轮C 与物体A 连接,绳的另一端和套在固定竖直杆上的物体B 连接,开始时,BC 连线沿水平方向。
高一物理下学期期中综合复习专题04 绳和杆的关联速度的合成与分解问题(解析版)
高一物理下学期期中综合复习(重点专练模拟检测)专题04 绳和杆的关联速度的合成与分解问题特训专题 特训内容专题1 绳的关联速度的合成与分解问题(1T—6T )专题2 杆的关联速度的合成与分解问题(7T—12T )【典例专练】一、绳的关联速度的合成与分解问题1.如图所示,绳子通过固定在天花板上的定滑轮,两端分别与同一水平面上的A B 、两物体连接,当两物体到达如图所示位置时,绳与水平面的夹角分别为37︒、53︒,两物体的速度大小分别为A B v v 、,已知3sin 375︒=、4cos375︒=,则A v 与B v 之比为( )A .3:4B .4:3C .4:5D .5:4【答案】A【详解】设此时绳子的速度大小为v 绳,将A 、B 的速度分别沿绳的方向和垂直绳的方向分解,可得 A cos37v v =绳;B co 53s v v =绳解得:3:4A B v v =故选A 。
2.如图所示,人用轻绳通过定滑轮拉穿在光滑竖直杆上的物块A ,人以速度v 0向左匀速拉绳,某一时刻,绳与竖直杆的夹角为θ,与水平面的夹角为α,此时物块A 的速度v 1为( )A .v 1=v 0sin αcos θB .v 1=0sin sin v αθC .v 1=v 0cos αcos θD .v 1=0cos cos v αθ【答案】D【详解】将A 的速度分解为沿绳子方向和垂直于绳子方向,如图所示拉绳子的速度等于A 沿绳子方向的分速度,设该速度为v ,根据平行四边形定则得,A 的实际速度为1cos v v θ= 同理对人的速度分解可得0cos v v α=联立可得01cos cos v v αθ=故选D 。
3.如图所示,一辆货车利用跨过光滑定滑轮的轻质不可伸长的缆绳提升一箱货物,货车向左做匀速直线运动,在将货物提升到图示的位置时,货物速度为v ,连接货车的缆绳与水平方向夹角为θ,不计一切摩擦,下列说法正确的是( )A .货车的速度等于v cos θB .货车的速度等于cos vθC .货物处于超重状态D .货车的对地面的压力大于货车的重力 【答案】BC【详解】AB .货车沿着绳子方向的速度等于货箱的速度,因此cos v v θ=车可得cos vv θ=车,A 错误,B 正确; C .货车匀速前进过程中,绳子倾角θ逐渐减小,可得货箱的速度逐渐增大,因此货箱向上做加速运动,处于超重状态, C 正确;D .由于货车受到缆绳的拉力,货车对地面的压力小于货车的重力,D 错误。
绳船模型中的速度和加速度关系深度分析
绳船模型中的速度和加速度关系深度分析摘要:速度合成和分解中,绳子两端绳上的点的速度沿绳子方向的分量才相等,而不是绳子两端的物体的速度沿绳子方向的分量相等。
同时,绳子两端的点的加速度沿绳子方向的分量也不是单纯意义上的相等,本文通过绳船模型定量给出速度及加速度的关系。
关键词:速度加速度分解相等绳杆端速度分解模型中,在绳子不松弛的情况下,在同一时刻必须具有相同的沿杆绳方向的分速度[1]。
这里的速度分量指,绳子两端点的速度沿绳子方向分量,而不是绳子两端物体的速度分量。
绳子两端点的速度与绳子两端物体的速度有很大的区别,如图1所示,数值方向的动滑轮模型,绳子端点C的速度是绳子两端物体(滑轮)速度的两倍。
本文将通过绳船模型详细说明速度关系。
图1在教学过程中,学生从速度关系直接类比加速度关系,绳子两端的点的加速度沿绳方向分量相等,这样的理解显然是不对的。
如图2所示,物体绕圆心o作匀速圆周运动,半径为r,速率为v,分析绳子两端的点的加速度沿绳方向分量的关系?绳子一端物体的加速度,这个加速度为物体的合加速度,此加速度沿半径方向的分量为,绳子一端圆心的加速度0,此加速度沿半径方向的分量为0,显然绳子两端的点的加速度沿绳方向的分量不相等。
本文将通过绳船模型详细说明加速度关系。
1、单绳船模型中速度关系如图3所示,人用轻质细绳通过定滑轮牵引小船靠岸,如果收绳的速度为,则在绳与水平方向夹角为的时刻,船头到滑轮的距离为,船的速度有多大[2]?分析:船在水面在直线运动,实际发生的运动就是合运动,这个合运动有两个运动效果,一是使小船沿绳拉力方向以速度运动,二是使小船随绳的一端绕滑轮做顺时针方向的圆周运动。
靠近船头绳上的速度和船的速度一样,由于绳子不松软,所以沿绳方向速度分量相等:①由①式变形得船的速度:②2、单绳船模型中加速度关系如图3所示,如果人拉绳子以恒定的加速度向前奔跑,则在绳与水平方向夹角为的时刻,船头到滑轮的距离为,船的速度有多大?错误的理解,由于绳子不松软,所以沿绳方向加速度分量相等。
(完整版)绳、杆相关联物体的速度求解带答案
绳、杆相关联物体的速度求解“关联速度”问题特点:沿杆或绳方向的速度分量大小相等。
绳或杆连体速度关系:①由于绳或杆具有不可伸缩的特点,则拉动绳或杆的速度等于绳或杆拉物的速度。
②在绳或杆连体中,物体实际运动方向就是合速度的方向。
③当物体实际运动方向与绳或杆成一定夹角时,可将合速度分解为沿绳或杆方向和垂直于绳或杆方向的两个分速度。
常用的解题思路和方法:先确定合运动的方向,即物体实际运动的方向,然后分析这个合运动所产生的实际效果,即一方面使绳或杆伸缩的效果;另一方面使绳或杆转动的效果。
以确定两个分速度的方向,沿绳或杆方向的分速度和垂直绳或杆方向的分速度,而沿绳或杆方向的分速度大小相同。
1.一绳一物题型⑴拉的物体匀速运【例1】如图1所示, 人在岸上拉船,已知船的质量为m,水的阻力恒为f,当轻绳与水平面的夹角为θ时,船的速度为v,此时人的拉力大小为T,则此时A.人拉绳行走的速度为v cosθB.人拉绳行走的速度为v/cosθC.船的加速度为D.船的加速度为解析:船的速度产生了两个效果: 一是滑轮与船间的绳缩短, 二是绳绕滑轮顺时针转动, 因此将船的速度进行分解如图所示, 人拉绳行走的速度v人=v cosθ, A对, B错;绳对船的拉力等于人拉绳的力,即绳的拉力大小为T,与水平方向成θ角,因此T cosθ-f=ma,解得:,C正确,D错误。
答案:AC。
点评:人拉绳行走的速度即绳的速度,易错误地采用力的分解法则,将人拉绳行走的速度。
即若按图3所示进行分解,则水平分速度为船的速度,得人拉绳行走的速度为v/cosθ,会错选B选项。
⑵匀速拉动物体【例2】如图4所示,在河岸上利用定滑轮拉绳索使小船靠岸,拉绳的速度为v,当拉船头的绳索与水平面的夹角为α时,船的速度是多少?2.两绳一物题型【例3】如图7所示,两绳通过等高的定滑轮共同对称地系住一个物体A,两边以v速度匀速地向下拉绳。
当两根细绳与竖直方向的夹角都为60°时,物体A上升的速度多大?解析:以右边绳子为研究对象,应用绳连体模型的结论,当绳端物体A在做既不沿绳方向,又不垂直于绳方向运动时,一般要将绳物体A的真实运动分解到沿绳收缩方向和垂直于绳子方向的两个分运动。
突破难点:绳末端速度分解问题及练习
突破难点:绳末端速度分解问题及练习1.如图所示,套在竖直细杆上的环 A 由跨过定滑轮的不可伸长的轻绳与重物B 相连.由于B 的质量较大,故在释放 B 后,A 将沿杆上升,当 A 环上升至定滑轮的连线处于水平位置 时,其上升速度 v i 丰0,若这时B 的速度为V 2,则( )B . V 2>v iD . V 2= 0[答案]D2.如图所示,A B 两物体系在跨过光滑定滑轮的一根轻绳的两端,当 A 物体以速度v向左运动时,系 A B 的绳分别与水平方向成 a B 角,此时B 物体的速度大小为 ______________ , 方向 _________ .[答案]cosa 水平向右cos 3[解析]根据A B 两物体的运动情况,将两物体此时的速度v 和V B 分别分解为两个分速度v i (沿绳的分量)和V 2(垂直绳的分量)以及vB i (沿绳的分量)和vB 2(垂直绳的分量),如图, 由于两物体沿绳的速度分量相等, v i = vBi , v cos a= V B Cos 3Cos a则B 物体的速度方向水平向右,其大小为V B =vcos3A. V 2= v i[解析]环上升过程其速度v i 可分解为两个分速度 v //和v i ,如图所示, v // = V 2 =v i c os 0,当 0= 90 °寸, cos 0= 0,3. 如图所示,点光源S到平面镜M的距离为d.光屏AB与平面镜的初始位置平行.当平面镜M绕垂直于纸面过中心O的转轴以3的角速度逆时针匀速转过 30°时,垂直射向平面[答案]83d镜的光线so 在光屏上的光斑P 的即时速度大小为多大?[解析] 当平面镜转过 30°角时,反射光线转过60 °角,反射光线转动的角速度为平面镜转动角速度的 2倍,即为2 3将P 点速度沿OP 方向和垂直于 OP 的方向进行分解,可得:v cos60 ° = 2w OP= 4w d ,所以 v = 8 cod .4.如图6所示,用一根长杆和两个定滑轮的组合装置来提升重物 长杆的一端放在地上通过铰链联结形成转轴,其端点恰好处于左侧滑轮正下方O 点处,在杆的中点 C 处拴一细绳,绕过两个滑轮后挂上重物MC 点与O 点距离为I .现在杆的另一端用力•使其逆时针匀速转动,由竖直位置以角速度w 缓缓转至水平位置(转过了 90°角),此过程中下述说法中正确的是A. 重物M 做匀速直线运动B. 重物M 做匀变速直线运动C. 重物M 的最大速度是 3D. 重物M 的速度先减小后增大解析:由题知,C 点的速度大小为 V C = 3,设V C 与绳之间的夹角为 0,把V C 沿绳和垂 直绳方向分解可得,V 绳=V C COS 0,在转动过程中 0先减小到零再反向增大,故 V 绳先增大后减小,重物 M 做变加速运动,其最大速度为w l , C 正确.5. 一辆车通过一根跨过定滑轮的轻绳子提升一个质量为m 的重物,开始车在滑轮的正下方, 绳子的端点离滑轮的距离是 H.车由静止 开始向左做匀加速运动,经过时间 t 绳子与水平方向的夹角为 0,如 图9所示,试求:⑴车向左运动的加速度的大小;⑵重物m 在t 时刻速度的大小.H解析:⑴汽车在时间t 内向左走的位移:X = t a n -0又汽车匀加速运动1x = 2at图6cos 06•如图4 — 1 — 3所示,物体A 和B 质量均为m 且分别与轻绳连接跨 过光滑轻质定滑轮, B 放在水平面上,A 与悬绳竖直•用力 F 拉B 沿 水平面向左匀速运动过程中,绳对 A 的拉力的大小是 ( )A. 一定大于 mgB.总等于 mgC.一定小于mg D.以上三项都不正确解析:物体B 向左的速度vB 是合速度, 根据其效果,分解为如右图所示的两 个速度v 1和v 2,其中v 2 = vA ,又因为v 2 =vB cos 0,所以当物体 B 向左匀速运动时,vB 大小不变,0变小,cos 0变大,即A 向上做加速运动,由牛 顿第二定律得 F T — mg= ma 所以绳的拉力 F T= mg+ ma> mg 故正确答 案为A.7.如图4 — 1 — 6所示,一个长直轻杆两端分别固定一个小球 A 和B,两球的质量均为 m ,两 球半径忽略不计,杆 AB 的长度为I ,现将杆AB 竖直靠放在竖直墙上, 轻轻振动小球 B 使小球B 在水平地面上由静止向右运动,求当A 球沿墙下滑距离为;时AB 两球的速度V A 和V B 的大小.(不计一切摩擦)V77777777777777777777777^A B 两球速度的分解情况如图4— 1 — 7所示,由题意知,0= 30°由运动的合成与分解得V A Sin 0= V B COS 02x所以a =〔2H2t tan 0(2)此时汽车的速度v 汽=at = t2H_ tan 0由运动的分解知识可知,汽车速度 v 汽沿绳的分速度与重物 m 的速度相等,即v 物=v 汽得v 物=2H cos 0t tan 0答案:2H'2t tan 02H Cost tan 0又A、B组成的系统机械能守恒,所以l 1 2 1 2 -mg 2= 2m\A + 2m\B ②由①②解得V A= 1 3gl , V B = 1 gl .欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绳(杆)端速度分解模型
一、基础知识
1、模型特点
沿绳(或杆)方向的速度分量大小相等.
2、思路与方法
合运动→绳拉物体的实际运动速度v
分运动→⎩⎨
⎧
其一:沿绳(或杆)的速度v 1
其二:与绳(或杆)垂直的分速度v 2
方法:v 1与v 2的合成遵循平行四边形定则.
3、解决此类问题时应把握以下两点:
(1)确定合速度,它应是小船的实际速度;
(2)小船的运动引起了两个效果:一是绳子的收缩,二是绳绕滑轮的转
动.应根据实际效果进行运动的分解.
二、练习
1、如图所示,轻绳通过定滑轮拉动物体,使其在水平面上运动.若拉绳的速度为v 0,当绳与水平方向夹角为θ时,物体的速度v 为________.若此时绳上的拉力大小为F ,物体的质量为m ,忽略地面的摩擦力,那么,此时物体的加速度为________.
答案
v
cos θ
F cos θ
m
解析物体的运动(即绳的末端的运动)可看做两个分运动的合成:
(1)沿绳的方向被牵引,绳长缩短,缩短的速度等于v0;(2)垂直于
绳以定滑轮为圆心的摆动,它不改变绳长.即速度v分解为沿绳
方向和垂直绳方向的分速度,如图所示,v cos θ=v0,v=
v
0 cos θ
.
拉力F产生竖直向上拉物体和水平向右拉物体的效果,其水平分量为F cos θ,加速度
a=F cos θ
m
.
2、如图所示,一人站在岸上,利用绳和定滑轮拉船靠岸,在某一时刻绳的速度为v,绳AO
段与水平面的夹角为θ,OB段与水平面的夹角为α.不计摩擦和轮的质量,则此时小船的速度多大
解析小船的运动引起了绳子的收缩以及绳子绕定滑轮转动的效果,
所以将小船的运动分解到绳子收缩的方向和垂直于绳子的方向,
分解如图所示,则由图可知
v A =
v cos θ
.
答案
v cos θ
3、如图所示,在水平地面上做匀速直线运动的小车,
通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一
时刻的速度分别为v1和v2,绳子对物体的拉力为F T,物体所
受重力为G,则下列说法正确的是( ) A.物体做匀速运动,且v1=v2
B.物体做加速运动,且v2>v1
C.物体做加速运动,且F T>G
D.物体做匀速运动,且F T=G
答案C
解析把v1分解如图所示,v2=v1cos α,α变小,v2变大,物体做加速运动,超重,F T>G,选项C正确.
4、人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度v0
匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为
θ,则物体A实际运动的速度是( )
A.v0sin θ B.
v
0 sin θ
C.v0cos θ D.
v
0 cos θ
答案D
解析由运动的合成与分解可知,物体A参与两个分运动:一个是沿着与它相连接的绳子的运动,另一个是垂直于绳子斜向上的运动.而物体A实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运
动就是物体A的合运动,它们之间的关系如图所示.由几何关系可得v=
v
cos θ
,所以
D项正确.
5、如图,人沿平直的河岸以速度v行走,且通过不可伸长的绳
拖船,船沿绳的方向行进,此过程中绳始终与水面平行.当绳与河岸的夹角为α时,船的速率为( )
A.v sin α B.
v sin α
C.v cos α D.
v cos α
答案C
解析如图所示,把人的速度沿绳和垂直绳的方向分解,由几何知识有v船=v cos α,所以C正确,A、B、D错误.
6、A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上,现物体A以v1的速度向右
匀速运动,当绳被拉成与水平面夹角分别为α、β时,如图所示.物体B的运动速度v
为(绳始终有拉力) ( )
B
A.v1sin α/sin βB.v1cos α/sin β
C.v1sin α/cos βD.v1cos α/cos β
答案D
解析A、B两物体的速度分解如图.
由图可知:v绳A=v1cos α
v
=v B cos β
绳B
由于v绳A=v绳B
所以v B=v1cos α/cos β,故D对.。
