直线方程(知识整理)
高中数学知识点总结 直线与方程

高中数学知识点总结直线与方程一、直线与方程
1.直线的倾斜角
3.直线方程的五种形式
111222
0A x B y C A x B y C ++=⎧⎨
++=⎩的解. (1)方程组有唯一解⇔1l 与2l 相交,交点坐标就是方程组的解; (2)方程组无解⇔1l ∥2l ;
(3)方程组有无数解⇔1l 与2l 重合.
3.距离问题
特别提醒
解决对称问题要抓住以下两点:
(1)已知点与对称点的连线与对称轴垂直;
(2)以已知点和对称点为端点的线段的中点在对称轴上.三、圆的方程
1.圆的标准方程与一般方程
(1)直线与圆相离,没有公共点;(2)直线与圆相切,只有一个公共点;(3)直线与圆相交,有两个公共点.
圆与圆的位置关系的判断方法有两种.
(1)几何法:
由两圆的圆心距d与半径长R,r的关系来判断(如下图,其中R r>).
(2)代数法:
设圆221111:0C x y D x E y F ++++= ①,圆22
2222:0C x y D x E y F ++++= ②,
联立①②,如果该方程组没有实数解,那么两圆相离;如果该方程组有两组相同的实数解,那么两圆相切;如果该方程组有两组不同的实数解,那么两圆相交.
特别提醒
设圆221111:0C x y D x E y F ++++= ①,圆222222:0C x y D x E y F ++++= ②,
若两圆相交,则有一条公共弦,由①−②,得121212()()0D D x E E y F F -+-+-=③. 方程③表示圆C 1与圆C 2的公共弦所在直线的方程.。
直线系方程知识点总结

直线系方程知识点总结一、直线的一般方程1、直线的一般方程形式为Ax+By+C=0。
其中A、B和C是常数,A和B不能都为0。
2、直线的一般方程可以表示为两个变量的线性关系,即直线上的任意一点(x,y)都满足方程Ax+By+C=0。
3、直线方程的一般形式中的A、B和C可以根据直线的性质进行设定和求解。
例如,A 和B的比值确定了直线的斜率,而C的取值可以确定直线与坐标轴的交点。
4、直线的一般方程适用于解决直线的各种性质和问题,如求直线的斜率、与坐标轴的交点、过定点的直线方程等。
二、直线的斜截式方程1、直线的斜截式方程形式为y=kx+b。
其中k是直线的斜率,b是直线在y轴上的截距。
2、直线的斜截式方程是表示直线的一种简化形式,通过斜率和截距可以直观地了解直线在平面上的位置和特征。
3、直线的斜截式方程可以直接通过直线的斜率和截距求解,对于一些特定的问题,可以更加方便地使用斜截式方程。
4、直线的斜截式方程和一般方程可以相互转化,通过斜截式方程可以求解直线的一般方程,反之也可以通过直线的一般方程求解斜截式方程。
三、直线的点斜式方程1、直线的点斜式方程形式为y-y1=k(x-x1)。
其中(x1,y1)是直线上的一个定点,k是直线的斜率。
2、直线的点斜式方程适用于已知直线上的一个定点和斜率的情况。
通过点斜式方程即可得到直线的方程。
3、直线的点斜式方程和斜截式方程可以相互转化,通过点斜式方程也可以求解直线的斜截式方程,反之也可以通过斜截式方程求解点斜式方程。
四、直线的截距式方程1、直线的截距式方程形式为x/a + y/b = 1。
其中a和b是直线在x轴和y轴上的截距。
2、直线的截距式方程是表示直线的一种特殊形式,通过截距可以直观地了解直线与坐标轴的交点。
3、直线的截距式方程可以直接通过直线在坐标轴上的截距求解,对于特定的问题可以更加方便地使用截距式方程。
4、直线的截距式方程和一般方程可以相互转化,通过截距式方程可以求解直线的一般方程,反之也可以通过直线的一般方程求解截距式方程。
直线与方程知识点总结

直线与方程知识点总结一、直线的表示1、比例表达式:对于任意的两个不同的点A(x1,y1)与B(x2,y2),它们所连成的直线上任意的一点P(x,y)都满足比例关系:$$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$$2、斜截式:也叫斜率表达式:对于任意的两个不同的点A(x1,y1)与B(x2,y2),它们所连成的直线可用如下斜率表达式:$$y-y_1=k(x-x_1)$$其中,k为斜率,可以根据两点A(x1,y1)与B(x2,y2),计算得出:$$k=\frac{y_2-y_1}{x_2-x_1}$$3、标准方程:直线可以用标准方程表达:$$Ax+By+C=0$$其中,A、B、C可以根据两点A(x1,y1)与B(x2,y2),计算得出:$$A=y_2-y_1,B=x_1-x_2,C=x_2y_1-x_1y_2$$二、方程的表示1、一元一次方程:一元一次方程可以按如下形式表示:$$Ax+B=0$$其中,A、B为常数,A≠0,解析解可以表示为:$$x=-\frac{B}{A}$$2、一元二次方程:一元二次方程可以按如下形式表示:$$Ax^2+Bx+C=0$$其中,A、B、C为常数,A≠0,解析解可以表示为:$$x=\frac{-B\pm\sqrt{B^2-4AC}}{2A}$$3、二元一次方程:二元一次方程可以按如下形式表示:$$Ax+By+C=0$$其中,A、B、C为常数,解析解可以表示为:$$x=\frac{-B\pm\sqrt{B^2-4AC}}{2A}$$$$y=\frac{-A\pm\sqrt{B^2-4AC}}{2B}$$4、同次及非同次线性方程组:。
直线方程知识点总结

直线与方程知识点总结一、直线基本知识1、直线得倾斜角与斜率(1)直线得倾斜角①关于倾斜角得概念要抓住三点:ⅰ、与x轴相交; ⅱ、x轴正向;ⅲ、直线向上方向、②直线与x轴平行或重合时,规定它得倾斜角为、③倾斜角得范围、④;(2)直线得斜率①直线得斜率就就是直线倾斜角得正切值,而倾斜角为得直线斜率不存在.②经过两点()得直线得斜率公式就是()③每条直线都有倾斜角,但并不就是每条直线都有斜率。
2、两条直线平行与垂直得判定(1)两条直线平行对于两条不重合得直线,其斜率分别为,则有。
特别地,当直线得斜率都不存在时,得关系为平行。
(2)两条直线垂直如果两条直线斜率存在,设为,则注:两条直线垂直得充要条件就是斜率之积为—1,这句话不正确;由两直线得斜率之积为-1,可以得出两直线垂直,反过来,两直线垂直,斜率之积不一定为-1。
如果中有一条直线得斜率不存在,另一条直线得斜率为0时,互相垂直。
二、直线得方程1、直线方程得几种形式x 轴,方程为;(2)若,直线垂直于y轴,方程为;(3)(3)若,直线方程可用两点式表示)2、线段得中点坐标公式若两点,且线段得中点得坐标为,则3、过定点得直线系①斜率为且过定点得直线系方程为;②过两条直线, 得交点得直线系方程为(为参数),其中直线l2不在直线系中、三、直线得交点坐标与距离公式1、两条直线得交点设两条直线得方程就是,两条直线得交点坐标就就是方程组得解,若方程组有唯一解,则这两条直线相交,此解就就是交点得坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立。
2、几种距离(1)两点间得距离平面上得两点间得距离公式特别地,原点与任一点得距离(2)点到直线得距离点到直线得距离(3)两条平行线间得距离两条平行线,间得距离(注意:①求点到直线得距离时,直线方程要化为一般式;②求两条平行线间得距离时,必须将两直线方程化为系数相同得一般形式后,才能套用公式计算.)补充:1、直线得倾斜角与斜率(1)直线得倾斜角(2)。
直线方程总结知识点

一、直线方程的概念直线方程是描述平面上一条直线的数学关系式。
通常情况下,直线方程可表示为y = kx + b,其中x和y分别表示直线上的点的横纵坐标,k表示直线的斜率,b表示直线的截距。
直线方程可以用于描述直线的位置、方向等性质,是解决几何和代数问题的基本工具之一。
二、直线方程的常见形式1.点斜式方程点斜式方程是一种常见的直线方程形式,它的形式为y - y1 = k(x - x1),其中(k,x1,y1)为直线上的已知点,k为直线的斜率。
点斜式方程直观地表示了直线斜率的概念,方便计算直线的位置和方向。
2.斜截式方程斜截式方程是另一种常见的直线方程形式,它的形式为y = kx + b,其中k为直线的斜率,b为直线与y轴的截距。
斜截式方程直观地表示了直线截距的概念,方便计算直线与坐标轴的交点。
3.截距式方程截距式方程是直线的截距与坐标轴的关系式,它的形式为x/a + y/b = 1,其中a和b分别表示直线在x轴和y轴上的截距。
截距式方程可以直观地表示直线截距的性质,方便计算直线的位置和方向。
三、直线方程的求解方法1.根据已知点和斜率求解如果已知直线上的一个点和斜率,可以使用点斜式方程来表示直线。
首先找到直线上的一个点(x1,y1),然后用直线的斜率k计算出直线方程y = kx + b中的截距b,最终得到直线方程。
2.根据已知点和截距求解如果已知直线上的两个点,可以使用截距式方程来表示直线。
首先根据已知的两点(x1,y1)和(x2,y2)计算出直线的斜率k,然后再计算出直线的截距a和b,最终得到直线方程。
3.根据两条直线的关系求解如果已知两条直线的关系,可以使用斜截式方程来表示直线。
首先根据两条直线的关系计算出直线的斜率k,截距b,最终得到直线方程。
1.几何问题中的应用直线方程可以用来描述几何问题中的直线性质,比如直线的位置、方向等。
例如,可以使用直线方程来描述平面上两点之间的连线,计算直线的斜率和截距等,从而解决几何问题。
高一数学必修:直线与方程(知识点)

α0°。
则直线的l 与x l 做直线的倾斜角。
当直线轴平行或重合时,我们规定它的倾斜角为倾斜角的取值2.确定一条直线的条件:直线上的一点和这个直线的倾斜角可以惟一确定一条直线。
3.确定平面直角坐标系中一条直线位置的几何要素是:直线上的一个定点以及它的倾斜角。
4.坡度(倾斜程度):日常生活中,我们用“升高量与前进量的比”表示倾斜面的“坡度”(倾斜程度),即α的正切值叫做这条直线的斜率5.斜率:一条直线的倾斜角,我们用斜率表示直线的倾斜程度。
斜率常用表示,小写字母k注意:倾斜角是90°的直线没有斜率。
的直线的斜率公式(,),(,)6.经过两点≠P x y P x y x x 11122212()为l 1与l 2l l 1k 1=k 2l 1和l 2注意:若直线可能重合时,我们得到⇔∥2或重合8.如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于-1;反之,如果它们的斜率之积等于1⊥2⇔12=--1,那么它们互相垂直,即l l k k 15二、直线的方程(个)-0==0,l l 与x l 的倾斜角为0°时,tan0°=0,即k=0y -y 0=k (x -x 01.直线的点斜式方程(简称点斜式):)【当直线,这是直线轴平行或重合,的方程就是y y y y 或0】注意:直线的点斜式方程仅适用于有斜率的情形,所以在求直线的方程时,应先讨论直线有无斜率。
0,y l x a l 与x 截距:我们把直线轴交点,0()的横坐标a 叫做直线在轴上的截距。
我们把直线与轴交点b () l 在y 的纵坐标b 叫做直线轴上的截距。
注意:截距不是距离,截距是数。
2.直线的斜截式方程(简称斜截式):=+y kx b 注意:直线的斜截式方程仅适用于有斜率的直线。
注意:①直线的两点式方程不适用于没有斜率或斜率为0的直线。
一、直线的倾斜角与斜率1.倾斜角:当直线l 与x 轴相交时,我们取x 轴作为基准,x 轴正向与直线l 向上方向之间所成的夹角α叫高一数学必修:直线与方程(知识点)②若P x y P x y ,,,111222()()中有=x x 12或=y y 12时,直线PP 12没有两点式方程。
关于直线的知识点总结

(2)点斜式:知道直线上一点(x0,y0),并且直线的斜率k存在,
则直线可表示为 y-y0=k(x-x0)
当k不存在时,直线可表示为 x=x0
(3)截距式:不适用于和任意坐标轴垂直的直线和过原点的直线
知道直线与x轴交于(a,0),与y轴交于(0,b),
二、直线方程的距离
1、点到直线的距离
点P(x0,y0)到直线 Ax+By+C=0的距离可表示为:
d=|Ax0+By0+C|/√(A^2+B^2)
2、两平行线间的距离
设两条直线方程为
Ax+By+C1=0
Ax+By+C2=0
两平行直线间距离公式d=|C1-C2|/√(A^2+B^2),
将B(8,2)代入,解得c=-38.
故所求对称直线方程为2x+11y-38=0.
点评 解法一利用所求的对称直线肯定与已知直线平行,再由点(对称中心)到此两直线距离相等,而求出c,使问题解决,而解法二是转化为点关于点对称问题,利用中点坐标公式,求出对称点坐标,再利用直线系方程,写出直线方程. 本题两种解法都体现了直线系方程的优越性.
则直线可表示为 x/a+y/b=1
(4)斜截式: Y=KX+B (K≠0)
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。
两直线平行时 K1=K2
两直线垂直时 K1 X K2 = -1
(5)两点式 x1不等于x2 y1不等于y2
五、定比分点问题
1、定比分点定义
直线L上两点P、O,它们的坐标分别为(x1,y1),(x2,y2),在直线L上一个不同于P, O的任一点M使PM/MO等于已知常数λ。即PM/MO=λ,我们就把M叫做有向线段PO的定比分点。 若设M的坐标为(x,y),
直线方程基础知识小结
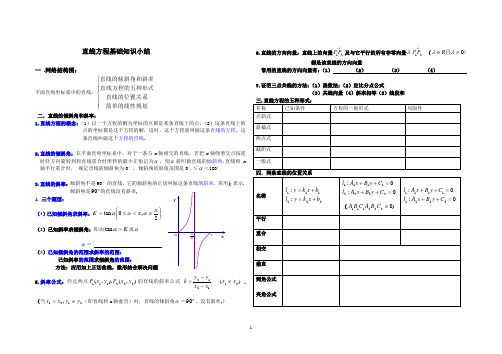
直线方程基础知识小结一 .网络结构图:平面直角坐标系中的直线:⎪⎪⎩⎪⎪⎨⎧简单的线性规划直线的位置关系直线方程的五种形式直线的倾斜角和斜率二.直线的倾斜角和斜率:1.直线方程的概念:(1,这条直线叫做这个方程的直线.2.直线的倾斜角:在平面直角坐标系中,对于一条与x 时针方向旋转到和直线重合时所转的最小正角记为αx 轴平行重合时, 规定直线的倾斜角为0°.3.直线的斜率:倾斜角不是90°的直线,k 表示.倾斜角是︒90的直线没有斜率4. 三个题型: (1)已知倾斜角求斜率:⎪⎭⎫ ⎝⎛≠<≤=2,0tan παπααK (2)已知斜率求倾斜角:即由K =αtan 求αα=(3)已知倾斜角的范围求斜率的范围:已知斜率的范围求倾斜角的范围:方法:应用如上正切曲线,数形结合解决问题5.斜率公式:经过两点),(),,(222111y x P y x P )2x ≠(当2121,y y x x ≠=(即直线和x6.直线的方向向量:直线上的向量→21P P 及与它平行的所有非零向量λ→21P P ()且0≠∈λλR 都是该直线的方向向量 常用的直线的方向向量有:(1) (2) (3) (4)7.证明三点共线的方法:(1)函数法;(2)定比分点公式(3)共线向量(4)斜率相等(5)线段和五.点到直线的距离公式:(1)P ()00,y x 到直线0:=++C By Ax l 的距离公式:(2)0:;0:2211=++=++C By Ax l C By Ax l 的距离公式:(3)P ()00,y x 到直线a x l =:的距离公式:P ()00,y x 到直线b y l =:的距离公式: 六.直线的对称问题:1.点关于点的对称点问题:()()())2,2(),(,,00y b x a y x y x ba ----任意点,坐标原点关于方法依据:中点坐标公式 2. 点关于直线的对称点问题:()()()()()()()()()(),,0,,,,2,,2,,=++=+-=++-=====-=+----------C By Ax c y x c y x xy xy by ax y y x x c x c y c x c y x y x y y b x y x a y x y x 直线直线直线直线直线直线直线直线直线关于说明:01(1)到(4)方法依据是中点坐标公式02(5)到(9)方法依据是:点关于直线对称点的基本解法3点关于直线对称的基本解法:直接法:设所求的对称点坐标是(),00y x 则由题意有:⎪⎪⎩⎪⎪⎨⎧-=-⨯--=++++1)(0220000B A x x y y C y y B xx A ⎩⎨⎧==∴00y x间接法 :3.三个典型题:(1)距离和的最小值问题:在定直线l 上取点P ,求P 到两定点A,B 距离和PB PA +的最小值当两定点A,B 在直线l 的两侧时:PB PA +AB ≥,最小值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的同侧时:先求点B 关于定直线l 的对称点 /B ,则PB PA +=//AB PB PA ≥+,最小值是/AB此时点P 坐标由方程组 ⎩⎨⎧=++:0:/AB l C By Ax l 决定 (2)距离差的最大值问题:在定直线l 上取点P ,求P 到两定点A,B 距离差PB PA -的最大值当两定点A,B 在直线l 的同侧时:PB PA -AB ≥,最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:AB l C By Ax l 决定 当两定点A,B 在直线l 的两侧时:先求点B 关于定直线l 的对称点 /B ,PB PA -=//AB PB PA ≤- ,最大值是,AB 此时点P 坐标由方程组⎩⎨⎧=++:0:/AB l C By Ax l 决定(3)入射光线和反射光线问题:入射光线上的点关于界面的对称点在反射光线上;反射光线上的点关于界面的对称点在入射光线上; 入射光线与界面的交点在反射光线上; 反射光线与界面的交点在入射光线上;界面是x 轴(y 轴)时,考虑入射光线与反射光线的斜率互为相反数; 界面是直线y=x(y=-x)时,考虑入射光线与反射光线上点的对称 例5光线由点)4,1(-A 射出,遇到直线l :0632=-+y x 后被反射,已知其)1362,3(B , 求反射光线所在直线的方程.七.几组特殊的直线系方程:1.直线系方程的定义:具有某种共同性质(过某点、共斜率等)的所有直线的集合叫做直线系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线方程(知识整理).一.基础知识回顾 (1)直线的倾斜角一条直线向上的方向与x 轴正方向所成的最小正角叫做这条直线的倾斜角,其中直线与x 轴平行或重合时,其倾斜角为0,故直线倾斜角的范围是)0(1800παα ≤≤.注:①当 90=α或12x x =时,直线l 垂直于x 轴,它的斜率不存在.②每一条直线都存在惟一的倾斜角,除与x 轴垂直的直线不存在斜率外,其余每一条直线都有惟一的斜率,并且当直线的斜率一定时,其倾斜角也对应确定.(2) 直线方程的几种形式点斜式、截距式、两点式、斜截式.特别地,当直线经过两点),0(),0,(b a ,即直线在x 轴,y 轴上的截距分别为)0,0(,≠≠b a b a 时,直线方程是:1=+b ya x .附直线系:对于直线的斜截式方程b kx y +=,当b k ,均为确定的数值时,它表示一条确定的直线,如果b k ,变化时,对应的直线也会变化.①当b 为定植,k 变化时,它们表示过定点(0,b )的直线束.②当k 为定值,b 变化时,它们表示一组平行直线.(3)两条直线的位置关系 10两条直线平行1l ∥212k k l =⇔两条直线平行的条件是:①1l 和2l 是两条不重合的直线. ②在1l 和2l 的斜率都存在的前提下得到的. 因此,应特别注意,抽掉或忽视其中任一个“前提”都会导致结论的错误.(一般的结论是:对于两条直线21,l l ,它们在y 轴上的纵截距是21,b b ,则1l ∥212k k l =⇔,且21b b ≠或21,l l 的斜率均不存在,即2121A B B A =是平行的必要不充分条件,且21C C ≠)推论:如果两条直线21,l l 的倾斜角为21,αα则1l ∥212αα=⇔l . 20两条直线垂直两条直线垂直的条件:①设两条直线1l 和2l 的斜率分别为1k 和2k ,则有12121-=⇔⊥k k l l 这里的前提是21,l l 的斜率都存在. ②0121=⇔⊥k l l ,且2l 的斜率不存在或02=k ,且1l 的斜率不存在. (即01221=+B A B A 是垂直的充要条件)(4)两条直线的交角①直线1l 到2l 的角(方向角);直线1l 到2l 的角,是指直线1l 绕交点依逆时针方向旋转到与2l 重合时所转动的角θ,它的范围是),0(π,当 90≠θ时21121tan k k kk +-=θ.②两条相交直线1l 与2l 的夹角:两条相交直线1l 与2l 的夹角,是指由1l 与2l 相交所成的四个角中最小的正角θ,又称为1l 和2l 所成的角,它的取值范围是 ⎝⎛⎥⎦⎤2,0π,当90≠θ,则有21121tan k k k k +-=θ.(5)点到直线的距离 ①点到直线的距离公式:设点),(00y x P ,直线P C By Ax l ,0:=++到l 的距离为d ,则有2200BA C By Ax d +++=.②两条平行线间的距离公式:设两条平行直线)(0:,0:212211C C C By Ax l C By Ax l ≠=++=++,它们之间的距离2221BA C C d +-=.(6)对称问题:①关于点对称的两条直线一定是平行直线,且这个点到两直线的距离相等.②关于某直线对称的两条直线性质:若两条直线平行,则对称直线也平行,且两直线到对称直线距离相等.若两条直线不平行,则对称直线必过两条直线的交点,且对称直线为两直线夹角的角平分线.③点关于某一条直线对称,用中点表示两对称点,则中点在对称直线上(方程①),过两对称点的直线方程与对称直线方程垂直(方程②)①②可解得所求对称点.注:①曲线、直线关于一直线b x y +±=对称的解法:y 换x ,x 换y . 例:曲线f(x ,y)=0关于直线y=x –2对称曲线方程是f(y+2 ,x –2)=0.②曲线C: f (x ,y )=0关于点(a ,b)的对称曲线方程是f(a – x, 2b – y)=0. 二.范例解析例1.已知直线l 过点P(-1,1)且与A(-2, 3)、B(3,2)为端点的线段相交,试求直线l 倾斜角α的取值范围。
[思路]1)分别求出直线PA 、PB 的斜率;2)数形结合,利用正切函数的单调性求解。
[破解]1)先求出12,4PA PB K K =-=; 2)由图7-3知,满足题意的直线l 的斜率为1,24k k ≥≤-。
因为直线l 的倾斜角[0,)απ∈,而tan [0,),(,)22y x πππ=在上分别是增函数,从而知11tan tan 2tan tan 24422arc arc ππααααπ≥≤-⇒≤≤<≤-或或,又知2π也满足条件,故倾斜角α取值范围为1[tan ,tan 2].4arc arc π-[收获]1)直线的斜率是判定两直线位置关系的重要依据; 2)数形结合思想方法是求解解析几何问题的重要方法之一;3)已知斜率范围探求倾斜角的范围,最关键的一环是利用正切函数的单调性处理。
例2.∆ABC 的顶点(1,3),(2,1),(3,1)A B C --,试求∠A 平分线AT 所在直线方程。
[思路] 利用角平线性质∠CA T=∠BA T 结合到角公式求出直线AT 的斜率即可。
[破解] 如图7-1,由已知易求1,2AC AB K K ==-。
由角平线的性质∠CA T=∠BAT知AC 到AT 的角与AT 到AB 的角相等。
11AT AC AB AT AT AC AT AB k k k k k k k k --=++即可求出16AT k =-,从而∠A 平分线AT 所在直线方程为:6190x y +-=[收获] 1)充分利用平面几何性质将问题转化成解析几何中的有关问题是研究平面几何问题的关键。
2)注意夹角与到角公式的区别,分清什么时候用夹角(或到角)公式,以免产生错解。
3)处理有关几何问题最好作出图形增强直观效果,为寻找解题突破口提供依据。
例3.某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为α(90°≤α<180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a >b ) 问学生距离镜框下缘多远看画的效果最佳?命题意图 本题是一个非常实际的数学问题,它不仅考查了直线的有关概念以及对三角知识的综合运用,而且更重要的是考查了把实际问题转化为数学问题的能力知识依托 三角函数的定义,两点连线的斜率公式,不等式法求最值错解分析 解决本题有几处至关重要,一是建立恰当的坐标系,使问题转化成解析几何问题求解;二是把问题进一步转化成求tan ACB 的最大值 如果坐标系选择不当,或选择求sin ACB 的最大值 都将使问题变得复杂起来 技巧与方法 欲使看画的效果最佳,应使∠ACB 取最大值,欲求角的最值,又需求角的一个三角函数值解 建立如图所示的直角坐标系,AO 为镜框边,AB 为画的宽度,O 为下边缘上的一点,在x 轴的正半轴上找一点C (x ,0)(x >0),欲使看画的效果最佳,应使∠ACB 取得最大值由三角函数的定义知 A 、B 两点坐标分别为(a cos α,a sin α)、 (b cos α,b sin α),于是直线AC 、BC 的斜率分别为k AC =tan xCA =x a a -ααcos sin ,.cos sin tan xb b xCB k BC -==αα于是tan ACB =AC BC AC BC k k k k ⋅+-1ααααcos )(sin )(cos )(sin )(2⋅+-+⋅-=++-⋅-=b a x xabb a x x b a ab x b a 由于∠ACB 为锐角,且x >0,则tan ACB ≤ααcos )(2sin )(b a ab b a +-⋅-,当且仅当xab=x ,即x =ab 时,等号成立, 此时∠ACB 取最大值,对应的点为C (ab ,0),因此,学生距离镜框下缘ab cm 处时,视角最大,即看画效果最佳例4.等腰三角形一腰所在的直线1l 的方程是x -2y -2=0.底边所在的直线2l 的方程是:x+y -1=0,点(-2,0)在另一腰上,求这腰所在直线3l 的方程.解:设1l ,2l ,3l 的斜率分别为1k ,2k ,3k 1l 到2l 的角是1θ2l 到3l 的角是2θ,则121,12k k ==-。
21112tan 31k k k k θ-==-+ 因为1l ,2l ,3l 所围成的三角形为等腰三角形,所以1221tan tan 3θθθθ=⇒==-即32233231, 2.1k k k k k k -=-=-∴=+又直线 3l 经过点(-2,0),故其方程为:2[(2)]24y x x y =---+即。
αC BA o yx例5.已知M(x,y)是以A(-2, 3)、B(3,2)为端点的线段上一动点,试求11y x -+的取值范围。
[思路]1)若令11y t x -=+,代入线段AB 所在的直线方程消去y 可得到()(231)t f x x x =-≤≤≠-且可求出t 的范围,但计算较繁。
2)变换角度,由数入形,联想直线斜率公式可使问题轻松解决。
[破解] 1) 令11y t x -=+,不难发现t 就是线段AB 一动点M 与定点P (-1,1)连线的的斜率(如图3)2) 易求出12,4PA PB K K =-=3) 由图7-5知,满足题意的直线PM 的斜率为1,24k k ≥≤-,即11y x -+的取值范围为1(,2][,)4-∞-+∞。
[收获]形如“11y y t x x -=-”的最值范围问题,可联想直线斜率公式,数形结合解决。
[拓展] 对于曲线y=f(x)上任一动点P (x,y ),探求0y y t x x +=+的范围问题都可联想直线斜率公式,数形结合解决。
例6.过直线2x +y +8=0和直线x +y +3=0的交点作一条直线,使它夹在两条平行直线x -y -5=0和x -y -2=0之间的线段长为5,求该直线的方程.[思路]1) 利用距离公式求出两平行直线的距离;2) 利用勾股定理求出此直线夹在两平行直线间的线段长; 3) 利用夹角公式求出直线斜率,即可求出直线方程。
[破解]如图7-9所示, 由28030x y x y ++=⎧⎨++=⎩求出交点M (-5,2).设所求直线 l 与12,l l 分别交于B 、A 两点, 由已知 |AB|=5,又l 1、l 2间距离3||2AC =,在 Rt △ABC图7-9中,||BC =. 设l 1到l 的角为α,则||tan 3||AC BC α==. 设直线 l 的斜率为k ,由夹角公式得 |1|1tan 32|1|2k k k k α-==⇒=-=-+或 .所求直线的方程为 2x +y +8=0或x +2y +1=0.[收获]1、 数形结合,利用图形直观特征,能有效地找到解题思路。
