2008年新疆乌鲁木齐市中考数学试题及答案(扫描版)
2010中考数学专题复习——反比例函数试卷

中考数学专题复习——反比例函数一、选择题1. (08浙江温州)已知反比例函数k y x=的图象经过点(32)-,,则k 的值是( ) A .6- B .6 C .23D .23-2.(2008山东烟台)在反比例函数12m y x -=的图象上有两点A ()11,x y ,B ()22,x y ,当120x x <<时,有12y y <,则m 的取值范围是( )A 、0m <B 、0m >C 、12m < D 、12m >3.(2008浙江宁波)如图,正方形ABOC 的边长为2,反比例函数k y x=过点A ,则k 的值是( )A .2B .2-C .4D .4-6.(2008年沈阳市)下列各点中,在反比例函数2y x=-图象上的是( )A .(21),B .233⎛⎫ ⎪⎝⎭,C .(21)--,D .(12)-,7.(2008年湖南省邵阳市)若反比例函数k y x=的图象经过点(12)-,,则这个函数的图象一定经过点( )A .(12),B .(21),C .(12)-,D .(12)--,8.(2008湖北黄冈)已知反比例函数2y x=,下列结论中,不正确...的是( ) A .图象必经过点(12), B .y 随x 的增大而减少 C .图象在第一、三象限内D .若1x >,则2y <9.(2008湖南株洲)已知函数1y x=的图象如下,当1x ≥-时,y 的取值范围是( )A .1y <-B .1y ≤-C .1y ≤- 或0y >D .1y <-或0y ≥10.(2008黑龙江哈尔滨)已知反比例函数y =x2k -的图象位于第一、第三象限,则k 的取值范围是( ).(A )k >2 (B ) k ≥2 (C )k ≤2 (D ) k <211.(2008年山东省青岛市)如果点11()A x y ,和点22()B x y ,是直线y kx b =-上的两点,且当12x x <时,12y y <,那么函数k y x=的图象大致是( )-1-1yxO12.(2008年江苏省连云港市)已知某反比例函数的图象经过点()m n ,,则它一定也经过点( )A .()m n -,B .()n m ,C .()m n -,D .()m n ,13.(2008年云南省双柏县)已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )14.(2008新疆乌鲁木齐市)反比例函数6y x=-的图象位于( )A .第一、三象限B .第二、四象限C .第二、三象限D .第一、二象限15.(2008浙江温州)已知反比例函数k y x=的图象经过点(32)-,,则k 的值是( ) A .6- B .6 C .23D .23-16.(2008宁夏)反比例函数xk y =(k >0)的部分图象如图所示,A 、B 是图象上两点,AC ⊥x轴于点C ,BD ⊥x 轴于点D ,若△AOC 的面积为S 1,△BOD 的面积为S 2,则S 1和S 2 的大小关系为( )A . S 1> S 2B . S 1= S 2C . S 1 <S 2D . 无法确定xxxxA . D .v /(km/h)v/(km/h)v /(km/h)A .B .C ..17.(2008湖南益阳市)物理学知识告诉我们,一个物体所受到的压强P 与所受压力F 及受力面积S 之间的计算公式为SF P=. 当一个物体所受压力为定值时,那么该物体所受压强P 与受力面积S 之间的关系用图象表示大致为( )18.(2008湖南常德市)下面的函数是反比例函数的是 ( )A . 13+=x yB .x x y 22+=C . 2x y = D .xy 2=19.(2008年浙江省嘉兴市)某反比例函数的图象经过点(23)-,,则此函数图象也经过点( )A .(23)-,B .(33)--,C .(23),D .(46)-,20。
新疆乌鲁木齐市2008年高中招生考试

新疆乌鲁木齐市2008年高中招生考试物理试卷(90分)说明:本卷中的g都取10N/Kg。
作图可用铅笔。
答题可用计算器。
一、选择题(本题有10个小题,每小题3分,共30分。
每小题4个选项,其中只有1个选项是符合题意的,请将正确选项前的字母序号填在答卷相应的表格里。
选对得3分,多选、不选、错选均不得分)1.图示是2008年北京奥运会传递圣火的手持火炬—“祥云”的照片。
关于它的质量和长度合理的是A.质量985g,长度72cm B.质量985Kg,长度72cmC.质量985g,长度72dmD.质量985kg,长度72dm2.国际单位制中,电荷量的单位是A.库仑B.伏特C.欧姆D.瓦特3.乌鲁木齐市某街道旁的电子显示屏显示的噪声等级为80 dB。
如果人处在此噪声等级的环境中A.对人的听力会产生严重危害B.对人的学习会产生影响C.对人的睡眠不会产生影响D.对人的学习、睡眠都不会产生影响4.在清澈的湖面上空,小燕子正在向下俯冲捕食。
在小燕子向下俯冲的过程中,关于它在湖水中的像的虚实、它和像之间的距离,正确的说法是A.实像,距离变大B.实像,距离变小C.虚像,距离变小D.虚像,距离变大5.下列不属于电磁波的是A.无线电波B.微波C.光波D.声波6.下列说法正确的是A.扩散现象只发生在液体之间B.物体温度越高,分子热运动越剧烈C.只有热传递才能改变物体的内能D.0℃的物体没有内能7.掉在水平地面上的弹性小球会跳起,而且弹跳的高度会越来越低。
图示是小球弹跳的频闪照片,小球在1、2位置的高度一样。
下面说法正确的是A.小球在1、2位置的动能相同,机械能也相同B.小球在1、2位置的动能相同,2位置的机械能较小C.小球在1、2位置的机械能相同,2位置的动能较小D.小球在2位置的动能较小,机械能也较小8.如图所示,均匀木棒AB长为1m,水平放置在O、O'两个支点上。
已知AO、O'B长度均为 0.25m。
若把B端竖直向上稍微抬起一点距离,至少需要用力20N;若把B端竖直向下稍微压下一点距离,则至少需要用力A.20N B.40N C.60N D.8ON9.如图所示,容积为3 dm3的圆柱形容器放在水平桌面上,容器内装有质量为1㎏的水,现将一个密度为0.6×103㎏/m3 的木块放入容器中,木块与容器壁不接触,水恰好没有溢出,则木块的质量为A.0.6㎏B.1.2㎏C.1.8㎏D.2.0㎏10.某调光灯电路如图所示,当滑动变阻器达到滑片P滑至a端时,灯泡L的功率为36W;滑片P滑至b端时,灯泡L的功率为9W,则滑片P滑至ab的中点时,灯泡L的功率为A.16W B.18WC.22.5W D.25W二、填空题(本题有4个小题,每空1分,共30分。
乌鲁木齐中考数学试题及答案

2010年新疆乌鲁木齐市初中毕业生学业水平测试数学试卷一、选择题(本大题共10小题,每小题4分,共40分)每题的选项中只有一项符合题目要求. 1.在0,2-,1,2-这四个数中负整数是 A.2- B. 0 C.22- D. 12.如图1是由五个相同的小正方体组成的几何体,则它的左视图是3.“十二五”期间,新疆将建成横贯东西、沟通天山的“十”字形高速公路主骨架,全疆高 速公路总里程突破4 000km ,交通运输条件得到全面改善,将4 000用科学记数法可以表 示为A.24010⨯B. 3410⨯C. 40.410⨯ D. 4410⨯4.阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获得20%,则这种 电子产品的标价为A. 26元B. 27元C. 28元D. 29元 5.已知整式252x x -的值为6,则2256x x -+的值为 A. 9 B. 12 C. 18 D. 246.如图2,在平面直角坐标系中,点A B C 、、的坐标为 (1,4)、(5,4)、(1、2-),则ABC △外接圆的圆心 坐标是A.(2,3)B.(3,2)C.(1,3)D.(3,1)7.有若干张面积分别为22a b ab 、、的正方形和长方形纸片,阳阳从中抽取了1张面积为2a的正方形纸片,4张面积为ab 的长方形纸片,若他想拼成一个大正方形,则还需要抽取 面积为2b 的正方形纸片A. 2张B.4张C.6张D.8张8.某校九年级(2)班50名同学为玉树灾区献爱心捐款情况如下表:捐款(元) 10 15 30 40 50 60人数3611 11 136则该班捐款金额的众数和中位数分别是A. 13,11B. 50,35C. 50,40D. 40,509.如图3,四边形OABC 为菱形,点A B 、在以点O 为圆心的DE 上,若312OA =∠=∠,,则扇形ODE 的面积为A.3π2 B. 2π C.5π2D. 3π 10.将边长为3cm 的正三角形各边三等分,以这六个分点为顶点构 成一个正六边形,则这个正六边形的面积为 A.332cm 2 B.334cm 2 C.338cm 2D.33cm 2 图2 ADO ECB图3二、填空题(本大题共5小题,每小题4分,共20分)把答案直接填在答题卡的相应位置处. 11.计算:18322-+=_____________.12.如图4,AB 是O ⊙的直径,C D 、为O ⊙上的两点, 若35CDB ∠=°,则ABC ∠的度数为__________. 13.在数轴上,点A B 、对应的数分别为2,51x x -+,且A B 、 两点关于原点对称,则x 的值为___________.14.已知点1(1)A y -,,2(1)B y ,,3(2)C y ,在反比例函数(0)k y k x=<的图象上,则 123y y y 、、的大小关系为_________(用“>”或“<”连接).15.暑假期间,瑞瑞打算参观上海世博会.她要从中国馆、澳大利亚馆、德国馆、英国馆、日本馆和瑞士馆中预约两个馆重点参观,想用抽签的方式来作决定,于是她做了分别写有以上馆名的六张卡片,从中任意抽取两张来确定预约的场馆,则他恰好抽中中国馆、澳大利亚馆的概率是___________.三、解答题(本大题Ⅰ—Ⅴ,共9小题,共90分)解答时对应在答题卡的相应位置处写出文字说明、证明过程或演算过程.Ⅰ.(本题满分15分,第16题6分,第17题9分)16.解不等式组1(4)223(1) 5.x x x ⎧+<⎪⎨⎪-->⎩,17.先化简,再求值:21111211a a a a a a ++-÷+-+-,其中 2.a = 四.(本题满分30分,第18题8分,第19题、20题,每题11分)18.如图5,在平行四边形ABCD 中,BE 平分ABC ∠交AD 于点E ,DF 平分∠ADC 交 BC 于点F . 求证:(1)ABE CDF △≌;(2)若BD EF ⊥,则判断四边形EBFD 是什么特殊四边形,请证明你的结论.19.如图6,在平面直角坐标系中,直线4:43l y x =-+分别交x 轴、y 轴于点A B 、,将AOB △绕点O 顺时针旋转90°后得到A OB ''△. (1)求直线A B ''的解析式;(2)若直线A B ''与直线l 相交于点C ,求A BC '△的面积.CO图4BDAFD 图5E C AB 图6CA y x OlA 'B '20.某过街天桥的截面图为梯形,如图7所示,其中天桥斜面CD 的坡度为1:3i =(1:3i =是指铅直高度DE 与水平宽度CE 的比),CD 的长为10m ,天桥另一斜面AB 坡角ABG ∠=45°.(1)写出过街天桥斜面AB 的坡度; (2)求DE 的长;(3)若决定对该过街天桥进行改建,使AB 斜面的坡度变缓,将其45°坡角改为30°, 方便过路群众,改建后斜面为AF .试计算此改建需占路面的宽度FB 的长(结果精确0.01)Ⅲ.(本题满分23分,第21题11分,第22题12分)21.2010年5月中央召开了新疆工作座谈会,为实现新疆跨越式发展和长治久安,作出了重 要战略决策部署.为此我市抓住机遇,加快发展,决定今年投入5亿元用于城市基础设施 维护和建设,以后逐年增加,计划到2012年当年用于城市基础设施维护与建设资金达到 8.45亿元.(1)求从2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率; (2)若2010年至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率相同, 预计我市这三年用于城市基础设施维护和建设资金共多少亿元?22.2010年6月4日,乌鲁木齐市政府通报了首府2009年环境质量公报,其中空气质量级别分布统计图如图8所示,请根据统计图解答以下问题:(1)写出2009年乌鲁木齐市全年三级轻度污染天数:(2)求出空气质量为二级所对应扇形圆心角的度数(结果保留到个位);(3)若到2012年,首府空气质量良好(二级及二级以上)的天数与全年天数(2012年是闰年,全年有366天)之比超过85%,求2012年空气质量良好的天数要比2009年至少增加多少天?Ⅳ.(本题满分10分)23.已知二次函数2(0)y ax bx c a =++≠的图象经过(00)(1)O M ,,,1和()(0)N n n ≠,0 三点.(1)若该函数图象顶点恰为点M ,写出此时n 的值及y 的最大值;(2)当2n =-时,确定这个二次函数的解析式,并判断此时y 是否有最大值; (3)由(1)、(2)可知,n 的取值变化,会影响该函数图象的开口方向.请你求出n 满足 什么条件时,y 有最小值?F AB G D E C图7图8Ⅴ.(本题满分12分)24.如图9,边长为5的正方形OABC 的顶点O 在坐标原点处,点A C 、分别在x 轴、y 轴 的正半轴上,点E 是OA 边上的点(不与点A 重合),EF CE ⊥,且与正方形外角平分 线AC 交于点P .(1)当点E 坐标为(30),时,试证明CE EP =;(2)如果将上述条件“点E 坐标为(3,0)”改为“点E 坐标为(t ,0)(0t >)”,结论 CE EP =是否仍然成立,请说明理由;(3)在y 轴上是否存在点M ,使得四边形BMEP 是平行四边形?若存在,用t 表示点M 的坐标;若不存在,说明理由.数学试题参考答案及评分标准一、选择题(本大题共10小题,每小题4分,共40分)题号 1 2 3 4 5 6 7 8 9 10 答案 ADBCCDBCDA二、填空题(本大题共5小题,每小题4分,共20分)11.0 12.55° 13. 1 14. 231y y y <<或132y y y >> 15.115三、解答题(本大题1-V 题,共9小题,共90分) 16.解:由(1)得:440x x +<<, ··························································································· 2′由(2)得:3351x x x -+><-, ·················································································· 4′ ∴不等式组的解集是:1x <- ··························································································· 6′ 17.解:原式=()2111111a a a a a +--++-································································································ 3′ =1111a a -+- ············································································································· 4′ =221a -- ···················································································································· 7′当2a =时,原式=()22221-=-- ····································································· 9′ 18. 证明:(1)∵四边形ABCD 是平行四边形,∴A C AB CD ABC ADC ∠=∠=∠=∠,,∵BE 平分ABC ∠,DF 平分ADC ∠,∴ABE CDF ∠=∠ ································ 2′ ∴()ABE CDF ASA △≌△ ·················································································· 4′ (2)由ABE CDF △≌△,得AE CF = ····································································· 5′ 在平行四边形ABCD 中,AD BC AD BC =∥,∴DE BF DE BF =∥,∴四边形EBFD 是平行四边形 ··············································································· 6′ 若BD EF ⊥,则四边形EBFD 是菱形 ··································································· 8′19.解:(1)由直线l :443y x =-+分别交x 轴、y 轴于点A B 、,可知;()()3004A B ,,,∵AOB △绕点O 顺时针旋转90°而得到A OB ''△ ∴AOB A OB ''△≌△故()()0340A B ''-,,, ······································································································· 2′ 设直线A B ''的解析式为y kx b =+(0k k b ≠,,为常数)∴有340b k b =-⎧⎨+=⎩解之得:343k b ⎧=⎪⎨⎪=-⎩∴直线A B ''的解析式为334y x =- ·················································································· 5′ (2)由题意得:334443y x y x ⎧=-⎪⎪⎨⎪=-+⎪⎩解之得:84251225x y ⎧=⎪⎪⎨⎪=-⎪⎩∴84122525C ⎛⎫- ⎪⎝⎭, ··················································· 9′ 又7A B '=∴184294722525A CB S =⨯⨯=△′ ···························································································· 11′ 20.解:(1)在Rt AGB △中,45ABG ∠=° ∴AG BG =∴AB 的坡度=1AGBG= ······································································································· 2′ (2)在Rt DEC △中,∵3tan 3DE C EC ∠==∴30C ∠=° 又∵10CD = ∴()15m 2DE CD == ······································································· 5′ (3)由(1)知,5AG BG ==,在Rt AFG △中,30AFG ∠=°tan AGAFG FG∠=,即3535FB =+ ········································································· 7′ 解得535 3.66FB =-≈ ························································································ 10′答:改建后需占路面宽度约为3.66m. ···································································· 11′21.解:(1)设从2010至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率为x ,由题意得:()2518.45x += ······························································································ 3′解得,1230% 2.3x x ==-,(不合题意舍去) ····························································· 6′答:从2010至2012年我市每年投入城市基础设施维护和建设资金的年平均增长率为30%. ··························································································································································· 7′(2)这三年共投资()5518.45x +++()5510.38.4519.95=+++=(亿元) ······························································· 10′ 答:预计我市这三年用于城市建设基础设施维护和建设资金共19.95亿元 ··············· 11′ 22. 解:(1)21.6%36578.8479⨯=≈(天) ······································································ 2′(2)()19.0% 2.7% 3.9%21.6%360-+++⨯⎡⎤⎣⎦°226.08=°226≈° ···················································································································· 5′ (3)设到2012年首府空气质量良好的天数比2009年增加了x 天,由题意得:()9.0%36562.8%36585%365x +⨯+⨯>···························································· 8′49.03x > ············································································································ 10′ 由题意知x 应为正整数,∴50x ≥ ································································ 11′答:2012年首府空气质量良好的天数比2009年首府空气质量良好的天数至少增加50天. ················································································································ 12′23.解:(1)由二次函数图象的对称性可知2n =;y 的最大值为1. ··································· 2′(2)由题意得:1420a b a b +=⎧⎨-=⎩,解这个方程组得:1323a b ⎧=⎪⎪⎨⎪=⎪⎩故这个二次函数的解析式为21233y x x =+ ···························································· 5′ ∵103> ∴y 没有最大值. ·················································································· 6′ (3)由题意,得210a b an bn +=⎧⎨+=⎩,整理得:()210an a n +-= ·································· 8′∵0n ≠ ∴10an a +-=故()11n a -=,而1n ≠ 若y 有最小值,则需0a > ∴10n -> 即1n <∴1n <时,y 有最小值. ························································································· 10′24.解:(1)过点P 作PH x ⊥轴,垂足为H∴2190∠=∠=° ∵EF CE ⊥ ∴34∠=∠ ∴COE EHP △∽△ARHOM Cy BGPFx∴CO EHOE HP=················································· 2′ 由题意知:5CO = 3OE = 2EH EA AH HP =+=+ ∴523HP HP += 得3HP = ∴5EH = ·························································································································· 3′ 在Rt COE △和Rt EHP △中∴2234CE CO OE =+= 2234EP EH PH =+=故CE EP = ······················································································································· 5′ (2)CE EP =仍成立.同理.COE EHP △∽△ ∴CO EHOE HP=········································································ 6′ 由题意知:5CO = OE t = 5EH t HP =-+ ∴55t HP t HP-+= 整理得()()55t HP t t -=- ∵点E 不与点A 重合 ∴50t -≠ ∴HP t = 5EH = ∴在Rt COE △和Rt EHP △中225CE t =+ 225EP t =+ ∴CE EP = ··························································· 5′ (3)y 轴上存在点M ,使得四边形BMEP 是平行四边形. ············································· 9′过点B 作BM EP ∥交y 轴于点M ∴590CEP ∠=∠=° ∴64∠=∠在BCM △和COE △中64BC OCBCM COE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴BCM COE △≌△ ∴BM CE = 而CE EP = ∴BM EP =由于BM EP ∥ ∴四边形BMEP 是平行四边形. ················································ 11′ 故BCM COE △≌△可得CM OE t == ∴5OM CO CM t =-=-故点M 的坐标为()05t -, ···························································································· 12′。
2008年中考数学试题及答案解析
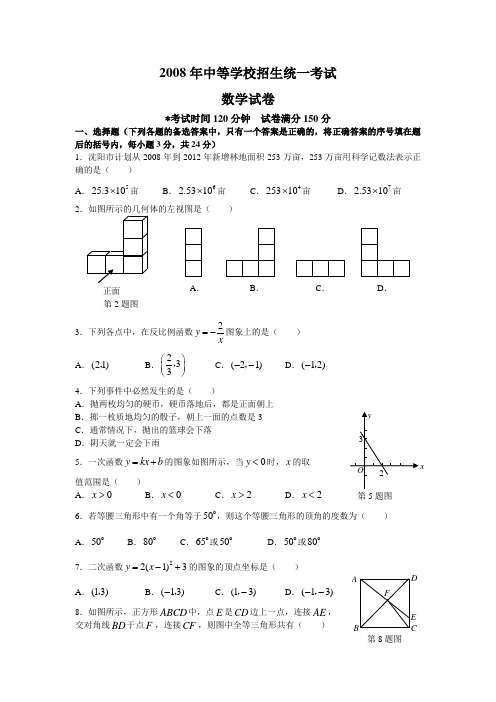
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( ) A .525.310⨯亩B .62.5310⨯亩C .425310⨯亩D .72.5310⨯亩2)3.下列各点中,在反比例函数2y x=-图象上的是()A .(21),B .233⎛⎫⎪⎝⎭,C .(21)--,D .(12)-,4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨5.一次函数y kx b =+的图象如图所示,当0y <时,x 的取 值范围是( ) A .0x > B .0x <C .2x >D .2x <6.若等腰三角形中有一个角等于50,则这个等腰三角形的顶角的度数为( ) A .50B .80C .65或50D .50或807.二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-,D .(13)--, 8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )正面第2题图A .B .C .D .第5题图xADCEFB第8题图A .1对B .2对C .3对D .4对二、填空题(每小题3分,共24分)9.已知A ∠与B ∠互余,若70A ∠=,则B ∠的度数为 . 10.分解因式:328m m -= .11.已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 .12.如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补 充一个条件能使菱形ABCD 成为正方形,则这个条件是 (只填一个条件即可). 13.不等式26x x -<-的解集为 .14.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米.15.观察下列图形的构成规律,根据此规律,第8第15题图16.在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.计算:101(1)52-⎛⎫π-+-+- ⎪⎝⎭18.解分式方程:1233xx x=+--.19.先化简,再求值:222()()2y x y x y x y ++---,其中13x =-,3y =.第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20.如图所示,在66⨯的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形,如图①中的三角形是格点三角形. (1)请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两个不同的格点四边形,并将这两个格点四边形分别画在图②,图③中; (2)直接写出这两个格点四边形的周长.四、(每小题10分,共20分)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O 上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局. (1)一次出牌小刚出“象”牌的概率是多少?(2)如果用A B C ,,分别表示小刚的象、虎、鼠三张牌,用1A ,1B ,1C 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析:①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩. 六、(本题12分)24.一辆经营长途运输的货车在高速公路的A 处加满油后,以每小时80千米的速度匀速行驶,前往与A 处相距636千米的B 地,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达C 处,求此时油箱内余油多少升?(3)在(2)的前提下,C 处前方18千米的D 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B 地.(货车在D 处加油过程中的时间和路程忽略不计)第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25.已知:如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AMN △是等腰三角形.(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长ED 交线段BC 于点P .求证:PBD AMN △∽△.八、(本题14分) 26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题(每小题3分,共24分) 1.B 2.A 3.D 4.C 5.C 6.D7.A8.C二、填空题(每小题3分,共24分) 9.2010.2(2)(2)m m m +-11.12012.90BAD ∠=(或AD AB ⊥,AC BD =等)13.4x >14.1215.65 16.8 三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.解:原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18.解:12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验:将7x =代入原方程,左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 (将7x =代入最简公分母检验同样给分)19.解:原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-,3y =时,原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20.解:(1)答案不唯一,如分割线为三角形的三条中位线中任意一条所在的直线等.································· 2分拼接的图形不唯一,例如下面给出的三种情况:图① 图② 图③ 图④图①~图④,图⑤~图⑦,图⑧~图⑨,画出其中一组图中的两个图形. ······················ 6分 (2)对应(1)中所给图①~图④的周长分别为4+8,4+4+ 图⑤~图⑦的周长分别为10,8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、(每小题10分,共20分) 21.解:(1)OD AB ⊥,AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 (2)OD AB ⊥,AC BC ∴=,AOC △为直角三角形, 3OC =,5OA =,由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22.解:(1)1()3P =一次出牌小刚出象牌“” ··················································· 4分(2)树状图(树形图):·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种. ········································································ 9分1()3P ∴=一次出牌小刚胜小明. ····································································· 10分 五、(本题12分) 23.解:(1)21······························································································ 2分 (2)一班众数为90,二班中位数为80 ······························································· 6分 (3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好; ···································································································· 8分 ②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好; ················································································································· 10分 ③从B 级以上(包括B 级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好. ······························································································· 12分 六、(本题12分) 24.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+ ················ 1分将(0100),,(180),代入上式得, 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证:当2x =时,20210060y =-⨯+=,符合一次函数; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律. ··················································· 5分 y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ··························· 6分 (2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升. ····························································· 8分 (3)方法不唯一,如:方法一:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 设在D 处至少加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯+=+, ··················································· 11分 解得,69a =(升) ····················································································· 12分方法二:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 汽车行驶18千米的耗油量:1820 4.580⨯=(升) D B ,之间路程为:63680 4.218282-⨯-=(千米)汽车行驶282千米的耗油量:2822070.580⨯=(升) ················································································· 11分 70.510(16 4.5)69+--=(升) ···································································· 12分 方法三:由(1)得,货车行驶中每小时耗油20升, ············································· 9分设在D 处加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯++≤,解得,69a ≥ ····························································································· 11分 ∴在D 处至少加油69升,货车才能到达B 地. ················································· 12分七、(本题12分) 25.证明:(1)①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =,AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠,BE CD =M N ,分别是BE CD ,的中点,BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=,即AMN △为等腰三角形 ···························································· 6分 (2)(1)中的两个结论仍然成立. ···································································· 8分 (3)在图②中正确画出线段PD由(1)同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△,ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠,PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、(本题14分)26.解:(1)点E 在y 轴上 ·············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ································································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,2OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ················································································ 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =--+ ·················································· 9分(3)存在符合条件的点P ,点Q . ································································· 10分。
2008年中考数学试卷汇编(圆)及答案

2008年中考数学试题汇编(圆)11.(某某市2008年)在Rt ABC △中,90C ∠=,8AC =,6BC =,两等圆A ,B 外切,那么图中两个扇形(即阴影部分)的面积之和为( A )A .254πB .258πC .2516πD .2532π7.(某某省某某市2008年)已知两圆的半径分别为3cm 和2cm ,圆心距为5cm ,则两圆的位置关系是( B ) A .外离B .外切C .相交D .内切9.(某某省某某市2008年)如图,已知圆心角78BOC ∠=,则圆周角BAC ∠的度数是( C ) A .156B .78C .39D .129.如图3 ,一个扇形铁皮OAB.已知OA =60cm ,∠AOB =120°,小华将OA 、OB 合拢制成了一个圆锥形烟囱帽(接缝忽略不计),则烟囱帽的底面圆的半径为( )B A. 10cm B. 20cm C. 24cm D. 30cm6.(某某市2008年)如图1,正方形ABCD 是⊙O 的内接正方形,点P 在劣弧CD 上不同于点C 得到任意一点,则∠BPC 的度数是( )A .45B .60C .75D .90(第11题图)ABC120°O AB 图3A PBO图4CDAO B E12.(某某市2008年)如图3,PA 切⊙O 于A ,PO 交⊙O 于B ,若PA=6,PB=4,则⊙O 的半径是( )A .52B .56C .2D .58.(某某市2008年)如图,O 是等边三角形ABC 的外接圆,O 的半径为2则等边三角形ABC 的边长为( ) ABC .D .10.(某某市2008年)如图,已知O 的半径为1,AB 与O O 交于点C ,OD OA ⊥,垂足为D ,则cos AOB ∠的值等于( ) A .OD B .OAC .CDD .AB3.(庆阳市试题)两圆半径分别为3和4,圆心距为7,则这两个圆( )A.外切B.相交C.相离D.内切9.(庆阳市试题) 如图4,AB 是O 的直径,CD 为弦,CD AB ⊥于E ,则下列结论中不成立...的是( ) A.COE DOE ∠=∠B.CE DE = C.=OE BE D.BD BC =8.(某某省2008年)如图所示,AB 是⊙O 的直径,AD =DE ,AE与BD 交于点C ,则图中与∠BCE 相等的角有( )A .2个B .3个C .4个D .5个9. (2008年潍坊市)如图,ABC △内接于圆O ,50A =∠,60ABC =∠,BD 是圆O 的(第10题)(第8题) BE DA CO直径, BD 交AC 于点E ,连结DC ,则AEB ∠等于( ) A .70 B .110 C .90 D .1208.(某某市2008年)如图,A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O —C —D —O 路线作匀速运动.设运动时间为t (s ),∠APB=y (°),则下列图象中表示y 与t 之间函数关系最恰当的是( )9.(某某市2008年)在Rt △ABC 中,∠C=90°,AC=12,BC=5,将△ABC 绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是( ) A .25πB .65πC .90πD .130π7、(某某市2008年)如图,已知CD 是⊙O 的直径,过点D 的弦DE 平行于半径OA ,若∠D 的度数是50o,则∠C 的度数是( )A 、50oB 、40oC 、30oD 、25o16.( 某某自治州2008年) 如图6,扇形OAB 是一个圆锥的侧面展开图, 若小正方形方格的边长为1,则这个圆锥的 底面半径为A.21B. 22C. 2D. 222.(枣庄市2008年)右图是奥运会自行车比赛项目标志,图中两车轮所在圆的位置关系是 A .内含 B .相交 C .相切第8题图 OPDCBA y t9045y t9045y t 0904545900t y A B C DBAO图6第2题图D .外离6.(枣庄市2008年)如图,已知⊙O 的半径为5,弦AB =6,M 是AB 上任意一点, 则线段OM 的长可能是A .2.5B .3.5C .4.5D .5.511.(枣庄市2008年)如图,扇形OAB 是圆锥的侧面展开图,若小正方形方格的边长为1 cm ,则这个圆锥的底面半径为 A .22cm B .2cmC .22cm D .21cm 9.(2008年某某省某某市)如图,正方形ABCD 中,E 是BC 边上一点,以E 为圆心、EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则sin EAB 的值为() A .43B .34 C .45D .352.(某某省某某市2008年)右图是一个“众志成城,奉献爱心”的图标,图标中两圆的位置关系是A .外离 B .相交C .外切D .内切4.左边圆锥的主视图是( )A BOM第6题图AOB第11题图ABC第13题图(第9题)(第2题)A10.(某某省某某市2008年)如图,已知⊙O 是以数轴的原点O 为圆心,半径为1的圆,45AOB ∠=︒,点P 在数轴上运动,若过点P 且与OA 平行的直线与⊙O 有公共点, 设OP x =,则x 的取值X 围是 A .O≤x≤2 B .≤x ≤2 C .-1≤x ≤1 D .x >28..(2008年某某某某)已知⊙O 1和⊙O 2外切,它们的半径分别为2cm 和5cm ,则O 1O 2的长是( )(A )2cm (B )3cm (C )5cm (D )7cm5、(某某市2008年)如图,AB 是⊙O 的直径,点C 在⊙O 上,则∠ACB 的度数为()A 、30°B 、45°C 、60°D 、90°6.(某某市二○○八年)如图,在O 中,AOB ∠的度数为m C ,是ACB 上一点,D E ,是AB 上不同的两点(不与A B ,两点重合),则 D E ∠+∠的度数为()A .mB .1802m -C .902m +D .2m 11.如图,圆锥的侧面积恰好等于其底面积的2图所对应扇形圆心角的度数为() A .60 B .90 C .120D .18010.(某某市2008年)如图2,边长为1的菱形ABCD 绕点A 旋转,当B 、C 两点恰好落在扇形AEF 的弧EF 上时,弧BC 的长度等于A.6π B.4πC.3πD.2π(第10题)6题)(第11题)图 2FE D CBA8. (某某市二00八年)如图,小红同学要用纸板制作一个高4cm ,底面周长是6πcm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是(A )12πcm 2(B )15πcm 2(C )18πcm 2(D )24πcm 26.(威海市2008年)如图,AB 是⊙O 的直径,点C ,D 在⊙O 上,OD ∥AC ,下列结论错误的是A .∠BOD =∠BACB .∠BOD =∠CODC .∠BAD =∠CAD D .∠C =∠D12.(威海市2008年)如图,⊙O 的半径为2,点A 的坐标为(2,32),直线AB 为⊙O 的切线,B 为切点.则B 点的坐标为A .⎪⎪⎭⎫ ⎝⎛-5823, B .()13,-C .⎪⎭⎫ ⎝⎛-5954,D .()31,-18.(2008年某某省)如图,有一圆心角为120 o 、半径长为6cm 的扇形,若将OA 、OB 重合后围成一圆锥侧面,那么圆锥的高是A .24cmB .35cmC .62cmD .32cm6.(2008年某某市)下列结论中,正确的是B OACDxy O11BA(A )圆的切线必垂直于半径; (B )垂直于切线的直线必经过圆心; (C )垂直于切线的直线必经过切点; (D )经过圆心与切点的直线必垂直于切线. 10、(某某市2008年)如图(4),在直角坐标系中,四边形OABC 为正方形,顶点A 、C 在坐标轴上,以边AB 为弦的⊙M 与x 轴相切,若点A 的坐标为(0,8),则圆心M 的坐标为( )A 、(4,5)B 、(-5,4)C 、(-4,6)D 、(-4,5)6.(某某省2008年)在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( A ) A .与x 轴相离、与y 轴相切 B .与x 轴、y 轴都相离 C .与x 轴相切、与y 轴相离D .与x 轴、y 轴都相切12.(滨州市2008年)如图所示,AB 是⊙O 的直径,AD =DE ,AE 与BD 交于点C ,则图中与∠BCE 相等的角有 (D )A .2个B .3个C .4个D .5 个13.如图,等腰梯形ABCD 中,AD ∥BC ,以A 为圆心,AD 为半径的圆与BC 切于点M ,与AB 交于点E ,若AD =2,BC =6,则⌒DE的长为( A ) A .23π B .43π C .83π D .π39、(2008年某某市)如图,水平地面上有一面积为230cm π的扇形AOB ,半径OA=6cm ,且OA 与地面垂直.在没有滑动的情况下,将扇形向右滚动至OB 与地面垂直为止,则O 点移动的距离为()CA 、20cmB 、24cmC 、10cm πD 、30cm π5、(2008年某某省某某市)如图,AB 是⊙O 的直径,弦CD ⊥AB,垂足为E, 如果AB=20,CD=16, 那么线段OE 的长为【 】C A 、10 B 、8 C 、6 D 、410、(2008年某某省某某市)在△ABC 中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是BE D ACO 第14题图F A GEBCCBOA【 】BA .23B .1C .2D .3211、(2008年某某省某某市)如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r ,扇形的半径为R ,扇形的圆心角等于90°,则r 与R 之间的关系是【 】DA 、R =2r ;B 、3R r =;C 、R =3r ;D 、R =4r .13、(2008年某某省某某市)如图,在△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交AC 于F ,点P 是⊙A 上一点,且∠EPF =40°,则图中阴影部分的面积是【 B 】 A .94π- B .984π-C .948π-D .988π-7.(2008年某某省某某市)如图,在Rt △ABC 中,∠C=90°,AC=1,BC=2.以边BC 所在直线为轴,把△ABC 旋转一周,得到的几何体的侧面积是A .πB .2πC . 5πD .25π7.( 某某巿2008年)⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是A.内含B. 内切C.相交D.外切5、(某某市2008年)如图,AB 是⊙O 的直径,点C 在⊙O 上,则∠ACB 的度数为()A 、30°B 、45°C 、60°D 、90°9.高速公路的隧道和桥梁最多.图7是一个隧道的横截面,若它的形状是以O 为圆心的圆P AEFDC的一部分,路面AB =10米,净高CD =7米,则此圆的半径OA =( D ) A .5 B .7C .375 D .3777.( 2008年某某市)如图是一个五环图案,它由五个圆组成,下排的两个圆的位置关系是 ( D ).A.内含 B.外切 C.相交 D.外离4.(某某省某某市2008年)在Rt △ABC 中,∠C =90︒,AB =4,AC =1,则cos A 的值是( )BA 15B .14C 15D .44.(某某市2008年)如图,已知以直角梯形ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相切,切点分别是D 、C 、E 。
2008年乌鲁木齐中考数学试题及答案

新疆乌鲁木齐市2008年高中招生统一考试数学试卷(问卷)注意事项:1.本卷共三个大题,23个小题,总分150分,考试时间120分钟;2.本试卷共8页,由两部分组成,其中问卷4页,答卷4页.考生要先在答卷密封区内规定位置认真填写考点、考场号、学校、姓名、准考证号,并在卷头指定位置上填写座位号; 3.所有答案必须用黑色或蓝色钢笔、中性笔(画图可用铅笔)写在答卷上,写在问卷上或另加页均无效.答题时请对准题号,把答案写在答卷的规定位置上; 4.答题时允许使用科学计算器.一、选择题(本大题共7小题,每小题4分,共28分)每题所给的四个选项中只有一项是符合题目要求的,请将所选项的代号字母填在答卷的相应位置处. 1的相反数是( ) A.BC. D2.反比例函数6y x=-的图象位于( ) A .第一、三象限 B .第二、四象限 C .第二、三象限 D .第一、二象限 3.下列运算正确的是( ) A .33--=B .1133-⎛⎫=- ⎪⎝⎭C3=± D3=-4.一名射击运动员连续打靶8次,命中的环数如图1所示, 这组数据的众数与中位数分别为( ) A .9与8 B .8与9 C .8与8.5 D .8.5与95.某等腰三角形的两条边长分别为3cm 和6cm , 则它的周长为( ) A .9cm B .12cm C .15cm D .12cm 或15cm6.一次函数y kx b =+(k b ,是常数,0k ≠)的图象如图2所示, 则不等式0kx b +>的解集是( ) A .2x >- B .0x > C .2x <- D .0x < 7.若0a >且2xa =,3ya =,则x ya -的值为( ) A .1-B .1C .23 D .32图1图2xb +二、填空题(本大题共6小题,每小题4分,共24分)把答案直接填在答卷的相应位置处. 8.将点(12),向左平移1个单位,再向下平移2个单位后得到对应点的坐标是 . 9.如图3,在四边形ABCD 中,AD BC ∥,90D ∠=,若再添加一个条件,就能推出四边形ABCD 是矩形,你所添加的条件是 .(写出一种情况即可)10.乌鲁木齐农牧区校舍改造工程初见成效,农牧区最漂亮的房子是学校.2005年市政府对农牧区校舍改造的投入资金是5786万元,2007年校舍改造的投入资金是8058.9万元,若设这两年投入农牧区校舍改造资金的年平均增长率为x ,则根据题意可列方程为 .11.我们知道利用相似三角形可以计算不能直接测量的物体的高度,阳阳的身高是1.6m ,他在阳光下的影长是1.2m ,在同一时刻测得某棵树的影长为3.6m ,则这棵树的高度约为 m . 12.如图4所示的半圆中,AD 是直径,且3AD =,2AC =, 则sin B 的值是 .13.如图5所示是一个圆锥在某平面上的正投影,则该圆锥的侧 面积是 . 三、解答题(本大题Ⅰ—Ⅴ题,共10小题,共98分)解答时应在答卷的相应位置处写出文字说明、证明过程或演算过程. Ⅰ.(本题满分12分,第14题6分,第15题6分) 14.解不等式组2392593x x x x++⎧⎨+>-⎩≥15.先化简,再求值:221111121x x x x x +-÷+--+,其中1x =. Ⅱ.(本题满分28分,第16题7分,第17题10分,第18题11分) 16.在一次数学课上,王老师在黑板上画出图6,并写下了四个等式: ①AB DC =,②BE CE =,③B C ∠=∠,④BAE CDE ∠=∠.要求同学从这四个等式中选出两个作为条件,推出AED △是等腰三角形.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)已知:求证:AED △是等腰三角形. 证明:D图3 C B D A图4图5C17.2008年5月12日14时28分在我国四川省汶川地区发生了里氏8.0级强烈地震,灾情牵动全国人民的心,“一方有难、八方支援”.某厂计划加工1500顶帐篷支援灾区人民,在加工了300顶帐篷后,由于救灾需要工作效率提高到原来的1.5倍,结果提前4天完成了任务.求原来每天加工多少顶帐篷?18.某公司在A B ,两地分别库存挖掘机16台和12台,现在运往甲、乙两地支援建设,其中甲地需要15台,乙地需要13台.从A 地运一台到甲、乙两地的费用分别是500元和400元;从B 地运一台到甲、乙两地的费用分别是300元和600元.设从A 地运往甲地x 台挖掘机,运这批挖掘机的总费用为y 元.(1)请填写下表,并写出y 与x 之间的函数关系式;(2)公司应设计怎样的方案,能使运这批挖掘机的总费用最省?Ⅲ.(本题满分36分,第19题12分,第20题12分,第21题12分)19.宝宝和贝贝是一对双胞胎,他们参加奥运志愿者选拔并与甲、乙、丙三人都进入了前5名.现从这5名入选者中确定2名作为志愿者.试用画树形图或列表的方法求出: (1)宝宝和贝贝同时入选的概率;(2)宝宝和贝贝至少有一人入选的概率.20.如图7,河流两岸a b ,互相平行,C D ,是河岸a 上间隔50m 的两个电线杆.某人在河岸b 上的A 处测得30DAB ∠=,然后沿河岸走了100m 到达B 处,测得60CBF ∠=,求河流的宽度CF 的值(结果精确到个位).BED CFab A图721.如图8,在四边形ABCD 中,点E 是线段AD 上的任意一点(E 与A D ,不重合),G F H ,,分别是BE BC CE ,,的中点.(1)证明四边形EGFH 是平行四边形; (2)在(1)的条件下,若EF BC ⊥,且12EF BC =,证明平行四边形EGFH 是正方形.Ⅳ(本题满分8分) 22.先阅读,再解答:我们在判断点(720)-,是否在直线26y x =+上时,常用的方法:把7x =-代入26y x =+中,由2(7)6820⨯-+=-≠,判断出点(720)-,不在直线26y x =+上.小明由此方法并根据“两点确定一条直线”,推断出点(12)(34)(16)A B C -,,,,,三点可以确定一个圆.你认为他的推断正确吗?请你利用上述方法说明理由.Ⅴ(本题满分14分)23.如图9,在平面直角坐标系中,以点(11)C ,为圆心,2为半径作圆,交x 轴于A B ,两点,开口向下的抛物线经过点A B ,,且其顶点P 在C 上.(1)求ACB ∠的大小;(2)写出A B ,两点的坐标; (3)试确定此抛物线的解析式;(4)在该抛物线上是否存在一点D ,使线段OP 与CD 互相平分?若存在,求出点D 的坐标;若不存在,请说明理由.BG A EF HD图8新疆乌鲁木齐市2008年高中招生统一考试数学试卷参考答案及评分建议一、选择题(本大题共7小题,每小题4分,共28分)二、填空题(本大题共6小题,每小题4分,共24分) 8.(00),9.90A ∠=或AD BC =或AB CD ∥10.25786(1)8058.9x +=11.4.812.23 13.15π4三、解答题(本大题Ⅰ—Ⅴ题,共10小题,共98分) Ⅰ.(本题满分12分,第14题6分,第15题6分) 14.解:由239x x ++≥,得6x ≥ ·································································· 2分由2593x x +>-,得45x >································································ 4分 所以,不等式组的解集是6x ≥ ····························································· 6分15.解:原式211(1)1(1)(1)1x x x x x -=-++-+ ······················································· 2分 2211(1)(1)1(1)(1)x x x x x x -+--=-=+++ ················································· 4分 22(1)x =+ ·················································································· 5分当1x =时,原式23== ····················································· 6分 Ⅱ.(本题满分28分,第16题7分,第17题10分,第18题11分)16.已知:①③(或①④,或②③,或②④) ······················································ 2分 证明:在ABE △和DCE △中,B C AEB DEC AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,ABE DCE ∴△≌△ ························································ 6分 AE DE ∴=,即AED △是等腰三角形 ······························································ 7分 17.解:设该厂原来每天生产x 顶帐篷 ······························································· 1分 据题意得:1500300120041.5x x x ⎛⎫-+= ⎪⎝⎭································································ 5分 解这个方程得100x = ····················································································· 8分经检验100x =是原分式方程的解 ······································································ 9分 答:该厂原来每天生产100顶帐篷. ································································ 10分 18··················································································································· 3分500400(16)300(15)600(3)y x x x x =+-+-+-4009100x =+ ······························································································ 6分 (2)30x -≥且150x -≥即315x ≤≤,又y 随x 增大而增大·························· 9分 ∴当3x =时,能使运这批挖掘机的总费用最省,运送方案是A 地的挖掘机运往甲地3台,运往乙地13台;B 地的挖掘机运往甲地12台,运往乙地0台 ······························· 11分Ⅲ.(本题满分36分,第19题12分,第20题12分,第21题12分) 19.解:树形图如下:共20种情况 ·································································································· 6分(1)宝宝和贝贝同时入选的概率为212010= ························································ 9分 (2)宝宝和贝贝至少有一人入选的概率为1472010= ············································· 12分 20.解:过点C 作CE AD ∥,交AB 于ECD AE ∥,CE AD ∥ ················································································ 2分 ∴四边形AECD 是平行四边形 ·········································································· 4分50AE CD ∴==m ,50EB AB AE =-=m ,30CEB DAB ∠=∠= ······················ 6分 又60CBF ∠=,故30ECB ∠=,50CB EB ∴==m ········································· 8分贝贝 甲 乙 丙 宝宝 甲 乙 丙 宝宝 贝贝 乙 丙 甲 丙 甲 宝宝 贝贝 乙 宝宝 贝贝 宝宝 贝贝 甲 丙 乙∴在Rt CFB △中,sin 50sin 6043CF CB CBF =∠=≈m ······························· 11分答:河流的宽度CF 的值为43m . ···································································· 12分 21.证明:(1)在BEC △中,G F ,分别是BE BC ,的中点GF EC ∴∥且12GF EC =············································································· 3分 又H 是EC 的中点,12EH EC =,GF EH ∴∥且GF EH = ··············································································· 4分 ∴四边形EGFH 是平行四边形 ········································································· 6分 (2)证明:G H ,分别是BE EC ,的中点GH BC ∴∥且12GH BC = ············································································· 8分 又EF BC ⊥,且12EF BC =,EF GH ∴⊥,且EF GH = ····························· 10分∴平行四边形EGFH 是正方形.Ⅳ.(本题满分8分)22.他的推断是正确的. ················································································· 1分 因为“两点确定一条直线”,设经过A B ,两点的直线解析式为y kx b =+ ·················· 2分由(12)(34)A B ,,,,得234k b k b +=⎧⎨+=⎩解得11k b =⎧⎨=⎩ ····················································· 4分∴经过A B ,两点的直线解析式为1y x =+ ························································· 5分把1x =-代入1y x =+中,由116-+≠,可知点(16)C -,不在直线AB 上,即A B C ,,三点不在同一直线上 ······································································ 7分 所以A B C ,,三点可以确定一个圆. ································································ 8分 Ⅴ.(本题满分14分) 23.解:(1)作CH x ⊥轴,H 为垂足,1CH =,半径2CB = ·············································· 1分 60BCH ∠=,120ACB ∴∠= ································· 3分(2)1CH =,半径2CB =HB ∴=(1A , ······································ 5分(10)B + ······························································· 6分(3)由圆与抛物线的对称性可知抛物线的顶点P 的坐标为(13), ······························ 7分 设抛物线解析式2(1)3y a x =-+ ······································································· 8分把点(1B 代入上式,解得1a =- ····························································· 9分222y x x ∴=-++ ······················································································· 10分(4)假设存在点D 使线段OP 与CD 互相平分,则四边形OCPD 是平行四边形 ······· 11分 PC OD ∴∥且PC OD =.PC y ∥轴,∴点D 在y 轴上. ··································································· 12分 又2PC =,2OD ∴=,即(02)D ,. 又(02)D ,满足222y x x =-++,∴点D 在抛物线上 ························································································ 13分所以存在(02)D ,使线段OP 与CD 互相平分. ···················································· 14分。
2008年中考数学试题分类汇编(阅读、规律、代数式)

以下是河北省柳超的分类(2008年贵阳市)13.符号“f ”表示一种运算,它对一些数的运算结果如下: (1)(1)0f =,(2)1f =,(3)2f =,(4)3f =,…(2)122f ⎛⎫=⎪⎝⎭,133f ⎛⎫= ⎪⎝⎭,144f ⎛⎫= ⎪⎝⎭,155f ⎛⎫= ⎪⎝⎭,…利用以上规律计算:1(2008)2008f f ⎛⎫-= ⎪⎝⎭.(2008年贵阳市)10.根据如图2所示的(1),(2),(3)三个图所表示的规律,依次下去第n个图中平行四边形的个数是( )A .3nB .3(1)n n +C .6nD .6(1)n n +(2008年遵义市)16.如图是与杨辉三角形有类似性质的三角形数垒,a b ,是某行的前两个数,当7a =时,b = .以下是江西康海芯的分类:1. (2008年郴州市)因式分解:24x -=____________ ()()22x x +-辽宁省 岳伟 分类2008年桂林市(图2)……(1)(2) (3)1 2 2 3 4 3 4 7 7 4 5 11 14 11 5· · · · · · · · · a b · · · · · · · · (16题图)如图,矩形1111ABCD的面积为4,顺次连结各边中点得到四边形2222ABCD,再顺次连结四边形2222ABCD四边中点得到四边形3333ABCD,依此类推,求四边形n n n n ABCD的面积是 。
18.(2008年湖州市)将自然数按以下规律排列,则2008所在的位置是第 行第 列.10. ( 2008年杭州市) 如图, 记抛物线12+-=x y 的图象与x 正半轴的交点为A , 将线段OA 分成n 等份, 设分点分别为121,,,-n P P P , 过每个分点作x 轴的垂线, 分别与抛物线交于点121,,,-n Q Q Q , 再记直角三角形 ,,22111Q P P Q OP 的面积分别为 ,,21S S ,这样就有,24,21322321nn S n n S -=-=… ; 记21S S W += 1-++n S , 当n 越来越大时, 你猜想W 最接近的常数是( C ) (A) 32 (B)21 (C)31(D) 41(第10题)16. ( 2008年杭州市) 如图, 一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形, 那么一个5×3的矩形用不同的方式分割后, 小正方形的个数可以是 ________________ .以下是安徽省马鞍山市成功中学的汪宗兴老师的分类1.(2008年·东莞市)(本题满分9分)(1)解方程求出两个解1x 、2x ,并计算两个解的写出你的结论.24.(2008年双柏县)(本小题9分)依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:(1)某工厂一名工人2008年3月的收入为2 400元,问他应交税款多少元? (2)设x 表示公民每月收入(单位:元),y 表示应交税款(单位:元),(第16题)当2500≤x ≤4000时,请写出y 关于x 的函数关系式;(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元?(08年宁夏回族自治区)商场为了促销,推出两种促销方式:方式①:所有商品打7.5折销售: 方式②:一次购物满200元送60元现金.(1)杨老师要购买标价为628元和788元的商品各一件,现有四种购买方案:方案一:628元和788元的商品均按促销方式①购买; 方案二:628元的商品按促销方式①购买,788元的商品按促销方式②购买; 方案三:628元的商品按促销方式②购买,788元的商品按促销方式①购买; 方案四:628元和788元的商品均按促销方式②购买. 你给杨老师提出的最合理购买方案是 .(2)通过计算下表中标价在600元到800元之间商品的付款金额,你总结出商品的购买规律是 。
中考数学应用题归类解析

中考数学应用题归类解析应用题源于生产、生活实践,是中考数学的常见题型.解题时,要求学生要熟悉其基本的生产、生活情景,善于积极地用数学观点和方法去解决实际问题.为了帮助九年级同学系统地复习这一题型,本文以2008年中考题为例,归纳其类型与解法,供参考. 一、方程型例1、(长沙市)“5·12”汶川大地震后,灾区急需大量帐篷.某服装厂原有4条成衣生产线和5条童装生产线,工厂决定转产,计划用3天时间赶制1000顶帐篷支援灾区.若启用1条成衣生产线和2条童装生产线,一天可以生产帐篷105顶;若启用2条成衣生产线和3条童装生产线,一天可生产帐篷178顶.(1)每条成衣生产线和童装生产线每天生产帐篷各多少顶?(2)工厂满负荷全面转产,是否可以如期完成任务?如果你是厂长,你会怎样体现你的社会责任感?解:(1)设每条成衣生产线和童装生产线平均每天生产帐篷x 、y 顶,则⎩⎨⎧==⎩⎨⎧=+=+32y 41x 178y 3x 2105y 2x 解得答:略(2)由1000972)325414(3<=⨯+⨯知,即使工厂满负荷全面转产,也不能如期完成任务.可以从加班生产、改进技术等方面进一步挖掘生产潜力,或动员其他厂家支援等,想法尽早完成生产任务,为灾区人民多做贡献.二、不等式型例2、(青岛市)2008年8月,北京奥运会帆船比赛将在青岛国际帆船中心举行.观看帆船比赛的船票分为两种:A 种船票600元/张,B 种船票120元/张.某旅行社要为一个旅行团代购部分船票,在购票费不超过5000元的情况下,购买A 、B 两种船票共15张,要求A 种船票的数量不少于B 种船票数量的一半.若设购买A 种船票x 张,请你解答下列问题: (1)共有几种符合题意的购票方案?写出解答过程; (2)根据计算判断:哪种购票方案更省钱? 解:(1)根据题意,得320x 55000)x 15(120x 6002x 15x ≤≤⎪⎩⎪⎨⎧≤-+-≥解得所以满足条件的x 为5或6。
