数学奥赛中数论问题的解题方法
数论题的解题诀窍
数论题的解题诀窍数论题是数学中的一个分支，研究整数之间的性质和关系。
解题的诀窍包括找规律、分类讨论、数形结合等方法。
下面将详细介绍这些解题的技巧，并以实例加以说明。
一、找规律是解决数论题的常用方法之一。
数论题通常需要找到或证明一种性质或关系。
这时我们可以从一些特殊情况入手，观察数列或方程中数值的变化规律，尝试找到规律并进行归纳。
举例说明：求证任意一个整数的平方必为偶数。
我们考察一些数字的平方和奇偶性：1^2=1，是奇数；2^2=4，是偶数；3^2=9，是奇数；4^2=16，是偶数；...我们发现，无论正整数n取多大，n^2的结果都是偶数。
所以可以得出结论：任意一个整数的平方都是偶数。
二、分类讨论是解决数论题的常用方法之一。
当数论题目中的数字或问题具有多种情况时，我们可以按照特定的规则进行分类讨论，从而找到问题的解决之道。
举例说明：有一袋中有100个球，其中有红球、蓝球和绿球，红球与蓝球的数量相等，绿球的数量是红球和蓝球的数量之和的一半。
问红球、蓝球和绿球分别的数量是多少？解析：设红球的数量为x，蓝球的数量为y，则绿球的数量为(x+y)/2。
根据题目条件可以列出方程组：x + y + (x + y)/2 = 100。
化简得到：3x + 3y = 200，即x+y = 200/3。
由于x和y都是整数，所以200/3必须是整数。
假设x和y都小于200/3，那么它们的和不可能等于200/3，所以x和y必然大于等于200/3。
但是，200/3在整数范围内最近的整数是67，所以x和y的和必然小于等于最大为67，因此只有一种情况。
分类讨论可用于解决类似的数论题目，当题目中数字或情况有多种组合时，我们可以采用这种方法。
三、数形结合是解决数论题的另一种方法。
有些数论问题可以通过数学模型的图形推理或与几何问题的联系相结合来解决。
举例说明：在一个等边三角形的顶点上依次标上1,2,…,100这一百个整数，要求将顶点上的整数分别用两个颜色红和蓝进行染色，使得对于每一个等边三角形的三个顶点，如果存在一个定的整数n，且其三个顶点的整数之和为n的话，则这三个顶点必须用同样的颜色染色。
高中奥林匹克数学竞赛解题方法
高中奥林匹克数学竞赛解题方法一、代数技巧代数是数学的基础，掌握代数技巧对于解决数学问题至关重要。
以下是一些常用的代数技巧：1、合并同类项：将同类项合并为一个项，可以简化计算过程。
2、提取公因式：将公因式提取出来，可以简化计算过程。
3、完全平方公式和平方差公式：这两个公式在代数中非常常用，可以用来进行化简和展开。
4、分式的约分：将分式约分为最简形式，可以简化计算过程。
5、根式与分数指数幂的互化：将根式转化为分数指数幂，或将分数指数幂转化为根式，可以用来解决一些复杂的问题。
二、几何技巧几何是数学中重要的分支之一，掌握几何技巧对于解决数学问题非常重要。
以下是一些常用的几何技巧：1、三角形的内心、外心和垂心：掌握这些特殊点的性质和作法，可以用来解决一些与三角形相关的问题。
2、圆的标准方程和一般方程：掌握圆的标准方程和一般方程，可以用来解决一些与圆相关的问题。
3、立体几何中的空间向量：通过空间向量的运算，可以用来解决一些立体几何问题。
4、解析几何中的直线、圆和椭圆：掌握直线、圆和椭圆的性质和作法，可以用来解决一些解析几何问题。
三、数据分析数据分析是数学中重要的应用之一，掌握数据分析技巧对于解决实际问题非常重要。
以下是一些常用的数据分析技巧：1、数据的集中趋势和离散程度：掌握数据的集中趋势和离散程度，可以用来评估数据的分布情况。
2、数据的可视化：通过图表等可视化工具，可以更加直观地展示数据和分析结果。
3、回归分析：通过回归分析，可以找出变量之间的关系，从而对数据进行更加深入的分析。
4、方差分析：通过方差分析，可以检验多个样本之间是否存在显著性差异。
5、时间序列分析：通过时间序列分析，可以预测未来一段时间内的数据变化趋势。
四、数学建模数学建模是数学中重要的应用之一，掌握数学建模技巧对于解决实际问题非常重要。
以下是一些常用的数学建模技巧：1、建立数学模型：根据实际问题建立相应的数学模型，可以是方程、不等式、图形等。
奥数秘技数论的高级技巧
奥数秘技数论的高级技巧数论是奥林匹克数学竞赛中的重要一环，它要求考生具备深厚的数学基础和解题能力。
本文将介绍奥数秘技数论的高级技巧，帮助读者在奥数竞赛中取得更好的成绩。
一、整除性与同余在数论中，整除性与同余是常见的概念，它们在解题过程中经常起到关键作用。
1. 整除性整除性是指一个数能够被另一个数整除，常用的整除性定理包括带余除法定理、最大公约数定理、最小公倍数定理等。
熟练掌握这些定理，并能够灵活应用于解题过程中，将有助于提升解题效率。
2. 同余同余是指两个数之间满足某个特定模的关系，常用的同余性质和定理包括同余定理、欧拉定理、费马小定理等。
在解题过程中，通过利用同余关系可以简化问题，减少计算量，提高解题速度。
二、模运算及其应用模运算是奥数秘技数论的重要组成部分，它是指将整数除以一个模数的操作。
模运算在奥数竞赛中的应用非常广泛，以下是几个常用的模运算应用示例：1. 求幂取模当需要求一个数的幂对某个模数取模时，可以利用模运算的性质进行简化计算。
例如，欧拉定理和费马小定理提供了在计算大数的幂取模时的快速方法。
2. 同余方程求解同余方程是奥数竞赛中常见的问题类型，通过模运算的性质，可以求解同余方程并给出满足条件的整数解。
三、数列与排列组合数列与排列组合是奥数秘技数论中的另一大类，掌握它们的性质和解题方法能够帮助读者快速解决相关问题。
1. 等差数列与等比数列等差数列和等比数列是奥数竞赛中常见的数列类型，通过观察和推导，可以求解数列的通项公式、前n项和等相关问题。
2. 排列组合计数排列组合是奥数竞赛中常见的计数问题类型，通过运用排列组合的原理，可以解决选择问题、放置问题等各种计数问题。
四、二次剩余与二次剩余定理二次剩余是奥数竞赛中较为复杂的问题类型，涉及到高级数论知识。
二次剩余定理是解决二次剩余问题的重要工具，它可以通过特定模下的同余关系来判断一个数是否是二次剩余，并给出相应的解。
五、进阶话题与拓展除了上述内容，奥数秘技数论还涉及到一些进阶话题和拓展应用。
小学奥数讲解 关于数论的问题
奥数题讲解数论问题所用知识不超过小学5年级，题目难度5颗星。
a,b,c,d都是个位数，由它们组成的四位数abcd和两位数ab、cd满.足(ab+cd) *(ab+cd)=abcd。
请问满.足条件的四位数abcd共有多少个?答案: 3个。
辅导办法:将题目写给小朋友，让他自行思考解答，若20分钟还不能解答,由家长进行讲解。
讲解思路:这种类型的题目,关键是要寻找ab和cd的关系,再根据关系寻找满足条件的数。
步骤1:先思考第一个问题,ab+cd的范围是什么?这个问题很简单, 由于ab+cd的平方是四位数,而32*32=1024 ,99*99=9801,因此ab+cd在32到99之间。
步骤2:再思考第二个问题,db和cd满足什么关系?由题意，(ab+cd) *(ab+cd) =100*ab+cd,化简有(ab+cd)*(ab+cd-l)=99*ab 因此，(ab+cd) *(ab+cd-1)是99的倍数。
步骤3:再思考第二个问题,ab+cd可能的取值是多少?由于99=3*3*11,而(ab+cd)和(ab+cd-1)不可能同时是9的倍数,因此只可能有3种情况,结合步骤1中ab+cd的范围讨论。
情况一：ab+cd是9的倍数,ab+cd-1是11的倍数,此时只有ab+cd 是45才满足条件;情况二:ab+cd是11的倍数,ab+cd-1是9的倍数,此时只有ab+cd是55才满足条件;情况三:ab+cd或ab+cd-1是99的倍数,此时只有xb+cd是99才满足条件。
步骤4:综合上述几个问题,代入验证，45*45=2025=(20+25)*(20+25)55*55=3025= (30+25)*(30+25)99*99=9801= (98+1) *(98+1),都满足条件,所以满足条件的数是3个。
数学奥赛中数论问题的解题与方法研究
数学奥赛中数论问题的解题与方法研究1引言在数学竞赛中，数论问题始终是一个重要内容．数论是研究数规律和性质的数学分支．数论分为初等数论、解析数论和代数数论．据统计初等数论的内容在数学奥赛中用的比较多，因此本文的讨论均为初等数论中与数学奥赛相关的数论知识．２ 背景介绍２.１ 理论背景对数学奥赛中数论问题的解题与方法研究，我们首先要了解与数学奥赛相关的数论内容．从近年来的数学竞赛试题来看，整数的奇偶性、整除性、同余、不定方程等在数学奥赛中占的比重较大．这些问题貌似简单，但真正掌握并灵活运用并非易事，它的内容严谨简洁，方法奇巧多变，蕴涵了丰富的数学思想方法，其数学思想方法又往往隐含在数学知识形成和问题解决的过程中．初等数论基础知识比较简单，但处理问题方法技巧性很强，在培养人们思维能力方面起着重要作用．２.２ 历史背景毕达哥拉斯被称为数论的远祖．自古以来，数学主要考虑的是数的表示和计算以及求解实用的问题，这叫算术，但毕达哥拉斯开始把数本身作为数学研究的对象，这就成为了数论即数的理论．此后由于费尔马的研究，整数论才成为一门独立的学科，他被称为数论之父)119117](1[.-P３ 整数３.１ 整数的奇偶性偶数﹕能被２整除的整数；奇数：不能被２整除的整数． 关于奇数和偶数有如下的性质)3635](2[:-P⑴ 奇数＋奇数＝偶数，奇数＋偶数＝奇数，偶数＋偶数＝偶数．⑵ 若干个整数之和为奇数，则这些数中必有奇数，且奇数的个数为奇数个；若干个整数之和为偶数，则这些数中若有奇数，奇数的个数必为偶数个．⑶ 奇数×奇数＝奇数；奇数×偶数＝偶数．⑷ 若干个整数之积为奇数，则这些数必为奇数；若干个整数之积为偶数，则这些数中至少有一个是偶数．⑸ 若a 是整数，则 a 与a 有相同的奇偶性．⑹ 若a 、b 是整数，则b a b a -+与奇偶性相同．上述性质显而易见，证明也很简单，运用上面的性质可以解决关于奇偶性的问题．以下我们通过例子加以说明.例 1 设n 为奇数，，，21a a …，n a 是n ，，， 21的任意一个排列，证明()()()1121-+--n a n a n a 必是偶数.证明 （反证法）假设这个乘积是奇数，根据以上性质4，得1121-+--n a n a n a ，，， 必都为奇数，且已知n 为奇数，于是﹙1a －n ﹚＋﹙2a －n ＋1﹚＋…＋﹙n a －1﹚＝奇数， 而由于1a ，2a …，n a 是１，２，…，n 的一个排列，故﹙1a －n ﹚＋﹙2a －n ＋1﹚＋…＋﹙n a －1﹚ ＝﹙1a ＋2a ＋…n a ﹚－（１＋２＋…n ）＝０ 因为０是偶数不是奇数，矛盾.所以乘积﹙1a －n ﹚﹙2a －n ＋1﹚…﹙n a －1﹚必是偶数.例 2 在1000999321，，，， 这1000个数的前面任意添加一个正号或负号，问他们的代数和是奇数还是偶数.解 因为b a +与b a -的奇偶性相同，所以在1000999321，，，，， 这1000个数的前面任意添加一个正号或负号，它的奇偶性都与1000999321+++++ 的奇偶性相同，由于1000999321+++++ 是偶数，所以在1000999321，，， 这1000个数的前面任意添加一个正号或负号，它们的代数和一定是偶数.大量练习这类习题，灵活运用奇偶数的这些性质，对于一些表面看来棘手的问题也可迎刃而解. 3.2 整除性理论整除:设z b a ∈，，若z q ∈存在，使得bq a =,则称b 整除a ，记做a b |. 整除的性质(1) 能被4﹙或25﹚整除的数的特征是这个数的末二位数能被4﹙或25﹚整除；(2) 能被8（或125）整除的数的特征是这个数的末三位上的数字所组成的数能被8（或125）整除；(3) 能被11整除的数的特征是这个数的偶位上的数字之和与奇数位上的数字之和的差能被11整除)80](3[P ；(4) 如果一个数能被3或9整除，那么这个数各位上的数字之和能被3或9整除，反之成立)35](4[.P 例 3 已知一个七位自然数42762xy 是99的倍数(其中y x ，是阿拉伯数字)，试求100330520++y x 之值，简写出求解过程.解 由99｜42762xy 知9｜42762xy 且11｜42762xy ，所以72426++++++y x 是9的倍数，即3++y x m 9=(m 为自然数)，又因为9090≤≤≤≤y x ，，所以2133≤++≤y x ，从而156=+=+y x y x 或.由11｜42762xy 可知()22746++-+++y x 是11的倍数，所以k y x 1113=-+(k 为整数)，又，99≤-≤-y x 即，22134≤-+≤y x 所以92=--=-y x y x 或.因为y x +与y x -同奇偶，所以42==y x ，或312==y x ，(不符合舍去).从而2460100330520=++y x . 3.3 平方数平方数:如果一个整数是某一个整数的平方，这样的数叫平方数，也叫完全平方数，如0，1，9，100等.平方数有许多优美的特性，与平方数有关的问题常出现在国内外数学竞赛上，这些习题往往结论奇妙，耐人寻味我们来看看关于平方数的性质.(1) 偶数的平方一定能被4整除； (2) 奇数的平方除以8余1；(3) 凡个位数为651，，的数的平方其个位数不变；(4) 凡个位数字为8732，，，或末尾数字为5但不是25的数，一定不是平方数； (5) 凡个位数字是6而十位数字为偶数的一定不是平方数； (6) 平方数若是奇数，则它的十位数字必是偶数.例 4 已知222n m l =+，n m l ，，，均为自然数，l 为素数.证明:)(2n m l ++为完全平方数.证明 222n m l =+，则))((2222m n m n l m n l +-=-=，即，由l 是素数，，0>->+m n n m 只有121211222-=+=++=-=+=l m m m m l m n m n l ，即，，，因此，222)1(12212222)1(2+=++=+-+=++=++l l l l l m l m l即)1(2++m l 为完全平方数.另外我们介绍在数论问题中进行恰当估计的一些典型方法和技巧，在做数学题中我们容易漏掉一些显而易见的性质，从而被绊住.例5 设p 和q 是两个给定的正整数，且满足pq q p 11+++是整数.求证:p 和q 的最大公约数不超过q p +.分析和解 设p 和q 的最大公约数是d ，则我们可以得到，，d q q d p p 11== (其中11q p ，是互质的整数)由1121121212)()(11q p d q p d q p d p q q p +++=+++是整数 所以2d ｜)()(1121212q p d q p d +++故2d ︱)(11q p d +亦即d ｜)(11q p +.显然我们熟知的一个结论，一个正整数的约数必定不超过它本身)6](5[P ，因此d ≤dqp q p +=+11即d ≤q p +. 4 不定方程不定方程是数论中最古老的一个分支，且不定方程问题富有趣味，耐人寻味，具有优美的技巧.我们熟知不定方程的一些性质后，对生活中比较棘手的问题就很容易解决了.定理)2625](6[1-P 二元一次不定方程()0≠∈=+b a z c b a c by ax ，，，，，有整数解的充分必要条件是()cb a ，.定理2 若1)(=b a ，，且00y x ，为c by ax =+之一组解，则此二元一次不定方程的全部解为z t bty y bt x x ∈⎩⎨⎧-=+=00.例6 某团体搞郊游活动，需要kg 6水，小张拿来两只空桶去水井里提水，一只可盛kg 7水，一只可盛kg 5水，试问小张应该如何操作才能得到kg 6水?解 由于一只桶可盛kg 5水，因此必须在另一只桶内有kg 1的水，这样就能得到kg 6的水，因此要求如何利用这两只空桶得到kg 1水，设可盛kg 5水的水桶装了x 次水， 可盛kg 7水的水桶装了y 次水，则175=-y x .2300==y x ，整数解为：为任意整数）t ty tx (5273⎩⎨⎧-=-= 由此可知取水的操作过程：可装kg 5水的水桶盛水3次，倒入装kg 7的大桶2次，将剩下的kg 1水倒在大桶内，再用小桶盛水kg 5，合起来就得kg 6的水.5 同余定义：如果两个整数b a ，被同一个正整数m 去除，所得的余数相同：mr r ms b m r r mt a <≤+=<≤+=00，，则称a 与b 模m 同余，记作)(mod m b a ≡，否则称a 与b 模m 不同余.定理 1 如果n n b b b a a a ，，，，，，， 2121都是整数，且.21)(m od n i m b a i i ，，，， =≡ 那么).(mod ).(mod 21212121m b b b a a a m b b b a a a n n n n ≡+++≡+++性质1 对于数字)90(≤≤a a ，与一切自然数n ，a a n 与14+的个位数相同；224a a n 与+的个位数字相同；334a an 与+的个位数字相同；444a a n 与+个位数字相同.由以上定理和性质我们可以解很多复杂的问题，对以下这道题就是利用了上面的定理和性质.例7 求5013分别被5，11除所得的余数. 解 因为)5(mod 313≡，)5(mod 134≡，所以).5m od 491333132485050（≡⨯≡⨯≡≡因为)11(m od 102)11(m od 2135≡≡，，而 )11(mod 1102≡，所以)11(m od 11)10(10)2(213552101055050≡≡≡≡≡≡，因此，5013除以11余1.例8 求整数12756839-=p 的个位数字.解 因为)4(mod 3756839≡，因此，7568392的个位数字与32的个位数字相同， 而823=，则p 的个位数字是7.利用同余知识，还能解决整除问题，因为要证b ｜a ，则只要证)(mod 0b a ≡即可，这样同余及有关性质成为处理整除问题的有力工具.例如我们利用同余的性质证明前面介绍的整除的性质3. 例9 证明能被11整除的数的特征是这个数的偶位上的数字之和与奇位上的数字之和的差能被11整除.证 设.1010100111011a a a a N a a a a N n n n n n n ++++==--- ，则因).11(m od )1(10)11(m od 110kk-≡-≡，则因此)11(m od )1()1()1(0111a a a a N n n n n +-++-+-≡-- ，当t n 2=时，由上式 )11(mod )1()1()1(01121222a a a a N t t t t +-++-+-≡-- 即 N ≡[)()(1321202222a a a a a a a t t t t +++-++++--- ])11(mod ，当12-=t n 时，)11(m od )1()1()1()1(012222221212a a a a a N t t t t +-+-++-+-≡---- 即 [])11(m od )()(132********a a a a a a a N t t t t +++-+++≡---- .即不论n 是奇数还是偶数，N 的偶数位的数字之和与奇数位上的数字之和的差对于模11同余，若这个差记为M ，即)11(mod M N ≡，因此，11｜N 当且仅当11｜M ．通过上面的论述，我们加深了对初等数论的认识，随着对初等数论知识的不断运用，我们对它出现的任何形式的题型都会游刃有余.初等数论在数学奥赛中出现的比重较大，学透以上初等数论知识后我们对数学奥赛中的数论问题也就容易解决了.希望以上的讨论为参加数学奥赛的同学提供一定的帮助.参考文献:[1] 胡作玄. 从毕达哥拉斯到费尔马 [M]，河南: 河南科学技术出版社2001，1 [2] 陈传理，张同君.竞赛数学教程[M]，北京：高等教育出版社1996.10 [3] 阎满富，王朝霞.初等数论及其应用[M]，北京：中国铁道出版社1999.4 [4] 判春雷， 数学竞赛中的数论问题选讲[J], 中华期刊网 2007 [5] 章复春， 数论问题中的不等式估计[J], 2000 ，5.[6] 闵嗣鹤，严士健.初等数论[M]，北京：高等教育出版社1996.10[7] Crux Mathematicorum.22.No.4.May∕1996。
【奥赛】小学数学竞赛：容斥原理之数论问题.学生版解题技巧 培优 易错 难
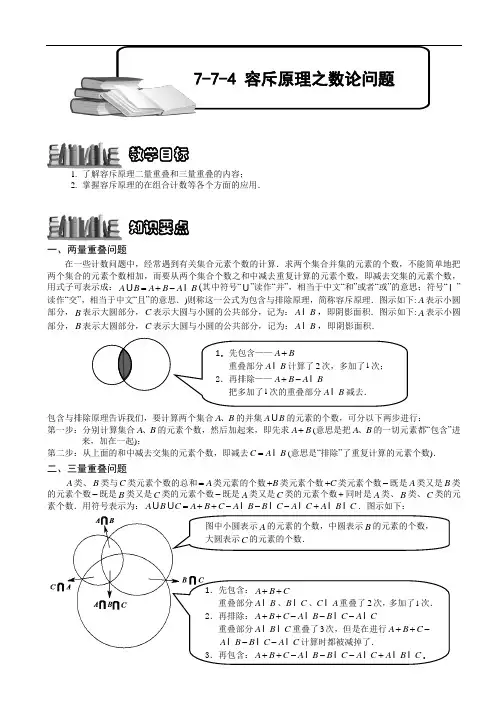
1. 了解容斥原理二量重叠和三量重叠的内容；2. 掌握容斥原理的在组合计数等各个方面的应用．一、两量重叠问题在一些计数问题中，经常遇到有关集合元素个数的计算．求两个集合并集的元素的个数，不能简单地把两个集合的元素个数相加，而要从两个集合个数之和中减去重复计算的元素个数，即减去交集的元素个数，用式子可表示成：A B A B A B =+-U I (其中符号“U ”读作“并”，相当于中文“和”或者“或”的意思；符号“I ”读作“交”，相当于中文“且”的意思．)则称这一公式为包含与排除原理，简称容斥原理．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．图示如下:A 表示小圆部分，B 表示大圆部分，C 表示大圆与小圆的公共部分，记为：A B I ，即阴影面积．包含与排除原理告诉我们，要计算两个集合A B 、的并集A B U 的元素的个数，可分以下两步进行：第一步：分别计算集合A B 、的元素个数，然后加起来，即先求A B +(意思是把A B 、的一切元素都“包含”进来，加在一起)；第二步：从上面的和中减去交集的元素个数，即减去C A B =I (意思是“排除”了重复计算的元素个数)．二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数．用符号表示为：A B C A B C A B B C A C A B C =++---+U U I I I I I ．图示如下：教学目标知识要点1．先包含——A B +重叠部分A B I 计算了2次，多加了1次； 2．再排除——A B A B +-I把多加了1次的重叠部分A B I 减去．图中小圆表示A 的元素的个数，中圆表示B 的元素的个数，大圆表示C 的元素的个数．1．先包含：A B C ++重叠部分A B I 、B C I 、C A I 重叠了2次，多加了1次． 2．再排除：A B C A B B C A C ++---I I I重叠部分A B C I I 重叠了3次，但是在进行A B C ++- A B B C A C --I I I 计算时都被减掉了． 3．再包含：A B C A B B C A C A B C ++---+I I I I I ．7-7-4 容斥原理之数论问题在解答有关包含排除问题时，我们常常利用圆圈图(韦恩图)来帮助分析思考．例题精讲【例 1】在1~100的全部自然数中，不是3的倍数也不是5的倍数的数有多少个？【巩固】在自然数1100~中，能被3或5中任一个整除的数有多少个？【巩固】在前100个自然数中，能被2或3整除的数有多少个？【例 2】在从1至1000的自然数中，既不能被5除尽，又不能被7除尽的数有多少个?【巩固】求在1至100的自然数中能被3或7整除的数的个数．【例 3】以105为分母的最简真分数共有多少个？它们的和为多少？【巩固】分母是385的最简真分数有多少个？并求这些真分数的和.【例 4】在1至2008这2008个自然数中，恰好是3、5、7中两个数的倍数的数共有个．【例 5】求1到100内有____个数不能被2、3、7中的任何一个整除。
数学竞赛常见解题方法总结
数学竞赛常见解题方法总结数学竞赛常见解题方法可以分为几个大类，包括代数、几何、概率与统计以及数论。
每个类别下又有不同的方法和技巧，适用于解答不同类型的题目。
下面将对这些常见解题方法进行总结和分析。
一、代数类解题方法1. 数列求和：对于给定的数列，可以用等差数列或等比数列的求和公式来快速求解。
此外，还可以利用差分法、二次差分法等方法求和。
2. 方程求解：对于一元二次方程、一次方程及其他更复杂的方程，可以运用配方法、因式分解、绝对值法、韦达定理等方法求解。
3. 不等式求解：针对不等式问题，可以运用代换法、区间判断法、平方运算法等方法，求解不等式的解集。
4. 函数图像分析：可以通过求导、极值问题等方法，对函数的图像进行分析和求解。
5. 组合函数求解：针对给定的复合函数，可以通过逆函数定义、复合函数的性质等方法进行求解。
二、几何类解题方法1. 平面几何定理：常用平面几何定理包括平行线定理、相似三角形定理、勾股定理等。
在解题过程中，可以通过画图、构造辅助线等方法，将问题转化为已知几何定理的形式进行求解。
2. 三角形性质利用：针对三角形问题，可以应用三角形中位线、垂心定理、欧拉定理等几何性质进行解题。
3. 向量方法：向量方法在几何问题中有广泛应用，常用于求解线段的中点、平行四边形的性质、共线问题等。
4. 坐标系与方程运用：对于平面几何问题，可以通过建立坐标系，利用坐标运算进行解题。
此外，还可以通过方程的运用，表示几何图形，进而求解问题。
三、概率与统计类解题方法1. 随机事件计算：针对概率问题，可以利用集合论的知识进行解题，包括用频率定义概率、利用互斥事件和对立事件计算概率等方法。
2. 组合计数：在概率和统计问题中，常常需要进行组合和计数的运算。
可以利用阶乘、排列组合等方法进行计算。
3. 数据处理与分析：对于给定的数据集合，可以通过构造频率分布表、绘制直方图、计算中位数、算术平均数等方法进行数据的处理和分析。
高中数学竞赛数论
高中数学竞赛数论数论作为数学的一个重要分支，研究自然数的性质及其相关的运算规律，是高中数学竞赛中的一道重要题型。
本文将从数论的基本概念、常见题型以及解题技巧三个方面来介绍高中数学竞赛中的数论问题。
一、基本概念1.1 整数与自然数整数是由自然数和其相反数构成的数集，用Z表示。
自然数是人们日常生活中使用的正整数，用N表示。
1.2 质数与合数质数是只能被1和自身整除的自然数，合数是除了1和自身之外还有其他因数的自然数。
1.3 最大公约数与最小公倍数对于两个自然数a和b，最大的能够同时整除它们的自然数称为它们的最大公约数，用gcd(a, b)表示；最小的能够同时被它们整除的自然数称为它们的最小公倍数，用lcm(a, b)表示。
1.4 同余定理如果两个整数a和b，它们除以某个正整数n得到的余数相同，即a 和b对n取余相等，可以表示为a≡b(mod n)。
二、常见题型2.1 求因数、质因数分解求一个数的因数，可以通过试除法来找到它的所有因数。
质因数分解是将一个数分解为质数的乘积，通过不断地除以最小的质因数来完成。
2.2 同余关系通过同余关系的性质，可以解决一些数的性质问题。
例如，通过同余定理可以求解方程、证明数的整除关系等。
2.3 数列问题数论中的数列问题是指根据给定的数列规律，求解数列的性质或是推导数列的通项公式。
三、解题技巧3.1 取模运算大多数数论问题都可以通过取模运算来简化问题的复杂度。
当计算一个数的幂时，可以通过取模运算降低计算量。
3.2 数论恒等式熟练掌握一些常见的数论恒等式对于解题非常有帮助。
例如费马小定理、欧拉定理等，适时运用可以大大简化问题的解答过程。
3.3 奇偶性讨论对于一些数论问题，可以通过分别讨论奇数和偶数的情况来解决，从而得到问题的解。
3.4 数论规律数论中存在一些常见的规律，比如质数取值范围、奇偶性的性质等。
通过深入研究这些规律，可以更好地理解数论问题，并找到有效的解题方法。
结语高中数学竞赛数论作为数学竞赛中的一个重要部分，涉及的内容较为广泛。
高中数学竞赛中数论问题的常用方法
高中数学竞赛中数论问题的常用方法数论是研究数的性质的一门科学,它与中学数学教育有密切的联系.数论问题解法灵活,题型丰富,它是中学数学竞赛试题的源泉之一.下面介绍数论试题的常用方法.1.基本原理为了使用方便,我们将数论中的一些概念和结论摘录如下:我们用),...,,(21n a a a 表示整数1a ,2a ,…,n a 的最大公约数.用[1a ,2a ,…,n a ]表示1a ,2a ,…,n a 的 最小公倍数.对于实数x ,用[x ]表示不超过x 的最大整数,用{x }=x -[x ]表示x 的小数部分.对于整数b a ,,若)(|b a m -,,1≥m 则称b a ,关于模m 同余,记为)(mod m b a ≡.对于正整数m ,用)(m ϕ表示{1,2,…,m }中与m 互质的整数的个数,并称)(m ϕ为欧拉函数.对于正整数m ,若整数m r r r ,...,,21中任何两个数对模m 均不同余,则称{m r r r ,...,,21}为模m 的一个完全剩余系；若整数)(21,...,,m r r r ϕ中每一个数都与m 互质,且其中任何两个数关于模m 不同余,则称{)(21,...,,m r r r ϕ}为模m 的简化剩余系.定理1 设b a ,的最大公约数为d ,则存在整数y x ,,使得yb xa d +=.定理2(1)若)(mod m b a i i ≡,1=i ,2,…,n ,)(m od 21m x x =,则11ni i i a x =∑≡21ni ii b x=∑；(2)若)(mod m b a ≡,),(b a d =,m d |,则)(mod d m d b d a ≡； (3)若b a ≡,),(b a d =,且1),(=m d ,则)(mod m dbd a ≡；(4)若b a ≡(i m mod ),n i ,...,2,1=,M=[n m m m ,...,,21],则b a ≡(M mod ). 定理3(1)1][][1+<≤<-x x x x ； (2)][][][y x y x +≥+；(3)设p 为素数,则在!n 质因数分解中,p 的指数为∑≥1k kpn.定理4 (1)若{m r r r ,...,,21}是模m 的完全剩余系,1),(=m a ,则{b ar b ar b ar m +++,...,,21}也是模m 的完全剩余系；(2)若{)(21,...,,m r r r ϕ}是模m 的简化剩余系,1),(=m a ,则{)(21...,,m ar ar ar ϕ}是模m 的简化剩余系. 定理5(1)若1),(=n m ,则)()()(n m mn ϕϕϕ=.(2)若n 的标准分解式为k kp p p n ααα (2)121=,其中k ααα,...,21为正整数,k p p p ,...,21为互不相同的素数,则)11)...(11)(11()(21kp p p n n ---=ϕ. 对于以上结论的证明,有兴趣的读者可查阅初等数论教材.2 方法解读对于数论试题,除直接运用数论的基本原理外,常用的基本方法还有因式(因数)分解法,配对法,分组法,估值法,同余方法,构造法,调整法,数学归纳法与反证法.下面分别予以说明2.1基本原理的应用例1 设正整数a ,b ,c 的最大公约数为1,并且c ba ab=- (1),证明:)(b a -是一个完全平方数. 证:设d b a =),(,d a a 1=,d b b 1=,其中1),(11=b a .由于1),,(=c b a ,故有1),(=c d .由(1)得c b c ad b a 1111-= (2)由(2)知,c b a 11|,又1),(11=b a ,∴ c a |1.同理可证c b |1,从而有c b a |11,设k b a c 11=,k 为正整数,代入(2)得)(11b a k d -= (3)由(3)知d k |,又c k |,∴1),(|=c d k ,∴1=k . ∴11b a d -=.∴211)(d b a d b a =-=-.故成立. 例2 设n 为大于1的奇数,1k ,2k ,…,n k 为给定的整数.对于{n ,...,2,1}的排列12(,,...,)n P a a a =, 记1()ni i i s P k a ==∑,试证存在{n ,...,2,1}的两个不同的排列B 、C,使得)()(!|C s B s n -.证:假设对于任意两个不同的排列B 、C,均有!n 不整除)()(C S B s -.令X 为{n ,...,2,1}的所有排列构成的集合,则{()|s P P X ∈}为模!n 的一个完全剩余系,从而有!1(1!)!()(mod !)2n P Xi n n s P i n ∈=+≡=∑∑ (1) 又 1()()ni i P X P X i s P k a ∈∈==∑∑∑=∑=+ni i k n n 12)1(! (2) 而n 为大于1的奇数,所以由(1),(2)得)!(mod 02)1(!2!)!1(1n k n n n n ni i ≡+≡+∑=. 又1)!,!1(=+n n ,所以)!(mod 02!n n ≡,矛盾.故,存在B 、C X ∈,B ≠C,使得)()(!|C s B s n -. 2.2 因式(数)分解数论中许多问题直接与因式(数)分解相关联,如合数问题,整除问题等常常是要证明某种分解式的存在.数的标准分解式本身就是一种特定形式的因数分解.在不定方程的求解与一些代数式的求值中,因式(数)分解能帮助我们确定某些变量的取值范围,寻找到解题的方法.例3 求三个素数,使得它们的积为和的5倍.解:易知a ,b ,c 中必有一个为5,不妨设5c =,则有5++=b a ab ,从而有6)1)(1(=--b a .因为1-a 与1-b 均为正整数,不妨设b a <,则有⎩⎨⎧=-=-6111b a 或⎩⎨⎧=-=-3121b a ,从而知2=a ,7=b .故所求的三个素数为2,5,7.2.3 配对例4 设k 为正奇数,证明:n ++++...321整除kk k n +++...21. 分析 因为2)1(...321+=++++n n n .故需证)...21(2|)1(kk k n n n ++++,注意到当k 为奇数时,kk y x +可因式分解,因此可将)...21(2kkkn +++中的n 2个数两两配对.证 )...21(2kkkn +++=kkkkkkkn n n n 2]1)1[(...])2(2[])1(1[++-++-++-+, 而当k 为奇数时,kkb a b a ++|,从而知()kk k n n +++...212| (1)又 ()kk k n+++...212=]1[...])1(2[]1[k k k k k kn n n +++-+++,∴)...21(2|)1(kk kn n ++++ (2) 由(1)(2)知,)...21(2|)1(kkkn n n ++++,故结论成立.2.4 分组例5 (1990年高中联赛试题)设}200,...,2,1{=E ,},...,,{10021a a a G =E ⊆,且G 具有下列性质:(1)对任何1001≤<≤j i ,201≠+j i a a ；(2)100801001=∑=i ia.试证:G 中的奇数的个数是4的倍数,且G 中所有数的平方和是一定数.证:对于1001≤≤i ,令12-=i i α,i i αβ-=201.},{i i i E βα=,则G 中恰含i E 中的一个元素.设G中有k 个奇数1i α,2i α,…,k i α,有s 个偶数s j j j βββ,...,,21,这里},...,,,,...,,{2121s k j j j i i i =}100,...,2,1{.由题设知,10080=∑∑∑∑====+-=+sr j kt i sr j kt i r t rt1111)201(βββα=∑∑==-kt i k t t 112201β+⎪⎭⎫⎝⎛+∑∑==k t sr j i r t 11ββ =-k 2012∑=kt i t1β+)200...642(++++=1010022011+-∑=kt i tk β.∴2022011-=-∑=kt i tk β(1)由于t i β为偶数,所以∑=kt i t12|4β,又20|4,所以k 201|4,∴k |4,即k 是4的倍数.∑∑∑===+=sr j kt i i irta121210012βα=∑∑==+-sr j kt i rt 1212)201(ββ=∑∑==⨯-kt i kt t 1122012201β+)(1212∑∑==+sr j kt i r tββ=∑=⨯-kt i tk 122012201β+)200...642(2222++++=)2201(2011∑=-kt i tk β+6)1200)(1100(1004++⨯(2)将(1)代入(2)得62011011004)20(20110012⨯⨯⨯+-⨯=∑=i i a =1349380.2.5估值例6 令n a 表示前n 个质数之和,即21=a ,5322=+=a ,105323=++=a ,…,证明:对任意的正整数n ,区间[1,+n n a a ]中包含有一个完全平方数.分析:设质数从小到大依次为12,,...,k p p p …,要结论成立,只要存在正整数m ,使得12+≤≤n n a m a ,只要1+≤≤n n a m a ,只要11≥-+n n a a ,只要n n n a a a 211+≥-+,只要n n a p 211+≥+,只要)...(44)1(2121k n n p p p a p +++=≥-+ (1)证:直接验证易知[2,1,a a ],[32,a a ],[43,a a ],[54,a a ]中都含有1个完全平方数.当5≥n 时,我们证明:(1)式成立.为此,令2112(1)(1)4(...)n k f n p p p p ++=--+++,则n n n p p p n f n f 4)1()1()()1(221----=-++=n n n n n p p p p p 4)2)((11--+-++.当2≥n 时,n p 为奇数,故21≥-+n n p p ,1(1)()2(22)n n n f n f n p p p ++-≥+--=)2(21--+n n p p 0≥, 故当2≥n 时,数列)(n f 为递增数列.由于)(4)1()5(432125p p p p p f +++--==)7532(4)111(2+++--=32>0所以当5≥n 时,0)5()(>≥f n f .故当5≥n 时(1)式成立.例7 求出不定方程1)!1(-=-kn n (1)的全部正整数解.解 当2=n 时,易得1=k ；当2>n 时,(1)式左边为偶数,故右边也是偶数,所以n 为奇数.当3=n 时,由13!2-=k,得1=k .当5=n 时,由15!4-=k,得2=k .当5>n 且为奇数时,321-<-n n ,221≠-n ,故)!2(|212--⋅n n ,即)!2(|)1(--n n ,因此2(1)|(1)!n n --,所以)1(|)1(2--k n n .另一方面,由二项式定理知1)1)1((1-+-=-kkn n =A(2)1-n +)1(-n k .其中A 为整数,所以)1(|)1(2--n k n ,故k n |)1(-,因此1-≥n k ,故有)!1(111->-≥--n n n n k.这说明当5>n 时,方程(1)无解,故方程(1)的解为)1,2(),(=k n ,)1,3(,)2,5(.2.6同余 例8 证明991993991993+能被1984整除.证 993993993)991(-≡=9912)991()991(--=)1984(m od )991()991)(11984495(991991-≡-+⨯,∴)1984(m od 0991)991(991993991991991993≡+-≡+.∴991993991993|1984+.例9 用1,2,3,4,5,6,7组成的无重复数字的7位数,证明:这些7位数中没有一个是另一个的倍数. 证:若有两个7位数a ,b ,使得kb a = (1) 由于a ,b 均是由1,2,...,7所排成,故72≤≤k 由(1)得)9(mod kb a ≡, ∴)9(mod 11⋅≡k ,即)9(mod 1≡k ,这与92≤≤k 矛盾,故结论成立. 2.7构造例10 若一个正整数的标准分解中,每个素约数的幂次都大于1,则称它为幂数,证明:存在无穷多个互不相同的正整数,它们及它们中任意多个不同数的和都不是幂数.证:将全体素数从小到大依次记为1p ,2p ,...,n p ,….令11p a =,2212p p a =,当2≥n 时,n n n n n n p p p p p p a a 21222111...---==,下证:1a ,2a ,…,n a ,…合题意. 事实上, n n a p |,但2n p |/n a ,所以n a 不是幂数.又对于k i i i <<<≤ 211,)1(112121i i i i i i i i a a a a a a a a k k +++=+++ =)1(11i i Ap a +=)1(111212221i i i Ap p p p p +- , 其中A 为正整数.因为1)1,(11=+i i Ap p ,所以1i p 在)(21k i i i a a a +++ 的标准分解中的幂次为1,因而不是幂数.例11 设}2011,,3,2,1{ 中质数的个数为a ,n 为正整数且a n ≤<1,求证必有2011个连续正整数, 其中恰有n 个质数.证:令}2010,,2,1,{+++=k k k k A k ,并令)(k f 为k A 中质数的个数,则易知a f =)1(,0)2!2012(=+f . 对于)1!2012(,,2,1+= k ,显然有1|)()1(|≤-+k f k f ,所以对于a n ≤<0,必存在一个0k ,使得n k f =)(0,从而0k A 中的2011个连续整数满足要求.2.8 数学归纳法例12 设n 是正整数,求证:124323|51222-+-n n n.证:令22()332241nf n n n =-+-.因为0)1(=f ,所以)1(|512f ,假设)(|512n f ,那么对于1+n ,因为)183(8)()1(2--=-+n n f n f n,所以要证)1(|512+n f ,只需证)183(8|5122--n n ,即只需证明)183(|642--n n .为此,令183)(2--=n n g n .显然有0)1(|64=g ,假设)(|64n g ,由于)199(64)19(8)()1(21+++=-=-+-- n n nn g n g ,因此)1(|64+n g ,由归纳法原理知对一切n ,有183|642--n n,从而有)1(|512+n f ,再由归纳法原理知,对于正整数n ,有)(|512n f .2.9 反证法例13 试证方程042333=--z y x (1)无正整数解.分析:若(z y x ,,)为(1)的一组解,则x 为偶数,令12x x =,则0243331=--z y x ,从而知y 为偶数,再令12y y =,代入得04233131=--z y x ,故z 为偶数,再令12z z =,代入得042313131=--z y x ,因此),,(111z y x 也是方程(1)的解.这样由方程(1)的一组正整数解),,(z y x 必可得到另一组正整数解),,(111z y x ,且x x <1.因此,若开始取得的正整数解使得x 达到最小,则这种下降不可能进行.证:反证法. 若方程(1)存在正整数解,设),,(000z y x 是使得x 达到最小的正整数解,那么依分析的过程知必可得到方程(1)的一组正整数解),,(111z y x ,且01x x <,这与0x 达到最小相矛盾,这个矛盾表明方程(1)无正整数解. 习题1．设1≥≥n m ,m ,n 为整数,证明nm C mn m ),(是整数. 2．设a ,b 为整数,证明:))1(()2)((|)!(1b n a b a b a a bn n -+++- .3.设n 是大于3的奇数,证明可将集合}1,,3,2,1{-n 的元素分成两组,每组21-n 个元素,使得两组数的和模n 同余.。
初中数学竞赛中的数论问题
初中数学竞赛中的数论问题
近年来，数学竞赛在初中教育中变得越来越受欢迎。
在竞赛中，学生们开始着重于探索数论问题并研究如何解决。
当学生们对数论的思维有了更深的理解后，数学竞赛便变得更加有趣，也更有价值。
本文重点阐述初中数学竞赛中的数论问题，以及如何解决它们。
在初中数学竞赛中，数论问题是比较重要的部分。
它们包括计算机算法、数学逻辑、数论等。
首先，计算机算法是解决问题的基础。
学生们需要用涉及如搜索、排序、字符串匹配等算法的知识，来实现一些数学模型的自动化求解。
其次，学生们也要掌握数学逻辑，例如，通过构造函数、求解方程组等，从而推演出相关模型，实现目标。
最后，学生们需要学习数论，以解决竞赛中有关素数、因数分解、逆元等概念的问题。
解决数论问题需要综合运用算法、数学逻辑和数论的技巧。
一般来说，学生在解决这些问题之前，需要先考虑清楚各种条件，把问题用数学语言描述出来，然后结合算法、数学逻辑和数论的技巧进行分析，最后给出解决方案。
另外，除了掌握数论方面的知识，学生们还需要培养良好的学习习惯和思维素质。
一方面，学生们要熟悉数论知识，并结合实际，不断提高自己的应用能力和思维水平。
另一方面，学生们要学会从容应对，并勇于探索。
有时候，数论的问题可能会比较棘手，但学生们要学会积极主动地去思考和探索，找出最佳的解决方案。
通过上述介绍，可以看到，初中数学竞赛中的数论问题既难又好
玩。
学生们不仅要掌握数论知识，还需要持之以恒地学习，培养良好的学习习惯和思维素质。
当学生掌握了这些技巧，便能解决竞赛中的复杂数论问题，获得取得更理想的成绩。
数学竞赛中的数论问题
数学竞赛中的数论问题数论是一门研究整数性质和整数运算规律的数学学科。
在数学竞赛中，数论问题经常会成为让人头痛的难题，因为数论问题经常需要具有深刻的数学思维和技巧才能解决。
一、简单的数论问题首先，我们先了解一些简单的数论问题。
例如：如果一个正整数能被15整除，则它一定也能被几个整数整除呢？首先我们可以列出15的因数，即1、3、5、15。
由此可知，如果一个正整数能被15整除，那么它一定也能被1、3、5、15这几个整数整除。
再比如，如果一个正整数能够同时被2和3整除，那么它一定也能被哪个整数整除呢？可以先求出2和3的最小公倍数，即6。
因此，如果一个正整数能够同时被2和3整除，那么它一定也能被6整除。
二、进阶的数论问题接着，我们来看一些进阶的数论问题。
例如：对于一个正整数n，如果n的因子个数是奇数个，那么n是不是一个完全平方数呢？我们用3作为例子来探讨。
3的因子只有1和3，那么它的因子个数是偶数。
但是，假如n的因子个数是奇数个，那么n一定是一个完全平方数。
再来看一个例子，已知a、b、c、d都是正整数，且满足a^2 +b^2 = c^2 + d^2，问a和b是否相等。
这个问题需要用到一些数学技巧来解决。
首先我们可以通过等式变形得到(b-a)(b+a) = (d-c)(d+c)这个等式。
设x=b-a，y=d-c，那么等式变为x(x+2a) =y(y+2c)。
因为x和2a、y和2c都是偶奇配对，所以x、y必定有一个为偶数。
设x=2k，则y(y+2c) = 4k(k+a)。
由于y(y+2c)是一个偶数，而k和k+a一定有奇偶性之分，因此k(k+a)是一个奇数。
因为两个奇数的积一定是一个奇数，所以k、k+a两者必有一个为奇数。
考虑将y(y+2c)分解质因数，如果y为偶数，则y和y+2c有公因数2，那么它们的积就有一个不止一个因子2，和k和k+a成了矛盾；如果y为奇数，则y和y+2c互质，那么它们的积y(y+2c)就有一个不止一个奇素因子，和k和k+a同样成了矛盾。
奥数闯关数论与整数问题
奥数闯关数论与整数问题数论作为数学的一个分支，主要研究整数的性质和相互关系。
在奥林匹克数学竞赛中，数论问题常常是考察选手逻辑思维和数学推理能力的重要环节之一。
本文将介绍奥数闯关中的数论问题，重点关注整数问题，并分析解题思路和方法。
一、质数：素数的魅力质数是指除了1和自身外，没有其他因数的自然数。
质数在奥数闯关中经常出现，因此了解质数的性质及特点对解决问题至关重要。
例如，欧几里得算法是求解两个数最大公约数的重要方法，而质数的性质在这一算法中发挥了重要作用。
二、模运算：数字之间的奇妙运算模运算是指在一定范围内，通过除法运算得到的余数。
在奥数闯关中，模运算常用于寻找某个整数与其他数之间的特殊关系。
比如，当我们需要判断一个整数是否能同时被2和3整除时，可以使用模2和模3运算的性质来解决。
三、同余：数的等价性同余是指两个整数除以同一个正整数所得的余数相等。
在奥数闯关中，同余问题经常被用来证明和推导数学命题。
通过建立同余关系，我们可以将原问题转化为更易解的数论问题，从而简化解题过程。
四、因数分解：拆解质因数因数分解是将一个数分解为若干个质数乘积的过程。
因数分解在奥数闯关中起到关键作用，能够帮助我们快速求解问题。
掌握因数分解的方法，不仅可以拆解数学问题，还可以解决实际生活中与整数相关的困惑。
五、整数方程：数之间的相互关系整数方程是奥数闯关中的常见考点之一，要求我们求解满足特定条件的整数解。
通过建立代数方程，运用数论知识和数学推理，我们可以找到合适的整数解，并得到问题的正确答案。
六、整数的特殊性质：奇偶性、除尽和倍增等整数拥有许多与其他数不同的特殊性质，例如奇偶性、除尽和倍增等。
这些性质在奥数闯关中广泛应用，为解题提供了便利。
对于给定问题，我们可以利用整数的特殊性质来缩小解空间，找到有效的求解方法。
七、数论技巧与策略：掌握解题要领在奥数闯关中，除了掌握数论的基础知识外，还需要灵活运用各种数论技巧与策略。
这些技巧包括递推关系、特殊取模方法、数列性质等。
数学奥林匹克专题讲座 第02讲 数论的方法技巧(下)
《数学奥林匹克专题讲座》第2讲数论的方法技巧（下）四、反证法 反证法即首先对命题的结论作出相反的假设，并从此假设出发，经过正确的推理，导出矛盾的结果，这就否定了作为推理出发点的假设，从而肯定了原结论是正确的。
反证法的过程可简述为以下三个步骤： 1．反设：假设所要证明的结论不成立，而其反面成立； 2．归谬：由“反设”出发，通过正确的推理，导出矛盾——与已知条件、公理、定义、定理、反设及明显的事实矛盾或自相矛盾； 3．结论：因为推理正确，产生矛盾的原因在于“反设”的谬误，既然结论的反面不成立，从而肯定了结论成立。
运用反证法的关键在于导致矛盾。
在数论中，不少问题是通过奇偶分析或同余等方法引出矛盾的。
解：如果存在这样的三位数，那么就有 100a+10b+c=（10a+b）+（10b+c）+（10a+c）。
上式可化简为80a=b+c，而这显然是不可能的，因为a≥1，b≤9，c≤9。
这表明所找的数是不存在的。
说明：在证明不存在性的问题时，常用反证法：先假设存在，即至少有一个元素，它符合命题中所述的一切要求，然后从这个存在的元素出发，进行推理，直到产生矛盾。
例2 将某个17位数的数字的排列顺序颠倒，再将得到的数与原来的数相加。
试说明，得到的和中至少有一个数字是偶数。
解：假设得到的和中没有一个数字是偶数，即全是奇数。
在如下式所示的加法算式中，末一列数字的和d+a为奇数，从而第一列也是如此，因此第二列数字的和b+c≤9。
将已知数的前两位数字a，b与末两位数字c，d去掉，所得的13位数仍具有“将它的数字颠倒，得到的数与它相加，和的数字都是奇数”这一性质。
照此进行，每次去掉首末各两位数字，最后得到一位数，它与自身相加是偶数，矛盾。
故和的数字中必有偶数。
说明：显然结论对（4k+1）位数也成立。
但对其他位数的数不一定成立。
如12+21，506+605等。
例3 有一个魔术钱币机，当塞入1枚1分硬币时，退出1枚1角和1枚5分的硬币；当塞入1枚5分硬币时，退出4枚1角硬币；当塞入1枚1角硬币时，退出3枚1分硬币。
数学奥赛中数论问题的解题方法
数学奥赛中数论问题的解题方法1 引言在历年的国内外数学奥林匹克中，几乎每年都离不开数论问题。
分析历年奥林匹克数学竞赛试题易知，奥林匹克数学中的数论问题主要有：（1）整除性问题；（2）数性的判断；（3）余数问题；（4）整数的分解与分析；（5）不定方程问题；（6）与高斯函数[x]有关的问题。
本文对奥林匹克数学中的数论问题的常用解题方法做进一步的分析总结。
2 常用的部分解题方法2．1 奇偶分析法奇偶数的性质：（1）两个奇数的和与差为偶数，而积为奇数；（2）两个偶数的和、差、积为偶数；奇数与偶数的和、差为奇数，而积为偶数；（3）如果为整数，为奇数，则的奇偶性与相反；如果为整数，为偶数，则的奇偶性与相同。
例设N是正整数，如果存在大于1的正整数k，使得N- 是k的正整数倍，则称N为一个“千禧数”。
试确定1，2，3，…，2000中“千禧数”的个数，并说明理由。
解设是“千禧数”，则存在正整数，使得，即；显然与的奇偶性不同，且,,所以有大于1的奇因子,从而有大于1的奇因子。
反过来,若有大于1的奇因子,则可设,其中, 的奇偶性不同,且,则且，其中为正整数。
综上,只有当有大于1的奇因子时,是“千禧数”而在1,2,3,…2000中，只有1，，…，不是“千禧数”，故有“千禧数”2000-11=1989个。
评析：奇偶分析法是从未知数，系数的奇偶性入手讨论未知数的可能取值情况，以达到缩小考察范围，得出相应的结果。
在解决与正整数有关的问题（如数性有关的问题）能灵活运用奇偶分析的方法，往往有“四两拔千斤”的效果。
2．2 分类讨论依据数学研究对象的本质属性的相同点和差异点，将数学对象进行分类，然后对划分的每类分别进行研究和求解的方法，叫分类讨论的方法。
分类讨论必须遵循的原则：（1）分类讨论的对象必须是确定的；（2）每次分类的标准必须是同一的；（3）分类必须不重复，不遗漏；（4）连续多次分类，按层次逐级进行，不得越级。
例解方程解将方程变形为,由不等式,可得由此又可以得到(1)因为当时,所以此时方程无解(因方程的解必须满足(1))又因为当时,所以此时方程也无解。
奥数竞赛的常见题型及解题思路
奥数竞赛的常见题型及解题思路奥数竞赛是一项智力竞赛活动，旨在培养学生的逻辑思维、数学能力和解决问题的能力。
在奥数竞赛中，常见的题型包括数论题、几何题、代数题和概率题等。
本文将介绍这些常见的题型及解题思路。
一、数论题数论题是奥数竞赛中的重要题型，主要考察的是学生对数学知识的掌握和运用能力。
解决数论题的关键在于找到规律，以下是几种常见的数论题：1. 除法余数问题：常用于考察除法的性质和整数的性质。
解题思路是通过观察被除数和除数之间的关系，找出规律，从而得出答案。
2. 同余问题：同余问题要求找出一组满足指定条件的整数解。
解题思路是先列出满足条件的第一个整数解，然后根据模的性质，得出满足条件的其他整数解。
3. 素数问题：素数问题要求判断一个数是否为素数，或找出一段连续的素数。
解题思路是通过试除法或其他数学方法来判断一个数是否为素数，或者使用筛法来找出一段连续的素数。
二、几何题几何题是奥数竞赛中的重要题型之一，主要考察学生的几何图形判断和计算能力。
以下是几种常见的几何题：1. 角度和：角度和问题要求计算几个角的总和。
解题思路是根据角的性质，利用已知条件求出每个角的大小，然后求和。
2. 三角形问题：三角形问题要求计算三角形的面积、周长或边长等。
解题思路是根据已知条件，利用三角形的性质和公式，求解未知量。
3. 平面镶嵌问题：平面镶嵌问题要求将一些特定形状的图形组合在一起，使其完全填满一个平面。
解题思路是观察给定的图形，找到它们的共同特点，然后进行合理的组合。
三、代数题代数题是奥数竞赛中的重要题型之一，主要考察学生对代数方程和不等式的理解和运用能力。
以下是几种常见的代数题：1. 方程求解问题：方程求解问题要求求解一个或多个未知数的方程。
解题思路是通过对方程进行化简、因式分解、移项等运算，将方程转化为易解的形式，找到方程的解。
2. 不等式问题：不等式问题要求求解一个或多个未知数的不等式。
解题思路是通过对不等式进行化简、移项等运算，找到不等式的解集。
高中数学竞赛数论
高中数学竞赛数论数论作为数学的一个分支，是数学竞赛中重要的考查内容之一。
高中数学竞赛数论题目常常涵盖了整数性质、模运算、质数等各个方面的知识。
在数论的学习和应用中，往往需要我们灵活运用各种技巧和方法来解决问题。
本文将从基本概念、常见性质、解题技巧等方面来介绍高中数学竞赛数论的相关内容。
一、基本概念1. 整数的性质：整数的奇偶性、整数的除尽性等都是数论中基本的概念。
在解题过程中，我们常常需要利用整数的性质来简化问题。
2. 算术基本定理：任何一个大于1的正整数，都可以表示为若干个质数的乘积，且这种表示方法是唯一的。
这一定理在数论中有着非常重要的作用，解决了很多关于因数分解的问题。
3. 同余方程：在数论中，我们常常会接触到模运算和同余方程。
同余方程是指在整数集合Z上定义的一种关系，通常用符号“≡”来表示。
在解决问题时，求解同余方程是一个常见的手段。
二、常见性质1. 质数性质：质数是指只有1和它本身两个正因数的自然数。
在解题中，我们需要掌握质数的性质，如质数的判定方法、质数之间的性质等。
2. 欧拉定理：欧拉定理是数论中的一个重要定理，它描述了正整数幂的同余性质。
欧拉定理在数论中的应用非常广泛，是解决一类数论问题的重要工具。
3. 数列与递推关系：在数论竞赛中，常常会涉及到数列和递推关系。
我们需要熟练掌握数列的性质和常见的数列递推方法，以便解题时能够迅速找到规律。
三、解题技巧1. 数学归纳法：数学归纳法是数论中常用的证明方法，通过数学归纳法可以证明某个结论对于所有正整数都成立。
在数论竞赛中，经常可以用到数学归纳法来解决问题。
2. 等价转化：有时候，我们需要将原来的问题进行等价转化，从而简化解题过程。
通过巧妙的等价转化，我们可以找到更容易解决的问题。
3. 假设反证法：假设反证法是一种解题思路，通过假设问题的否定，再通过逻辑推导得出矛盾，从而证明原命题成立。
在数论中，假设反证法常常被用来解决一些猜想和证明问题。
数论的基本解法
数论的基本解法概述数论是研究整数和整数之间的关系、性质以及应用的数学分支。
在数学竞赛中，数论问题常常出现，并且往往需要一些基本的解法来解决。
本文将介绍数论问题的一些基本解法，帮助读者更好地应对数论问题。
解法一：质因数分解质因数分解是数论问题中最常见的解法之一。
质因数分解可以将一个数分解为若干个质数的乘积。
通过质因数分解，我们可以得到一个数的质因数，在进一步求解时会更加方便。
例如，对于一个正整数 n，我们可以通过如下步骤进行质因数分解：1.从最小的质数 2 开始，不断尝试将 n 整除，直到无法整除。
2.如果某个质数 p 能够整除 n，我们就可以得到一个质因数，同时将 n 除以 p。
反复执行这一步骤，直到 n 变为 1.解法二：同余模运算同余模运算是另一种经常用到的数论解法。
同余模运算是指对于给定的两个整数 a 和 b，当它们除以一个正整数 m 所得的余数相等时，就称 a 与 b 在模 m 下同余，记作a ≡ b (mod m)。
同余模运算的性质可以帮助我们简化问题的求解。
例如，我们可以利用同余模运算来简化大数运算、判断奇偶性、求解线性同余方程等。
解法三：欧拉函数欧拉函数是数论中另一个重要的概念。
欧拉函数 phi(n) 表示小于等于 n 且与 n 互质的数的个数。
欧拉函数有许多重要的性质，比如欧拉函数的递推公式：如果p 是质数，那么 phi(p) = p-1.通过欧拉函数，我们可以求解一些与模运算有关的问题。
解法四：扩展欧几里得算法扩展欧几里得算法是解决线性同余方程ax ≡ b (mod m) 的常用工具。
扩展欧几里得算法可以在给定 a、b 和 m 的情况下，快速求解出同余方程的解。
扩展欧几里得算法的核心思想是利用欧几里得算法求解最大公约数，同时获得一组特殊解。
通过这个特殊解，我们可以得到同余方程的一般解，并利用模运算得到其中的整数解。
结语以上是数论问题的一些基本解法，质因数分解、同余模运算、欧拉函数以及扩展欧几里得算法是数论问题中常用的工具。
小学数学奥赛数论与代数问题几何推理与证明组合与概率题型解题思路与策略等
小学数学奥赛数论与代数问题几何推理与证明组合与概率题型解题思路与策略等小学数学奥赛数论与代数问题、几何推理与证明、组合与概率题型解题思路与策略等小学数学奥赛是培养小学生数学兴趣和能力的一项重要活动。
而在数学奥赛中，数论与代数、几何推理与证明、组合与概率是常见的题型。
掌握这些题型的解题思路与策略对于小学生的数学竞赛至关重要。
本文将就小学数学奥赛中的这几类题型，分享一些解题的思路和策略。
一、数论与代数问题的解题思路与策略在小学数学奥赛中，数论与代数问题是常见的题型。
在解决这类问题时，可以采用以下的解题思路与策略。
1. 分析问题：首先要仔细阅读题目，理解题意，明确要求和条件。
然后根据题目的特点进行分类，将复杂的问题分解为若干个简单的部分。
通过对每个部分的分析，找出问题的关键点，确定解题思路。
2. 建立方程：根据题目中的条件，可以将问题中的未知数用字母表示，建立方程或等式来描述问题。
方程的建立可以帮助我们清晰地理解问题，更好地解决问题。
3. 利用性质和定理：数论与代数问题通常涉及到数的性质和运算规则，通过灵活运用性质和定理，可以减少计算量，简化解题过程。
例如，利用倍数的性质判断一个数是否是某个数的倍数，利用奇偶性质来解决奇偶问题等。
4. 智斗选项：当遇到多个选项时，可以尝试替换选项的值，判断方程的成立与否，从而排除不符合条件的选项。
这样可以快速缩小答案范围，提高解题效率。
二、几何推理与证明的解题思路与策略几何推理与证明是数学竞赛中的一个需要一定几何知识基础以及逻辑思维能力的题型。
以下是解决几何推理与证明问题的一些思路与策略。
1. 图形分析：对于几何问题，首先要对给定图形进行仔细地观察和分析，明确图形之间的关系和性质，找出问题的关键点，从而找到解题的线索。
2. 利用已知条件：几何题通常给出一些已知条件，可以通过利用这些已知条件来推导出其他未知条件，进而解决问题。
熟悉常见的定理和性质对于应用已知条件进行推理和证明是非常有帮助的。