_幂函数及图象变换_基础
幂函数知识点
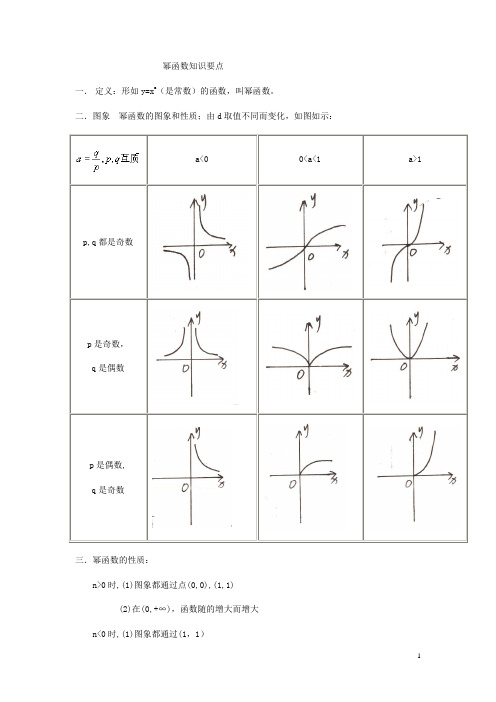
幂函数知识要点一.定义:形如y=x a(是常数)的函数,叫幂函数。
二.图象幂函数的图象和性质;由d取值不同而变化,如图如示:三.幂函数的性质:n>0时,(1)图象都通过点(0,0),(1,1)(2)在(0,+∞),函数随的增大而增大n<0时,(1)图象都通过(1,1)(2)在(0,+∞),函数随x的增加而减小(3)在第一象限内,图象向上与y轴无限地接近,向右与x轴无限地接近。
注意事项:1.判断幂函数的定义域的方法可概括为(对指数)“先看正负,是负去零,再看奇偶,是偶非负”2.根据幂函数的定义域,值域及指数特点画其图象。
函数位于第一象限的图象在“n>1”时,往上翘;0<n<1,往右拐;n<0向下滑。
四.例析:分析:底数分别不同而指数相同,可以看作是和。
两个幂函数,利用幂函数的单调性质去理解。
解:(1)(0,+∞)是递增的又∵1.1<1.4 ∴利用幂函数的性质比较数的大小。
例3.比较的大小。
分析:三个量比较大小,先考虑取值的符号。
启示:当直接比较大小难以进行时,可以考虑借助一些中间量特殊值,如0,1或其他数来解决。
分析:在指数运算中,注重运算顺序和灵活运用乘法合成。
启示:此处化简过程可与初中代数式的运算联系。
五.自测题:1.计算的值()2.下列命题中正确的是()A.当n=0时,函数y=x n的图象是一条直线B.幂函数的图象都经过(0,0),(1,1)两点C.若幂函数y=x n的图象关于原点对称,则y=x n在定义域内y随x的增大而增大D.幂函数的图象不可能在第四象限3.实数a,b满足0<c<b<1,则下列不等式正确的是()A.a b<ba B.a-b<b-b C.a-a<b-b D.b b<a a4.在幂函数y=x a,y=x b,y=x c,y=x d在第1象限的图象中(右图),的大小关系为()A.a>b>c>d B.d>b>c>a C.d>c>b>aD.b>c>d>a5.下列函数中是幂函数的是)6.设幂函数y=x n的图象经过(8,4),则函数y=x n的值域为_______。
高中幂函数知识点总结

引言:高中幂函数是高中数学中的重要部分,它在数学研究和实际问题中有着广泛的应用。
本文将对高中幂函数的知识点进行总结和整理,帮助学生完善对幂函数的理解和掌握。
概述:幂函数是指形如y=x^n的函数,其中n是常数。
幂函数的特点是具有单调性和奇偶性,其图象通常为一条曲线。
在研究幂函数时,需要掌握其定义、性质和应用。
正文:一、幂函数的定义1.1 幂函数的基本形式幂函数的基本形式是y=x^n,其中n是常数。
幂函数的定义域为所有实数,且n可以是正整数、负整数、零和有理数。
1.2 幂函数的图象当n为正奇数时,幂函数的图象在第一象限和第三象限上单调递增;当n为正偶数时,幂函数的图象在第一象限上单调递增,且具有对称轴y=0;当n为负数时,幂函数的图象在第一、三象限上单调递减。
1.3 幂函数的特殊情况当n=1时,幂函数变为一次函数;当n=0时,幂函数变为常数函数;当n为正无穷大时,幂函数趋向于正无穷大;当n为负无穷大时,幂函数趋向于零。
二、幂函数的性质2.1 幂函数的单调性幂函数在定义域上的单调性与n的值有关。
当n为正奇数时,幂函数是增函数;当n为正偶数时,在非负区间上是增函数,在负区间上是减函数;当n为负数时,在非负区间上是减函数,在负区间上是增函数。
2.2 幂函数的奇偶性幂函数的奇偶性与n的奇偶性有关。
当n为奇数时,幂函数是奇函数;当n为偶数时,幂函数是偶函数。
2.3 幂函数的零点当n为正奇数时,幂函数的零点为x=0;当n为正偶数时,幂函数的零点为x=0;当n为负奇数时,幂函数没有零点;当n为负偶数时,幂函数的零点为x=0。
三、幂函数的图象变换3.1 幂函数的平移幂函数的平移是指将幂函数的图象沿横轴或纵轴方向移动。
平移的方向和距离与平移的规律有关,具体可利用平移的公式进行计算。
3.2 幂函数的伸缩幂函数的伸缩是指将幂函数的图象进行纵向或横向的拉伸或压缩。
伸缩的方式和伸缩的规律有关,可利用伸缩的公式进行计算。
3.3 幂函数的翻折幂函数的翻折是指将幂函数的图象进行关于横轴或纵轴的翻折。
基本初等函数(Ⅰ) 幂函数

解析 答案
类型二 幂函数的图象及应用 例 2 若点( 2,2)在幂函数 f(x)的图象上,点(-2,14)在幂函数 g(x)的图象上, 问当 x 为何值时,(1)f(x)>g(x);(2)f(x)=g(x);(3)f(x)<g(x).
解答
引申探究 若对于例 2 中的 f(x),g(x),定义 h(x)=fgxx,,ffxx≤>ggxx,, 试画出 h(x)的图象. 解 h(x)的图象如图所示:
类型三 幂函数性质的综合应用
命题角度1 比较大小
例3
设
a=23
2 3
,b=23
1 3
,c=25
2 3
,则a,b,c的大小关系是
A.a>b>c
B.b>a>c
C.b>c>a
D.c>b>a
解析 ∵y=23x 在 R 上为减函数,
∴23
2 3
<23
1 3
,即
a<b;∵f(x)=x
2 3
在(0,+∞)上为增函数,
1
1
A.16
B.16
C.2
√D.2
12345
答案
3.设α∈{-1,1,1 ,3},则使函数y=xα的定义域为R的所有α的值为
2
√A.1,3
B.-1,1
C.-1,3
D.-1,1,3
12345
答案
2
4.下列是y=x 3 的图象的是
√
12345
答案
5.以下结论正确的是 A.当α=0时,函数y=xα的图象是一条直线 B.幂函数的图象都经过(0,0),(1,1)两点 C.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大
高中数学必修一第15讲:幂函数及图象变换(中等)

幂函数及图象变换【学习目标】1.通过实例,了解幂函数的概念;结合幂函数的图象,了解它们的变化情况. 2.掌握幂函数的图象和性质,并能熟练运用图象和性质去解题。
3.掌握初等函数图象变换的常用方法. 【要点梳理】 幂函数概念形如的函数,叫做幂函数,其中α为常数. 要点诠释:幂函数必须是形如的函数,幂函数底数为单一的自变量x ,系数为1,指数为常数.例如:()2423,1,2y x y x y x ==+=-等都不是幂函数.幂函数的图象及性质 1.作出下列函数的图象:(1)x y =;(2)21x y =;(3)2x y =;(4)1-=x y ;(5)3x y =.要点诠释:幂函数随着α的取值不同,它们的定义域、性质和图象也不尽相同,但它们有一些共同的性质: (1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);(2)0>α时,幂函数的图象通过原点,并且在区间),0[+∞上是增函数.特别地,当1>α时,幂函数的图象下凸;当10<<α时,幂函数的图象上凸;(3)0<α时,幂函数的图象在区间),0(+∞上是减函数.在第一象限内,当x 从右边趋向原点时,图象在y()y x R αα=∈()y x R αα=∈轴右方无限地逼近y 轴正半轴,当x 趋于∞+时,图象在x 轴上方无限地逼近x 轴正半轴. 2.作幂函数图象的步骤如下: (1)先作出第一象限内的图象;(2)若幂函数的定义域为(0,+∞)或[0,+∞),作图已完成; 若在(-∞,0)或(-∞,0]上也有意义,则应先判断函数的奇偶性 如果为偶函数,则根据y 轴对称作出第二象限的图象; 如果为奇函数,则根据原点对称作出第三象限的图象. 3.幂函数解析式的确定(1)借助幂函数的定义,设幂函数或确定函数中相应量的值. (2)结合幂函数的性质,分析幂函数中指数的特征.(3)如函数()af x k x =⋅是幂函数,求()f x 的表达式,就应由定义知必有1k =,即()af x x =. 4.幂函数值大小的比较(1)比较函数值的大小问题一般是利用函数的单调性,当不便于利用单调性时,可与0和1进行比较.常称为“搭桥”法.(2)比较幂函数值的大小,一般先构造幂函数并明确其单调性,然后由单调性判断值的大小. (3)常用的步骤是:①构造幂函数;②比较底的大小;③由单调性确定函数值的大小. 要点三、初等函数图象变换基本初等函数包含以下九种函数:正比例函数、反比例函数、一次函数、二次函数、幂函数、指数函数、对数函数.(三角函数、反三角函数待讲)由基本初等函数经过四则运算以及简单复合所得的函数叫初等函数.如:2()f x x =的图象变换,22(1),1,y x y x =+=+222,||y x y x ==(1)平移变换y=f(x)→y=f(x +a) 图象左(0a >)、右(0a <)平移 y=f(x)→y=f(x)+b 图象上(b 0>)、下(b 0<)平移 (2)对称变换y=f(x) →y=f(-x), 图象关于y 轴对称 y=f(x) →y=-f(x) , 图象关于x 轴对称 y=f(x) →y=-f(-x) 图象关于原点对称 y=f(x)→1()y fx -= 图象关于直线y=x 对称(3)翻折变换:y=f(x) →y=f(|x|),把y 轴右边的图象保留,然后将y 轴左边部分 关于y 轴对称.(注意:它是一个偶函数)y=f(x) →y=|f(x)| 把x 轴上方的图象保留,x 轴下方的图象 关于x 轴对称 要点诠释:(1)函数图象是由基本初等函数的图象经过以上变换变化而来。
第二章-4.2-简单幂函数的图象和性质高中数学必修第一册北师大版

§4 函数的奇偶性与简单的幂函数
4.2 简单幂函数的图象和性质
教材帮|必备知识解读
知识点1 幂函数的概念
例1-1 在函数 = −4 , = 3 2 , = 2 + 2, = 1中,幂函数的个数为( B
A.0
B.1
C.2
D.3
【解析】函数 = −4 为幂函数;
函数 = 3 2 中 2 的系数不是1,所以它不是幂函数;
的增大而减小;
当 = −3时,2 − 2 − 3 = 12, = 12 是幂函数,但不满足当 ∈ 0, +∞ 时,
随的增大而减小,故舍去.
∴ 实数的值为2.
【学会了吗|变式题】
2.(2024·广东省汕头市期末)已知函数 = 2 − 2 − 2 ⋅ −2 是幂函数,且在
故A正确;
幂函数 = 的图象只在第一象限内和原点,故B不正确;
当 > 0时, > 0,所以幂函数的图象不可能在第四象限,故C不正确;
幂函数 = 与 = 3 的图象的交点为 −1, −1 , 0,0 , 1,1 ,共三个,故D不正确.
方法帮|关键能力构建
题型1 幂函数的定义域和值域
0, +∞ 上单调递增,则实数 =( C
A.−1
B.−1或3
)
C.3
D.2
【解析】由题意知,2 − 2 − 2 = 1,即 + 1 − 3 = 0,
解得 = −1或 = 3,
∴ 当 = −1时, − 2 = −3,则 = −3 在 0, +∞ 上单调递减,不合题意;
当 = 3时, − 2 = 1,则 = 在 0, +∞ 上单调递增,符合题意,∴ = 3,
幂函数图象规律
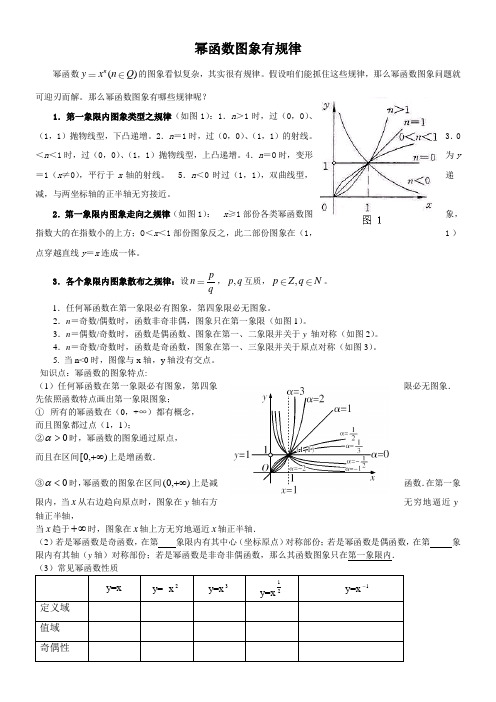
幂函数图象有规律幂函数()n yx n Q 的图象看似复杂,其实很有规律。
假设咱们能抓住这些规律,那么幂函数图象问题就可迎刃而解。
那么幂函数图象有哪些规律呢?1.第一象限内图象类型之规律(如图1):1.n >1时,过(0,0)、(1,1)抛物线型,下凸递增。
2.n =1时,过(0,0)、(1,1)的射线。
3.0<n <1时,过(0,0)、(1,1)抛物线型,上凸递增。
4.n =O 时,变形为y =1(x ≠0),平行于x 轴的射线。
5.n <0时过(1,1),双曲线型,递减,与两坐标轴的正半轴无穷接近。
2.第一象限内图象走向之规律(如图1): x ≥1部份各类幂函数图象,指数大的在指数小的上方;O <x <1部份图象反之,此二部份图象在(1,1)点穿越直线y =x 连成一体。
3.各个象限内图象散布之规律:设pnq,,p q 互质,,p Z q N 。
1.任何幂函数在第一象限必有图象,第四象限必无图象。
2.n =奇数/偶数时,函数非奇非偶,图象只在第一象限(如图1)。
3.n =偶数/奇数时,函数是偶函数、图象在第一、二象限并关于y 轴对称(如图2)。
4.n =奇数/奇数时,函数是奇函数,图象在第一、三象限并关于原点对称(如图3)。
5. 当n<0时,图像与x 轴,y 轴没有交点。
知识点:幂函数的图象特点:(1)任何幂函数在第一象限必有图象,第四象限必无图象.先依照函数特点画出第一象限图象;① 所有的幂函数在(0,+∞)都有概念, 而且图象都过点(1,1); ②0>α时,幂函数的图象通过原点, 而且在区间),0[+∞上是增函数.③0<α时,幂函数的图象在区间),0(+∞上是减函数.在第一象限内,当x 从右边趋向原点时,图象在y 轴右方无穷地逼近y轴正半轴,当x 趋于∞+时,图象在x 轴上方无穷地逼近x 轴正半轴. (2)若是幂函数是奇函数,在第 象限内有其中心(坐标原点)对称部份;若是幂函数是偶函数,在第 象限内有其轴(y 轴)对称部份;若是幂函数是非奇非偶函数,那么其函数图象只在第一象限内. y=xy=x 2y=x 3y=x 21y=x 1-定义域 值域 奇偶性单调性 定点(1);(2);(3);(4);(5);(6);(7);(8);(9)。
2.3 幂函数图像与性质
(指数函数)
y x1
(幂函数)
y 3x
(指数函数)
1
y x2
(幂函数)
y 5x
(指数函数)
y5 x
(幂函数)
幂函数的图象及性质
对于幂函数,我们只讨论 =1,2,3,1 , 2
-1时的情形。
五个常用幂函数的图像和性质
(1) y x (2) y x2 (3) y x3
2
(4,2)
1
(-1,1)
(1,1)
y=x-1
2、在第一象限内, k >0,在
4
6 k <0,在(0,+∞)上为减函数.
-1
(-1,-1)
-2
3、k为奇数时,幂函数为奇函数,
k为偶数时,幂函数为偶函数.
-3
-4
4、幂函数图像不过第四象限。
例3
若m
4
1 2
23 4
3 4… 27 64 …
3 2…
1
y=x 2
x
函数 y x3 的图像
定义域: R 值 域: R
奇偶性:在R上是奇函数 单调性:在R上是增函数
1
函数 y x 2 的图像
定义域:[0,)
值 域:[0,)
奇偶性:非奇非偶函数
单调性:在[0,)上是增函数
4
3
2
1
(1,1)
-6
意
2、定义域与k的值有关系.
例1、下列函数中,哪几个函
数是幂函数? 答案:(1)(4)
(1)y = 1
x2
(3)y=2x
(2)y=2x2
(4)y=
1 x
(5) y=x2 +2
北师大版高中数学课件第二章 4.2 简单幂函数的图象和性质
(3)由幂函数的图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象
限内的图象(类似于 y=x 或
-1
1
y= 2 ,y=x3)来判断.
(4)当α>0时,幂函数在区间(0,+∞)上都单调递增;当α<0时,幂函数在区间
(0,+∞)上都单调递减.
变式训练 2如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的
断a,b,c的大小关系.
解析由幂函数的图象特征,知c<0,a>1,0<b<1.故c<b<a.
答案A
反思感悟 对于函数y=xα(α为常数)而言,其图象有以下特点:
(1)恒过点(1,1).
(2)当x∈(0,1)时,指数越大,幂函数图象越靠近x轴(简记为“指大图低”);当
x∈(1,+∞)时,指数越大,幂函数的图象越远离x轴(简记为“指大图高”).
设 g(x)=xb(b∈R).
1
∵点 -2, 4 在幂函数 g(x)的图象上,
1
∴4=(-2)b,解得 b=-2.∴g(x)=x-2.
在同一直角坐标系中作出f(x)=x2和g(x)=x-2的图象,如图所示:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
数)的形式,即:(1)系数为1;(2)指数为常数;(3)后面不加任何项.反之,若一个
函数为幂函数,则该函数必具有这种形式.
变式训练1如果幂函数y=(m2-3m+3)
2 --2
的图象不过原点,求实数m的取值.
解由幂函数的定义得m2-3m+3=1,解得m=1,或m=2;
幂函数的概念和图象
R [0, ) y | y 0
奇偶性
奇
偶
奇
非奇非偶
奇
单调性 定点
[0, )
增
上增
(, 0]
上减
(1,1) (1,1) (0,0) (0,0)
(0, )
增
增
上减
(, 0)
上减
(1,1) (1,1) (1,1) (0,0) (0,0)
【P64】
在下列四个图形中,y=x-12的图象大致是( )
幂函数 的概念和图象
高一数学 黄海忠
指数函数的概念
函数 y a(x a 0且a 1)叫做指数函数, 其中 x 是自变量,a 为常数.
a 1
0 a 1
一、幂函数的概念
形如 y x 的函数叫做幂函数, 其中 x 是自变量, 为常数.
(1)下列函数:①y=x3;②y=12x;③y=4x2;④y=x5
+1;⑤y=(x-1)2;⑥y=x;⑦y=ax(a>1).其中幂函数的个数
为( )
A.1 C.3
B.2
D.4
【P64】
(2)若函数 y=(m2+2m-2)xm 为幂函数且在第一象限为增函数,
则 m 的值为( A )
A.1
B.-3
C.-1
Hale Waihona Puke D.3二、幂函数的图像
对于幂函数,约定:只讨论 1, 2,3, 1 , 1的情形。
1
(4) y x2 , x 0; (5) y x1 , x 0.
y x3 y x2
yx
1
y x2 y x1
定点(1,1)
三.幂函数的性质
【课本P78表格】
yx
3-3幂函数
2 3 数,又∵ > , 3 5 2 0.5 3 0.5 ∴(3) >(5) .
第三章
基本初等函数(I)
人 教 B 版 数 学
第三章
基本初等函数(I)
[点评]
利用函数单调性比较两实数的大小首先要
通过观察分析,构造出适当的函数来,对于幂的形式的数,
若同指数不同底数,则考虑幂函数;若同底数不同指数,
人 教 B 版 数 学
f(x)=x-4的图象如图所示:
第三章
基本初等函数(I)
人 教 B 版 数 学
第三章
基本初等函数(I)
已知幂函数f(x)的图象过点( 1 象过点(2, ). 4 (1)求f(x),g(x)的解析式;
2 ,2),幂函数g(x)的图
人 教 B 版 数 学
(2)当x为何值时:①f(x)>g(x);②f(x)=g(x); ③f(x)<g(x).
第三章
基本初等函数(I)
[解析]
(1)设f(x)=xα,∵其图象过点(
2 ,2),故2
=( 2)α,∴α=2,∴f(x)=x2. 1 设g(x)=x ,∵其图象过点(2,4),
β
人 教 B 版 数 学
1 - ∴4=2β,∴β=-2,∴g(x)=x 2. (2)在同一坐标系下作出f(x)=x2与g(x)=x-2的图象, 如图所示:
人 教 B 版 数 学
,
2 解得a<3且a≠-1或a>4.
第三章
基本初等函数(I)
2 ∴a 的取值范围为(-∞,-1)∪(-1, )∪(4,+∞). 3
人 教 B 版 数 学
第三章
基本初等函数(I)
1 1 若(a+1)- <(3-2a)- ,试求 a 的取值范围. 3 3 [分析] 1 考查幂函数 y=x- ,可知它在(-∞,0)和(0, 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
_幂函数及图象变换_基础
巩固练习
1.下列函数中,35431,21,,yyxyxxyxx是幂函数的个数是( ).
A.1 B.2 C.3 D.4
2.函数12yx的定义域是( )
A.[0,+∞) B.(-∞,0) C.(0,+∞) D.R
3.函数23yx的图象是( )
4.下列函数中,既是偶函数,又在区间0,上单调递减的函数是( )
A.2yx B. 1yx C. 2yx D. 13yx
5.幂函数35myx,其中m∈N,且在(0,+∞)上是减函数,又()()fxfx,则m=( )
A.0 B.1 C.2 D.3
6.若幂函数yx的图象在0
7.下列结论中正确的个数有( )
(1)幂函数的图象一定过原点; (2) 当<0时,幂函数yx是减函数;
(3)当>0时,幂函数yx是增函数;(4)函数22yx既是二次函数,又是幂函数.
A.0 B.1 C.2 D.3
8. 三个数121.2a,120.9b,11c的大小顺序是( ) 9.若幂函数()yfx的图象经过点1(9,)3,则(25)f的值是 . 10.若幂函数224(317)mmymmx的图象不过原点,则m的值为 . (1)6611110.60.7与; (2)5533(0.88)(0.89).与 1.B 根据幂函数的定义判断,5354431,yxyxxx是幂函数. 数,故(3)不对.函数22yx是二次函数,不是幂函数,故(4)不对. 8. A 11112222101.2,0.9(),1.19abc,易知101.21.19,又函数12yx在0,上单调递 11.1,3 由题意知10,220,122.aaaa解得13a. (2)函数),0(35在xy上增函数且89.088.00 0 0 ,即00,xxyy,因为点0,0()Qxy在函数()yfx的图象上,所以2()2()yxx, 即2()2gxxx.
A.c
11.若1144(1)(22)aa,则实数a的取值范围是 .
12.函数1(1)yx的单调递减区间为 .
13.比较下列各组中两个值大小
14. 已知函数()fx和()gx的图象关于原点对称,且2()2fxxx.
(1)求函数()gx的解析式;
(2)解不等式函数()()|1|gxfxx.
答案与解析
2.C 函数121211yxxx,所以函数的定义域是0,.
3.C 函数2323yxx,因为3223()()()fxxxfx,所以这个函数为偶函数,图象关于
y
轴对称,可能是B或C,又2013,所以当1x时,图象应在yx直线的下方,故选C.
4. A 函数221yxx,所以函数是偶函数,又20,所以函数在区间0,上单调递减,
故选A.
5.B 因为函数35myx,其中m∈N,且在(0,+∞)上是减函数,所以350m,即53m,又函
数是偶函数,故1m.
6.B 幂函数1,01yxxxx,考察指数函数(01)xyaa的增减性知,1.
7.A 幂函数yx,当0时,图象一定过原点,当0时,图象一定不过原点,故(1)不对.当
0时,幂函数图象在0,上是减函数,故(2)不对.当0
时,幂函数图象在0,上是增函
增,所以cba,故选A.
9. 15 设()fxx,则1(9)3f,即193,得112211,(),(25)2525fxxf.
10.-6 由23171mm,解得3m或6m.又当3m时,指数240mm不合题意;当
6m时,240mm,所以6m
.
12.,1和1, 将函数1yx的单调区间向左平移一个单位即可.
13.解:(1)7.06.00),0(116上是增函数且在函数xy
11611
6
7.06.0
.)89.0()88.0(,89.088.089.088.0353535353535即
14. 解析:(1)设函数()yfx的图象上任一点0,0()Qxy关于原点的对称点为,Pxy,则
0,20.2xxyy
(2)由()()|1|gxfxx,得22|1|0xx
当1x时,2210xx,由函数221yxx的图象可知,此不等式无解.
当1x时,2210xx,由函数221yxx的图象,解得112x.
原不等式的解集为11,.2
