2018年春季高考数学真题版
山东省2018届高三普通高校招生春季考试数学试题

山东省2018年普通高校招生(春季)考试数学试题卷一一、选择题(本大题20个小题,每小题3分,共60分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上)1. 已知集合{,}M a b =,{,}N b c =,则M N 等于( )A .∅B .{}bC .{,}a cD .{,,}a b c2. 函数()11xf x x x =++-的定义域是( )A .(1,)-+∞B .(1,1)(1,)-+∞C .[1,)-+∞D .[1,1)(1,)-+∞3. 奇函数()y f x =的局部图像如图所示,则( )A .(2)0(4)f f >>B .(2)0(4)f f <<C .(2)(4)0f f >>D .(2)(4)0f f <<4. 不等式11g ||0x +<的解集是( )A .11(,0)(0,)1010-B .11(,)1010-C. (10,0)(0,10)- D .(10,10)-5. 在数列{}n a 中, 121,0a a =-=,21n n n a a a ++=+,则S a 等于()A .0B .1- C. 2- D .3-6. 在如图所示的平面直角坐标系中,向量AB 的坐标是( )A .(2,2)B .(2,2)--C. (1,1) D .(1,1)--7. 22(1)(1)1x y ++-=的圆心在( )A .第一象限B .第二象限 C. 第三象限 D .第四象限8. 已知,a b R ∈,则“a b >”是“22a b >”的( )A .充分不必要条件B .必要不充分条件C.允要条件 D .既不允分也不必要条件9. 关于直线:320l x y -+=,下列说法正确的是( )A .直线l 的倾斜角为60B .向量(3,1)v =是直线l 的一个方向向量C. 直线l 经过点(1,3)- D .向量(1,3)n =是直线l 的一个法向量10. 景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的面走到山顶后,接着从另一面下山,则不同走法的种数是( )A .6B .10 C. 12 D .2011. 在平面直角坐标系中,关于,x y 的不等式0Ax By AB ++>(0)AB ≠表示的区域(阴影部分)可能 是( )A .B . C. D .12. 已知两个非零向量a 与b 的夹角为锐角,则( )A .0a b ⋅>B .0a b ⋅< C. 0a b ⋅≥ D .0a b ⋅≤13. 若坐标原点(0,0)到直线sin 20x y θ-+=的距离等于22,则角θ的取值集合是( )A .{|,}4k k Z πθθπ=±∈ B .{|,}2k k Z πθθπ=±∈ C. {|2,}4k k Z πθθπ=±∈ D .{|2,}2k k Z πθθπ=±∈14. 关于,x y 的方程222(0)x ay a a +=≠,表示的图形不可能是( )A .B . C. D .15. 在5(2)x y -的展开式中,所有项的系数之和等于( )A .32B .-32 C. 1 D .-116. 设命题:53p ≥,命题:{1}{0,1,2}q ⊆,则下列命题中为真命题的是( )A .p q ∧B .p q ⌝∧ C. p q ∧⌝ D .p q ⌝∨⌝17. 已知抛物线2(0)x ay a =≠的焦点为F ,准线为l ,该抛物线上的点M 到x 轴的距离为5,且||7MF =,则焦点F 到准线l 的距离是( )A .2B .3 C. 4 D .518. 某停车场只有并挂的8个停车位,恰好仝部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概半是( )A .514 B .1528 C. 914 D .6719. 己知矩形ABCD ,2AB BC =,把这个矩形分别以AB BC 、所在直线为轴旋转一周,所成几何体的侧面积分别记为12S S 、,则1S 与2S 的比值等于( )A .12 B .1 C. 2 D .420.若由函数sin(2)2y x π=+的图像变换得到sin()23y ππ=+的图像,则可以通过以下两个步骤完成:第一步,把sin(2)2y x π=+图像上所有点的横坐标变为原来的4倍,纵坐标不变:第二步,可以把所得图像沿x轴( )A .向石移3π个单位 B .向右平移512π个单位C. 向左平移3π个单位 D .同左平移512π个单位卷二二、填空题(本大题5个小题,每小题4分,共20分。
(完整版)2018年春季高考数学真题

2018春季高考真题一、选择题1、已知集合,,则等于 M ={a,b}N ={b,c}M ∩N A 、 B 、 C 、D 、∅{b} {a,c}{a,b,c} 2、函数的定义域是f (x )=x +1+xx ‒1A 、B 、(-1,+∞)(-1,1)∪(1,+∞)C 、 D 、[ -1,+∞) [ -1,1)∪(3、奇函数的布局如图所示,则 y =f(x)A 、 B 、 f(2)>0>f(4) f(2)<0<f(4)C 、 D 、f(2)> f(4)>0 f(2)<f(4)<04、已知不等式的解集是1+lg|x|<0AB 、、(‒110,0)∪ (0,110)(‒110,110)C 、D 、(‒10,0)∪ (0,10)(‒10,10)5、在数列中, =-1 ,=0,=+,则等于{a n }a 1 a 2a n +2a n +1a n a 5A 、B 、C 、D 、0 - 1 -2-36、在如图所示的平面直角坐标系中,向量的坐标是 AB A 、 B 、 C 、D 、(2,2)(‒2,‒2)(1,1)(-1,-1)7、圆(x +1)2+(y ‒1)2=1的圆心在A 、第一象限B 、第二象限C 、第三象限D 、第四象限8、已知,则“”是“”的a 、b ∈R a >b 2a >2bA 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件9、关于直线,下列说法正确的是l:x ‒3y +2=0A 、直线l 的倾斜角为 B 、向量是直线l 的一个方向向量 60。
v =(3,1)C 、直线l 经过点D 、向量是直线l 的一个法向量(1,3)n =(1,3)10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A 、6B 、10C 、12D 、2011、在平面直角坐标系中,关于的不等式表示的区域(阴影部分)可能是x,y Ax +By +AB >0(AB ≠0)12、已知两个非零向量a 与b 的夹角为锐角,则 A 、 B 、 C 、D 、a ∙b >0a ∙b <0a ∙b ≥0a ∙b ≤013、若坐标原点到直线的距离等于,则角的取值集合是 (0,0)x -y +sin 2θ=022θA 、{}B 、{} θ|θ=kπ±π4,k ∈Zθ|θ=kπ±π2,k ∈ZC 、{}D 、{}θ|θ=2kπ±π4,k ∈Zθ|θ=2kπ±π2,k ∈Zl e15、在 (x ‒2y )2的展开式中,所有项的系数之和等于A 、32B 、-32C 、1D 、-116、设命题,命题,则下列命题中为真命题的是p:5≥3q:{1}⊑{0,1,2}A 、p B 、 C 、 D 、 ∧q ¬p ∧q p ∧¬q ¬p ∨¬q 17、已知抛物线的焦点为,准线为,该抛物线上的点到轴的距离为,且=7,则焦点到准线距x 2=ay(a ≠0)F l M x 5|MF|F l 离是A 、2B 、C 、D 、34518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A 、B 、C 、D 、51415289146719、已知矩形ABCD ,AB=2BC ,把这个矩形分别以AB ,BC 所在直线为轴旋转一周,所围成集合体的侧面积分别记为S 1、S 2 ,则S 1、S 2的比值等于A 、B 、C 、D 、1212420、若由函数图像变换得到的图像,则可以通过以下两个步骤完成:第一步,把y =sin (2x +π2)y =sin(x2+π3)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x 轴y =sin (2x +π2)A 、向右平移个单位B 、向右平移个单位C 、向左平移个单位D 、向左平移个单位π35π12π35π12二、填空题21、已知函数,则的值等于 。
2018年上海春考数学试题有答案详解

2018年上海市普通高等学校春季招生统一文化考试数学试卷一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.不等式||1x >的解集为__________. 2.计算:31lim 2n n n →∞-=+__________.3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B =__________.4.若复数z i i =+(i 是虚数单位),则2z z+=__________. 5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=__________.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹为__________.7.如图,在长方形1111B ABC A C D D -中,3AB =,4BC =,15AA =, O 是11A C 的中点,则三棱锥11A AOB -的体积为__________.第7题图 第12题图 8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、 四辩.若其中学生 甲必须参赛且不担任四辩,则不同的安排方法种数为__________.9.设a R ∈,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =__________.10.设m R ∈,若z 是关于x 的方程2210xmx m -+=+的一个虚根,则||z 的取值范围是__________.11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图象有且仅有两个不同的公共点,则a 的取值范围是__________.12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中.已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度 从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为__________秒(精确到0.1)二、选择题(本大题共有4题,满分20分,每题5分)13.下列函数中,为偶函数的是( ) (A )2y x-= (B )13y x =(C )12y x-=(D )3y x =14.如图,在直三棱柱111AB A B C C -的棱虽在的直线中,与直线1BC异面的直线条数为( ) (A )1 (B )2(C )3(D )415.记n S 为数列{}n a 的前n 项和.“{}n a 是递增数列”是“n S 为递增数列”的( ) (A )充分非必要条件 (B )必要非充分条件(C )充要条件(D )既非充分也非必要条件16.已知A 、B 为平面上的两个定点,且|2|AB =.该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AB AP ⋅=,2AQ AP =-,则动线段PQ 所形成图形的面积为( )(A )36(B )60(C )81(D )108三、解答题(本大题共有5题,满分76分,第17~19题每题14分,20题16分,21题18分)17.(本题满分14分,第1小题满分6分,第2小题满分8分) 已知cos y x =.(1)若3(1)f α=,且[0,]απ∈,求()3f πα-的值;(2)求函数(2)2()y f x f x =-的最小值.18. (本题满分14分,第1小题满分6分,第2小题满分8分)已知a R ∈,双曲线222:1x y aΓ-=.(1)若点(2,1)在Γ上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分7分,第2小题满分7分)利用“平行于圆锥曲线的母线截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥视为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影出的抛物线的平面图,图3是一个射灯的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).图1 图2 图3 20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分) 设0a>,函数1()12xf x a =+⋅.(1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x ⋅-=的最大值(用a 表示);(3)设()()(1)g x f x f x =--.若对任意(,0]x ∈-∞,)(()0g x g ≥恒成立,求a 的取值范围.21.(本题满分18分,第1小题满分3分,第2小题满分6分,第3小题满分9分)若{}n c 是递增数列,数列{}n a 满足:对任意*n N ∈,存在*m N ∈,使得10m nm n a c a c +-≤-,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的“分隔数列”;(2)设4nc n =-,n S 是{}n c 的前n 项和,31n nd c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n nc aq -=,n T {}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.参考答案一、填空题1.(,1)(1,)-∞-+∞2.33.(0,1)4.25.156.22143x y +=7.5 8.180 9.410.)+∞ 11.1119(,]66ππ12.4.4二、选择题13.A14.C15.D16.B三、解答题17.(1)16+;(2)32-18.(1))(;(2. 19.(1)14;(2)9.59︒. 20.(1)121()log (01)x f x x x --=<<;(2)2112max y a a =++(0x =时取最值);(3)21.(1)证明略;(2)不是.反例:4n=时,m 无解;(3)02a q ≥>⎧⎨⎩.参考答案一、填空题1.(,1)(1,)-∞-+∞2.33.(0,1)4.25.156.22143x y +=7.5 8.180 9.410.)+∞ 11.1119(,]66ππ提示:1212(1)sin()12(1)sin()sin()2x x x ax x x ax ax --=-⇒-=-⇒=-711711711,,2,2,4,4,666666ax ππππππππππ∴=++++0ax a << 117266a πππ∴<≤+ 12.4.4 提示:以A 为原点建立坐标系,设时刻为t ,则40(0,1.5),(20,20),03P t Q t t -≤≤则0 1.5:20020 1.5PQx y tl t t--=---,化简得(8)8120t x y t --+= 点(10,10)O 到直线PQ1≤,化简得23161280t t +-≤即8833t ---+≤≤880 4.433t t -+-+≤≤⇒∆=≈ 二、选择题13.A14.C15.D16.B 提示:建系(0,0),(2,0)A B ,则(,)P x y 的轨迹为线段3,44x y =-≤≤,AP 扫过的三角形面积为12,则利用相似三角形可知AQ 扫过的面积为48,因此和为60三、解答题17.(1;(2)32-18.(1)(;(2. 19.(1)14;(2)9.59︒. 20.(1)121()log (01)x f x x x --=<<;(2)2112max y a a =++(0x =时取最值); (3)提示:1211()21212232x x x xa g x a a a a --=-=+⋅+⋅⋅++2,(2(0,1])23x at a t at-=∈⋅++ 因为-a <0,所以当x =0,t =1时,分母取到最小值从而分式值取到最小值,此时2210a t t a t =⇒=≥⇒<≤21.(1)证明:存在2m n =,此时*1,22122n m n n c n a n c n +∀∈=<=+<=+N 证毕 (2)不是.反例:4n=时,m 无解;(3)02a q ≥>⎧⎨⎩.提示:因为1{}n aq -为递增数列,因此01a q >⎧⎨>⎩或者001a q <⎧⎨<<⎩①当001a q <⎧⎨<<⎩时,*,0n n c ∈<N ,因此321123T T T c c c <<<=<<<因此不存在23m c T c ≤<,不合题意。
2018届上海春季高考数学试卷(附解析)

2018年上海市春季高考数学试卷2018.01一.填空题(本大题共12题,满分54分,第1~6题每题4分,第7~12题每题5分)1.不等式||1x >的解集为2.计算:31lim 2n n n →∞-=+3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B = 4.若复数1i z =+(i 是虚数单位),则2z z+=5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹方程为7.如图,在长方体1111ABCD A B C D -中,3AB =,4BC =,15AA =,O 是11A C 的中点,则三棱锥11A A OB -的体积为(第7题)(第12题)8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为(结果用数值表示)9.设a ∈R ,若292()x x +与92()a x x+的二项展开式中的常数项相等,则a =10.设m ∈R ,若z 是关于x 的方程2210x mx m ++-=的一个虚根,则||z 的取值范围是11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图像有且仅有两个不同的公共点,则a 的取值范围是12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为秒(精确到0.1)二.选择题(本大题共4题,每题5分,共20分)13.下列函数中,为偶函数的是()A.2y x -= B.13y x =C.12y x -= D.3y x =14.如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为()A.1 B.2 C.3 D.415.设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}n S 是递增数列”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件16.已知A 、B 为平面上的两个定点,且||2AB = ,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤ ,6AP AB ⋅= ,2AQ AP =- ,则动线段PQ 所形成图形的面积为()A.36B.60C.72D.108三.解答题(本大题共5题,共14+14+14+16+18=76分)17.已知cos y x =.(1)若1()3f α=,且[0,]απ∈,求()3f πα-的值;(2)求函数(2)2()y f x f x =-的最小值.18.已知a R ∈,双曲线222:1x y aΓ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).(图1)(图2)(图3)20.设0a >,函数1()12xf x a =+⋅.(1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 取值范围.21.若{}n c 是递增数列,数列{}n a 满足:对任意*n N ∈,存在*m N ∈,使得10m n m n a c +-≤-,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的分隔数列;(2)设4n c n =-,n S 是{}n c 的前n 项和,32n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T 是{}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.参考答案一.填空题1.(,1)(1,)-∞-+∞2.33.(0,1)4.25.156.22143x y +=7.58.1809.410.3,)3+∞11.1119(,]66ππ12.4.4二.选择题13.A14.C 15.D 16.B 三.解答题17.(1)1266+;(2)32-.18.(1),(;(2)12.19.(1)14;(2)9.59°.20.(1)121()log x f x x --=(01x <<);(2)max 2112y a a =++(0x =时取最值);(3).21.(1)证明略;(2)不是,反例:4n =时,m 无解;(3)02a q >⎧⎨≥⎩.。
山东省2018年普通高校招生(春季)考试 数学试题-答案

三 、解 答 题 (本 大 题 5 个 小 题 ,共 40 分 ) 26.(本 小 题 6 分 )
文
博 解:(1)函数f(x)=x2+(m -1)x+4的对称轴为x=-m2-1,……………………… (1分) 东 因为函数f(x)在区间(-∞,0)上单调递减,
所以-m2-1≥0,…………………………………………………………………………… (1分)
(2 7)2=(3 7)2+72-2×3 7×7×cos∠B,
解 得 cos∠B =277,
媒
传 所以sin∠B=
1-
æç2
7
ö2
÷
=
è7ø
21,… … … … … … … … … … … … … … … … … … … … … 7
(1 分 )
化 sin∠APB
=sin(180°-30°-
∠B
)=sin150°cos∠B
山东省2018年普通高校招生(春季)考试 数学试题答案及评分标准
卷 一 (选 择 题 ,共 60 分 )
一 、选 择 题 (本 大 题 20 个 小 题 ,每 小 题 3 分 ,共 60 分 )
题号
1
2
3
4
5
6
7
8
9 10
答案
B
D
A
A
C
D
B
C
B
C
题号
11 12 13 14 15 16 17 18 19 20
-cos150°sin∠B
=
1 2
27 ×7-
æ
ç
è
-
3ö÷ 2ø
×
文 721=5147,………………………………………………………………………………… (1分)
2018年上海市春考数学试卷

上海市教育考试院保留版权2018年春考数学第1页(共4页)2018年上海市普通高校春季招生统一文化考试数学试卷考生注意:1.本场考试时间120分钟.试卷共4页,满分150分,答题纸共2页.2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名.将核对后的条形码贴在指定位置.3.所有作答必须涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一、填空题(本大题共有12题,满分54分,第1~6题每题4分,第7~12题每题5分)考生应在答题纸相应编号的空格内直接填写结果.1.不等式||1x >的解集为.2.计算:31lim 2n n n →∞-=+.3.设集合{|02}A x x =<<,{|11}B x x =-<<,则A B = .4.若复数1i z =+(i 是虚数单位),则2z z +=.5.已知{}n a 是等差数列,若2810a a +=,则357a a a ++=.6.已知平面上动点P 到两个定点(1,0)和(1,0)-的距离之和等于4,则动点P 的轨迹方程为.7.如图,在长方体1111ABCD A B C D -中,3AB =,4BC =,15AA =,O 是11A C 的中点,则三棱锥11A A OB -的体积为.8.某校组队参加辩论赛,从6名学生中选出4人分别担任一、二、三、四辩,若其中学生甲必须参赛且不担任四辩,则不同的安排方法种数为.(结果用数值表示)9.设a ∈R ,若922x x ⎛⎫+ ⎪⎝⎭与92a x x ⎛⎫+ ⎪⎝⎭的二项展开式中的常数项相等,则a =.10.设m ∈R ,若z 是关于x 的方程2210x mx m ++-=的一个虚根,则||z 的取值范围是.2018年春考数学第2页(共4页)11.设0a >,函数()2(1)sin()f x x x ax =+-,(0,1)x ∈,若函数21y x =-与()y f x =的图像有且仅有两个不同的公共点,则a 的取值范围是.12.如图,正方形ABCD 的边长为20米,圆O 的半径为1米,圆心是正方形的中心,点P 、Q 分别在线段AD 、CB 上,若线段PQ 与圆O 有公共点,则称点Q 在点P 的“盲区”中,已知点P 以1.5米/秒的速度从A 出发向D 移动,同时,点Q 以1米/秒的速度从C 出发向B 移动,则在点P 从A 移动到D 的过程中,点Q 在点P 的盲区中的时长约为.二、选择题(本大题共有4题,满分20分,每题5分)每题有且只有一个正确答案,考生应在答题纸的相应位置,将代表正确选项的小方格涂黑.13.下列函数中,为偶函数的是().(A)2y x -=(B)13y x =(C)12y x -=(D)3y x =14.如图,在直三棱柱111ABC A B C -的棱所在的直线中,与直线1BC 异面的直线的条数为().(A)1(B)2(C)3(D)415.设n S 为数列{}n a 的前n 项和,“{}n a 是递增数列”是“{}n S 是递增数列”的().(A)充分非必要条件(B)必要非充分条件(C)充要条件(D)既非充分又非必要条件16.已知A 、B 为平面上的两个定点,且||2AB = ,该平面上的动线段PQ 的端点P 、Q ,满足||5AP ≤,6AP AB ⋅= ,2AQ AP =- ,则动线段PQ 所形成图形的面积为().(A)36(B)60(C)72(D)108三、解答题(本大题满分76分)本大题共有5题,解答下列各题必须在答题纸的相应位置写出必要的步骤.17.(本题满分14分,第1小题满分6分,第2小题满分8分)已知函数()cos f x x =.(1)若1()3f α=,且[0,π]α∈,求π3f α⎛⎫- ⎪⎝⎭的值;(2)求函数(2)2()y f x f x =-的最小值.2018年春考数学第3页(共4页)18.(本题满分14分,第1小题满分6分,第2小题满分8分)已知a ∈R ,双曲线222:1x y aΓ-=.(1)若点(2,1)在上,求Γ的焦点坐标;(2)若1a =,直线1y kx =+与Γ相交于A 、B 两点,且线段AB 中点的横坐标为1,求实数k 的值.19.(本题满分14分,第1小题满分6分,第2小题满分8分)利用“平行于圆锥母线的平面截圆锥面,所得截线是抛物线”的几何原理,某快餐店用两个射灯(射出的光锥为圆锥)在广告牌上投影出其标识,如图1所示,图2是投影射出的抛物线的平面图,图3是一个射灯投影的直观图,在图2与图3中,点O 、A 、B 在抛物线上,OC 是抛物线的对称轴,OC AB ⊥于C ,3AB =米, 4.5OC =米.(1)求抛物线的焦点到准线的距离;(2)在图3中,已知OC 平行于圆锥的母线SD ,AB 、DE 是圆锥底面的直径,求圆锥的母线与轴的夹角的大小(精确到0.01°).20.(本题满分16分,第1小题满分4分,第2小题满分6分,第3小题满分6分)设0a >,函数1()12x f x a =+⋅.(1)若1a =,求()f x 的反函数1()f x -;(2)求函数()()y f x f x =⋅-的最大值(用a 表示);(3)设()()(1)g x f x f x =--,若对任意(,0]x ∈-∞,()(0)g x g ≥恒成立,求a 的取值范围.图1图3图22018年春考数学第4页(共4页)21.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小题满分8分)若{}n c 是递增数列,数列{}n a 满足:对任意*n ∈N ,存在*m ∈N ,使得10m n m n a c a c +--≤,则称{}n a 是{}n c 的“分隔数列”.(1)设2n c n =,1n a n =+,证明:数列{}n a 是{}n c 的分隔数列;(2)设4n c n =-,n S 是{}n c 的前n 项和,32n n d c -=,判断数列{}n S 是否是数列{}n d 的分隔数列,并说明理由;(3)设1n n c aq -=,n T 是{}n c 的前n 项和,若数列{}n T 是{}n c 的分隔数列,求实数a 、q 的取值范围.。
(完整版)2018年春季高考数学真题

2018春季高考真题一、选择题1、已知集合M={a,b},N={b,c},则M∩N等于A、∅B、{b}C、{a,c}D、{a,b,c}2、函数f(x)=√x+1+xx−1的定义域是A、(−1,+∞)B、(−1,1)∪(1,+∞)C、[ −1,+∞)D、 [ −1,1)∪(1,+∞)3、奇函数y=f(x)的布局如图所示,则A、f(2)>0>f(4)B、f(2)<0<f(4)C、f(2)> f(4)>0D、f(2)<f(4)<04、已知不等式1+lg|x|<0的解集是A、(−110,0)∪(0,110)B、(−110,110)C、(−10,0)∪(0,10)D、(−10,10)5、在数列{a n}中,a1=-1 , a2=0,a n+2=a n+1+a n,则a5等于A、0B、−1C、−2D、−36、在如图所示的平面直角坐标系中,向量AB⃗⃗⃗⃗⃗ 的坐标是A、(2,2)B、(−2,−2)C、(1,1)D、(−1,−1)7、圆(x+1)2+(y−1)2=1的圆心在A、第一象限B、第二象限C、第三象限D、第四象限8、已知a、b∈R,则“a>b”是“2a>2b”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、关于直线l:x−√3y+2=0,下列说法正确的是A、直线l的倾斜角为60。
B、向量v=(√3,1)是直线l的一个方向向量C、直线l经过点(1,√3)D、向量n=(1,√3)是直线l的一个法向量10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是A、6B、10C、12D、2011、在平面直角坐标系中,关于x,y的不等式Ax+By+AB>0(AB≠0)表示的区域(阴影部分)可能是12、已知两个非零向量a与b 的夹角为锐角,则A、a∙b>0B、a∙b<0C、a∙b≥0D、a∙b≤013、若坐标原点(0,0)到直线x−y+sin2θ=0的距离等于√22,则角θ的取值集合是A、{θ|θ=kπ±π4,k∈Z} B、{θ|θ=kπ±π2,k∈Z}C、{θ|θ=2kπ±π4,k∈Z} D、{θ|θ=2kπ±π2,k∈Z}14、关于x,y的方程x2+ay2=a2(a≠0),表示的图形不可能是15、在(x−2y)2的展开式中,所有项的系数之和等于A、32B、-32C、1D、-116、设命题p:5≥3,命题q:{1}⊑{0,1,2},则下列命题中为真命题的是A、p∧qB、¬p∧qC、p∧¬qD、¬p∨¬q17、已知抛物线x2=ay(a≠0)的焦点为F,准线为l,该抛物线上的点M到x轴的距离为5,且|MF|=7,则焦点F到准线l距离是A、2B、3C、4D、518、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是A、514B、1528C、914D、6719、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于A、12B、1C、2D、420、若由函数y=sin(2x+π2)图像变换得到y=sin(x2+π3)的图像,则可以通过以下两个步骤完成:第一步,把y=sin(2x+π2)上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴A、向右平移π3个单位B、向右平移5π12个单位C、向左平移π3个单位D、向左平移5π12个单位二、填空题21、已知函数f(x)={x 2+1,x>0−5,x≤0,则f[f(0)]的值等于。
2018山东春季高考数学试题及答案(word)(可编辑修改word版)
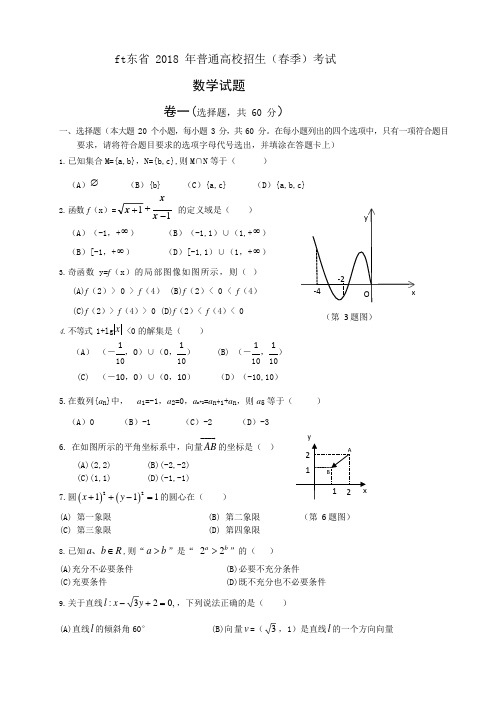
3 ft 东省 2018 年普通高校招生(春季)考试数学试题 卷一(选择题,共 60 分)一、选择题(本大题 20 个小题,每小题 3 分,共 60 分。
在每小题列出的四个选项中,只有一项符合题目要求,请将符合题目要求的选项字母代号选出,并填涂在答题卡上)1. 已知集合 M={a,b},N={b,c},则 M∩N 等于()(A )∅ (B ){b} (C ){a,c} (D ){a,b,c} x 2. 函数 f (x )=+x -1的定义域是()(A )(-1,+ ∞ ) (B )(-1,1)∪(1,+ ∞ ) (B )[-1,+∞ ) (D )[-1,1)∪(1,+∞ )3. 奇函数 y=f (x )的局部图像如图所示,则( )(A)f (2)> 0 > f (4) (B)f (2)< 0 < f (4) (C)f (2)> f (4)> 0 (D)f (2)< f (4)< 0(第 3 题图)4. 不等式 1+lg x <0 的解集是()1 11 1(A ) (- ,0)∪(0, )(B) (- , )10 10 10 10 (C) (-10,0)∪(0,10)(D )(-10,10)5.在数列{a n }中, a 1=-1,a 2=0,a n+2=a n+1+a n ,则 a 5 等于()(A )0 (B )-1 (C )-2 (D )-36. 在如图所示的平角坐标系中,向量 AB 的坐标是( )(A)(2,2)(B)(-2,-2) (C)(1,1)(D)(-1,-1)7.圆( x +1)2+ ( y -1)2= 1 的圆心在( )(A) 第一象限 (B) 第二象限 (C) 第三象限(D) 第四象限y(第 6 题图)8. 已知 a 、b ∈ R ,则“ a > b ”是“ 2a > 2b ”的()(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件9. 关于直线l : x - 3y + 2 = 0, ,下列说法正确的是( )(A)直线l 的倾斜角 60° (B)向量v =( ,1)是直线l 的一个方向向量2 1A1 2xBx +1 y-2-4 Ox3 3 (C)直线l 经过(1,- )(D)向量n =(1, )是直线l 的一个法向量10. 景区中有一座ft ,ft 的南面有 2 条道路,ft 的北面有 3 条道路,均可用于游客上ft 或下ft ,假设没有其他道路,某游客计划从ft 的一面走到ft 顶后,接着从另一面下ft ,则不同走发的种数是( ) (A) 6 (B) 10 (C) 12(D) 2011. 在平面直角坐标系中,关于 x ,y 的不等式 Ax+By+AB>0(AB≠ 0)表示的区域(阴影部分)可能是() yyOxOxAB CD12. 已知两个非零向量 a 与 b 的夹角为锐角,则()(A) a ⋅ b > 0 (B )a ⋅b < 0(B) (C )a ⋅b ≥ 0 (D ) a ⋅ b ≤ 013. 若坐标原点(0,0)到直线 x - y + sin= 0 的距离等于2,则角的取值集合是( )2(A)⎧|= k ±∈ Z ⎫ (B) ⎧|= k ±∈ Z ⎫ ⎨ , k ⎬ ⎨ 4 2 , k ⎬ ⎩ ⎭ ⎩ ⎭(C) ⎧|= 2k ± ∈ Z ⎫ )(D) ⎧|= 2k ±∈ Z ⎫ ⎨ , k ⎬ ⎨ 4 2 , k ⎬ ⎩ ⎭ ⎩ ⎭ 14. 关于 x,y 的方程 x 2 + ay 2 = a 2(a ≠ 0),表示的图形不可能是( )yOXAB CD15.在(x - 2 y )5 的展开式中,所有项的系数之和等于( )(A )32(B )-32 (C )1 (D )-116. 设命題 p: 5 ≥ 3,命題 q: {1} ⊆{0, 1, 2},则下列命題中为真命題的是( )(A) p ∧q(B) ﹁p ∧q (C) p ∧﹁q (D) ﹁p ∨﹁q17. 己知抛物线 x²=ay(a≠0)的焦点为 F,准线为 l,该抛物线上的点 M 到 x 轴的距离为 5,且|MF |=7,则焦点 F 到准线 l 的距离是( )(A) 2(B) 3(C) 4(D) 518. 某停车场只有并排的 8 个停车位,恰好全部空闲,现有 3 辆汽车依次驶入,并且随机停放在不同车位,yOxyOXy OXy OXyOx⎛ ⎫ 则至少有 2 辆汽车停放在相邻车位的概率是 ( )(A)5 14 (B)15 28 (C) 914(D) 67 19. 已知矩形 ABCD ,AB= 2BC ,把这个矩形分别以 AB 、BC 所在直线为轴旋转一周,所围成几何体的侧面积分别记为 S 1、S 2,则 S 1 与 S 2 的比值等于() 1 (A)(B) 1(C) 2(D) 4220. 若由函数 y= sin(2x+ )的图像变换得到 y=sin( 3x + 2 3 )的图像,则可以通过以下两个步骤完成:第一步 把 y= sin(2x+ )图像上所有点的横坐标变为原来的 4 倍,纵坐标不变;第二步,可以把所得,3图像沿 x 轴()5(A) 向右平移 个单位(B)向右平移 个单位312 5 (C) 向左平移 个单位(D)向左平移个单位312二、填空题(本大题 5 个小题,每小题 4 分,共 20 分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018春季高考真题
一、选择题
1、已知集合,,则等于
A、B、C、D、
2、函数的定义域是
A、B、
C、D、
3、奇函数的布局如图所示,则
A、B、
C、D、
4、已知不等式的解集是
A B、
C、D、
5、在数列中,=-1 ,=0,=+,则等于
A、B、C、D、
6、在如图所示的平面直角坐标系中,向量的坐标是
A、B、C、D、
7、圆
A、第一象限
B、第二象限
C、第三象限
D、第四象限
8、已知,则“”是“”的
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
9、关于直线,下列说法正确的是
A、直线l的倾斜角为
B、向量是直线l的一个方向向量
C、直线l经过点
D、向量是直线l的一个法向量
10、景区中有一座山,山的南面有2条道路,山的北面有3条道路,均可用于游客上山或下山,假设没有其他道路,某游客计划从山的一面走到山顶后,接着从另一面下山,则不同的走法的种数是
A、6
B、10
C、12
D、20
11、在平面直角坐标系中,关于的不等式表示的区域(阴影部分)可能是
12、已知两个非零向量a与b 的夹角为锐角,则
A、B、C、D、
13、若坐标原点到直线的距离等于,则角的取值集合是
A、{}
B、{}
C、{}
D、{}
14、关于的方程,表示的图形不可能是
15、在
A、32
B、-32
C、1
D、-1
16、设命题,命题,则下列命题中为真命题的是
A、p
B、
C、
D、
17、已知抛物线的焦点为,准线为,该抛物线上的点到轴的距离为,且=7,则焦点到准线距离是
A、2
B、
C、
D、
18、某停车场只有并排的8个停车位,恰好全部空闲,现有3辆汽车依次驶入,并且随机停放在不同车位,则至少有2辆汽车停放在相邻车位的概率是
A、B、C、D、
19、已知矩形ABCD,AB=2BC,把这个矩形分别以AB,BC所在直线为轴旋转一周,所围成集合体的侧面积分别记为S1、S2 ,则S1、S2的比值等于
A、B、C、D、
20、若由函数图像变换得到的图像,则可以通过以下两个步骤完成:第一步,把
上所有点的横坐标变为原来的4倍,纵坐标不变;第二步,可以把图像沿x轴
A、向右平移个单位
B、向右平移个单位
C、向左平移个单位
D、向左平移个单位
二、填空题
21、已知函数,则的值等于。
22、已知,则等于。
23、如图所示,已知正方体ABCD-A1B1C1D1 ,E,F分别是D1B,A1C上不重合的两个动
点,给出下列四个结论:
①CE||D1F ;②平面AFD||平面B1EC1;
③AB1EF ;④平面AED||平面ABB1A1
其中,正确的结论的序号是。
24、已知椭圆C的中心在坐标原点,一个焦点的坐标是(0,3),若点(4,0)在椭圆C上,则椭圆C的离心率等于
25、在一批棉花中随机抽测了500根棉花纤维的长度(精确到1mm)作为样本,并绘制了如图所示的频率分布直方图,由图可知,样本中棉花纤维的长度大于225mm的频数是。
三、解答题
26、已知函数,其中m为常数。
(1)若函数f(x)在区间(-)上单调递减,求实数m的取值范围;
(2)若,都有,求实数m的取值范围。
27、已知在等比数列{}中,=,=。
(1)求数列{}的通项公式;
(2)若数列{}满足,求{}的前n项和.
28、如图所示的几何体中,四边形ABCD是矩形,MA平面ABCD,NB平面ABCD,且AB=NB=1,AD=MA=2。
(1)求证:NC||平面MAD;
(2)求棱锥M-NAD的体积。
29、如图所示,在ABC中,BC=7,2AB=3AC,点P在BC上,且求线段AP的长。
30、双曲线 1 (a>0,b>0)的左、右焦点分别是F1 ,F2,抛物线的焦
点与点F2重合,点M(2,2)是抛物线与双曲线的一个交点,如图所示。
(1)求双曲线及抛物线的标准方程;
(2)设直线l与双曲线的过一、三象限的渐近线平行,且交抛物线与A,B两点,交双
曲线于点C。
若点C是线段AB的中点,求直线l的方程。
