高三数学第二次周练试题(文科)
安徽省六校教育研究会2020届高三数学第二次素质测试试题 文(含答案)
安徽省六校教育研究会2020届高三数学第二次素质测试试题 文一、选择题：本大题共12小题，每题5分．满分60分。
在每小题给出的四个选项中，只有一个是符合题目要求的。
1．己知集合A={x|-2≤x<1或2<x ≤3}，集合B={-2，-1，1，2，3}，则集合A ∩B 中的元素个数为A ．2B ．3C ．4D ．52．已知复数z 满足：zi=3+4i （i 为虚数单位），则z = A. 4+3i B.4- 3i C.-4+3i D. -4-3i 3．已知命题p: ,1log 2,12≥-≥∀x x x 则p ⌝为A. 1log 2,12<-<∀x x x B ．1log 2,12<-≥∀x x x C ．1log 2,12<-<∃x x x D ．1log 2,12<-≥∃x x x4．为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度．某地区在2015年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为70%．2015年开始全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占2019年贫困户总数的比）及该项目的脱贫率见下表：那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )倍A ．57 B ．3548 C. 3547 D ．2837 5．已知首项为正数的等比数列{a n }中，149744229,29=⋅=⋅a a a a 则a 13=A ．923 B. 1223 C ．923± D ．1223±6．已知函数)3sin(π+=x y 的定义域为[a ，b]，值域为]1,21[，则b-a 的值可能为A ．3πB ．πC ．23π D.2π7．已知双曲线C: 2222by a x -=l （a>0，b>0）的右焦点为F ，O 为坐标原点，以OF 为直径的圆与双曲线C 的一条渐近线交于点O 及点A )23,23(，则双曲线C 的方程为 A ．1322=-y x B ．1322=-y x C ．12622=-y x D. 16222=-y x8．《易经>包含着很多哲理，在信息学、天文学中都有广泛的应用，《易经》的博大精深， 对今天的几何学和其它学科仍有深刻的影响，下图就是《易经》中记载的几何图形一一八卦田，图中正八边形代表八卦，中间的圆代表阴阳太极图，图中八块面积相等的曲边梯形代表八卦田．已知正八边形的边长为l0m ，代表阴阳太极图的圆的半径为4m ，则每块八卦田的面积约为A ．114 m2B. 57m2C ．54 m2D ．48 m 29．锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若0)cos(2)4sin(=+++C B A π13,6+==c b ，则角C 的大小为A ．12πB ．6πC ．3πD ．125π 10.函数y=sin|x|+x 在x ∈[-2π，2π ]上的大致图象是11．若定义在R 上的增函数y=f(x-l)的图象关于点(1，0)对称，且f(2)=2，令g(x)==f(x)-l ，则下列结论不一定成立的是A ．g(1)=0B ．g(0)= -1C ．g(-1)+g(1)<0D ．g(-1)+g(2)> -212．如图所示，棱长为l 的正方体ABCD - A 1B 1C 1D 1中，P 为线段AB 1的中点，M ，N 分别 为体对角线AC 1和棱C 1D,上任意一点，则MN PM 22+的最小值为A.42 B ．22 C ．1 D ．2 二、填空题：本题共4小题，每题5分，共20分。
2021年高三第二次统练(数学文含答案)
顺义区xx届高三第二次统练数学试卷（文科）审核：贾玉雷本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。
考试时间120分钟。
考试结束后，将本试卷和答题卡一并交回。
注意事项：1．考生务必将答案答在答题卡上，在试卷上作答无效。
2．答题前考生务必用黑色字迹的签字笔在答题卡上填写姓名、准考证号，然后再用2B铅笔将与准考证号对应的信息点涂黑。
3．答题卡上第Ⅰ卷必须用2B铅笔作答，将选中项涂满涂黑，黑度以盖住框内字母为准，修改时用橡皮擦除干净。
第Ⅱ卷必须用黑色字迹的签字笔按照题号顺序在各题目的答题区域内作答，未在对应的答题区域内作答或超出答题区域作答的均不得分。
第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，选出符合题目要求的一项.1．已知集合，集合，则( )A. B. C. D.2. 已知复数，则( )A. B. C. D.3. 已知等比数列中，，，，则( )A. 5B. 6C. 7D. 84.已知向量，，且，则锐角等于（）A. B. C. D.5.“”是“直线与圆相交”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.阅读下面的程序框图，执行相应的程序，则输出的结果是（）n=n+1s=s+(-1)n n n=1, s=0n ≤ 10 ?开始是否A. 4B. 5C. 6D. 77. 以双曲线的中心为顶点，左焦点为焦点的抛物线方程是（）A. B. C. D.8.在圆内，过点作条弦（），它们的长构成等差数列，若为过该点最短的弦，为过该点最长的弦，且公差，则的值为（）A. B. C. D.2021年高三第二次统练（数学文含答案）二、填空题：本大题共6小题，每小题5分，共30分.二.填空题(本大题共6个小题,每小题5分,共30分,把答案填在题中横线上)9. 在总体为的一批零件中，抽取一个容量为的样本，若每个零件被抽取的可能性为25%，则的值为_________.10.已知向量与向量，则与的夹角为_________.11.已知、满足约束条件，则的最小值为______________.12.函数，则不等式的解集是____________.13.如图所示，墙上挂有一长为宽为2的矩形木板，它的阴影部分是由，的图象和直线围成的图形，某人向此板投飞镖，假设每次都能击中木板，且击中木板上每一点的可能性相同，则他击中阴影部分的概率是______________.14．某同学在研究函数时，分别给出下面几个结论：（1）函数是奇函数（2）函数的值域为（3）函数在上是增函数（4）函数（为常数，）必有一个零点其中正确结论的序号为___________（把所有正确结论的序号都填上）三．解答题（本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤）15．（本小题共12分）已知函数，．（Ⅰ）求的值；（Ⅱ）如果函数，求函数的最小正周期和最大值.16．（本小题共13分）甲、乙两位同学参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次，绘制成茎叶图如下Ⅰ.从甲、乙两人的成绩中各随机抽取一个，用列举法计算甲的成绩比乙高的概率；Ⅱ.现要从中选派一人参加数学竞赛，从统计学的角度考虑，你认为选派哪位学生参加合适？请说明理由. 17．（本小题共14分）一个直三棱柱的直观图及三视图如图所示，（其中为的中点） Ⅰ.求证：平面Ⅱ.当点在棱上的什么位置时，有平面， 请证明你的结论 Ⅲ.对（2）中确定的点，求三棱锥的体积． 18．（本小题共14分） 已知函数 （为常数，） Ⅰ若时，函数取得极大值，求实数的值；Ⅱ.若不等式在函数定义域上恒成立，（其中为的导函数）求的取值范围.19. （本小题共14分）已知：椭圆 过点，离心率；直线与圆:相切,并与椭圆交于不同的两点、,（为坐标原点）. Ⅰ.求椭圆的方程及与的关系式； Ⅱ.设，且满足，， 求直线的方程；Ⅲ.在Ⅱ.的条件下，求三角形的面积. 20．（本小题共13分）设数列的前项和为，点在直线上，其中为常数，且. Ⅰ.求证：是等比数列，并求其通项； Ⅱ若数列的公比，数列满足，, ， ），求证：是等差数列，并求;Ⅲ.设数列满足，为数列的前项和，且存在实数满足，求的最大值.俯视图侧视图主视图21112DC 1B 1A 1BC A高三数学试题（文科）参考答案及评分标准二.填空题(本大题共6个小题,每小题5分,共30分)其它答案参考给分 9． ；10.; 11. ；12.；13．；14．;（注：14题少解给2分，有错解不给分） 三．解答题（本大题共6小题，共80分） 15. （本小题共12分） 解：（Ⅰ）．_______4分（Ⅱ）()()()(sin cos )[sin()cos()]g x f x f x x x x x =-=+-+- _______6分_______8分，的最小正周期为．_______10分 ，因此，函数的最大值是．_______12分16．（本小题共13分）解： Ⅰ.由茎叶图知甲乙两同学的成绩分别为： 甲：82 81 79 88 80乙：85 77 83 80 85 ______2分 记从甲、乙两人的成绩中各随机抽取一个为， 用列举法表示如下：______4分甲的成绩比乙高的概率为 ______7分Ⅱ.本小题的结论唯一但理由不唯一，只要考生从统计学的角度给出其合理解答即可得分. （1）派乙参赛比较合适， ______9分 . 理由如下： 甲的平均分，乙的平均分，甲乙平均分相同；又甲的标准差的平方（即方差），乙的标准差的平方（即方差），______11分甲乙平均分相同，但乙的成绩比甲稳定，派乙去比较合适；______13分（2）派乙去比较合适，理由如下：从统计学的角度看，甲获得分以上（含85分）的概率乙获得分以上（含85分）的概率，甲的平均分，乙的平均分，平均分相同；派乙去比较合适.若学生或从得分以上(含82分)去分析：甲获得分以上（含82分）的概率,乙获得分以上（含82分）的概率，甲的平均分，乙的平均分，平均分相同；派乙去比较合适.（同样给此问的分）.17．（本小题共14分）证明：由三视图知该多面体为底面为直角三角形的直三棱柱，，棱平面，，，；______2分Ⅰ. 为的中点，，平面平面，，，平面______5分Ⅱ. 当点在棱上的中点时，有平面______7分证明：连结，，，，四边形为正方形，，，由Ⅰ知，平面______10分Ⅲ.设，为三棱锥的高，，______12分可求得，体积.______14分18.（本小题共14分）解：定义域，______2分Ⅰ在处取得极值，______4分，令，解得在上单调递增，在上单调递减，满足在处取得极大值，.______7分Ⅱ. 方法1：若不等式在函数定义域上恒成立______9分俯视图侧视图主视图21112DC1B1 A1B CA即在上恒成立，在上恒成立 ，“”当且仅当时取到，______12分 （不验证“=”成立扣1分） .______14分方法2：令 ，，易知在递减，在递增；有最小值（即极小值）为， . 19．（本小题共14分） 解：Ⅰ.椭圆，过点，，______1分，______2分椭圆方程为：；______3分 直线与圆相切，，，即 ______5分 Ⅱ.方法1：消去得， ， ______6分 设，，则，，2||||cos 3OA OB OA OB θ⋅=⋅==又211221212212(,)(,)213k OA OB x y x y x x y y k +⋅==+=⋅⋅⋅==+ ______8分 ，；，直线的方程为：或 ______10分Ⅲ.由Ⅱ.知；消去得，，由弦长公式：， ______14分 方法2： 直线过点 ＜＞ ，且 ， ：，与联立解得：， 或， 即，，由两点得的方程为：，由前面解知：为三角形的底边，为三角形的高， ， 20．（本小题共13分） 解：解：Ⅰ.点在直线 上， * ______1分 当时，，， ， ______2分当时，由*式知**，两式相减得 ， ，又当时也适合，是等比数列，通项；____5分 Ⅱ.由Ⅰ知， ，即，又也适合，成等差数列，______7分其通项，______9分Ⅲ. 满足为数列的前项和，递增；______11分，要满足对任意都成立，. 的最大值为. ______13分32789 8015 耕30556 775C 睜R6?28939 710B 焋#34659 8763 蝣5B(39486 9A3E 騾。
广州市高三二模数学试题及答案(文科)
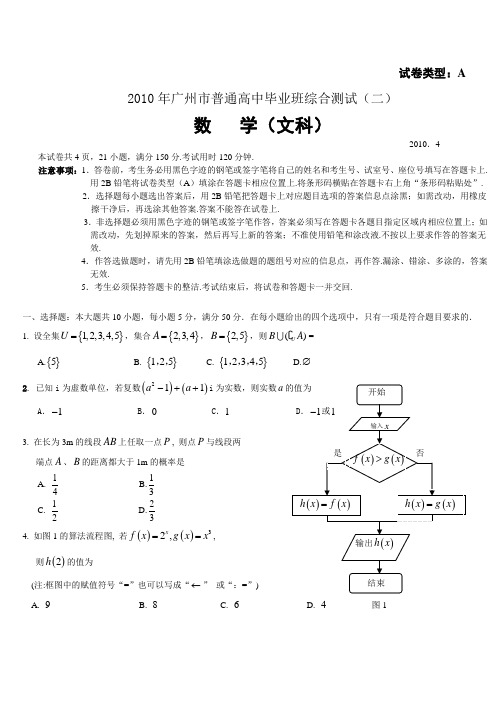
试卷类型：A2010年广州市普通高中毕业班综合测试（二）数 学（文科）2010．4 本试卷共4页，21小题，满分150分.考试用时120分钟.注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B 铅笔将试卷类型（A ）填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”. 2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案.答案不能答在试卷上.3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4．作答选做题时，请先用2B 铅笔填涂选做题的题组号对应的信息点，再作答.漏涂、错涂、多涂的，答案无效.5．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 设全集{}1,2,3,4,5U =，集合{}2,3,4A =，{}2,5B =，则()U BA =A.{}5B. {}125，，C. {}12345，，，，D.∅2. 已知i 为虚数单位，若复数()()211a a -++i 为实数，则实数a A ．1- B ．0 C ．13. 在长为3m 的线段AB 上任取一点P , 则点P 与线段两 端点A 、B 的距离都大于1m 的概率是A.14 B.13 C. 12 D.234. 如图1的算法流程图, 若()()32,xf xg x x ==,则()2h 的值为(注:框图中的赋值符号“=”也可以写成“←” 或“：=”)A. 9B. 8C. 6D. 4 图15. 命题“若,x y 都是偶数，则x y +也是偶数”的逆否命题是A ．若x y +是偶数，则x 与y 不都是偶数B ．若x y +是偶数，则x 与y 都不是偶数C ．若x y +不是偶数，则x 与y 不都是偶数D ．若x y +不是偶数，则x 与y 都不是偶数6. 设变量,x y 满足约束条件2,, 2.x y x x y ≤⎧⎪≤⎨⎪+≥⎩则目标函数2z x y =+的最小值为A. 6B. 4C. 3D. 2 7. 若0x <且1xxa b >>, 则下列不等式成立的是A. 01b a <<<B. 01a b <<<C. 1b a <<D. 1a b << 8. 函数()cos sin 44f x x x ππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭12-是 A. 最小正周期为2π的偶函数 B. 最小正周期为π的偶函数 C. 最小正周期为2π的奇函数 D. 最小正周期为π的奇函数9. 高8m 和4m 的两根旗杆笔直地竖在水平地面上, 且相距10m , 则地面上观察两旗杆顶端仰角相等的点的轨迹为A. 圆B. 椭圆C. 双曲线D. 抛物线 10. 已知函数()sin f x x x =-,若12,,22x x ππ⎡⎤∈-⎢⎥⎣⎦且()()120f x f x +>,则下列不等式中 正确的是A. 12x x >B. 12x x <C. 120x x +>D. 120x x +< 二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（11～13题）11．已知向量a ,b 满足1=a ,b =2, a b 1=, 则a 与b 的夹角大小是 .12. 已知双曲线C :()2222100x y a ,b a b-=>>的离心率2e =, 且它的一个顶点到相应焦点的距离为1, 则双曲线C 的方程为 . 13.图2是一个有n 层()2n ≥的六边形点阵.它的中心是一个点,算作第一层, 第2层每边有2个点,第3层每边有3个点 ,…,第n 层每边有n 个点,则这个点阵的点数共有 个图3（二）选做题（14~ 15题，考生只能从中选做一题） 14.(坐标系与参数方程选做题)已知直线l 的参数方程为1,42.x t y t =+⎧⎨=-⎩(参数t ∈R ),圆C 的参数方程为2cos 2,2sin .x y θθ=+⎧⎨=⎩(参数[]0,2θπ∈),则直线l 被圆C 所截得的弦长为 .15.(几何证明选讲选做题)如图3, 半径为5的圆O 的两条弦 AD 和BC 相交于点P , ,OD BC P ⊥为AD 的中点, 6BC =, 则弦AD 的长度为 .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤，16. （本小题满分12分）已知1sin 0,,tan 523⎛⎫=∈= ⎪⎝⎭πααβ. (1) 求tan α的值; (2) 求()tan 2+αβ的值.某学校课题组为了研究学生的数学成绩与物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（满分100分）如下表所示：若单科成绩85分以上（含85分），则该科成绩为优秀． （1）根据上表完成下面的2×2列联表(单位:人)：数学成绩优秀数学成绩不优秀合 计物理成绩优秀 物理成绩不优秀合 计20 关系？（3）若从这20个人中抽出1人来了解有关情况，求抽到的学生数学成绩与物理成绩至少有一门 不优秀的概率. 参考数据:① 假设有两个分类变量X 和Y ,它们的值域分别为{}12,x x 和{}12,y y ,其样本频数列联表(称 为22⨯列联表)为:则随机变量()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++为样本容量；②独立检验随机变量2K 的临界值参考表：序号12345678910 11 12 13 14 15 16 17 18 19 20 数学成绩 95 75 80 94 92 65 67 84 98 71 67 93 64 78 77 90 57 83 72 83 物理成绩 90 63 72 87 91 71 58 82 93 81 77 82 48 85 69 91 61 84 78 861y 2y合计1x a b a b +2xcd c d + 合计a c +b d +a b c d +++()20P K k ≥ 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.0010k0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828NMB 1C 1D 1A 1DCBA在长方体1111ABCD A B C D -中, 11,2AB BC AA ===, 点M 是BC 的中点,点N 是1AA 的中点. (1) 求证: //MN 平面1A CD ;(2) 过,,N C D 三点的平面把长方体1111ABCD A B C D -截成 两部分几何体, 求所截成的两部分几何体的体积的比值.19. （本小题满分14分）我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是：水费=基本费+超额费+定额损耗费,且有如下三条规定：①若每月用水量不超过最低限量m立方米时，只付基本费9元和每户每月定额损耗费a元；②若每月用水量超过m立方米时，除了付基本费和定额损耗费外，超过部分每立方米付n元的超额费；③每户每月的定额损耗费a不超过5元.(1) 求每户每月水费y（元）与月用水量x（立方米）的函数关系；(2) 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示：试分析该家庭今年一、二、三各月份的用水量是否超过最低限量，并求m,n,a的值.20. （本小题满分14分）已知椭圆22122:1(0)x y C a b a b+=>>的右焦点2F 与抛物线22:4C y x =的焦点重合，椭圆1C 与抛物线2C 在第一象限的交点为P ，25||3PF =.圆3C 的圆心T 是抛物线2C 上的动点, 圆3C 与y 轴交于,M N 两点，且||4MN =. （1）求椭圆1C 的方程；（2）证明:无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点.21. （本小题满分14分）已知数列{}n a 和{}n b 满足11a b =,且对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-. (1) 判断数列1n a ⎧⎫⎨⎬⎩⎭是否为等差数列, 并说明理由; (2) 证明: ()111n nn n a b ++>.2010年广州市普通高中毕业班综合测试（二）数学（文科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如 果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力比照评分标准给以相应的分数． 2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容 和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半； 如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题：本大题主要考查基本知识和基本运算．共10小题，每小题5分，满分50分．二、填空题：本大题主要考查基本知识和基本运算．本大题共5小题，考生作答4小题，每小题5分， 满分20分．其中14～15题是选做题，考生只能选做一题．11．3π12. 2213y x -=13. 2331n n -+ 14. 515.三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.16．（本小题满分12分）(本小题主要考查同角三角函数的基本关系、两角和与差的正切等知识, 考查化归与转化的数学思想方法 和运算求解能力) (1) 解:∵sin 0,,52⎛⎫=∈ ⎪⎝⎭παα ∴ cos ===α. …2分 ∴sin 1tan cos 25===ααα. …4分(2)解法1:∵1tan 3=β, ∴22tan tan 21tan βββ=- …6分2123113⨯=⎛⎫- ⎪⎝⎭34=. …8分 ∴()tan tan 2tan 21tan tan 2++=-αβαβαβ…10分132413124+=-⨯ 2=. …12分 解法2: ∵1tan 3=β, ∴()tan tan tan 1tan tan ++=-αβαβαβ…6分112311123+=-⨯1=. …8分 ∴()()()tan tan tan 21tan tan +++=-+αββαβαββ …10分1131113+=-⨯2=. …12分P NMB 1C 1D 1A 1DCBA17．（本小题满分12分）(本小题主要考查独立性检验的基本思想、方法及其简单应用和概率等知识, 考查或然与必然的数学思想方法， 以及数据处理能力、运算求解能力和应用意识) （1）解：2×2列联表为(单位:人):…4分 （2）解：提出假设0H ：学生数学成绩与物理成绩之间没有关系.根据列联表可以求得22121214720(5)8.8027.879136K ⨯-⨯⨯⨯⨯⨯=≈>. …6分当0H 成立时，2(7.879)0.005P K >=.所以我们有99.5%的把握认为：学生的数学成绩与物理成绩之间有关系. …8分 （3）解：由(1)可知数学成绩与物理成绩都优秀的学生的人数为5人，则数学成绩与物理成绩至少有一门不优秀的学生人数为15人. …10分 故从20名学生中抽出1名,抽到的学生数学成绩与物理成绩至少有一门不优秀的概率为153204=. …12分 18. （本小题满分14分）(本小题主要考查空间线面关系、几何体的体积等知识, 考查数形结合、化归与转化的数学思想方法， 以及空间想象能力、推理论证能力和运算求解能力) （1）证法1：设点P 为AD 的中点，连接,MP NP .∵ 点M 是BC 的中点, ∴ //MP CD .∵ CD ⊂平面1A CD ,MP ⊄平面1A CD , ∴ //MP 平面1A CD . …2分 ∵ 点N 是1AA 的中点, ∴ 1//NP A D .∵ 1A D ⊂平面1A CD ,NP ⊄平面1A CD ,∴ //NP 平面1A CD . …4分PNMB 1C 1D 1A 1DCBAQN MB 1C 1D 1A 1DCB A∵ MP NP P =,MP ⊂平面MNP ,NP ⊂平面MNP ,∴ 平面//MNP 平面1A CD . ∵ MN ⊂平面MNP ,∴//MN 平面1A CD . …6分 证法2: 连接AM 并延长AM 与DC 的延长线交于点P , 连接1A P , ∵ 点M 是BC 的中点, ∴ BM MC =.∵ BMA CMP ∠=∠, 90MBA MCP ︒∠=∠=, ∴ Rt MBA ≅Rt MCP . …2分∴ AM MP =. ∵ 点N 是1AA 的中点,∴ 1MN //A P . …4分∵ 1A P ⊂平面1A CD ,MN ⊄平面1A CD ,∴ //MN 平面1A CD . …6分(2) 解: 取1BB 的中点Q , 连接NQ ,CQ , ∵ 点N 是1AA 的中点, ∴ //NQ AB . ∵ //AB CD , ∴ //NQ CD .∴ 过,,N C D 三点的平面NQCD 把长方体1111ABCD A B C D -截成两部分几何体,其中一部分几何体为直三棱柱QBC -NAD , 另一部分几何体为直四棱柱1111B QCC A NDD -. …8分 ∴ 11111222QBC S QB BC ∆==⨯⨯=, ∴ 直三棱柱QBC -NAD 的体积112QBC V S AB ∆==, …10分 ∵ 长方体1111ABCD A B C D -的体积112V =⨯⨯2=, ∴直四棱柱1111B QCC A NDD -体积2132V V V =-=. …12分∴ 12V V =1232=13.∴ 所截成的两部分几何体的体积的比值为13. …14分(说明:213V V =也给分) 19．（本小题满分14分）(本小题主要考查函数和方程、分段函数等知识, 考查函数与方程、分类与整合的数学思想方法，以及抽象 概括能力、推理论证能力、运算求解能力和应用意识)（1）解：依题意，得()()()909a,x m,y n x m a,x m.+<≤*⎧⎪=⎨+-+>**⎪⎩其中05a <≤. …2分（2）解：∵05a <≤，∴9914a <+≤.由于该家庭今年一、二月份的水费均大于14元，故用水量4立方米，5立方米都大于最低限量m 立方米. …4分 将417x ,y =⎧⎨=⎩和523x ,y =⎧⎨=⎩分别代入()**，得()()1794,2395.n m a n m a =+-+⎧⎪⎨=+-+⎪⎩…6分两式相减, 得6n =.代入()1794n m a,=+-+得616a m =-. …8分 又三月份用水量为2.5立方米，若25m .<，将2511x .,y =⎧⎨=⎩代入()**，得613a m =-，这与616a m =-矛盾. …10分 ∴25m .≥，即该家庭三月份用水量2.5立方米没有超最低限量.将 2.5,11x y =⎧⎨=⎩代入()*，得119a =+，由616119a m ,a.=-⎧⎨=+⎩ 解得23a ,m .=⎧⎨=⎩ …13分答：该家庭今年一、二月份用水超过最低限量，三月份用水没有超过最低限量，且362m ,n ,a ===. …14分 20．（本小题满分14分）(本小题主要考查直线、圆、抛物线、椭圆等知识, 考查数形结合、化归与转化、特殊与一般、函数 与方程的数学思想方法，以及推理论证能力、运算求解能力和创新意识)（1）解法1：∵抛物线22:4C y x =的焦点坐标为(1,0)， …1分∴点2F 的坐标为(1,0).∴椭圆1C 的左焦点1F 的坐标为1(1,0)F -，抛物线2C 的准线方程为1x =-. 设点P 的坐标为11(,)x y ，由抛物线的定义可知211PF x =+,∵253PF =, ∴1513x +=，解得123x =.由211843y x ==，且10y >,得1y =∴点P 的坐标为23,⎛⎝. …3分 在椭圆1C :22221(0)x y a b a b+=>>中，1c =.122||||4a PF PF =+=+=.∴2,a b === ∴椭圆1C 的方程为22143x y +=. …6分 解法2：∵抛物线22:4C y x =的焦点坐标为(1,0)， …1分∴点2F 的坐标为(1,0).∴ 抛物线2C 的准线方程为1x =-.设点P 的坐标为11(,)x y ，由抛物线的定义可知211PF x =+, ∵253PF =,∴1513x +=，解得123x =. 由211843y x ==，且10y >得1y = ∴点P的坐标为2(3. …3分在椭圆1C :22221(0)x y a b a b+=>>中，1c =.由222221424199c ,a b c ,.ab ⎧⎪=⎪=+⎨⎪⎪+=⎩解得2,a b == ∴椭圆1C 的方程为22143x y +=. …6分 （2）证法1: 设点T 的坐标为00(,)x y ,圆3C 的半径为r ， ∵ 圆3C 与y 轴交于,M N 两点，且||4MN =, ∴||4MN ==.∴r =∴圆3C 的方程为222000()()4x x y y x -+-=+. ()* …8分∵ 点T 是抛物线22:4C y x =上的动点, ∴ 2004y x =(00x ≥).∴20014x y =. 把20014x y =代入()* 消去0x 整理得:22200(1)2()024x y yy x y +---+=.()** …10分方程()**对任意实数0y 恒成立，∴2210,220,40.xy x y ⎧-=⎪⎪-=⎨⎪+-=⎪⎩解得2,0.x y =⎧⎨=⎩ …12分∵点(2,0)在椭圆1C :22143x y +=上, ∴无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点()2,0. …14分 证法2: 设点T 的坐标为00(,)x y ,圆3C 的半径为r ，∵ 点T 是抛物线22:4C y x =上的动点,∴ 2004y x =(00x ≥). …7分∵ 圆3C 与y 轴交于,M N 两点，且||4MN =, ∴||4MN ==. ∴r =∴ 圆3C 的方程为222000()()4x x y y x -+-=+.()*** …9分令00x =,则2004y x =0=,得00y =.此时圆3C 的方程为224x y +=. …10分由22224,1,43x y x y⎧+=⎪⎨+=⎪⎩解得2,0.x y =±⎧⎨=⎩ ∴圆3C :224x y +=与椭圆1C 的两个交点为()2,0、()2,0-. …12分分别把点()2,0、()2,0-代入方程()***进行检验，可知点()2,0恒符合方程()***，点()2,0-不恒符合方程()***.∴无论点T 运动到何处,圆3C 恒经过椭圆1C 上一定点()2,0. …14分 21．（本小题满分14分）(本小题主要考查导数及其应用、数列、不等式等知识, 考查化归与转化的数学思想方法，以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1) 解: 数列1n a ⎧⎫⎨⎬⎩⎭为等差数列. …1分理由如下:∵对任意n ∈N *都有1n n a b +=,121n n n na ba a +=-, ∴12211111n n n n n n na b a a a a a +-===--+. ∴1111n na a +=+,即1111n n a a +-=. …3分 ∴数列1n a ⎧⎫⎨⎬⎩⎭是首项为11a ,公差为1的等差数列. …4分 (2) 证明: ∵11a b =, 且111a b +=, ∴11a b =12=. 由(1)知()1211nn n a =+-=+. ∴ 11n a n =+, 11n n n b a n =-=+. …6分 所证不等式()111n nn n a b ++>,即111111n nn n n +⎛⎫⎛⎫+> ⎪⎪++⎝⎭⎝⎭, 也即证明111111n nn n +⎛⎫⎛⎫+>+ ⎪⎪+⎝⎭⎝⎭. 令()()ln 11xf x x x =>-, 则()'21ln (1)x xx f x x --=-. 再令()1ln x g x x x-=-, 则()'211g x x x =-21x x-=. …8分当1x >时, ()'0g x <,∴函数()g x 在[)1,+∞上单调递减. ∴当1x >时,()()10g x g <=,即1ln 0x x x--<.∴当1x >时, ()'21ln (1)x xx f x x --=-0<.∴函数()ln 1xf x x =-在()1,+∞上单调递减. …10分 ∵111111n n<+<++,∴11111f f n n ⎛⎫⎛⎫+>+ ⎪ ⎪+⎝⎭⎝⎭. ∴11ln 1ln 111111111n n n n⎛⎫⎛⎫++ ⎪ ⎪+⎝⎭⎝⎭>+-+-+. …12分∴111ln 1ln 11n nn n +⎛⎫⎛⎫+>+ ⎪⎪+⎝⎭⎝⎭.∴111111n nn n +⎛⎫⎛⎫+>+ ⎪ ⎪+⎝⎭⎝⎭. ∴()111n n n n a b ++>成立. …14分。
高三数学二轮复习文科系列周考卷一 试题
2021届高三数学二轮复习文科系列周考卷一制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日第一卷(选择题 一共50分)一、选择题：本大题一一共10小题，每一小题5分，一共50分，在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的. 1．函数y=lg(1－x ) (x <0) 的反函数是 ( )A ．y=101－x(x <0) B ．y=101－x(x >0)C ．y=1－10x(x <0)D ．y=1－10x(x >0)2．“1>a 〞是“11<a〞的 ( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．函数)4(sin )4(cos 22ππ+-+=x x y 是 ( )A ．周期为π的奇函数B ．周期为π的偶函数C ．周期2π的奇函数D ．周期为2π的偶函数4．设函数f (x )是定义在R 上以3为周期的奇函数，假设f (1)＜1，f (2)＝2a －3a ＋1，那么〔 〕A .a ＜23B .a ＜23且a ≠－1C .a ＞23或者a ＜－1D .1＜a ＜235．由0，1，2，…，9这十个数字组成的、无重复数字的四位数中，个位数字与百位之差的绝对值等于8的个数为 〔 〕 A.180 B.196 C6．在△ABC 中，cotA 是等差数列{a n }的公差，且B a a cot ,4,473=-=是等比数列{b n }的公比，且9,3163==b b ，那么这个三角形是 ( )A ．锐角三角形B ．钝角三角形C ．直角三角形D ．等腰三角形7．正方形ABCD ，沿对角线BD 折成直二面角后不会成立的结论是 〔 〕 A ．AC ⊥BDB ．△ADC 为等边三角形 C ．AB 、CD 所成角为60°D ．AB 与平面BCD 所成角为60°8．如图，目的函数y ax P -=仅在闭区域OACB 的点 )54,32(C 处获得最小值，那么a 的取值范围是 〔 〕 〔A 〕)125,310(-- 〔B 〕)103,512(--〔C 〕)512,103(〔D 〕)103,512(- 9．棱长为3的正方体ABCD —A 1B 1C 1D 1中，长为2的线段MN 的一个端点M 在DD 1 上运动，另一个端 点 N 在底面 ABCD 上运动。
四川省内江市第六中学2022-2023学年高三上学期第二次月考《文科》数学(解析版)
内江六中2022—2023学年（上）高2023第二次月考文科数学试题第Ⅰ卷 选择题（满分60分）一、选择题（每题5分，共60分）1. 已知向量()1,2a =r ，()1,1b = ，若c a kb =+ ，且b c ⊥ ，则实数k =（ ）A. 32B. 53-C. 53D. 32-【答案】D 【解析】【分析】根据平面向量坐标的线性运算得c得坐标，在根据向量垂直的坐标关系，即可得实数k 的值.【详解】解：因为向量()1,2a =r ，()1,1b = ，所以()1,2c a kb k k =+=++ ，又b c ⊥，所以120b c k k ⋅=+++= ，解得32k =-.故选：D.2. 复数13i2iz -=+的虚部为（ ）A. 75-B. 7i 5-C. 73-D. 7i 3-【答案】A 【解析】【分析】利用复数的除法运算化简，即可得复数的虚部.【详解】解：复数13i (13i)(2i)17i 17i 2i (2i)(2i)555z -----====--++-故z 的虚部为75-.故选：A ．3. 若集合{1A =-，0，1}，2{|1B y y x ==-，}x A ∈，则A B = （ ）A. {0} B. {1}C. {0，1}D. {0，1}-【答案】D 【解析】【分析】把A 中元素代入B 中解析式求出y 的值，确定出B ，找出两集合的交集即可．【详解】解：把A 中=1x -，0，1代入B 中得：0y =，1，即{0B =，1}，则{0A B = ，1}-，故选：D ．4. 若变量x 、y 满足约束条件211y x x y y ≤⎧⎪+≤⎨⎪≥-⎩，则目标函数2z x y =+取最大值时的最优解是（ ）A. 5,03⎛⎫ ⎪⎝⎭B. 1,12⎛⎫-- ⎪⎝⎭C. 12,33⎛⎫⎪⎝⎭D. ()2,1-【答案】C 【解析】【分析】作出满足约束条件的可行域，平移直线20x y +=，即可得出结果.【详解】作出满足约束条件的可行域（如图中阴影部分所示）.2z x y =+可化为20x y z +-=，平移直线20x y +=，当其经过点C 时，目标函数2z x y =+取得最大值，联立21y x x y =⎧⎨+=⎩，解得13x =，23y =，故最优解是12,33⎛⎫⎪⎝⎭，故选：C.5. 若a ，b 均为实数，则“ln ln a b >”是“e e a b >”的（ ）A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据函数ln y x =与e x y =解不等式，即可判断.【详解】解：因为ln ln a b >，由函数ln y x =在()0,+∞上单调递增得：0a b >>又e e a b >，由于函数e x y =在R 上单调递增得：a b >由“0a b >>”是“a b >”的充分不必要条件可得“ln ln a b >”是“e e a b >”的充分不必要条件.故选：A.6. 如图是函数()()sin 0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的图象的一部分，则函数()f x 的解析式为（ ）A. ()2sin 26f x x π⎛⎫=+⎪⎝⎭B. ()2sin 23f x x π⎛⎫=+⎪⎝⎭C. ()sin 3f x x π⎛⎫=+ ⎪⎝⎭D. ()2sin 23f x x π⎛⎫=-⎪⎝⎭【答案】B 【解析】【分析】由图象可确定()f x 最小正周期T ，由此可得ω；根据712f A π⎛⎫=- ⎪⎝⎭可求得ϕ；由()0f =可求得A ，由此可得()f x .【详解】由图象可知：()f x 最小正周期23471T πππ⎛⎫-=⎪⎝⎭=⨯，22T πω∴==；又77sin 126f A A ππϕ⎛⎫⎛⎫=+=-⎪ ⎪⎝⎭⎝⎭，()73262k k ππϕπ∴+=+∈Z ，解得：()23k k πϕπ=+∈Z ，又02πϕ<<，3πϕ∴=，()sin 23f x A x π⎛⎫∴=+⎪⎝⎭，()0sin 3f A A π=== ，2A ∴=，()2sin 23f x x π⎛⎫∴=+ ⎪⎝⎭.故选：B.7. 已知向量,a b 的夹角为4π，且1||4,(23)122a a b a b ⎛⎫=+⋅-= ⎪⎝⎭，则向量b 在向量a 方向上的投影是（ ）A.B. 3C. D. 1【答案】D 【解析】【分析】由题意，根据数量积的运算，化简等式，解得模长，结合投影的计算公式，可得答案.【详解】由()123122a b a b ⎛⎫+⋅-= ⎪⎝⎭，22323122a a b a b b -⋅+⋅-= ，2213122a a b b +⋅-= ，21164cos 31224b b π+⨯⋅-=，230b -= ，(30b += ，解得b = b 在向量a 方向上的投影为cos 14b π= ，故选：D.8. 蒙特卡洛算法是以概率和统计的理论、方法为基础的一种计算方法，将所求解的问题同一定的概率模型相联系．用均匀投点实现统计模拟和抽样，以获得问题的近似解，故又称统计模拟法或统计实验法，现设计一个实验计算圆周率的近似值，向两直角边长分别为6和8的直角三角形中均匀投点40个．落入其内切圆中的点有22个，则圆周率π≈（ ）A.6320B.3310C.7825D.9429【答案】B 【解析】【分析】根据几何概型的计算公式和题意即可求出结果.【详解】直角三角形内切圆的直径等于两直角边的和与斜边的差，即268104r =+-=，由几何概型得2222140682π⨯≈⨯⨯，从而3310π≈.故选：B.9. 双碳，即碳达峰与碳中和的简称，2020年9月中国明确提出2030年实现“碳达峰”，2060年实现“碳中和”．为了实现这一目标，中国加大了电动汽车的研究与推广，到2060年，纯电动汽车在整体汽车中的渗透率有望超过70%，新型动力电池随之也迎来了蓬勃发展的机遇．Peukert 于1898年提出蓄电池的容量C （单位：A·h ），放电时间t （单位：h ）与放电电流I （单位：A ）之间关系的经验公式n C I t =⋅，其中32log 2n =为Peukert 常数．在电池容量不变的条件下，当放电电流10A I =时，放电时间57h t =，则当放电电流15A I =，放电时间为（ ）A. 28h B. 28.5hC. 29hD. 29.5h【答案】B 【解析】【分析】根据题意求出蓄电池的容量C ，再把15A I =代入，结合指数与对数的运算性质即可得解.【详解】解：根据题意可得5710n C =⋅，则当15A I =时，571015n n t ⋅=⋅，所以32231log 2log 222257575728.5h 333nt ⎛⎫⎛⎫⎛⎫=⋅=⋅=⋅= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，即当放电电流15A I =，放电时间为28.5h.故选：B .10. 已知函数()32e ,0461,0x x f x x x x ⎧<=⎨-+≥⎩，则函数()()()2232g x f x f x =--⎡⎤⎣⎦的零点个数为（ ）．A. 2 B. 3 C. 4 D. 5【答案】B 【解析】【分析】首先根据()()22320f x f x --=⎡⎤⎣⎦，得到()2f x =或1()2f x =-，然后利用导数分析0x ≥时函数的单调性，结合单调性画出函数的图象，通过图象即可观察出函数零点的个数.【详解】由()()()22320g x f x f x =--=⎡⎤⎣⎦，得()2f x =或1()2f x =-.当0x ≥时，2()121212(1)f x x x x x '=-=-，所以当(0,1)x ∈，()0,()'<f x f x 单调递减；当()1,x ∈+∞，()0,()'>f x f x 单调递增，所以1x =时，()f x 有极小值(1)4611f =-+=-.又0x <时，()x f x e =，画出函数()f x 的图象如图所示，由图可知：函数()()()2232g x f x f x =--⎡⎤⎣⎦的零点个数为3.故选：B .11. 已知()f x 是定义在R 上的函数满足(4)()f x f x -=-，且满足(31)f x -为奇函数，则下列说法一定正确的是（ ）A. 函数()f x 图象关于直线=2x 对称B. 函数()f x 的周期为2C. 函数()f x 关于点1,03⎛⎫- ⎪⎝⎭中心对称 D. (2023)0f =【答案】D 【解析】【分析】对于A.令2x x =+代入(4)()f x f x -=-即可判断.对于C.可考虑图像平移或者将3x 换元进行判断.对于BD.通过AB对称轴和对称中心即可判断出函数周期，继而计算出(2023)f 【详解】因为函数()f x 关于直线2x =-对称，不能确定()f x 是否关于直线2x =对称，A 错误；因为(31)f x -为奇函数，所以(31)(31)f x f x -=---，所以(1)(1)f x f x -=---，所以()(2)f x f x =---，所以函数()f x 关于点(1,0)-中心对称，故C 错误;由()(4)f x f x =--与()(2)f x f x =---得(4)(2)f x f x --=---，即(4)(2)f x f x -=--，故(4)()f x f x -=，所以函数()f x 的周期为4，故B 错误；(2023)(50641)(1)0f f f =⨯-=-=，故D 正确．故选:D的的12. 已知关于x 的不等式(e )e ->x x x x m m 有且仅有两个正整数解（其中e 2.71828= 为自然对数的底数），则实数m 的取值范围是（ ）A. 43169(,]5e 4eB. 3294(,4e 3eC. 43169[,5e 4eD. 3294[,e 3e 4【答案】D 【解析】【分析】问题转化为2(1)e x x m x +<（0x >）有且仅有两个正整数解，讨论0m ≤、0m >并构造()(1)f x m x =+、2()ex x g x =，利用导数研究单调性，进而数形结合列出不等式组求参数范围.【详解】当0x >时，由2e e 0xxx mx m -->，可得2(1)ex x m x +<（0x >），显然当0m ≤时，不等式2(1)ex x m x +<在(0,)+∞恒成立，不合题意；当0m >时，令()(1)f x m x =+，则()f x 在(0,)+∞上单调递增，令2()ex x g x =，则(2)()e xx x g x '-=，故(0,2)上()0g x '>，(2,)+∞上()0g x '<，∴()g x 在(0,2)上递增，在(2,)+∞上递减，又(0)(0)0f m g =>=且x 趋向正无穷时()g x 趋向0，故()240,e g x ⎛⎤∈ ⎥⎝⎦，综上，(),()f x g x 图象如下：由图知：要使()()f x g x <有两个正整数解，则()()()()()()11{2233f g f g f g <<≥，即2312e 43e 94e m m m ⎧<⎪⎪⎪<⎨⎪⎪≥⎪⎩，解得32944e 3e m ≤<．故选：D【点睛】关键点点睛：问题转化为2(1)ex x m x +<（0x >）有且仅有两个正整数解，根据不等式两边的单调性及正整数解个数列不等式组求范围.第Ⅱ卷非选择题（满分90分）二、填空题（每题5分，共20分）13. 1289log 24⎛⎫+= ⎪⎝⎭______ ．【答案】116##516【解析】【分析】利用指数幂与对数运算即可求解.【详解】112388893111log 2log 8log 84236⎛⎫+=+=+= ⎪⎝⎭.故答案为：116.14. 曲线123x y x -=+在点()1,2--处的切线方程为________．（用一般式表示）【答案】530x y -+=【解析】【分析】利用导数的几何意义即得.【详解】由123x y x -=+，得22(23)2(1)5(23)(23)x x y x x +--'==++，所以切线的斜率为255(23)k ==-+，所以所求的切线方程为(2)5[(1)]y x --=--，即530x y -+=.故答案为：530x y -+=.15. 已知π4sin 35α⎛⎫+= ⎪⎝⎭，则πsin 26α⎛⎫+= ⎪⎝⎭___________.【答案】725##0.28【解析】分析】利用倍角余弦公式求得2π7cos(2)325α+=-，由诱导公式π2πsin(2cos(263αα+=-+，即可求值.【详解】22ππ167cos(212sin 12332525αα⎛⎫+=-+=-⨯=- ⎪⎝⎭，而πππ2π7sin(2cos(2)cos(2)662325ααα+=-++=-+=.故答案为：72516. 已知函数()sin 3f x x πω⎛⎫=+ ⎪⎝⎭(ω>0)，若()f x 在20,3π⎡⎤⎢⎥⎣⎦上恰有两个零点，且在,424ππ⎡⎤-⎢⎥⎣⎦上单调递增，则ω的取值范围是________.【答案】510,23⎡⎤⎢⎥⎣⎦【解析】【分析】由()f x 在20,3π⎡⎤⎢⎥⎣⎦上恰有两个零点，令3x k πωπ+=，Z k ∈，可得52338233ππωππω⎧≤⎪⎪⎨⎪>⎪⎩，令22232k x k ππππωπ-+≤+≤+，Z k ∈，可得f (x )在5,66ππωω⎡⎤-⎢⎥⎣⎦上单调递增，从而有5646240ππωππωω⎧-≤-⎪⎪⎪≥⎨⎪>⎪⎪⎩，联立求解即可得答案.【详解】解：由题意，令3x k πωπ+=，Z k ∈，得x ＝33k ππω-，Z k ∈，∴f (x )的第2个、第3个正零点分别为53πω，83πω，【∴52338233ππωππω⎧≤⎪⎪⎨⎪>⎪⎩，解得542ω≤<，令22232k x k ππππωπ-+≤+≤+，Z k ∈，∴52266k k x ππππωωωω-+≤≤+，Z k ∈，令k ＝0，f (x )在5,66ππωω⎡⎤-⎢⎥⎣⎦上单调递增，∴5,,42466ππππωω⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦，∴5646240ππωππωω⎧-≤-⎪⎪⎪≥⎨⎪>⎪⎪⎩，解得1003ω<≤，综上，ω的取值范围是51023ω≤≤.故答案为：510,23⎡⎤⎢⎥⎣⎦.三、解答题（共70分）（一）必考题（共60分）17. 在锐角ABC 中，内角,,A B C 所对的边分别为,,a b c，已知sin sin ,2A Ca b A b +==.（1）求角B 的大小；（2）求2a c -的取值范围.【答案】（1）3π（2）()0,6【解析】【分析】（1）结合A C B π+=-，以及诱导公式、二倍角公式、正弦定理化简原式，即得解；（2）利用正弦定理，辅助角公式可化简26a c A π⎛⎫-=-⎪⎝⎭，结合A 的范围即得解【小问1详解】A CB π+=- ，sinsin 2B a b A π-∴=cos sin 2B a b A ∴=sin cos sin sin 2B A B A ∴=cos sin 2sin cos 222B B B B ∴==1sin 22B ∴=，又B 为锐角,263B B ππ∴==【小问2详解】由正弦定理4sin sin sin a b c A B C ====，214sin ,4sin 4sin 4sin 2sin 32a A c C A A A A A π⎫⎛⎫∴===-=+=+⎪ ⎪⎪⎝⎭⎭，128sin 2sin 6sin cos 2a c A A A A A A A ⎫∴-=--=-=-⎪⎪⎭6A π⎛⎫=- ⎪⎝⎭由锐角ABC ，故20,0232A C A πππ<<<=-<故(),sin ,20,6626A A a c πππ⎛⎛⎫<<∴-∈∴-∈ ⎪ ⎝⎭⎝.18. 已知等差数列{}n a 的前n 项和为n S ，2512a a +=，424S S =．（1）求n a 及n S ；（2）若11n n n n a b S S ++=⋅，求数列{}n b 的前n 项和n T ．【答案】（1）21n a n =-，2n S n =（2）()2111n T n =-+【解析】【分析】（1）设出等差数列的首项和公差，利用等差数列的通项公式、前n 项和公式得到关于首项和公差的方程组求出1a 和d ，进而求出n a 及n S ；（2）利用（1）求出n b ，再利用裂项抵消法进行求和.【小问1详解】设等差数列{}n a 的公差为d ，则11125124344(2)2a d a d a d +=⎧⎪⎨⨯+=+⎪⎩，解得112a d =⎧⎨=⎩，所以()12121n a n n =+-=-，()21212n n n S n n -⨯=⨯+=．【小问2详解】由（1）得：+121n a n =+，21(1)n S n +=+，则()()122221211111n n n n a n b S S n n n n +++===-⋅++，所以123n nT b b b b =+++⋅⋅⋅+()22222222111111122331114n n =-+-+-+⋅⋅-+⋅+()2111n =-+..19. 已知()2ex x a f x -=.（1）当1a =时，求曲线()y f x =在点()()0,0f 处的切线方程；（2）若()1f x x ≤-对[)1,x ∞∈+恒成立，求a 的取值范围.【答案】（1）10x y --=（2）1a ≥【解析】【分析】（1）利用导数的几何意义以及直线方程的点斜式即可求解.（2）分离参数a ，转化成不等式恒成立问题，利用导数求最值即可.【小问1详解】当1a =时，()21ex x f x -=，()01f =-，()22(1)ex x x f x --'=，(0)1k f '∴==，所以切线方程为：11(0)y x +=⨯-，即10x y --=.【小问2详解】()1f x x ≤-恒成立，即2(1)e x a x x ≥--在[)1,x ∞∈+上恒成立，设2()(1)e x g x x x =--，()(2e )x g x x '=-，令()0g x '=，得120,ln 2x x ==，在[)1,+∞上，()0g x '<，所以函数2()(1)e x g x x x =--在[)1,+∞上单调递减，所以max ()(1)1g x g ==，max ()a g x ∴≥，故有1a ≥.20. 2022年2月4日北京冬奥运会正式开幕，“冰墩墩”作为冬奥会的吉祥物之一，受到各国运动员的“追捧”，成为新晋“网红”，尤其在我国，广大网友纷纷倡导“一户一墩”，为了了解人们对“冰墩墩”需求量，某电商平台采用预售的方式，预售时间段为2022年2月5日至2022年2月20日，该电商平台统计了2月5日至2月9日的相关数据，这5天的第x 天到该电商平台参与预售的人数y （单位：万人）的数据如下表：日期2月5日2月6日2月7日2月8日2月9日第x 天12345人数y （单位：万人）4556646872（1）依据表中的统计数据，请判断该电商平台的第x 天与到该电商平台参与预售的人数y （单位：万人）是否具有较高的线性相关程度？（参考：若0.300.75r <<，则线性相关程度一般，若0.75r ≥，则线性相关程度较高，计算r 时精确度为0.01）（2）求参与预售人数y 与预售的第x 天的线性回归方程；用样本估计总体，请预测2022年2月20日该电商平台的预售人数（单位：万人）.参考数据：()()()55211460, 6.78i i i i i y y x x y y ==-=--=≈∑∑，附：相关系数()()()121ˆˆˆ,n i i i n i i x x y y r b ay bx x x ==--===--∑∑【答案】（1）具有较高的线性相关程度（2）ˆ 6.641.2yx =+，146.8万人【解析】【分析】（1）根据已知数据计算出相关系数r 可得；（2）由已知数据求出回归方程的系数得回归方程，然后在回归方程中令16x =代入计算可得估计值．【小问1详解】由表中数据可得1234545566468723,6155x y ++++++++====，所以()52110i i x x =-=∑又()()()55211460,66i i i i i y y x x y y ==-=--=∑∑所以0.970.75nx x y y r --==≈>所以该电商平台的第x 天与到该电商平台参与预售的人数y （单位：万人）具有较高的线性相关程度即可用线性回归模型拟合人数y 与天数x 之间的关系.【小问2详解】由表中数据可得()()()12166ˆ 6.610ni ii n i i x x y y b x x ==--===-∑∑则ˆˆ61 6.6341.2a y bx=-=-⨯=所以ˆ 6.641.2yx =+令16x =，可得ˆ 6.61641.2146.8y=⨯+=（万人）故预测2022年2月20日该电商平台预售人数146.8万人21. 已知()()2e 2ln x f x x a x x =-+（1）当e a =时，求()f x 的单调性；（2）讨论()f x 的零点个数．【答案】（1）()f x 在()0,1上单调递减，在()1,+∞上单调递增； （2）当0e ≤<a ，0个零点；当e a =或a<0，1个零点；e a >，2个零点【解析】【分析】（1）求出函数的导函数()()e 2e x f x x x x ⎛⎫'=+- ⎪⎝⎭，可得()10f '=，令()e e x g x x x =-，利用导数说明()g x 的单调性，即可求出()f x 的单调区间；（2）依题意可得()()2ln e 2ln 0x x f x a x x +=-+=，令2ln t x x =+，则问题转化为e t at =，R t ∈，利用零点存在定理结合单调性可判断方程的解的个数.【小问1详解】解：因为e a =，0x >，()()2e e 2ln x f x x x x =-+所以()()()()()2e 22e 2e e 12e 2e x x x x f x x x x x x x x x x +⎛⎫⎛⎫'=+-+=+-=+- ⎪ ⎪⎝⎭⎝⎭，()10f '=令()e e xg x x x =-，()()2e 1e 0x g x x x '=++>，所以()g x 在()0,+∞单增，且()10g =，当()0,1∈x 时()e e 0x g x x x =-<，当()1,x ∈+∞时()e e 0x g x x x =->，所以当()0,1∈x 时()0f x ¢<，当()1,x ∈+∞时()0f x ¢>，所以()f x 在()0,1单调递减，在()1,+∞单调递增【小问2详解】解：因为()()()2ln 2ln e e 2ln e 2ln 0x x x x f x a x x a x x +=⋅-+=-+=令2ln t x x =+，易知2ln t x x =+在()0,+∞上单调递增，且R t ∈，故()f x 零点转化为()()2ln e 2ln e 0x x t f x a x x at +=-+=-=即e t at =，R t ∈，的设()e t g t at =-，则()e tg t a '=-，当0a =时，()e tg t =无零点；当a<0时，()e 0t g t a '=->，故()g t 为R 上的增函数，而()010g =>，11e 10a g a ⎛⎫=-< ⎪⎝⎭，故()g t 在R 上有且只有一个零点；当0a >时，若(),ln t a ∈-∞，则()0g t '<；()ln ,t a ∈+∞，则()0g t '>；故()()()min ln 1ln g t g a a a ==-，若e a =，则()min 0g t =，故()g t 在R 上有且只有一个零点；若0e a <<，则()min 0g t >，故()g t 在R 上无零点；若e a >，则()min 0g t <，此时ln 1a >，而()010g =>，()()22ln 2ln 2ln g a a a a a a a =-=-，设()2ln h a a a =-，e a >，则()20a h a a-'=>，故()h a 在()e,+∞上为增函数，故()()e e 20h a h >=->即()2ln 0g a >，故此时()g t 在R 上有且只有两个不同的零点；综上：当0e ≤<a 时，0个零点；当e a =或a<0时，1个零点；e a >时，2个零点；【点睛】思路点睛：导数背景下的零点问题，注意利用零点存在定理结合函数单调性来讨论.（二）选考题（10分）请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.选修4-4：坐标系与参数方程22. 已知曲线1C 的参数方程为e e e e t tt t x y --⎧=+⎨=-⎩（t 为参数），以直角坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系．曲线2C 的极坐标方程4cos ρθ=.（1）求1C 的极坐标方程；（2）若曲线π(0)6θρ=>与曲线1C 、曲线2C 分别交于两点A ，B ，点(40)P ， ，求△PAB 的面积.【答案】（1）24ππ(cos 244ρθθ=-<<（2）【解析】【分析】（1）将1C 的参数方程化为普通方程，再根据极坐标与直角坐标的转化公式即可得答案;（2）联立方程，分别求得点A ，B 的极坐标，根据三角形面积公式即可求得答案.【小问1详解】由e e e et tt t x y --⎧=+⎨=-⎩消去参数t ，得224x y -=,因为e e 2t t -+≥，所以曲线1C 的直角坐标方程为224(2)x y x -=≥，因为cos sin x y ρθρθ=⎧⎨=⎩，所以曲线1C 的极坐标方程为24ππ()cos 244ρθθ=-<< ；【小问2详解】由2π64cos2θρθ⎧=⎪⎪⎨⎪=⎪⎩得:A ρ=所以曲线π(0)6θρ=>与曲线1C 交于点A π)6，由π64cos θρθ⎧=⎪⎨⎪=⎩,得:B ρ=， 所以曲线π(0)6θρ=>与曲线2C :4cos ρθ=交于点B π6，则PAB S =△PA PBS S -△O △O 1π4()sin 26B A ρρ=⨯⨯-=选修4-5：不等式选讲23. 己知函数()221f x x a x a =+++-．（1）当0a =时，求不等式()2f x ≥的解集；（2）若对于任意x ∈R ，都有()2f x ≥，求实数a 的取值范围．【答案】（1）()1,1,3⎡⎫-∞-⋃+∞⎪⎢⎣⎭（2）32a ≤-或1a ≥．【解析】【分析】（1）分0x ≥，102x -≤<，12x <-三种情况打开绝对值，求解即可；（2）打开绝对值，将函数()f x 写成分段函数，结合单调性求解即可【小问1详解】()21f x x x=++当0x ≥时，()312f x x =+≥，解得13x ≥，当102x -≤<时，()12f x x =+≥，解得x ∈∅，当12x <-时，()312f x x =--≥，解得1x ≤-，所以不等式()2f x >的解集为()1,1,3⎡⎫-∞-⋃+∞⎪⎢⎣⎭．【小问2详解】因为222172()12148(0222a a a a a +++++--==>，故212a a +>-所以()2222231,11,2131,2x a a x a a f x x a a x a a x a a x ⎧⎪++-≥⎪+⎪=+++-≤<⎨⎪+⎪---+<-⎪⎩所以函数()f x 在1,2a +⎛⎤-∞- ⎥⎝⎦上递减，在1,2a +⎡⎫-+∞⎪⎢⎣⎭上递增，所以函数()f x 在R 上的最小值为21122a a f a ++⎛⎫-=+ ⎪⎝⎭．所以2122a a ++≥，即223(23)(1)0a a a a +-=+-≥解得32a ≤-或1a ≥。
河北省唐山市届高三下学期第二次模拟考试数学(文)试题
河北省唐山市2011—2012学年度高三年级第二次模拟考试数学（文）试题说明：一、本试卷共4页,包括三道大题，24道小题，共150分,其中1．～(21)小题为必做题，（22)～（24)小题为选做题．二、答题前请仔细阅读答题卡上的“注意事项”，按照“注意事项"的规定答题．三、做选择题时，每小题选出答案后,用2B 铅笔把答题卡上对应题目的标号涂黑．如需改动，用橡皮将原选涂答案擦干净后，再选涂其他答案，四、考试结束后，将本试卷与原答题卡一并交回, 参考公式：样本数据n x xx ,,,21的标准差；x x x x x x x ns n 其中],)()()[(122221-+-+-=为样本平均数; 柱体体积公式：为底面面积其中S Sh V ,=、h 为高； 锥体体积公式:h S Sh V ,,31为底面面积其中=为高;球的表面积、体积公式：,34,432R V RS ππ==其中R 为球的半径。
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中,有且只有一项符合题目要求．1．已知1zi-=2+i ，则复数z 的共轭复数为A ．3+iB ．3-iC ．-3-iD ．—3+i2．己知集合A=｛l ，2，3)，集合B=（2，3，4），则A()N C B =A ．｛l ｝B ．f0，1}C ．｛1,2，3｝D ．（2,3,4）3．己知命题p ：“a>b”是“2a >2b ”的充要条件；q ：x ∃∈R，lx+l l≤x，则A ．⌝p ∨q 为真命题B ．p ∨q 为真命题C ．p ∧q 为真命题D ．p ∧⌝q 为假命题4．已知α是第三象限的角，且tan α=2，则sin(α+4π）=A ．1010-B ．1010C ．31010-D ．310105．设变量x 、y满足1,0,220,x y x y x y +≥⎧⎪-≥⎨⎪--≥⎩则目标函数z=2x+y 的最小值为A ．32B ．2C ．4D ．66．把函数y=sin （2x —6π)的图象向左平移6π个单位后，所得函数图象的一条对称轴为A ．x=0B ．x=2π C ．x=6π D ．x=—12π7．执行如图所示的算法，若输出的结果y≥2，则输入的x 满足A ．x≥4B ．x≤-lC ．—1≤x≤4D ．x≤一l 或x≥48．已知某几何体的三视图如图所示，则其体积为 A ．2 B ．lC ．43D ．539．曲线y=11x x -+在点（0，一1）处的切线与两坐标轴围成的封闭图形的面积为A ．1B ．－12C ．43D ．1810．奇函数f （x ）、偶函数g （x ）的图象分别如图1、2所示，方程f （g(x)）=0、g （f(x ））=0 的实根个数分别为a 、b ，则a+b=A ．3B ．7C．10D ．1411．直线l 与双曲线C ：22221(0,0)x y a b a b-=>>交于A 、B 两点，M 是线段AB 的中 点,若l 与OM （O 是原点)的斜率的乘积等于1，则此双曲线的离心率为A ．2B 2C ．3D 312．把一个皮球放入如图所示的由8根长均为20 cm 的铁丝接成的四棱锥形骨架内，使皮球的表面与8根铁丝都有接触点,则皮球的半径为A ．3B ．10 cmC ．2cmD ．30cm二、填空题：本大题共4小题，每小题5分，共20分13．函数y=1102x-的定义域为 .14．向圆（x 一2)2+（y —23=4内随机掷一点，则该点落在x 轴下方的概率为 。
安徽省合肥市2021届高三二模数学试题及答案(文科)
2021年安徽省合肥市高考数学第二次教学质量检测试卷（文科）一、选择题（每小题5分）.1．复数（i是虚数单位）的模等于（）A．2B．2C．D．2．已知A＝{x|x2＜4x}，B＝{x|y＝lg（x﹣2）}，则A∩B＝（）A．（0，2]B．（﹣∞，2]C．（2，+∞）D．（2，4）3．下列双曲线中，焦点在y轴上，且渐近线互相垂直的是（）A．x2﹣y2＝﹣4B．﹣y2＝1C．﹣x2＝1D．x2﹣y2＝14．声强级（单位：dB）由公式L I＝10lg给出，其中I为声强（单位：W/m2）．某班级为规范同学在公共场所说话的文明礼仪，开展了“不敢高声语，恐惊读书人”主题活动，要求课下同学之间交流时，每人的声强级不超过40dB．现已知4位同学课间交流时，每人的声强分别为10﹣7W/m2，2×10﹣9W/m2，5×10﹣10W/m2，9×10﹣11W/m2，则这4人中达到班级要求的有（）A．1人B．2人C．3人D．4人5．设正项等比数列{a n}的前n项和为S n，若a2a6＝16，2S3＝a2+a3+a4，则a1＝（）A．B．2C．D．46．秦九韶是我国南宋时期的数学家，他在所著《数书九章》中提出的多项式求值算法，至今仍是比较先进的算法．如图是秦九韶算法的一个程序框图，执行该程序框图，若输入x ＝a，n＝2，输出s＝26，则输入的实数a的值为（）A．﹣4或﹣3B．﹣3或4C．﹣4或3D．3或47．设抛物线C：y2＝4x的焦点为F，点A是抛物线C的准线与x轴的交点．若抛物线C上的点M满足|MA|＝|MF|，则|MF|＝（）A．B．2C．2D．48．函数f（x）＝的图象大致是（）A．B．C．D．9．在文明城市创建过程中，某市创建办公室对市区内从事小吃、衣帽、果蔬、玩具等6类商户数进行了统计并绘成如图所示的条形统计图，对商户进行了文明城市知识教育培训．2021年初，该市创建办公室计划从2000户商户中，按照商户类型进行分层抽样，随机抽取100户进行文明城市知识教育培训效果调查，则衣帽类和果蔬类商户抽取的户数分别为（）A．50，15B．50，30C．30，25D．25，1510．若a，b是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（）A．若a⊥b，b⊥α，α⊥β，则a⊥βB．若α⊥β，a⊥α，b∥β，则a⊥bC．若a∥α，a∥β，α∩β＝b，则a∥bD．若a∥b，a⊥α，b∥β，则α∥β11．如图，在△ABC中，D，E是AB边上两点，，且△BDM，△EDM，△AEM，△ACM的面积成等差数列．若在△ABC内随机取一点，则该点取自△AEM的概率是（）A．B．C．D．12．在《通用技术》课上，某小组同学准备用一个棱长为6的正四面体坯料制作一个正三棱柱模型（其底面在正四面体一个面上），要求削去的材料尽可能少，则所制作的正三棱柱模型的高为（）A．B．C．4D．2二、填空题（共4小题）.13．已知向量＝（x，1），＝（1，﹣2），且⊥，则|﹣|＝．14．若直线l：y＝kx与圆C：（x﹣2）2+y2＝3相交，则实数k的取值范围是．15．已知函数f（x）＝lnx，g（x）＝xlnx．若当x∈（0，+∞）时，f（x）≤kx+b≤g（x）恒成立，则实数k﹣b的值等于．16．如图数表，它的第一行数由正整数从小到大排列得到，此后下一行数由前一行每两个相邻的数的和写在这两个数正中间下方得到．依此类推，则该数表中，第n行第1个数是．三、解答题：本大题共5小题，满分60分．解答应写出文说明、证明过程或演算步骤。
2021届江西省南昌市高三二模文科数学试题扫描版附答案
NCS20210607项目第二次模拟测试卷「’ 文科数学木试卷共4页，23小题，满分150分.考试时间120分钟.注意事项：1. 答卷前，考生务必将自己的姓名、准•考证号填涂在答题卡上.并在相应位置贴好条形码.2•作答选择题时.选出每小題答案后，用2B铅笔把答题卡上对应题目的答案信息涂黑：如需改动，用橡皮擦干净后•再选涂其它答案.3•非选择题必须用黑色水笔作答，答案必须写在答题卡各题目指定区域内相应位置上：如需改动，先划掉原来答案，然后再写上新答案，不准使用铅笔和涂改液•不按以上要求作答无效.4•考生必须保证答题卡整洁.考试结束后，将试卷和答题卡一并交回.选择番本题共12小题，每小题5分，共60分•在每小题给出的四个选项中，只有一项是符合题目要求的.1. 复数Z = l + V3i，则z2在复平面上所对应的点在A・第一彖限B・第二象限 C.第三象限 D.第四象限2. 己知集合/ = {(XJ)|(X + y + l)(2x_y + l) = 0},则集合/中元素个数是A.0个B.1个C.2个D无数个’3. 从编号依次为01,02,…，20的20人中选取5人，现从随机数表的第一行第3列和第4列数字开始,由左向右依次选取两个数字，则_______________________________5308 3395 5502^ 6215 2702 4369 3218826^ 099£_7846_i充莎刁?莎乙丽巧両亍9527 _肓匕_药方_而厂'A709B^of C^l'5 D. 184. 在平面直角坐标系x®中，若点/与点8(2,1)关于直线y = x对称，则血乙46等于A.15. 己知/⑴二竺二1，则5+勺=：0"是“/(州)+ /(兀)二0”的e” + 1A・充分不必要条件B.必要不充分条件C.充要条件D.坯不充分也不必要条件6 •函数/(x) = sin伽+讣⑺＞0)部分图象如图所示, 若厶ABC的面积为?则血二7. 己知F是抛物线y2=4x的焦点，P是抛物线上的一个动点, 值为A. 2 + 275B. 4 +亦C. 3 + V?8. 直线l:y = k(x±2)上存在两个不同点到原点距离等丁1,则斤的取值范围是D.2龙川3,1),则AJPF周长的最小D・6+7勺A. (-2,2)B. (-73,73) 'C. (-1J)—高三文科数学（模拟二）第2页（共4页）一B9.已知/（x ） = F" ，"（（）」），若/（x ）= 1有两解，则a 的取值范圈是 log, AXE [L2） -A. （0,—）B.（0,才C.（1,2]D.（1,2）10・如图是默默无"蚊”的广告创意图，图中网格是单位正方形，阴影部分由若干个牡两迈首尾相连组成的图形.最外层的半圆弧与矩形相切• 从矩形屮任取一点，则落在阴影部分的概率是 TCB. 3rr28A.C.5TID ・71567H •如图，正四棱锥P —ABCD 的高为12, AB = 6近• 分别为PA 、PC 的中点，过点B.E.F二.填空题：本题共4小题，每小题5分■共20分.13. 已知7 = （—1、2）,乙=（3,—1）,则与a-b 同方向的单位向疑足 ________ • Y 2 1 14. 若曲线y = J — 在X = 处的切线的斜率为三，则勺二 ______________ ・‘ 4 215. 四面体 A BCD 中，Z.ABC = Z.BCD = 90°, AB = BC = CD = 2,AD= 2^3，则该四面体的 外接球表面积为 ________ •16. 如图，平面凹四边形A BCD ,其中力〃 =5, BC = &ZMBC = 60°, AZ.ADC = 120°则四边形A BCD 血积的最小值为―__・12. 将双曲线绕其对称中心旋转，会得到我们熟悉的函数图彖，例如将双曲线--^1 = 1的图象22绕原点逆时针旋转45°后，能得到反比例函数尹=丄的图象x（其渐近线分别为X 轴和y 轴）：同样的，如图所示，常见 的“对勾函数° =加：+巴（加> 0〃 > 0）也能由双曲线的x 图象绕原点旋转得到（其渐近线分别为『=加兀和y 轴）・ 设m 二写小二屈・则此“对勾函数”所对应的双曲线的实轴长为A.価B. 4C. 2&D. 2^7的截面交PD 于点A/ , 将四棱锥分成上下两个部分, 规定丽为主视图方向，则几何体CDAB — FME 的俯视图为A B三.解答题：共70分.解答应写出文•字说明、证明过程或演算步骤.第17il21题为必考题，每个试题考生都必须作答；第22. 23题为选考题.考生根据要求作答.（一）必考题：共60分.17. （12 分〉己知数列何｝中，=2,a2=l（we N*）.（1 ）求鸟，兔的值；（H）求｛%｝的前2021项和S?⑵.18. （12分）春节期间，防疫常态化要求减少人员聚集，某商场为了应对防疫要求，但又不影响群众购物.采取推广使用••某某到家'•线上购物APP,再由物流人员送货到家.下左图为从某区随机抽取100位年龄在卩0,70）的人口年龄段的频率分布直方图，下右图是该样本中使用了柱某某到家"线上购物APP人数占抽取总人数比的频率柱状图•（1 ）从年龄段在［60,70）的样本中，随机抽取两人•估计都不使用••某某到家"线上购物APP的概率；：U1）若把年龄低于40岁（不含）的人称为^青年人S为确定是否有99.9%的把握认为••青年人” 更愿童使用"某某到家"线上购物APP,填写下列2x2联表，并作出判断.参考数据:-bc\（a 4 6）（c + 〃）（a + c）（b + 〃）其中n-a^b^c^d・19. (12分)如图，菱形ABCD 的边长为6,对角线交于点E, ZABC =芒~,将△/4DC 沿FC 折起得到三棱锥D - ABC ，点D 在底面ABC 的投影为点O ・20. (12分)已知椭圆E:-^- + ^- = l(a>6>0)的离心率,椭圆£与“轴交干人B 两点, 与夕轴交于C,D 两点，四边形ACBD 的面积为4.(I )求椭圆E 的方程；(H)若P 是椭圆E 上一点(不在坐标轴上)，直线PC.PD 分别与乂轴相交于两点，设 PC,PD,OP 的斜率分别为人也扎,过点P 的直线/的斜率为且k& = kk 、,直线/与x 轴 交于点Q,求|M0 — |N0|的值.21. (】2分)已知函数f(x) = e\g(x) = x 9直线y = a(a> 0)分别与函数y = f(x).y = g(x)的 图象交于儿B 两点，O 为坐标原点. (I )求I FBI 长度的最小值；(H)求最大整数使得k<OA OB 对*(0,xo)恒成立.(二)选考题：共10分请考生在第22. 23题中任选一题作答.如果多做，则按所做的第一题计分. 22. (10分)选修4-4：坐标系与参数方程x = 2 cos 0r-在直角坐标系xOr 中，曲线G 的参数方程为彳 — a(。
2020-2021学年度安徽省淮北市高三第二次模拟数学文科试题及答案
高三第二次模拟考试数学（文科）试卷一、选 择 题（每 小 题 5 分，共 12 小 题，满 分 60 分） 1．已知集合 A {2, 1,1, 2}， B x x2 2 ，则 A B （）A.{1, 2, 2} B.{1,1} C.{2, 2}D.{2, 1,1, 2}2.复数 z(1 i) i ,则 z 为（ ） A. 2 B.1 C. 2D. 1223. 已知 ABC 是边长为 2 的正三角形，在 ABC 内任取一点，则该点落在 ABC 内切圆内的概率是（）A. 3 6B. 3 3C.1 3 6D. 3 94.已 知F1, F2 是双曲 线C:x2 a2y2 b2 1(a 0, b 0) 的左右焦点，F1 坐标 (7, 0) ，双 曲 线右支上 一点 P ，满足 PF1 PF2 4，则 它 的 渐 近 线 方 程 为（ ）A. y 3 x 2B. y 2 3 x 3C. y 3 x 4D. y 4 x 35.⟪九章算术⟪是中国古代数学名著，体现了古代劳动人民数学的智慧，其中第六章“均输”中，有一竹节容量问题，根据这一问题的思想设计了如下所示的程序框图，若输出的 m 的值为 35，则输入的 a 的值为（ ）A.4B.5C.7D.116.如图，在正方体 ABCD A1B1C1D1 中， P 为 BD1 的中点，则 PAC 在该正方体各个面上的正投影可能是（）A.①②B. ②④C.②③D.①④x 07.若 x, y 满足约束条件 xy30，则zx2y的最大值为（）x 2 y 0A.3B.4C.5D.6 8.已知等差数列 an 的 公 差 为 d ，前 n 项和为 Sn ，则“ d 0 ”是“ S2 S4 2S3 ”的（ ）A.充分不必要条件 B.必要不充分条件 C. 既不充分也不必要条件 D.充要条件 9.已知函数 f (x) 是定义在 R 上的奇函数，且在区间 ,0 上单调递增，若实数 a 满足 f 2log3 a f 2 ，则 a 的取值范围是（ ）A. ( 3, )B. (1, 3)C. (0, 3) D. (, 3)10.将函数 f (x) 2sin x cos x 2 3 cos2 x 的图像向右平移 个单位长度后，得到函数 g(x) 的图像，则函6 数 g(x) 的图像的一个对称中心是( )A. ( , 3) B. ( , 3)34C. ( , 3) D. ( , 3)122 11. 已知函数 fx1 5x 1( x1)则方程f(x)kx恰有两个不同的实根时，实数 k的取值范围ln x(x 1)是（ ）A. (0, 1) eB. (0, 1) 5C.1 5,1) eD. 1 5,1 e 12.设 F是椭圆 C:x2 a2y2 b2 1(ab 0) 的一个焦点， P 是 C 上的 点，圆x2 y2 a2 与 直 9线PF 交 于 A, B 两 点，若 A, B 是 线 段 PF 的 两 个三 等 分 点，则 C 的 离 心 率 为（ ）A. 3 3B. 5 3C. 10 4D. 17 5二、填空题（每小题 5 分，共 4 小题，满分 20 分）rrr r r rr13.已知向量 a (1, 2),b (m, 1) ，若 a / /(a b) ，则 agb =_____________14. 已 知 定 义 在 R 上 的 函 数 f (x) 满 足 f (x 2) 1 ， 当 x 0, 2时，f (x) x ex ， 则f (x) f (2018) _____________15.三棱锥 P ABC 中，已知 PA 底面 ABC ，BAC 600, PA 4 , AB AC 2 ,若三棱锥的所有顶点3都在同一个球面上，则该球的体积为_____________ 16.已知等比数列 an 的前 n 项和为 Sn n N ,且 a2 a1 ， S4 a1 28, a3 2 是 a2 , a4 的等差中项，若数列 an1 Sn Sn1 的前n项和Tn M 恒成立，则 M 的最小值为___________三、解答题（共 6 小题，满分 70 分）17.（本题满分 12 分）已知 a,b, c 分别是 ABC 三个内角 A, B,C 所对的边，且 sin2 B 5 cosB 2 2（Ⅰ）求角 B 的大小. （Ⅱ）已知 b 2 ，求 ABC 面积的最大值.18. （本题满分 12 分）如图，在三棱锥 S ABC 中，侧面 SAB 与侧面 SAC 均为边长为 2 的等边三角形， BAC 90°， O 为 BC 中点． （Ⅰ）证明： AC SO ； （Ⅱ）求点 C 到平面 SAB 的距离．A19．（本题满分 12 分）我国自改革开放以来，生活越来越好，肥胖问题也日渐显著，为分析肥胖程度对总胆固醇与空腹血糖的影响, 在肥胖人群中随机抽出 8 人,他们的肥胖指数值、总胆固醇腹血糖指标值（单位：）如下表所示：指标值（单位：）、空人员编号值指标值指标值（Ⅰ）用变量 与 与 的相关系数, 分别说明 指标值与值、指标值与值的相关程度；（Ⅱ）求 与 的线性回归方程, 已知 指标值超过 为总胆固醇偏高, 据此模型分析当值达到多大时, 需要注意监控总胆固醇偏高情况的出现（上述数据均要精确到 ）.参考公式：相关系数nn (xi x)( yi y) (xi x)( yi y) r i 1nn(xi x)2 ( yi y)2b i1n(xi x)2，a y bxi 1i 1i 1参考数据： 8282828x 33, y 6, z 8, (xi x) 244, ( yi y) 3.66, (zi z) 5.4, (xi x) yi y 28.3,i1i1i1i 1 8 (xi x) zi z 35.4, 244 15.6, 3.6 1.9, 5.4 2.3 ,i 120．（本题满分 12 分）已知抛物线 C 的顶点在原点，焦点在 y 轴上，且抛物线上有一点 P(m,5) 到焦点的距离为 6. （Ⅰ）求该抛物线 C 的方程； （Ⅱ）已知抛物线上一点 M (4, t) ，过点 M 作抛物线的两条弦 MD 和 ME ，且 MD ME ，判断直线 DE是否过定点，并说明理由.21.（本小题满分 12 分）已知函数 f (x) ln(x 1) a x a R ．（Ⅰ）讨论函数 f (x) 的单调性；（Ⅱ）当 x 1时，设 g(x) f (x 1), h(x) ln x x 1，满足g(x)h(x) 恒成立，求 a 的取值范围．四、选做题请考生在 22,23 三题中任选一题做答，如果多做，则按所做的第一题记分.做答时用 2B 铅笔在答题卡把所选题目的题号涂黑. 22．（本小题满分 10 分）选修 4－4：坐标系与参数方程已知直线l 的参数方程： x y 1 t cos（ t sint为参数），曲线C的参数方程：x 3 cos（ y sin为 参 数），且 直 线 交 曲 线 C 于 A，B 两点．（Ⅰ）将 曲 线 C 的 参 数 方 程 化 为 普 通 方 程，并 求 时， AB 的 长 度；4（Ⅱ）已 知 点 P(1,0) ，求 当 直 线 倾 斜 角 变 化 时， PA PB 的 范 围．23．（本小题满分 10 分）选修 4－5：不等式选讲已知函数 f (x) x 2 x 1（Ⅰ）解不等式 f (x) x 0 .（Ⅱ ）若关于 x 的不等式 f (x) a2 2a 的解集为 R ，求实数 a 的取值范围.第二次模拟考试数学文科参考答案一.选择题1-5 B C D A A6-10 D B D A A11-12 C D二．填空题13 . 5 214.115.256 811 16. 2三. 解答题17.解（Ⅰ）Q ABC 中， sin2 B 5 cos B 2 21 cos2 B 5 cos B 2 即 cos2 B 5 cos B 1 022解得 cos B 2(舍)或cos B 1 2所以 B= --------6 分 3（Ⅱ）由（Ⅰ）知 B= ，Q b 2 3根据余弦定理得 b2 a2 c2 2ac cos B 代入得 a2 c2 ac 4 ，得 a2 c2 ac 4 2ac ，解得 ac 4 ，QSABC1 2ac sinB1 4 23 23所以 ABC 的面积最大值为 3 --------12 分18. 证 明 ：（ Ⅰ ） 由 题 设 AB= AC= SB= SC SA ， 连 结 OA ， △ABC 为 等 腰 直 角 三 角 形 ， 所 以OA OB OC 2 SA 2 ，且 AO BC ，----------2 分又 △SBC 为 等 腰 三 角 形 ， 故 SO BC ， 且SO 2 SA 2，从而 OA2 SO2 SA2 ．所以 △SOA 为直角三角形，又 AO I BO O ．所以 SO 平面 ABC 即 AC SO ---------5 分（Ⅱ）设 C 到平面 SAB 的距离为 d ，则由（Ⅰ）知：三棱锥VSABC VCSAB即1 3SABCSO1 3SSABd------7分∵ △ABC 为等腰直角三角形,且腰长为 2.SO AO ．∴ BC 2 2∴ SO SB2 OB2 4 2 2 ---------8 分∴△SAB的面积为SSAB=1 222sin603△ABC 面积为 SABC 2 , ∴ 223d,d26 326 ∴C 到平面 SAB 的距离为 3----------------12 分19．解（Ⅰ）变量 y 与 x 的相关系数分别是 r 28.3 0.95---------2 分 15.6 1.9变量 z 与 x 的相关系数分别是 r ' 35.4 0.99 ---------4 分 15.6 2.3可以看出TC 指标值与 BMI 值、 GLU 指标值与 BMI 值都是高度正相关.---------6 分 （Ⅱ） y 与 x 的线性回归方程, $y bx a .根据所给的数据, 可以计算出b 28.3 0.12, a 6 0.12 33 2.04 ---------8 分 244所以 y 与 x 的回归方程是 $y 0.12x 2.04 ---------10 分由 0.12x 2.04 5.2,可得 x 26.33, 据此模型分析 BMI 值达到 26.33时, 需要注意监控总胆固醇偏高情况出现.---------12 分20.解：由题意设抛物线方程为x22 py，其准线方程为yp 2，Q P(m,5) 到焦点的距离等于 P 到其准线的距离，5 p 6, p 2 2 所以抛物线方程为 x2 4 y --------4 分（2）由（1）可得点 M 4, 4 ，设直线 MD 的方程为： y k(x 4) 4 ，联立y k(x x24y4)4，得x24kx16k160，--------5分设 D x1, y1 , E x2, y2 ，则 xM x1 16k 16 ， x1 16k 16 4 4k4y1(4k 4)2 44(k 1)2同理可得 x24 k4y24( 1 k1)2 --------8 分4(k 1)2 4( 1 1)2所以直线 DE 的方程为 y 4(k 1)2 k (x 4k 4)4k 4 4 4k=(k1 k)(k1 k2)(x4k4)(k12)(x4k4)k 1kk化简的 y (k 1 2)x 4k 4 (k 1 2)(x 4) 8 --------11 分kkk∴直线 DE 过定点 4,8 --------12 分21．解：(I)因为 f (x) ln(x 1) a x ，所以定义域为 (1, )f / (x) 1 a 1 a(x 1) (x 0)x 1x 1所以（1）当 a 0 时， f / (x) 0 恒成立，所以 f (x) 在 0, 上单调递增。
安徽省潜山野寨中学2012届下学期高三第二次周考文科数学试题
俯视图侧视图正视图433图1第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题。
每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设全集R U =,=A (2){|21},{|ln(1)}x x x B x y x -<==-，则图中阴影部分表示的集合A ． {|1}x x ≥B ．{|12}x x ≤<C ．{|01}x x <≤D ．{|1}x x ≤2．已知,x y R ∈，为虚数单位，且1xi y i -=-+，则(1)x y i ++的值为 A ． 2 B ． 2i - C ． 4- D ． 2i3．如果执行如右图所示的程序框图，则输出的S 值为A ．3-B ．12-C ．2D ．134．设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π，且()()f x f x -=则A ． ()y f x =在3(,)44ππ单调递增B ． ()y f x =在(0,)2π单调递增C ． ()y f x =在3(,)44ππ单调递减D ． ()y f x =在(0,)2π单调递减 5．下列命题正确的个数（1）命题“0x ∃∈R ，20x +1>3x 0”的否定是“∀x ∈R ，x 2 +1<3x”：（2）函数f (x)= cos 2 ax －sin 2 ax 的最小正周期为π”是“a=l”的必要不充分条件。
（3）“x ∈[1,2]时x 2 +2x≥ax 恒成立”⇔ “（x 2+2x ）min ≥（ax ）max 在x ∈[l ，2]上恒成立”；（4）“平面向量a 与b 的夹角是钝角”的充分必要条件是“a ·b <0”。
A ． l B ．2 C ．3 D ． 46．已知四棱锥P ABCD -的三视图如右图1所示，则四棱锥P ABCD -的四个侧面中的最大面积是A ．6B ．8C． D ． 37．若直线y kx =与圆22(2)1x y -+=的两个交点关于直线20x y b ++=对称，则,k b 的值分别为A ． 1,42k b ==- B ． 1,42k b =-= C ． 1,42k b == D ． 1,42k b =-=- 8．已知等比数列{}n a 满足0,1,2,n a n >= ，且25252(3)n n a a n -⋅=≥，则当1n ≥时，2123221log log log n a a a -+++=A ．(21)n n -B ．2(1)n +C ．2nD ．2(1)n -9．如图，PAB ∆所在的平面α 和四边形ABCD 所在的平面β互相垂直，且 ,AD B C αα⊥⊥，4AD =， 8BC =，6A B =,若tan 2tan 10ADP BCP ∠+∠=，则点P 在平面α内的轨迹是A ．圆的一部分B ．椭圆的一部分C ．双曲线的一部分D ．抛物线的一部分 10．椭圆221369x y +=上有两个动点P 、Q ，(3,0)E ，EP EQ ⊥，则 EP QP⋅ · EP QP 的最小值为 A ． 6 B ．3- C ． 9 D ．12-11．若曲线f （x ，y ）= 0上两个不同点处的切线重合，则称这条切线为曲线f （x ，y ）= 0的“自公切线”．下列方程：①221x y -=；②2||y x x =-，③3sin 4cos y x x =+；④||1x +=对应的曲线中存在“自公切线”的有A ．①②B ．②③C ．①④D ．③④12．将甲、乙、丙、丁、戊共五位同学分别保送到北大、上海交大和浙大3所大学，若每所大学至少保送1人，且甲不能被保送到北大，则不同的保送方案共有多少种?A ．150B ．114C ．100D ．72第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题5分，共20分．13．某产品的广告费用x 与销售额y 的统计数据如下表：β α P A B CD根据上表可得回归方程y bx a =+∧∧∧中的b ∧为7．据此模型预报广告费用为10万元时销售额为（万元）．14．设60sin (a xdx,π=⎰则二项式的展开式中的常数项等于 ． 15．已知实数x 、y 满足22224,2(1)(1)(0)y x x y y x y r r ≤⎧⎪+≤⎪⎨≥-⎪⎪++-=>⎩则r 的最小值为 ． 16．设数列{}n a 的各项均为正数，前n 项和为n S ，对于任意的n N +∈，2,,n n n a S a 成等差数列，设数列{}n b 的前n 项和为n T ，且2(ln )nn nx b a =，若对任意的实数(]1,x e ∈（e 是自然对数的底）和任意正整数n ，总有n T r <()r N +∈．则r 的最小值为．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）在锐角三角形ABC 中，a 、b 、c 分别是角A 、B 、C 2sin 0c A -=．（Ⅰ）求角C 的大小； （Ⅱ）若2c =，求a ＋b 的最大值．18．（本小题满分12分）从甲、乙两名运动员的若干次训练成绩中随机抽取6次，分别为甲：7.7, 7.8, 8.1, 8.6, 9.3,9.5．乙：7.6, 8.0, 8.2, 8.5, 9.2, 9.5。
山西省长治市第二中学2014届高三第二次练考数学(文)试题
高三二练文科数学试题 第 1 页 共 8 页山西省长治市第二中学2014届高三第二次练考数学试题（文）（满分150分，考试时间120分）一、选择题(5×12＝60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号)1.已知集合2{|log (1)}A x y x ==+,集合1{|(),0}2x B y y x ==>,则A B I =A ．(1,)+∞B ．(1,1)-C ．(0,)+∞D ．(0,1)2.下面是关于复数21z i=- 的四个命题 1p :2z =, 2:p 22z i = 3:p z 的共轭复数为1i -+ 4:p z 的虚部为1其中真命题为A. 23,p pB. 12,p pC. 24,p pD. 34,p p 3.下列命题正确的是A ．2000,230x R x x ∃∈++= B ．32,x N x x ∀∈> C ．21x >是1x >的必要不充分条件 D ．若a b >,则22a b > 4.下列函数在其定义域内,既是奇函数又存在零点的是A ．()1xf x e =- B ．1()f x x x -=- C.1()f x x x -=+ D ．()|sin |f x x =- 5.函数f (x )＝sin 2⎪⎭⎫ ⎝⎛4π＋x －sin 2⎪⎭⎫ ⎝⎛4π－x 是A ．周期为π的奇函数B ．周期为π的偶函数C ．周期为2π的偶函数D ．周期为2π的奇函数6.已知函数()f x =Acos(x ωϕ+)的图象如图所示，2()23f π=-，则(0)f = A. 23- B. 23 C. 12- D. 127.等差数列{}n a 的前n 项和为S n ，且132,12a S ==，高三二练文科数学试题 第 2 页 共 8 页则64n nS a +的最小值是 A ．7 B ．152 C ．8 D ． 1728.已知函数()()()2,0,0,a x f x a x b x+=>∈则下列判断正确的是A.当b > 时，()f x的最小值为B.当0b <≤时，()f x的最小值为C.当0b <≤时，()f x 的最小值为2a b b+；D.对任意的0b > 时，()f x的最小值均为9.在直角三角形ABC 中，2C π∠=，3AC =取点,D E ，使2,3BD DA AB BE ==那么CD CA CE CA ⋅+⋅=A ．3B ． 6C ． -3D -6，10.函数()2tan f x x x =-在(,)22ππ-上的图象大致为11.函数()f x 是定义在()0,+∞上的单调函数，且对任意的,x y 都有()()()f x y f x f y ⋅=+，若数列{}n a 的前项和为n s ，且满足()()()()*23n n f s f a f n N+-=∈，则na=A ．12n - B ． n C ．21n - D ． 132n -⎛⎫ ⎪⎝⎭高三二练文科数学试题 第 3 页 共 8 页12.已知定义在R 上的函数()f x 满足()()1f x f x +=-，当()1,1x ∈-时，()2f x x =，函数()()3lg 1121xo x x g x x ⎧->=⎨≤⎩为,那么函数()()()h x f x g x =-在区间[]5,5-上零点的个数为 A ．9 B ．8C ． 7D ．6二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的相应位置上)13. 若12,e e 是两个不共线的向量，已知1212122,3,2AB e ke CB e e CD e e =+=+=-，若A ，B ，D 三点共线，则k =14.已知y x ,满足⎪⎩⎪⎨⎧≥++-≤+≥0242c y x y x x ，且目标函数y x z +=3的最小值是5，则z 的最大值____.15.已知数列{}n a 中，()12121,2,23n n n a a a a a n --===+≥，则12360a a a a ++++= 16.在ABC ∆中，若060,A BC ==ABC ∆周长的最大值为三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤，并把解答写在答题纸的相应位置上) 17．（本小题满分10分）已知函数()25f x x x =--- （I ）证明：3()3f x -＃；（II ）求不等式2()815f x x x ?+的解集.18.(本小题满分12分)已知向量(sin ,cos ),,cos )m x x n x x == ，且函数()f x m n a =+（1）求函数()f x 的最小正周期和单调递减区间；(2）若函数()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值的和为32，求a 的值.高三二练文科数学试题 第 4 页 共 8 页19．(本小题满分12分)已知正项递增的等差数列{}n a ，n s 为数列{}n a 的前n 项和，若3s =12，且1232,,1a a a +成等比数列.（1）求{}n a 的通项公式； （2）令3nn n a c =，求数列{}n c 的前n 项和n T .20. (本小题满分12分)在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且22()(2a b c bc --=，2sin sin cos 2CA B =，BC 边上的中线AM. (1)求角A 和角B 的大小； (2)求ABC ∆的面积.21. (本小题满分12分)已知函数21()ln ()2a f x x ax x a R -=+- (1)当1a =时，求函数()f x 的极值.(2)当1a >时，讨论函数()f x 的单调性.（3）若对任意(3,4)a ∈及任意[]12,1,2x x ∈恒有212(1)ln 2()()2a m f x f x -+>-成立，求实数m 的取值范围.22. (本小题满分12分)椭圆)0(12222>>=+b a by a x 左右两焦点分别为21,F F ，且离心率36=e ；（1） 设E 是直线2+=x y 与椭圆的一个交点，求||||21EF EF +取最小值时椭圆的方程； （2） 已知)1,0(N ，是否存在斜率为k 的直线l 与（1）中的椭圆交与不同的两点B A ,，使得点N 在线段AB 的垂直平分线上，若存在，求出直线l 在y 轴上截距的范围；若不存在，说明理由.高三二练文科数学试题答案 第 5 页 共 8 页山西省长治市第二中学2014届高三第二次练考数学试题（文）参考答案一、选择题（每小题5分） 1-12 DCCBA BDAAC DB 二、填空题（每小题5分）13 -8 14 10 15 6021-1617．解答题解:（I ）3,2,()|2||5|27,25,3, 5.x f x x x x x x -≤⎧⎪=---=-<<⎨⎪≥⎩当25,327 3.x x <<-<-<时所以3() 3.f x -≤≤ ………………5分 （II ）由（I ）可知，当22,()815x f x x x ≤≥-+时的解集为空集；当225,()815{|55}x f x x x x x <<≥-+-≤<时的解集为； 当25,()815{|56}x f x x x x x ≥≥-+≤≤时的解集为.综上，不等式2()815{|56}.f x x x x x ≥-+-≤≤的解集为 …………10分 18.解：（1）1()sin(2)62f x x a π=+++，所以T π=， 函数()f x 的单调区间是2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦高三二练文科数学试题答案 第 6 页 共 8 页（2）5,2,636661sin(2)126x x x ππππππ-≤≤∴-≤+≤∴-≤+≤1113(1)()22220a a a ∴+++-++=∴=19.解：（1）31232212,12,312,4s a a a a a =++=\==即设数列{}n a 的公差为d （d >0）,由题意得，22132(1)a a a =+，22222()(1)a a d a d =-++ 得3d =或4()d =-舍，121a a d ∴=-=，所以32n a n =------------------------4分 （2）321(32),333n n n n n a n b n -===-所以 231111147(32),3333n n T n =⨯+⨯+⨯++-⨯ （1）2311111114(35)(32)33333n n n T n n +=⨯+⨯++-⨯+-⨯ ，（2） （1）-（2）：211121111511133(32)(32)333336233n n n n n T n n +-+=+⨯++⨯--⨯=-⨯--⨯所以5651443n n n T +=-⨯-----------------------------------------------------12分。
黑龙江省大庆市高三下学期第二次教学质量监测试题(二模)(4月) 数学(文)
高三年级第二次教学质量检测试题文科数学注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
第I 卷(选择题共60分)一、选择题：本大题共12小题，每小题5分满分60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知集合A ＝{x|x>2}，B ＝{0，1，2，3，4}，则A ∩B ＝ A.{3，4} B.{0，3，4} C.{0，1，2} D.{0}2.设i 是虚数单位，则复数z ＝2i(3－2i)对应的点在复平面内位于 A.第一象限 B.第二象限 C.第三象限 D.第四象限3.命题“∀x ∈R ，x 2－x ＋2021>0”的否定是A.∃x 0∈R ，x 02－x 0＋2021<0B.∀x ∈R ，x 2－x ＋2021≤0C.∀x ∈R ，x 2－x ＋2021<0D.∃x 0∈R ，x 02－x 0＋2021≤0 4.sincos1212ππ=A.12 B.143 35.已知直线l ：x ＋y ＋1＝0与圆C ：(x ＋1)2＋(y ＋2)2＝8相交于A ，B 两点，则弦AB 的长度为 6 2 6 26.已知m ，n ，l 是三条不同的直线，α，β是两个不同的平面，则下列判断不正确的是 A.若m ⊥α，n ⊂α，则m ⊥n 。
B.若m ，n 都与l 相交且m//n ，则直线m ，n ，l 共面。
C.若m ⊥α，n ⊥β，m//n ，则α//β。
D.若m ，n ，l 两两相交，且交于同一点，则直线m ，n ，l 共面。
7.已知向量a ＝(2，1)，b ＝(－1，x)，(2a ＋b )⊥a ，则x 的值为 A.－4 B.－8 C.4 D.88.日晷是我国古代按照日影测定时刻的仪器，晷长即为所测量影子的长度。
2021-2022年高三第二次数学模拟考试(文科)
2021年高三第二次数学模拟考试（文科）本试卷分第I卷（选择题）和第II卷（非选择题）两部分。
第I卷1至2页，第II卷3至4页，答题纸5至7页，共150分。
测试时间120分钟。
第I卷（共60分）一、选择题：（本大题共12小题。
每小题5分。
共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．设集合，则满足的集合B的个数为（）A．1 B．3 C．4 D．82．已知，其中是实数，是虚数单位，则（）A．B．C．D．3．已知，且，则（）A．B．C．D．4．设函数，则（）A．在区间内均有零点B．在区间内均无零点C．在区间内有零点，在区间内无零点D．在区间内无零点，在区间内有零点5．实数满足，则的值为（）A．8 B．C．0 D．106．设函数为定义在R上的奇函数，当时，（为常数），则（）A．3 B．1 C．D．7．如果若干个函数的图象经过平移后能够重合，则称这些函数为“互为生成函数”。
给出下列函数①；②；③；④其中“互为生成函数”的是（）A．①②B．①③C．③④D．②④8．在内，内角的对边分别是，若，，则A=（）A．B．C．D．9．已知是实数，则函数的图象不可能是（）10．设命题非零向量是的充要条件；命题“”是“”的充要条件，则（）A．为真命题B．为假命题C．为假命题D．为真命题11．已知二次函数，满足：对任意实数，都有，且当时，有成立，又，则为（）A．1 B．C．2 D．012．若，且，则下面结论正确的是（）A．B．C．D．第II卷（非选择题共90分）二、填空题：本大题共4个小题，每小题4分，共16分。
（将答案填在答题纸上）13．设曲线在点处的切线与直线平行，则.14．如果，那么= .15．在中，，则.16．O是平面上一点，点是平面上不共线的三点。
平面内的动点P满足，若，则·的值等于.三、解答题：本大题共6个小题，共74分。
解答应写出文字说明，证明过程或演算步骤。
（将答案写在答题纸上。
东北三省三校2021年高三第二次联合模拟文科数学试题Word版含解析
东北三省三校2021年高三第二次联合模拟文科数学试题一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A、B均为集合U＝{1，2，3，4，5，6}的子集，且（∁U A）∩B＝{3}，（∁U B）∩A＝{6}，A∩B ＝{1，2}，则集合B＝（）A．{1，2，3} B．{1，2，6} C．{1，2} D．{1，2，3，4，5}2．若a+2i＝（1﹣i）（1+bi）（a，b∈R，i为虚数单位），则复数a﹣bi在复平面内对应的点所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限3．若实数x、y满足，则y﹣x的最大值为（）A．3 B．0 C．﹣3 D．﹣94．已知α，β是两个不同的平面，直线m⊂α，下列命题中正确的是（）A．若α⊥β，则m∥βB．若α⊥β，则m⊥βC．若m∥β，则α∥βD．若m⊥β，则α⊥β5．课堂上数学老师和同学们做游戏，随机询问甲、乙、丙、丁4位同学的作业完成情况，甲说：“丙未完成作业或丁未完成作业”；乙说：“丁未完成作业”；丙说：“我完成作业了”；丁说：“我完成作业了”．他们中恰有一个人说了谎话，请问：是谁说了谎话？（）A．甲B．乙C．丙D．丁6．已知正项等比数列{a n}，若向量，则log2a1+log2a2+…+log2a9＝（）A．12 B．8+log25 C．5 D．187．我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中，积累了丰富的经验，总结出了一套有关体积、容积计算的方法，这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中．《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，如图所示的阳马三视图，则它的体积为（）A．B．1 C．2 D．38．已知两个不相等的非零向量，满足，且与的夹角为45°，则的取值范围是（）A．B．C．（0，2] D．9．已知，则sin（60°+α）的值为（）A．B．C．D．10．设函数f（x）＝sin x+cos x+sin x cos x+1，则下列说法中正确的是（）A．f（x）关于（0，1）中心对称B．f（x）的极小值为C．f（x）的最小正周期为πD．f（x）图象的一条对称轴为11．已知双曲线上存在一点M，过点M向圆x2+y2＝1做两条切线MA、MB，若，则实数a的取值范围是（）A．B．C．D．12．已知函数f（x）＝9（lnx）2+（a﹣3）•xlnx+3（3﹣a）x2有三个不同的零点x1，x2，x3，且x1＜1＜x2＜x3，则的值为（）A．81 B．﹣81 C．﹣9 D．9二、填空题：本题共4小题，每小题5分，共20分．把答案填写在答题纸相应位置上．13．我校高一、高二、高三共有学生1800名，为了了解同学们对“智慧课堂”的意见，计划采用分层抽样的方法，从这1800名学生中抽取一个容量为36的样本．若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数，则我校高三年级的学生人数为．14．已知实数a、c满足c＜1＜a，关于x的不等式的解集为．15．直线l经过抛物线y2＝2px（p＞0）的焦点F，与抛物线交于A，B两点，与直线交于点M，若，且，则抛物线的方程为．16．设△ABC的内角A、B、C所对的边分别为a、b、c，且（a+b+c）（a﹣b+c）＝3ac，则B＝；若边AC上的点D满足BD＝CD＝2AD＝2，则△ABC的面积S＝．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．（一）必考题：共60分．17．已知数列是公差不为0的等差数列，且a1＝1，a2•a3＝a8．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若，求数列{b n}的前n项和S n．18．如图，在四棱锥P﹣ABCD中，平面ABCD⊥平面PAD，AD∥BC，AB＝BC AD＝1，∠APD＝∠BAD＝90°．（Ⅰ）求证：PD⊥PB；（Ⅱ）当PA＝PD时，求三棱锥P﹣BCD的体积．19．2022年冬奥会将由北京和张家口联合举办，其中冰壶比赛将在改造一新的水立方进行．女子冰壶比赛将由来自全球的十支最优秀的队伍参加，中国女子冰壶队作为东道主，将对奥运冠军发起冲击．（Ⅰ）已知参赛球队包括来自亚洲的中国队、日本队和韩国队，来自美洲的加拿大对和美国队，以及来自欧洲的瑞士队、英国对、瑞典队、丹麦队和德国队．每支球队有四名参赛队员．若赛前安排球员代表合影，需要以分层抽样的方式从三个大洲的运动员中抽取10名运动员，则每个大洲各需要抽取多少运动员？（Ⅱ）此次参赛的夺冠热门队伍包括加拿大对、瑞士队、英国对、瑞典队和东道主中国队，若比赛的揭幕战随机的从这五支球队中选择两支球队出站，求中国队被选中的概率．20．已知函数．（Ⅰ）求f（x）的单调区间；（Ⅱ）当x∈（0，+∞）时，若函数f（x）与g（x）图象交于P（x1，y1）、Q（x2，y2）（x2＞x1）两点，求实数a的取值范围21．已知椭圆，动直线l与椭圆E交于不同的两点A（x1，y1），B（x2，y2），且△AOB的面积为1，其中O为坐标原点．（Ⅰ）为定值；（Ⅱ）设线段AB的中点为M，求|OM|•|AB|的最大值．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分，作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑．[选修4-4：坐标系与参数方程]22．在直角坐标系xOy中，直线l的方程是y＝2，曲线C的参数方程是（φ为参数）．以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．（Ⅰ）求直线l和曲线C的极坐标方程；（Ⅱ）若A（ρ1，α）是曲线C上一点，是直线l上一点，求的最大值．[选修4-5：不等式选讲]23．已知a、b、c∈R+，且a+b+c＝6．（Ⅰ）当c＝5时，求的最小值；（Ⅱ）证明：a2+b2﹣2b+c2﹣4c≥﹣2．东北三省三校2021年高三第二次联合模拟文科数学试题参考答案一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A、B均为集合U＝{1，2，3，4，5，6}的子集，且（∁U A）∩B＝{3}，（∁U B）∩A＝{6}，A∩B ＝{1，2}，则集合B＝（）A．{1，2，3} B．{1，2，6} C．{1，2} D．{1，2，3，4，5}根据两个集合的交集，看出两个集合中都含有这两个元素，根据A的补集与B的交集的元素，看出B中不含有元素6，得到结果．因为集合A、B均为集合U＝{1，2，3，4，5，6}的子集，且（∁U A）∩B＝{3}，（∁U B）∩A＝{6}，A∩B＝{1，2}，所以：3∈B，6∉B，1，2∈B，4，5∉B，4，5∉A；故集合B＝{1，2，3}．故选：A．本题考查子集与交集，并集的转换，是一个基础题，本题典型的解法是利用文恩图看出集合B中的元素．2．若a+2i＝（1﹣i）（1+bi）（a，b∈R，i为虚数单位），则复数a﹣bi在复平面内对应的点所在的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限利用复数代数形式的乘除运算化简，再由复数相等的条件求得a，b的值，则答案可求．因为a+2i＝（1﹣i）（1+bi）＝（1+b）+（b﹣1）i，∴a＝1+b且2＝b﹣1；所以：a＝4，b＝3；∴复数a﹣bi在复平面内对应的点（4，﹣3）所在的象限为第四象限．故选：D．本题考查复数代数形式的乘除运算，考查复数相等的条件，考查复数的代数表示法及其几何意义，是基础题．3．若实数x、y满足，则y﹣x的最大值为（）A．3 B．0 C．﹣3 D．﹣9画出可行域，将目标函数变形画出相应的直线，将直线平移至B时纵截距最大，z最大．画出的可行域如图：⇒B（6，6）．令z＝y﹣x变形为y＝x+z作直线y＝x将其平移至B（6，6）时，直线的纵截距最大，最大为：0．故选：B．本题主要考查利用线性规划求函数的最值，关键是将目标函数赋予几何意义．4．已知α，β是两个不同的平面，直线m⊂α，下列命题中正确的是（）A．若α⊥β，则m∥βB．若α⊥β，则m⊥βC．若m∥β，则α∥βD．若m⊥β，则α⊥β直接利用线面垂直和平行的判定和性质的应用求出结果．对于选项A：若α⊥β，则m∥β也可能m⊥β，故错误．对于选项B：若α⊥β，则m⊥β也可能m∥β，故错误．对于选项C：若m∥β，则α∥β也可能α与β相交，故错误．对于选项D，直线m⊂α，m⊥β，则α⊥β是面面垂直的判定，故正确．故选：D．本题考查的知识要点：线面垂直和平行的判定和性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．5．课堂上数学老师和同学们做游戏，随机询问甲、乙、丙、丁4位同学的作业完成情况，甲说：“丙未完成作业或丁未完成作业”；乙说：“丁未完成作业”；丙说：“我完成作业了”；丁说：“我完成作业了”．他们中恰有一个人说了谎话，请问：是谁说了谎话？（）A．甲B．乙C．丙D．丁根据题意判断其中两人说话矛盾，有人说话，其他人说真话，可推出．由乙说：“丁未完成作业，与丁说：“我完成作业了”，则乙丁有一人说谎，则甲丙说的真话，可知丙完成作业了，丁未完成作业，进而可以判断丁说了假话．故选：D．本题考查简单的合情推理，属于基础题．6．已知正项等比数列{a n}，若向量，则log2a1+log2a2+…+log2a9＝（）A．12 B．8+log25 C．5 D．18本题先根据平行向量的坐标运算可得a2•a8＝16，再根据等比中项的知识，可计算出a5＝4，在求和时根据对数的运算及等比中项的性质可得到正确选项．由题意，向量，则8•2﹣a2•a8＝0，即a2•a8＝16，根据等比中项的知识，可得a2•a816，∵a5＞0，∴a5＝4，∴log2a1+log2a2+…+log2a9＝log2（a1a2 (9)＝log2[（a1a9）•（a2a8）•（a3a7）•（a4a6）•a5]＝log2a59＝9log24＝18．故选：D．本题主要考查等比数列的性质应用，以及数列与向量的综合问题．考查了转化与化归思想，平行向量的运算，对数的计算，逻辑思维能力和数学运算能力．本题属中档题．7．我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中，积累了丰富的经验，总结出了一套有关体积、容积计算的方法，这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中．《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，如图所示的阳马三视图，则它的体积为（）A．B．1 C．2 D．3由三视图还原原几何体，可知该几何体为四棱锥，底面ABCD为矩形，AB＝2，AD＝3，侧棱PA⊥底面ABCD，且PA＝1．再由棱锥体积公式求解．由三视图还原原几何体如图，可知该几何体为四棱锥，底面ABCD为矩形，AB＝2，AD＝3，侧棱PA⊥底面ABCD，且PA＝1．∴该几何体的体积V．故选：C．本题考查由三视图求面积、体积，关键是由三视图还原原几何体，是中档题．8．已知两个不相等的非零向量，满足，且与的夹角为45°，则的取值范围是（）A．B．C．（0，2] D．如图所示，设，，∠CAB＝45°，由图可知，当BC⊥AC时，||的取值最小，求出最小值，没有最大值，即可得到结果．如图所示，设，，∠CAB＝45°，由图可知，当BC⊥AC时，||的取值最小，此时，则||，而||没有最大值，故则的取值范围为[，+∞），故选：D．本题主要考查两个向量的加减法的法则，以及其几何意义，属于基础题．9．已知，则sin（60°+α）的值为（）A．B．C．D．由已知结合同角平方关系，诱导公式及二倍角公式进行化简即可求解．∵，则sin（60°+α）＝sin（90°﹣30°+α）＝cos（α﹣30°）＝cos（30°﹣α），＝1﹣2sin2（15°﹣α）＝1．故选：A．本题主要考查了诱导公式及二倍角公式在三角化简求值中的应用，属于基础试题．10．设函数f（x）＝sin x+cos x+sin x cos x+1，则下列说法中正确的是（）A．f（x）关于（0，1）中心对称B．f（x）的极小值为C．f（x）的最小正周期为πD．f（x）图象的一条对称轴为借助于三角函数的性质逐项进行判断，选出正确选项．对于A选项，f（x）关于（0，1）中心对称，首先表达错误，应该说f（x）的图象关于某个点中心对称，其次f（x）+f（﹣x）＝2cos x+2不恒等于2，所以A错误；对于B选项，∵f（x）＝sin x+cos x+sin x cos x+1∴f′（x）＝cos x﹣sin x+cos2x，令f′（x）＝0有sin x ＝cos x或sin x+cos x＝﹣1．当sin x＝cos x＝±时，有f（x）＝±，当sin x+cos x＝﹣1时，两边平方可得1+2sin x cos x＝1，sin x cos x＝0，此时f（x）＝sin x+cos x+sin x cos x+1＝0，所以f（x）的极小值不可能为，所以B错误；对于C选项，f（x+π）＝﹣sin x﹣cos x+sin x cos x+1≠f（x），所以π不是f（x）的最小正周期，所以C 错误；对于D选项，∵f（）＝sin（）+cos（）+sin（）cos（）+1＝cos x+sin x+sin x cos x+1＝f（x），∴f（）＝f（x），所以f（x）图象的一条对称轴为x，故D正确．故选：D．本题考查三角函数的性质，属于中档题．11．已知双曲线上存在一点M，过点M向圆x2+y2＝1做两条切线MA、MB，若，则实数a的取值范围是（）A．B．C．D．利用已知条件，推出a的关系式，即可求解结果．双曲线上存在一点M，过点M向圆x2+y2＝1做两条切线MA、MB，若，可知MAOB是正方形，MO，所以双曲线的实半轴长的最大值为，所以a∈．故选：B．本题考查双曲线的简单性质，圆的切线性质的应用，考查分析问题解决问题的能力，是中档题．12．已知函数f（x）＝9（lnx）2+（a﹣3）•xlnx+3（3﹣a）x2有三个不同的零点x1，x2，x3，且x1＜1＜x2＜x3，则的值为（）A．81 B．﹣81 C．﹣9 D．9把f（x）的零点转化为a﹣3的零点，令t＝3，t∈（0，+∞），可得方程9t2﹣（51+a）t+81＝0有两实根t1，t2，由判别式大于0解得a的范围，再由根与系数的关系可得6，t1t2＝9，进一步得到t1＞3，3，结合x1＜1＜x2＜x3，可得3，3，33，则可知t1，3t2，则．f（x）＝9（lnx）2+（a﹣3）•xlnx+3（3﹣a）x2＝0⇒（a﹣3）（xlnx﹣3x2）＝﹣9（lnx）2⇒a﹣3，令t＝3，则，t∈[3，+∞），⇒a﹣3⇒9t2﹣（51+a）t+81＝0．设关于t的一元二次方程有两实根t1，t2，∴△＝（51+a）2﹣4×9×81＞0，可得a＞3或a＜﹣105．∴6，t1t2＝9．又∵t1+t2，当且仅当t1＝t2＝3时等号成立，由于t1+t2≠6，∴t1＞3，3（不妨设t1＞t2）．∵x1＜1＜x2＜x3，∴3，3，33．则可知t1，3t2．∴．故选：A．本题考查函数零点与方程根的关系，考查数学转化思想方法，考查一元二次方程根的分布，属难题．二、填空题：本题共4小题，每小题5分，共20分．把答案填写在答题纸相应位置上．13．我校高一、高二、高三共有学生1800名，为了了解同学们对“智慧课堂”的意见，计划采用分层抽样的方法，从这1800名学生中抽取一个容量为36的样本．若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数，则我校高三年级的学生人数为700 ．设从高三年级抽取的学生人数为2x人，由题意利用分层抽样的定义和方法，求出x的值，可得高三年级的学生人数．设从高三年级抽取的学生人数为2x人，则从高二、高一年级抽取的人数分别为2x﹣2，2x﹣4．由题意可得2x+（2x﹣2）+（2x﹣4）＝36，∴x＝7．设我校高三年级的学生人数为N，再根据，求得N＝700，故答案为：700．本题主要考查分层抽样，属于基础题．14．已知实数a、c满足c＜1＜a，关于x的不等式的解集为{x|x≥a或x≤c} ．由已知可转化为二次不等式即可求解．由题意可得（x﹣a）（x﹣c）≥0且x≠1，因为c＜1＜a，所以x≥a或x≤c，故不等式的解集为{x|x≥a或x≤c}．故答案为：{x|x≥a或x≤c}．本题主要考查了分式不等式的求解，体现了转化思想的应用．15．直线l经过抛物线y2＝2px（p＞0）的焦点F，与抛物线交于A，B两点，与直线交于点M，若，且，则抛物线的方程为y2＝4x．由抛物线的方程可得焦点F的坐标，由向量的关系可得F为AM的中点，可得A的横坐标，代入抛物线的方程可得A的纵坐标，进而求出直线AB的方程与抛物线联立求出两根之和，再由抛物线的性质可得AB 的值，由题意可得p的值，进而求出抛物线的方程．由题意如图所示，因为，F为AM的中点，所以AF＝AA'＝NF＝2p，设A（x1，y1），B（x2，y2），所以2p＝x1，所以x1，代入抛物线的方程可得y1p 即A（，p）所以k AB，所以直线AB的方程为：y（x），直线与抛物线的方程联立可得：，整理可得：3x2﹣5px0，x1+x2，由抛物线的性质可得AB＝x1+x2+p p，解得p＝2，所以抛物线的方程为：y2＝4x，故答案为：y2＝4x．本题考查向量与点的位置关系，以及抛物线的性质，属于中档题．16．设△ABC的内角A、B、C所对的边分别为a、b、c，且（a+b+c）（a﹣b+c）＝3ac，则B＝；若边AC上的点D满足BD＝CD＝2AD＝2，则△ABC的面积S＝．（l）利用余弦定理容易求出B的大小；（2）引入角α＝∠DBC，根据BD＝DC得α＝C，再利用内角和定理将A用α表示出来，最后在△ABD中利用正弦定理可求出α，问题迎刃而解．（1）根据题意（a+b+c）（a﹣b+c）＝3ac，化简得a2+c2﹣b2＝ac，所以cos B，∵B∈（0，π），∴B；（2）做出图形如下：由题意不妨设∠DBC＝α，则∠ABDα，∠C＝α，所以Aα，在△ABD中由正弦定理得，将AD＝1，BD＝2代入化简得，∴．∴A，C，易得AB．∴．故答案为：．本题考查三角形中的几何计算问题，涉及内角和定理、正余弦定理的应用，属于中档题．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．（一）必考题：共60分．17．已知数列是公差不为0的等差数列，且a1＝1，a2•a3＝a8．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若，求数列{b n}的前n项和S n．本题第（Ⅰ）题先根据数列是公差不为0的等差数列可知1，再列出、、关于d的表达式，根据a2•a3＝a8有•，代入表达式可得关于d的方程，解出d 的值，即可得到等差数列的通项公式，进一步可得数列{a n}的通项公式；第（Ⅱ）题先根据第（Ⅰ）题的结果计算出数列{b n}的通项公式，然后运用裂项相消法计算前n项和S n．（Ⅰ）由题意，可知1，1+d，1+2d，1+7d，∵a2•a3＝a8，∴•，即（1+d）（1+2d）＝（1+7d），整理，得d2﹣2d＝0，解得d＝0（舍去），或d＝2．∴1+2（n﹣1）＝2n﹣1，∴a n＝（2n﹣1）2，n∈N*．（Ⅱ）由（Ⅰ）知，[]，∴S n＝b1+b2+…+b n（1）（）[][1][1]．本题主要考查数列求通项公式的计算，以及运用裂项相消法计算前n项和．考查了转化与化归思想，方程思想，裂项相消法的运用，以及逻辑思维能力和数学运算能力．本题属中档题．18．如图，在四棱锥P﹣ABCD中，平面ABCD⊥平面PAD，AD∥BC，AB＝BC AD＝1，∠APD＝∠BAD＝90°．（Ⅰ）求证：PD⊥PB；（Ⅱ）当PA＝PD时，求三棱锥P﹣BCD的体积．（Ⅰ）推导出BA⊥AD，BA⊥PD，AP⊥PD，从而PD⊥平面PAB，由此能证明PD⊥PB；（Ⅱ）取AD中点O，连接PO，则PO⊥AD，证明PO⊥平面ABCD，再由棱锥体积公式求解．证明：（Ⅰ）∵∠BAD＝90°，∴BA⊥AD，∵平面ABCD⊥平面PAD，交线为AD，∴BA⊥平面PAD，从而BA⊥PD，∵∠APD＝90°，∴AP⊥PD，∵BA∩AP＝A，∴PD⊥平面PAB，∵PB⊂平面PAB，∴PD⊥PB；解：（Ⅱ）∵PA＝PD，取AD中点O，连接PO，则PO⊥AD，由平面ABCD⊥平面PAD，交线为AD，得PO⊥平面ABCD．又∠APD＝90°，AD＝2，得PO＝1，∴．即三棱锥P﹣BCD的体积为．本题考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．19．2022年冬奥会将由北京和张家口联合举办，其中冰壶比赛将在改造一新的水立方进行．女子冰壶比赛将由来自全球的十支最优秀的队伍参加，中国女子冰壶队作为东道主，将对奥运冠军发起冲击．（Ⅰ）已知参赛球队包括来自亚洲的中国队、日本队和韩国队，来自美洲的加拿大对和美国队，以及来自欧洲的瑞士队、英国对、瑞典队、丹麦队和德国队．每支球队有四名参赛队员．若赛前安排球员代表合影，需要以分层抽样的方式从三个大洲的运动员中抽取10名运动员，则每个大洲各需要抽取多少运动员？（Ⅱ）此次参赛的夺冠热门队伍包括加拿大对、瑞士队、英国对、瑞典队和东道主中国队，若比赛的揭幕战随机的从这五支球队中选择两支球队出站，求中国队被选中的概率．（Ⅰ）利用分层抽样法求出从亚洲、美洲、欧洲运动员中抽取的人数；（Ⅱ）利用列举法求出基本事件数，计算所求的概率值．（Ⅰ）利用分层抽样法从亚洲运动员中抽取103（人），从美洲运动员中抽取102（人），从欧洲运动员中抽取105（人）；（Ⅱ）从“加拿大队、瑞士队、英国队、瑞典队和中国队”中任选两队，基本事件是{加拿大队，瑞士队}，{加拿大队，英国队}，{加拿大队，瑞典队}，{加拿大队，中国队}，{瑞士队，英国队}，{瑞士队，瑞典队}，{瑞士队，中国队}，{英国队，瑞典队}，{英国队，中国队}，{瑞典队，中国队}共有10种不同取法；其中中国队被选中的基本事件有4种，故所求的概率为P．本题考查了分层抽样方法与列举法求古典概型的概率问题，是基础题．20．已知函数．（Ⅰ）求f（x）的单调区间；（Ⅱ）当x∈（0，+∞）时，若函数f（x）与g（x）图象交于P（x1，y1）、Q（x2，y2）（x2＞x1）两点，求实数a的取值范围（1）先对函数求导，然后结合导数可求函数的单调区间；（2）由已知分离参数可得a在（0，+∞）上有2个不同的零点，构造函数h（x），x∈（0，+∞），然后结合导数及函数的性质可求．（I），当x＞1时，f′（x）＜0，函数单调递减，当x＜1时，f′（x）＞0，函数单调递增，故f（x）的单调递增区间（﹣∞，1），单调递减区间（1，+∞）；（II）由题意可得在（0，+∞）上有2个不同的零点，即a在（0，+∞）上有2个不同的零点，令h（x），x∈（0，+∞），则，当0＜x＜1时，h′（x）＞0，函数单调递增，当x＞1时，h′（x）＜0，函数单调递减，且h（0）＝﹣1，x→+∞时，h（x）＜0，h（x）max＝h（1），故﹣1．本题主要考查了利用导数求解函数的单调区间及函数的零点个数的求解，体现了转化思想的应用．21．已知椭圆，动直线l与椭圆E交于不同的两点A（x1，y1），B（x2，y2），且△AOB的面积为1，其中O为坐标原点．（Ⅰ）为定值；（Ⅱ）设线段AB的中点为M，求|OM|•|AB|的最大值．（Ⅰ）当直线l的斜率不存在时，设l：x＝m，代入椭圆方程求解|AB|，结合△AOB的面积为1求得m值，可得为定值4，当直线l的斜率存在时，设y＝kx+t，联立椭圆方程，可得A，B横坐标的和与积，利用弦长公式求弦长，再由点到直线的距离公式求得|OM|，结合△AOB的面积为1，可得1+4k2＝2t2，则的值可求，从而说明为定值；（Ⅱ）设M（x0，y0），当直线的斜率不存在时，|OM|，|AB|，则|OM|•|AB|＝2；当直线的斜率存在时，由（Ⅰ）可得M的坐标，求得|OM|，写出|OM|•|AB|，结合1+4k2＝2t2转化为关于的二次函数求最值．（Ⅰ）当直线l的斜率不存在，设l：x＝m，代入椭圆方程可得y2＝1，由△AOB的面积为1，可得|m|•21，解得m＝±，则；当直线l的斜率存在，设y＝kx+t，联立椭圆方程可得（1+4k2）x2+8ktx+4t2﹣4＝0，设A（x1，y1），B（x2，y2），可得x1+x2，x1x2，|AB|•••，由△AOB的面积为1，可得••|AB|＝1，化简可得1+4k2＝2t2，则（）2﹣2•4，而4，综上可得，为定值4；（Ⅱ）设M（x0，y0），当直线的斜率不存在时，|OM|，|AB|，则|OM|•|AB|＝2；当直线的斜率存在时，由（Ⅰ）可得x0，y0＝kx0+t，则|OM|，可得|OM|•|AB|•．∵，∴0．可知|OM|•|AB|＜2．综上，|OM|•|AB|的最大值为2．本题考查直线与椭圆位置关系的应用，训练了利用二次函数求最值，考查化简运算能力和推理能力，属于中档题．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分，作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑．[选修4-4：坐标系与参数方程]22．在直角坐标系xOy中，直线l的方程是y＝2，曲线C的参数方程是（φ为参数）．以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系．（Ⅰ）求直线l和曲线C的极坐标方程；（Ⅱ）若A（ρ1，α）是曲线C上一点，是直线l上一点，求的最大值．（Ⅰ）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．（Ⅱ）利用三角函数关系式的变换和正弦型函数的性质的应用求出结果．（Ⅰ）直线l的方程是y＝2，转换为极坐标方程为ρsinθ＝2，曲线C的参数方程是（φ为参数）．转换为直角坐标方程为，转换为极坐标方程为．（Ⅱ）点A（ρ1，α）是曲线C上一点，所以：，所以，点是直线l上一点，所以，所以，，当时，最大值为．本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，三角函数关系式的恒等变换，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．[选修4-5：不等式选讲]23．已知a、b、c∈R+，且a+b+c＝6．（Ⅰ）当c＝5时，求的最小值；（Ⅱ）证明：a2+b2﹣2b+c2﹣4c≥﹣2．（Ⅰ）依题意，a+b＝1，将目标式化简可得，再利用基本不等式求最值即可；（Ⅱ）将不等式左边化简可得a2+b2﹣2b+c2﹣4c＝a2+（b﹣1）2+（c﹣2）2﹣5，运用柯西不等式即可得证．（Ⅰ）当c＝5时，a+b＝1，∴，又（当且仅当a＝b时取等号），则，∴，即的最小值为9；（Ⅱ）证明：a2+b2﹣2b+c2﹣4c＝a2+（b﹣1）2+（c﹣2）2﹣5，由柯西不等式有，[a2+（b﹣1）2+（c﹣2）2]•（1+1+1）≥（a+b﹣1+c﹣2）2（当且仅当a＝b﹣1＝c﹣2时取等号），∴，又a+b+c＝6，∴a2+（b﹣1）2+（c﹣2）2≥3，即a2+b2﹣2b+c2﹣4c≥﹣2（当且仅当a＝1，b＝2，c＝3时取等号）．本题考查利用基本不等式求最值，以及柯西不等式的运用，考查不等式的证明，考查推理能力，属于基础题．。
江苏省黄桥中学分校高三数学(文科)双周练试
江苏省黄桥中学分校高三数学（文科）双周练试卷 （三角函数、平面向量、数列） 2008-9-16命题人：徐卫华 审核人：徐学兵一、填空题（本大题共14小题，每小题5分，共70分，请把答案填答题纸上）1、已知数列{}n a 的前n 项和n n S 23+=，则其通项n a ＝★2、已知向量(2,4)=a ，(1,1)=b ，若向量()m ⊥+b a b ，则m = ★3、在等差数列{n a }中，22,16610a a x x --=是方程的两根，则5691213a a a a a ++++=★4、曲线y y x x y 在和直线21)4cos()4sin(2=-+=ππ轴右侧的交点按横坐标从小到大依次记为P 1，P 2，P 3，…，则|P 2P 4|= ★5、设20062005,1}{a a q a n 和若的等比数列为公比>是方程03842=+-x x 的两根，则a 2007+a 2008=★6、在(0,2π)内，使sin cos x x ≥成立的x 的取值范围为： ★7、各项均正的数列{}n a 中, 21=a ,nn n n a a n a a -+=+++111，则n a =★ 8、若数列}{n a 满足12 (01),1 (1).n n n n n a a a a a +≤≤⎧=⎨->⎩且167a =,则2008a =★边BC上一点，9、如图,在ABC △中，12021BAC AB AC ∠===，，°，D 是2DC BD =，则AD BC ⋅=★记作1i i t t + ，10、将半径为1的圆周十二等分，从分点i 到分点i+1的向量依次1223233412112t t t t t t t t t t t t ⋅+⋅++⋅=则★11、已知a n ＝(2n －1)⋅⎝⎛⎭⎫13n，把数列{a n }的各项排成三角形状；记A (m ，n )表示第m 行，第n 列的项，则A (5，2)＝★12、已知向量OB ＝(2，0)，OC ＝(2，2)，CA ＝(cos α，sin α)( α∈R)，则OA 与OB夹角的取值范围是★13、已知,a b 是两个互相垂直的单位向量, 且1⋅=c a ,1⋅=c b,||=c 则对任意的正实数t ,1||t t++c a b 的最小值是★14、在计算“1223(1)n n ⨯+⨯+⋅⋅⋅++”时，某同学学到了如下一种方法：ABDCa 1a 2 a 3 a 4a 5 a 6 a 7 a 8 a 9…………………………先改写第k 项：1(1)[(1)(2)(1)(1)],3k k k k k k k k +=++--+由此得112(123012),3⨯=⨯⨯-⨯⨯123(234123),3⨯=⨯⨯-⨯⨯…1(1)[(1)(2)(1)(1)].3n n n n n n n n +=++--+相加，得11223(1)(1)(2).3n n n n n ⨯+⨯+⋅⋅⋅++=++类比上述方法，请你计算“123234(1)(2)n n n ⨯⨯+⨯⨯+⋅⋅⋅+++”，其结果为 ★二、解答题（本题共6小题，总分90分）15、（本小题14分）已知向量m =()B B cos 1,sin -, 向量n =（2，0），且m 与n 所成角为3π，其中A 、B 、C 是ABC ∆的内角。
高三数学文科模拟考试 (含答案)
高三数学文科模拟考试 (含答案)高三模拟考试数学（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），共4页，满分150分，考试时间120分钟。
考生作答时，请将答案涂在答题卡上，不要在试题卷和草稿纸上作答。
考试结束后，请将答题卡交回。
第Ⅰ卷（选择题，共60分）注意事项：请使用2B铅笔在答题卡上涂黑所选答案对应的标号。
第Ⅰ卷共12小题。
1.设集合A={x∈Z|x+1<4}，集合B={2,3,4}，则A∩B的值为A.{2,4}。
B.{2,3}。
C.{3}。
D.空集2.已知x>y，且x+y=2，则下列不等式成立的是A.x1.D.y<-113.已知向量a=(x-1,2)，b=(x,1)，且a∥b，则x的值为A.-1.B.0.C.1.D.24.若___(π/2-θ)=2，则tan2θ的值为A.-3.B.3.C.-3/3.D.3/35.某单位规定，每位职工每月用水不超过10立方米的，按每立方米3元收费；用水超过10立方米的，超过的部分按每立方米5元收费。
某职工某月缴水费55元，则该职工这个月实际用水为（）立方米。
A.13.B.14.C.15.D.166.已知命题p：“存在实数x使得e^x=1”，命题q：“对于任意实数a和b，如果a-1=b-2，则a-b=-1”，下列命题为真的是A.p。
B.非q。
C.p或q。
D.p且q7.函数f(x)满足f(x+2)=f(x)，且当-1≤x≤1时，f(x)=|x|。
若函数y=f(x)的图象与函数y=log_a(x)（a>0且a≠1）的图象有且仅有4个交点，则a的取值集合为A.(4,5)。
B.(4,6)。
C.{5}。
D.{6}8.已知函数f(x)=sin(θx)+3cos(θx)（θ>0），函数y=f(x)的最高点与相邻最低点的距离是17.若将y=f(x)的图象向右平移1个单位得到y=g(x)的图象，则函数y=g(x)图象的一条对称轴方程是A.x=1.B.x=2.C.x=5.D.x=6删除了格式错误的部分，对每段话进行了简单的改写，使其更流畅易懂。
四川省成都市石室中学2022-2023学年高三下学期二诊模拟考试文科数学试题含答案
成都石室中学2022-2023学年度下期高2023届二诊模拟考试文科数学（全卷满分150分，考试时间120分钟）第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题列出的四个选项中，只有一项是符合题目要求的．1．已知集合{}230A x x x =-<，{3xB x =≥，则A B ⋃=（）A ．10,2⎛⎫ ⎪⎝⎭B ．1,32⎡⎫⎪⎢⎣⎭C ．()0,+∞D ．1,2⎡+∞⎫⎪⎢⎣⎭2．已知z 的共轭复数是z ，且12i z z =+-（i 为虚数单位），则复数z 的虚部为（）A ．32B ．32-C ．-2D ．-2i3．下图是我国跨境电商在2016~2022年的交易规模与增速统计图，则下列结论正确的是（）A ．这7年我国跨境电商交易规模的平均数为8.0万亿元B ．这7年我国跨境电商交易规模的增速越来越大C ．这7年我国跨境电商交易规模的极差为7.6万亿元D ．图中我国跨境电商交易规模的6个增速的中位数为13.8%4．设实数x ，y 满足约束条件20,20,2360,x y x y x y -+≥⎧⎪-≤⎨⎪++≥⎩则2z x y =-的最小值为（）A ．-8B ．-6C ．-4D ．-25．已知π6sin 46α⎛⎫-=⎪⎝⎭，则sin 2α的值为（）A ．13B ．23C．3D．36．已知a ，b ，c 为直线，α，β，γ平面，下列说法正确的是（）A ．若a c ⊥，b c ⊥，则a b∥B ．若αγ⊥，βγ⊥，则αβ⊥C ．若a α∥，b α∥，则a b ∥D ．若αγ∥，βγ∥，则αβ∥7．若正整数N 除以正整数m 后的余数为n ，则记为()mod N n m =，例如()102mod 4=．如图所示程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的n 等于（）A ．20B ．21C ．22D ．238．已知双曲线22221x y a b-=的右焦点为)F ，点P ，Q 在双曲线上，且关于原点O 对称．若PF QF ⊥，且PQF △的面积为4，则双曲线的离心率为（）A ．52B ．2C D ．39．某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（）A ．B ．C ．4D ．10．已知函数()f x 满足()()0f x f x +-=，()()110f x f x ++-=，当()0,1x ∈时，()2x f x =()4log 80f =（）A ．55-B ．455-C D ．5511．已知抛物线2:8C y x =与直线()()20y k x k =+>相交于A ，B 两点，F 为抛物线C的焦点，若2FA FB =，则AB 的中点的横坐标为（）A ．52B ．3C ．5D ．612．设2log 3a =，3log 4b =，log a c b =，则下列关系正确的是（）A ．a b c>>B ．b a c>>C ．c b a>>D ．c a b>>第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分．13．平面向量a ，b 满足()3,2a b +=- ，()1,a b x -=，且0a b ⋅= ，则x 的值为______．14．已知直线1:0l y =，2:l y =，圆C 的圆心在第一象限，且与1l ，2l 都相切，则圆C 的一个方程为______．（写出满足题意的任意一个即可）15．已知三棱锥P ABC -的体积为233，各顶点均在以PC 为直径的球面上，AC =，2AB =，2BC =，则该球的表面积为______．16．已知函数()()π2sin 0,02f x x ωϕωϕ=+><<⎛⎫ ⎪⎝⎭，π04f ⎛⎫-= ⎪⎝⎭，ππ44f x f x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭，且()f x 在π2π,189⎛⎫⎪⎝⎭上单调，则ω的最大值为______．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答；第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（本小题满分12分）针对我国老龄化问题日益突出，人社部将推出延迟退休方案．某机构进行了网上调查，所有参与调查的人中，持“支持”“保留”和“不支持”态度的人数如下表所示．支持保留不支持50岁以下80004000200050岁以上（含50岁）100020003000（Ⅰ）在所有参与调查的人中，用分层抽样的方法抽取n 个人，已知从持“不支持”态度的人中抽取了30人，求n 的值；（Ⅱ）在持“不支持”态度的人中，用分层抽样的方法抽取5人看成一个总体，从这5人中任意选取2人，求至少有1人年龄在50岁以下的概率．18．（本小题满分12分）已知数列{}n a 的前n 项和为n S ，12a =，12n n S a +=-．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令2log n n b a =，从①n n n c b a =⋅，②2141n nc b =-，③()21nn n b c =-⋅三个条件中任选一个，求数列{}n c 的前n 项和n T ．19．（本小题满分12分）如图，ABC △是正三角形，在等腰梯形ABEF 中，AB EF ∥，12AF EF BE AB ===，平面ABC ⊥平面ABEF ，M ，N 分别是AF ，CE 的中点，4CE =．（Ⅰ）求证：MN ∥平面ABC ；（Ⅱ）求三棱锥N ABC -的体积．20．（本小题满分12分）已知函数()()2ln ln 0f x x ax x a a =-++>．（Ⅰ）当1a =时，求()f x 的最大值；（Ⅱ）若[)1,x ∀∈+∞，()0f x ≤，求a 的取值范围．21．（本小题满分12分）已知椭圆()2222:10x y C a b a b +=>>经过点13,2⎫⎪⎭，其右焦点为)3,0F．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）椭圆C 的右顶点为A ，若点P ，Q 在椭圆C 上，且满足直线AP 与AQ 的斜率之积为120，求APQ △面积的最大值．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，那么按所做的第一题计分．22．［选修4-4：坐标系与参数方程］（本小题满分10分）在平面直角坐标系xOy 中，已知直线:1l x y +=与曲线2221:21x t C t y t ⎧=⎪⎪+⎨⎪=⎪+⎩，（t 为参数）．以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系．（Ⅰ）求曲线C 的普通方程；（Ⅱ）在极坐标系中，射线3π:08m θαα⎛=<<⎫⎪⎝⎭与直线l 和曲线C 分别交于点A ，B ，若)31OA OB =-，求α的值．23．［选修4-5：不等式选讲］（本小题满分10分）已知存在0x ∈R ，使得0024x a x b +--≥成立，0a >，0b >．（Ⅰ）求2a b +的取值范围；（Ⅱ）求22a b +的最小值．成都石室中学2022-2023学年度下期高2023届二诊模拟考试文科数学参考答案答案及解析1．C 【解析】由题意可得，集合{}03A x x =<<，12B x x ⎧⎫=≥⎨⎬⎩⎭，所以{}0A B x x ⋃=>．故选C ．2．C 【解析】设()i ,z x y x y =+∈R ．因为12i z z =+-，所以()()i 12i 12i x y x y =-+-=+-+，221,20,x y x y ⎧+=+⎨+=⎩解得3,22,x y ⎧=⎪⎨⎪=-⎩则32i 2z =-，所以复数z 的虚部为-2．故选C ．3．D 【解析】这7年我国跨境电商交易规模的平均数为5.56.37.18.039.711.512.18.07++++++>（万亿元），故A 错误；这7年我国跨境电商交易规模的增速有升有降，故B 错误；这7年我国跨境电商交易规模的极差为12.1 5.5 6.6-=（万亿元），故C 错误；我国跨境电商交易规模的6个增速的中位数为13.1%14.5%13.8%2+=，故D 正确．故选D ．4．B 【解析】作出可行域如图中阴影部分所示，2z x y =-可化简为1122y x z =-，即斜率为12的平行直线．由20,20,x y x y -+=⎧⎨-=⎩解得2,4,x y =⎧⎨=⎩则()2,4A ．结合图形可知，当直线2z x y =-过点()2,4A 时，z 取最小值，min 2246z =-⨯=-．故选B．5．B 【解析】由已知，得2ππ2sin 2cos 212sin 243ααα⎛⎫⎛⎫=-=--=⎪ ⎪⎝⎭⎝⎭．故选B ．6．D 【解析】可借助正方体进行判断．对于A 选项，正方体中从同一顶点出发的三条棱两两垂直，故A 错误；对于B 选项，选取正方体的上、下底面为α，β以及一个侧面为γ，则αβ∥，故B 错误；对于C 选项，选取正方体的上底面的对角线为a ，b ，下底面为α，则a b ∥不成立，故C 错误；对于D 选项，选取正方体的上、下底面为α，γ，任意作一个平面β平行于下底面γ，则有αβ∥成立，故D 正确．故选D ．7．C 【解析】由已知中的程序框图可得，该程序的功能是利用循环结构计算并输出同时满足条件：①被3除余1，②被5除余2，且最小为两位数，所以输出的22n =．故选C ．8．C 【解析】因为双曲线的右焦点为)F，所以c =．设其左焦点为1F ．因为PF QF ⊥，点P ，Q 关于原点O 对称，所以2PQ OF ==．由PQF △的面积为4，得142S PF QF =⋅=，则8PF QF ⋅=．又22220PF QF PQ +==，所以2PF QF -=．又由双曲线的对称性可得1QF PF =，则由双曲线的定义可得122PF PF a ==-，所以1a =，则离心率ce a==．故选C ．9．B 【解析】如图，该几何体是棱长为2的正方体中的三棱锥P ABC -，其中面积最大为(21322PBCS =⨯⨯=△．故选B ．10．D 【解析】因为()f x 满足()()0f x f x +-=，所以()f x 为奇函数．又因为()()110f x f x ++-=，所以()()()()()21111f x f x f x x f f x -⎡⎤⎡+=++=--+=-⎤⎣⎦=⎣⎦，所以()f x 是周期为2的奇函数．又因为()0,1x ∈时，()2xf x =-所以()()()(()44422log 802log 5log 5log log 2f f f f f =+===(2log 22log 2f -=--=-5=+=．故选D ．11．A 【解析】如图，设AB 的中点为G ，抛物线2:8C y x =的准线为:2l x =-，焦点为()2,0F ，直线()()20y k x k =+>过定点()2,0P -，过点A ，B 分别作AM l ⊥于点M ，BN l ⊥于点N ．由2FA FB =，得2AM BN =，所以点B 为AP 的中点．连接OB ，则12OB FA FB ==，做点B 的横坐标为1，则点A 的横坐标为4，所以AB 的中点G 的横坐标为14522+=．故选A ．12．A 【解析】因为2log 31a =>，3log 41b =>，所以222333333log 2log 4log 8log 9log 2log 41222b a ⎛⎫⎛⎫⎛⎫ ⎪+ ⎪ ⎪⎝⎭⎝⎭⎝<<⎭=⨯==，所以1a b >>，所以log log 1a a c b a =<=，所以a b c >>．故选A ．13．3±【解析】因为()3,2a b +=- ，()1,a b x -= ，所以22,2x a -+⎛⎫= ⎪⎝⎭ ，21,2x b --⎛⎫= ⎪⎝⎭ ．又因为0a b ⋅= ，所以2221022x x-+--⨯+⨯=，解得23x =±．14．(()22311x y +-=（答案不唯一）【解析】由题意可得，圆心C 在直线33y x =上，圆C 的方程形如()()()22230x ay a a a -+-=>．15．20π【解析】由3AC =2AB =，2BC =，得2π3ABC ∠=，所以242πsin 3AC r ==，得2r =（r 为ABC △外接圆半径）．又1sin 32ABC S AB BC ABC =⋅⋅∠=△，则1323333P ABC ABC V S h h -=⋅==△，所以2h =，即点P 到平面ABC 的距离为2，所以外接球球心O （PC 的中点）到平面ABC 的距离1d =，所以外接球半径2225R r d =+=，所以24π20πS R ==球．16．5【解析】因为函数()()2sin f x x ωϕ=+，π04f ⎛⎫-= ⎪⎝⎭，所以ππ4m ωϕ-+=，m ∈Z ①．又因为ππ44f x f x ⎛⎫⎛⎫-=+⎪ ⎪⎝⎭⎝⎭，所以直线π4x =是()f x 图象的对称轴，所以πππ42n ωϕ+=+，n ∈Z ②．由①②可得，()ππ24m n ϕ=++．又π02ϕ<<．所以π4ϕ=，则41n ω=+，n ∈Z ．又()f x 在π2π,189⎛⎫⎪⎝⎭上单调，()f x 的最小正周期为2πω，所以2πππ918ω-≤，即116ω≤，解得6ω≤，故ω的最大值为5．17．解：（Ⅰ）参与调查的总人数为80004000200010002000300020000+++++=，其中从持“不支持”态度的人数200030005000+=中抽取了30人，所以30200001205000n =⨯=．（Ⅱ）由已知易得，抽取的5人中，50岁以下与50岁以上人数分别为2人（记为1A ，2A ），3人（记为1B ，2B ，3B ）．画树状图如下：由树状图可知，从这5人中任意选取2人，基本事件共10个，其中，至少有1人年龄在50岁以下的事件有7个，故所求概率为710．18．解：（Ⅰ）因为12n n S a +=-，所以()122n n S a n -=-≥．将上述两式相减，得()122n n a a n +=≥．因为12a =，122S a =-，即122a a =-，所以24a =，所以212a a =，所以()*12n n a a n +=∈N ．因为120a =≠，所以()*12n na n a +=∈N ，所以数列{}n a 是以2为首项，2为公比的等比数列，所以2n n a =．（Ⅱ）由（Ⅰ）可知，22log log 2n n nb a n ===．若选①：2n n n nc b a n =⋅=⋅，则1231222322n n T n =⋅+⋅+⋅+⋅⋅⋅+⋅，()23121222122n n n T n n +=⋅+⋅+⋅⋅⋅+-⋅+⋅．将上述两式相减，得123112222222212n nn n n T n n +++--=+++⋅⋅⋅+-⋅=-⋅-，所以()1122n n T n +=-⋅+．若选②：()()221111114141212122121n n c b n n n n n ⎛⎫====⎪---+-+⎝⎭，则111111111111111232352572212122121n nT n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+⋅⋅⋅+-=-= ⎪ ⎪ ⎪ ⎪ ⎪-+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭．若选③：()()2211nnn n c b n =-⋅=-⋅．当n 为偶数时，()()()()222222112341122n n n T n n n ⎡⎤⎣+=-++-++⋅⋅⋅+--+=++⋅⋅⋅+=⎦；当n 为奇数时，()()()()211121122n n n n n n n T T n c +++++=-=-+=-．综上，()()121nn T n n +=-．19．（Ⅰ）证明：如图，取CF 的中点D ，连接DM ，DN ．因为M ，N 分别是AF ，CE 的中点，所以DM AC ∥，DN EF ∥．又因为DM ⊄平面ABC ，AC ⊂平面ABC ，所以DM ∥平面ABC ．又因为EF AB ∥，所以DN AB ∥，同理可得，DN ∥平面ABC ．因为DM ⊂平面MND ，DN ⊂平面MND ，DM DN D ⋂=，所以平面MND ∥平面ABC ．又因为MN ⊂平面MND ，所以MN ∥平面ABC ．（Ⅱ）解：如图，取AB 的中点O ，连接OC ，OE ．由已知可得，OA EF ∥且OA EF =，所以四边形OAFE 是平行四边形，所以OE AF ∥且OE AF =．因为ABC △是正三角形，O 是AB 的中点，所以OC AB ⊥．又因为平面ABC ⊥平面ABEF ，平面ABC ⋂平面ABEF AB =，所以OC ⊥平面ABEF ．又OE ⊂平面ABEF ，所以OC OE ⊥．设12AF EF EB AB a ====，则OC =，OE a =．在Rt COE △中，由222OC OE CE +=，得)2224a +=，则2a =，所以OC =122AF EF EB AB ====，则4AB =，112AM AF ==．由题意易得，60FAB ∠=︒，则点M 到AB的距离sin 602h AM =⋅︒=，即点M 到平面ABC的距离为2．又MN ∥平面ABC ，所以1113423322N ABC M ABC ABC V V S h --==⋅⋅=⨯⨯⨯=△．20．解：（Ⅰ）当1a =时，()2ln f x x x x =-+，()()()211121x x f x x x x+-=-+=-，当()0,1x ∈时，()0f x '>；当()1,x ∈+∞时，()0f x '<，所以()f x 在()0,1上单调递增，在()1,+∞上单调递减，所以()()max 10f x f ==．（Ⅱ）由()()2ln ln 0f x x ax x a a =-++>，得()()1210f x ax a x'=-+>，易知()f x '在()0,+∞上单调递减．①由（Ⅰ）可知，当1a =时，()0f x ≤，符合题意．②当01a <<时，()()1210f a '=->，110f a a ⎛⎫⎪⎝⎭'=-<，所以存在111,x a ⎛⎫∈ ⎪⎝⎭时，使得()10f x '=，故当11,x x a ⎛⎫∈ ⎪⎝⎭时，()0f x '<，()f x 单调递减，所以()2111l 1n ln 0f x f a a a a aa >=-⋅⎛⎫⎛⎫ ⎪ ⎪⎭++⎝⎭=⎝，不符题意，舍去．③当1a >时，()()1210f a '=-<，110f a a ⎛⎫'=-> ⎪⎝⎭，所以存在21,1x a ⎛⎫∈⎪⎝⎭，使得()20f x '=，故当[)1,x ∈+∞时，()0f x '<，()f x 单调递减，()()1ln 1f x f a a ≤=-+．令()()ln 11g a a a a =-+>，则()1110ag a a a-'=-=<，故()g a 在()1,+∞上单调递减，所以()()10g a g <=，故()0f x <，符合题意．综上所述，a 的取值范围是[)1,+∞．21．解：（Ⅰ）依题意，得22222311,4,c a b a b c ⎧=⎪⎪+=⎨⎪=+⎪⎩解得2,1,a b c ⎧=⎪=⎨⎪=⎩所以椭圆C 的标准方程为2214x y +=．（Ⅱ）易知直线AP 与AQ 的斜率同号，所以直线PQ 不垂直于x 轴，故可设:PQ y kx m =+，()11,P x y ，()22,Q x y ．由221,4,x y y kx m ⎧+=⎪⎨⎪=+⎩得()222148440k x mkx m +++-=，所以122814mk x x k-+=+，21224414m x x k -=+，()2216410k m ∆=+->，即2241k m +>．由120AP AQ k k ⋅=，得121212220y y x x ⋅=--，消去1y ，2y 得()()()()12122022kx m kx m x x ++=--，即()()221212121220202024k x x km x x m x x x x +++=-++，所以222222224484482020202414141414m mk m mk k km m k k k k ----⋅+⋅+=-⋅++++，整理得2260m km k --=，所以2m k =-或3m k =，所以直线():2PQ y k x =-或()3y k x =+．又因为直线PQ 不经过点()2,0A ，所以直线PQ 经过定点()3,0-，所以直线PQ 的方程为()3y k x =+，易知0k ≠，设定点()3,0B -，则APQ ABP ABQS S S =-△△△1212AB y y =-1252k x x =-52=52=52k ==因为0∆>即2241k m +>，且3m k =，所以2150k ->，所以2105k <<，所以()22215955533143APQ k k S k -+==≤⋅=+△，当且仅当2114k =时取等号，所以APQ △面积的最大值为53．22．解：（Ⅰ）曲线C 的普通方程为()2211x y -+=，(]0,2x ∈．（Ⅱ）直线l 的极坐标方程为()sin cos 1ρθθ+=，易得1sin cos OA αα=+．曲线C 的极坐标方程为2cos ρθ=，易得2cos OB α=．由已知，得)121cos sin cos ααα=+，231sin 22cos 2αα++=，31sin 21cos 22αα+++=，31sin 2cos 22αα-+=，两边平方并整理得3sin 42α=-．又3π08α<<，即3π042α<<，所以4π43α<，则π3α=．23．解：（Ⅰ）由题意，知()()2222x a x b x a x b a b a b +--≤+--=+=+．因为存在0x ∈R ，使得0024x a x b +--≥，所以只需24a b +≥，即2a b +的取值范围是[)4,+∞．（Ⅱ）由柯西不等式，得()()()2222212216a b a b ++≥+≥，当45a =，85b =时，22a b +取得最小值165．。
湖北武汉乐学教育高三文科数学周测试题(2)
乐学教育数学周测试题一、选择题：（共15小题，每题4分）1．已知集合U ＝{1,2,3,4,5,7}，集合A ＝{4,7}，集合B ＝{1,3,4,7}，则( )A ．U ＝A ∪B B ．U ＝(∁U A )∪BC ．U ＝A ∪(∁U B )D ．U ＝(∁U A )∪(∁U B )2、设x R ∈,则“12x >”是“2210x x +->”的 （ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3、已知集合{}320A x R x =∈+>,{}(1)(3)0B x R x x =∈+->,则A B ∩=（ ） A ．(),1-∞- B ．21,3⎛⎫-- ⎪⎝⎭C ．2,33⎛⎫- ⎪⎝⎭D ．()3,+∞ 4、若全集U={x ∈R|2x ≤4} A={x ∈R||x+1|≤1}的补集CuA 为 （ ）A ．{x ∈R |0<x<2}B ．{x ∈R |0≤x<2}C ．{x ∈R |0<x≤2}D ．{x ∈R |0≤x≤2}5、已知命题p:∀x1,x2∈R,(f(x2)-f(x1)(x2-x1)≥0,则⌝p 是 （ ）A ．∃x1,x2∈R,(f(x2)-f(x1)(x2-x1)≤0B ．∀x1,x2∈R,(f(x2)-f(x1)(x2-x1)≤0C ．∃x1,x2∈R,(f(x2)-f(x1)(x2-x1)<0D ．∀x1,x2∈R,(f(x2)-f(x1)(x2-x1)<06、命题“若α=4π,则tanα=1”的逆否命题是 （ ） A ．若α≠4π,则tanα≠1 B ．若α=4π,则tanα≠1 C ．若tanα≠1,则α≠4π D ．若tanα≠1,则α=4π 7、命题“存在实数x ,,使1x >”的否定是 （ ）A ．对任意实数x , 都有1x >B ．不存在实数x ,使1x ≤C ．对任意实数x , 都有1x ≤D ．存在实数x ,使1x ≤8、已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈;,则B 中所含元素 的个数为（ ） A ．3 B ．6C ．8D ．10 9、若a ∈R ，则a=2是（a-1）（a-2）=0的 ( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分又不必要条件10、设全集U=*{|6}x N x ∈<，集合A={1,3}，B={3,5}，()U C A B ∪= ( ) （A ）{}1,4 （B ）{}1,5 （C ）{}2,4 （D ）{}2,511、若集合{}A=|1x x x R ≤∈，，{}2B=|y y x x R =∈，，则A B ⋂=（ ） A. {}|11x x -≤≤ B. {}|0x x ≥ C. {}|01x x ≤≤ D. ∅12、下列选项叙述错误的是A.命题“若1x ≠，则2320x x -+≠”的逆否命题是“若2320x x -+=，则1x =”B.若命题p ：2,10x R x x ∀∈++≠，则p ⌝：2,10x R x x ∃∈++= C.若p q ∨为真命题，则p ，q 均为真命题D.“2x >”是“2320x x -+>”的充分不必要条件13、设1,()0,1,f x ⎧⎪⎪=⎨⎪-⎪⎩0(0)(0)x x x >=<,1,()0,g x ⎧⎪=⎨⎪⎩()(x x 为有理数为无理数),则(())f g π的值为（ ）A ．1B ．0C ．1-D ．π 14、根据统计，一名工人组装第x 件某产品所用的时间（单位：分钟）为,(),c x A x f x c x A A⎧<⎪⎪=⎨⎪≥⎪⎩（A ，c 为常数）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
盂县一中高三第二次周练（文科）命题人：岳志义一、选择题（每题5分，共60分）1．含有三个实数的集合可表示为{a ，ab，1}，也可表示为{a 2， a +b ，0}，则a 2006+b 2006的值为 （ ） A ．0 B ．1 C ．－1 D ．±12．已知全集I ＝{0，1，2}，满足C I （A ∪B ）＝{2}的A 、B 共有的组数为 （ ） A ．5 B ．7 C ．9 D ．113．设集合M ={x |x =412+k ，k ∈Z }，N ={x |x =214+k ，k ∈Z }，则( ）A ．M =NB ．M NC ．M ND ．M ∩N =∅4．对于任意的两个实数对（a ，b ）和（c ，d ），规定（a ，b ）＝（c ，d ）当且仅当a ＝c ，b＝d ；运算“⊗”为：),(),(),(ad bc bd ac d c b a +-=⊗，运算“⊕”为：),(),(d c b a ⊕),(d b c a ++=，设R q p ∈,，若)0,5(),()2,1(=⊗q p 则=⊕),()2,1(q p （ ）A ．)0,4(B ．)0,2(C ．)2,0(D ．)4,0(-5．已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨≥⎩ 是(,)-∞+∞上的增函数，那么 a 的取值范围是（ ）A ．（0，1）B ．（0，13）C.17⎡⎢⎣，13⎤⎥⎦ D ．]1,17⎡⎢⎣ 6．函数2()lg(31)f x x ++的定义域（ ）A ．1(,)3-+∞ B ．1(,1)3-C ．11(,)33-D ．1(,)3-∞-7．已知函数)(x f y =，对任意的两个不相等的实数21,x x ，都有)()()(2121x f x f x x f ⋅=+成立，且0)0(≠f ，则)2006()2005(...........)2005()2006(f f f f ⋅⋅-⋅-的值是（ ） A ．0 B ．1 C ．2006！D ．（2006！）28．如图所示，f i （x ）（i =1，2，3，4）是定义在［0，1］上的四个函数，其中满足性质：“对［0，1］中任意的x 1和x 2，任意λ∈［0，1］，f ［λx 1+（1－λ）x 2］≤λf （x 1）+（1－λ）f （x 2）恒成立”的只有 （ ）f 1（x ） f 2（x ） f 3（x ） f 4（x ）A ．f 1（x ），f 3（x ）B ．f 2（x ）C ．f 2（x ），f 3（x ）D ．f 4（x ） 9．不等式|x 2－x －6|＞3－x 的解集是（ ）（A ）（3，＋∞） （B ）（－∞，－3）∪（3，＋∞） （C ）（－∞，－3）∪（－1，＋∞） （D ）（－∞，－3）∪（－1，3）∪（3，＋∞）10、设2()lg 2x f x x +=-，则2()()2x f f x +的定义域为A ．(4,0)(0,4)-B ．(4,1)(1,4)--C ．(2,1)(1,2)--D ．(4,2)(2,4)--11、若不等式x 2＋ax ＋1≥0对于一切x ∈（0，12〕成立，则a 的取值范围是（ ） A ．0 B. –2 C.-52D.-312、若关于x 的不等式x k )1(2+≤4k ＋4的解集是M ，则对任意实常数k ，总有（ ） （A ）2∈M ，0∈M ； （B ）2∉M ，0∉M ； （C ）2∈M ，0∉M ； （D ）2∉M ，0∈M ．二、填空题（每题4分，共16分）13、函数()f x 对于任意实数x 满足条件()()12f x f x +=，若()15,f =-则()()5f f =__________.14、设不等式2x －1＞m(x 2－1)对满足|m|≤2的一切实数m 的取值都成立，x 的取值范围为 15、设函数y ＝f （x ）是最小正周期为2的偶函数，它在区间［0，1］上的图象为如图14所示的线段AB ，则在区间［1，2］上f （x ）＝ .16、已知直线l 过点)1,2(P ，且与x 轴、y 轴的正半轴分别交于BA 、两点，O 为坐标原点，则三角形OAB 面积的最小值为 ．三、解答题17、（12分）已知向量)23sin 23(cos x x ，=a ，)2sin 2(cos xx -=，b ，)13(-=，c ，其中R ∈x ．（１）当b a ⊥时，求x 值的集合； （２）求||c a -的最大值．18．（12分）设A B a x a x x B x x x A ⊆=-+++==+=若},01)1(2{},04{222，求实数a 的取值范围。
. 19、（本小题满分12分）如图3，四棱锥P —ABCD 的底面边长为1的正方形，PD ⊥BC ，且PD=1，PC=2. （Ⅰ）求证：PD ⊥平面ABCD ； （Ⅱ）求二面角A —PB —D 的大小. 20．（本小题满分12分）从4名男生和2名女生中任选3人参加演讲比赛，求： （Ⅰ）所选3人中恰有1名女生的概率； （Ⅱ）所选3人中至少有1名女生的概率.21、（12分）已知函数32()f x x ax bx c =+++在23x =-与1x =时都取得极值.(1) 求a 、b 的值及函数()f x 的单调区间;(2) 若对[]1,2x ∈-,不等式2()f x c <恒成立,求c 的取值范围.22．（14分）已知二次函数c bx ax x f ++=2)(．（1）若a>b >c ， 且f （1）=0，证明f （x ）的图象与x 轴有2个交点；（2）在（1）的条件下，是否存在m ∈R ，使池f （m ）=－ a 成立时，f （m +3）为正数，若 存在，证明你的结论，若不存在，说明理由；（3）若对)()(,,,212121x f x f x x R x x ≠<∈且，方程)]()([21)(21x f x f x f +=有2个不等实根，),(21x x 证明必有一个根属于答案一、1．B ；2．C ；3．B ；4．B 5．C ；6．B ；7．B ； 8．A ．9、D 10、B 11、C 12、A二、13．51-14、213x 217＋＜＜－ 15、x 16、4 三、17、讲解 （１）由b a ⊥，得0=⋅b a ，即02sin 23sin 2cos 23cos =-xx x x ．则 02cos =x ， 得 )(4π2πZ ∈+=k k x ． ∴ ⎭⎬⎫⎩⎨⎧∈+=Z k k x x ，4π2π|为所求．（２）+-=-22)323(cos||x c a =+2)123(sin x )3π23sin(45-+x ， 所以||c a -有最大值为3．18、解：由2{40}{04}{0,4}A x x x x x x =+====-=-或. ∵B A ⊆，∴{0}{4}{0,4}B B B B =∅==-=-或或或. 当B =∅时，即01)1(222=-+++a x a x 无实根，由0<∆，即0)1(4)1(422<--+a a ，解得1-<a ；当{0}B =时，由根与系数的关系：2002(1)0011a a a ++⨯-⇒=-＝－，＝； 当{4}B =-时，由根与系数的关系：2442(1)(4)1a a a --+⨯--⇒∈∅＝－，(-4)＝； 当{0,4}B =-时，由根与系数的关系：2042(1)0(4)11a a a -+⨯--⇒=＝－，＝；综上所得11-≤=a a 或19、解答：（Ⅰ）∵PD=CD=1，PC=2 ∴PD 2+CD 2=PC 2，即PD ⊥CD.（3分） 又PD ⊥BC.BC ∩CD=C ∴PD ⊥平面ABCD（6分）（Ⅱ）如图，连结AC 交BD 于O ，则AC ⊥BD.∵PD ⊥平面ABCD ， ∴PD ⊥AC.∴AC ⊥平面PBD.（8分）过O 点作OE ⊥PB 于E ，连结AE ， 则AE ⊥PB ，故∠AEO 为二面角 A —PB —D 的平面 角.（10分）由Rt △OEB ∽Rt △PDB ，得OE=66=⋅PB OB PD . ∴tan ∠AEO=,3=OEAO即∠AEO=60° 20、解答：（I ）设所选3人中恰有1名女生为事件A ，则532062)(362412=⨯=⋅=C C C A P 6分（II ）设所选人中至少有1名女生为事件B ，则所选3人中没有女生为事件B . 8分51204)(3634===C C B P10分54)(1)(=-=∴B P B P 21、解答：322(1)(),()32,f x x ax bx c f x x ax b '=+++=++22124()0,(1)320,3931,2,2()32(32)(1),():f a b f a b a b f x x x x x f x ''-=-+==++==-=-'=--=+-由得函数的单调区间如下表所以函数()f x 的递增区间为2(,)3-∞-与(1,)+∞;递减区间为2(,1)3-.[][]32221(2)()222221,2,,(),327(2)2,(2)2.()(1,2),(2)2,1 2.f x x x x c x x f x c f c f c f x c x c f c c c =--+∈-=-=+=+=+∈-=+-当时为极大值而则为最大值要使恒成立只须解得或<> <>22、解: （1）)(,04,00,0)1(2x f ac b c a c b a c b a f ∴>-=∆∴<>∴>>=++=且且 的图象与x轴有两个交点.（2）0)(1,0)1(=∴=x f f 为 的一个根，由韦达定理知另一根为a c ,,,10,00c abc b a acc a --=>><<∴<>∴又且 10)1)((<<∴<-=--m a c a m a c m a 则13233=+->+>+∴acm)(x f 在（1，+∞）单调递增，0)1()3(=>+∴f m f ，即存在这样的m 使 0)3(>+m f（3）令)]()([21)()(21x f x f x f x g +-=，则)(x g 是二次函数.0)]()([41]2)()()(][2)()()([)()(22121221121≤--=+-+-=⋅x f x f x f x f x f x f x f x f x g x g 0)(0)()(),()(2121=∴<⋅≠x g x g x g x f x f 又的根必有一个属于),(21x x .沁园春·雪 <毛泽东>北国风光，千里冰封，万里雪飘。