电磁场与电磁兼容习题答案与详解_第2章
电磁场与电磁波 第2章习题解答

第二章习题解答【习题2.1】101929=.=101.6102.0810e qR R mq e Cp m Ce e 解:电偶极矩p 其中 1.3可得电偶极矩p 的大小其方向为从负电荷指向正电荷,即从氯离子指向氢离子。
---´== =醋【习题2.2】解1解:由例2.2得,电偶极子所产生的电场为533()1[]4e e P R RP E RRπε=-0()R R << ……………………①其中 0e P qR = ,0R方向从负电荷指向正电荷,R是从电偶极子指向电场中任一点的矢量,起点在正负电荷连线的中点。
(如图)本题 100 1.310R m -=⨯ 1010010R m -=⨯满足 0R R << .将①式整理:32013[()]4e e E P R R P RRπε=-令 ()e m k P R R P =-(23k R=)则 304m E Rπε=…………………………②欲求E的最大值,求出m最大值即可.222222[()]()2()()e e e e e e m k P R R P k P R R P k P R P R =-=+- 2222(2)()e e k R k P R P =-+2224296()()e e R P R P R R=-+ 2223()e e P R P R=+其中 00cos e P R qR R qR R θ== , (θ是0R 和R之间的夹角)易见,当cos 1θ=,即0θ=时,2m可取最大值22222m ax 234e e e m R P P P R=+=则 m=2e P 代入②式得 m a x33m ax042e P mERRπεπε==将习题2.1中的结论 e P=2.082910c m -⨯⋅ 代入得29112103max2.08102 3.148.910(10010)EV m ----⨯=⋅⨯⨯⨯⨯⨯513.710V m-≈⨯⋅距离自由电子处的电场 191712121020 1.6101.41044 3.148.910(10010)e E V mV mRπε-----⨯==⋅≈⨯⋅⨯⨯⨯⨯⨯故 距离电偶极子处的电场最大值为 513.710V m -⨯⋅ 距离自由电子处的电场为 711.410V m -⨯⋅【习题2.2】解2解:设矢量0R e的方向从电荷C L -指向电荷H +R n 是从由C L - H +构成的电偶极子指向电场中的任一点的矢量,起点在正负电荷连线的中点,且0R 〈〈R. ( e , n 为单位矢量,θ是e , n的夹角)(1)003303cos 1[]4qR qR E n e R R θπε=- (41P )由向量减法的三角形法则及余弦定理得:=03024qR R πε⎛⎫⎪⎝⎭E =由上题得290( 2.110)e p qR cm -==⨯因此,当0θ=或θπ=时E有最大值, 03024qR E R πε==50302 3.7104qR V M R πε=⨯ (2)7201() 1.4104q R VE M R R πε==⨯【习题2.3】证明: 电偶极距qRe p =其方向为从负电荷指向正电荷。
电磁场与电磁波理论基础 第二章 课后答案

1 q1 q2 u (r ) = + 4πε 0 R1 R2
式中
+q
Z
P ( x, y,z )
R1
r
r2
o
R2
R1 = r - r1 = ( x + a ) e x + ye y + e z R1 = ( x + a ) + y 2 + z 2 R 2 = r - r2 = ( x - a ) e x + ye y + e z R2 = ( x - a ) + y 2 + z 2
②当 a <
ρ < b ,此时 Q = 2π al ρ S1 ,由高斯定理可得
D ⋅ dS = 2π l ρ Dρ = Q = 2π al ρ
(S )
S1
Dρ =
a ρS1
ρ
D =
a ρS1
ρ
eρ
E =
a ρS1
ε0ρ
eρ
③当 ρ > b ,此时高斯面内的 Q = 2π al ρ S 1 + 2π bl ρ S 2 ,由高斯定理可得
代入得到
2 2
2
2
é ù 1 ê 8 (4e x - 4e z ) 4 (4e x - 4e y ) ú ê ú E (r ) = 3 3 ú 4pe 0 ê 4 2 4 2 êë úû 1 ée x + e y - 2e z ù = ê ûú 32 2pe 0 ë
(
)
(
)
2-7.一个点电荷+q 位于(-a, 0, 0)处,另一点电荷-2q 位于(a, 0, 0)处,求电位等于零的 面;空间有电场强度等于零的点吗? 解 根据点电荷电位叠加原理,有
电磁场第二章习题解答-推荐下载

d
d
d2
d
0
(
(
4 9
4 9
4 9
0U 0 d
0U
0U
0d
0
d
4
4
4
3 x2
3
3
x
2
x2
3
3
3
,式中
)S
)S
d
d
x
x
故
J
v
e
Q 4 a3 3
Q 4 a3
2.4 一个半径为 a 的导体球带总电荷量为 Q ,同样以匀角速度 绕一个直 径旋转,求球表面的面电流密度。
解 以球心为坐标原点,转轴(一直径)为 z 轴。设球内任一点 P 的位置 矢量为 r ,且 r 与 z 轴的夹角为 ,则 P 点的线速度为
v r er sin
球内的电荷体密度为
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
电磁场与电磁波(第四版)课后答案_谢处方_第二章习题

JdD t ex15.261014377cos377t117.1z ex57.531012cos377t117.1zA/m2
Jd 57.531012A/m2
2
2.6 一个平行板真空二极管内的电荷 体位密于度x=为0,阳极94板0U0位(d于43)xx23=,d,式极中间阴电极压板 为U0。如果U0 =40V,d=lcm,横截 面积s =10cm2。 求:
(1) x=0和x=d 区域内的总电荷量; (2) x=d/2和x=d区域内的总电荷量。
精选2021版课件
dE
R ez a er a a (ez ex cos ' e y sin '),
E
r
l 4 0
c
R R3dl '
a
l
4 0
(ez ex cos ' e y sin ')a 2 d '
0
3
2a
8
l 2a 0
(ez
ey 2)
x
z
R a d '
y
ldl '
精选2021版课件
解:先求出平行双线在回路中的磁感应强度
BL
0i 2 r
BR2bc0 i dr
回路中的感应电动势为
in d d tsB d s d d t sB Ld ssB Rd s sB Ld sb b c20 ira d r2 0 a iln b bc
sB R d s d c d 2b c 0 精i选d 20 21版r 课件r a d r 2 0 a iln b b c 16
电磁场与电磁波课后习题及答案二章习题解答

二章习题解答2.1 一个平行板真空二极管内的电荷体密度为4320049U d x ρε--=-,式中阴极板位于0x =,阳极板位于x d =,极间电压为0U 。
如果040V U =、1cm d =、横截面210cm S =,求:(1)0x =和x d =区域内的总电荷量Q ;(2)2x d =和x d =区域内的总电荷量Q '。
解 (1) 43230004d ()d 9dQ U d x S x τρτε--==-=⎰⎰110044.7210C 3U S dε--=-⨯ (2) 43230024d ()d 9dd Q U d x S x τρτε--''==-=⎰⎰11004(10.9710C 3U S d ε--=-⨯ 2.2 一个体密度为732.3210C m ρ-=⨯的质子束,通过1000V 的电压加速后形成等速的质子束,质子束内的电荷均匀分布,束直径为2mm ,束外没有电荷分布,试求电流密度和电流。
解 质子的质量271.710kg m -=⨯、电量191.610C q -=⨯。
由212mv qU = 得61.3710v ==⨯ m s 故 0.318J v == 2A m26(2)10I J d π-== A2.3 一个半径为a 的球体内均匀分布总电荷量为Q 的电荷,球体以匀角速度ω绕一个直径旋转,求球内的电流密度。
解 以球心为坐标原点,转轴(一直径)为z 轴。
设球内任一点P 的位置矢量为r ,且r 与z 轴的夹角为θ,则P 点的线速度为sin r φωθ=⨯=v r e ω球内的电荷体密度为343Qa ρπ=故 333sin sin 434Q Q r r a aφφωρωθθππ===J v e e 2.4 一个半径为a 的导体球带总电荷量为Q ,同样以匀角速度ω绕一个直径旋转,求球表面的面电流密度。
解 以球心为坐标原点,转轴(一直径)为z 轴。
设球面上任一点P 的位置矢量为r ,且r 与z 轴的夹角为θ,则P 点的线速度为sin a φωθ=⨯=v r e ω球面的上电荷面密度为24Q a σπ=故 2sin sin 44S Q Q a a aφφωσωθθππ===J v e e 2.5 两点电荷18C q =位于z 轴上4z =处,24C q =-位于y 轴上4y =处,求(4,0,0)处的电场强度。
电磁场答案第2章下
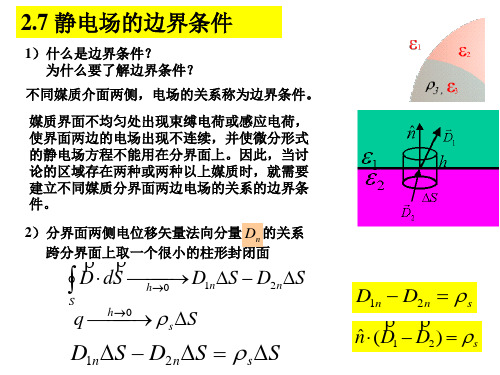
I J dS
S
对电流分布在曲面附近很薄的一层中的情况,当不需 分析计算这一薄层中的场时,可忽略薄层的厚度,将 电流近似看成是面电流。面电流用面电流密度Js表示.
3)电流面密度 Js
面电荷ρs以速度 v 运动形成的电流。 电流密度 电流
J s v
I J dS
s
电流面密度矢量
E dl 0
l
E1t E 2t
E dl 0
l
D dS 0
S
D1n D2n J1n J 2n
J dS 0
S
说明分界面上 E 切向分量连续,J 的法向分量连续。
上 页 下 页
回顾: 恒定电流场的边界条件
J dS 0
界面上的束缚面电荷
s ' 0 ( E1n E2n ) s
s ' 0 ( E1n E2n )
5)导体表面(导体与介质界面)的边界条件
D1n D2n s
E1t E2t
Dn S
Et 0
电场垂直于导体表面,且表面上的感应 电荷面密度等于表面上的电位移矢量的 大小。 对应的电位的边界条件为
J dS 0
s
l l1
应用到电 路的结点
dl E dl E dl
l2
U1 U2 U e
恒定电场的基本方程是基尔霍夫定律的场的表示。
上 页
下 页
5.分界面上的衔接条件 采用与静电场类比的方式可以方便的得 到恒定电场中不同媒质分界面的衔接条件。 静电场(=0) 恒定电场(无源区)
S
J1n J 2n 1E1n 2 E2n E1t E2t
电磁场与电磁兼容习题答案与详解第2章

电磁场与电磁兼容习题答案与详解-第2章第2章:电磁场基础知识1.题目:电场强度的方向与电荷正负有关吗?答案:是的,电场强度的方向与电荷的正负有关。
正电荷的电场强度方向指向远离电荷的方向,负电荷的电场强度方向指向靠近电荷的方向。
详解:电场强度的方向由正电荷指向负电荷,这是由于电荷之间存在相互作用力。
根据库仑定律,同性电荷之间的相互作用力是斥力,异性电荷之间的相互作用力是吸引力。
电场强度的方向就是这种相互作用力的方向。
2.题目:什么是电场线?答案:电场线是描述电场强度方向的线条。
在电场中,电场线的方向与电场强度的方向一致,电场线之间不会相交。
详解:电场线是静电场中电场强度方向的图形表示。
它可以用来表示电场强度的大小和方向。
电场线的方向由正电荷指向负电荷,线的密度表示电场强度的大小。
电场线之间不会相交,这是因为在相交点上电场强度有多个值,与实际不符。
3.题目:什么是电场强度?答案:电场强度是描述电场对单位正电荷施加的力的大小和方向。
详解:电场强度是电场的物理量,它表示电场对单位正电荷施加的力的大小和方向。
电场强度的单位是牛顿/库仑。
电场强度的方向由正电荷指向负电荷。
4.题目:电场强度与电场线之间的关系是什么?答案:电场强度和电场线是相互对应的。
电场强度的方向与电场线的方向一致,电场线的密度表示电场强度的大小。
详解:电场强度和电场线是相互对应的。
电场强度的方向由正电荷指向负电荷,电场线的方向也是由正电荷指向负电荷。
电场线的密度表示电场强度的大小,密度越大,表示电场强度越大。
5.题目:电场强度的大小与电荷量有关吗?答案:是的,电场强度的大小与电荷量有关。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
详解:电场强度的大小与电荷量有关。
根据库仑定律,电场强度与电荷量成正比,与距离的平方成反比。
在距离电荷越远的地方,电场强度越小;在距离电荷越近的地方,电场强度越大。
电磁场原理习题与解答(第2章)

(4)长圆柱中,有体密度为的电荷,与它偏轴地放有一半 径为a的无限长圆柱空洞,两者轴线平行且距离为d,如图2-6所示,求 空洞内的电场强度。 x y o
b (b)0 x y o d ( c) 图2-6 (a) 解:由于空洞存在,电荷分布不具有对称性,由此产生的场亦无对称 性,因此不能用高斯定律求解。这是可把空洞看作也充满,使圆柱体内 无空洞,然后再令空洞中充满-,并单独作用,分别求出两种场的分布 后叠加即可。设空洞内的电场强度为。 第一步 单独作用,如图(b)所示, 由体密度为的电荷产生的电场强 度为,由高斯定理
将电位参考点设在外导体上,即 则 , , 即 ,所以,内,外
2-9 用双层电介质制成的同轴电缆如题图2-9所示,介电常数 , 内、外导 体单位长度上所带电荷分别为和 (1)求两种电介质中以及 和处的电场强度与电通密度;
(2)求两种电介质中的电极化强度; (3)问何处有极化电荷,并求其密度。 解: (1)由高斯定理可得:
因此
(3) 球内电场, (r<a)
球外电场,由高斯定理:
, (r>a) 或
2-8 具有两层同轴介质的圆柱形电容器,内导体的直径为2cm,内层介 质的相对介电常数,外层的相对介电常数,要使两层介质中的最大场强 相等,并且内层介质所承受的电压和外层介质相等,问两层介质的厚度 各为多少? 解:以圆柱心为坐标原点,径向为轴,设单位长度上带电荷为,由高斯 定理,。 ,,
2-32 空气中,相隔1cm的两块平行导电平板充电到100V后脱离电 源,然后将一厚度为1mm的绝缘导电片插入两极间,问:
(1)忽略边缘效应,导电片吸收了多少能量?这部分能量起到了什 么作用?两板间的电压和电荷的改变量各为多少?最后存储在其中的能 量多大?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场与电磁兼容习题答案与详解
第二章
麦克斯韦方程组:
.在均匀的非导电媒质(0=σ,1=r μ)中,已知时变电磁场为
()V /m 34cos 300⎪⎭⎫ ⎝⎛-=y t z ωπa E ,()A/m 34cos 10⎪⎭⎫ ⎝
⎛-=y t x ωa H ,利用麦克斯韦方程组求出ω和r ε。
解:将E 和H 用复数表示:
由复数形式的麦克斯韦方程,有:
比较(1)与(3),(2)与(4),得 :
由此得:
16
/108==r s rad εϖ
.已知无源空间中的电场为()()()V/m 106cos 100.1sin 9z t x y βππ-⨯=a E , 利用麦克斯韦方程求H 及常数β。
解:E 复数形式:
由复数形式麦克斯韦方程
将上式与题给的电场E 相比较,即可得:
而磁场的瞬时表达式为:
高斯定理:
.两个相同的均匀线电荷沿x 轴和y 轴放置,电荷密度μc/m l 20=ρ,求点(3,3,3)处的电位移矢量D 。
解:设x 轴上线电荷在P (3,3,3)点上产生的电位移矢量为D 1,x 轴上线电荷在P (3,3,
3)点上产生的电位移矢量为D 2。
D 1
y z D 2
x z +
因为以x 轴为轴心,l ds D ρ=⋅⎰1 l D ρπ=⋅⋅2321 即πμπμ2310232201=⋅=
D 同理πμ
23102=D
z y x z y x a a a a a a D D D π
μπμπμπμ3103535)22121(231021++=++=
+= .μc/m l 30=ρ的均匀线电荷沿z 轴放置,以z 轴为轴心另有一半径为2m 的无限长圆柱面,其上分布有密度为2μc/m 41.5πρ-=s 的电荷,利用高斯定理求各区域内的电位移矢量D 。
解:建立圆柱坐标系,以z 轴为轴心,设一单位长度的圆柱面
(1) 当r<2m 时 因为⎰=
⋅l ds D ρ,所以l r D ρπ=⋅2 故r D l πρ2=,D =l l l a r
u a r ππρ152= (2)当r>2m 时1221⋅⋅⋅+⋅=⋅⎰πρρs l ds D
故c u c u c u r D ⋅⋅=⋅⋅-⋅⋅=⋅5.285.1302π 所以l a r
c u D π25.28⋅⋅= 安培定律:
.半径为a 的实心圆柱导体,电流I 在其截面上均匀分布,求磁场强度H 。
解:根据⎰
=⋅I u dl B 0可知 当a ≤ρ时,I a
I a I 22
22ρππρ==' I a u B dl B 2202ρπρϕ=⋅=⋅⎰
所以2
02a I u B πρϕ= 当a >ρ时,πρϕ20I u B =
.求半径为a 的圆形电流回路中心轴上的磁场H ,并给出回路中心的磁场。
y
解:取圆柱坐标,使z 轴与圆环的轴线相合,并使圆环在z=0的平面上,中心轴上任一点的坐标为(0,0,z ),并且ϕa 是ϕ的函数,即
ρϕ
ϕa a -=∂∂
根据比-萨定理得 ⎰⨯=2
04R a dl I u B R π (1) ϕϕad a dl = (2)
ααρcos sin z R a a a +-= (3)
22z a R += (4)
(2),(3),(4)代入(1)中得
⎰++-⨯=2
20)cos sin (4z a a a d a Ia u B z ααϕπρϕ =ϕααπρd a a z a Ia u z )cos sin ()
(4220⎰++ =
⎪⎭⎫ ⎝⎛++⎰⎰ππρϕαϕαπ20202204d cos a d sin a )z a (Ia u z 括号中的第二项积分为零,因为ρa 是φ的函数,在[0,2π]的范围内各个单位矢量互相抵消,积分为零。
=z a sin )
z a (Ia u ⋅+αππ24220 =z a )z a (Ia u 23
222
02+
在中心点处z=0,所以z a a I u B 20=
边界条件:
.在两导体平板(分别位于z=0和z=d 处)之间的空气中 ,已知电场强度为
()()V /m cos sin 0x k t z d E x y -⎪⎭
⎫ ⎝⎛=ωπa E ,式中0E 和x k 为常数。
试求:(1)磁场强度H ;(2)两导体表面上的电流密度J s 。
解:(1 )将E 表示为复数形式,由复数形式的麦克斯韦方程,得磁场的复数形式:
磁场的瞬时表达式为:
(2)z=0处的导体表面的电流密度为:
z=d 处的导体表面的电流密度为
电磁场的能量:
2.19 电场强度和磁场强度分别为()e t ϕω+=cos 0E E 和()m t ϕω+=cos 0H H ,证明其坡印廷矢量的平均值为:()m e ϕϕ-⨯=
cos 2100H E S av 。
解:⎰⎰++⨯=⨯=T m e T
av dt t t H E T
dt H E T S 00)cos()cos()(1)(1
ϕωϕω (1) 设αϕω=+e t ;βϕω=+m t
且[])cos()cos(2
1cos cos βαβαβα++-=⋅ (2) 将(2)代入(1)中得
[]dt t H E T
S T m e m e av ⎰+++-⨯=000)2cos()cos()(21ϕϕωϕϕ =dt t H E T
H E T m e m e ⎰++⨯+⨯-00000)2cos()(21))(cos(21ϕϕωϕϕ =)cos()(2100m e H E ϕϕ-⋅⨯。
