《电磁场与电磁波》经典例题
电磁场与电磁波试题
电磁场与电磁波试题一、选择题1.物体自带的静电荷可以产生（）电场。
A. 近距离的 B. 远距离的 C. 高速的 D. 恒定的2.下列哪个物理量是电场强度的定义？ A. 电荷的大小 B. 电势差的变化C. 电场线的形状D. 电场力的大小3.两个相同电量的电荷之间的力为F，若电荷1的电量变为原来的4倍，电荷2的电量变为原来的2倍，则两个电荷之间的力变为原来的（）倍。
A. 1/8B. 1/4C. 1/2D. 24.以下哪个物理量在电路中是守恒的？ A. 电流 B. 电荷 C. 电压 D. 电功5.电流方向由正极流动到负极。
这是因为电流是由（）极到（）极流动的。
A. 正极，负极 B. 负极，正极 C. 高电势，低电势 D. 低电势，高电势二、填空题1.电场强度的单位是（）。
2.在均匀介质中，电位与电势之间的关系是：（）。
3.电容的单位是（）。
4.电容和电容器的关系是：（）。
三、解答题1.简述电场的概念及其性质。
答：电场是由电荷周围的空间所产生的物理现象。
当电荷存在时，它会在其周围产生一个电场。
电场有以下性质：–电场是矢量量，具有大小和方向。
–电场的强度随着距离的增加而减弱，遵循反比例关系。
–电场由正电荷指向负电荷，或由高电势指向低电势。
–电场相互叠加，遵循矢量相加原则。
–电场线表示了电场的方向和强度，线的密度表示电场强度的大小。
2.简述电流的概念及其特性。
答：电流是指单位时间内通过导体截面的电荷量，用符号I表示，单位是安培（A）。
电流具有以下特性：–电流的方向由正极流向负极，与电子的运动方向相反。
–电流是守恒量，即在封闭电路中，电流的大小不会改变。
–电流的大小与导体电阻、电势差和电阻之间的关系符合欧姆定律：I = U/R，其中I为电流，U为电势差，R为电阻。
3.电容器与电场之间有怎样的关系？答：电容器是一种用于储存电荷和电能的元件。
当电容器充电时，电荷会从一极板移动到另一极板，形成了电场。
电容器的电容决定了电容器储存电荷和电能的能力。
电磁场与电磁波练习题
电磁场与电磁波练习题一、单项选择题(每小题1分，共15分)1、电位不相等的两个等位面（）A. 可以相交B. 可以重合C. 可以相切D. 不能相交或相切2、从宏观效应看，物质对电磁场的响应包括三种现象，下列选项中错误的是（）A.磁化B.极化C.色散D.传导3、电荷Q 均匀分布在半径为a 的导体球面上，当导体球以角速度ω绕通过球心的Z 轴旋转时，导体球面上的面电流密度为（）A.sin 4q e a ?ωθπB.cos 4q e a ?ωθπC.2sin 4q e a ?ωθπD.33sin 4q e r aωθπ 4、下面说法错误的是（）A.梯度是矢量, 其大小为最大方向导数,方向为最大方向导数所在的方向。
B.矢量场的散度是标量，若有一个矢量场的散度恒为零，则总可以把该矢量场表示为另一个矢量场的旋度。
C.梯度的散度恒为零。
D.一个标量场的性质可由其梯度来描述。
5、已知一均匀平面波以相位系数30rad/m 在空气中沿x 轴方向传播，则该平面波的频率为（）A.81510π?HzB.8910?HzC.84510π?Hz D.9910?Hz6、坡印廷矢量表示（）A.穿过与能量流动方向相垂直的单位面积的能量B.能流密度矢量C.时变电磁场中空间各点的电磁场能量密度D.时变电磁场中单位体积内的功率损耗7、在给定尺寸的矩形波导中，传输模式的阶数越高，相应的截止波长（）A.越小B.越大C.与阶数无关D.与波的频率有关8、已知电磁波的电场强度为(,)cos()sin()x y E z t e t z e t z ωβωβ=---，则该电磁波为（）A. 左旋圆极化波B. 右旋圆极化波C. 椭圆极化波D.直线极化波9、以下矢量函数中，可能表示磁感应强度的是（）A. 3x y B e xy e y =+B.x y B e x e y =+C.22x y B e x e y =+D. x y B e y e x =+10、对于自由空间，其本征阻抗为（）A. 0η=B.0η=C. 0η=D. 0η=11、自感和互感与回路的（）无关。
电磁场与电磁波大题
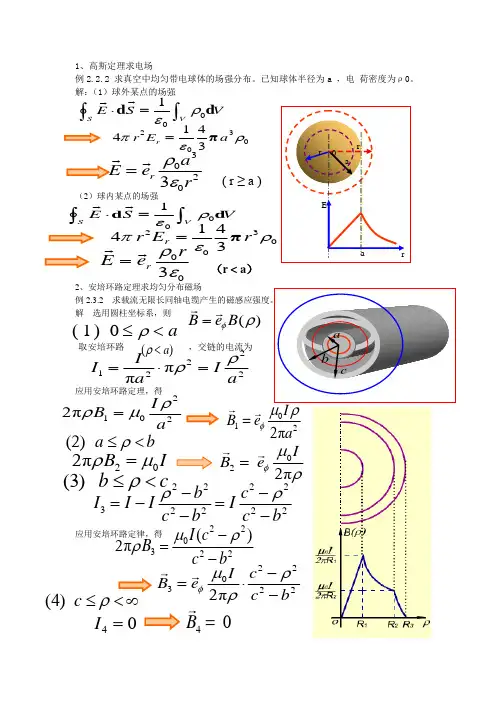
1、高斯定理求电场例2.2.2求真空中均匀带电球体的场强分布。
已知球体半径为a ，电 荷密度为ρ0。
解：（1）球外某点的场强（2）球内某点的场强2、安培环路定理求均匀分布磁场例2.3.2 求载流无限长同轴电缆产生的磁感应强度。
解 选用圆柱坐标系，则应用安培环路定理，得应用安培环路定律，得ar 0 r r E a V S E V S ⎰⎰=⋅d d 001ρε 03023414ρεπa E r r π=2303ra eE r ερ =( r ≥ a ) VS E V S ⎰⎰=⋅d d 001ρε 03023414ρεπr E r r π=003ερr eE r =（r < a ）a b c()B e B φρ=(1)0aρ≤<取安培环路 ，交链的电流为 ()a ρ<22122ππI I I a a ρρ=⋅=21022πI B aρρμ=0122πI B eaφμρ=(2)a bρ≤<202πB I ρμ=022πIB eφμρ=(3)b c ρ≤<222232222b c I I I I c b c b ρρ--=-=--220322()2πI c B c b μρρ-=-2203222πI c B e c b φμρρ-=⋅-(4)cρ≤<∞40I =40B =3、拉普拉斯方程 点位 电场强度 书例3.1.3 习题3.74、双导体电容 球型电容例3.1.5 同轴线内导体半径为a ，外导体半径为b 均匀介质，求同轴线单位长度的电容。
解 设同轴线的内、外导体单位长度带电量分别为+ρl 和－ρl ，应用高斯定理可得到内外导体间任一点的电场强度为内外导体间的电位差故得同轴线单位长度的电容为练习：同心球形电容器的内导体半径为、外导体半径为b ，其间填充介电常数为ε的均匀介质。
求此球形电容器的电容。
解：设内导体的电荷为q ，则由高斯定理可求得内外 导体间的电场同心导体间的电压球形电容器的电容εa b 同轴线 ()2πl E eρρρερ=1()d d 2πb b la a U E e ρρρρρερ=⋅=⎰⎰ln(/)2πl b a ρε=12π(F/m)ln(/)l C U b a ρε==a bεo 4π4πr r 22qqD e ,E er rε==0011d ()4π4πba q qb aU E r a b abεε-==-=⋅⎰4πab q C U b aε==-当 时，∞→b 04πC aε=孤立导体球的电容5、电感例3.3.3b ，空气填充。
电磁场与电磁波例题
1、如图1－1，平板电容器间由两种媒质完全填充，厚度分别为1d 和2d ，介电常数分别为1ε和2ε，电导率分别为1σ和2σ，当外加电压0U 时，求分界面上的自由电荷密度。
解：设电容器极之间的电流密度为J ，则： 2211E E J σσ==11σJ E = ，22σJ E = 于是+=101σJd U 22σJd 即：22110σσd d U J +=分界面上的自由面电荷密度为：J E E n D n D s )1122(112212σεσεεερ-=-=-=)1122(σεσε-=22110σσd d U +2、一个截面如图2－1所示的长槽，向y 方向无限延伸，两则的电位是零，槽内∞→y ，0→ϕ，底部的电位为：0)0,(U x =ϕ。
求槽内的电位。
解：由于在0=x 和a x =两个边界的电位为零，故在x 方向选取周期解，且仅仅取正弦函数，即：)(sin an n k x n k n X π==在y 方向，区域包含无穷远处，故选取指数函数，在∞→y 时，电位趋于零，所以选取y n k e nY -= 由基本解的叠加构成电位的表示式为：∑∞=-=1sin n a y n e a x n n C ππϕ待定系数由0=y 的边界条件确定。
在电位表示式，令0=y ，得：∑∞==1sin 0n a x n n C U π⎰-==a n n aUdx a x n U a n C 0)cos 1(0sin 02πππ 当n 为奇数时， πn U n C4=，当n 为偶数时，00=C 。
最后，电位的解为：a y n e n a x n n U πππϕ-∑∞==5,3,1sin 043、在两导体平板（0=z 和d z =）之间的空气中传输的电磁波，其电场强度矢量)cos()sin(0x x k t z dE y e E -=ωπ其中x k 为常数。
试求：（1）磁场强度矢量H 。
（2）两导体表面上的面电流密度s J 。
电磁场与电磁波例题集合
带电体位于真空，计算该带电圆柱内、外的电场强度。
z S1
L y
S
E dS
q
0
E dS
S
S1
EdS E dS 2πrLE
S1
x a
当 r < a 时，则电荷量q 为 q πr 2 L , 求
得电场强度为
r E er 2 0
当 r > a 时，则电荷量q 为 q πa 2 L , 求
功率损耗密度分别为
pl1 1E12 ,
2 pl 2 2 E2
两种特殊情况： 若 1 0 ， + U –
d1 d2
1= 0
E2 = 0
则 E2 0
we 2 0 pl 2 0
+ E1 U / d1 U –
d1 E1 = 0 d2 2 = 0
若 2 0， 则 E1 0
1E1 2 E2
边界垂直，求得 又
E1d1 E2d2 U
求出两种介质中的电场强度分别为 2 1 E1 U E2 U d1 2 d 2 1 d1 2 d 2 1
两种介质中电场储能密度分别为
1 we1 1 E12 , 2 1 2 we2 2 E2 2
2I H1 e π r ( 1 2 )
H2 I ( 1 2 ) I e e 2π r 2π r ( 1 2 )
B1 1H1
B2 2 H2
例1 计算无限长直导线与矩形线圈之间的互感。
设线圈与导线平行，周围介质为真空，如图所示。
q 4π 0 r l cos 2 q 4π 0 r
2
电磁场与电磁波经典例题
电磁场与电磁波
6
在无源（ 0, J 0）的自由空间中，已知时
时谐电磁场
变电磁场的磁场强度的复矢量为： j z H 2e eyA/m， 式中β为常数。试求： 1）磁场强度的瞬时表达式？ 2）电场强度的复矢量表达式、瞬时表达式？ 3）瞬时坡印廷矢量，平均坡印廷矢量？
电磁场与电磁波
电磁场与电磁波
小测3：时谐电磁场分析
5
时谐电磁场 Maxwell方程组的应用
已知理想介质（4 0 , 0）中均匀平面波电磁场的电场分量 瞬时表达式为： 5 E ( z , t ) 2 cos(6000 t - 4 10 z )e y V / m 试求： （ ）电场强度的复矢量？ 1 （2）伴随的磁场强度的瞬时表达式？复矢量？ （3）该电磁波的瞬时坡印廷矢量S？平均坡印廷矢量S av？
电磁场与电磁波
小测11参数为1 0 ,1 0 , 1 0，
且媒质1中的磁场强度为： 1 1 8 H1 ( z , t ) ey [ cos(15 10 t 5 z ) cos(15 108 t 5 z )] A/m； 2 6 z 0区域的媒质2参数为 2 5 0 ,2 20 0 , 2 0， 且媒质2中的电场强度为:E2 ( z , t ) ex 80 cos(15 108 t 50 z ) V/m。 1、请写出时域积分、微分形式的Maxwell方程组； 一般形式的边界条件。 2、用Maxwell方程组求解媒质1的电场强度， 媒质2的磁场强度,给出求解依据。 3、验证z 0的分界面电磁场满足边界条件。
小测3：电磁场与电磁波综合分析
7
电磁场与电磁波综合分析
已知理想介质（4 0 , 0）中均匀平面波的电场强度的 5 瞬时表达式为：E ( z , t ) 2 cos(6000 t - 4 10 z )ey V / m （ ）利用时域Maxwell方程组求解伴随的磁场强度H ( z, t )？ 1 （2）利用频域Maxwell方程组求解伴随的瞬时表达式H ( z, t )？ （3）利用均匀平面波的性质求解伴随的磁场强度H ( z, t )？ （4）求该电磁波的瞬时坡印廷矢量S？平均坡印廷矢量S av？
电磁场与电磁波姚毅版考试例题及习题精简版
1、例2.2.4（38P ）半径为0r 的无限长导体柱面，单位长度上均匀分布的电荷密度为l ρ。
试计算空间中各点的电场强度。
解：作一与导体柱面同轴、半径为r 、长为l 的闭合面S ，应用高斯定律计算电场强度的通量。
当0r r <时，由于导体内无电荷，因此有0=⋅⎰→→SS d E ，故有0=→E ，导体内无电场。
当0r r >时，由于电场只在r 方向有分量，电场在两个底面无通量，因此2ερπlrl E dS E dS a a ES d E l r Sr r Sr r r rS=⋅=⋅=⋅=⋅⎰⎰⎰→→→→ 则有：rE l r 02περ=例 2. 2. 6 圆柱坐标系中, 在 r = 2 m 与 r = 4 m 之间 的 体 积 内 均 匀 分 布 有 电 荷, 其 电 荷 密 度 为ρ/C ·m- 3。
利用高斯定律求各区域中的电场强度。
解：当 0≤r ≤2m 时, 有 即Er = 0当 2 m ≤r ≤4 m 时, 有因此当r ≥ 4 m 时, 有例 2. 3. 1 真空中, 电荷按体密度 ρ= ρ0 ( 1 -r2/a2) 分布在半径为 a 的球形区域内, 其中 ρ0为常数。
试计算球内、外的电场强度和电位函数。
解 由于电荷分布具有球对称分布, 电场也应具有球对称分布, 因此, E_沿半径方向, 且只是 r 的函数。
作一半径为 r 的同心球面 S, 应用高斯定律的积分形式可得。
当 r > a 时而 Q 为球面 S 包围的总电荷, 即球形区域内的总电荷。
因此当 r < a 时取无穷远的电位为零, 得球外的电位分布为球面上( r = a ) 的电位为 当 r < a 时由于 Q = ( 8 /15 ) πρ0 a3, 在球外, 电场和电位还可以写成由此可见, 具有球对称分布的电荷, 在球外的电场和电位与点电荷的电场和电位具有相同的分布。
例 2. 5. 1 在 图 2. 5. 3 中 的 电 介 质 分 界 面 附 近,E_1 = a_x2 - a_y3 + a_z5V/m, 分界面上没有自由电荷分布, 求D_2 、角 θ1 和 θ2 。
电磁场与电磁波(必考题)
1 / 91.已知自由空间中均匀平面波磁场强度瞬时值为：())]43(cos[31,,z x t-e t z x H +=πωπy A/m ，求①该平面波角频率ω、频率f 、波长λ ②电场、磁场强度复矢量③瞬时坡印廷矢量、平均坡印廷矢量。
解：① z x z k y k x k z y x ππ43+=++；π3=x k ，0=yk ，π4=z k ；)/(5)4()3(22222m rad k k k k z y x πππ=+=++=；λπ2=k ，)(4.02m k ==πλ c v f ==λ（因是自由空间），)(105.74.010388Hz c f ⨯=⨯==λ；)/(101528s rad f ⨯==ππω②)/(31),()43(m A e e z x H z x j y +-=ππ； )/()243254331120),(),(),()43()43(m V e e e e e e e k k z x H e z x H z x E z x j z x z x z x j y n +-+--=+⨯⨯=⨯=⨯=πππππππηη（③ ()[])/()43(cos 2432),,(m V z x t e e t z x E z x +--=πω())]43(cos[31,,z x t-e t z x H +=πωπy （A/m ） ()[]()[])/()43(cos 322431)]43(cos[31)43(cos 243222m W z x t e e z x t-e z x t e e H E S z x z x +-+=+⨯+--=⨯=πωππωππωy ())43(2432),(z x j z x e e e z x E +--=π，)43(31),(z x j y e e z x H +-=ππ()())/(322461312432Re 21Re 212*)43()43(*m W e e e e e e e H E S z x z x j y z x j z x av +=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⨯-=⎪⎭⎫ ⎝⎛⨯=+-+-ππππ2.横截面为矩形的无限长接地金属导体槽，上部有电位为 的金属盖板；导体槽的侧壁与盖板间有非常小的间隙以保证相互绝缘。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、选择题
1、以下关于时变电磁场的叙述中，正确的是（ ）
A 、电场是无旋场
B 、电场和磁场相互激发
C 、电场与磁场无关
2、区域V 全部用非导电媒质填充，当此区域中的电磁场能量减少时，一定是（ ）
A 、能量流出了区域
B 、能量在区域中被消耗
C 、电磁场做了功
D 、同时选择A 、C
3、两个载流线圈之间存在互感，对互感没有影响的的是（ ）
A 、线圈的尺寸
B 、两个线圈的相对位置
C 、线圈上的电流
D 、空间介质
4、导电介质中的恒定电场E 满足（ ）
A 、0∇⨯=E
B 、0∇∙=E
C 、∇⨯=E J
5、用镜像法求解电场边值问题时，判断镜像电荷的选取是否正确的根据是（ ）
A 、镜像电荷是否对称
B 、电位方程和边界条件不改变
C 、同时选择A 和B
6、在静电场中，电场强度表达式为3(32)()y x z cy ε=+--+x y z E e e e ，试确定常数
ε的值是（ ）
A 、ε=2
B 、ε=3
C 、ε=4
7、若矢量A 为磁感应强度B 的磁矢位，则下列表达式正确的是（ ） A 、=∇B
A B 、=∇∙B A C 、=∇⨯B A D 、2=∇B A 8、空气（介电常数10εε=）与电介质（介电常数204εε=）的分界面是0z =平面，
若已知空气中的电场强度124=
+x z E e e 。
则电介质中的电场强度应为（ ） A 、1216=+x z E e e B 、184=+x z E e e C 、12=+x z E e e
9、理想介质中的均匀平面波解是（ ）
A 、TM 波
B 、TEM 波
C 、TE 波
10、以下关于导电媒质中传播的电磁波的叙述中，正确的是（ ）
A 、不再是平面波
B 、电场和磁场不同相
C 、振幅不变
D 、以T
E 波的形式传播
二、填空
1、一个半径为α的导体球作为电极深埋地下，土壤的电导率为
σ，略去地面的影响，则电极的接地电阻R =
2、 内外半径分别为a 、b 的无限长空心圆柱中均匀的分布着轴向电流I ，设空间离轴距离为()r r a <的某点处，B=
3、 自由空间中，某移动天线发射的电磁波的磁场强度
80.15cos(9.3610 3.12)/x t y A m =⨯-H e ， 则位移电流d
J = 4、 磁场强度cos()y m H t z ωβ=-H e ，则其复数形式为
5、 设海水的衰减系数为α ，则电磁波在海水中穿透深度（趋肤深度）为
6、 在无源的真空中，已知均匀的平面波电场为0j z x jE e β-=E e ，则此波的极化方式
为
7、 平面电磁波在空气中的传播速度
8310/o v c m s ==⨯，在04εε=的电介质中传播时，则速度v =
8、 均匀平面波垂直入射到理想导体表面上，入射波电场振幅
1m E 与反射波电场的振幅2m E 的关系是
9、 均匀平面波垂直入射到三层无损耗媒质上，两个分界面分别平行，其中特征阻抗12ηη=，媒质2中的波长为2λ，当媒质2的深度d = 时，电磁波可以无损耗的通过媒质2。
10，一均匀平面波自空气垂直入射到半无限大的无耗媒质表面上，已知空气中合成着的驻波比S=3 ，则 =
三、简答题
Maxwell 引入位移电流，建立了Maxwell 方程组，并预言了电磁波的存在，Maxwell 电磁场理论是电磁学的最核心内容，其地位相当于经典力学中的牛顿运动定律所处的地位。
请写出时域微分形式的Maxwell 方程组（每个方程1分），并简述每个方程的物理意义（每条1分），假设分界面的电荷密度为
s ρ，电流密度为S J ，请写出电磁场基本方程对应的
边界条件（每个边界条件1分）
四，综合计算题
1， 在自由空间传播的均匀平面波的电场强度复矢量为
(20)4204210110j j x y e e ππεπε-+---=+-E e e 求：
（1） 平面波的传播方向；（2分）
（2） 电磁波的频率；（2分）
（3） 波长λ；（2分）
（4） 磁场强度H ；（4）
（5） 电磁波流过沿传播方向单位面积的平均功率；（4分）
2， 入射波电场
9110cos(31010)/z t z V m ππ=⨯-E e ，从空气（z<0区域）中垂直入射到z=0的分界面上，在z>0区域中
1,4,0r r μεσ=== ，求： （1） z<0区域的电场1E 和磁场1H ；（8分）
（2） z>0区域的电场2E 和磁场2H ；（6分）。