高中数学 3.1.2《两角和与差的正弦、余弦、正切公式》导学案 新人教A版必修4
人教版高中数学全套教案导学案3.1.2两角和与差的正弦、余弦、正切公式(教、学案)

3. 1.2两角和与差的正弦、余弦、正切公式一、教材分析本节的主要内容是两角和与差的正弦、余弦和正切公式,为了引起学生学习本章的兴趣,理解以两角差的余弦公式为基础,推导两角和、差正弦和正切公式的方法,体会三角恒等变换特点的过程,理解推导过程,掌握其应用从而激发学生对本章内容的学习兴趣和求知欲。
二、教学目标⒈掌握两角和与差公式的推导过程;⒉培养学生利用公式求值、化简的分析、转化、推理能力; ⒊发展学生的正、逆向思维能力,构建良好的思维品质。
三、教学重点难点重点:两角和与差公式的应用和旋转变换公式;难点:两角和与差公式变aSina +bCosa 为一个角的三角函数的形式。
四、学情分析 五、教学方法1.温故、推新,循序渐进,以学生为主体逐步掌握本节知识要点 2.学案导学:见后面的学案。
3.新授课教学基本环节:预习检查、总结疑惑→情境导入、展示目标→合作探究、精讲点拨→反思总结、当堂检测→发导学案、布置预习六、课前准备 多媒体课件七、课时安排:1课时 八、教学过程(一)复习式导入:大家首先回顾一下两角和与差的余弦公式:()cos cos cos sin sin αβαβαβ+=-;()cos cos cos sin sin αβαβαβ-=+.这是两角和与差的余弦公式,下面大家思考一下两角和与差的正弦公式是怎样的呢? 提示:在第一章我们用诱导公式五(或六)可以实现正弦、余弦的互化,这对我们解决今天的问题有帮助吗?让学生动手完成两角和与差正弦和正切公式.()()sin cos cos cos cos sin sin 2222ππππαβαβαβαβαβ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫+=-+=-+=-+- ⎪ ⎪ ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎝⎭⎝⎭⎣⎦sin cos cos sin αβαβ=+.()()()()sin sin sin cos cos sin sin cos cos sin αβαβαβαβαβαβ-=+-=-+-=-⎡⎤⎣⎦ 让学生观察认识两角和与差正弦公式的特征,并思考两角和与差正切公式.(学生动手)()()()sin sin cos cos sin tan cos cos cos sin sin αβαβαβαβαβαβαβ+++==+-. 通过什么途径可以把上面的式子化成只含有tan α、tan β的形式呢?(分式分子、分母同时除以cos cos αβ,得到()tan tan tan 1tan tan αβαβαβ++=-.注意:,,()222k k k k z πππαβπαπβπ+≠+≠+≠+∈以上我们得到两角和的正切公式,我们能否推倒出两角差的正切公式呢?()()()()tan tan tan tan tan tan 1tan tan 1tan tan αβαβαβαβαβαβ+---=+-==⎡⎤⎣⎦--+ 注意:,,()222k k k k z πππαβπαπβπ+≠+≠+≠+∈.(二)例题讲解例1、已知3sin ,5αα=-是第四象限角,求sin ,cos ,tan 444πππααα⎛⎫⎛⎫⎛⎫-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值.解:因为3sin ,5αα=-是第四象限角,得4cos 5α===,3sin 35tan 4cos 45ααα-===- ,于是有43sin sin cos cos sin 444252510πππααα⎛⎫⎛⎫-=-=--=⎪ ⎪⎝⎭⎝⎭43cos cos cos sin sin 44455πππααα⎛⎫⎛⎫+=-=-=⎪ ⎪⎝⎭⎝⎭两结果一样,我们能否用第一章知识证明?3tan tan144tan 7341tan tan 144παπαπα---⎛⎫-===- ⎪⎛⎫⎝⎭++- ⎪⎝⎭例2、利用和(差)角公式计算下列各式的值: (1)、s i n 72c o s 42c o s 72s i n 42-;(2)、c o s 20c o s 70s i n 20s i n 70-;(3)、1t a n 151t a n 15+-.解:分析:解此类题首先要学会观察,看题目当中所给的式子与我们所学的两角和与差正弦、余弦和正切公式中哪个相象.(1)、()1s i n 72c o s 42c o s 72s i n 42s i n7242s i n 302-=-==; (2)、()c o s 20c o s 70s i n 20s i n 70c o s 2070c o s 900-=+==;(3)、()1t a n 15t a n 45t a n 15t a n 4515t a n 6031t a n 151t a n 45t a n 15++==+==--.例3x x解:此题与我们所学的两角和与差正弦、余弦和正切公式不相象,但我们能否发现规律呢?)()1cos sin 30cos cos30sin 22sin 302x x x x x x x ⎫-==-=-⎪⎪⎭思考:=余弦分别等于12.(三)反思总结,当堂检测。
3.1.2两角和差的正弦正切公式(导学案)

3.1.2 两角和与差的正弦公式【学习目标】1、掌握两角和与差的正弦公式及其推导方法。
2、通过公式的推导,了解它们的内在联系,培养逻辑推理能力。
并运用进行简单的三角函数式的化简、求值和恒等变形。
3、掌握诱导公式 sin =cos α,sin = cos α,sin =- cos α, sin =- cos α,【学习重点难点】 (一)预习指导: 两角和与差的余弦公式:cos(α+β)= cos(α-β)=(二)基本概念: 基本概念:1.两角和的正弦公式的推导sin(α+β)= sin(α-β)=(二)、典型例题选讲: 例1 不查表,求下列各式的值. (1)sin105°(2)sin80°cos20°- cos80°sin20°(3)cos(4)cos80°sin40°+cos10°sin50°⎪⎭⎫ ⎝⎛+απ2⎪⎭⎫ ⎝⎛-απ2⎪⎭⎫ ⎝⎛+απ23⎪⎭⎫⎝⎛-απ23103cos 5sin 103sin 5ππππ+例2已知sin α= ,α∈ ,cos β= - ,β是第三象限角,求sin (α-β)的值.【课堂练习】1.在△ABC 中,已知cosA = ,cosB= ,则cosC 的值为2.已知 <α< ,0<β<α,cos( +α)=- ,sin( +β)= ,求sin(α+β)的值.3.化简(1)sin α+cos α (2)sin α-cos α(3)sin α3+cos α (4)2sin α32-cos α(5)2cos χ-6sin χ (6)3sin α4-cos α31544π43π4π5343π13554⎝⎛⎪⎭⎫ππ,2135我们得到一组有用的公式:(1)sin α±sin α=2sin =2cos .(2)sin α3±cos α=2sin =2cos(3)αsin α+bcos α=22b a +sin (α+ϕ)=22b a +cos(α-θ)6.化解3cos χχsin -7.求证:cos χ+sin χ=2cos (χ - )8.求证:cos α+3sin α=2sin ( ).9.已知 ,将函数у=cos ( )-cos 化简.10.求 的值.【课堂小结】⎝⎛⎪⎭⎫±4πα ⎝⎛⎪⎭⎫4πα ⎝⎛⎪⎭⎫±3πα ⎝⎛⎪⎭⎫3πα 4παπ+6︒︒-︒20cos 20sin 10cos 2⎥⎦⎤⎢⎣⎡∈2,0πχχπ-12⎝⎛⎪⎭⎫+χπ1253.1.3 两角和与差的正切公式【学习目标】1.掌握两角和与差的正切公式及其推导方法。
高中数学3.1两角和与差的正弦余弦和正切公式3.1.2第2课时两角和与差的正切公式课件新人教A版必修四1

T(α-β)
[ 基础自测] 1.思考辨析 (1)存在α,β∈R,使tan(α+β)=tan α+tan β成立.( tan α+tan β (2)ቤተ መጻሕፍቲ ባይዱ任意α,β∈R,tan(α+β)= 都成立.( 1-tan αtan β ) )
tan α+tan β (3)tan(α+β)= 等价于tan α+tan β=tan(α+β)· (1-tan αtan β). 1-tan αtan β ( )
[自 主 预 习· 探 新 知]
两角和与差的正切公式 名称 两角和 的正切 两角差 的正切 简记 符号 T(α+β) 公式 tan(α+β)= tan α+tan β 1-tan αtan β _____________ tan(α-β)= tan α-tan β 1+tan αtan β ____________ 使用条件 π α,β,α+β≠kπ+2(k∈Z) 且 tan α· tan β≠1 π α,β,α-β≠kπ+2(k∈Z) 且 tan α· tan β≠-1
第三章
三角恒等变换
3.1 两角和与差的正弦、余弦和正切公式
3.1.2 两角和与差的正弦、余弦、正切公式 第2课时 两角和与差的正切公式
学习目标:1.能利用两角和与差的正弦、余弦公式推导出两角和与差的正 切公式.2.能利用两角和与差的正切公式进行化简、求值、证明.(重点)3.熟悉两 角和与差的正切公式的常见变形,并能灵活应用.(难点)
∵α,β 均为锐角, ∴α+β∈(0,π), π ∴α+β=4. (2)∵AD⊥BC 且 BD∶CD∶AD=2∶3∶6, BD 1 ∴tan∠BAD=AD=3, CD 1 tan∠CAD=AD =2, tan∠BAC=tan(∠CAD-∠BAD)
tan∠CAD-tan∠BAD = 1+tan∠CADtan∠BAD 1 1 2-3 = 1 1 1+2×3 1 =7.]
高中数学新人教版A版精品教案《3.1.2 两角和与差的正弦、余弦、正切公式》

例3:
引导学生小结:
学生说出了本节课学习的主要内容,还有化简中用到类比、整体代入的、化归与的数学思想。
学生自己先独立完成不会的组内讨论,
最后得出结果
例3的解决有两种方法
方法一、将例1中的
tan15°=
直接代入原式=
方法二、观察例2(3)题的形式发现
原式=
=tan(45°15°)
课题名称《两角和与差的正弦、余弦、正切公式》设 计 者谢君玉
单 位内蒙古巴彦淖尔市磴口县第一中学授课年级高一
章节名称
人教版普通高中课程标准实验教科书必修四
第三章三角恒等变换§两角和与差的正弦、余弦、正切公式(第1课时)
学 时
40分
课标要求
>对本节内容的要求是:
(1)经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用。
(让学生知道要到哪里去)
磴口电信公司准备将信号发射塔建在阿贵庙附近的一座小山上。
如图所示小山高BC约30米,在地平面上有一点A,测得A,C两点间的距离为60米,从A点观测电视发射塔的视角(∠CAD )约45°,求这座信号发射塔的高度。
由本地实际出发,提高学生学习兴趣。通过老师引导,学生发现,想解决发射塔的高度,需要知道 从而导入新课,让学生了解学习数学很有用
由同角三角函数的关系:tanα= 类比推导3:tanαβ=
思考:如何用tanα、tanβ表示tanαβ
思路:弦化切
(分子分母同除以coαcoβ)
注意:α、β的范围
(α、β、αβ≠ )
由两角和的正切推导4:tanα-β=
学生先猜想,接着证明,得出结论注意:(α、β、α-β≠ )
3.1.2两角和与差的正弦、正切公式-导学案

导学案年级: 高一 科目: 数学 主备: 审核:课题:两角和与差的正弦、正切公式 课型:新授课 课时 :2 课时 【三维目标】●知识与技能:能利用两角和与差的余弦公式,利用化归思想等推导出两角和与差的正弦、正切公式,体会它们的内在联系并进行简单的应用。
●过程与方法:进一步提高学生运用对比、联系、转化的观点去处理和分析问题的自觉性。
●情感态度与价值观:培养学生积极动手,勇于探索,善于发现,团结协作,独立意识以及不断超越自我的创新品质。
【学习重点】:引导学生通过独立探索和讨论交流,利用已学知识,推导出两角和与差的正弦和正切公式,并体会它们的内在联系。
【学习难点】:掌握两角和与差正弦、余弦、正切公式的逆用和变用。
【教学资源】教师导学过程(导案)学生学习活动(学案) 【导学过程1:】复习式导入:(1)大家首先回顾一下两角和与差的余弦公式:()βαβαβαsin sin cos cos cos =±;(2)()cos sin =α; (3)()()=αtan . 【学生学习活动1:】(1)回忆上节课所学知识,诱导公式和同角的基本关系为本节课学习作铺垫【导学过程2:】 讲授新课怎样由上述知识得到两角和与差的正弦和正切公式呢?活动1、学生动手完成两角和的正弦公式推导()()()诱导公式五βαβαβαπβαπβαπβαπβαsin cos cos sin sin 2sin cos 2cos 2cos 2cos sin +=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=+【学生学习活动2:】活动1、学生动手完成两角和的正弦公式推导()()()诱导公式五βαβαβαπβαπβαπβαπβαsin cos cos sin sin 2sin cos 2cos 2cos 2cos sin +=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-=⎥⎦⎤⎢⎣⎡+-=+ 活动2、怎样继而得到两角差的正弦公式;观察两角和与差的正弦公式的特征()()[]()()()换元的思想βαβαβαβαβαβαsin cos cos sin sin cos cos sin sin sin -=-+-=-+=-活动2、怎样继而得到两角差的正弦公式;观察两角和与差的正弦公式的特征()()[]()()()换元的思想βαβαβαβαβαβαsin cos cos sin sin cos cos sin sin sin -=-+-=-+=-小结1:()βαβαβαsin cos cos sin sin ±=±活动3、学生动手完成两角和的正切公式推导()()()()系同角三角函数的基本关βαβαβαβαβαβαβαβαβαtan tan 1tan tan sin sin cos cos sin cos cos sin cos sin tan -+=-+=++=+ 活动4、怎样继而得到两角差的正切公式;观察两角和与差的 正弦公式的特征()()[]()()()换元的思想----βαβαβαβαβαβαtan tan 1tan tan tan tan 1tan tan tan tan +-=-+=+=小结2:()βαβαβαtan tan 1tan tan tan ±=±其中,,,()222k k k k z πππαβπαπβπ+≠+≠+≠+∈将()βα+S 、()βα+C 、()βα+T 称为和角公式;()βα-S 、()βα-C 、()βα-T 称为差角公式。
高中数学3.1.2两角和与差的正弦、余弦、正切公式(一)教案新人教A版必修4
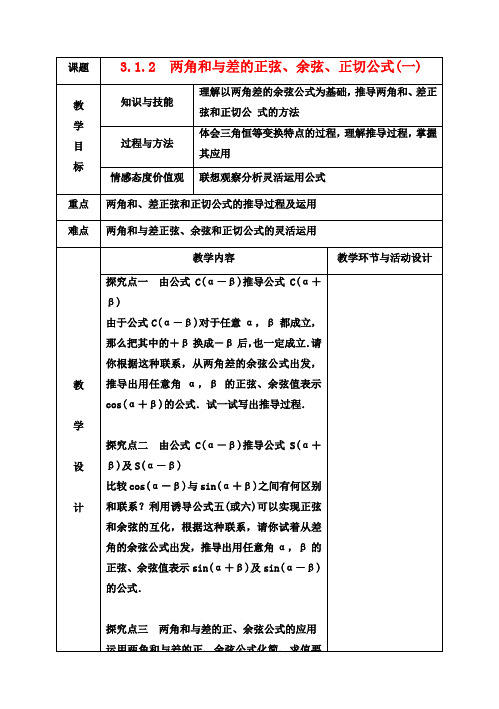
小结 此类题是给值求角题,步骤如下:(1)求所求角的某一个三角函数值;(2)确定所求角的范围,此类题常犯的错误是对角的范围不加讨论,范围讨论的程度过大或过小,会使求出的角不合题意或者漏解,同时要根据角的范围确定取该角的哪一种三角函数值.
跟踪训练2 已知sin α=35,cos β=-5
13,α
为第二象限角,
β为第三象限角.求sin(α+β)和sin (α-β)的值.
例3 已知sin(2α+β)=3sin β,求证:tan(α+β)=2tan α.
小结 证明三角恒等式一般采用“由繁到简”、“等价转化”、“往中间凑”等办法,注意等式两边角的差异、函数名称的差异、结构形式的差异.
跟踪训练3 证明:sin
2α+βsin α
-2cos(α+
β)=sin β
sin α
.。
高中数学3.1.2两角和与差的正弦、余弦、正切公式二教案新人教A版必修4

探究点一 两角和与差的正切公式的推导
问题 1 你能根据同角三角函数基本关系式tan α=sin α
cos α
,从两角和与差的正弦、余弦公式出发,推导出
用任意角α,β的正切值表示tan(α+β),tan(α-β)的公式吗?试一试.
探究点二 两角和与差的正切公式的变形公式 两角和与差的正切公式变形形式较多,例如:
tan α±tan β=tan(α±β)(1∓tan αtan β), tan αtan β=1-
tan α+tan βtan α+β=
tan α-tan β
tan α-β
-1.
答 当cos(α+β)≠0时,tan(α+β)=sin (α+β)cos (α+β)=sin αcos β+cos αsin β
cos αcos β-sin αsin β
.
当cos αcos β≠0时,分子分母同除以cos αcos β,得
tan(α+β)=tan α+tan β
1-tan αtan β
.
根据α,β的任意性,在上面式子中,以-β代替β得
tan(α-β)=tan α+tan (-β)1-tan αtan (-β)=tan α-tan β
1+tan αtan β
.
问题2 在两角和与差的正切公式中,α,β,α±β的取值是任意的吗?
答 在公式T (α+β),T (α-β)中α,β,α±β都不能等于k π+π2(k ∈Z ).
=tan 120°=- 3.。
高中数学第三章.2两角和与差的正弦余弦正切公式知识巧解学案新人教A版必修

学习资料专题3.1.2 两角和与差的正弦、余弦和正切公式疱工巧解牛知识•巧学一、两角和的余弦公式1.比较cos(α-β)与cos(α+β),根据α+β与α-β之间的联系:α+β=α-(-β),则由两角差的公式得cos(α+β)=cos[α-(-β)]=cosαcos(-β)+sinαsin(-β)=cosαcosβ-sinαsinβ,即cos(α+β)=cosαcosβ-sinαsinβ.学法一得这种以-β代β的变换角的方式在三角函数的恒等变形中有着重要应用,同时也启发我们要辩证地看待和角与差角.在公式C(α-β)中,因为角α、β是任意角,所以在C(α+β)中,角α、β也是任意角.2.用两点间的距离公式推导C(α+β).图3-1-5如图3-1-5,在直角坐标系xOy内作单位圆O,以O为顶点,以x轴的非负半轴为始边,作出角α、-β,使角α、-β的终边分别交单位圆于点P2、P4,再以OP2为始边,作角β,使它的终边交单位圆于点P3,这样就出现了α、β、α+β这样的角,设角α、-β的始边交单位圆于点P1,则P1(1,0).设P2(x,y),根据任意角的三角函数的定义,有sinα=y,cosα=x,即P2(cosα,sinα);同理,可得P3(cos(α+β),sin(α+β)),P4(cos(-β),sin(-β)).由整个作图过程可知△P3OP1≌△P2OP4,所以|P1P3|=|P2P4|.|P1P3|2=|P2P4|2,即[cos(α+β)-1]2+sin2(α+β)=[cos(-β)-cosα]2+[sin(-β)-sinα]2.根据同角三角函数的基本关系,整理得2-2cos(α+β)=2-2(cosαcosβ-sinαsinβ),即cos(α+β)=cosαcosβ-sinαsinβ.3.利用向量的数量积推导C(α+β).图3-1-6如图3-1-6,在平面直角坐标系xOy 内作单位圆,以Ox 为始边作角α、-β,它们与单位圆的交点分别为A 、B.显然,=(cos α,sin α),=(cos(-β),sin(-β)).根据向量数量积的定义,有·=(cos α,sin α)·(cos(-β),sin(-β))=cos αcos(-β)+sin αsin(-β)=cos αcos β-sin αsin β.于是cos(α+β)=cos αcos β-sin αsin β.学法一得 ①在处理问题的过程中,把有待解决或难解决的问题,通过某种转化,归结为一类已经解决或比较容易解决的问题,最终求得原问题的解,这种思想方法叫做化归思想. ②以任意角的三角函数的定义为载体,我们推导了同角的三角函数的基本关系式、诱导公式和两角和的余弦公式.熟记公式中角、函数的排列顺序及式中的正负号是正确使用公式的关键.记忆要诀 公式右端的两部分为同名三角函数之积,连接符号与左边的连接符号相反. 二、两角和与差的正弦 1.公式的推导sin(α-β)=cos[2π-(α-β)]=cos [(2π-α)+β]=cos(2π-α)cos β-sin(2π-α)sin β=sin αcos β-cos αsin β.在上面的公式中,以-β代β,即可得到sin(α+β)=sin αcos β+cos αsin β. 2.和差公式是诱导公式的推广,诱导公式是和差公式的特例.如sin(2π-α)=sin2πcos α-cos2πsin α=0×cos α-1×sin α=-sin α. 当α或β中有一个角是2π的整数倍时,通常使用诱导公式较为方便;上面公式中的α、β均为任意角.误区警示 公式对分配律不成立,即sin(α±β)≠sin α±sin β,学习时一定要注意这一点.学法一得 公式使用时不仅要会正用,还要能够逆用,如化简sin(α+β)cos β-cos(α+β)sin β,不要将sin(α+β)和cos(α+β)展开,而应当整体考察,进行如下变形:sin(α+β)cos β-cos(α+β)sin β=sin [(α+β)-β]=sin α,这也体现了数学中的整体原则.记忆要诀 记忆时要与两角和与差的余弦公式区别开来,两角和与差的正弦公式的右端的两部分为异名三角函数之积,连接符号与左边的连接符号相同. 三、两角和与差的正切 1.公式的推导利用两角和的正弦、余弦公式,可以推导出两角和的正切公式: tan(α+β)=βαβαβαβαβαβαsin sin cos cos sin cos cos sin )cos()sin(-+=++,当cos αcos β≠0时,我们可以将上式的分子、分母同时除以cos αcos β, 即得用tan α和tan β表示的公式:tan(α+β)=βαβαtan tan 1tan tan -+,在上面的公式中,以-β代β,可得两角差的正切公式:tan(α-β)=βαβαtan tan 1tan tan +-.2.公式成立的条件要能应用公式,首先要使公式本身有意义,即tan α、tan β存在.并且1+tan αtan β的值不为零,所以可得α、β需满足的条件:α≠k π+2π,β≠k π+2π,α+β≠k π+2π或α-β≠k π+2π,以上k∈Z .当tan α、tan β、tan(α±β)不存在时,可以改用诱导公式或其他方法解决.学法一得 两角和与差的正切同样不仅可以正用,而且可以逆用、变形用,逆用和变形用都是化简三角恒等式的重要手段,如tan α+tan β=tan(α+β)(1-tan αtan β)就可以解决诸如tan15°+tan30°+tan15°tan30°的问题.所以在处理问题时要注意考察式子的特征,巧妙运用公式或其变形,使变换过程简单明了. 典题•热题知识点一 所求角可表示成两个特殊角的和、差 例1 求sin 75°,tan15°的值.解:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30° =42621222322+=⨯+⨯; tan15°=tan(60°-45°)=32311345tan 60tan 145tan 60tan -=+-=︒︒+︒-︒,或tan15°=tan(45°-30°)=3233133130tan 45tan 130tan 45tan -=+-=︒︒+︒-︒. 例2 求︒︒-︒︒︒+︒8sin 15sin 7cos 8sin 15cos 7sin 的值.思路分析:观察被求式的函数名称的特点和角的特点,其中7°=15°-8°,15°=8°+7°,8°=15°-7°.无论采取哪种代换方式,都可减少角的个数.利用和角或差角公式展开,进行约分、化简、求值.若用7°=15°-8°代换,分子、分母是二次齐次式;若用15°=8°+7°或8°=15°-7°代换,分子、分母将会出现三次式,显然选择后者更好,不妨比较一下. 答案:原式=︒︒+︒-︒︒︒+︒+︒8sin )87sin(7cos 8sin )87cos(7sin︒︒︒-︒-︒︒︒︒+︒-︒=︒∙︒-︒︒︒-︒︒∙︒-︒︒︒+︒=8sin 8cos 7sin )8sin 1(7cos 8sin 8cos 7cos )8sin 1(7sin 8sin 7cos 8sin 8cos 7sin 7cos 8sin 7sin 8sin 8cos 7cos 7sin 2222︒︒-︒︒︒︒+︒︒=︒︒︒-︒∙︒︒︒︒+︒∙︒=8sin 7sin 8cos 7cos 8sin 7cos 8cos 7sin 8sin 8cos 7sin 8cos 7cos 8sin 8cos 7cos 8cos 7sin 22 3215tan 15cos 15sin -=︒=︒︒=.巧解提示:原式=︒∙︒-︒-︒︒∙︒+︒-︒8sin 15sin )815cos(8sin 15cos )815sin(︒∙︒-︒∙︒+︒∙︒︒∙︒+︒∙︒-︒∙︒=8sin 15sin 8sin 15sin 8cos 15cos 8sin 15cos 8sin 15cos 8cos 15sin︒∙︒︒∙︒=8cos 15cos 8cos 15sin =tan15°=tan(45°-30°) 3233133130tan 45tan 130tan 45tan -=+-=︒∙︒+︒-︒=. 方法归纳 三角函数式的结构一般由角、三角函数符号及运算符号三部分组成.因此三角恒等变换常常首先寻找式子所包含的各个角之间的联系,并以此为依据选择可以联系它们的适当公式,这是三角恒等变换的重要特点.无论是化简、求值,还是证明,其结果应遵循以下几个原则:①能求值的要求值;②三角函数的种类尽可能少;③角的种类尽可能少;④次数尽可能低;⑤尽可能不含根号和分母.知识点二 已知α、β的三角函数值,求α±β的三角函数值例3 已知sin α=31,求cos(3π+α)的值. 思路分析:因为3π是个特殊角,所以根据C (α+β)的展开式,只需求出cos α的值即可.由于条件只告诉了sin α=31,没有明确角α所在的象限,所以应分类讨论,先求cos α的值,再代入展开式确定cos(3π+α)的值.解:∵sin α=31>0,∴α位于第一、二象限.当α是第一象限角时,cos α=322)31(12=-, ∴cos(3π+α)=cos 3πcos α-sin 3πsin α=6322312332221-=⨯-⨯;同理,当α是第二象限角时,cos α=322-, ∴cos(3π+α)=6332+-.方法归纳 解这类给值求值问题的关键是先分清S (α±β)、C (α±β)、T (α±β)的展开式中所需要的条件,结合题设,明确谁是已知的,谁是待求的.其中在利用同角三角函数的基本关系求值时,应先解决与已知具有平方关系的三角函数值.但是,对于cos(π+α)、cos(2π+α)这样的函数求值,由于它们的角与2π的整数倍有关,所以无需按它们的展开式求值,直接利用诱导公式可能更简单. 例4 已知cos(α-2β)=91-,sin(2α-β)=32,并且2π<α<π,0<β<2π,求2c o sβα+的值.思路分析:观察给出的角)2()2(2βαβαβα---=+,结合公式C (α-β)展开式的特点,只需利用同角三角函数的基本关系计算出sin(α-2β)、cos(2α-β)的值即可. 解:∵2π<α<π,0<β<2π,∴4π<2α<2π,0<2β<4π.∴4π<α-2β<π,-4π<2α-β<2π. 又∵cos(α-2β)=91-<0,∴πβαπ<-<<22.∴954)91(1)2(sin 1)2sin(22=--=--=-βαβα. 同理,∵sin(2α-β)=32>0,∴220πβα<-<.∴35)32(1)2(sin 1)2cos(22=-=--=-βαβα. 故)]2()2cos[(2cosβαβαβα---=+=cos(α-2β)cos(2α-β)+sin(α-2β)sin(2α-β) 2757329543591=⨯+⨯-=.例5 在△ABC 中,sinA=53,cosB=135,求cosC. 思路分析:本题主要考查三角形中的三角函数问题.若不注意“△ABC”这个条件,就会产生多解,所以解这类问题时一定要注意尽量压缩角的范围,避开分类讨论,同时要注意结论是否符合题意. 解: ∵cosB=22135<,∴B∈(4π,2π)且sinB=1312.∵sinA=2253<,∴A∈(0,4π)∪(43π,π). 若A∈(43π,π),B∈(4π,2π),则A+B∈(π,23π)与A+B+C=π矛盾, ∴A ∉(43π,π).因此A∈(0,4π)且cosA=54.从而cosC=cos [π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=6516131********=⨯+⨯-. 例6 如图3-1-7,已知向量=(3,4)绕原点旋转45°到OP′的位置,求点P′(x′,y′)的坐标.图3-1-7思路分析:本题相当于已知角α的三角函数值,求α+45°的三角函数值. 解:设∠xOP=α.因为|OP|=54322=+,所以cos α=53,sin α=54. 因为x′=5cos(α+45°)=5(cos αcos45°-sin αsin45°)22)22542253(5-=⨯-⨯=,同理,可求得y′=5sin(α+45°)=227,所以P′(22-,227). 方法归纳 ①已知角α的某一三角函数值和角α所在的象限,则角α的其他三角函数值唯一;已知角α的某一三角函数值,不知角α所在的象限,应先分类讨论,再求α的其他三角函数值.②一般地,90°±α,270°±α的三角函数值,等于α的余名函数值,前面加上一个把α看成锐角时原函数值的符号,它的证明也可通过两角和、差的三角函数式进行.③在给值求值的题型中,要灵活处理已知与未知的关系,合理进行角的变换,使所求角能用已知角表示出来,所求角的三角函数值能用已知角的三角函数值表示出来. 知识点三 已知三角函数值求角 例7 已知sin α=55,sin β=1010,且α、β都是锐角,求α+β的值. 思路分析:(1)根据已知条件可先求出α+β的某个三角函数值,如cos(α+β).(2)由两角和的余弦公式及题设条件知只需求出cos α、cos β即可.(3)由于α、β都是锐角,所以0<α+β<π,y=cosx 在(0,π)上是减函数,从而根据cos(α+β)的值即可求出α+β的值.解:∵sin α=55,sin β=1010,且α、β都是锐角,∴cos α=552sin 12=-α,cos β= 10103sin 12=-β. ∴cos(α+β)=cos αcos β-sin αsin β=2210105510103552=⨯-⨯. 又∵0<α+β<π,∴α+β=4π. 方法归纳 给值求角的一般步骤是:①确定所求角的范围;②找到该范围内具有单调性的某一三角函数值;③先找到一个与之相关的锐角,再由诱导公式导出所求角的值. 知识点四 利用两角和、差的三角函数公式证明恒等式例8 已知3sin β=sin(2α+β),求证:tan(α+β)=2tan α.思路分析:观察条件等式和结论等式中的角,条件中含有β、2α+β,结论中含有α+β、α,若从条件入手,可采用角的变换,β=(α+β)-α,2α+β=(α+β)+α,展开后转化成齐次整式,约分得出结论.证明:∵3sin β=3sin [(α+β)-α]=3sin(α+β)cos α-3cos(α+β)sin α, sin(2α+β)=sin [(α+β)+α]=sin(α+β)cos α+cos(α+β)sin α, 又3sin β=sin(2α+β),∴3sin(α+β)cos α-3cos(α+β)sin α=sin(α+β)cos α+cos(α+β)sin α. ∴2sin(α+β)cos α=4cos(α+β)sin α. ∴tan(α+β)=2tan α.方法归纳 对条件恒等式的证明,若条件复杂,可从化简条件入手得出结论;若结论复杂,可化简结论得出条件;若条件和结论都较为复杂,可同时化简它们,直到找到它们间的联系. 知识点五 变用两角和差的三角函数公式化简求值 例9 用和、差公式证明tan12°+tan18°+33 tan12°·tan18°=33. 解:∵︒∙︒-︒+︒18tan 12tan 118tan 12tan =tan(12°+18°)=tan30°=33,∴tan12°+tan18°=33(1-tan12°·tan18°), 即左边=33(1-tan12°tan18°)+33tan12°tan18°=33=右边. ∴tan12°+tan18°+33tan12°·tan18°=33. 方法归纳 三角公式通过等价变形,可正用,可逆用,也可变用,主要是通过对函数结构式的变形与对角的分、拆、组合来实现的.例10 求(1+tan1°)(1+tan2°)(1+tan3°)……(1+tan45°)的值. 解:因为α+β=45°时,tan(α+β)=βαβαtan tan 1tan tan --+=1,所以tan α+tan β+tan αtan β=1,即(1+tan α)(1+tan β)=2.于是(1+tan1°)(1+tan44°)=(1+tan2°)(1+tan43°)=……=(1+tan22°)(1+tan23°)=2.又因为1+tan45°=2,所以原式=223. 方法归纳 当α+β=k π+4π,k∈Z 时,(1+tan α)(1+tan β)=2; 当α+β=k π-4π,k∈Z 时,(1+tan α)(1+tan β)=2tan αtan β. 问题•探究 思想方法探究问题1 在三角恒等变换中,三角公式众多,公式变换也是解决问题的有效手段,在应用这些公式时要注意些什么问题?探究过程:使用任何一个公式都要注意它的逆向变换、多向变换,这是灵活使用公式所必须的,尤其是面对那么多三角公式,把这些公式变活,显得更加重要,这也是学好三角函数的基本功.如:cos(α-β)cos β-sin(α-β)sin β化简为__________.将α-β看作一个角,β看作另一个角,则cos(α-β)cos β-sin(α-β)sin β=cos [(α-β)+β]=cos α. 解答本题时不仅利用角的变换:α=(α-β)+β,同时运用了公式的逆向变换. 探究结论:两角和的正切公式tan(α+β)=βαβαtan tan 1tan tan -+.除了掌握其正向使用之外,还需掌握如下变换:1-tan αtan β=)tan(tan tan βαβα++;tan α+tan β=tan(α+β)(1-tan αtan β);tan αtan βtan(α+β)=tan (α+β)-tan α-tan β等.两角和的正切公式的三种变形要熟悉,其在以后解题中经常使用,要能灵活处理.问题2 2004年重庆高考有一题为:求函数y=sin 4x+32sinxcosx-cos 4x 的最小正周期和最小值,并写出该函数在[0,π]上的单调递增区间.该函数变形后就需要用到形如asinx+bcosx(a 、b 不同时为零)的式子的变换,我们称之为辅助角变换,那么如何进行辅助角变换?探究过程:形如asinx+bcosx(a 、b 不同时为零)的式子可以引入辅助角变形为Asin(x+φ)的形式.asinx+bcosx=)cos sin (222222x ba b x b a a b a -+++,令cos φ=22ba a +,sin φ=22ba b +,则原式=22b a +(sinxcos φ+cosxsin φ)=22b a +sin(x+φ).(其中φ角所在象限由a 、b 的符号确定,φ角的值由tan φ=a b 确定,常常取φ=arctan ab). 探究结论:辅助角变换是三角变形的重要形式,它的应用十分广泛,特别是在数学中求三角函数的最值及物理学当中波的合成时,都是重要的工具.例如2sinx-3cosx ,就可以利用这一结论将其化为一个三角函数的形式,从而确定其最值,因为a=2,b=-3,A=1322=+b a ,所以2sinx-3cosx=13sin(x+φ),(其中φ在第四象限,且tan φ=23-),所以2sinx-3cosx 的最大值是13,最小值是13-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.2 《两角和与差的正弦、余弦、正切公式》导学案
【学习目标】
1. 能从两角差的余弦公式导出两角和的余弦公式,以及两角和与差的正弦、正切公式,了解公式间的内在联系。
2.能应用公式解决比较简单的有关应用的问题。
【重点难点】
1. 教学重点:两角和、差正弦和正切公式的推导过程及运用;
2. 教学难点:两角和与差正弦、余弦和正切公式的灵活运用. 【学法指导】
1.理解并掌握两角和与差的正弦、余弦、正切公式,初步运用公式求一些角的三角函数值;
2.经历两角和与差的三角公式的探究过程,提高发现问题、分析问题、解决问题的能力; 【知识链接】
1、在一般情况下sin(α+β)≠sin α+sin β,cos(α+β)≠cos α+cos β.
3sin ,sin()_________;sin()_________.
544ππ
θθθθ=-=-=则若是第四象限角,则
.___________)6
tan(,2tan =-=π
θθθ是第三象限角,求
2、等。
灵活运用,如注意角的变换及公式的)2
()2(2
),
()(2;)(βα
βαβ
αβαβααββαα---=+--+=-+=
已知=-=
+)tan(,5
2
)tan(βαβα41,那么的值为)5
tan(π
α+( ) A 、-
183 B 、183 C 、1213 D 、22
3
3.在运用公式解题时,既要注意公式的正用,也要注意公式的反用和变式运用.如公式tan(α±β)=
β
αβ
αtan tan 1tan tan ±可变形为:tan α±ta n β=tan(α±β)(1 tan αtan β);
±tan αtan β=1-
)
tan(tan tan βαβ
α±±,
.___________40tan 20tan 340tan 20tan =++
4、又如:asin α+bcos α=2
2
b a + (sin αcos φ+cos αsin φ)= 2
2
b a + sin(α+φ),其中tan φ=
a
b
等,有时能收到事半功倍之效. ;__________cos sin =+αα .___________cos sin =-αα
x x sin cos 3-=_____________.
提出疑惑
【学习过程】
(一)复习式导入:大家首先回顾一下两角和与差的余弦公式:
动手完成两角和与差正弦和正切公式.
观察认识两角和与差正弦公式的特征,并思考两角和与差正切公式.
通过什么途径可以把上面的式子化成只含有tan α、tan β的形式呢?(分式分子、分母同时除以
cos cos αβ,得到()tan tan tan 1tan tan αβ
αβαβ
++=
-.
注意:,,()2
2
2
k k k k z π
π
π
αβπαπβπ+≠
+≠
+≠
+∈
以上我们得到两角和的正切公式,我们能否推倒出两角差的正切公式呢?
()()()()
tan tan tan tan tan tan 1tan tan 1tan tan αβαβ
αβαβαβαβ
+---=+-=
=
⎡⎤⎣⎦--+
注意:,,()2
2
2
k k k k z π
π
π
αβπαπβπ+≠
+≠
+≠
+∈.
(二)例题讲解
例1、已知3sin ,5
αα=-是第四象限角,求sin ,cos ,tan 444πππααα⎛⎫⎛⎫⎛
⎫-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝
⎭的值.
例2、利用和(差)角公式计算下列各式的值: (1)、s i n 72c o s 42c o s 72s i n 42-
;(2)、c o s 20c o s 70s i n 20s i n 70
-
;(3)、
1t a n 151t
a n 15+-
.
例3x x
【学习反思】
【基础达标】
)(
37sin 83sin 37cos 7sin 1的值为、︒︒-︒︒
(A)23
-
(B)2
1-
(C)2
1
(D)2
3
)(
75tan 75tan 1 22的值为、︒
︒-
(A)32
(B)33
2
()32
-C (D)3
3
2-
)(
,3cos 2cos 3sin 2sin 3的值是则若、x x x x x =
(A)10
π
(B)6π
(C)5
π
(D)4
π
.________3sin ,2,23,51cos 4=⎪⎭⎫ ⎝⎛
+⎪⎭⎫ ⎝⎛∈=πθππθθ则若、
._________15tan 3115tan 3 5=︒
+︒
-、 ()()._________sin sin cos cos 6=+++ββαββα、
参考答案 1、2
1
-
2、C
3、A
4、10362+-
5、1
6、αcos
【拓展提升】
1. 已知()21tan ,tan ,544παββ⎛⎫+=-= ⎪⎝⎭求tan 4πα⎛
⎫+ ⎪⎝
⎭的值.
( )
2. 若.)tan(,2
1
cos cos ,21sin sin ,=-=--=-βαβαβαβα则均为锐角,且 3、函数⋅=x y 2
cos
π
)1(2
cos -x π的最小正周期是___________________.
4、α为第二象限角,)的值。
求为第一象限角,βαββα-==
2tan(.13
5
cos ,53sin
.
2
tan
22,1312)2cos(,54)2
sin(.5β
αβα
βαβαβ
α+---=-=
-
求为第三象限角,为第二象限角,且已知。
