组合数学第三章习题解答
组合数学第三章习题解答
m
i 0 nm
(c )
C (m l 1, m 1) C (m l , m) C (m l , m 1) C (m l , m 2) ...
(1)l C (m l , m l )
(a)
C (n m, n k ) C (n m, k m)
设这66个元素为a1<a2<a3<...<a66
构造b1=a2-a1, b2=a3-a1,…, b65=a66-a1, 令B={b1,b2,…,b65} 这65个元素属于1到326，如果这65个元素有任何一个属于P1， 则定理得证。 否则： B p2 p3 p4 p5 (2)因为。 65 1 1 17 4 因此至少有一个集合含至少B中17个元素，设这个集合为p2。 设这6个元素为： bi1 bi2 ... bi1 7
证明(a)
(a) A B与A B关于B互为余集， 因此 A B B A B
(b) A BC C AC B C A B C A B C与(C B) (C A)互为余集. A B C C (C B) (C A) C C A C B A B C
否则： e1 , e2 p5 构造： e2 e1 同样可证明e2-e1既可表示成p1中数之差，也可表示成p2p3p4中 数之差。 e2-e1是1到326中的数，设f=d2-d1
e p1 p2 p3 p4
因此：1到326的326个整数任意分成5部分，其中必有一部分 其中有一个数是另两个数之差，设ai=aj-ah,那么反过来： aj=ai+ah
3.12,一年级有100名学生参加中文、英文和数学的考试，其中92 人通过中文考试，75人通过英语考试，65人通过数学考试；其中 65人通过中英文考试，54人通过中文和数学考试，45人通过英语 和数学考试，求通过三门学科考试的学生数？
组合数学卢开澄课后习题答案
组合数学卢开澄课后习题答案组合数学是一门研究离散结构和组合对象的数学学科，它广泛应用于计算机科学、统计学、密码学等领域。
卢开澄是中国著名的组合数学家，他的教材《组合数学》是该领域的经典之作。
在学习组合数学的过程中，课后习题是巩固知识、提高能力的重要途径。
下面我将为大家提供一些卢开澄课后习题的答案。
第一章：集合与命题逻辑1.1 集合及其运算习题1：设集合A={1,2,3}，B={2,3,4}，求A∪B和A∩B的结果。
答案：A∪B={1,2,3,4}，A∩B={2,3}。
习题2：证明若A∩B=A∩C，且A∪B=A∪C，则B=C。
答案：首先，由A∩B=A∩C可得B⊆C，同理可得C⊆B，因此B=C。
然后，由A∪B=A∪C可得B⊆C，同理可得C⊆B，因此B=C。
综上所述，B=C。
1.2 命题逻辑习题1：将下列命题用命题变元表示：（1）如果今天下雨，那么我就带伞。
（2）要么他很聪明，要么他很勤奋。
答案：（1）命题变元P表示今天下雨，命题变元Q表示我带伞，命题可表示为P→Q。
（2）命题变元P表示他很聪明，命题变元Q表示他很勤奋，命题可表示为P∨Q。
习题2：判断下列命题是否为永真式、矛盾式或可满足式：（1）(P∨Q)→(P∧Q)（2）(P→Q)∧(Q→P)答案：（1）该命题为可满足式，因为当P为真，Q为假时，命题为真。
（2）该命题为永真式，因为无论P和Q取何值，命题都为真。
第二章：排列与组合2.1 排列习题1：从10个人中选取3个人，按照顺序排成一队，有多少种不同的结果？答案：根据排列的计算公式，共有10×9×8=720种不同的结果。
习题2：从10个人中选取3个人，不考虑顺序，有多少种不同的结果？答案：根据组合的计算公式，共有C(10,3)=120种不同的结果。
2.2 组合习题1：证明组合恒等式C(n,k)=C(n,n-k)。
答案：根据组合的计算公式可得C(n,k)=C(n,n-k)，因此组合恒等式成立。
3、组合数学第三章排列组合(1)
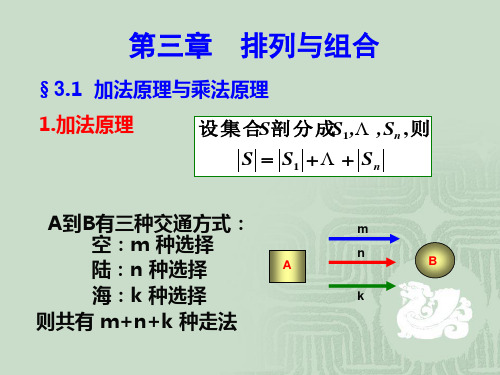
P（5，3）
（2）同（1），若不限制每天考试的次数，问有多 少种排法？
53
例3.8 排列26个字母，使得在a 和 b之间正好有7个 字母，问有多少种排法？
例3 用26个字母排列，是元音 a,e,i,o,u 组不相继 出现，有多少种排法？
（1）排列所有辅音：P(21,21)=21！ （2）在辅音前后的22个空档中排元音:
n2 +... + nk .
2若r=n,则N= n! ; n1 !n2 !...nk !
3若r < n且对一切i,i =1, 2,..., k,有ni ? r,则N=kr ; 4若r < n,且存在着某个ni < r,则对N没有一般的求解公式。
§3.5 多重集的组合
多重集S中r个元素进行无序选择，构成一个多重 集的r-组合。 篮子里有2个苹果，1个桔子，3个香蕉，篮子里 的水果构成“多重集”。
解1 (1)任意坐： n=9! (2)不相邻：A先就坐，B不相邻：7 其余8人排序：8！ m=7*8！ (3) P=m/n=7*8!/9!=7/9
例6 10个人为圆桌任意就坐，求指定的两个人 A与B不相邻的概率。
解2 (1)任意坐： n=9! (2)A,B相邻：A先就坐，B左右相邻：2 其余8人排序：8！ k=2*8！ (3)不相邻：m=9!-2*8! (4) 两人不相邻的概率 P=m/n=（9!-2*8!)/9!=1-2/9=7/9
证明
(1) 从{ 1,2,…,n }中选出2-组合有
C
2 n
(2) 另一种选法：
最大数为k的2-组合共有k-1个，k=1,2,…,n
有加法原理，共有 0+1+2+…+(n-1) 个2-组合
2021_2022学年新教材高中数学第三章排列组合与二项式定理3.1.3.2组合数的应用课时作业含解
课时作业(六) 组合数的应用一、选择题1．圆上有10个点，过每三个点画一个圆内接三角形，如此一共可以画的三角形个数为( )A．720 B．360C．240 D．1202．某电视台连续播放5个广告，其中有3个不同的商业广告和2个不同的奥运广告．要求最后必须播放奥运广告，且2个奥运广告不能连续播放，如此不同的播放方式有( )A．120种B．48种C．36种D．18种3．假如从1,2,3，…，9这9个整数中同时取4个不同的数，其和为偶数，如此不同的取法共有( )A．60种B．63种C．65种D．66种4．将标号为1,2，…，10的10个球放入标号为1,2，…，10的10个盒子里，每个盒内放一个球，恰好3个球的标号与其在盒子的标号不一致的放入方法种数为( )A．120 B．240C．360 D．720二、填空题5．某单位有15名成员，其中男性10人，女性5人，现需要从中选出6名成员组成考察团外出参观学习，如果按性别分层，并在各层按比例随机抽样，如此此考察团的组成方法种数是________．6．某球队有2名队长和10名队员，现选派6人上场参加比赛，如果场上最少有1名队长，那么共有________种不同的选法．7．现有6X风景区门票分配给6位游客，假如其中A，B风景区门票各2X，C，D风景区门票各1X，如此不同的分配方案共有________种．三、解答题8．某医院有内科医生12名，外科医生8名，现选派5名参加赈灾医疗队．(1)假如内科医生甲与外科医生乙必须参加，共有多少种不同选法？(2)假如甲、乙均不能参加，有多少种选法？(3)假如甲、乙2人至少有1人参加，有多少种选法？(4)假如医疗队中至少有1名内科医生和1名外科医生，有多少种选法？9．10件不同产品中有4件是次品，现对它们进展一一测试，直至找出所有4件次品为止．(1)假如恰在第5次测试，才测试到第一件次品，第10次才找到最后一件次品，如此这样的不同测试方法数是多少？(2)假如恰在第5次测试后，就找出了所有4件次品，如此这样的不同测试方法数是多少？[尖子生题库]10．按照如下要求，分别求有多少种不同的方法？(1)6个不同的小球放入4个不同的盒子；(2)6个不同的小球放入4个不同的盒子，每个盒子至少一个小球；(3)6个一样的小球放入4个不同的盒子，每个盒子至少一个小球．课时作业(六) 组合数的应用1．解析：确定三角形的个数为C310＝120.答案：D2．解析：最后必须播放奥运广告有C12种，2个奥运广告不能连续播放，倒数第2个广告有C13种，故共有C12C13A33＝36种不同的播放方式．答案：C3．解析：均为奇数时，有C45＝5种；均为偶数时，有C44＝1种；两奇两偶时，有C24·C25＝60种，共有66种．答案：D4．解析：先选出3个球有C310＝120种方法，不妨设为1,2,3号球，如此1,2,3号盒中能放的球为2,3,1或3,1,2两种．这3个放入标号不一致的盒子中有2种不同的方法，故共有120×2＝240种方法．答案：B5．解析：按性别分层，并在各层按比例随机抽样，如此需从10名男性中抽取4人，5名女性中抽取2人，共有C410C25＝2 100种抽法．答案：2 1006．解析：假如只有1名队长入选，如此选法种数为C12·C510；假如两名队长均入选，如此选法种数为C410，故不同选法有C12·C510＋C410＝714(种)．答案：7147．解析：6位游客选2人去A风景区，有C26种，余下4位游客选2人去B风景区，有C24种，余下2人去C，D风景区，有A22种，所以分配方案共有C26C24A22＝180(种)．答案：1808．解析：(1)只需从其他18人中选3人即可，共有C318＝816(种)选法．(2)只需从其他18人中选5人即可，共有C518＝8 568(种)选法．(3)分两类：甲、乙中有1人参加；甲、乙都参加．如此共有C12C418＋C318＝6 936(种)选法．(4)方法一(直接法)：至少有1名内科医生和1名外科医生的选法可分4类：1内4外；2内3外；3内2外；4内1外．所以共有C112C48＋C212C38＋C312C28＋C412C18＝14 656(种)选法．方法二：从无限制条件的选法总数中减去5名都是内科医生和5名都是外科医生的选法种数所得的结果即为所求，即共有C520－(C512＋C58)＝14 656(种)选法．9．解析：(1)先排前4次测试，只能取正品，有A46种不同测试方法，再从4件次品中选2件排在第5和第10的位置上测试，有C24A22＝A24种测法，再排余下4件的测试位置，有A44种测法．所以共有不同测试方法A46·A24·A44＝103 680种．(2)第5次测试恰为最后一件次品，另3件在前4次中出现，从而前4次有一件正品出现，所以共有不同测试方法C16·C34·A44＝576种．10．解析：(1)每个小球都有4种方法，根据分步乘法计数原理，共有46＝4 096种不同放法．(2)分两类：第1类，6个小球分3,1,1,1放入盒中；第2类，6个小球分2,2,1,1放入盒中，共有C36·C14·A33＋C26·C24·A24＝1 560(种)不同放法．(3)方法一：按3,1,1,1放入有C14种方法，按2,2,1,1，放入有C24种方法，共有C14＋C24＝10(种)不同放法．方法二：(挡板法)在6个球之间的5个空中插入三个挡板，将6个球分成四组，共有C35＝10(种)不同放法．。
组合数学习题解答
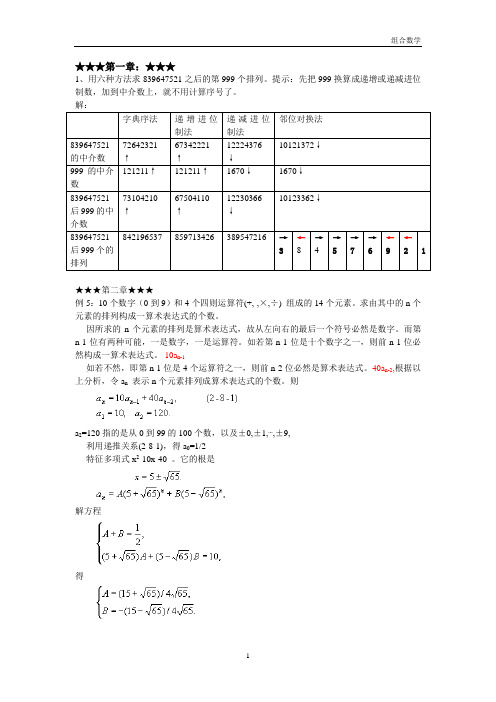
★★★第一章：★★★1、用六种方法求839647521之后的第999个排列。
提示：先把999换算成递增或递减进位制数，加到中介数上，就不用计算序号了。
解：字典序法递增进位制法递减进位制法邻位对换法839647521的中介数72642321↑67342221↑12224376↓10121372↓999的中介数121211↑121211↑1670↓1670↓839647521后999的中介数73104210↑67504110↑12230366↓10123362↓839647521后999个的排列842196537 859713426 389547216 →3←8→4→5→7→6←9←21★★★第二章★★★例5：10个数字（0到9）和4个四则运算符(+,-,×,÷) 组成的14个元素。
求由其中的n个元素的排列构成一算术表达式的个数。
因所求的n个元素的排列是算术表达式，故从左向右的最后一个符号必然是数字。
而第n-1位有两种可能，一是数字，一是运算符。
如若第n-1位是十个数字之一，则前n-1位必然构成一算术表达式。
10a n-1如若不然，即第n-1位是4个运算符之一，则前n-2位必然是算术表达式。
40a n-2,根据以上分析，令a n表示n个元素排列成算术表达式的个数。
则a2=120指的是从0到99的100个数，以及±0,±1,...,±9,利用递推关系(2-8-1)，得a0=1/2特征多项式x2-10x-40 。
它的根是解方程得例7：平面上有一点P，它是n个域D1,D2,...,D n的共同交界点，见图2-8-4现取k种颜色对这n个域进行着色，要求相邻两个域着的颜色不同。
试求着色的方案数。
令a n表示这n个域的着色方案数。
无非有两种情况（1）D1和D n-1有相同的颜色；（2）D1和D n-1所着颜色不同。
第一种情形，域有k-1种颜色可用，即D1D n-1域所用颜色除外；而且从D1到D n-2的着色方案，和n-2个域的着色方案一一对应。
《组合数学》第二版(姜建国著)-课后习题答案全
习题一（排列与组合）1．在1到9999之间，有多少个每位上数字全不相同而且由奇数构成的整数？解：该题相当于从“1，3，5，7，9”五个数字中分别选出1，2，3，4作排列的方案数；（1）选1个，即构成1位数，共有15P 个；（2）选2个，即构成两位数，共有25P 个；（3）选3个，即构成3位数，共有35P 个；（4）选4个，即构成4位数，共有45P 个；由加法法则可知，所求的整数共有：12345555205P P P P +++=个。
2．比5400小并具有下列性质的正整数有多少个？（1）每位的数字全不同；（2）每位数字不同且不出现数字2与7；解：（1）比5400小且每位数字全不同的正整数；按正整数的位数可分为以下几种情况：① 一位数，可从1～9中任取一个，共有9个；② 两位数。
十位上的数可从1～9中选取，个位数上的数可从其余9个数字中选取，根据乘法法则，共有9981⨯=个；③ 三位数。
百位上的数可从1～9中选取，剩下的两位数可从其余9个数中选2个进行排列，根据乘法法则，共有299648P ⨯=个；④ 四位数。
又可分三种情况：⏹ 千位上的数从1～4中选取，剩下的三位数从剩下的9个数字中选3个进行排列，根据乘法法则，共有3942016P ⨯=个；⏹ 千位上的数取5，百位上的数从1～3中选取，剩下的两位数从剩下的8个数字中选2个进行排列，共有283168P ⨯=个；⏹ 千位上的数取5，百位上的数取0，剩下的两位数从剩下的8个数字中选2个进行排列，共有2856P =个；根据加法法则，满足条件的正整数共有：9816482016168562978+++++=个；（2）比5400小且每位数字不同且不出现数字2与7的正整数；按正整数的位数可分为以下几种情况：设{0,1,3,4,5,6,8,9}A =① 一位数，可从{0}A -中任取一个，共有7个；② 两位数。
十位上的数可从{0}A -中选取，个位数上的数可从A 中其余7个数字中选取，根据乘法法则，共有7749⨯=个；③ 三位数。
组合数学(第3章3.3)
多重集的排列及组合
主要内容
多重集排列应用 多重集的组合及应用
回顾：多重集排列计数
定理3.4.2：令S是多重集，它有k个不同的 元素，每个元素的重复数分别为n1，n2，…， nk，那么，S的排列数等于 n! n1! n 2 !… n k ! 其中n= n1+n2+…+nk
多重集排列与集合划分
6 = 84
解：（1）方程x1+x2+x3+x4=10 （B）的正整数
例
3. 方程x1+x2+x3+x4=20的整数解的个数是多少？其中 x1≥3, x2≥1, x3≥0, x4≥5. 解：作变量代换：y1=x13， y2=x21， y3=x3， y4=x45，那么，得到方程： y1+y2+y3+y4=11。原 方程的解个数与该方程的非负整数解个数相同。 故为：
r + k - 1 r + k - 1 = r k -1
定理的证明
(1) 令S＝{∞a1, ∞a2,…, ∞ak}，那么S的一个r-组合 具有形式{x1a1, x2a2,…, xkak}，其中 x1+x2+…+xk=r （A） A xi是非负整数。 (2) 方程（A）的任何一个解确定S的一个r-组合，因 此，S的r-组合个数等于方程（A）解的个数。
11 + 4 1 14 11 = 11
问题？
令多重集S={n1a1, n2a2, …, nkak}，n= n1+n2+…+nk ，求S的r-组合数，其中0≤r≤n. 方程： x1+x2+…+xk=r 满足条件 0≤x1≤n1，0≤x2≤n2，…, 0≤xk≤nk 的整数解的个数。
《组合数学》第二版 姜建国著 课后习题答案全
只需证明 f 是满射函数即可。又因为 f 是定义在两个有限且基数相等的函
数上，因此如果能证明 f 单射，则 f 必是满射。
假设 f 不是单射，则存在 (am1, am2 ,, a2 , a1), (bm1, bm2 ,, b2 , b1) M ， (am1, am2 ,, a2 , a1) (bm1, bm2 ,, b2 , b1) ，且有 K0 N ，使得 K0 f (am1, am2 ,, a2 , a1) f (bm1, bm2 ,, b2 , b1) 由于 (am1, am2 ,, a2 , a1) (bm1, bm2 ,, b2 , b1) ，故必存在 j m 1 ，使得 a j bj 。不妨设这个 j 是第一个使之不相等的，即 ai bi (i m 1,, j 1) ， aj bj 且 aj bj ，
2．比 5400 小并具有下列性质的正整数有多少个？ （1）每位的数字全不同； （2）每位数字不同且不出现数字 2 与 7； 解：（1）比 5400 小且每位数字全不同的正整数； 按正整数的位数可分为以下几种情况： ① 一位数，可从 1～9 中任取一个，共有 9 个； ② 两位数。十位上的数可从 1～9 中选取，个位数上的数可从其余 9 个数 字中选取，根据乘法法则，共有 9 9 81个； ③ 三位数。百位上的数可从 1～9 中选取，剩下的两位数可从其余 9 个数 中选 2 个进行排列，根据乘法法则，共有 9 P92 648 个； ④ 四位数。又可分三种情况： 千位上的数从 1～4 中选取，剩下的三位数从剩下的 9 个数字中选 3 个进行排列，根据乘法法则，共有 4 P93 2016 个； 千位上的数取 5，百位上的数从 1～3 中选取，剩下的两位数从剩 下的 8 个数字中选 2 个进行排列，共有 3 P82 168 个； 千位上的数取 5，百位上的数取 0，剩下的两位数从剩下的 8 个数 字中选 2 个进行排列，共有 P82 56 个； 根据加法法则，满足条件的正整数共有：9 81 648 2016 168 56 2978 个；
李凡长版组合数学课后习题答案习题3
f(2)=1,f(3)=1,f(4)=2.
6. 求 n 位 0,1 序列中“ 010”只出现一次且在第 n 位出现的序列数 f(n). 解：最后三位是“ 010”的序列共有 2n-3 个。包括以下情况：
f(n) 包含了在最后三位第一次出现 010 的个数，同时排除了从
n-4 到 n-2 位第一次出现 010 的可能；
13. 在一个平面上画一个圆 , 然后一条一条地画 n 条与圆相交的直线 . 当 r 是 大于 1 的奇数时 , 第 r 条直线只与前 r －1 条直线之一在圆内相交 . 当 r 是偶数时 , 第 r 条直线与前 r －1 条直线都在圆内相交 . 如果无 3 条直线在 圆内共点 , 这 n 条直线把圆分割成多少个不重叠的部分？
2) 证明 f r (n, k)
n rk r , n r k( r 1)
k
解：可将本题转换为构造相应的 0－1 串的问题。将这样的 n 位 0－1 串与 1 到 n 的正整数对位，与 1 相应的整数选取，与 0 相应的不取。一个 0－1 串 对应一个选取方案。这也对应将相同的球放入不同的盒子的方案数。
解：设 f(n) 表示 n 个椭圆将平面分割成的部分的个数， 则有： 一个椭圆将平
面分成内、外两个部分，两个椭圆将平面分成 4 个部分。第二个椭圆的周界
被第一个椭圆分成两部分，这恰恰是新增加的域的边界。依此类推，第三个
椭圆曲线被前面两个椭圆分割成 4 部分，将平面分割成 4＋4＝8 个部分。若
n－ 1 个椭圆将平面分割成 f(n-1) 个部分， 第 n 个椭圆和前 n－1 个椭圆两两
f (n) (n 2) f (n 1) ( n 1)
（6）
；
f (0) 1
解： f(n)=(n+2)f(n-1)=(n+2)(n+1)f(n-2)=
组合数学讲义及答案 3章 递推关系
A 图 3.1.1
B Hanoi 塔问题
C
（解）特例：a1＝1，a2＝3，对于任何 n≥3。 一般情形： ： 第一步，将套在柱 A 的上部的 n－1 个盘按要求移到柱 B 上，共搬动了 a n1 次；
第二步，将柱 A 上的最大一个盘移到柱 C 上，只要搬动一 次； 第三步，再从柱 B 将 n－1 个盘按要求移到柱 C 上，也要 用 a n1 次。 由加法法则：
《组合数学》
第三章 递推关系
第三章
递推关系
§3.1 基本概念
（一） 递 推 关 系 定义3.1.1 （隐式）对数列 a i i 0和任意自然数 n，一
个关系到 an 和某些个 a i i n 的方程式， 称为递推关系， 记 作 F a0 , a1 , , a n 0 (3.1.1) 例
4／75
《组合数学》
第三章 递推关系
n 1 n -1 n n - 1 n - 2 2 2 2 an ＝ n 为奇数： 0 1 r 2 r ＋…＋ n - 1 r 2
后两项求和：
m 1 m 1 2m j 2 j r r r ＋ m 1 r j j 0
m2 m 1
＝r
2m 2 j j 0
j j r ＝ r
n 2 2
an 3an1 2an2 2a1 1
（二） 分 类 （1） 按常量部分： ① 齐 次 递 推 关 系 ： 指 常 量 ＝ 0 ， 如
Fn Fn1 Fn 2 ；
② 非齐次递推关系，即常量≠0，如 hn 2hn 1 1 。 （2） 按 a i 的运算关系：
组合数学【第5版】(英文版)第3章答案
Math475Text:Brualdi,Introductory Combinatorics5th Ed. Prof:Paul TerwilligerSelected solutions for Chapter31.For1≤k≤22we show that there exists a succession of consecutive days during which the grandmaster plays exactly k games.For1≤i≤77let b i denote the number of gamesplayed on day i.Consider the numbers{b1+b2+···+b i+k}76i=0∪{b1+b2+···+b j}77j=1.There are154numbers in the list,all among1,2,...,153.Therefore the numbers{b1+b2+···+b i+k}76i=0∪{b1+b2+···+b j}77j=1.are not distinct.Therefore there exist integers i,j(0≤i<j≤77)such that b i+1+···+b j=k.During the days i+1,...,j the grandmaster plays exactly k games.2.Let S denote a set of100integers chosen from1,2,...,200such that i does not divide j for all distinct i,j∈S.We show that i∈S for1≤i≤15.Certainly1∈S since 1divides every integer.By construction the odd parts of the elements in S are mutually distinct and at most199.There are100numbers in the list1,3,5,...,199.Therefore each of 1,3,5,...,199is the odd part of an element of S.We have3×5×13=195∈S.Therefore none of3,5,13,15are in S.We have33×7=189∈S.Therefore neither of7,9is in S.We have11×17=187∈S.Therefore11∈S.We have shown that none of1,3,5,7,9,11,13,15 is in S.We show neither of6,14is in S.Recall33×7=189∈S.Therefore32×7=63∈S. Therefore2×32×7=126∈S.Therefore2×3=6∈S and2×7=14∈S.We show10∈S. Recall3×5×13=195∈S.Therefore5×13=65∈S.Therefore2×5×13=130∈S. Therefore2×5=10∈S.We now show that none of2,4,8,12are in S.Below we list the integers of the form2r3s that are at most200:1,2,4,8,16,32,64,128,3,6,12,24,48,96,192,9,18,36,72,144,27,54,108,81,162.In the above array each element divides everything that lies to the southeast.Also,each row contains exactly one element of S.For1≤i≤5let r i denote the element of row i that is contained in S,and let c i denote the number of the column that contains r i.We must have c i<c i−1for2≤i≤5.Therefore c i≥6−i for1≤i≤5.In particular c1≥5so r1≥16,and c2≥4so r2≥24.We have shown that none of2,4,8,12is in S.By the above comments i∈S for1≤i≤15.3.See the course notes.4,5,6.Given integers n≥1and k≥2suppose that n+1distinct elements are chosen from{1,2,...,kn}.We show that there exist two that differ by less than k.Partition{1,2,...,nk}=∪ni=1S i where S i={ki,ki−1,ki−2,...,ki−k+1}.Among our n+1chosen elements,there exist two in the same S i.These two differ by less than k.17.Partition the set{0,1,...,99}=∪50i=0S i where S0={0},S i={i,100−i}for1≤i≤49,S50={50}.For each of the given52integers,divide by100and consider the remainder. The remainder is contained in S i for a unique i.By the pigeonhole principle,there exist two of the52integers for which these remainders lie in the same S i.For these two integers the sum or difference is divisible by100.8.For positive integers m,n we consider the rational number m/n.For0≤i≤n divide the integer10i m by n,and call the remainder r i.By construction0≤r i≤n−1.By the pigeonhole principle there exist integers i,j(0≤i<j≤n)such that r i=r j.The integer n divides10j m−10i m.For notational convenience define =j−i.Then there exists a positive integer q such that nq=10i(10 −1)m.Divide q by10 −1and call the remainder r. So0≤r≤10 −2.By construction there exists an integer b≥0such that q=(10 −1)b+r. Writingθ=m/n we have10iθ=b+r 10 −1=b+r10+r102+r103+···Since the integer r is in the range0≤r≤10 −2this yields a repeating decimal expansion forθ.9.Consider the set of10people.The number of subsets is210=1024.For each subset consider the sum of the ages of its members.This sum is among0,1,...,600.By the pigeonhole principle the1024sums are not distinct.The result follows.Now suppose we consider at set of9people.Then the number of subsets is29=512<600.Therefore we cannot invoke the pigeonhole principle.10.For1≤i≤49let b i denote the number of hours the child watches TV on day i.Consider the numbers{b1+b2+···+b i+20}48i=0∪{b1+b2+···+b j}49j=1.There are98numbers in the list,all among1,2,...,96.By the pigeonhole principle the numbers{b1+b2+···+b i+20}48i=0∪{b1+b2+···+b j}49j=1.are not distinct.Therefore there existintegers i,j(0≤i<j≤49)such that b i+1+···+b j=20.During the days i+1,...,j the child watches TV for exactly20hours.11.For1≤i≤37let b i denote the number of hours the student studies on day i.Considerthe numbers{b1+b2+···+b i+13}36i=0∪{b1+b2+···+b j}37j=1.There are74numbers in the list,all among1,2,...,72.By the pigeonhole principle the numbers{b1+b2+···+b i+13}36i=0∪{b1+b2+···+b j}37j=1are not distinct.Therefore there exist integers i,j(0≤i<j≤37)such that b i+1+···+b j=13.During the days i+1,...,j the student will have studied exactly13hours.12.Take m=4and n=6.Pick a among0,1,2,3and b among0,1,2,3,4,5such that a+b is odd.Suppose that there exists a positive integer x that yields a remainder of a(resp.b) when divided by4(resp.by6).Then there exist integers r,s such that x=4r+a and x=6s+bining these equations we obtain2x−4r−6s=a+b.In this equation the2left-hand side is even and the right-hand side is odd,for a contradiction.Therefore x does not exist.13.Since r (3,3)=6there exists a K 3subgraph of K 6that is red or blue.We assume that this K 3subgraph is unique,and get a contradiction.Without loss we may assume that the above K 3subgraph is red.Let x denote one of the vertices of this K 3subgraph,and let {x i }5i =1denote the remaining five vertices of K 6.Consider the K 5subgraph with vertices{x i }5i =1.By assumption this subgraph has no K 3subgraph that is red or blue.The only edge coloring of K 5with this feature is shown in figure 3.2of the text.Therefore we may assume that the vertices {x i }5i =1are labelled such that for distinct i,j (1≤i,j ≤5)the edge connecting x i ,x j is red (resp.blue)if i −j =±1modulo 5(resp.i −j =±2modulo5).By construction and without loss of generality,we may assume that each of x 1,x 2is connected to x by a red edge.Thus the vertices x,x 1,x 2give a red K 3subgraph.Now the edge connecting x and x 3is blue;otherwise the vertices x,x 2,x 3give a second red K 3subgraph.Similarly the edge connecting x and x 5is blue;otherwise the vertices x,x 1,x 5give a second red K 3subgraph.Now the vertices x,x 3,x 5give a blue K 3subgraph.14.After n minutes we have removed n pieces of fruit from the bag.Suppose that among the removed fruit there are at most 11pieces for each of the four kinds.Then our total n must be at most 4×11=44.After n =45minutes we will have picked at least a dozen pieces of fruit of the same kind.15.For 1≤i ≤n +1divide a i by n and call the reminder r i .By construction 0≤r i ≤n −1.By the pigeonhole principle there exist distinct integers i,j among 1,2,...,n +1such that r i =r j .Now n divides a i −a j .bel the people 1,2,...,n .For 1≤i ≤n let a i denote the number of people aquainted with person i .By construction 0≤a i ≤n −1.Suppose the numbers {a i }n i =1are mutually distinct.Then for 0≤j ≤n −1there exists a unique integer i (1≤i ≤n )such that a i =j .Taking j =0and j =n −1,we see that there exists a person aquainted with nobody else,and a person aquainted with everybody else.These people are distinct since n ≥2.These two people know each other and do not know each other,for a contradiction.Therefore the numbers {a i }n i =1are not mutually distinct.17.We assume that the conclusion is false and get a bel the people 1,2,...,100.For 1≤i ≤100let a i denote the number of people aquainted with person i .By construction 0≤a i ≤99.By assumption a i is even.Therefore a i is among 0,2,4,...,98.In this list there are 50numbers.Now by our initial assumption,for each even integer j (0≤j ≤98)there exists a unique pair of integers (r,s )(1≤r <s ≤100)such that a r =j and a s =j .Taking j =0and j =98,we see that there exist two people who know nobody else,and two people who know everybody else except one.This is a contradiction.18.Divide the 2×2square into four 1×1squares.By the pigeonhole principle there exists a 1×1square that contains at least two of the five points.For these two points the distance apart is at most √2.319.Divide the equilateral triangle into a grid,with each piece an equilateral triangle of side length1/n.In this grid there are1+3+5+···+2n−1=n2pieces.Suppose we place m n=n2+1points within the equilateral triangle.Then by the pigeonhole principle there exists a piece that contains two or more points.For these two points the distance apart is at most1/n.20.Color the edges of K17red or blue or green.We show that there exists a K3subgraph of K17that is red or blue or green.Pick a vertex x of K17.In K17there are16edges that contain x.By the pigeonhole principle,at least6of these are the same color(let us say red).Pick distinct vertices{x i}6i=1of K17that are connected to x via a red edge.Consider theK6subgraph with vertices{x i}6i=1.If this K6subgraph contains a red edge,then the twovertices involved together with x form the vertex set of a red K3subgraph.On the other hand,if the K6subgraph does not contain a red edge,then since r(3,3)=6,it contains a K3subgraph that is blue or green.We have shown that K17has a K3subgraph that is red or blue or green.21.Let X denote the set of sequences(a1,a2,a3,a4,a5)such that a i∈{1,−1}for1≤i≤5 and a1a2a3a4a5=1.Note that|X|=16.Consider the complete graph K16with vertex set X.We display an edge coloring of K16with colors red,blue,green such that no K3 subgraph is red or blue or green.For distinct x,y in X consider the edge connecting x and y.Color this edge red(resp.blue)(resp.green)whenever the sequences x,y differ in exactly 4coordinates(resp.differ in exactly2coordinates i,j with i−j=±1modulo5)(resp. differ in exactly2coordinates i,j with i−j=±2modulo5).Each edge of K16is now colored red or blue or green.For this edge coloring of K16there is no K3subgraph that is red or blue or green.22.For an integer k≥2abbreviate r k=r(3,3,...,3)(k3’s).We show that r k+1≤(k+1)(r k−1)+2.Define n=r k and m=(k+1)(n−1)+2.Color the edges of K m with k+1colors C1,C2,...,C k+1.We show that there exists a K3subgraph with all edges the same color.Pick a vertex x of K m.In K m there are m−1edges that contain x.By the pigeonhole principle,at least n of these are the same color(which we may assume is C1).Pick distinct vertices{x i}ni=1of K m that are connected to x by an edge colored C1.Considerthe K n subgraph with vertices{x i}ni=1.If this K n subgraph contains an edge colored C1,then the two vertices involved together with x give a K3subgraph that is colored C1.On the other hand,if the K n subgraph does not contain an edge colored C1,then since r k=n, it contains a K3subgraph that is colored C i for some i(2≤i≤k+1).In all cases K m hasa K3subgraph that is colored C i for some i(1≤i≤k+1).Therefore r k≤m.23.We proved earlier thatr(m,n)≤m+n−2n−1.Applying this result with m=3and n=4we obtain r(3,4)≤10.24.We show that r t(t,t,q3)=q3.By construction r t(t,t,q3)≥q3.To show the reverse inequality,consider the complete graph with q3vertices.Let X denote the vertex set of this4graph.Color the t -element subsets of X red or blue or green.Then either (i)there exists a t -element subset of X that is red,or (ii)there exists a t -element subset of X that is blue,or (iii)every t -element subset of X is green.Therefore r t (t,t,q 3)≤q 3so r t (t,t,q 3)=q 3.25.Abbreviate N =r t (m,m,...,m )(k m ’s).We show r t (q 1,q 2,...,q k )≤N .Consider the complete graph K N with vertex set X .Color each t -element subset of X with k colors C 1,C 2,...,C k .By definition there exists a K m subgraph all of whose t -element subsets are colored C i for some i (1≤i ≤k ).Since q i ≤m there exists a subgraph of that K m with q i vertices.For this subgraph every t -element subset is colored C i .26.In the m ×n array assume the rows (resp.columns)are indexed in increasing order from front to back (resp.left to right).Consider two adjacent columns j −1and j .A person in column j −1and a person in column j are called matched if they occupy the same row of the original formation.Thus a person in column j is taller than their match in column j −1.Now consider the adjusted formation.Let L and R denote adjacent people in some row i ,with L in column j −1and R in column j .We show that R is taller than L.We assume that L is at least as tall as R,and get a contradiction.In column j −1,the people in rows i,i +1,...,m are at least as tall as L.In column j ,the people in rows 1,2,...,i are at most as tall as R.Therefore everyone in rows i,i +1,...,m of column j −1is at least as tall as anyone in rows 1,2,...,i of column j .Now for the people in rows 1,2,...,i of column j their match stands among rows 1,2,...,i −1of column j −1.This contradicts the pigeonhole principle,so L is shorter than R.27.Let s 1,s 2,...,s k denote the subsets in the collection.By assumption these subsets are mutually distinct.Consider their complements s 1,s 2,...,s k .These complements are mutu-ally distinct.Also,none of these complements are in the collection.Therefore s 1,s 2,...,s k ,s 1,s 2,...,s k are mutually distinct.Therefore 2k ≤2n so k ≤2n −1.There are at most 2n −1subsets in the collection.28.The answer is 1620.Note that 1620=81×20.First assume that 100i =1a i <1620.We show that no matter how the dance lists are selected,there exists a group of 20men that cannot be paired with the 20women.Let the dance lists be bel the women 1,2,...,20.For 1≤j ≤20let b j denote the number of men among the 100that listed woman j .Note that 20j =1b j = 100i =1a i so ( 20j =1b j )/20<81.By the pigeonhole principle there exists an integer j (1≤j ≤20)such that b j ≤80.We have 100−b j ≥20.Therefore there exist at least 20men that did not list woman j .This group of 20men cannot be paired with the 20women.Consider the following selection of dance lists.For 1≤i ≤20man i lists woman i and no one else.For 21≤i ≤100man i lists all 20women.Thus a i =1for 1≤i ≤20and a i =20for 21≤i ≤100.Note that 100i =1a i =20+80×20=1620.Note also that every group of 20men can be paired with the 20women.29.Without loss we may assume |B 1|≤|B 2|≤···≤|B n |and |B ∗1|≤|B ∗2|≤···≤|B ∗n +1|.By assumption |B ∗1|is positive.Let N denote the total number of objects.Thus N = n i =1|B i |and N = n +1i =1|B ∗i |.For 0≤i ≤n define∆i =|B ∗1|+|B ∗2|+···+|B ∗i +1|−|B 1|−|B 2|−···−|B i |.5We have∆0=|B∗1|>0and∆n=N−N=0.Therefore there exists an integer r(1≤r≤n)such that∆r−1>0and∆r≤0.Now0<∆r−1−∆r=|B r|−|B∗r+1|so|B∗r+1|<|B r|.So far we have|B∗1|≤|B∗2|≤···≤|B∗r+1|<|B r|≤|B r+1|≤···≤|B n|.Thus|B∗i|<|B j|for1≤i≤r+1and r≤j≤n.Defineθ=|(B∗1∪B∗2∪···∪B∗r+1)∩(B r∪B r+1∪···∪B n)|.We showθ≥ing∆r−1>0we have|B∗1|+|B∗2|+···+|B∗r|>|B1|+|B2|+···+|B r−1|=|B1∪B2∪···∪B r−1|≥|(B1∪B2∪···∪B r−1)∩(B∗1∪B∗2∪···∪B∗r+1)|=|B∗1∪B∗2∪···∪B∗r+1|−θ=|B∗1|+|B∗2|+···+|B∗r+1|−θ≥|B∗1|+|B∗2|+···+|B∗r|+1−θ.Thereforeθ>1soθ≥2.6。
组合数学习题解答ex3
解
（c）的另一种解法：用格路说明组合意义 各点坐标：A0(m-1,l) Ai(m-1+i,l-i) Bj(m-1+j,l-j+1) 左=C(m+l-1,m-1)，为 O->A0 的路径数。设 O->P 的路径数为|P| 则，|A0|=|B1|-|A1|=|B1|-(|B2|-|A2|)=|B1|-|B2|+|A2|=|B1|-|B2|+|B3|-|A3|=
(1) 方案数=(n-1)!·2n (2) 设第 I 个单位的代表相邻的方案数为 Ai,i=1,2,…,n.
I ∑ ∑ I ∑ n
Ai
i =1
n
= (−1)k
Ai
k =0
I∈Φ(n,k ) i∈I
=
n k =0
(−1) k
n k
(2n
−
2k
− 1)!2 k
13. 一书架有 m 层，分别放置 m 类不同种类的书，每层 n 册。先将书架上的图书全部取出 清理。清理过程要求不打乱所有的类别。试问: （1）m 类书全不在各自原来层次上的方案数有多少？ （2）每层的 n 本书都不在原来位置上的方案数等于多少？ （3）m 层书都不在原来层次，每层 n 本书也不在原来位置上的方案数又有多少？ 解
解法二：用~a 代表 a
设三角形三点为(x1,y1), (x2,y2), (x3,y3)，则重心为((x1+x2+x3)/3, (y1+y2+y3)/3)。将整数分为等 价类~x1=~x2 mod 3，则有三类：~0, ~1, ~2。考察一维三点组的和被 3 整除对情况，共有四种： {~a,~a,~a}, {~0,~1,~2}，即每组含有一种或三种元素，若含有两种元素，其和必不能被 3 整除。 一维中最大的不满足集合为：{~0,~0,~1,~1}, {~1,~1,~2,~2}, {~0,~0, ~2,~2}。每组四个元素，发现
组合数学习题解答
第一章：1.2. 求在1000和9999之间各位数字都不相同，而且由奇数构成的整数个数。
解：由奇数构成的4位数只能是由1，3，5，7，9这5个数字构成，又要求各位数字都不相同，因此这是一组从5个不同元素中选4个的排列，所以，所求个数为：P(5,4)=120。
1.4. 10个人坐在一排看戏有多少种就坐方式？如果其中有两人不愿坐在一起，问有多少种就坐方式？解：这显然是一组10个人的全排列问题，故共有10！种就坐方式。
如果两个人坐在一起，则可把这两个人捆绑在一起，如是问题就变成9个人的全排列，共有9！种就坐方式。
而这两个人相捆绑的方式又有2种（甲在乙的左面或右面）。
故两人坐在一起的方式数共有2*9！，于是两人不坐在一 起的方式共有 10！- 2*9！。
1.5. 10个人围圆桌而坐，其中两人不愿坐在一起，问有多少种就坐方式？解：这是一组圆排列问题，10个人围圆就坐共有10!10 种方式。
两人坐在一起的方式数为9!92⨯,故两人不坐在一起的方式数为：9！-2*8！。
1.14. 求1到10000中，有多少正数，它的数字之和等于5？又有多少数字之和小于5的整数？解：(1)在1到9999中考虑，不是4位数的整数前面补足0，例如235写成0235,则问题就变为求：x 1+x 2+x 3+x 4=5 的非负整数解的个数，故有F （4，5）=⎪⎪⎭⎫ ⎝⎛-+=515456 (2)分为求：x 1+x 2+x 3+x 4=4 的非负整数解，其个数为F （4，4）=35x 1+x 2+x 3+x 4=3 的非负整数解，其个数为F （4，3）=20x 1+x 2+x 3+x 4=2 的非负整数解，其个数为F （4，2）=10x 1+x 2+x 3+x 4=1 的非负整数解，其个数为F （4，1）=4x 1+x 2+x 3+x 4=0 的非负整数解，其个数为F （4，0）=1将它们相加即得，F （4，4）+F （4，3）+F （4，2）+F （4，1）+F （4，0）=70。
组合数学第四版卢开澄标准答案-第三章解析
第三章3.12.一年级有100名学生参加中文，英语和数学的考试，其中92人通过中文考试，75人通过英语考试，65人通过数学考试；其中65人通过中，英文考试，54人通过中文和数学考试，45人通过英语和数学考试，试求通过3门学科考试的学生数。
[解].令：A 1={通过中文考试的学生}A 2={通过英语考试的学生}A 3={通过数学考试的学生}于是 |Z| =100，|A 1|=92，|A 2|=75，|A 3|=65|A 1∩A 2|=65，|A 1∩A 3|=54，|A 2∩A 3|=45此题没有给出：有多少人通过三门中至少一门；有多少人一门都没通过。
但是由 max{ |A 1|,|A 2|,|A 3| }=max{92,75,65}=92故可以认为：至少有92人通过三门中至少一门考试，即100≥|A 1∪A 2∪A 3|≥92至多有8人没通过一门考试，即0≤|1A ∩2A ∩3A | ≤8于是，根据容斥原理，有|A 1∪A 2∪A 3|=(|A 1|+|A 2|+|A 3|)-(|A 1∩A 2|+|A 1∩A 3|+|A 2∩A 3|)+|A 1∩A 2∩A 3|即 |A 1∩A 2∩A 3|=|A 1∪A 2∪A 3|-(|A 1|+|A 2|+|A 3|)+(|A 1∩A 2|+|A 1∩A 3|+|A 2∩A 3|)=|A 1∪A 2∪A 3|-(92+75+65)+(65+54+45)=|A 1∪A 2∪A 3|-232+164=|A 1∪A 2∪A 3|-68从而由 92-68≤|A 1∪A 2∪A 3|-68≤100-68即 24≤|A 1∪A 2∪A 3|-68≤32可得 24≤|A 1∩A 2∩A 3| ≤32故此，通过3门学科考试的学生数在24到32人之间。
也可用容斥原理，即|1A ∩2A ∩3A |=|Z|-(|A 1|+|A 2|+|A 3|)+(|A 1∩A 2|+|A 1∩A 3|+|A 2∩A 3|)-|A 1∩A 2∩A 3|=100-(92+75+65)+(65+54+45)-|A 1∩A 2∩A 3|=100-232+164-|A 1∩A 2∩A 3|=32－|A 1∩A 2∩A 3|从而有 |A 1∩A 2∩A 3|=32-|1A ∩2A ∩3A |由已知 0≤|1A ∩2A ∩3A |≤8，可得24≤|A 1∩A 2∩A 3|≤32故此，通过3门学科考试的学生数在24到32之间。
组合数学习题答案.
第一章答案 第二章答案 第三章答案 第四章答案第一章答案1．(a) 45 ( {1,6},{2,7},{3,8},…,{45,50} )(b) 45⨯5+(4+3+2+1) = 235( 1→2~6, 2→3~7, 3→4~8, …,45→46~50, 46→47~50, 47→48~50, 49→50 ) 2．(a) 5!8!(b) 7! P(8,5) (c) 2 P(5,3) 8! 3. (a) n!P(n+1, m) (b) n!(m+1)!(c) 2!((m+n-2)+1)! 4. 2 P(24,5) 20!5. 2⨯5⨯P(8,2)+3⨯4⨯P(8,2)6. (n+1)!-17. 用数学归纳法易证。
8. 41⨯319. 设 n=p 1n 1p 2n 2…p kn k , 则n 2的除数个数为 ( 2p 1+1) (2p 2+1) …(2p k+1).10．1）用数学归纳法可证n 能表示成题中表达式的形式；2）如果某n 可以表示成题中表达式的形式，则等式两端除以2取余数，可以确定a 1；再对等式两端的商除以3取余数，又可得a 2；对等式两端的商除以4取余数，又可得a 3；…；这说明表达式是唯一的。
11．易用C(m,n)=m!/(n!(m-n)!)验证等式成立。
组合意义：右：从n 个不同元素中任取r+1个出来，再从这r+1个中取一个的全体组合的个数；左：上述组合中，先从n 个不同元素中任取1个出来，每一个相同的组合要生复 C(n-1,r) 次。
12．考虑,)1(,)1(101-=-=+=+=∑∑n nk k k n nnk kknx n x kC x x C 求导数后有令x=1, 即知.210-==∑n nk kn n kC13. 设此n 个不同的数由小到大排列后为a 1, a 2, …, a n 。
当第二组最大数为a k 时，第二组共有2k-1种不同的可能，第一组有2n-k -1种不同的可能。
组合数学第三章课后习题答案
3.1题（宗传玉）某甲参加一种会议，会上有6位朋友，某甲和其中每人在会上各相遇12次，每二人各相遇6次，每三人各相遇3次，每五人各相遇2次，每六人各相遇一次，1人也没有遇见的有5次，问某甲共参加了几次会议解:设A i为甲与第i个朋友相遇的会议集，i＝1，…，6．则故甲参加的会议数为:28+5=33.3.2题（宗传玉）求从1到500的整数中被3和5整除但不被7整除的数的个数.解:设A3：被3整除的数的集合A5：被5整除的数的集合A7：被7整除的数的集合所以3.3.题（宗传玉）n个代表参加会议，试证其中至少有2人各自的朋友数相等。
解:每个人的朋友数只能取0，1，…，n－1．但若有人的朋友数为0，即此人和其他人都不认识，则其他人的最大取数不超过n－2．故这n个人的朋友数的实际取数只有n－1种可能．，所以至少有２人的朋友数相等．3.4题（宗传玉）试给出下列等式的组合意义.解:(a) 从n 个元素中取k 个元素的组合，总含有指定的m 个元素的组合数为)()(kn mn m k m n --=--。
设这m 个元素为a 1,a 2,…,a m ,Ai 为不含a i 的组合（子集），i=1,…,m.()∑∑∑==∈⊄==⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-+⎪⎪⎭⎫ ⎝⎛==⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫⎝⎛-=ml l m l l m i i lj i lk l n k m A k n k n m n k l n l j 01),(),...,(1m1i i i i i 1)1(A A A A 111213.5题（宗传玉）设有三个7位的二进制数：a1a2a3a4a5a6a7，b1b2b3b4b5b6b7，c1c2c3c4c5c6c7．试证存在整数i 和j，1≤i≤j≤7，使得下列之一必定成立：a i=a j=b i=b j，a i=a j=c i=c j，b i=b j=c i=c j．证：显然，每列中必有两数字相同，共有种模式，有０或１两种选择．故共有·2种选择．·2=6．现有7列，．即必有２列在相同的两行选择相同的数字，即有一矩形，四角的数字相等．3.6题（宗传玉）在边长为1的正方形内任取5个点试证其中至少有两点，其间距离小于证：把１×１正方形分成四个(1/2)×.则这５点中必有两点落在同一个小正方形内．而小正方形内的任两点的距离都小于．3.7题（王星）在边长为1的等边三角形内任取5个点试证其中至少有两点，期间距离小于1/2．证：把边长为１的三角形分成四个边长为1/2的三角形，如上图：则这５点中必有两点落在同一个小三角形中．小三角形中任意两点间的距离都小于1/2．3.8题（王星）任取11个整数，求证其中至少有两个数它们的差是10的倍数。
2024新教材高中数学3-1-3组合与组合数第2课时组合数的应用作业新人教B版选择性必修第二册
D．90
解析 C120－10＝35(条)．故选B.
解析 答案
4．某地招募了20名志愿者，他们编号分别为1号，2号，…，19号，
20号，如果要从中任意选取4人再按编号大小分成两组去做一些预备服务
工作，其中两个编号较小的人在一组，两个编号较大的人在另一组，那么
确保5号与14号入选并被分配到同一组的选取种数是( )
第一类：一个盒子内放1个小球，另一个盒子内放3个小球．先把小球
分为两组，其中一组1个，另一组3个，有C
1 4
种分法，再放到2个盒子内，
有A24种放法，共有C41A24种放法．
解
第二类：2个盒子内各放2个小球．先从4个盒子中选出2个盒子，有C42 种选法，然后把4个小球平均分成2组，每组2个，有C24种分法，共有C42C42种 放法．
解析 每个被选的人都无顺序差别，是组合问题．分两步完成：第一
步，选女工，有C
1 3
种选法；第二步，选男工，有C
2 7
种选法．故共有C31
C 27
种
不同的选法．
解析 答案
知识点二 有限制条件的组合问题
2. 某班级要从4名男生、2名女生中选派4人参加某次社区服务，如果
要求至少有1名女生，那么不同的选派方案种数为( )
解析
5．要排出某班一天中语文、数学、政治、英语、体育、艺术6堂课的 课程表，要求数学排在上午(前4节)，体育排在下午(后2节)，不同的排法种 数是________．
答案 192 解析 由题意，要求数学课排在上午(前4节)，体育课排在下午(后2 节)，有C14C12＝8种． 再排其余4节，有A44＝24种， 根据分步乘法计数原理知，共有8×24＝192种方法．
＝75种．
新教材高中数学第三章第1课时组合与组合数及组合数性质学生用书新人教B版选择性必修第二册(含答案)
新教材高中数学学生用书新人教B版选择性必修第二册：第1课时组合与组合数及组合数性质[课标解读] 1.通过实例，理解组合的概念；能利用计数原理、排列定义推导组合数公式.2.能够结合具体实例，理解排列、组合与两个计数原理的关系，能够运用两个计数原理推导排列、组合的相关公式，并能够运用它们解决简单的实际问题．【教材要点】知识点一组合的概念一般地，从n个不同对象中取出m(m≤n)个对象并成________，称为从n个不同对象中取出m个对象的一个组合．知识点二组合数的概念从n个不同对象中取出m(m≤n)个对象的________的个数，称为从n个不同对象中取出表示．m个对象的组合数，用符号C mn知识点三组合数公式及其性质(1)公式：C n m＝________＝________．(2)性质：C n m＝________，C n m＋C n m−1＝________．(3)规定：C n0＝________．【基础自测】1.下列判断不正确的是( )A.两个组合相同的充要条件是组成组合的对象完全相同B．从a1，a2，a3三个不同对象中任取两个对象组成一个组合，所有组合的个数为C23 C．从甲、乙、丙3名同学中选出2名去参加某两个乡镇的社会调查，有多少种不同的选法是组合问题D．从甲、乙、丙3名同学中选出2名，有3种不同的选法2．从2，3，5，7，11中每次选出两个不同的数作为分数的分子、分母，则可产生不同的分数的个数是________，其中真分数的个数是________．3．C62＝________，C1817＝________．4．从3，5，7，11这四个数中任取两个相乘，可以得到不相等的积的个数为________．题型1 组合的概念例1 判断下列各事件是排列问题还是组合问题．(1)10支球队以单循环进行比赛(每两队比赛一次)，这次比赛需要进行多少场次？(2)10支球队以单循环进行比赛，这次比赛冠、亚军获得者有多少种可能？(3)从10个人里选3个代表去开会，有多少种选法？(4)从10个人里选出3个不同学科的课代表，有多少种选法？状元随笔要确定是组合还是排列问题，只需确定取出的对象是否与顺序有关．方法归纳1．根据排列与组合的定义进行判断，区分排列与组合问题，先确定完成的是什么事件，然后看问题是否与顺序有关，与顺序有关的是排列，与顺序无关的是组合．2．区分有无顺序的方法把问题的一个选择结果写出来，然后交换这个结果中任意两个对象的位置，看是否会产生新的变化，若有新变化，即说明有顺序，是排列问题；若无新变化，即说明无顺序，是组合问题．跟踪训练1 判断下列问题是组合还是排列，并用组合数或排列数表示出来．(1)若已知集合{1，2，3，4，5，6，7}，则集合的子集中有3个元素的有多少？(2)8人相互发一个电子邮件，共发了多少个邮件？(3)在北京、上海、广州、成都四个民航站之间的直达航线上，有多少种不同的飞机票？有多少种不同的飞机票价？(4)从集合{1，2，3，4}中任取两个不同对象相乘，有多少个不同的结果？完成的“这件事”指的是什么？(5)从集合{1，2，3，4}中任取两个不同对象相除，有多少个不同结果？这是排列问题，还是组合问题？完成的“这件事”指的是什么？题型2 组合的列举问题(逻辑推理)例2 已知A ，B ，C ，D ，E 五个元素，写出每次取出3个元素的所有组合．方法归纳1．此类列举所有从n 个不同元素中选出m 个元素的组合，可借助本例所示的“顺序后移法”(如法一)或“树形图法”(如法二)，直观地写出组合，做到不重复不遗漏．2．由于组合与顺序无关．故利用“顺序后移法”时箭头向后逐步推进，且写出的一个组合不可交换位置．如写出ab 后，不必再交换位置为ba ，因为它们是同一组合．画“树形图”时，应注意顶层及下枝的排列思路，防止重复或遗漏．跟踪训练2 从5个不同的对象a ，b ，c ，d ，e 中取出2个，写出所有不同的组合．题型3 组合数公式的应用例3 (1)计算C 104－C 73·A 33.(2)求证：C n m ＝m ＋1n ＋1C n+1m+1. (3)从乒乓球运动员男5名、女6名中组织一场混合双打比赛，不同的组合方法种数为( )A ．C 52C 62B ．C 52A 62C ．C 52A 22C 62A 22D ．A 52A 62状元随笔 根据题目的特点，选择适当的组合数公式进行求值或证明．方法归纳关于组合数计算公式的选取1．涉及具体数字的可以直接用公式C n m＝A n m A mm ＝n (n−1)(n−2)···(n−m+1)m!计算．2．涉及字母的可以用阶乘式C n m ＝n!m!(n−m )!计算．3．计算时应注意利用组合数的性质C n m ＝C n n−m 简化运算．跟踪训练3 (1)10×9×8×···×41×2×3×···×7可表示为( )A ．A 106B ．A 107C ．C 106D ．C 107(2)算式m (m+1)(m+2)···(m+20)20!可以表示为( )A ．A m+2020B ．C m+2020 C ．21C m+2020D ．21C m+2021(3)新冠病毒爆发初期，全国支援武汉的活动中，需要从A 医院某科室的6名男医生、4名女医生中分别选派3名男医生和2名女医生，则不同的选派方案共有________种．(用数字作答)题型4 组合的性质 【思考探究】1．试用两种方法求：从a ，b ，c ，d ，e 5人中选出3人参加数学竞赛，2人参加英语竞赛，共有多少种选法？你有什么发现？你能得到一般结论吗？[提示] 方法一：从5人中选出3人参加数学竞赛，剩余2人参加英语竞赛，共C 53＝5×4×33×2×1＝10(种)选法．方法二：从5人中选出2人参加英语竞赛，剩余3人参加数学竞赛，共C 52＝5×42＝10(种)不同选法．经求解发现C 53＝C 52.推广到一般结论有C n m ＝C n n−m.2．从含有队长的10名排球队员中选出6人参加比赛，共有多少种选法？[提示] 共有C 106＝10×9×8×7×4×56×5×4×3×2×1＝210(种)选法．3．在2中，若队长必须参加，有多少种选法？若队长不能参加有多少种选法？由2，3，你发现什么结论？你能推广到一般结论吗？[提示] 若队长必须参加，共C 95＝126(种)选法．若队长不能参加，共C 96＝84(种)选法． 由2，3发现从10名队员中选出6人可分为队长参赛与队长不参赛两类，由分类加法计数原理可得：C 106 ＝C 95＋C 96.一般地：C n+1m ＝C n m ＋C n m−1.例4 (1)计算C 43＋C 53＋C 63＋…＋C 20183的值为( )A ．C 20194B ．C 20195C ．C 20194－1 D ．C 20195－1(2)解方程C 14x ＝C 142x−4的解为________．方法归纳1．性质“C n m ＝C n n−m”的意义及作用2．与排列组合有关的方程或不等式问题要用到排列数、组合数公式，以及组合数的性质，求解时，要注意由C n m中的m ∈N ＋，n ∈N ＋，且n ≥m 确定m ，n 的范围，因此求解后要验证所得结果是否适合题意．跟踪训练4 (1)化简：C m 9－C m+19＋C m 8＝________；(2)计算C 9996＋C 9997＝________．(3)若C 202n−3＝C 20n+2(n ∈N ＋)，则n ＝( ) A ．5 B ．7 C ．5或7 D ．5或6(4)若3A n 3－6A n 2＝4C n+1n−1，则n ＝( ) A ．8 B ．7 C ．6 D ．5教材反思3．1.3 组合与组合数第1课时组合与组合数及组合数性质新知初探·自主学习[教材要点]知识点一一组知识点二所有组合知识点三(1)A n mA m mn！m！(n−m)！(2)C n n−m C n+1m(3)1[基础自测]1．解析：A正确．因为只要两个组合的元素相同，不论元素的顺序如何，都是相同的组合．B正确．由组合数的定义可知正确．C错误．因为选出2名同学还要分到不同的两个乡镇，这是排列问题．D正确．因为从甲、乙、丙3人中选两名有：甲乙，甲丙，乙丙，共3个组合，即有3种不同选法．答案：C2．解析：产生分数可分两步：第一步，产生分子有5种方法；第二步，产生分母有4种方法，共有5×4＝20个分数，且各不相同．产生真分数，可分四类：第一类，当分子是2时，有4个真分数，同理，当分子分别是3，5，7时，真分数的个数分别是3，2，1，共有4＋3＋2＋1＝10个真分数．答案：20 10＝15，3．解析：C62＝6×52C1817＝C181＝18.答案：15 184．解析：从四个数中任取两个数的取法为C42＝6.答案：6课堂探究·素养提升例 1 解析：(1)是组合问题，因为每两个队比赛一次并不需要考虑谁先谁后，没有顺序的区别．(2)是排列问题，因为甲队得冠军、乙队得亚军与甲队得亚军、乙队得冠军是不一样的，是有顺序的区别．(3)是组合问题，因为3个代表之间没有顺序的区别．(4)是排列问题，因为3个人中，担任哪一科的课代表是有顺序的区别．跟踪训练1 解析：(1)已知集合的对象具有无序性，因此含3个元素的子集个数与元素的顺序无关，是组合问题，共有C73个．(2)发邮件与顺序有关，是排列问题，共发了A82个电子邮件．(3)飞机票与起点站、终点站有关，故求飞机票的种数是排列问题，有A42种飞机票；票价只与两站的距离有关，故票价的种数是组合问题，有C42种票价．＝6(个)不同结果．(4)共有C42＝4×32完成的“这件事”是指：从集合{1，2，3，4}中任取两个不同对象并相乘．(5)共有A42－2＝10(个)不同结果；这个问题属于排列问题；完成的“这件事”是指：从集合{1，2，3，4}中任取两个不同对象并相除．例2 解析：方法一：可按AB→AC →AD →BC →BD →CD 顺序写出，即所以所有组合为ABC ，ABD ，ABE ，ACD ，ACE ，ADE ，BCD ，BCE ，BDE ，CDE .方法二：画出树形图，如图所示．由此可以写出所有的组合：ABC ，ABD ，ABE ，ACD ，ACE ，ADE ，BCD ，BCE ，BDE ，CDE . 注意书写的规范性： ①注意是否与顺序有关；②注意按顺序列举，不重不漏．列举法适合总数比较少的情形．跟踪训练2 解析：要想写出所有组合，就要先将元素按照一定顺序排好，然后按顺序用图示的方法将各个组合逐个标出来，如图所示：由此可得所有的组合为ab ，ac ，ad ，ae ，bc ，bd ，be ，cd ，ce ，de .例3 解析：(1)原式＝C 104−A 73＝10×9×8×74×3×2×1－7×6×5＝210－210＝0.(2)证明：∵右边＝m+1n+1C n+1m+1＝m+1n+1·(n+1)！(m+1)！(n−m )！＝n ！m ！(n−m )！＝C n m，左边＝C n m ，∴左边＝右边，故原式成立．(3)分两步进行：第一步，选出两名男选手，有C 52种方法；第二步，从6名女生中选出2名且与已选好的男生配对，有A 62种．故有C 52A 62种．故选B.答案：(1)见解析 (2)见解析 (3)B 跟踪训练3 解析：(1)10×9×8×…×41×2×3×…×7＝A 107A 77＝C 107A 77A 77＝C 107.(2)m (m+1)(m+2)…(m+20)20！＝(m+20)！(m−1)！20！＝(m+20)！(m−1)！[(m+20)−(m−1)]！×21＝21C m+2021.(3)根据题意，从6名男医生、4名女医生中分别选派3名男医生和2名女医生，共有C 63·C 42＝20×6＝120种选派方案． 答案：(1)D (2)D (3)120例4 解析：(1)C +43C 53+C 63+⋯+C 2 0183＝C 44+C 43+C 53+…+C 2 0183−C 44＝C 54+C 53+…+C 2 0183－1＝…＝C 2 0184+C 2 0183－1＝C 2 0194－1.(2)由题意知{x =2x −4，2x −4≤14，x ≤14或{x =14−(2x −4)，2x −4≤14，x ≤14，解得x ＝4或6.答案：(1)C (2)4或6跟踪训练4 解析：(1)原式＝(C m 9+C m 8)－C m+19＝C m+19 −C m ＋19＝0. (2)C 9996+C 9997＝C 10097＝C 1003＝161 700.(3)由题意知{2n −3=n +20≤2n −3≤200≤n +2≤20n ∈N +或{2n −3+n +2=200≤2n −3≤200≤n +2≤20n ∈N +，即n ＝5或7.(4)由题意知，3n (n －1)(n －2)－6n (n －1)＝4×(n+1)n 2×1，解得n ＝5(n =23舍去).答案：(1)0 (2)161 700 (3)C (4)D。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.9 把从1到326的326个整数任意分为5个部分，试证其中有一部 分至少有一个数是某两个数之和，或是另一个数的两倍。 证明：用反证法，设存在划分。
P P2 P3 P4 P5 {1,...,326} 1
326 1 因为 1 66,因此必存在有一子集含66个元素 5 不妨设为P 1
i 1
6
i
12 C (6,1)
Ai 12 C (6,1) 6 C (6,2) 4 C (6,3) 3 C (6,4) 2 C (6,5) C (6,6) 72 90 80 45 12 1 28
28 5 33
共33次会议
2.求从1到500的整数中被3和5整除但不被7整除的数的个数.
解 设A3：被3整除的数的集合 A5：被5整除的数的集合 A7：被7整除的数的集合
A7 A5 A3 A5 A3 A7 A5 A3 500 500 3 5 7 33 4 29 3 5
3.6 在边长为1的正方形内任取5点，试证其中至少有两点，其间 距离小于 2 证 把１×１正方形分成四个相等的小正 方形．如下图：
2
则这５点中必有两点落在同一个小正方形 内．而小正方形内的任两点的距离都小于
1 2 1 2 2 ( ) ( ) 2 2 2
3.7 在边长为1的等边三角形内任取5点，试证至少有两点距离 小于1/2
第三章习题 3.1 某甲参加一种会议，会上有6位朋友，某甲和其中每人在 会上各相遇12次，每二人各相遇6次，每三人各相遇4次，每四 人各相遇3次，每五人各相遇2次，每六人各相遇一次，1人也没 有遇见的有5次，问某甲共参加了几次会议？ 1．解 设Ai为甲与第i个朋友相遇的会议集，i＝1，…，6．则
A
3.4 试给下列等式以组合意义
(a) C (n m, n k ) (1)l C (m, l )C (n l , k ), n k m
m
(b)
(c )
C (l 1, n m 1) (1) j C (n m, j )C (n m j l 1, l )
120 120 120 A2 A3 20, A2 A5 12, A2 A7 8 2 3 25 2 7 120 120 120 A3 A5 8, A3 A7 5, A5 A7 3, 3 5 3 7 5 7
bi j ai j 1 a1
c1 bi2 bi1 , c2 bi3 bi1 ,..., c16 bi1 7 bi1 ,
c j bi j1 bi1 ai j1 1 a1 ai1 1 a1 ai j1 1 ai1 1
设C={c1,c2,…,c16} 如果： C ( p1 p2 ) 否则：
证把边长为１的三角形分成四个边长为－的三角形，如下图：
则这５点中必有两点落在同一个小三角 形中．
3.8 任取11个数，求证其中至少有两个数它们的差是10的倍数。 证明：一个数是不是10的倍数取决于这个数的个位数是不是0，是 0就是10的倍数。 一个数的个位数只可能是0,1,...,9十个数，任取11个数，其中必 有两个个位数相同，那么这两个数的差的个位数必然是0。
3.12,一年级有100名学生参加中文、英文和数学的考试，其中92 人通过中文考试，75人通过英语考试，65人通过数学考试；其中 65人通过中英文考试，54人通过中文和数学考试，45人通过英语 和数学考试，求通过三门学科考试的学生数？
3.13,试证
(a) (b) A B B A B A BC C AC B C A B C
设这66个元素为a1<a2<a3<...<a66
构造b1=a2-a1, b2=a3-a1,…, b65=a66-a1, 令B={b1,b2,…,b65} 这65个元素属于1到326，如果这65个元素有任何一个属于P1， 则定理得证。 否则： B p2 p3 p4 p5 (2)因为。 65 1 1 17 4 因此至少有一个集合含至少B中17个元素，设这个集合为p2。 设这6个元素为： bi1 bi2 ... bi1 7 构造：
3. n代表参加会议，试证其中至少有2人各自的朋友数相等。 解：每个人的朋友数只能取0，1，…，n－1．以下分两种 情况讨论。 若有人的朋友数为0，即此人和其他人都不认识，则其他n1个人的最大取数不超过n－2．必有两人认识人数相等。 若没有人的朋友数为0，则这n个人的朋友数的实际取数只 有n－1种可能．所以至少有２人的朋友数相等。
3.5 设有3个7位的二进制数 a1 a2 a3 a4 a5 a6 a7, b1 b2 b3 b4 b5 b6 b7, c1 c2 c3 c4 c5 c6 c7, 试证存在整数i和j，1≤i<j≤7，使得下列之一必然成立： ai=aj=bi=bj,ai=aj=ci=cj,bi=bj=ci=cj 证明： 显然，每列中必有两数字相同，共有C(3,2)种模式，有０或１ 两种选择．故共有C(3,2)· 2种选择。C(3,2)· 2=6．现有7列，即 必有２列在相同的两行选择相同的数字，即有一矩形，四角的 数字相等．
(a)从n个元素中取k个元素的组合，总含m个指定的元素的组合 数为C(n-m,k-m),设这m个元素为a1,a2,...,am.Ai为不含ai的组 合，i=1,2,...,m
Ai C (n 1, k ) Ai1 Ai 2 ... Ail C (n l , k )
Ai1 Ai 2 ... Aim C (n, k ) C (m,1)C (n 1, k ) C (m,2)C (n 2, k ) ... (1) m C (m, m)C (n m, k )
di j ci j 1 ci1
e1 d i2 d i1 , e2 d i3 d i1
同样可证明ei既可表示成p1中元素之差，也可表示成p2p3p4 中元素之差，
否则： e1 , e2 p5 构造： e2 e1 同样可证明e2-e1既可表示成p1中数之差，也可表示成p2p3p4中 数之差。 e2-e1是1到326中的数，设f=d2-d1
Ai N i Ai , i 1,2,..., l
A0 N 0 A0 N 0 A1 N 0 ( N1 A1 ) ... N 0 N1 N 2 ... (1)l N l C (m l , m) C (m l , m 1) C (m l , m 2) ... C (m l , m l )
C p3 p4 p5
16 1 3 1 6
则定理得证
(3)因为。
因此至少有一个集合含至少C中6个元素，设这个集合为p3。 设这11个元素为： ci1 ci2 ... ci6
ci j bi j 1 bi1
构造： d1 ci2 ci1 , d 2 ci3 ci1 ,..., d 5 ci6 ci1 同样可证明d1和d2既可表示成p1中元素之差，也可表示成p2p3 中元素之差，
j 0
i 0 nm
C (m l 1, m 1) C (m l , m) C (m l , m 1) C (m l , m 2) ...
(1)l C (m l , m l )
(a)
C (n m, n k ) C (n m, k m)
A
B
C
R(
)
Ⅰ
=R( ) R( ) =(1+x)(1+3x+x2 ) =1+4x+4x2 + x3
故方案数＝3!－4· 2!+4 · 1!－1 · 0!＝1
Ⅱ
Ⅲ
3.11,n个球放到m个盒子中去，n<m(m-1)/2,试证其中必有两个盒 子有相同的球数。
证明：用反证法
假如没有两个盒子的球数相同，那么m个盒子中最少需要 0,1,2,...(m-1)共m(m-1)/2,因此必有两个盒子有相同的球数。
e p1 p2 p3 p4
因此：1到326的326个整数任意分成5部分，其中必有一部分 其中有一个数是另两个数之差，设ai=aj-ah,那么反过来： aj=ai+ah
3.10 A,B,C三种材料用作产品I,II,III的原料，但要求I禁止 用B和C作原料，II不能用B作原料，III不允许用A作原料，问 有多少种安排方案？ 解 按题意可得如下的带禁区的棋盘其中有阴影的表示禁 区． 禁区的棋子多项式为：
证明(a)
(a) A B与A B关于B互为余集， 因此 A B B A B
(b) A BC C AC B C A B C A B C与(C B) (C A)互为余集. A B C C (C B) (C A) C C A C B A B C
设D={d1,d2,…,d5} 如果： D ( p1 p2 p3)因为。
5 1 2 1 3
因此至少有一个集合含至少D中3个元素，设这个集合为p4。 设这3个元素为： 构造：
d i1 d i2 d i3
j1 n -m
l个相同的球放入n个不同的盒子里，指定的m个盒子为空，其他 盒子不空的方案数为C(l-1,n-m-1)
( c ) 设Ai为m+l个元素中取m+i个，含特定元素a的方案集；Ni为 m+l个元素中取m+i个的方案数．则：
N i C (m l , m i )
Ai C (m l 1, m i 1) Ai N i Ai C (m l , m i ) C (m l 1, m i 1) C (m l 1, m i ) Ai 1