天体物理导论作业
高中物理高考题解析-认识天体运动-考题及答案

课时分层作业(八)认识天体运动题组一开普勒定律的理解1.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于()A.B B.F1C.A D.F2B[根据开普勒第二定律,对任意一个行星来说,它与太阳的连线在相等时间内扫过相等的面积。
行星在近日点速率大于在远日点速率,即A为近日点,B 为远日点,太阳位于F1,故B正确。
]2.开普勒行星运动定律为万有引力定律的发现奠定了基础,根据开普勒定律可知,以下说法中正确的是()A.开普勒定律只适用于行星绕太阳的运动,不适用于卫星绕地球的运动B.若某一人造地球卫星的轨道是椭圆,则地球处在该椭圆的一个焦点上C.开普勒第三定律a3T2=k中的k值,不仅与中心天体有关,还与绕中心天体运动的行星(或卫星)有关D.在探究太阳对行星的引力规律时,得到了开普勒第三定律a3T2=k,它是可以在实验室中得到证明的B[开普勒定律既适用于行星绕太阳的运动,也适用于卫星绕行星的运动,故A错误;根据开普勒第一定律知,人造地球卫星的轨道是椭圆时,地球处在椭圆的一个焦点上,故B正确;开普勒第三定律a3T2=k中的k值只与中心天体有关,与绕中心天体运动的行星(或卫星)无关,故C错误;开普勒第三定律是通过观测到的数据研究归纳出来的,不能在实验室中得到证明,故D错误。
]3.(多选)以下关于开普勒行星运动的公式a3T2=k的理解正确的是()A.k是一个与环绕天体无关的量B.T表示行星运动的自转周期C.T表示行星运动的公转周期D.若地球绕太阳运转轨道的半长轴为a地,周期为T地;月球绕地球运转轨道的半长轴为a月,周期为T月,则a3地T2地=a3月T2月AC[公式a3T2=k中的k与中心天体有关,与环绕天体无关,中心天体不一样时,k值不一样,地球公转的中心天体是太阳,月球公转的中心天体是地球,故A正确,D错误。
T表示行星运动的公转周期,故B错误,C正确。
实测天体物理习题1D

《观测天体物理学》第一章 习题解答一、填空1. 目前获得天体信息的五个主要渠道(载体)是 电磁辐射 , 物质采样 ,宇宙射线, 中微子 , 引力波 。
2.天文台选址定点观测,主要是测定大气的 视宁度 , 大气积分水气含量,_大气消光天光背景__及___气象参数__。
3. 一个完整的天文光学观测仪器系统包括 望远镜;辐射分析仪;辐射探测器;计算机。
4 .对于地面天文观测,地球大气只有三个“大气窗口”,它们是: 光学 , 红外 , 射电 。
5. 现代地面大望远镜一定要有_主动光学___和__自适应光学__的先进技术来克服镜面由于温度变化和重力形变以及地球大气湍流的影响。
6. 哈勃空间望远镜的口径是_2.4__m 的_卡塞格林(R-C )__式望远镜, 它比地面望远镜的优点是:是不受地球大气的吸收、散射和抖动的影响 。
二、问答题:1. 计算正常情况和黑暗中人眼的理论分辨本领。
(正常情况下,人眼光瞳直径d 为2mm, 黑暗环境中d 为6mm )解答:由分辨本领公式:δ″=140/D正常情况下人眼的分辨角为140/2= 70″ ;黑暗中人眼的分辨角为140/6=23.″3。
2. 美国帕洛马天文台的 5.33 米望远镜(A =D/F=5.33/51.6),在卡塞格林焦点上附加目镜,计算最小的目镜焦距以及它的最低放大倍数。
解答:最大放大率 10)5330/"140/("704"/"4max≈⨯=∆⨯=θG 最小目镜焦距 m mm G F f 510660/51600/maxmin ≈== 最低放大倍数886/5330/min ≈==eyed d G 美国5米望远镜附加目镜的最短焦距为5mm; 最低放大倍数为D/d(人眼)=5330/6=888倍3 美国的凯克10米口径望远镜,目视时的分辨率是多少?解答:理论分辨角δ″=140/D=0.014″, 分辨率为1/δ″=71.4。
物理学导论试题及课后答案
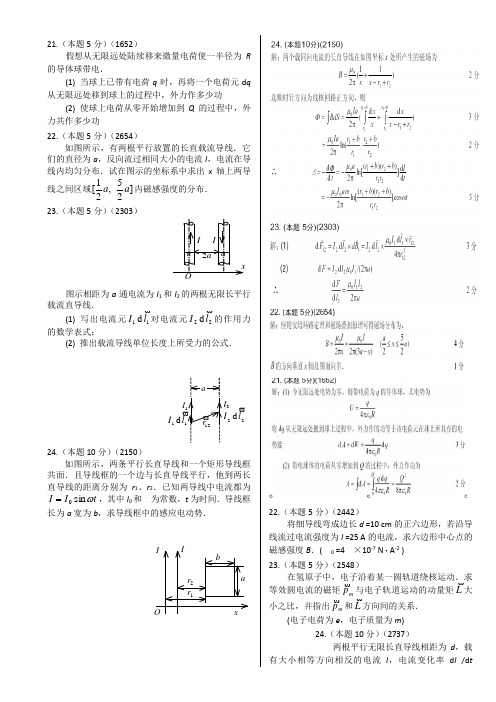
21.(本题5分)(1652)假想从无限远处陆续移来微量电荷使一半径为R 的导体球带电.(1) 当球上已带有电荷q 时,再将一个电荷元d q从无限远处移到球上的过程中,外力作多少功 (2) 使球上电荷从零开始增加到Q 的过程中,外力共作多少功22.(本题5分)(2654)如图所示,有两根平行放置的长直载流导线.它们的直径为a ,反向流过相同大小的电流I ,电流在导线内均匀分布.试在图示的坐标系中求出x 轴上两导线之间区域]25,21[a a 内磁感强度的分布. 23.(本题5分)(2303)图示相距为a 通电流为I 1和I 2的两根无限长平行载流直导线.(1) 写出电流元11d l I 对电流元22d l I 的作用力的数学表式;(2) 推出载流导线单位长度上所受力的公式.24.(本题10分)(2150)如图所示,两条平行长直导线和一个矩形导线框共面.且导线框的一个边与长直导线平行,他到两长直导线的距离分别为r 1、r 2.已知两导线中电流都为t I I sin 0 ,其中I 0和为常数,t 为时间.导线框长为a 宽为b ,求导线框中的感应电动势.22.(本题5分)(2442)将细导线弯成边长d =10 cm 的正六边形,若沿导线流过电流强度为I =25 A 的电流,求六边形中心点的磁感强度B .(0 =4×10-7 N ·A -2 )23.(本题5分)(2548)在氢原子中,电子沿着某一圆轨道绕核运动.求等效圆电流的磁矩m p与电子轨道运动的动量矩L 大小之比,并指出m p和L 方向间的关系.(电子电荷为e ,电子质量为m )24.(本题10分)(2737)两根平行无限长直导线相距为d ,载有大小相等方向相反的电流I ,电流变化率d I /d tIa aI xO2aII 21d l I22d l Ia12rIIOxr 1r 2 ab=>0.一个边长为d的正方形线圈位于导线平面内与一根导线相距d,如图所示.求线圈中的感应电动势,并说明线圈中感应电流是顺时针还是逆时针方向.ddII7-3 计算和证明题7-3-1解Q所受合力为零,即224l,求得Q7-3-2解场强大小为20044()a ladx lE dEx a a l,沿带电直线方向.7-3-3解如图建立坐标系,正负电荷关于x对称,它们在O点产生的场强沿y轴负向,在圆上取dl=Rdφdq=λdl=Rλdφ,它在O点产生场强大小为dE=24RRd方向沿半径向外则dE x=dEsinφ=dRsin4dE y=dEcos(π-φ)=R4cosφdφ积分22sin04xE dR2220002cos42yqE dR R R方向沿y轴负向.7-3-4解如图所示,dq dl Rd,它在圆心O点产生的场强200cos44Rd A ddER R其在x轴上的场强为cos()x xE dE dE2200cos44A d AR R方向沿x轴负向,其在y轴上的场强为sin()y yE dE dE2cos sin4A dR7-3-5解小球受力如图所示,由图可知,qE mgtg即2q mgtg,有622308.010/mgtgC mq7-3-6解在r R处取一细圆环,其带电量2dq dS rdr,根据教材例7-2-4结果可知,圆环在轴线上P点产生的场强大小223/2223/2223/200024()4()2()xdq x rdr x rdrdEx r x r x rxqEr22223/2223/222000()2()4()2RR x rdr x d x r E x r x r x R7-3-7解(1)11122222(2)(21) 1.05/e bd S b d S bd d N m C (2)由高斯定理可得,1209.2910ie iqC7-3-8解半圆柱薄筒的横截面如图所示,建立直角坐标系Oxy ,沿弧长方向取一宽度为dl 的细条,此细条单位长度上的带电量为dl Rd d R R, 此细条等同于无限长均匀带电直线,因此它在O 点产生的场强为20022d dE R R,20cos cos()2x d dE dE R, 20sin sin()2y d dE dE R,20cos 02x x d E dE R, 22000sin 2y y d E dE R R,20x y y E E i E j E j j Rr r r r r7-3-9解(1)以地面为高斯面,由高斯定理可得2111114ne iSi E dS E S E R qr r Ò,所以2510149.0310nii qE R C(2)如下图,由高斯定理1()e SE dS E E S nShr r Ò下上,所以有122120 1.0610/E E E E n C m h h下上7-3-10解我们可以设想不带电空腔内分布着体密度相同的正负电荷.由电场的叠加原理可知,有空腔的带电球体的电场,可以看作一个半径为R 电荷体密度为 的均匀带正电球体和一个半径为r 电荷体密度为 的均匀带负电球体所激发电场的叠加.即000E E E r r r由高斯定理可求出00E r,302004343a a E a r , 所以O 点的场强大小为0003a E E,方向沿OO u u u u r .同理,O 点的场强大小为 00003a E E E,方向仍沿OO u u u u r . 7-3-11解由电荷的轴对称性分析可知,场强也具有轴对称性,可利用高斯定理求场强.(1) 在r R 处,作一同轴圆柱形高斯面,由高斯定理n rn rE r 下E r 上hS 2S 1dl 1120ne iSi E dS rlE qr r Ò311110191436410 1.610910q U R C所以 0E (2) 在12R r R 处,类似(1),有102l rlE所以 102E r(3) 在2r R 处,类似(1),有1202rlE l所以 1202E r7-3-12解(1)A点电势为104A q U r,B点电势为B U,63.610J注 式中90210q C(2)C点电势为204C q U r,D 点电势为1202D q q U d,2120000())42CD C D q q q A q U U q r d63.610J 7-3-13解 (1)00E ,9493104104910 2.881040.05iO i iq U Vr(2)9360()010 2.8810 2.8810O O A q U U J ,0q 电势能的改变为60 2.8810O W A J (3)60 2.8810O W W A J7-3-14解(1)雨滴的电势为11014q U R,有(21,这时雨滴表面电势为9112202574q U V R 7-3-15解根据电势叠加原理,O 点的电势可看作直线AB 、DE 和半圆周BCD 所带电荷在O 点产生电势的叠加,AB 、DE 在O 点产生的电势为 21300ln 244RRdx U U x,半圆周BCD 在O 点产生的电势为 22000444q R U RR所以O 点产生的电势为1230(2ln 2)4U U U U1000()(4AB A B q A q U U q r12121122200044R R rR R q q q dr dr drr r7-3-16解 金核表面的电势为,金核中心的电势为7-3-17解 由高斯定理可求得Ⅰ、Ⅱ、Ⅲ区域的场强大小分别为10E ,12204q E r123204q q E r设1P 、2P 、3P 分别为Ⅰ、Ⅱ、Ⅲ区域内任一点, (1) Ⅰ区域内任一点1P 的电势由电势的定义式计算,有11P U E dlr r 1212123R R rR R E dl E dl E dl r r r r r r12121()4q q R R(2) Ⅱ区域内任一点2P 的电势由电势的定义式计算,有22P U E dlr r 2223R rR E dl E dl r r r r22112220044R rR q q q dr dr r r1221()4q q r R(3) Ⅲ区域内任一点3P 的电势由电势的定义式计算,有33P U E dlr r 3r E dl r r12204rq q dr r1204q q r7-3-18解 两“无限长”共轴圆柱面之间场强可由高斯定理求得为02E r式中 为单位长度上所带电量.由电势差的定义,两圆柱面之间的电势差为212001ln 22BR AB AR R U E dl dr r Rr r , 则8092124502.0810/102910ln ln 3AB U C m R R7-3-19解 由高斯定理可得场强分布为a x a 0E; x a 或x a 0E ;由电势的定义式计算电势分布在x a 区域,000axxaU Edx dx dx a在a x a 区域, 000xx U Edx dx x在a x区域,9197115091079 1.610 1.61047.010qU V R 72132000033 2.41044242RR qr q q U dr dr U V R r R00[ln ln()]ln 2l a a l a x l x a000axx a U Edx dx dx a电势U 随在x 分布如图所示7-3-20解 设坐标原点在左边导线轴线上,x 轴通过两导线并与之垂直.在两导线之间,坐标为x 的任一点P 的场强为0022()E x l x, 所以两导线间电势差为 00()22()l aAB aU dx x l x7-3-21解(1)在带电直线上取电荷元dq dx ,它在P 点的电势为 004()4()dq dxdU r x r x整个带电直线在P 点的电势为000ln 4()4lP r l U dx r x r(2)根据场强与电势的微分关系dUE dr,有 04()lE r r l7-3-22解 由高斯定理可求得均匀带电球体内外的场强分布为r R ,103rE; r R ,32203R E r(1)r R ,33220033r rrR R U E dr dr r r(2)r R ,320033R R R U R(3)r R,322122000(2)336RRr rRrR r R U E dr E dr dr dr R r r7-3-23解(1)r R 处,在圆柱体内任取一点,该点到轴线距离为r ,过该点作一半径为r ,高为l 的同轴闭合圆柱形高斯面,由高斯定理 11ne iSi E dS qr r Ò,可得312223ral rlE ar rldr r求得 23ar E 内,方向沿径向向外.对r R ,同理由高斯定理可得312223Ral rlE ar rldr R求得 30 3aR E r外(2)设1r m 处为电势零参考位置且假设该点在圆柱体外,则在r R区域内,33110ln 33r r aR aR U E dr dr r r 外外在r R区域内,23110033RRrRrR ar aR U E dr E dr dr dr r外内内33300()ln 93a aR R r R 8-3 计算和证明题8-3-1解 请参见教材P342题8-3-1图(1)由于静电感应,球壳内表面带电量为q ,外表面带电量为q ;球壳电势为33200344R R q q U E dl dr r Rr r 3(2)内表面带电量为q ,外表面带电量为0;球壳电势为0U 3(3)内球接地时,内球的电势0U 1,设内球此时带电量为q ,则球壳内表面带电量为q ;外表面带电量为q q ,空间场强分布为: 12R r R ,1204q E r;23R r R ,20E ;3r R ,3204q qE r; 因此,内球的电势 231231123R R R R R U E dr E dr E dr213220044R R R q q qdr drr r120311()044q q q R R R 求得12122313R R qq R R R R R R球壳的电势为3123303012231344R R R q q qU E dr R R R R R R R电势的改变为12333012231304R R qU U U U R R R R R R 8-3-2解 请参见教材P342题8-3-2图(1)设导体球上的感应电量为q ,这些感应电荷到球心O 点的距离都为R ,因此感应电荷q 在O 点产生的电势为04q R,点电荷q 在O 点产生的电势为042qR,故O 点的电势为000048q q U RR(导体球接地), 求得2q q(2)因O 点场强为零,故q 在O 点产生的场强大小等于q 在O 点产生的场强大小,方向相反,即为00q q E E E r r r所以 2016q q E R8-3-3解请参见教材P342题8-3-3图(1)设A 板两表面中左侧表面带电量为1q ,右侧表面带电量为2q ,其电荷面密度分别为11q S,22qS,由于B 、C 板都接地,故有 AC AB U UAC AC AB AB E d E d写成1200AC AB d d有12002q qS S① 又 12q q Q ② 由①②解得 12/3q Q ,2/3q Q 因此C板带电为712/3 2.010()C q q Q C ,72/3 1.010()B q q Q C(2)3200 2.2610()3A AB AB AB q Q U U d d V S S8-3-4解设导体片C 插入后,AC 间场强为1E ,CB 间场强为2E ,并假设0q ,则各板带电分布如图所示,并作如图所示的高斯面,两底面与板平行,由高斯定理可得120Sq S E dS E S E S Sr r Ò 即有 210qE E S① 由题意得 2122d dU E E② 由①②解得 20224C CB d U qdU U E S8-3-5解对于半径为R 的金属球,不论是实心还是空心,当带电量为q 时,其电势均为04q U R,则电容为04qC R U,可见电容是相同的. 对于地球,711C F 8-3-6解(1)设内、外金属膜圆筒半径分别为1R 和2R ,高度均为L ,其上分别带电量为Q ,则玻璃内的场强为12R r R , 02r Q E Lr内外圆筒之间的电势差为21201ln2R R r R Q U E dl LRr r 莱顿瓶的电容为 90212 2.2810ln r L qC F R U R(2)圆柱形电容器两金属膜之间靠近内膜处场强为最大,令该处场强等于击穿场强,即 101()2r Q E R E LR击穿所以 5012 6.6710r Q LR E C 击穿 8-3-7解 (1)由123111AB C C C C ,求得3.75AB C F(2)总电量43.7510AB AB Q C U C因为1C 和2C 并联,故有1212Q Q C C 即有 122Q Q ①又 12Q Q Q ② 由①②求得2C 带电量为4211.25103Q Q C,2C 上的电压22225QU V C(3)3100U U V ,4333510Q C U C8-3-8解(1)作一高斯面,使其两底面分别在板中和介质中且平行于板面,由介质中的高斯定理1n iSi D dS qrr Ò可得0D S S 求得 0Q D S又0()[()]r U E d t Et d t t E求得 ()r UE d t t因此 00()r r r UD E d t t(2)由上面结果可知 00()r r USQ S DS d t t(3)0()r r S QC U d t t8-3-9解(1)由题意极板间带电量Q 不变,00000SQ Q C U U d(2)电位移00SQ D S d,介质中的场强000rU DE d(3)电容大小与带电量多少无关,由题意可知 0()r r SC d t t8-3-10解设单位长度带电量为,则两极板间场强2E r,击穿场强0E 一定时,02rE 最大,电容器两极板电压为0ln ln 2RrR R U Edr rE r r式中r 是变量,适当选择r 的值,可使U 有极大值,即令 00ln 0dU RE E dr r , 求得0Rr e故当0Rr e时,电容器可能承受的最大电压为 0max 000ln 147RE R U r E KV r e8-3-11解(1)当1R r R ,由介质中的高斯定理可得0SD dS Qrr Ò,即有204r D Q求得 024QD r ,所以有 012004rr Q DE r当2R r R ,02204Q DE r(2)电势差为222220000041121()()222142312r Q Q Q Q C U C C C C () 2112RR R RU E dr E dr2100220044RR R Rr Q Q dr drr r01211()4r rrQ R R R(3)001221124()()r r Q RR R C U R R R R R R (4)2122220102114422RR r R R W E r dr E r dr2001211()8r rrQ R R R(5)00211(1)(1)4rrQ R8-3-12解(1)在12R r R 区域内作以r 为半径,长为l 的同轴柱面为高斯面,则由介质中的高斯定理1n i Si D dS qrr Ò,有2rlD l所以 2D r又 0r D E我们得到离轴线距离为r 处的场强为 02r E r, 方向沿径向向外(2)22112001ln 22R R R R r r R U Edr dr r R(3)2122200112ln 24R r R r R W E rdr R8-3-13解(1)282014.410/2e w E J m (2)3354[()]7.6103e W R h R w J式中R 为地球半径并取6370R km8-3-14解(1)浸入煤油后,电容器电容增加为原来的r 倍,即002r C C C ,而电量不变.能量损失为2222210200000111(1)9109002222444Q Q Q Q W C U C C C C 41.8210J(2)若将两电容器并联,则要发生电荷转移,但电荷总量不变,仍为2Q .并联后总电容为001r C C C C 总(), 两电容器并联后总能量为22024221rQ Q W C C总()() 并联后能量损失为0W W W W() 56.110J8-3-15解K接到1处,1C 带电为641108101209.610()Q C U C ;再将K 接到2后,1C 和2C 总带电量仍为1Q ,两电容器电压为4169.6108010Q U V C 总(8+4) 电容器1C 中的能量2622111181080 2.561022W C U J电容器2C 中的能量22221 1.28102W C U J8-3-16解据题意,把电子看作电荷均匀分布在外表面上,其静电能为222200200111()422424R e e W E dV r dr r R在估计电子半径的数量级时,一般可以略去上式中的系数,因此204eW R,据题意2204e em C R,我们可以求得21520 2.8104e e R m m C8-3-17解当介质板插入x 距离时,电容器的电容为000()[(1)]r x r a x a xaaC a x ddd此时电容器储能为220()22[(1)]x r Q Q dW x C a a x电介质未插入时,电容器储能为22020022Q Q dW C a当电介质插入x 时,电场力F 对电介质板所作的功等于电容器储能的减少量,即0()W W x ,电场力为当插入一半时,2ax ,则电场力为,方向平行极板向右.8-3-18解(1)因电压U 不变,拉开前的静电能为 222001111222SS W C U U U d d拉开后的静电能为2220022112224S S W C U U U d d则系统静电能的改变为222000210424SSSW W W U U U ddd结果表明当极板拉开后,系统的静电能减少.(2)当保持电压一定时,电场对电源作功为 A U Q两板距离从d 拉开到2d 时,极板上电荷的增量Q 为0002121()22S SSQ Q Q C U CU U Ud dd因此 200()022SSA U Q U U U dd结果表明当极板拉开后,在保持U 不变时,电场对电源作正功.(3)外力F 对极板作的功为2222220021(222dd d dd d SU SU CU A F dl dx dx x d dr r外力F 对极板作的功,也可由功能关系得到222000()424SU SU SU A W A ddd所得结果相同. 8-3-19解(1)令无限远处电势为零,则带电荷为q 的导体球,其电势为04q U R,将dq 从无限远处搬到球上的过程中,外力作的功等于该电荷元在球上所具有的电势能 04q dA dW dq R(2)外力作功为200048Qq Q A dA dq RR2020[()](1)2[(1)]r r W W x Q d F x a a x23302(1)()2(1)r r Q d a F a8-3-20解因为电荷保持不变,故有、无介质时,电场中各点的电位移矢量D r不变,电场能量密度为2000111222e e r r rw D D w DE D电场总能量为e rW W9-3计算题9-3-1. 解:(1)导线水平段在P 点产生的磁感应强度为零, 因此P 点的磁感应强度由竖直段产生, 即,4)90cos 0(cos 400aIa I B根据右手定则可判断其方向垂直纸面向外. (2)两水平段半长直导线在P 点产生的磁场方向相同,因此相当于一无限长直导线. 所以P 点的磁场为一无限长直导线和半圆共同产生的,即,4200rIr I B方向垂直纸面向里.(3)三边在P 点产生的磁场完全相同,因此P 点的磁感应强度为,29)150cos 30(cos 3024300a I tg a I B 方向垂直纸面向里.9-3-2. 解: O 点磁感应强度大小为部分圆弧和直线段共同产生,且它们的方向相同,所以),222(4)22cos(22cos 4222000tg R I R I R I B B B BA ACB •• •方向垂直纸面向里.9-3-3. 解:导线可分为四段,其中水平部分在O 点不产生磁场,因此O 点的磁场为两半圆和竖直向下半无限长直导线共同产生的,即磁感应强度大小为,444202010R IR IR IB方向垂直纸面向里. 9-3-4. 解:取薄金属板上宽度为dx 的长直电流元,其电流为,aIdxdI 到P 点的距离为x ,该线电流在点P 激发的磁感应强度大小为.,20方向垂直纸面向外xdIdB因所有线电流在点P 激发的磁场方向均相同,故点P 的磁感应强度为ab bdx axIdB B 20,ln20b b a a I 方向垂直纸面向外.9-3-5. 解:环心O 在两根通电直导线的延长线上,故它们在O 点产生的磁场为零,长为l 的载流圆弧在其圆心处的磁场为2001422rIlr l r I B,设左右两段圆弧的弧长分别为21,l l ,则两者在O 点的磁感应强度分别为,方向垂直纸方向垂直纸面向外;22202211014,4r l I B r l I B考虑到两段圆弧在电路中是并联关系,而在并联电路中,电流分配与电阻成反比,电阻又与导线长度成正比,所以212112l l R R I I,因此可得2211l I l I .由此可得, 两段圆弧在O 点的磁感应强度大小相等,方向相反.所以总磁感应强度为零,即021OB B B .9-3-6. 解: 将无限长载流圆柱形金属薄片看作是由许多平行而无限长直导线组成,对应于 d 到范围内无限长直导线的电流为Id dI ,它在环心处产生的磁感应强度为.cos 2cos ,sin 2sin 2sin 20200 d RIdB dB d R I R dI dB dB y x对整个半圆柱金属薄片积分,得20020200cos 2,sin 2d RI B R I d R I B y x ,故环心处磁感应强度为RIB B x 20 ,方向沿x 轴正向.9-3-7. 解: 由于此平面螺旋线圈绕得很密,可近似看成是由许多同心圆组成的,因为绕制均匀,所以沿半径方向单位长度的匝数为rR Nn,在线圈平面内,取半径为'',dr r 宽为的圆环作电流元,则此圆环的匝数为r d r R N r nd,等效电流为r d rR NIdI ,该圆环电流在O产生的磁场为:]2/22[]22[]22/2[B 2/2002/2/002/002• a d a d a d d m d r a I r I r a I r I r a Id Ir dS )()()()()( ,)(2200r r d r R NI r dIdB方向垂直纸面向外;所以由叠加原理,O点磁感应强度为.ln )(2d )(200r R r R NIr r r R NIdB B Rr方向垂直纸面向外9-3-8 解: 沿圆周单位长度的线圈匝数为R N/2R N/0.5n ,在距O 点x 处取一弧宽为dl 、半径为y 的圆环,则圆环上绕有 /2Nd ndl dN 匝线圈.通过圆环上的电流大小为 /2INd dN dI I ,该圆电流在球心处产生的磁感应强度为2/32202)(2y x dIy dB ,方向沿x 轴正向.由于所有小圆环电流产生的磁场方向相同,所以RNIy x Iy dB 4/2Nd )(2B 02/322202,方向沿x 轴正向.9-3-9 解: 根据电子绕核运动的角动量量子化假说:L=mva 0=h/2π, 可得电子的速率v=h/2πma 0,从而求出等效电流i=ev/2πa 0=he/4π2ma 02. 该电流在圆心处产生的磁感应强度为320008a 2ima heB. 9-3-10. 解: 带电圆环旋转时相当于一圆形电流nR T q 2/I ,根据教材P358-359中圆形电流在圆心和轴线上任意点产生磁场的规律可得,(1)圆心处: n R B 002/I ;(2)轴线上:232230232220)()(2x R R n x R IR B.9-3-11. 解: 带电直线沿直线运动相当于一无限长直线电流v q t /I ,根据无限长直线电流的磁感应强度分布规律可得rvr I B 2200. 9-3-12. 解: 参考例9-4可得abIl ln 20 .9-3-13 解: 无限长通电柱体的磁感应强度分布为202/2,2/d )(内d IrB r,rIB r d 2,2/0外. 题中两导线轴线间区域中的磁场为两导线单独产生的磁场的叠加,而且两分磁场方向相同.因此磁通量 对该式积分可得)2ln 21(0daI m. 9-3-14 解:(1)根据安培环路定理,磁感应强度的环路积分只与闭合路径所包围的电流有关,故参考上题可得21012,r Ir B r r;rIB r r r 2,021;0,3 B r r ;][2,2223223032r r rr r I B r r r .(2)两柱面间磁通量为120r 0ln 22B 21r r Il r Ildr dS r m •.9-3-15解: 单块无限大平面电流产生的磁感应强度为2/0j B ,方向见下图.由题意,电流流向相反,使得两平面电流在之间产生的磁场方向相同,两侧方向相反,因此有:(1)之间:j j B 00212/2B B ,(2)两侧:0B B 21 B .9-3-16解: 参考例9-2,可利用补偿法求解.本题中电流密度为)(22a R Ij,(1)圆柱体轴线上的磁感应强度为空腔中方向电流产生,即2)(2ln 222022a22a 0a02a1ba b a Iv vdr r I vdr r I vdr B vdr B ba b a b a ba )(2)(2222022201a R b Ia a R r a I B ;(2)利用例9-2的结果可得)(2220a R IbB.9-3-17 证明略. 提示:直接参考教材P371的例题9-5-1的解答过程及其具有普遍性的结论.9-3-18 解:设导线2上一点P 到O 点的距离为l ,则导线1在P 点产生的磁场 sin 2B 0l I,P 点附近的电流元Idl 受到的磁场力为sin 220l dlI BIdl dF ,它对O 点的力矩为ldF dM ,所以单位长度导线所受磁力对O 点的力矩为sin 2sin 220201I dl I dM M l l. 9-3-19 解:(1)见例题9-6,RI F 220 ,方向沿x 轴正向;(2)若将圆柱面换成直导线,则两直导线间作用力可参考教材P371-372,为d220 I F ,令F F 可求得R d 2.9-3-20 解:线圈左边受力为alII l F 2I B 10111 ,方向向左,右边受力为)(2I B 10122b a lII l F,方向向右,线圈上下两边受力为一对平衡力. 所以,它所受合力为)(2F 1021b a a lbII F F方向向左;因为线圈磁矩与磁场平行,所以0 M .10-3-1 解:由安培环路定理可得磁介质内部:LNInI H,SL NI B ro .所以NIS Lr 0,带入数据可求得:(1)31021 r (2)5302r .10-3-2 解:(1)导体内任选一以轴线为圆心的圆形路径,有I d l•l H , 而22r RII.因此,在导体内部:22RIr H)(R r ,2r 02R rI H B ;(2)导体外部,类似有I d l•l H ,得rI H 2,从而rIH B 200)(R r ;(3)4r B S B 0SSILLd d r• . 11-3计算题11-3-1 解:通过圆形线圈的磁通量为)3cos(10)583(a S B 422• t t ,因此电动势为)3cos(10)86(a 42t dt d ,将t=2代入可得(1),1014.35V A I 21014.3R=感;(2)C Rdt Rdt d q t t 202104.4)(1idt.11-3-2解:定义电动势方向向右,则由动生电动势的公式可得:,方向从C 到D ,即D 端电势高.11-3-3解:(1)磁通量为:abt l I r il bln 2sin 2S B 00a 0 •; (2)电动势为:abt l I dt d ln cos 200 .11-3-4 解: (1)大线圈中电流在小线圈处产生的磁感应强度近似为R I2B 0 ,原因在于小线圈很小.t 时刻通过小线圈的磁通量为wt S B cos a B 2 • 小,从而小线圈中的电流为:t bRa I Rdt d isin 220 ;(2) 小线圈受到大线圈的磁力矩大小为:tba I R wt B iS wt B P B P M m m 2220sin )2(sin sin 小,要保持小线圈匀速转动,要求合力矩为零,即外界施加的力矩也为t sin )2(2220 ba I R .(3) 互感系数为wt cos a 2bI M 2,因此小线圈中的电流在大线圈中产生磁通量为t ba R I 2sin )2(2Mi 220 ,所以大线圈中的感应电动势为t ba R I dt d 2cos 220 .11-3-5 解:(1) 由动生电动势公式可得V v AB 8Bl 1 ,方向由A 指向B ;同理,V CD 4 ,方向由C 指向D.(2)两棒与金属轨道构成的闭合回路中,电流为5.0RI CDAB,方向为ABCDA ,所以V U V U CD AB 6IR ,6-IR AB =CD (3) =05050ABOODC U U U .. .11-3-6 解:设当线圈转过角度为wt 时,与导线平行的两边到轴线的距离分别为r 1和r 2,则通过线圈的磁通量为wtab b a wtab b a Ia adr r I S r r cos 2cos 2ln 22d B 22220S021•,所以)cos 2)(cos 2(sin )(222222220t ab b a t ab b a tb a b Ia dt d11-3-7 解:旋转角度为wt 时,磁通量为:• S2cos 5.0BScoswt B wt r B dS ,所以电动势为Hznt Rn r B R i nt n r B wt w r B dt d 60n ,2sin ,2sin sin 5.022222= ,所以A Rnr B i V w r B m m 72242103,1035.011-3-8 证明:作圆心到金属棒两端点的连线,金属棒和所做的两条连线围成的回路面积为2225.05.0S l R l .因此,回路中电动势的大小为222225.05.025.05.0l R l dtdB l R l dt dB dt dB S dt d.11-3-9 解:由题意及动生电动势公式可得:)ln (2)(2Bvdl 0L 00aLa a L I dl l a l I L,方向由O 点指向M 点.11-3-10解:由均匀磁场中动生电动势的性质可知AC 产生的电动势相当于OC,故222O sin 21OC 21L B B C AC )(,方向由A指向C.11-3-11 解:电势差与电动势刚好相反,即0CA BC B 30cos B B lv lv U U U A AC ,代入数据可得V U AC 3107 ,为正,所以A 端电势高. 11-3-12 解:螺线管中磁场变化时产生的涡旋电场总是与半径方向垂直,因此由电动势定义可知,0B DC A 同理,0O O D A 而AOD构成一个回路,因此,43d 2dtdBa dt dB S dt AD同理dt dBa dt dB a BC 22436,61所以,即为回路中的总电动势.11-3-13 解:(1)由上题分析,可知,0O aO d 所以,102)5.02(422V dtdBR R dt d abdO abd(2) 由螺线管内部变化磁场产生的感生电场性质可直接得.,,105242沿顺时针方向垂直于oa V OadtdB R E a11-3-14解:回路在运动过程中受合力为dtdvm l l R v B F R Blv B F F 22合,解方程可得:tmRl B e l B FR v 22122. 11-3-15解:回路中磁通量随时间的变化为tg t v tg x t 4222aob 25.05.05.0BS ,所以电动势为方向沿逆时针方向。
高三物理一轮二轮复习天体运动课时作业(含答案)

天体运动第1课时作业一、选择题1.关于行星运动定律和万有引力定律的建立过程,下列说法正确的是( )A.第谷通过整理大量的天文观测数据得到行星运动规律B.开普勒指出,地球绕太阳运动是因为受到来自太阳的引力C.牛顿通过比较月球公转的向心加速度和地球赤道上物体随地球自转的向心加速度,对万有引力定律进行了“月地检验”D.卡文迪许在实验室里通过几个铅球之间万有引力的测量,得出了引力常量的数值2.设太阳质量为M ,某行星绕太阳公转周期为T ,轨道可视作半径为r 的圆。
已知万有引力常量为G ,则描述该行星运动的上述物理量满足( )A .GM =4π2r 3T 2B .GM =4π2r2T2C .GM =4π2r 2T3 D .GM =4πr3T23.组成星球的物质靠引力吸引在一起随星球自转.如果某质量分布均匀的星球自转周期为T ,万有引力常量为G ,为使该星球不至于瓦解,该星球的密度至少是( ) A.4πGT 2 B.3πGT 2 C.2πGT 2 D.πGT24.北斗卫星导航系统(BDS)是中国自行研制的全球卫星导航系统,该系统由35颗卫星组成,卫星的轨道有三种:地球同步轨道、中轨道和倾斜轨道.其中,同步轨道半径大约是中轨道半径的1.5倍,那么同步卫星与中轨道卫星的周期之比约为( ) A.1232⎛⎫⎪⎝⎭ B.2332⎛⎫ ⎪⎝⎭ C.3232⎛⎫ ⎪⎝⎭D.⎝ ⎛⎭⎪⎫32 25.一艘宇宙飞船在某个星球附近做圆形轨道环绕飞行,宇航员要估测该星球的密度,只需要测出( ) A .飞船的环绕半径 B .行星的质量 C .飞船的环绕周期 D .飞船的环绕速度 6.过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg b ”的发现拉开了研究太阳系外行星的序幕.“51 peg b ”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的120,该中心恒星与太阳的质量比约为( ) A.110B.1C.5D.10 7.某同学在距地面高为h 处水平抛出一个小钢球,经时间t 落地,地球半径为R .在地球表面附近绕地球做匀速圆周运动的宇宙飞船速率约为( ) A .2B .C .D .8.卫星绕地球做匀速圆周运动,其轨道半径为r ,运动周期为T ,地球半径为R ,引力常量为G ,下列说法中正确的是( )A.卫星的线速度大小为v =2πRTB.地球的质量为M =4π2R 3GT2C.地球的平均密度为ρ=3πGT2D.地球表面重力加速度大小为g =4π2r3T 2R29.1798年英国物理学家卡文迪许测出万有引力常量G ,因此卡文迪许被人们称为“能称出地球质量的人”,若已知万有引力常量G ,地球表面处的重力加速度g ,地球半径为R ,地球上一个昼夜的时间为T 1(地球自转周期),一年的时间T 2(地球公转的周期),地球中心到月球中心的距离L 1,地球中心到太阳中心的距离为L 2.则下列说法正确的是( ) A .地球的质量B .太阳的质量C .月球的质量D .可求月球、地球及太阳的密度10.利用引力常量G 和下列某一组数据,不能计算出地球质量的是( )A.地球的半径及重力加速度(不考虑地球自转)B.人造卫星在地面附近绕地球做圆周运动的速度及周期C.月球绕地球做圆周运动的周期及月球与地球间的距离D.地球绕太阳做圆周运动的周期及地球与太阳间的距离 11.(多选)假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是( )(球体体积公式V=πR 3)A .地球的向心力变为缩小前的一半B .地球的向心力变为缩小前的C .地球绕太阳公转周期与缩小前的相同D .地球绕太阳公转周期变为缩小前的一半12.理论上可以证明,质量均匀分布的球壳对壳内物体的引力为零.假定地球的密度均匀,半径为R .若矿井底部和地面处的重力加速度大小之比为k ,则矿井的深度为( )A.(1-k )RB.kRC.⎝ ⎛⎭⎪⎫1-1k R D.kR二、非选择题13.我国月球探测计划“嫦娥工程”已经启动,科学家对月球的探索会越来越深入.(1)若已知地球半径为R ,地球表面的重力加速度为g ,月球绕地球运动的周期为T ,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径.(2)若宇航员随登月飞船登陆月球后,在月球表面高度为h 的某处以速度v 0水平抛出一个小球,小球飞出的水平距离为x .已知月球半径为R 月,引力常量为G ,试求出月球的质量M 月.天体运动第2课时作业1.如图所示,某极地轨道卫星的运行轨道平面通过地球的南北两极,已知该卫星从北纬60°的正上方按图示方向第一次运行到南纬60°的正上方时所用时间为1 h ,则下列说法正确的是( )A.该卫星与同步卫星的运行半径之比为1∶4B.该卫星与同步卫星的运行速度之比为1∶2C.该卫星的运行速度一定大于7.9 km/sD.该卫星的机械能一定大于同步卫星的机械能 2.(多选)地球同步卫星离地心的距离为r ,运行速率为v 1,加速度为a 1,地球赤道上的物体随地球自转的向心加速度为a 2,地球的第一宇宙速度为v 2,半径为R ,则下列比例关系中正确的是( )A.a 1a 2=r RB.a 1a 2=(r R )2C.v 1v 2=r RD.v 1v 2=R r3.研究表明,地球自转在逐渐变慢,3亿年前地球自转的周期约为22小时.假设这种趋势会持续下去,地球的其他条件都不变,未来人类发射的地球同步卫星与现在的相比( )A.距地面的高度变大B.向心加速度变大C.线速度变大D.角速度变大4.(多选)石墨烯是目前世界上已知的强度最高的材料,它的发现使“太空电梯”的制造成为可能,人类将有望通过“太空电梯”进入太空.设想在地球赤道平面内有一垂直于地面延伸到太空的轻质电梯,电梯顶端可超过地球的同步卫星A 的高度延伸到太空深处,这种所谓的太空电梯可用于降低成本发射绕地人造卫星.如图所示,假设某物体B 乘坐太空电梯到达了图示的位置并停在此处,与同高度运行的卫星C 相比较( )A.B 的线速度大于C 的线速度B.B 的线速度小于C 的线速度C.若B 突然脱离电梯,B 将做离心运动D.若B 突然脱离电梯,B 将做近心运动5.a 、b 、c 、d 是在地球大气层外的圆形轨道上运行的四颗人造卫星。
必修2物理第三章1天体运动课时作业(教科版附答案和解释)

必修2物理第三章1天体运动课时作业(教科版附答案和解释)一、选择题 1.关于开普勒第二定律,正确的理解是( ) A.行星绕太阳运动时,一定是匀速曲线运动 B.行星绕太阳运动时,一定是变速曲线运动 C.行星绕太阳运动时,由于角速度相等,故在近日点处的线速度小于它在远日点处的线速度 D.行星绕太阳运动时,由于它与太阳的连线在相等的时间内扫过的面积相等,故它在近日点的速率大于它在远日点的速度解析:选BD.由于行星与太阳的连线在相等的时间内扫过的面积相等,所以相等时间里通过的曲线长度不同,线速度和角速度都不相同. 2.关于行星绕太阳运动的下列说法中正确的是( ) A.所有行星都在同一椭圆轨道上绕太阳运动 B.行星绕太阳运动时太阳位于行星轨道的中心处 C.离太阳越近的行星的运动周期越长 D.所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等解析:选D.不同的行星,有不同的椭圆轨道,太阳在椭圆轨道的一个焦点上,故A、B错误;由开普勒第三定律知,所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等,半长轴越大,其公转周期越长,故C错误,D正确. 3.关于开普勒第三定律a3T2=k,下列说法中正确的是( ) A.公式只适用于绕太阳做椭圆轨道运行的行星 B.公式适用于宇宙中所有围绕星球运行的行星(或卫星) C.式中的k值,对所有的行星(或卫星)都相等 D.围绕不同星球运行的行星(或卫星),其k值不同解析:选BD.开普勒第三定律a3T2=k适用于所有天体,即适用于行星围绕恒星和卫星围绕行星的运转,故A错误,B正确;式中的常数k是由中心天体决定的,同一中心天体k值相同,不同的中心天体k值不同,故C错误,D正确. 4.如图所示是行星m绕恒星M运动情况的示意图,下列说法正确的是( ) A.速度最大点是B点 B.速度最小点是C点 C.m 从A到B做减速运动 D.m从B到A做减速运动解析:选C.由开普勒第二定律可知,近日点时行星运行速度最大,因此,A、B错误;行星由A向B运动的过程中,行星与恒星的连线变长,其速度减小,故C正确,D错误. 5.地球绕太阳公转,地球本身绕地轴自转,形成了一年四季:春夏秋冬,则下面说法中正确的是( ) A.春分地球公转速率最小 B.夏至地球公转速率最小 C.秋分地球公转速率最小 D.冬至地球公转速率最小解析:选B.每年1月初,地球位于绕日公转轨道的近日点,速度最大;每年7月初,地球位于绕日公转轨道的远日点,速度最小. 6.某行星沿椭圆轨道运行,近日点离太阳距离为a,远日点离太阳的距离为b,过近日点时行星的速率为va,则过远日点时的速率为( ) A.vb=bava B.vb=abva C.vb=abva D.vb=bava解析:选C.如图所示,A、B分别为近日点、远日点,由开普勒第二定律,太阳和行星的连线在相等的时间里扫过的面积相等,取足够短的时间Δt,则有:va•Δt•a=vb•Δt•b,所以vb=abvA. 7.目前的航天飞机的飞行轨道都是近地轨道,一般在地球上空300~700 km 飞行,绕地球飞行一周的时间为90 min左右.这样,航天飞机里的宇航员在24 h内可以见到日落日出的次数应为( ) A.0.38 B.1 C.2.7 D.16 解析:选D.航天飞机绕行到地球向阳的区域,阳光能照射到它时为白昼,当飞到地球背阳的区域,阳光被地球挡住时就是黑夜.因航天飞机绕地球一周所需时间为90 min,而地球昼夜交替的周期是24×60 min,所以,航天飞机里的宇航员在一天的时间内,看到的日落日出次数n=24×6090=16. 8.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳是位于( ) A.F2 B.A C.F1 D.B 解析:选A.根据开普勒第二定律:太阳和行星的连线在相等时间内扫过相等的面积,因为行星在A点的速率比在B点大,所以太阳位于F2. ☆9.下表所示为太阳系八大行星的星球半径和轨道半径,若将八大行星绕太阳运行的轨迹粗略地认为是圆,可以估算出海王星的公转周期最接近( ) 行星名称水星金星地球火星木星土星天王星海王星星球半径(×106m) 2.44 6.05 6.37 3.39 69.8 58.2 23.7 22.4 轨道半径(×1011 m) 0.579 1.08 1.50 2.28 7.78 14.3 28.7 45.0 A.80年 B.120年 C.165年 D.200年解析:选C.设海王星绕太阳运行的平均轨道半径为r1, 周期为T1,地球绕太阳公转的轨道半径为R2,周期为T2(T2=1年),由开普勒第三定律有r31T21=r32T22,故T1=r31r32•T2≈164年,故选C.二、非选择题 10.地球公转轨道的半径在天文学上常用来作为长度单位,叫做一个天文单位,用来量度太阳系内的天体与太阳的距离.已知火星公转的周期是1.84年,根据开普勒第三定律,火星公转轨道半径是多少个天文单位的长度?将地球和火星绕太阳公转的轨道近似看成圆形轨道.解析:设地球和火星的轨道半径分别为r1、r2,公转周期分别为T1、T2,根据开普勒第三定律:r31T21=r32T22,得r2=3T22T21•r1=1.5(个天文单位).答案:1.5 11.地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆.天文学家哈雷曾经在1684年跟踪过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍,并预言这颗彗星将每隔一定时间就会出现.哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星最近出现的时间是1986年,请你根据开普勒行星运动第三定律估算,它下一次飞近地球是哪一年?解析:根据开普勒第三定律可得 r3地T2地=r3彗T2彗 T彗=183≈76.4年则哈雷彗星下一次出现的时间为1986年+76年=2062年.答案:2062年☆12.有一个名叫谷神的小行星,质量为m=1.00×1021 kg,它的轨道半径是地球绕太阳运动半径的2.77倍,求谷神星绕太阳一周所需要的时间.解析:设地球的轨道半径为R0,则谷神星绕太阳运行的轨道半径为Rn=2.77R0 又知地球绕太阳运行周期为T0=365天据R30T20=R3nT2n得:谷神星绕太阳的运行周期 Tn=R3nR30T0=2.773×365天=1 683天=1 683×24×3 600 s=1.45×108 s. 答案:1 683天或1.45×108 s。
天体物理导论试卷

(7)正常星系的Hubble分类是什么?什么是活动星系核(AGN)的超大黑洞能源机制与视角统一模型?
(8)2003年12月14日嫦娥三号在月球表面着陆,试论述嫦娥三ቤተ መጻሕፍቲ ባይዱ与天体物理。
南京师范大学2013-2014学年第1学期
物科院学院《天体物理导论》课程期末试卷
学院:专业:班级:
学号:姓名:任课教师:卞维豪
(1)北京地理经度与纬度各约为:116度和40度,则对于北京一观测者,北天极的高度是多少度?赤道面与黄道面交角是多少?春分、夏至、秋分、冬至时,北京太阳的地平高度角各多大?
北天极高度:40度;赤道黄道交角23.5度;
绝对星等: 为视星等, 为绝对星等, 为天体据我们的实际位置(单位为pc),则
光度: 为太阳的绝对星等( ), 为太阳的光度(为 ), 为天体的绝对星等,L为天体的光度,则
(4)太阳能源机制是什么?PP链与CNO循环的区别?给出恒星内部结构方程组、辅助方程表达式。
(5)什么是主序星的演化与恒星主序后的演化?红巨星、水平支恒星、渐近巨型支恒星核燃烧的差异?什么是黑洞、中子星、脉冲星、白矮星?史瓦西黑洞与克尔黑洞区别?
春分与秋分,太阳高度角为90-40=50度;夏至与冬至:50 - + 23.5度
(2)发生日食、月食时,月相分别是什么?为什么每次发生这样的月相时,不一定发生日食或月食?
(3)某天体的视星等为15等,有一天体亮度比之暗1000倍,则该天体的视星等是多少?
视星等: 为两星的视星等, 比 亮100倍即 : =100,所以
天文学导论习题答案

(50)
该行星的密度与木星的密度比为:
ρp = Mp · ρJ MJ
Dp DJ
−3
= 0.69 ×
2.1 × 105 1.42 × 105
−3
= 0.21
(51)
11
12
第五章 望远镜的基本原理
1. 暗7个星等需要的放大倍数为:
A = 2.5127 = 631
(52)
由A = (D/d)2,其中D为望远镜的口径,d为人眼在夜间瞳孔的直径,
Npp
=
F ∗A ∆mc2
=
1300 × 1 4.6 × 10−29 × (3 × 108)2
=
3.14 × 1014
(30)
每个质子-质子链产生两个电子型的中微子,因此单位面积上照射的中微
子数目为:
Nν = 2Npp = 6.28 × 1014
(31)
7
在 北 纬620处 , 中 午 太 阳 照 射 的 角 度 与 地 面 的 法 线 方 向 的 夹 角 为θ = 620 − 23.50 = 38.50, 因此,照射到A = 1m2上的中微子数目为:
rperi = a(1 − e) = 3.844 × 108 × (1 − 0.056) = 3.629 × 108m
(25)
远地点为:
rap = a(1 + e) = 3.844 × 108 × (1 + 0.056) = 4.059 × 108m (26)
在地球上看来太阳的角直径为:
θ
d =
= 1.39 × 109 = 0.927 × 10−2
40其中5710278k4110如果t278100000773au4230101712142010181043转动周期p为121018102110066years44第第第四四四章章章太太太阳阳阳系系系外外外行行行星星星38101145由恒星的视向速度v3012610601046根据质心的定义得到行星的质量m6010381011157101au6010272010331510113010451048太阳的视向速度v为
【物理】2020届一轮复习人教版万有引力定律天体运动课时作业

2020届一轮复习人教版 万有引力定律天体运动 课时作业A 组1.(多选)中国志愿者王跃参与人类历史上第一次全过程模拟从地球往返火星的一次实验“火星-500”活动,王跃走出登陆舱,成功踏上模拟火星表面,在火星上首次留下中国人的足迹.假设将来人类一艘飞船从火星返回地球时,经历了如图所示的变轨过程,则下列说法中正确的是(AC)A .飞船在轨道Ⅱ上运动时,在P 点速度大于在Q 点的速度B .飞船在轨道Ⅰ上运动时的机械能大于轨道Ⅱ上运动的机械能C .飞船在轨道Ⅰ上运动到P 点时的加速度等于飞船在轨道Ⅱ上运动到P 点时的加速度D .飞船绕火星在轨道Ⅰ上的运动周期跟飞船返回地面的过程中绕地球以轨道Ⅰ同样半径运动的周期相同【解析】根据开普勒第二定律可知,飞船在轨道Ⅱ上运动时,在P 点速度大于在Q 点的速度.故A 正确.飞船在轨道Ⅰ上经过P 点时,要点火加速,使其速度增大做离心运动,从而转移到轨道Ⅱ上运动.所以飞船在轨道Ⅰ上运动时的机械能小于轨道Ⅱ上运动的机械能.故B 错误.飞船在轨道Ⅰ上运动到P 点时与飞船在轨道Ⅱ上运动到P 点时受到的万有引力大小相等,根据牛顿第二定律可知加速度必定相等.故C 正确.根据周期公式T =4π2r3GM,虽然r 相等,但是由于地球和火星的质量不等,所以周期T 不相等.故D 错误.2.某人造卫星绕地球做匀速圆周运动,设地球半径为R ,地面重力加速度为g ,下列说法错误的是(D)A .人造卫星的最小周期为2πR gB .卫星在距地面高度R 处的绕行速度为Rg 2C .卫星在距地面高度为R 处的重力加速度为g4D .地球同步卫星的速率比近地卫星速率小,所以发射同步卫星所需的能量较少【解析】人造卫星绕地球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m 、轨道半径为r 、地球质量为M ,有F =F 向其中F =G Mmr2F 向=m v 2r =m ω2r =m(2πT )2r =ma解得v =GMr① T =2πr v =2πr3GM② a =GMr2 ③地球表面重力加速度公式 g =GMR2 ④根据②④式,卫星的公转周期为 T =2πr 3gR2 当r =R 时,T 最小,为2πRg,故A 正确; 由①④式得到 v =Rg r当卫星距地面高度为R 时,即r =2R 时,v =Rg2,故B 正确; 由③④式得到 a =gR 2r2当卫星距地面高度为R 时,a =g4,故C 正确;地球同步卫星的速率比近地卫星速率小,但要将卫星发射到较高的轨道,需要克服引力做较多的功,故D 错误;本题选错误的,故选D.3.如图所示,一颗行星和一颗彗星绕同一恒星的运行轨道分别为A 和B ,A 是半径为r 的圆轨道,B 为椭圆轨道,椭圆长轴QQ ′为2r.P 点为两轨道的交点,以下说法正确的是(B)A .彗星和行星经过P 点时受到的万有引力相等B .彗星和行星在P 处的加速度相同C .彗星和行星经过P 点时的速度相同D .彗星在Q ′处加速度为行星加速度的14【解析】根据万有引力F =GMmr 2,由于行星和彗星质量未知,不能比较在P 点处所受万有引力的大小,故A 错误;根据牛顿第二定律,万有引力提供加速度,GMm r 2=ma ,则a =GMr 2,在P 点由于距离中心天体都一样,因此加速度相等,故B 正确;彗星和行星经过P 点时的速度大小和方向均不同,故C 错误;彗星在Q ′点处与恒星球心的距离小于2r ,加速度大于行星加速度的14,故D 错误.4.“黑洞”是近代引力理论所预言的宇宙中的一种特殊天体,在“黑洞”引力范围内,任何物体都不能脱离它的束缚,甚至连光也不能射出.2001年,欧洲航天局由卫星观察发现银河系中心存在一个超大型黑洞.假设银河系中心仅存此一个黑洞,已知太阳系绕银河系中心做匀速圆周运动,则根据下列哪组数据可以估算出该黑洞的质量(引力常量为已知)(D)A .太阳系的质量和太阳系绕该黑洞公转的周期B .太阳系的质量和太阳系到该黑洞的距离C .太阳系的运行速度和该黑洞的半径D .太阳系绕该黑洞公转的周期和公转的半径【解析】太阳系绕银河系中心“黑洞”做匀速圆周运动,万有引力提供向心力,设太阳系的质量为m 、轨道半径为r 、“黑洞”质量为M ,根据万有引力提供向心力得:GMm r 2=m 4π2T 2r =m v 2r=m ω2r , 从上式可以看出,要计算“黑洞”质量,要知道周期T 与轨道半径r ,或者线速度v 与轨道半径r ,或者轨道半径r 与角速度ω,由于太阳系质量m 在等式左右可以约去,故太阳系质量对求银河系中心“黑洞”的质量无用处;故A 、B 、C 错误,D 正确.5.2018年4月22日,我国第一艘货运飞船“天舟一号”与“天宫二号”空间实验室顺利完成自动交会对接,若“天舟一号”与“天宫二号”绕地球做半径为r 、逆时针方向的匀速圆周运动,它们与地心连线的夹角为θ,如图所示,已知地球半径为R ,地球表面的重力加速度为g ,不计“天舟一号”与“天宫二号”间的相互作用力,下列说法正确的是(D)A .“天舟一号”与“天宫二号”的向心加速度大小均为gr2R2B .“天舟一号”从图示位置运动到“天宫二号”所在位置所需时间为θrR g rC .“天舟一号”要想追上“天宫二号”,必须先向后喷气D .“天舟一号”追上“天宫二号”,该过程中万有引力对“天舟一号”先做正功后做负功 【解析】由万有引力提供向心力:G Mm r 2=ma ,可得a =Gm r 2,又GM =gR 2,则a =R 2r 2g ,则A 错误;“天舟一号”从图示位置运动到“天宫二号”所在位置所需时间为t =θω,又ω=GM r3=gR 2r 3,可得t =θr Rrg,则B 错误;“天舟一号”向后喷气,速度变大会做离心运动脱离原轨道,不可能追上“天宫二号”,C 错误;使“天舟一号”追上“天宫二号”要先降低轨道再加速运动升高轨道,则万有引力对“天舟一号”先做正功后做负功,则D 正确.6.卫星电话在抢险救灾中发挥着重要作用,第一代、第二代海事卫星只使用静止轨道卫星,不能覆盖地球上的高纬度地区.第三代海事卫星采用同步卫星和中轨道卫星结合的方案,它由4颗同步卫星与12颗中轨道卫星构成.中轨道卫星高度为10 354 km ,分布在几个轨道平面上(与赤道平面有一定的夹角).在这个高度上,卫星沿轨道运动一周的时间为四分之一天,下列说法正确的是(C)A .中轨道卫星的线速度小于同步卫星的线速度B .4颗同步卫星的轨道可能不在同一个平面,但轨道半径一定相同C .在中轨道卫星经过地面某点的正上方的一天后,该卫星还在地面该点的正上方D .如果某一时刻,中轨道卫星、同步卫星与地球的球心在同一直线上,那么经过6小时,它们仍在同一直线上【解析】因G Mm r 2=m v 2r =m ω2r =m(2πT )2r =ma解得:v =GMr① T =2πrv =2πr3GM② ω=GMr3 ③a =GMr2 ④由②可得中轨道卫星的轨道半径小于同步卫星.半径小的速度大,周期小,加速度大. 中轨道卫星的轨道半径小,其线速度大,故A 错误;同步卫星都在赤道平面内,所以4颗同步卫星的轨道在同一个平面,轨道半径一定相同,故B 错误; 一天后地球完成1周,中轨道卫星完成4周,则卫星仍在地面该点的正上方,故C 正确; 经过6小时,中轨道卫星完成一周,而同步卫星为14周.故不可能在一直线上,故D 错误.7.已知一颗人造卫星在半径为R 的某行星上空绕该行星做匀速圆周运动,经过时间t ,卫星运动的弧长为s ,卫星与行星的中心连线扫过的角度是θ弧度.(已知万有引力常量为G)求:(1)该行星的质量M ; (2)该行星的第一宇宙速度v 1. 【解析】(1)卫星的线速度为:v =st卫星的角速度为:ω=θt则卫星做圆周运动的轨道半径为:r =v ω=sθ根据牛顿第二定律,有:G Mm r 2=m v2r解得:M =s3θGt2(2)行星的第一宇宙速度是近地轨道卫星的环绕速度,根据万有引力提供向心力:G Mm R 2=m v 21R解得:v 1=sts θRB 组8.一宇航员到达半径为R 、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m 的小球,上端固定在O 点,如图甲所示,在最低点给小球某一初速度,使其在竖直面内绕O 点做圆周运动,测得绳的拉力F 的大小随时间t 的变化规律如图乙所示.F 1=7F 2,设R 、m 、引力常量G 以及F 1为已知量,忽略各种阻力.以下说法正确的是(C)A .该星球表面的重力加速度为7F 17mB .卫星绕该星球的第一宇宙速度为Gm RC .星球的密度为3F 128πGmRD .小球过最高点的最小速度为0【解析】设小球在最低点时细线的拉力为F 1,速度为v 1, 则F 1-mg =m v 21r①设小球在最高点细线的拉力为F 2,速度为v 2, 则F 2+mg =m v 22r②由机械能守恒定律得mg2r +12mv 22=12mv 21 ③由①②③解得g =F 1-F 26m④F 1=7F 2,所以该星球表面的重力加速度为F 17m ,故A 错误.根据万有引力提供向心力得:GMm R 2=m v2R 卫星绕该星球的第一宇宙速度为v =GM R ,故B 错误.在星球表面,万有引力近似等于重力GMm ′R2=m ′g ⑤ 由④、⑤解得M =F 1R 27Gm ,星球的密度:ρ=M 43πR 3=3F 128πGmR ,选项C 正确;小球在最高点受重力和绳子拉力,根据牛顿运动定律得:F 2+mg =m v 22R ≥mg所以小球在最高点的最小速度v 2≥gR.故D 错误.9.我国首颗量子科学实验卫星于2018年8月16日1点40分成功发射.量子卫星成功运行后,我国将在世界上首次实现卫星和地面之间的量子通信,构建天地一体化的量子保密通信与科学实验体系.假设量子卫星轨道在赤道平面,如图所示.已知量子卫星的轨道半径是地球半径的m 倍,同步卫星的轨道半径是地球半径的n 倍,图中P 点是地球赤道上一点,由此可知(D)A .同步卫星与量子卫星的运行周期之比为n3m 3B .同步卫星与P 点的速率之比为1nC .量子卫星与同步卫星的速率之比为nmD .量子卫星与P 点的速率之比为n 3m【解析】根据GMm ′r 2=m ′4π2T 2r ,得T =4π2r3GM,由题意知r 量子=mR ,r 同步=nR ,所以T 同T 量=r 3同r 3量=()nR 3()mR 3=n3m3,故A 错误;P 为地球赤道上一点,P 点角速度等于同步卫星的角速度,根据v =ωr,所以有v 同v P =r 同r P =nR R =n 1,故B 错误;根据GMm ′r 2=m ′v2r,得v =GM r ,所以v 量v 同=r 同r 量=nR mR=n m ,故C 错误;综合BC ,有v 同=nv P ,v 量v 同=n m ,得v 量v P=n3m,故D 正确;故选D. 10.假设站在赤道某地的人,日落后4 h 时,发现一颗从“天边”飞来的卫星正好处于自己头顶的上空,且此卫星即将消失在夜幕之中.若该卫星在赤道所在平面上绕地球做匀速圆周运动,其转动方向与地球自转方向相同,又已知地球的同步卫星绕地球运行的轨道半径约为地球半径的6.0倍.据此可知,此人造地球卫星绕地球运行的周期约为(B)A .3.6 hB .4.6 hC .5.6 hD .6.6 h【解析】日落时,过赤道上P 点的最后一缕阳光如图所示,设地球半径为R ,图中O 点为地心,所以OP =R ;由于4 h 远小于地球公转周期,故可以认为在日落后4 h 内地心相对于太阳的位置未发生变化,OP 的连线在4 h 内转过的角度θ=16×2π=π3.卫星即将消失在夜幕时,其所在位置位于图中的Q 点,则卫星的轨道半径r =R cos θ=2R 由开普勒三定律得T 卫T 同=r3(6R )3=127,卫星绕地球运行的周期约4.6 h ,正确答案为B.11.(多选)如图,赤道上空有2颗人造卫星A 、B 绕地球做同方向的匀速圆周运动,地球半径为R ,卫星A 、B 的轨道半径分别为54R 、53R ,卫星B 的运动周期为T ,某时刻2颗卫星与地心在同一直线上,两颗卫星之间保持用光信号直接通信.则(BC)A .卫星A 的加速度小于B 的加速度 B .卫星A 、B 的周期之比为338C .再经时间t =3()83+9T148,两颗卫星之间的通信将中断D .为了使赤道上任一点任一时刻均能接收到卫星A 所在轨道的卫星的信号,该轨道上至少需要3颗卫星【解析】根据G Mm r 2=ma ,解得:a =G M r 2,可知A 的加速度大于B 的加速度,故A 错误;根据G Mm r 2=m 4π2T2r ,解得:T =4π2r 3GM ,可得:T A T B =338,故B 正确;由题意可知当卫星A 与B 的连线与地球相切时信号将中断,由几何关系可知此时A 、B 卫星的距离为25R 12,角度关系为⎝ ⎛⎭⎪⎫2πT A -2πT B t =θ,(θ为卫星A 、B 与地心连线的夹角),依勾股定理,得θ=π2,解得t =3()83+9T 148,故C 正确;对于同步卫星来讲,由于赤道对应的圆心角为360度,而一颗卫星能覆盖120度,故要有3颗,才能全部覆盖地球表面,同步卫星距地心的距离大约7R ,而卫星A 的轨道半径为5R4,覆盖的范围比同步卫星还要小,因此至少需要3颗以上才可以,故D 错误.12.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用,设每个星体的质量均为m ,四颗星稳定地分布在边长为a 的正方形的四个顶点上,已知这四颗星均围绕正方形对角线的交点做匀速圆周运动,引力常量为G ,试求:(1)星体做匀速圆周运动的周期;(2)若假设能在其中某一个星上做这么一个实验:站在h 高处以v 速度将一个物体水平抛出,测得落地点离抛出点水平位移为s ,则该星半径R 为多少?【解析】(1)由星体均围绕正方形对角线的交点做匀速圆周运动可知,星体做匀速圆周运动的轨道半径r =22a 由万有引力定律和向心力公式得: G m2(2a )2+2G m 2a 2cos 45°=m 22a 4π2T 2 解得:T =2πa2a(22+1)Gm(2)由万有引力定律可知:G mm ′R 2=m ′g ′则星体表面的重力加速度:g ′=G mR 2由平抛规律: s =vt h =12g ′t 2 得:g ′=2h t 2=2hv 2s 2=G m R 2解得: R =s v Gm 2h。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天体物理学的发展
---暗物质和暗能量的探索
天体物理学既是天文学的一个分支,也是物理学的一个分支,是应用物理学的技术、方法和理论,研究天体的形态、结构、化学组成、物理状态和演化规律的学科,又可以说是天文学和物理学之间的一门交叉学科。
天文学和物理学的关系至为密切。
牛顿力学的基础之一技术天文学的观察。
天文观测和理论分析离不开物理学的基本定律。
光谱学许多发现都与天文学有关联。
19世纪末,氦元素技术守信从太阳光谱中发现的。
天体一直是物理学最理想的实验室。
例如,玻尔原子模型理论丛匹克林系找到了证据,爱因斯坦的广义相对论从日食得到了最初的验证,科学家在研究恒星能源时提出了热核聚变概念。
20世纪60年代天文学的四大发现---类星体、脉冲星、星际分子、微波背景辐射,促进了高能天体物理学等学科的发展。
天体物理学设计方方面面,其中有太阳物理学、太阳系物理学,恒星物理学、恒星天文学、星系天文学、宇宙学、射电天文学、空间天文学、高能天体物理学等分支。
每一方面在20世纪都有许多引人入胜的经历。
宇宙的起源和进化是天体物理学研究的最基本的问题之一。
简历在广义相对论和宇宙学原理之上的大爆炸宇宙模型告诉我们:宇宙诞生于一次大爆炸,时间约在大约137亿年前;大爆炸发生的那一刻,宇宙处于极致密、极高温的状态,形成了空间和时间;经过膨胀和冷却,逐步演化成现在这个样子;演化过程可以分成原初轻元素合成、光子退耦、中性原子形成、恒星形成等几个重要的时期,在这个不断膨胀的时空里,星系、地球、空气、水和生命逐渐形成。
20世纪20年代,基于从星系光谱的红移的大量观测,哈勃发现了宇宙中所有的星系都在彼此远离退行,距离越远,退行速度越大,二者成正比,从而提出哈勃定律。
大爆炸宇宙模型还是在这一基础上产生的。
20世纪大量的天文观测和天堂物理研究结果都证实这个模型。
到了20世纪
末,科学界普遍接受了这一模型,但是仍有学的困难无法解决,其中有一个旷日持久的问题就是所谓的暗物质问题。
多年来,暗物质的存在及其特性一直是天体物理学和宇宙学的一个难解之谜。
所谓暗物质,指的就是无法直接观测的物质。
既然无法直接观测,它的存在就必是分局某种简介的资料作出的推测。
早在20世纪30年代,荷兰天体物理学家奥尔特就曾指出:为了说明恒星的运动,需要假定在太阳附近存在着看不见的物质。
1、质量短缺
星系团的质量可以用两种方法测量。
一种是光度方法,根据测得的质光比求出质量;另一种是动力学方法,从星系团各个成员星系的红移得出各个星系的相对速度,再根据维里定理算出星系团的质量。
1933年,兹维基比较两种方法对后发星系团的动力学方法得到的质量比光度方法得到的质量竟大四百倍。
如果承认两种方法所得结果都是对的,就必然得出星系团中存在大量看不见的物质的结论。
人们把这一现象称为“质量短缺”。
但是当时“质量短缺”的问题并未引起科学界的重视,认为只是兹维基的一种大胆推测,知道20世纪70年代初,科学界还普遍认为“质量短缺”是根本不存在的,差异是由其他因素造成的。
2、进一步证实
1987年在华盛顿卡内基研究生工作的鲁宾等人发表了他们对形象旋转曲线的研究。
他们发现,像银河系,仙女星系和其他一些漩涡星系,星系内恒星与气体绕星系中心的轨道速度并不随它们与星系中心的距离而下降,取而代之的是,这些星系的旋转曲线趋于平坦。
换句话说,在整个星系晕中的恒星速度保持恒定。
这表明,这些星系的质量并不是集中在核球,而是均匀的分布在整个星系中。
由此可见,在星系晕中一定存在着大量看不见的暗物质。
这一事实对肯定暗物质的存在具有很强的说服力。
1983年,天文学家发现:在距银河系中心20万光年距离的R15星,其视向速度高达465公里/秒。
要产生这样大的速度,银河系的总质量至少要比现在知道的质量大10倍,这一事实表明银河系及其周围存在大量的暗物质。
通过计算,可以间接地得出宇宙中有90%甚至99%的物质不能用望远镜直接观测的结论。
1987年,天体物理学家研究分析了红外天文学人造卫星对2400个星系的观
测数据,得到了用光学手段无法得到的银河系附近5亿光年范围内的三维物质分布图。
该图显示,银河系被以室女、长蛇和人马为主的10多个星系团所吸引,它们的合力作用恰与银河现今运动情况相一致,而与微波背景辐射方向相反,因而对所观测到的各向同性微波背景辐射的微小不均匀性成功地作出了解释。
根据红外天文学人造卫星图所提供的数据,加上对银河系所受合引力的分析,也可以得出至少有90%或更多的宇宙暗物质存在的判断。
数据如此巨大的暗物质究竟是什么?最初,很自然地把它们设想为一些暗星,如不发光的行星、小恒星、冷却了的白矮星、中子星、黑洞以及弥散气体或宇宙尘等。
这一类物质都是由重子组成。
然而,根据大爆炸宇宙学关于轻元素原子的合成理论,可以推断出重子数与光子数之比小于7×10-10。
也就是说,宇宙中如果存在暗物质,它们不可能是重子组成的物质,看来答案只能从粒子物理学中寻求。
在众多候选的基本粒子之中,人们自然会想到行踪诡秘的中微子。
但是中微子究竟有没有质量,至今尚未有定论。
3、暗物质的存在终于得到了确证
1989年,美国国家航空航天局曾发射过一颗宇宙背景探测者卫星并观测到了宇宙微波背景辐射在不同方向上存在着微弱的温度涨落。
为了进一步研究这种各向异性现象,1995年美国国家航空航天局接受建议,2001年发射了威尔金森微波各向异性探测器,并于2003年第一次清晰地绘制了一张宇宙婴儿时期的图像。
宇宙的年龄大约是130亿年,38万年寿命宇宙的图像相当于一个80岁的人在他出生当天拍下的照片。
这一年,由威尔金森微波各向异性探测器以其对宇宙学参数的精确测量,取得了决定意义的成果。
这些成果告诉人们,宇宙中普通物质只占4%,23%的物质为暗物质,73%是暗能量。
这是迄今为止,暗物质存在最有说服力的证明。
同年,由斯隆基金会资助、众多单位参加的国际性天文研究项目:斯隆数字太空勘测,根据大量天文观测所得到的数据也给出了类似的结果。
探讨了多年的疑难问题终于有了明确的答案。
2003年年底,《科学》杂志把这一成果选为当年第一大科技成果。
然而究竟什么是暗物质,还没有定论。
中微子当然是一种暗物质粒子,但威尔金森微波各向异性探测器和斯隆数字太空勘测的结果表明,它即使有质量,也应当非常之小,在暗物质中只能占微小的比例,绝大部分应是所谓的中性弱作用
重粒子。
而中性弱作用重粒子究竟是什么,目前还不清楚。
理论物理学家猜测,它们可能是超对称理论中的最轻的超对称粒子,是稳定的,在宇宙演化过程中像微波背景光子意义被遗留下来。
目前,世界各国科学家,正在进行着各种加速器和非加速器的实验,试图找到这种暗物质粒子。
4、暗能量
暗能量是近年宇宙学研究中提出的一个热门课题。
支持暗能量的主要证据有四个。
一是对遥远的超新星所进行的大量观测表明,宇宙在加速膨胀,星系膨胀的速度不像哈勃定律描述的那样,是恒定的,而是在不断加速。
按照爱因斯坦引力场方程,加速膨胀的现象推论出宇宙中存在着压强为负的暗能量。
另一个证据来自于近年对微波背景辐射的研究精确地测量出宇宙中物质的总密度。
但是,我们知道所有的普通物质与暗物质加起来大约只占其1/3左右,所以仍有约2/3的短缺。
这一短缺的物质称为暗能量,其基本特征是具有负压,在宇宙空间中几乎均以分布或完全不结团。
最近威尔金森微波各向异性探测器数据显示,暗能量在宇宙中占总物质的73%。
值得注意的是,对于通常的能量、重子和冷暗物质,压强都是非负的,所以必定存在着一种未知的负压物质主导今天的宇宙。
然而,当前物理学基本理论尚未能解释这些观测判定其存在的暗能量。
解决这一问题需要新的理论,同时也有赖于发射更多的探测卫星,对空间进行更多更精确更系统的观察,以进一步研究宇宙的膨胀规律。
不同的暗能量形式将导致非常不同的宇宙膨胀的规律,由此可以确定暗能量的形式和物流特征。
这是向物理学提出的巨大挑战。
物理学整面临新的大突破,也就是说,在宏观低速运动、宏观高速运动、微观低速运动以及微观高速运动的规律的突破以后,物理学将进一步突破宇宙观的领域。
这样的理论很可能是各种相互作用同意的量子理论,把引力作用也包括在内的大统一理论。
这将是又一场重大的物理学革命。
暗物质和暗能量的探讨正方兴未艾。
解决这些新问题需要将描述微观世界的粒子物理学与描述宇宙观世界的宇宙学结合起来。
极大和极小联系在一起,将是21世纪物理学和天文学研究的一个新特点。
