金融经济学之不确定风险下的选择理论
金融经济学整理

金融经济学名词解释自然状态:特定的会影响个体行为的全部外部环境因素。
自然状态的信念:个体会对每一种状态的出现给予一个主观的推断,即某一特定状态s出现的概率P。
期望效用原则:人们在投资决策时不是用“钱的数学期望〞来作为决策准则,而是用“道德期望〞来行动的。
而道德期望并不与得利多少成正比,而与初始财富有关。
即人们关怀的是最终财富的效用,而不是财富的价值量,而且,财富增加所带来的边际效用〔货币的边际效用〕是递减的。
效用函数的定义:不确定性下的选择问题是其效用最大化的决定不仅对自己行动的选择,也取决于自然状态本身的选择或随机变化。
公平博彩:指不改变个体当前期望收益的赌局,如一个博彩的随机收益为ε,期望收益为E(ε)=0,我们就称其为公平博彩。
效用函数的凸凹性的局部性质:经济行为主体效用函数的凸凹性实际上是一种局部性质。
即一个经济主体可以在某些情况下是风险厌恶者,在另一种情况下是风险偏好者。
效用函数是几个不同的局部组成。
在人们财富较少时,局部投资者是风险厌恶的;随着财富的增加,投资者对风险有些漠不关怀;而在较高财富水平阶段,投资者则显示出风险偏好。
确定性等价值:是指经济行为主体对于某一博彩行为的支付意愿。
即与某一博彩行为的期望效用所对应的数学期望值〔财富价值〕。
风险溢价:是指风险厌恶者为防止承当风险而情愿放弃的投资收益。
或让一个风险厌恶的投资者参与一项博彩所必需获得的风险补偿。
阿罗-普拉特定理:对于递减绝对风险厌恶的经济主体,随着初始财富的增加,其对风险资产的投资逐渐增加,即他视风险资产为正常品;对于递增绝对风险厌恶的经济主体,随着初始财富的增加,他对风险资产的投资减少,即他视风险资产为劣等品;对于常数绝对风险厌恶的经济行为主体,他对风险资产的需求与其初始财富的变化无关。
相对风险厌恶的性质定理:对于递增相对风险厌恶的经济主体,其风险资产的财富需求弹性小于1〔即随着财富的增加,投资于风险资产的财富相对于总财富增加的比例下降〕;对于递减相对风险厌恶的经济行为主体,风险资产的财富需求弹性大于1;对于常数风险厌恶的经济行为主体,风险资产的需求弹性等于1。
第3章讲义(2010)
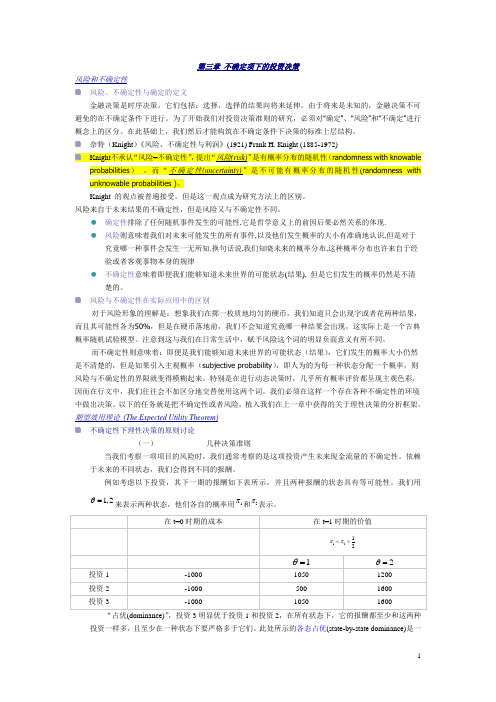
第三章 不确定项下的投资决策风险和不确定性风险、不确定性与确定的定义金融决策是时序决策,它们包括:选择,选择的结果向将来延伸。
由于将来是未知的,金融决策不可避免的在不确定条件下进行。
为了开始我们对投资决策准则的研究,必须对“确定”、“风险”和“不确定”进行概念上的区分。
在此基础上,我们然后才能构筑在不确定条件下决策的标准上层结构。
奈特(Knight )《风险、不确定性与利润》(1921) Frank H. Knight (1885-1972)Knight 不承认“风险=不确定性”,提出“风险(risk)”是有概率分布的随机性(randomness with knowableprobabilities ) ,而“不确定性(uncertainty)”是不可能有概率分布的随机性(randomness with unknowable probabilities )。
Knight 的观点被普遍接受。
但是这一观点成为研究方法上的区别。
风险来自于未来结果的不确定性,但是风险又与不确定性不同。
确定性排除了任何随机事件发生的可能性,它是哲学意义上的前因后果必然关系的体现. 风险则意味着我们对未来可能发生的所有事件,以及他们发生概率的大小有准确地认识,但是对于究竟哪一种事件会发生一无所知.换句话说,我们知晓未来的概率分布,这种概率分布也许来自于经验或者客观事物本身的规律不确定性意味着即便我们能够知道未来世界的可能状态(结果), 但是它们发生的概率仍然是不清楚的。
风险与不确定性在实际应用中的区别对于风险形象的理解是:想象我们在掷一枚质地均匀的硬币,我们知道只会出现字或者花两种结果,而且其可能性各为50%,但是在硬币落地前,我们不会知道究竟哪一种结果会出现,这实际上是一个古典概率随机试验模型。
注意到这与我们在日常生活中,赋予风险这个词的明显负面意义有所不同。
而不确定性则意味着:即便是我们能够知道未来世界的可能状态(结果),它们发生的概率大小仍然是不清楚的,但是如果引入主观概率(subjective probability ),即人为的为每一种状态分配一个概率,则风险与不确定性的界限就变得模糊起来。
浅谈金融风险的管理和方法

浅谈金融风险的管理和方法摘要金融机构作为资金融通和货币经营的组织,在其活动过程中必然存在或发生某一经济损失的可能性,这种可能性或不确定性是金融风险的根本特征。
自20世纪90年代以来,金融风险的发生和金融危机的频繁爆发,使许多国家的财富遭受重创,金融机构不断经受着各种风险带来的考验。
为此金融风险管理问题引发了社会、政府和金融界的高度关注。
一、金融风险的管理及其目的金融风险的管理是管理科学中的重要分支,是研究银行等金融机构的经营中各种风险的生成机理、计量方法、处理程序和决策措施的一门科学,美国风险管理的专家威廉姆和汉斯指出:风险管理是一种通过对风险的识别、衡量和控制,以最少的成本将风险导致的各种后果减少到最低限度的科学方法。
就目前国内金融风险的理论和政策领域来看,金融风险管理的目的主要是:维持社会公众的利益;保证金融机构和整个金融体系的稳健安全;保证国家宏观货币政策制定和贯彻执行;保证金融机构的公平竞争和较高的效率;。
(一)、维持社会公众的利益从现代经济学的观点来看,银行存款人、证券市场投资人及其他金融机构的公众客户,一方面将资金借给了各种金融筹资人,另一方面,这些存款人和投资人对资金的使用方向、金融等信息却知之甚少,而所有涉及存款和投资活动的客户又承担了几乎所有的系统性风险和某些非系统性的风险。
在这种信息存在典型不对称的背景下,政府的金融风险管理部门对公众的利益充当守业者和保护人的角色。
(二)、保证金融机构和整个金融体系的稳健安全从经营特征来看,商业银行除很少的自有资本之外,主要是靠从各种途径获取负债来维持经营,如果过分追求利益,吧过多的资金投入到期现长、收益高的资产上去,就可能影响资产的必要流动性,导致资产质量下降,致使到期本息的清收出现困难,甚至陷入流动性困难,或资不抵债的境地,并导致金融机构的连锁反应,最终带来整个金融系统的混乱和动荡。
因此,金融监管的首要目的是保证金融交易系统的顺畅运转、体系稳健运行,及时发现和防范可能的金融风险的出现和集中,防止金融系统性危机和市场的崩溃。
高级微观04-不确定性与消费者选择 2011

4 不确定性与消费者选择在本章以前,我们讨论的所有问题,都没有对理性行为人的行动和结果加以区分,每一个行动都确定地对应了一个特殊的最大化结果。
在本章,我们要讨论消费者选择的行动与其结果不确定地对应,即随机性对应。
这样,就可以把行动的选择看作是对于彩票的选择,而结果就是彩票中奖的奖金。
在本章以后,我们依然不专门考虑不确定性下的选择问题。
但是,有了本章的思考方式,我们的思考经济学问题的视野就不再局限于确定性世界了,博弈论和信息经济学的思考方式,都渗透了本章的因子。
当前,由美国次贷危机引发的日益蔓延的金融危机,说明经济学人充分思考不确定性问题的重要性。
4.1 确定性,不确定性,不完全理性与风险4.1.1 确定性,不确定性与不完全理性为了导出不确定性,先要了解确定性。
确定性与完全理性相关联。
决策者具有完全理性必须同时满足以下条件:(1) 影响决策者决策的任何因素是确定的;(2) 对于这些决策因素,决策者具有完备信息;(3) 在给定信息条件下,决策者具有处理信息的能力。
破坏(1)则成客观不确定性。
破坏(2)则成主观不确定性。
破坏(3)则成有限理性。
破坏上述任何一条,决策者就偏离了完全理性,其选择行为就是不完全理性的。
4.1.2 不确定性与风险这两者有所区别。
不确定性是风险存在的必要条件。
风险实际上是不同决策者关于彩票(赌局)偏好关系的特征。
换言之,风险可以用计算彩票的概率来刻画,而不确定性难以用概率刻画。
4.2 状态依存的收益函数4.2.1 确定性收益函数设决策者面临的有界的机会集合为A ={1a , …, n a }, i a 代表一种金融资产,其收益集合为X={1x , …, m x }。
如果是在确定性条件下决策,则连续函数x =)(a f , ,A a ∈ x ∈X此时的决策原则是选择*a ,使得)(*a f = max )(a f ,A a ∈。
4.2.2 彩票与状态依存收益函数在不确定性条件下,给定i a ,决策者不能确定i x ,这相当于他不知道)(i i a f x =,从而他不能做出最优选择。
金融经济学探究

金融经济学探究金融经济学是一门新兴的边绿科学,常被认为是应用数学的一个分支,是数学、经济学、金融学融合成的新学科,其被心内容是不确定环境下的最优投资选择理论和资产的定价理论。
时间和不确定性是影响金融行为主要因素。
本文े述了金融经济学的产生和发展,并就若干前沿问题作了简单介绍。
1.金融经济学的产生和发展概况1.1 华尔街第一次革命1.1.1 MM定理1956年F.Modigliani和ler通过计量经济学模型建立了Modigliani-Miller定理(MM定理)。
即在一定条件下,公司的市场价格只依赖于它的利润流,而与它的资本结构无关,即与债权与股权之间的比例无关,从而也与它的分红策略无关,即与债权者和股权者之间的利润分割无关,MM定理是用无套利假设通过数学推导西得到的第一条金融市场方面的定理。
此后形成一整套无套利定价理论,该定理目前已经成为公司财务理论的基础。
著名数理金融学家默顿曾对MM定理给予高度评价,MM理论是新旧理财学的分水岭。
旧的理财学分析会计规则,充满各种琐事的记录。
新的理财学在数学上是严谨的,它的原理在一定条件下是正确的,是经得起经济计量模型检验的。
1.1.2 证券组合选择理论Markowitz证券组合选择理论把投资组合的价格变化量料为随机变量,以它的均值来衡量收益,以它的方差来衡量风(从而Markowiz理论又称均值-方差分析);把投资组合中各种股票之间的比例作为变量,求收益一定的风险最小的投资组合问题就可归结为一个线性约束下二次规划问题。
1.1.3 请本资产定价模型(CAMP)Sharpe对金融资产的价格形成理论(即资本资产定价模型Capital Asset Pricing Model,CAPM),其思路起因Markowiz证券组合选择理论的计算量极大,改用投资组合的价格变化上“市场投资组合”的价格变化之间的回归系数来衡量股票交易由风险,该模型认为,当资本市场处于均衡时,所有风险资产的预期收益率是市场风险的线性函数,即所有风险资产的预期收主事于一个共同的因素(即“市场组合“-Market Porfolio)的p险之间有一个线性相关:2.华尔街第二次革命:期权定价理论早在1900年,法国数学家巴歇里(L.Bachelier)就在他的博士论文”投机的理论”中,把股票价格的变化描述为布朗运动(虽然严格的数学基础在19 23年才由美国数学家维纳建立起来)。
经济学与风险管理应用经济学原理于风险管理

经济学与风险管理应用经济学原理于风险管理经济学与风险管理:应用经济学原理于风险管理在如今复杂多变的市场环境中,风险管理成为企业和个人必不可少的一环。
为了应对不稳定的经济情况和不确定的市场波动,许多机构和个体开始探索经济学原理在风险管理中的应用。
本文将探讨经济学如何为风险管理提供理论基础,并将其应用于实际案例,以便更好地进行风险评估和决策。
1. 风险管理的概述风险管理旨在识别、评估和应对可能对目标的实现产生不利影响的因素。
在经济学中,风险被定义为不确定性的结果,并且可能导致损失或收益偏离预期值。
风险管理不仅适用于金融领域,也适用于其他行业和个人生活。
它通常包括风险识别、风险评估、风险控制和风险监管四个方面。
2. 风险管理中的经济学原理经济学提供了理论框架来解释市场行为和风险决策。
在风险管理中,经济学原理可以应用于以下几个方面:2.1 风险评估风险评估是风险管理流程的重要环节。
经济学原理中的概率理论和风险偏好理论可以用于量化和评估风险。
概率理论通过对过去数据和市场趋势进行分析,预测未来风险的概率。
而风险偏好理论则研究个体在面临不同风险时的选择行为,并帮助确定个体对风险的偏好程度。
2.2 风险决策风险决策是在面临不确定性时做出的决策。
经济学中的决策理论提供了决策者如何在风险情况下权衡利弊的方法。
决策树模型、期望效用理论和边际效用理论等经济学工具可以帮助决策者在风险管理中进行决策分析,并选择最优方案。
2.3 风险传导风险传导是指风险从一个经济主体传递到另一个经济主体的过程。
风险传导涉及到资源配置、市场机制和金融体系等方面。
经济学原理中的供求关系、市场竞争和金融机制等理论可以用于分析和理解风险在市场中的传导规律,进而采取相应的风险防范和控制措施。
3. 应用经济学原理于风险管理的案例研究以下案例研究将展示经济学原理在风险管理中的具体应用。
3.1 金融风险管理金融风险管理是金融机构面临的一项重要任务。
以银行业为例,经济学原理可以帮助银行测算信用风险、市场风险和流动性风险等,从而确定适宜的风险管理策略和措施。
不确定条件的选择理论资料

讲解
• 早期学者将不确定性和风险区分开来,将 不确定性分为确定的确定性(即风险)和 不确定、不可度量的不确定性(如奈特, 1957),现在一般不加区分。
• 所谓不确定性是指未来有多种可能情形发 生,每种情形下的结果(收益)已知,而 且各种情形发生的概率已知。通常用彩票 来代替之。
图示
• A Simple lottery: L=(x1,p1;…;xS,pS)
p1
x1 x2
p2
L
ps
xs
pS
xS
A Simple lottery and Machina Triangle
• The set of all lotteries on outcomes X is denoted {( p1,..., pS ) RS p1 ... pS 1}
不确定条件下的选择理论1期望效用理论2随机占优理论一期望效用理论vm公理化体系展望理论及其他1不确定条件下的选择公理体记号
不确定条件下的选择理论
熊和平 2009年秋季
主要内容
• 引言:问题的提出和简单历史 • 不确定条件下的选择公理与期望效用理论 • 期望效用理论的挑战 • 期望效用理论的一些替代 • 随机占优理论 • 风险厌恶及其度量 • 一些常见的效用函数
• C=(A,0.25) D=(B,0.25) • 结论?
A 选项7
6,000 (45%)
B 选项7
3,000 (90%)
C
6,000
选项8
(1%)
D 选项8
3,000 (2%)
0 (55%)
0 (10%)
0 ( 99%)
0 (98%)
风险中性原理

风险中性原理风险中性原理是指在特定情况下,个体对于风险的态度是中性的。
这意味着在面对不确定性和风险时,个体不会因为风险而改变其决策。
风险中性原理在金融领域和行为经济学中有着重要的应用,对于投资者和决策者来说,了解和理解风险中性原理对于做出理性的决策至关重要。
风险中性原理最早由马克·斯特恩斯坦在20世纪70年代提出。
斯特恩斯坦认为,个体在面对风险时,会根据概率来进行决策,而不会受到风险本身的影响。
这一理论对于解释人们在风险决策中的行为有着重要的意义。
在金融领域,风险中性原理对于投资者的决策具有重要影响。
根据风险中性原理,投资者在进行投资决策时,会将预期收益和风险同时考虑进去,而不会因为风险本身而改变其投资决策。
这意味着投资者会根据预期收益和风险来进行投资组合的选择,而不会因为风险而放弃高收益的投资机会。
此外,风险中性原理还对决策者的行为有着重要的指导意义。
在面对不确定性和风险的决策时,决策者应该根据风险中性原理来进行决策,而不是被风险所左右。
这意味着决策者在制定决策方案时,应该充分考虑风险因素,但不应该因为风险而改变其决策。
然而,风险中性原理并不意味着个体对于风险毫无感知。
相反,风险中性原理认为个体会根据风险的概率和预期收益来进行决策,而不是被风险所左右。
这意味着个体在决策时会对风险有所感知,但不会因为风险而改变其决策。
总之,风险中性原理在金融领域和行为经济学中有着重要的应用。
了解和理解风险中性原理对于投资者和决策者来说至关重要。
在面对不确定性和风险时,个体应该根据风险中性原理来进行决策,而不是被风险所左右。
这将有助于个体做出理性的决策,从而更好地应对风险和不确定性。
