第三章 稀溶液的依数性
无机化学第三章溶液的依数性

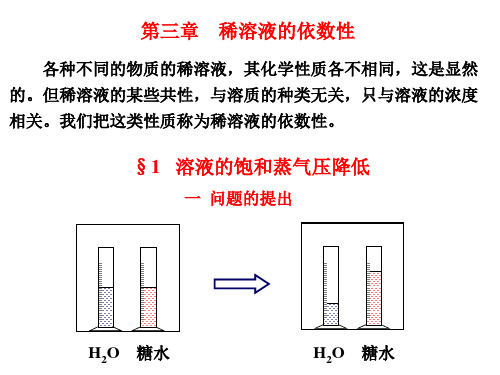
无机化学溶液的依数性第三章稀溶液的依数性§本章摘要§1. 溶液的饱和蒸气压下降问题的提出饱和蒸气压拉乌尔定律2. 沸点升高和凝固点下降沸点和凝固点饱和蒸气压图公式应用3. 渗透压渗透现象渗透压渗透压公式§1 溶液的饱和蒸气压下降一问题的提出水自动转移到糖水中去,为什么?这种转移, 只能通过蒸气来进行. 因此, 要研究蒸气的行为, 才能弄清楚问题的实质.二饱和蒸气压1. 纯溶剂的饱和蒸气压(P0)液体气体在密闭容器中, 在纯溶剂的单位表面上, 单位时间里, 有N0个分子蒸发到上方空间中。
随着上方空间里溶剂分子个数的增加, 密度的增加, 分子凝聚, 回到液相的机会增加. 当密度达到一定数值时, 凝聚的分子的个数也达到N0个。
这时起, 上方空间的蒸气密度不再改变, 保持恒定。
此时, 蒸气的压强也不再改变, 称为该温度下的饱和蒸汽压, 用P0表示。
达到平衡. 当蒸气压小于P0时, 平衡右移, 继续气化; 若蒸气压大于P0时, 平衡左移, 气体液化. 譬如, 改变上方的空间体积, 即可使平衡发生移动。
2.溶液的饱和蒸气压(P)当溶液中溶有难挥发的溶质时, 则有部分溶液表面被这种溶质分子所占据, 如图示:于是, 在溶液中, 单位表面在单位时间内蒸发的溶剂分子的数目N要小于N0。
凝聚分子的个数当然与蒸气密度有关. 当凝聚的分子数目达到N, 实现平衡时, 蒸气压已不会改变. 这时, 平衡状态下的饱和蒸气压为:P < P0对溶液来讲, 蒸气压大于P, 液化;蒸气压小于P, 气化。
3. 解释实验现象过程开始时, H2O 和糖水均以蒸发为主; 当蒸气压等于P 时, 糖水与上方蒸气达到平衡, 而P0 > P, 即H2O 并未平衡, 继续蒸发, 以致于蒸气压大于P. H2O 分子开始凝聚到糖水中, 使得蒸气压不能达到P0. 于是, H2O 分子从H2O 中蒸出而凝聚入糖水. 出现了本节开始提出的实验现象.变化的根本原因是溶液的饱和蒸气压下降。
无机化学03非电解质稀溶液的依数性

Ⅱ
7
渗透压在医学上的意义
9.0 g.L-1 NaCl 等渗溶液
5.0 g.L-1 NaCl 低渗溶液
15 g.L-1 NaCl 高渗溶液
Ⅲ
8
渗透压在医学上的意义
晶体渗透压和胶体渗透压
生物体液的渗 透压
(769.8kPa)
无机盐、葡萄
晶体渗透压(766kPa) 糖、氨基酸等 (由晶体物质产生) 小分子物质(1L
血浆含7.5g)
胶体渗透压(3.8kPa) 蛋白质、多糖
(由胶体物质产生)
、脂质等高分 子物质(1L血浆
含70g)
9
细胞
自由通过 水分子
细胞内液 细胞外液
晶体物质 胶体物质
晶体渗透压起决定作用!
4
例:计算18.7 g·L-1乳酸钠(M=112)溶液的渗透 浓度。并判断该溶液属于临床上的等渗、高渗还是 低渗溶液?
解:c = 18.7÷112×1000×2 = 334 mmol·L-1 334 mmol·L-1接近320 mmol·L-1,又因为
乳酸钠溶液的实际粒子活度略小于2,所以该溶液 仍然属于临床上的等渗溶液。
无机化学03非电解质稀溶液 的依数性
2
第三章 非电解质稀溶液的依数性
溶液的依数性
蒸气压下降 沸点升高 凝固点降低 渗透压
依数性的应用
3
什么是非电解质稀溶液?
溶液? 非电解质溶液? 稀溶液?
4
溶液的依数性
依数性
非电解质稀溶液的某些性质的大小只决定于溶 质的浓度而与溶质的本性无关,即只依赖于溶质粒 子的数目,称为依数性。包括溶液的蒸气压下降, 沸点升高,凝固点降低和渗透压。
根据公式
,则:
稀溶液依数性

仪器:温度计、烧杯、搅拌 器、滴定管等
实验步骤与操作
准备实验器材:烧杯、温度计、搅拌器、 滴定管等
配置稀溶液:按照一定比例配制不同浓 度的稀溶液
测量溶液温度:将溶液搅拌均匀后测量 其温度
滴定操作:将标准溶液滴加入稀溶液中 记录滴定数据
数据处理与分析:根据实验数据分析稀 溶液依数性的规律
实验结果与分析
在制药行业中稀溶 液依数性对于药物 的提取、分离和纯 化等过程具有重要 影响利用稀溶液依 数性可以提高药物 的纯度和收率。
稀溶液依数性在生物学中的应用
渗透压调节:稀 溶液中的溶质分 子可以影响细胞 的渗透压进而影 响细胞的吸水和 膨胀。
物质运输:稀溶 液中的溶质分子 可以影响物质的 跨膜运输例如葡 萄糖和氨基酸在 血液中的运输。
实验数据:测量 了不同浓度溶液 的蒸气压、凝固 点、沸点等数据
结果分析:通过 数据分析验证了 稀溶液依数性与 浓度之间的关系 得出了依数性的 规律
实验结论:实验 结果与理论预测 基本一致进一步 证实了稀溶液依 数性的存在
实验意义:实验 验证了稀溶液依 数性的理论为进 一步研究溶液性 质提供了实验依 据
添加标题
实例分析:以氯化钠为例 氯化钠溶于水后水分子的 偶极受到氯离子和钠离子 的静电吸引作用导致水分 子的偶极方向发生变化从 而影响了溶液的蒸气压、
沸点、凝固点等性质。
稀溶液依数性与溶剂性质的关系
溶剂的种类对稀溶液依数性有影响不同溶剂的稀溶液依数性不同。 溶剂的浓度对稀溶液依数性有影响溶剂浓度越高稀溶液依数性越明显。 溶剂的分子极性对稀溶液依数性有影响分子极性越强稀溶液依数性越明显。 溶剂的粘度对稀溶液依数性有影响粘度越大稀溶液依数性越不明显。
添加副标题
3稀溶液的依数性

1.7稀溶液的依数性之溶液的蒸气压下降一个神奇的问题处于室温中的一封闭箱内放有两杯液体,一段时间后,发现A 杯空了、B 杯满了。
B A 有什么神奇的力量? 稀溶液的依数性:溶液的蒸气压下降问题A B 纯水 糖水稀溶液的依数性:溶液的蒸气压下降1.纯溶剂的蒸气压 敞口水杯 密闭水杯示意图①蒸发(Evaporation ) ②凝结(Condensation )③饱和蒸气压(Saturated vapor pressure ):简称”蒸气压“,单位Pa 或kPa 。
液相 气相 蒸发凝结 v (蒸发)=v(凝结) 体系处于平衡状态上方蒸气对液面产生的压力1.纯溶剂的蒸气压温度(K ) 蒸气压(kPa ) 温度(K ) 蒸气压(kPa ) 冰 水 水 253 0.103 283 1.23 263 0.260 0.287 293 2.34 268 0.401 0.421 303 4.24 269 0.437 0.455 313 7.38 270 0.476 0.489 323 12.33 271 0.517 0.528 333 19.9 272 0.563 0.568 343 31.16273 0.611 0.611 373 101.325 不同温度下冰和水的蒸气压 温度高蒸气压高固体亦有蒸气压蒸气压低→难挥发性物质蒸气压高→易挥发性物质如:甘油、食盐如:苯、碘、乙醚 稀溶液的依数性:溶液的蒸气压下降2.溶液的蒸气压下降A :纯溶剂的蒸发 B:溶液的蒸发 原因:部分表面被占据。
P *:纯溶剂的蒸气压 P ΔP=P *-P P :溶液的蒸气压 溶液的蒸气压下降 P *稀溶液的依数性:溶液的蒸气压下降问题的答案处于室温中的一封闭箱内放有两杯液体,一段时间后,发现A 杯空了、B 杯满了。
B A 有什么神奇的力量? 稀溶液的依数性:溶液的蒸气压下降问题A B 纯水 糖水 溶液的蒸气压下降造成的。
3.拉乌尔定律(Raoult ,1887,法国物理学家)一定温度下,难挥发非电解质稀溶液的蒸气压,等于纯溶剂蒸汽压乘以溶剂在溶液中的物质的量分数。
稀溶液的依数性详解
三 拉乌尔定律
1 溶液的浓度
每 dm3 溶液中含溶质的物质的量为摩尔浓度,也经常称为体
积摩尔浓度。( 单位 mol · dm-3 )
这种浓度使用方便,唯一不足就是其数值要随温度变化。
若用每 kg 溶剂中含溶质的物质的量来表示溶液的浓度,则称
为质量摩尔浓度。( 单位 mol ·kg -1 ) 质量摩尔浓度经常用 m 表示。 摩尔分数
随着上方空间里溶剂分子个数的增加,密度的增加, 分子凝
聚回到液相的机会增加。当密度达到一定数值时,凝聚的分子的
个数也达到 N0 个。这时起,上方空间里溶剂分子的个数不再改变,
蒸气的密度也不再改变,保持恒定。
此时,蒸气的压强也不再改变。这个压强称为该温度下溶剂 的饱和蒸汽压,用 p0 表示。这时液相和气相之间实现相平衡。 蒸 凝 发 聚
故有
p = p0 · X质 。 对于稀的水溶液,有
m p p 0 55.5
一定温度下,p0 为常数。故上式可以写成
p = k ·m
( k 为常数,但对于不同溶剂 k 值不同 )
稀溶液饱和蒸气压下降值,与稀溶液的质量摩尔浓度成正比。 这是 Raoult 定律的又一种表述形式。
§2 溶液沸点升高和凝固点降低
液体
蒸 发
凝 聚
气体
3 解释实验现象 过程开始时,水和糖水均以蒸发为主。当蒸气压等于 p 时,
糖水与上方蒸气达到平衡。而 p0 > p ,即水并未与蒸汽达到平衡,
继续蒸发,以致于蒸气压大于 p , 水蒸气分子开始凝聚到糖 水中。
这又使得蒸气压不能达到 p0 于是, H2O 分子从水中蒸
611
大学化学 稀溶液的依数性

尿素的相对分子质量为60
稀溶液的依数性应用
溶液凝固点降低的性质还有许多实际应用。
——盐和冰的混合物可用作冷却剂
——严冬时节,汽车的散热水箱加入甘油或乙 二醇等物质,可防水箱结冰
b [K 3 Fe(CN) 6 ] 4.94 / 329 0.100 0.150 (mol kg
1 )
实验测得溶液中各种溶质的总质量摩尔浓度为
b总 T f Kf 1.1 1.86 0.591(mol k g
1
)
【例2-3】续解 b [ K3Fe(CN)6]不等于 b总是由于 K3Fe(CN)6 在水中溶解 成离子所致。设 1 个 K3Fe(CN)6 解离成 x 个离子,则
ΔTf = Tf0 - Tf = Kf bB
式中,ΔTf为凝固点下降数值;Kf为溶剂的质量摩尔凝固 点下降常数,也是溶剂的特征常数,单位为K· kg· mol-1 溶液的凝固点的下降是稀溶液的依数性 上式表明,难挥发性非电解质稀溶液的凝固点的下降只与 溶质的质量摩尔浓度有关,即与单位体积溶液中溶质质 点数的多少有关,而与溶质的本性无关。
③ 弱电解质的依数性计算可近似等同于非电解质。
例题(Example)
【例2-3】实验测得4.94g K3Fe(CN)6溶解在100g水中所得
溶液的凝固点为- 1.1℃ , M[K3Fe(CN)6] = 329g· mol-1 , 写出K3Fe(CN)6在水中的解离方程式。
【解】假定K3Fe(CN)6在水中不发生解离
表2.2 不同温度下冰和水的蒸气压
p/ kPa
稀溶液的依数性

稀溶液的依数性:当溶质溶解在溶剂中形成溶液后,溶液的蒸气压下降,沸点升高,凝固点降低及产生渗透压等性质,只与溶质中粒子的数目有关,而与溶质的本性无关。
由于这类性质的变化,只适用于稀溶液,故称之为稀溶液的依数性。
人工降雨:①根据开尔文公式RTlnPr/P0=2rVm/R’,最初生成的雨滴半径很小,所以其蒸气压很高,此时对平面液体过饱和度达4的水蒸气,对极小的水滴仍未达饱和,所以这个新的液构很难凝聚出来。
②而空气中的灰尘常会作为凝聚中心促使雨滴形成,若在这种水蒸气过饱和度已超过4的云层中,用火箭或撒入干冰提供凝聚中心,使凝聚水滴的曲率半径增大。
由laplace方程,Ps=2Y/R’,其相应的饱和蒸气压变小,蒸汽会还原凝结成冰。
暴沸:①通常在液态有机物中,溶解的空气很少,在蒸馏过程中,液体中形成的蒸汽泡内壁是一个凹液面。
②根据开尔文公式RTlnPr/P0=2rVm/R’可知,凹面上的R’越小,小蒸汽泡内的蒸气压就越低,所以在相同温度下,小蒸汽泡的蒸气压比平面液体的P0低很多;此时液体内部产生气泡所承受的压力P’1=P大气+P平面+Ps,所以当T超过正常沸点时,液体内部的小蒸汽泡无法形成,溶液无法沸腾。
③继续加热,直至小气泡开始形成,气泡一旦形成后便不断变大。
由laplace公式,Ps=2Y/R’,随着R’增大,Ps下降,而P静在气泡上升阶段中不断下降,此时Ti>T正常,故此很容易产生暴沸现象。
盐碱地农作物枯死:①农作物的生长需要水分,然而盐碱地中盐碱浓度大,此时化学势UA 较低,农作物的中心浓度较盐碱地低,其化学式势UB>UA。
②由UB>UA,土地中的渗透压>农作物中的渗透压,农作物中的水分通过细胞壁渗透到土壤中,导致细胞枯萎。
分解电压:电解质在电极上分解生成电解产物所需施加的最小电压。
析出电压:当外加电压等于分解电压时两极的电极电位,是开始析出物质时所必须的最小析出电位。
电极极化的意义:电极上有电流通过时,就会有净反应发生,表明电极失去了原有的平衡状态,电极电位将偏离平衡电位。
稀溶液的依数性

•
渗析实验
例18
5
凝固点下降的定性解释
A(g)
pA
A(l)
A*(s)
pamb 一定
A(l, Tf , p, x A )
A * (s, Tf , p)
o
a
由相平衡条件 A(l) A(s) pA(l) pA(s) A(g) RTln A(g) RTln p p pA(l) pA(s)
范特霍夫渗透压公式
p
pΠ
VAdp RT
xA
1
dlnxA
nB Π V RTlnxA RT A nA
V nB RT cB RT
4
渗透压
纯 水 向 红 萝 卜 内 渗 透
• 渗透原理被用 来处理尿毒症. 在人工肾里, 病人的血液在 玻璃软管(用作 半透膜)循环, 血液里的小分 子废物向管外 渗透, 从而使 血液得到净化.
RTf2
2 3 lnxA ln(1 xB ) ( xB xB / 2 xB / 3 ) xB ( xB 1) nB /(nA nB ) nB / nA M AbB
得到
R(Tf ) 2 M A Tf bB K f bB fus H m, A
继续
dlnxA
( S A(l) Sm, A(s) )
dlnxA
RT fus H m, A
RT 2
dT
( H A(l) H m, A(s) )
RT
2
dT
dT
H A(l) H m, A(s) fus H m, A 7
凝固点下降公式的推导
RT 若视fus Hm, A为与温度无关的常数 积分得 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章稀溶液的依数性
§本章摘要§1. 溶液的饱和蒸气压下降
问题的提出饱和蒸气压拉乌尔定律2. 沸点升高和凝固点下降
沸点和凝固点饱和蒸气压图公式
应用
3. 渗透压
渗透现象渗透压渗透压公式
§1 溶液的饱和蒸气压下降
一问题的提出
水自动转移到糖水中去, 为什么?
这种转移, 只能通过蒸气来进行.
因此, 要研究蒸气的行为, 才能弄清
楚问题的实质.
二饱和蒸气压
1. 纯溶剂的饱和蒸气压 (P0)
液体气
体
在密闭容器中, 在纯溶剂的单位表面上, 单位时间里,
有N0个分子蒸发到上方空间中。
随着上方空间里溶剂分
子个数的增加, 密度的增加, 分子凝聚, 回到液相的机会
增加. 当密度达到一定数值时, 凝聚的分子的个数也达到
N0个。
这时起, 上方空间的蒸气密度不再改变, 保持恒
定。
此时, 蒸气的压强也不再改变, 称为该温度下的饱和
蒸汽压, 用P0表示。
达到平衡. 当蒸气压小于P0时, 平衡右移, 继续气
化; 若蒸气压大于P0时, 平衡左移, 气体液化. 譬如,
改变上方的空间体积, 即可使平衡发生移动。
2.溶液的饱和蒸气压 (P)
当溶液中溶有难挥发的溶质时, 则有部分溶液表面被这种溶质分子所占据, 如图示:
于是, 在溶液中, 单位表面在单位时间内蒸发的溶剂分子的数目N 要小于N0。
凝聚分子的个数当然与蒸气密度有关. 当凝聚的分子数目
达到N, 实现平衡时, 蒸气压已不会改变. 这时, 平衡状态下的饱和蒸气
压为:P< P0对溶液来讲, 蒸气压大于P, 液化;蒸气压小于P, 气
化。
3. 解释实验现象
过程开始时, H2O 和糖水均以蒸发为主; 当蒸气压等于P 时, 糖水与上方蒸气达到平衡, 而P0> P, 即H2O 并未平衡, 继续蒸发, 以致于蒸气压大于P. H2O 分子开始凝聚到糖水中, 使得蒸气压不能达到P0. 于是, H2O 分子从H2O 中蒸出而凝聚入糖水. 出现了本节开始提出的实验现象.
变化的根本原因是溶液的饱和蒸气压下降。
三拉乌尔定律 (Laoult, 法国)
1. 溶液的浓度
每溶液中含溶质的摩尔数, 为摩尔浓度. 这种浓度使用方便, 唯一不足, 是和温度有关。
若用每Kg 溶剂中含溶质的摩尔数, 则称为质量摩尔浓度, 经常用m 表示。
摩尔分数:
对于稀溶液, 由于n质<< n剂, 故有:
对于稀的水溶液, 则有:
对于1000g 溶剂水, 则有:
这时, n质的意义是1000g 水中含的溶
质的摩尔数, 即质量摩尔浓度m, 故:
这是稀的水溶液中, x质与质量摩尔分数的关系, 其它溶剂, 则不是55.5, 但仍是一个已知数值。
2. 拉乌尔定律(Laoult)
在一定温度下, 溶液的饱和蒸气压等于纯溶剂的饱和蒸气压与溶剂摩尔分数之积.
即: P = P0·x剂
用P表示溶液的P与纯溶剂P0之差, 则有:P = P0 - P = P0 - P0·x剂= P0 (1- x 剂) 故有:P = P0·x质
对于稀的水溶液:
一定温度下, P0亦为常数, 故P0/55.5 也是常数, 令其等于k, 则有:P = k·m (对于不同溶剂, k 值不同)
稀溶液饱和蒸气压下降值, 与稀溶液的质量摩尔浓度成正比。
这是Raoult 定律的另一种表述形式。
§2 沸点升高和凝固点下降
一沸点和凝固点
蒸发: 表面气化现象称为蒸发;
沸腾: 表面和内部同时气化的现象;
沸点: 液体沸腾过程中的温度.
只有当液体的饱和蒸气压和外界大气的压强相等时, 液体的气化才能在表面和内部同时发生, 这时的温度即是沸点.
凝固点: 液体凝固成固体(严格说是晶体)是在一定温度下进行的, 这个温度称为凝固点。
凝固点的实质是, 在这个温度下, 液体和固体的饱和蒸气压相等.即为:
液体固体平衡
若P固> P液, 则固体要融化(熔解);
P固< P液, 液体要凝固;(和H2O自动向糖水转移是一个道理, 都是蒸气压在起作用)
二饱和蒸气压图
), , 三 公式
1. 沸点升高公式
用 Tb 表示沸点升高值, 即:
Tb = Tb- T0b ( T0b 是纯溶剂的沸点, Tb 是溶液的沸
点)。
Tb 是直接受P 影响的, 有:
Tb
P, 而
P = k·m, 故
Tb
m. 比例系数用
kb 表示, 则有:
Tb= kb ·m , kb 为沸点升高常数, 不同的溶剂, kb 值不同, 最常见的溶剂是H2O, 其kb= 0.512
2. 凝固点下降公式
用 Tf 表示凝固点降低值, 即: Tf = T0f - Tf T0f 是纯溶剂的凝固点, Tf 是溶液的凝固点. 总之, Tf 为正值, 且 Tf = kf ·m,
kf : 凝固点降低常数, H2O的kf = 1.86
3. 公式的成立条件
公式由P = k·m 推出, 在推导时, 有条件: 溶质不挥发, 且n质<< n剂, 即为稀溶液。
m(质量摩尔浓度)的大小, 要能与溶液表面上不挥发的质点的多少有定量关系, 溶质必须是非电解质. 若是NaCl, 电解产生Na+ 和Cl-, m = 1时, 质点数可能是2, 且Na+ 和Cl- 之间又有吸引, 则相当于在1-2 之间, 不好定量. Ba(OH)2 体系就更加复杂了. 因而, 公式成立的条件是: 不挥发的非电解质的稀溶液。
1) 挥发性溶质: 在后续课程中讲授。
2) 电解质溶液: 离解后, 相当于多少个粒子, 定
量关系不确切. 不能用此公式计算, 但同样0.1 m 的Al2(SO4)3 总比0.1m 的NaCl 产生的粒子多. 可以定性的推理, 即仍有蒸气压下降, 沸点升高和凝固点降低等性质.3) 浓溶液: 由于分子间的作用复杂, 虽然也有升高和降低等现象, 但定量关系不准确。
例题:将 1.09g 葡萄糖溶于20g 水中, 所得溶液的沸点升高了0.156K, 求葡萄糖的分子量。
解: 先求出m.
和实际分子量180 相近
利用凝固点法, 测分子量更准确. 因为kf 比kb 要大, 温度差要更明显一些. 就测定方法本身来讲, 凝固点的测定比沸点测定精确度高
四
§3 渗透压
一渗透现象
二渗透压
渗透现象发生以后,
1. H2O柱的高度降低, 静压减小, 使右行的H2O分子数目减少;
2. 糖水柱升高,使左行的H2O分子数目增加;
3. 糖水变稀, 膜右侧的H2O分子的分数增加, 亦使左行的H2O分子数目增加.
当过程进行到一定程度时, 右行和左行的H2O分子数目相等, 这时, 达到平衡, 即H2O 柱不再下降; 同时, 糖水柱不再升高. 液面高度差造成的静压, 称为溶液的渗透压, 用表示, 单位为Pa.
三渗透压公式
具有渗透压, 是溶液的依数性质, 它产生的根本原因也是相变界面上可发生变化的分子个数不同引起的. 经过长期研究, 人们发现:
1. 温度相同时, 和溶液的体积摩尔浓度成正比;
2. 浓度相同时, 和温度T 成正比. 即:
测得比例系数和气体常数R 相同, 则公式改写成:
即: V = nRT。
