高通有源滤波电路
有源高通滤波器电路设计(100Hz截止频率)

长沙学院课程设计说明书题目有源高通滤波器电路设计系(部) 电子与通信工程系专业(班级) 电气工程及其自动化姓名学号指导教师起止日期模拟电子技术课程设计任务书系(部):电子与通信工程系专业:电气工程及其自动化指导教师:长沙学院课程设计鉴定表目录摘要 (5)1.电路设计 (6)1.1.电路元件及参数的选择 (6)1.2.电路原理图绘制 (6)2.电路的仿真 (7)2.1.使用Multisim9仿真波特图示仪 (7)2.2.使用Multisim9仿真示波器 (7)2.2.1.输入信号频率小于截止频率时的仿真 (7)2.2.2.输入信号频率等于截止频率时的仿真 (8)2.2.3.输入信号频率大于截止频率时的仿真 (8)参考文献 (9)设计总结 (9)摘要滤波器是一种能使有用信号通过而大幅抑制无用信号的电子装置。
常用来进行信号处理、数据传输和抑制噪声等。
以往这种滤波电路主要采用无源R、L和C组成,20世纪60年代以来,集成运放获得了迅速发展,由它和R、C组成的有源滤波电路,具有不用电感、体积小、重量轻等优点。
此外,由于集成运放的开环电压和输入阻抗均很高,输出阻抗又低,构成有源滤波电路后还具有一定的电压放大和缓冲作用。
但是,集成运放的带宽有限,所以目前有源滤波电路的工作频率难以做的很高,以及难于对功率信号进行滤波,这是它的不足之处。
]1[在实际电子系统中,有源滤波器运用广泛,输入信号往往是含有多种频率成分的复杂信号,可能还会混入各种噪声、干扰及其它无用频率的信号,因此需要设法将有用频率信号挑选出来、将无用信号频率抑制掉。
完成此任务需要具有选频功能的电路。
本文主要内容是设计一个能阻挡低频信号、输出高频信号的有源高通滤波电路,以及利用Multisim9对电路进行仿真。
本电路所用到的运算放大器LM741EN,它的管脚1和5为调零端,管脚2为运放反相输入端,管脚3为同相输入端,管脚6为输出端,管脚7为正电源端,管脚4为负电源端,管脚8为空端。
有源滤波器的传递函数

有源滤波器的传递函数有源滤波器的传递函数可以通过不同的方法来推导,其中一种常用的方法是通过分析电路的放大器和反馈网络的连接方式和元件参数来得到。
下面以最常见的两种有源滤波器类型,低通滤波器和高通滤波器为例,分别推导它们的传递函数。
1. 低通滤波器(Low pass filter):为了推导低通滤波器的传递函数,我们可以以反馈放大器为基础。
假设输入信号为Vin,输出信号为Vout,放大器的放大倍数为A,反馈网络由电阻Rf和电容Cf组成。
首先,考虑放大器的输入和输出关系,我们有:Vout = A * Vin接下来,考虑反馈网络,根据电容器的性质,我们有:I = C * dVout/dt其中,I是电容器上的电流,C是电容器的容值。
根据欧姆定律,我们有:I = Vout / Rf根据上面两个方程,可以得到:C * dVout/dt = Vout / Rf经过简化和变形,可以得到:dVout/Vout = 1 / (A * Rf * C) * dt对上式两边进行积分,可得到:ln(Vout) = 1 / (A * Rf * C) * t + ln(C)取指数,可得到:Vout = e^(1 / (A * Rf * C) * t) * C其中,e是自然对数的底数。
上述方程描述了低通滤波器的传递函数,可以看到其形式为指数函数。
通过调节放大倍数A和反馈网络的参数Rf和Cf,可以实现不同的滤波效果。
2. 高通滤波器(High pass filter):高通滤波器的传递函数也可以通过类似的方法推导。
在这里,我们同样以反馈放大器为基础,输入信号为Vin,输出信号为Vout,放大倍数为A,反馈网络由电阻Rf和电容Cf组成。
首先,考虑输出和输入关系,我们有:Vout = A * Vin然后,考虑反馈网络,根据电容器的性质I = C * dVin/dt其中,I是电容器的电流,C是电容器的容值。
根据欧姆定律,我们有:I = Vin / Rf结合上述两个方程,可以得到:C * dVin/dt = Vin / Rf经过简化和变形,可得到:dVin/Vin = 1 / (A * Rf * C) * dt对上式两边进行积分,可得到:ln(Vin) = 1 / (A * Rf * C) * t + ln(C)取指数,可得到:Vin = e^(1 / (A * Rf * C) * t) * C上述方程描述了高通滤波器的传递函数,同样是一个指数函数。
滤波电路的原理

滤波电路的原理
滤波电路是一种用于去除信号中不需要的频率成分,保留有用信号的电路。
它的原理基于信号的频率特性,通过选择性地传递或阻止特定频率范围内的信号来实现滤波。
滤波电路通常由电容器、电感器和电阻器等元件组成。
根据元件的排列方式和连接方式,滤波电路可以分为低通滤波电路、高通滤波电路、带通滤波电路和带阻滤波电路。
低通滤波电路可以让低频信号通过,而阻止高频信号的传输。
它的原理是通过电容器对高频信号的阻抗产生作用,使高频信号流向地,从而实现对高频信号的滤波。
高通滤波电路则与低通滤波电路相反,它可以让高频信号通过,而阻止低频信号的传输。
高通滤波电路利用电感器对低频信号的阻抗产生作用,将低频信号流向地,从而实现对低频信号的滤波。
带通滤波电路可以选择某个频率范围内的信号通过,同时阻止其他频率范围的信号传输。
它通常由高通滤波和低通滤波两部分组成,可以实现对特定频率范围内信号的滤波。
带阻滤波电路则相反,它可以选择阻止某个频率范围内的信号通过,而允许其他频率的信号传输。
带阻滤波电路通常由低通滤波和高通滤波两部分组成。
通过合理选择滤波电路的元件和参数,可以实现对不同频率范
围内信号的有效滤波,从而去除噪音或干扰,提取出我们所需要的信号。
这是滤波电路的基本原理。
滤波电路主要有以下四种基本类型
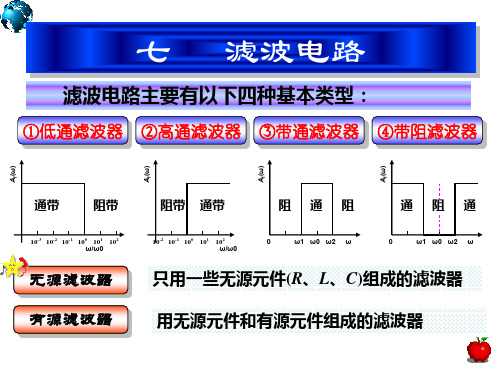
七
①低通滤波器
i
R 1 R jC
1 1 1 jRC
1 0 1 j
1 RC
0
(c)
C
o
U i
R
(b)
U o
它们的截止存在的问题 (1)电路的增益小,最大为1 (2)带负载能力差
1 0.707
0
o
(d )
如在无源滤波电路输 出端接一负载电阻RL, 则其截止频率和增益 均随RL而变化。
简单二阶低通滤波 电路的幅频特性
由幅频特性可见ω>>ω0时衰减 的斜率为-40dB/十倍频。但在 ω0附近,其幅频特性与理想的 低通滤波特性相差较大。
0 -3dB
20 lg
Af ( ) / dB Af
-40dB/十倍 频
0.1 0.37 1
10
ω/ω0
改进
R
1
R
U
2
f
将电容C1的接 地端改接到集成 运放的输出端。
o
up
o
A A
up
高通
1
通
1
阻
2
通
o
带阻滤波器电路图
C
C
R
1
R
f
1 o 1 j 2 Q o 2 Rf 1 1 Af 1 Q R1 RC 22 Af
有源滤波电路

(a) 图6-12 【例6-2】电路图
(b)
Vo Vn VP 0
该电路在频率低时有输出,频率高时无输出,因此电路(a)是低通滤波器。
在电路(b)中,在频率低时无输出,频率高时有输出,因此电路(b)是 高通滤波器。
(2) 电路(a)的通带增益为
Avp 1
Rf R1
电路(b)的通带增益为 Avp
【例6-2】电路如图6-12所示。已知集成运放均为理想运放; (1)分别说明各电路是低通滤波器还是高通滤波器,简述理由; (2)分别求出各电路的通带增益。
解: (1)在电路(a)中,若输入电压频率趋于零,则C1和C2相当于开路,集成运放构成 电压跟随器, 输出电压为 Vo Vi 若输入电压频率趋于无穷大,则C1和C2相当于短路,输出电压为
通带宽度 B
品质因数
Q
1 3 Avf
Avf 1
Rf R1
f0 Q
通带电压增益
Avp
Avf 3 Avf
上限截止频率
f p2
B f0 2
B 下限截止频率 f p1 f 0 2
【例6-3】图6-13(a)所示电路中,R=796kΩ,C=0.01μF,R1=243kΩ,
6.2 有源滤波电路
6.2.1 6.2.2 6.2.3 6.2.4 有源低通滤波器 有源高通滤波电路 有源带通滤波电路 有源带阻滤波电路
6.2.1 有源低通滤波器
低通滤波器的主要技术指标如下: (1)通带增益Aup 通带增益是指滤波器在通频带内的电压放大倍数。理想的 LPF通带内的幅频特性曲线是平坦的,阻带内的电压放大倍数 为零,如图6-1中虚线所示。 (2)通带截止频率fp 截止频率是滤波器通带与阻带的界限频率。低通滤波器 的截止频率指随着工作频率的提高,滤波器的传递函数的模 下降到0.707Aup时所对应的频率。 (3)衰减速率 实际滤波器的通带与阻带之间称为过渡带,如图6-1所 示。过渡带越窄,说明滤波器的选择性越好。通常用滤波器 在通带外每十倍频衰减了多少来表示。
二阶有源高通滤波器原理

二阶有源高通滤波器原理在电子电路中,滤波器是一种能够选择性地通过或者抑制特定频率信号的电路。
而有源高通滤波器则是一种常见的滤波器类型,用于将高频信号通过而抑制低频信号。
本文将介绍二阶有源高通滤波器的原理和工作方式。
1. 基本原理二阶有源高通滤波器通常由运算放大器、电容和电阻构成。
在这种滤波器中,运算放大器起到放大和相位移的作用,电容和电阻则构成滤波器的频率选择网络。
通过合适的设计,可以实现对特定频率以下信号的抑制,而对特定频率以上信号的通过。
2. 滤波器架构二阶有源高通滤波器的典型架构包括两个电容和两个电阻元件。
其中,电容和电阻的数值可以根据需要进行选择,以确定滤波器的截止频率和增益。
运算放大器的正负输入端分别连接这两个电容和两个电阻元件,输出端则连接到负反馈路径。
这样的架构可以实现对低频信号的衰减和对高频信号的放大。
3. 工作原理二阶有源高通滤波器的工作原理基于运算放大器的反馈机制。
当输入信号经过滤波器后,输出信号的幅度和相位将根据滤波器的频率响应而发生变化。
通过合理设置电容和电阻的数值,可以确定滤波器的截止频率和斜率,从而实现对特定频率信号的处理。
4. 频率响应二阶有源高通滤波器的频率响应通常呈现出一定的斜率,在截止频率处实现对低频信号的抑制。
随着频率的增加,滤波器对信号的放大倍率也会相应增加。
这种特性使得有源高通滤波器在许多应用中得到广泛应用,如音频处理、通信系统等方面。
5. 应用领域二阶有源高通滤波器在电子电路中有着广泛的应用。
比如在音频处理中,可以用于消除低频噪声或者实现声音效果;在通信系统中,可以用于滤除直流偏置或者实现信号调制。
由于其结构简单、性能稳定,因此在实际应用中得到了广泛的应用和认可。
综上所述,二阶有源高通滤波器作为一种常见的滤波器类型,在电子电路设计中扮演着重要的角色。
通过合理设计滤波器的参数,可以实现对特定频率信号的处理,满足不同应用场景的需求。
希望通过本文的介绍,读者能对二阶有源高通滤波器的原理和应用有更深入的理解。
第五章(二)有源滤波电路

模 : A uf
Au
1
2 2 1 ( L)
通 带 内 C 1视 为 短 路 : 电 压 放 大 倍 数 Au
滤波电路—使有用的频率信号通过,同时抑制无用频率成分的电路。 分类: 按处 按处理 按构成 理信 方法 器件分 号分 按频率特性分 低 通 滤 波 器 高 通 滤 波 器 带 通 滤 波 器 带 阻 滤 波 器 一 阶 滤 波 器 按传递函数分 二 阶 滤 波 器 N 阶 …… 滤 波 器
Au 1 (
Auf fn f ) j
2
fn Qf
对于二阶低通、高通电路, Auf 3时 , Q 电 路 产 生 自 激 振 荡 。 为防止自激,应使: Auf<3
3 Auf
三、有源带通滤波电路(BPF—Band Pass Filter)
电路只允许某一频段内信号通过,有上限和下限两个截止频 率,将高通滤波电路与低通滤波电 路进行适当组合,就可获得 带通滤波电路。下图为二阶有源带通滤波电路,图中R、C组成低 通电成路,C1、R3组成高通电路,要求RC<R3C1,故低通电路的上 限截止频率fH大于高通电路的下限截止频率fL,两 者之间形成了 一个通带,从而构成了带通滤波电路。
6
2 160 10 0.01 10 Rf 100 1 1 1.588 R1 170 1 3 Auf 1 3 1.588
99.5 H Z
0.708
Q 0.707时 : f H f n 上 限 截 止 频 率 : fH 99.5 H Z
2.内部电路:由输入级、中间级和输出级等组成。输入级有V2、V4组成双端输入 单端输出差分电路;V3、V5是其恒流源负载;V1、V6是射级跟随器,高 Ri;V7 V12为功率放大电路;V7 为驱动级(I0 为恒流源负载);V11、V12 用于消除交越失 真 ;V8、V10 构成 PNP 准互补对称 ;1、 8 开路时,负反馈最强,整个 电路的电压放大倍数Au = 20 ,若在1、 8 间外接旁路电容,以短路R5两 端的 交流压降,可使电压放大倍数提高到200;调整RP(典型应用电路图),可使集 成功放电压放大倍数在20~200之间变化;管脚7与地之间外接电解电容C5(典 型应用电路图),C5可与R2组成直流电源去耦电路。
滤波器电路分析

图5-3 m推演型LPF的特性示例
图5-5
表2 m推演型低通滤波电路元件归一化参数表
续表2
(9) 将上式(6)~(9)带入电路中得下图m推演型低通滤波电路,陷波点为 130MHZ,截止频率为100MHZ。
m推演型低通滤波电路,在f=130MHZ处有一个陷波点
仿真结果
回波损耗频率特性曲线,当在陷波点f=130MHZ时,电路的回拨损 耗最大,信号反射最厉害
2A
63.66 V
u1 (t ) [63.66 42.44cos(t ) 8.488cos(2t ) 3.638cos(3t ) ...]V
2. 对于基波,先计算转移电压比
| H ( j ) | 1 1 C
2
1 1 10
设计RC二阶低通滤波器电路,可以通过将两个RC一阶低通滤波电路 级联等到,RC二阶低通滤波电路。
图 14-9
下面给出一个fc=200KHZ的RC二阶低通滤波电路的仿真电路图
仿真结果:RC二阶电路的幅频特性 曲线,截止频率为28.199KHZ,
RC二阶高通滤波电路相频特性曲线
3.3RC二阶高通滤波电路
RC一阶高通滤波电路仿真原理图
RC一阶高通滤波电路幅频特性曲线,从图中可以看 出电路在幅度增益下降3.232dB时,截止为 100.901KHZ,滤波电路的性能能满足设计指标。
RC一阶高通滤波电路相频特性曲线,从图中可任意看 出当f=100.697KHZ时,相角超前46.497 deg。
3.3RC二阶低通滤波电路
图10
RC二阶高通滤波电路幅度表达式
RC二阶高通滤波电路截止频率
RC滤波电路所实现的频率特性,也可由相应的 RL电路来实现。在低频率应用的条件下,由于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南文理学院课程设计报告有源高通滤波电路目录第一章简介1.1 设计要求 (3)1.2 设计作用与目的 (3)1.3 所用仪器设备 (4)第二章设计原理2.1 设计方案及方案选择 (5)2.2 模块电路设计及分析 (6)2.3 总体设计 (10)2.4 元件参数 (11)第三章设计硬件及软件过程3.1 Multisim仿真图 (13)3.2 仿真结果 (14)3.3 系统调试结果分析 (16)第四章总结与展望第一章简介1.1设计要求有源高通滤波电路能传送输入信号中有用的频率成分,衰减或抑制无用的频率成分,并对有用的频率成分具有一定的电压放大作用。
有源高通滤波电路应包括:滤波电路;集成运放;反馈电路,三个部分。
滤波电路能有效滤除无用频率信号成分,保留有用频率信号成分。
集成运放和反馈电路使电路具有一定的电压放大作用,使电路滤波特性趋于理想。
通过对有源滤波电路的探究,设计了一四阶有源高通滤波电路。
在Multisim 10软件中进行仿真实验,对电路的频率特性和不同频率下输出的信号进行了分析,电路能有效滤除或衰弱频率为100Hz以下的电压信号,对频率100Hz以上的电压信号有放大作用。
最终结果基本达到了预期要求。
1.2设计作用与目的滤波器是减少或消除谐波对电力系统影响的电气部件,广泛应用于电力系统、通信发射机与接收机等电子设备中,它能减弱或消除谐波的危害,对无用信号尽可能大的衰减,让有用信号尽可能无衰减的通过,从而纠正信号波形畸变。
所以,无论信号的获取、传输,还是信号的处理和交换都离不开滤波技术。
在近代电信设备和各类控制系统中,滤波器应用极为广泛,尤其是有源高通滤波器。
它在通讯、声纳、测控、仪器仪表等领域中有着广泛的应用,有源高通滤波器的优劣直接决定产品的优劣。
所以研究滤波器,具有重大意义。
1.3 所用仪器设备表:有源高通滤波电路明细表第二章 设计原理2.1 设计方案及方案选择有源高通滤波器应分为三部分:滤波电路;集成运放;反馈电路。
滤波电路由R 、C 元件组成。
而集成运放和反馈电路构成了同相比例器或反相比例器。
选择不同的电路单元便有不同的设计方案。
2.1.1 方案一:二阶有源高通滤波器二阶有源高通滤波器由RC 滤波电路和同相比例放大电路组成,其特点是输入阻抗高,输出阻抗低。
其方框图如图2.1所示。
从方框图可以看出:二阶高通有源滤波器主要由RC 网络;集成运放;反馈网络几部分组成。
输入信号通过RC 网络选频,滤除或衰弱无用的频率信号成分,保留有用信号成分。
保留下来的信号成分通过集成运放和反馈网络进行放大,最后完整的输出。
2.1.2 方案二:四阶有源高通滤波器由前面分析可知,二阶有源高通电路能滤除无用频率信号。
而四阶有源高通滤波电路可由两个二阶高通滤波电路级联而得到。
则由图2.2可推断:四阶有源高通滤波器工作原理,输入信号经过电路第一级进行滤波,滤除、衰弱无用频率信号成分,有用成分被放大并被输入到电路第二级,再一次进行滤波和放大后,最后有用频率信号成分被完整输出。
图2.1 二阶有源高通电路框架图图2.2 四阶有源高通电路框架图2.1.3 有源高通滤波器设计方案选择滤波器的技术指标有通带和阻带之分,通带指标有通带的截止频率(没有特殊的说明时一般为-3dB截止频率),通带传输增益。
阻带指标为带外传输增益的衰减速度。
根据前面的设计分析,可设计出简单高通滤波电路和高阶高通滤波电路。
由于二阶高通滤波器滤波效果不够好,幅频特性衰减率较低,而阶数过高则电路复杂,成本较高。
因此,采用四阶有源高通滤波电路比较合理。
2.2 模块电路设计及分析设计电路时应先考虑电路的总体结构。
信号要有选择的被滤除,最主要的是滤波电路的设计。
而信号被筛选之后,最好应有一定的放大,这样才能保证有完整的输出。
因此,应先分析有源高通滤波器的框架图,再设计各单元电路,接着是总体电路的整合,最后是元器件参数的设计分析。
一,有源高通滤波器的基本组成滤波器是一个二端口网络,实现对输入信号的某些频率选择性通过的功能,而使其它频率的信号受到衰减或抑制。
实现这些功能的网络是振荡回路,即由RLC元件或RC元件构成的滤波器,也可以是由RC元件和有源器件构成的有源滤波器。
然后通过有源器件集成运放放大,实现滤波放大功能。
理想滤波器是不存在的,在实际滤波器的幅频特性图中,通带和阻带之间应没有严格的界限。
在通带和阻带之间存在一个过渡带,在过渡带内的频率成分不会被完全抑制,只会受到不同程度的衰减。
根据滤波器基本原理,易知有源高通滤波器的基本组成是:RC选频网络;集成运放;反馈网络。
首先输入信号接入电路,通过滤波电路进行滤波,滤除截止频率以外的信号。
然后通过集成运放电路,实现信号放大。
为了保证集成运放工作在线性区和稳定输出电压,电路中引入了反馈电路。
最后系统输出滤波后的信号。
各单元电路的作用:1、RC网络的作用在电路中RC网络起着滤波的作用,滤掉不需要的信号,这样在对波形的选取上起着至关重要的作用,通常主要由电阻和电容组成。
2、放大器的作用电路中运用了运放,同相放大器具有输入阻抗非常高,输出阻抗很低的特点,广泛用于前置放大级。
而反相放大器输入阻抗低,输出阻抗高。
3、反馈网络的作用将输出信号的一部分或全部通过电路反送到输入端,称为反馈,其中的电路称为反馈网络,反馈网络分为正、负反馈。
二,滤波电路部分设计根据放大电路的频率响应,由于电抗元件及半导体管极间电容的存在,当输入信号频率过低或过高时,导致放大倍数数值变小,产生超前或滞后的相移。
对于高通滤波电路,当信号频率较低时,耦合电容和发射极电容很大,分压作用不可忽略。
由于耦合电容的存在,对信号构成了高通电路,即对于频率足够高的信号电容相当于短路,信号几乎毫无损失地通过;而当信号频率低到一定程度时,电容的容抗不可忽略,信号将在其上产生压降,从而导致放大倍数的数值减小且产生相移。
RC网络在电路中起着重要的作用,滤掉不需要的信号,这样在对波形的选取上起着至关重要的作用,通常主要由电阻和电容组成。
1、一阶高通滤波电路图如图2.3所示。
由KCL分析得:1111oUiRUAU R jj c RCωω•••===+-式1;RCUi Uo图2.3一阶高通滤波电路令1l RC ω=, 有:122l l f RCωππ== 式2; 带入式1可得:1ar 1lU l f ctg A f f jf•==- 式3;则幅频特性:u A =,有:20lg u A =-式4;相频特性:lf arctgfϕ= 式5; 由以上各式可知:若l ff ,有1l f f,则:20lg 0u A ≈,00ϕ=;若l ff ,有1l f f,则:20lg 20lg20lg l u l f f A f f =-=,090ϕ=;若l f f =,有1lf f=,则:20lg 3u A =-,045ϕ=。
2、高阶滤波电路可以由低阶滤波电路级联而成,由此可得二阶高通滤波电路图如图2.4所示。
分析可得其传输函数:121212211111()//=1o U ijwc R R jwc jwc U A U R jwc •••-⨯++=+式6;由以上分析可得,一阶滤波器电路最简单,但带外传输系数衰减慢,过渡带较宽,幅频特性衰减小,一般在对带外衰减性要求不高的场合下选用。
增加RC 环节,变成二阶高通可加大衰减斜率。
三阶以上滤波器可由一阶和二阶滤波器级联而成。
图2.4 二阶高通滤波电路三,集成运放加反馈电路部分设计集成运放应用在信号的运算和处理中,以输入电压为自变量,以输出电压作为函数。
当输入电压变化时,输出电压将按一定的数学规律变化,即输出电压反映输入电压某种运算的结果。
为了实现本设计的通频带放大增益,对于基于理想运放的放大电路,采用“虚短”和“虚断”的分析方法,运放电路中应引入负反馈,使净输入量趋于零,才能保证集成运放工作在线性区。
为了稳定输出电压,引入电压负反馈。
运放电路的特征是从集成运放的输出端到其反相输出端存在反馈通路。
根据设计要求,输入端是信号电压源,输出端要求得到稳定的电压,因此放大电路中应引入电压串联负反馈或电压并联负反馈。
根据以上分析,可得电路设计如下:1) 同相比例运算电路:根据“虚短”和“虚断”的分析方法, 有p N iU U U ==,净输入电流为零,因而可解得输出电压和输入电压关系:110(1)N O Nff O iU U U R R R U U R --==+式7;2) 反相比例运算电路:根据“虚短”和“虚断”的分析方法,图2.5同相比例运算电路由输入电流为0P N i i ==,可得0p N U U ==为“虚地”,即可得:1fR R i i =;1i N N ofU U U U R R --= 式8;整理可得输出电压和输入电压关系:1f o iR U U R =-式9;由以上分析可知,两个运算电路特点如下:1) 反相比例运算电路引入了深度电压负反馈,且1AF +=∞,输出电阻0o R =。
尽管理想运放电路的输入电阻为无穷大,但是由于电路引入的是并联负反馈,故其输入电阻不大。
2)同相比例运算电路具有高输入电阻、低输出电阻的特点。
2.3 总体设计滤波器的设计任务是根据给定的技术指标选定电路形式和确定电路的元器件。
滤波器的技术指标有通带和阻带之分,通带指标有通带的截止频率(没有特殊的说明时一般为-3dB 截止频率),通带传输增益。
阻带指标为带外传输增益的衰减速度。
根据前面的分析,可设计出简单高通滤波电路和高阶滤波电路。
采用反相输入设计时,图2.6 反相比例运算电路系统的传输函数较复杂,故采用同相输入设计。
由于二阶高通滤波器滤波效果不够好,幅频特性衰减率较低,而阶数过高则电路复杂,成本较高。
因此,采用四阶有源滤波电路比较合理。
2.4 元器件参数设计实际滤波器的基本参数:理想滤波器是不存在的,在实际滤波器的幅频特性图中,通带和阻带之间应没有严格的界限。
在通带和阻带之间存在一个过渡带,在过渡带内的频率成分不会被完全抑制,只会受到不同程度的衰减。
当然,希望过渡带越窄越好,也就是希望对通带外的频率成分衰减得越快、越多越好。
因此,在设计实际滤波器时,总是通过各种方法使其尽量逼近理想滤波器。
理想滤波器的特性只需用截止频率描述,而实际滤波器的特性曲线无明显的转折点,故需用更多参数来描述。
理想滤波电路的频率响应在通带内应具有一定幅值和线性相移,而在阻带内其幅值应为零。
实际的滤波电路往往难以达到理想的要求。
如果同时在幅频和相频响应两方面都满足要求就更为困难。
巴特沃斯滤波电路的幅频响应在通带中具有最平幅度特性,本次设计采用巴特沃斯有源高通滤波电路。
设计截止频率100f Hz =的高通滤波器。
电容器C 的容量应在微法数量级,电阻的阻值应在几百千欧以内。
