初二上学期周周清试卷--一次函数单元测试
第四章一次函数 单元测试2024-2025学年北师大版数学八年级上册

O yx O y x x y O O y x 第四章 一次函数单元测试(共120分,100分钟)一、选择题:(每小题3分,共30分)1.一次函数83y x =-+的图象经过的象限是( )A.一、二、三B.二、三、四C.一、二、四D.一、三、四2.若y=(m -2)x+m 2-4是正比例函数,则m 的取值是( )A .2B .-2C .±2D .任意实数3.已知点()14,y -,()22,y 都在直线122y x =-+上,则1y ,2y 大小关系是( ) A.12y y > B.12y y = C.12y y < D.不能比较4.如图,函数y=kx+k 的图象可能是下列图象中( )A B C D5.下列函数中,是正比例函数,且y 随x 增大而减小的是( )A.14+-=x yB. 6)3(2+-=x yC. 6)2(3+-=x yD. 2x y -= 6.已知3-y 与x 成正比例,且x =2时,y =7,则y 与x 的函数关系式为( )A .32+=x yB .32-=x yC .323+=-x yD .33-=x y7.下列各点,在直线y =x +5上的是( )A . (0,4)B .(-1,2)C .(2,6)D . (-5, 0)8.若将直线23y x =-向下平移3个单位长度后得到直线y kx b =+,则下列关于直线y kx b =+说法正确的是( )A.经过第一、二、四象限B.与x 轴交于()2,0-C.与y 轴交于(0,6)D.y 随x 的增大而增大 9.关于x 的函数()3y k x k =-+,给出下列结论:①当3k ≠时,此函数是一次函数;②无论k 取什么值,函数图象必经过点()1,3-;③若图象经过二、三、四象限,则k 的取值范围是0k <;④若函数图象与x 轴的交点始终在正半轴,则k 的取值范围是03k <<.其中正确结论的序号是( )A.①②④B.①③④C.①②③④D.②③④10.如图,点B 在直线2y x =上,过点B 作BA x ⊥轴于点A ,作//BC x 轴与直线()0y kx k =≠交于点C ,若:1:2AB BC =,则k 的值是( )A.27B.23C.13D.25二、填空题:(每小题4分,共28分)11.一次函数图象过(1,2)且y 随x 的增大则减小,请写出一个符合条件的函数解析式 .12.直线y = -3x +6与x 轴交点坐标是 .13.一次函数y=kx+b 的图像位于第一、三、四,则y 随x 的增大而_________.14.直线63+=x y 与两坐标轴围成的三角形的面积是15.若函数32+=x y 与b x y 23-=的图象交于x 轴于同一点,则b =__________.16.若k x k y )1(-=-7是一次函数,则k = .17.若点A (x ,4),B (0,8)和C (-4,0)在同一直线上,则x = .三、解答下列各题:(共62分)18.(9分)已知一次函数2(2)312y k x k =--+.(1)k 为何值时,图象经过原点;(2)k 为何值时,图象与直线y = -2x +9的交点在y 轴上;(3)k 为何值时,图象平行于2y x =-的图象;19.(9分)如图是某汽车行驶的路程S (km )与时间t (min)的函数关系图.回答下列问题:(1)汽车在前9分钟内的平均速度是多少?(2)汽车在中途停了多长时间?(3)当16≤t ≤30时,求S 与t 的函数关系式.20.(10分)直线122y x =-+分别交x 轴,y 轴于A,B 两点,O 是原点,直线y=kx+b 经过AOB △的顶点A 或B,且把AOB △分成面积相等的两部分,求该直线所对应的函数表达式.9 16 30 t /minS /km40 1221.(10分)如图,直线132y x =-+与x,y 轴分别交于A,B 两点.(1)分别求点A 、点B 的坐标.(2)在x 轴上有一点M,线段AB 上有一点N,当OMN △是以ON 为斜边的等腰直角三角形时,求点M 的坐标。
2024八年级数学上册第四章一次函数周周清检测内容4

检测内容:4.1-4.4得分________ 卷后分________ 评价________一、选择题(每小题4分,共28分)1.下列函数:①y =πx ;②y =2x -1;③y =1x ;④y =2-1-3x ;⑤y =x 2-1中,是一次函数的有( B )A .4个B .3个C .2个D .1个 2.(开封期末)已知函数y =(m +1)xm 2-3是正比例函数,且图象在其次、四象限内,则m 的值是( B )A .2B .-2C .±2D .123.已知点A (x 1,y 1)和点B (x 2,y 2)是一次函数y =(k 2+1)x +2图象上的两点,且x 1>x 2,则y 1和y 2的大小关系是( C )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .不确定4.若a ,b 为实数,且1-2b +2b -1 -a =3,则直线y =ax +b 不经过的象限是( C ) A .第一象限 B .其次象限 C .第三象限 D .第四象限5.直线y =kx +3与y =3x +k 在同一坐标系内,其位置可能是( A )ABCD6.将直线y =x +b 沿y 轴向下平移3个单位长度,点A (-1,2)关于y 轴的对称点落在平移后的直线上,则b 的值为( C )A .-3B .3C .4D .-47.如图,等边三角形ABC 中,AB =4,有一动点P 从点A 动身,以每秒一个单位长度的速度沿着折线A -B -C 运动至点C ,若点P 的运动时间记作t 秒,△APC 的面积记作S ,则S 与t 的函数关系应满意如下图象中的( A )ABCD二、填空题(每小题5分,共20分)8.若一次函数y =mx +|m -1|的图象过点(0,3),且y 随x 的增大而增大,则m 的值为__4__.9.已知一次函数y =kx +b 的图象如图所示,则关于x 的方程kx +b =0的解为__x =-2__.第9题图第10题图10.甲、乙两人沿相同的路途前往离学校12 km 的地方参与植树活动,他们前往目的地所行驶的路程s (km)随时间t (min)改变的函数图象如图所示,则每分钟乙比甲多行驶的路程是__0.5__km.11.如图,在平面直角坐标系中,A (2,0),B (0,1),AC =AB 且AC ⊥AB 于点A ,则OC 所在直线的关系式是__y =23x __.三、解答题(共52分)12.(10分)如图,过点A 的一次函数的图象与正比例函数y =2x 的图象相交于点B . (1)求该一次函数的表达式;(2)判定点C (4,-2)是否在该函数的图象上,并说明理由.解:(1)当x =1时,y =2x =2,所以点B 的坐标为(1,2).设该一次函数的表达式为y =kx +b ,因为一次函数的图象经过点A (0,3)和点B (1,2),所以b =3,k +b =2,所以k =-1,所以该一次函数的表达式y =-x +3 (2)点C (4,-2)不在该函数的图象上,理由如下:当x =4时,y =-x +3=-1≠-2,所以点C (4,-2)不在该函数的图象上13.(12分)如图,函数y =34 x +3的图象与x 轴、y 轴的交点分别为A ,B 两点.(1)求A ,B 两点的坐标;(2)若直线y =mx 经过线段AB 的中点P ,求m 的值.解:(1)A (-4,0),B (0,3) (2)m =-3414.(14分)某学校的复印任务原来由甲复印社承接,其收费y (元)与复印页数x (页)的关系如下表:x /页 100 200 400 1 000 … y /元4080160400…(1)已知y 与x 满意一次函数关系,求该函数的表达式;(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费,则乙复印社每月收费y (元)与复印页数x (页)之间的函数表达式为__y =0.15x +200__;(不须要写出自变量的取值范围)(3)在如图所示的直角坐标系内画出(1)(2)中的函数图象,并回答每月复印页数在1 200页左右时,选择哪个复印社更合算.题图答图解:(1)y =0.4x(3)画函数图象如图所示,由图象可知,当每月复印页数在1 200页左右时,应选择乙复印社更合算15.(16分)(河北中考)如图,在平面直角坐标系xOy 中,一次函数y =-12 x +5的图象l 1分别与x 轴、y 轴交于A ,B 两点,正比例函数的图象l 2与l 1交于点C (m ,4).(1)求m 的值及l 2的表达式; (2)求S △AOC -S △BOC 的值;(3)一次函数y =kx +1的图象为l 3,且l 1,l 2,l 3不能围成三角形,干脆写出k 的值.解:(1)m =2,l 2:y =2x (2)过点C 作CD ⊥AO 于点D ,CE ⊥BO 于点E ,则CD =4,CE =2.易知A (10,0),B (0,5),所以AO =10,BO =5,所以S △AOC -S △BOC =12 ×10×4-12×5×2=15 (3)当l 3经过点C (2,4)时,k =32 ;当l 2,l 3平行时,k =2;当l 1,l 3平行时,k=-12 ,所以k 的值为32 或2或-12。
初二数学一次函数单元试卷

一、选择题(每题5分,共50分)1. 下列函数中,表示一次函数的是()A. y = 2x + 3B. y = x^2 + 2C. y = 3x - 4xD. y = 5x^3 - 22. 已知一次函数y = kx + b,若k > 0,则函数图象()A. 在一、二、三象限B. 在一、二、四象限C. 在一、三、四象限D. 在一、二、三、四象限3. 一次函数y = -2x + 1中,当x = 2时,y的值为()A. -3B. -1C. 0D. 14. 下列关于一次函数的说法正确的是()A. 一次函数的图象是一条直线B. 一次函数的图象是一条曲线C. 一次函数的图象是一条抛物线D. 一次函数的图象是一条指数函数曲线5. 一次函数y = 3x - 2中,若k = 3,则b的值为()A. -2B. 0C. 2D. 3二、填空题(每题5分,共50分)6. 一次函数y = 2x + 1中,当x = 0时,y的值为______。
7. 一次函数y = -3x + 5中,当x = 2时,y的值为______。
8. 一次函数y = 4x - 7中,当x = -1时,y的值为______。
9. 一次函数y = -2x + 3中,当x = 4时,y的值为______。
10. 一次函数y = 5x - 6中,当x = 0时,y的值为______。
三、解答题(每题10分,共40分)11. 已知一次函数y = kx + b,若k = 2,b = -3,求该函数图象与x轴、y轴的交点坐标。
12. 已知一次函数y = 3x - 2,若x = 4时,y的值为10,求该函数图象与x轴、y轴的交点坐标。
13. 已知一次函数y = -2x + 5,若x的取值范围为-3 ≤ x ≤ 2,求y的取值范围。
14. 已知一次函数y = 4x - 7,若x = 3时,y的值为5,求该函数图象与x轴、y轴的交点坐标。
四、应用题(每题15分,共30分)15. 小明骑自行车从家出发,每小时骑行5公里。
八年级上数学一次函数周清题

八年级数学(一次函数)周清测试班级 姓名一、填空题(每空4分,共44分)1、若函数22+-=m x y 是正比例函数,则m 的值是 .2、若函数(1)3y m x =++图象经过点(1,2),则m =3、直线x y 39-=与x 轴交点坐标是_______,与y 轴交点坐标是_______.4、若点P(a ,b)在第二象限,则直线y =ax +b 不经过第_____限.5、一次函数42+-=x y 的图象与坐标轴所围成的三角形面积是 .6、已知一次函数y=-3x+1的图象经过点(a ,1)和点(-2,b ),则a=________,b=______.7、函数y=(m+6)x+(m-2),当m 时是正比例函数;当m 时它是一次函数。
8、某一次函数的图象经过点(-1,2),且函数y 的值随自变量x 的增大而减小,请你写出一个符合上述条件的函数关系式: 。
二、选择题(每空4分,共24分)9、下列函数 (1)12-=x y (2)xy 1= (3)x y 3-= (4)12+=x y 中,是一次函数的有 ( )A.3个B.2个C.1个D.0个10、直线x y 2=,12-=x y ,13+=x y 共同具有的特征是 ( )A 、经过原点B 、与y 轴交于负半轴C 、y 随x 增大而增大D 、y 随x 增大而减小11、.函数 y = x 图象向下平移 2 个单位长度后,对应函数关系式是 ( )A .x 2y =B .x y =C .2x y +=D .2x y -= 12、下面哪个点在函数y=12x+1的图象上( ) A 、(2,1) B 、(-2,1) C 、(2,0) D 、(-2,0)13、一次函数y=-5x+3的图象经过第( )象限A .一、二、三B .二、三、四C .一、二、四D .一、三、四14、已知正比例函数)0k (kx y ≠= 的函数值随的增大而增大,则一次函数kxy+=的图象大致是( )三、解答题(15题:6分,16题:12分,17题:14分)15、体沿一个斜坡下滑,它的速度v(米/秒)与其下滑t(秒)的关系如图所示,则①、下滑2秒时物体的速度为___________.②、V(米/秒)与t(秒)之间的函数关系式为_________.③、下滑3秒时物体的速度为_____________.16、次函数y=kx+b的图象如图所示,看图填空:(1)当x=0时,y=____________;当x=____________时,y=0.(2)k=________,b=________.(3)当x=5时,y=__________;当y=30时,x=___________.17、位计划10月份组织员工到外地旅游,估计人数在6~15人之间。
数学周周清考试卷(一次函数)
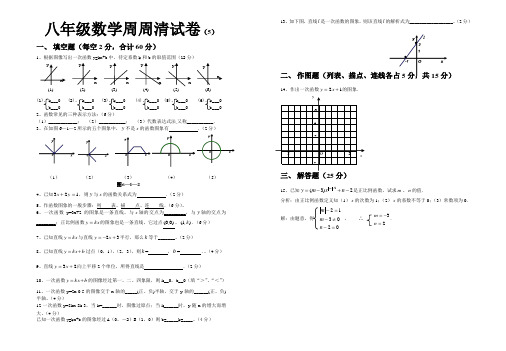
图6—1—2八年级数学周周清试卷(5)一、填空题(每空2分,合计60分)1、根据图像写出一次函数y=kx+b中,待定系数k和b的取值范围(12分)(1)、k___0 (2)、 k___0 (3)、k___0 (4)、k___0 (5)、k___0 (6)、k___0b___0 b___0 b___0 b___0 b___0 b___02、函数常见的三种表示方法:(6分)(1)____________;(2)___________;(3)代数表达式法,又称___________.3、在如图6—1—2所示的五个图象中,y不是x的函数图象有.(2分)(1)(2)(3)(4)(5)4、已知123=+yx,则y与x的函数关系式为.(2分)5、作函数图象的一般步骤:列表、描点、连线.(6分)。
6、一次函数y=3x+2的图象是一条直线,与x轴的交点为_________,与y轴的交点为________;正比例函数kxy=的图象也是一条直线,它过点)0,0(,),1(k.(6分)7、已知直线kxy=与直线32+-=xy平行,那么k等于_______。
(2分)8、已知直线bkxy+=过点(0,1),(2,3),则k= ,b= .。
(4分)9、直线23+=xy向上平移2个单位,所得直线是.(2分)10、一次函数bkxy+=的图像经过第一、二、四象限,则k__0,b__0(填“>”、“<”)11、一次函数y=2x-0.5的图像交于x轴的_____(正、负)半轴,交于y轴的______(正、负)半轴。
(4分)12一次函数y=5kx-5k-3,当k=______时,图像过原点;当k______时,y随x的增大而增大。
(4分)已知一次函数y=kx+b的图象经过A(0,-2)B(1,0)则b=_____k=____。
(4分)13、如下图,直线l是一次函数的图象,则该直线l的解析式为__________________。
(2分)●●二、作图题(列表、描点、连线各占5分,共15分)14、作出一次函数12+=xy的图象.三、解答题(25分)15、已知2)3(2-+-=-nxmy m是正比例函数,试求m、n的值.分析:由正比例函数定义知(1)x的次数为1;(2)x的系数不等于0;(3)常数项为0.解:由题意,得2312=-≠-=-nmm,∴23=-=nm.。
2019年秋季北师大版本八年级数学上册周周清测试卷 第四章 一次函数周周测2(4.3)

第四章一次函数周周测2一、选择题1. 若正比例函数的图象经过点(2,-3),则这个图象必经过点()A. (-3,-2)B. (2,3)C. (3,-2)D. (-2,3)2. 如果函数y=3x+m的图象一定经过第二象限,那么m的取值范围是()A. m>0B. m≥0C. m<0D. m≤03. 函数y=-x+2的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 设0<k<2,关于x的一次函数y=kx+2(1-x),当1≤x≤2时的最大值是()A. 2k-2B. k-1C. kD. k+15. 已知正比例函数y=kx(k≠0)的图象如图所示,则在下列选项中k值可能是()A. 1B. 2C. 3D. 46. 如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是()A. a>b>cB. c>b>aC. b>a>cD. b>c>a7. 在平面直角坐标系中,一次函数y=2x+1的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限8. 已知正比例函数y=kx(k≠0),当x=-1时,y=-2,则它的图象大致是()A. B. C. D.9. 已知点P(m,n)在第四象限,则直线y=nx+m图象大致是下列的()A. B. C. D.10. 一次函数y=kx+k(k<0)的图象大致是()A. B. C. D.11. 在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是()A. 第一象限B. 第二象限C. 第三象限D. 第四象限12. 如图为一次函数y=kx+b(k≠0)的图象,则下列正确的是()A. k>0,b>0B. k>0,b<0C. k<0,b>0D. k<0,b<013. 将直线y=-2x向下平移两个单位,所得到的直线为()A. y=-2(x+2)B. y=-2(x-2)C. y=-2x-2D. y=-2x+214. 将下列函数的图象沿y轴向下平移3个单位长度后,图象经过原点的是()A. y=-x-3B. y=3xC. y=x+3D. y=2x+515. 将一次函数y=-2x+4的图象平移得到图象的函数关系式为y=-2x,则移动方法为()A. 向左平移4个单位B. 向右平移4个单位C. 向上平移4个单位D. 向下平移4个单位二、填空题16. 在一次函数y=kx+3中,y的值随着x值的增大而增大,请你写出符合条件的k的一个值: _____________17. 一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是______18. 直线y=2x+1经过点(0,a),则a= _______19. 直线y=2x-1沿y轴向上平移3个单位,则平移后直线与x轴的交点坐标为________20. 矩形ABCD在平面直角坐标系中,且顶点O为坐标原点,已知点B(3,2),则对角线AC所在的直线l对应的解析式为_____三、解答题21. 已知函数y=(2m-2)x+m+1的图象过一、二、四象限,求m的取值范围.22. 已知函数y=(2m-2)x+m+1,(1)m为何值时,图象过原点.(2)已知y随x增大而增大,求m的取值范围.23. 已知一次函数y=kx+3的图象经过点(1,4).(1)求这个一次函数的解析式;(2)求关于x的不等式kx+3≤6的解集.24. 一次函数y=kx+b经过点(-1,1)和点(2,7).(1)求这个一次函数的解析表达式.(2)将所得函数图象平移,使它经过点(2,-1),求平移后直线的解析式.25. 一次函数y=1.5x-3(1)请在平面直角坐标系中画出此函数的图象.(2)求出此函数与坐标轴围成的三角形的面积.。
第四章一次函数单元测试 2024—2025学年北师大版数学八年级上册

第四章一次函数单元测试北师大版2024—2025学年秋季八年级上册(考试时间:120 分钟试卷满分: 120分)注意事项:1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
笞卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷一、选择题(每题只有一个正确选项,每小题3分,满分30分)1.若点(3,m)在函数y=x+2的图象上.则m的值为()A.0B.1C.2D.32.一个正比例函数的图象经过点(﹣2,4),它的表达式为()A.y=﹣2x B.y=2x C.y=﹣x D.y=x3.在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为()A.(2,0)B.(﹣2,0)C.(6,0)D.(﹣6,0)4.关于一次函数y=2x+4,下列说法正确的是()A.图象经过第一、三、四象限B.图象与y轴交于点(0,﹣2)C.函数值y随自变量x的增大而增大D.当x>﹣1时,y<25.点A(2,y1)与点B(3,y2)在直线y=﹣2024x+2024上,则y1与y2的关系是()A.y1<y2B.y1≤y2C.y1>y2D.y1=y26.小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中,如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象,则下列结论中不正确的是()A.公园离小明家1600米B.小明出发分钟后与爸爸第一次相遇C.小明在公园停留的时间为5分钟D.小明与爸爸第二次相遇时,离家的距离是960米7.若一次函数y=(4﹣3k)x﹣2的图象经过点A(x1,y1)和点B(x2,y2),当x1>x2时,y1<y2,则k的取值范围是()A.B.C.D.8.一次函数y=kx﹣k和正比例函数y=kx在同一平面直角坐标系中的函数图象可能是()A.B.C.D.9.将直线y=2x+1向右平移2个单位后所得图象对应的函数表达式为()A.y=2x+5B.y=2x+3C.y=2x﹣2D.y=2x﹣3 10.一次函数y=(m﹣1)x+m+2的图象过一、二、三象限,则m的取值范围是()A.m>1B.﹣1<m<2C.﹣2<m<1D.m>﹣2二、填空题(每小题3分,满分18分)11.已知关于x的函数y=(k﹣1)x|k﹣2|是正比例函数,则k=.12.当直线y=(2﹣2k)x+k﹣3,不经过第一象限时,则k的取值范围是.13.在函数y=中,自变量x的取值范围是.14.若,则直线y=kx﹣k必经过第象限.15.如图,直线y=x+4与x轴、y轴分别交于A、B两点,点C在OB 上,若将△ABC沿AC折叠,使点B恰好落在x轴上的点D处,则点C的坐标是.16.如图,在平面直角坐标系中,一次函数y=k(x﹣1)的图象分别交x 轴,y轴于A,B两点,且OB=2OA,将直线AB绕点B按顺时针方向旋转45°,交x 轴于点C,则直线BC的函数表达式是.第II卷第四章一次函数单元测试北师大版2024—2025学年秋季八年级上册考生注意:本试卷共三道大题,24道小题,满分120分,时量120分钟姓名:____________ 学号:_____________座位号:___________一、选择题题号12345678910答案二、填空题11、_______ 12、______13、_______ 14、______15、_______ 16、______三、解答题(17、18题每题8分,19、20、21、22每题9分,23、24每题10分,共计72分,解答题要有必要的文字说明)17.如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.(1)写出点P2的坐标;(2)求直线l所表示的一次函数的表达式;(3)若将点P2先向右平移3个单位,再向上平移6个单位得到像点P3.请判断点P3是否在直线l上,并说明理由.18.如图,直线l1:y=2x+4与x轴交于点A,与y轴交于点B,直线l2:y=﹣x+1与y轴交于点C,直线l1和直线l2相交于点D.(1)直接写出点A、B、C的坐标分别为:A,B,C;(2)在x轴上是否存在一点P,使得S△ADP=4,若存在,求点P坐标;若不存在,请说明理由.19.“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:(1)小明家到学校的路程是多少米?(2)小明在书店停留了多少分钟?(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?20.已知y=y1+y2,y1与x成正比例,y2与x﹣2成正比例,当x=1时,y=﹣3;当x=﹣2时,y=0.(1)求y与x的函数关系式;(2)当x=3时,求y的值.21.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A 型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?22.如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.(1)求直线AB的解析式.(2)求△OAC的面积.(3)是否存在点M,使△OMC的面积是△OAC的面积的?若存在求出此时点M的坐标;若不存在,说明理由.23.已知函数y=其中m为常数,该函数的图象记为G.(1)当m=﹣2时,若点D(3,n)在图象G上,求n的值;(2)当3﹣m≤x≤4﹣m时,若函数最大值与最小值的差为,求m的值;(3)已知点A(0,1),B(0,﹣2),C(2,1),当图象G与△ABC有两个公共点时,直接写出m的取值范围.24.如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C,D,且点D的坐标为(1,n).(1)求一次函数y=kx+b的解析式;(2)求四边形AOCD的面积;(3)在平面内直线CD的右侧是否存在点P,使得以点P,C,D为顶点的三角形是以CD为腰的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.。
一次函数试卷

)八年级数学一次函数检测试卷班级_________ 姓名_________ 学号_________ 成绩_________一、填空题(每题2分,共20分)1、在匀速运动公式:vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______. 2、函数y =x 的取值范围是___________.3、若关于x 的函数1(1)m y n x-=+是一次函数,则m = ,n .4、正比例函数(35)y m x =+,当m 时,y 随x 的增大而增大.5、若函数(1)3y m x =++图象经过点(1,2),则m = .6、已知函数43y x =-,那么函数图象与x 轴、y 轴的交点坐标分别是__________、__________.7、分别用x 和y 表示等腰三角形的顶角和底角的度数, y 与x 之间的函数解析式为_______________.8、王华和线强同学在合作电学实验时,记录下电流I (安培)与电阻R (欧)有如下对应关系.观察下表:你认为I 与R 间的函数关系式为__________________;当电阻R =5欧时,电流I =_______安培.9、拖拉机开始工作时,油箱中有油40升,如果每小时耗油5升,如图是拖拉机工作时,油箱中的余油量Q (升)与工作时间 t (小时)的函数关系图像,那么图中?应是_______.10、在某公用电话亭打电话时,需付电话费y (元)与通话时间 x (分钟)之间的函数关系用图象表示如图.小明打了2分钟需付费______元;小莉打了8分钟需付费_______元.(第8题图) (第10题图) 二、选择题 (每题3分,共24分)11、下列给出的四个点中,不在直线y =2x -3上的是 ( ) A.(1, -1) B.(0, -3) C.(2, 1) D.(-1,5)A.1B.2C.21D.0 13、若23y x b =+-是正比例函数,则b 的值是 ( ) A.0 B.23 C.23- D.32- 14、当3-=x 时,函数732--=x x y 的函数值为 ( ) A.-25 B.-7 C. 8 D.1115、函数y =(k -1)x ,y 随x 增大而减小,则k 的范围是 ( ) A.0<k B.1>k C.1≤k D.1<k16、如图,OA 、BA 分别表示甲、乙两名学生运动的一次函数, 图中S 和t 分别表示运动路程和时间,根据图象判断快者比 慢者每秒快 ( )A. m 1B. m 5.1C. m 2D. m 5.217、函数y =ax +b 与y =bx +a 的图象在同一坐标系内的大致位置正确的是( )A. B. C. D.三、解答题:18、已知直线y kx b =+经过点(1,2)和点(1-,4),求这条直线的解析式.19、将函数y =2x +3的图象平移,使它经过点(2,-1).求平移后得到的直线的解析式.20、甲市到乙市的包裹邮资为每千克0.9元,每件另加手续费0.2元.求总邮资y (元)与包裹重量x (千克)之间的函数解析式,并计算5千克重的包裹的邮资.21、已知直线12+=x y .(1) 求已知直线与y 轴的交点A 的坐标; (2) 若直线b kx y +=与已知直线关于y 轴对称,求k 与b 的值.22、一天上午8时,小华去县城购物,到下午2时 返回家,结合图象回答:(1)小华何时第一次休息? (2)小华离家最远的距离时多少? (3)返回时平均速度是多少?(4)请你描述一下小华购物的情况.23、爱动脑筋的小明同学在买一双新的运动鞋时,发现了一些有趣现象,即鞋子的号码与鞋子的长(cm )之间存在着某种联系,经过收集数据,得到下表:请你代替小明解决下列问题:(1)根据表中数据,在同一直角坐标系中描出相应的点,你发现这些点在哪一种图形上?(2)猜想y 与x 之间满足怎样的函数关系式,并求出y 与x 之间的函数关系式,验证这些点的坐标是否满足函数关系式.(3)当鞋码是40码时,鞋长是多长?四、附加题(做对另加10分,若整卷总分超过100分以100分计算)24、已知一次函数y =k x +b 的自变量的取值范围是―3≤x ≤6,相应的函数值的范围是 ―5≤y ≤―2,求这个函数的解析式.八年级一次函数数学检测试卷班级_________ 姓名_________ 学号_________ 成绩_________一、填空题(每题2分,共20分)1.在圆的周长公式C=2πr 中,变量是________,常量是_________.2.在函数2-=x y 中,自变量x 的取值范围是_________.3.函数221x y =中,当x =___________时,函数的值等于2. 4.一次函数的图象经过点(-2,3)与(1 ,-1),它的解析式是___ _____.5.将直线y =3x 向下平移5个单位,得到直线 ;将直线y =-x -5向上平移5个单位,得到直线 .6.东方超市鲜鸡蛋每个0.4元,那么所付款y 元与买鲜鸡蛋个数x (个)之间的函数关系式是_______________.7.平行四边形相邻的两边长为x 、y ,周长是30,则y 与x 的函数关系式是__________. 8.出租车收费按路程计算,3km 内(包括3km )收费8元;超过3km 每增加1km 加收1元,则路程x ≥3km 时,车费y (元)与x (km )之间的函数关系式是________________. 9.已知点P (3a – 1,a + 3)是第二象限内坐标为整数的点,则整数a 的值是_______. 10.若直线a x y +-=和直线b x y +=的交点坐标为(8,m ),则=+b a ____________. 二、选择题(每题3分,共24分)11.下列函数中,与y =x 表示同一个函数的是 ( ) A.y =x 2x B.y =x2 C.y =(x )2 D.y =3x 312.下列关系式中,不是函数关系的是 ( )A.y =-x (x <0) B.y =±x (x >0) C.y =x (x >0) D.y =-x (x>0) 13.若m <0, n >0, 则一次函数y=mx+n 的图象不经过 ( ) A.第一象限 B. 第二象限 C.第三象限 D.第四象限 14.已知函数y =3x +1,当自变量增加m 时,相应的函数值增加( ) A.3m +1 B.3m C.m D.3m -115.汽车由A地驶往相距120km 的B 地,它的平均速度是30km /h ,则汽车距B地路程s(km )与行驶时间t (h )的函数关系式及自变量t 的取值范围是( ) A.S =120-30t (0≤t ≤4) B.S =120-30t (t >0) C.S =30t (0≤t ≤40) D.S =30t (t <4) 16.已知函数221+-=x y ,当11≤<-x 时,y 的取值范围是 ( ) A.2325≤<-y B.2523<<y C.2523<≤y D.2523≤<y17.小明的父亲饭后散步,从家中走20分钟到一个离家900米的报亭看10分钟的报纸后,用15分钟返回家中,下列图形中表示小明父亲离家的时间与距离之间的关系是( )A. B. C. D.18.当00><b ,a 时,函数y =a x+b 与a bx y +=在同一坐标系中的图象大致是( )A. B. C. D.三、解答题(第19题6分,其余每题10分,共56分)19.地壳的厚度约为8到40km ,在地表以下不太深的地方,温度可按y =3.5x +t 计算,其中x 是深度,t 是地球表面温度,y 是所达深度的温度. (1)在这个变化过程中,自变量和因变量分别是什么? (2)如果地表温度为2℃,计算当x 为5km 时地壳的温度.20.已知3-y 与x 成正比例,且2=x 时,7=y . (1)求y 与x 的函数关系式; (2)当21-=x 时,求y 的值; (3)将所得函数图象平移,使它过点(2,-1).求平移后直线的解析式.21.已知弹簧的长度y (厘米)在一定的限度内是所挂物质量x (千克)的一次函数.现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式.22.王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).(1)小强让爷爷先上多少米?(2)山顶离山脚的距离有多少米?谁先爬上山顶? (3)小强经过多少时间追上爷爷?23. 如图,在边长为2的正方形ABCD 的一边BC 上,一点P 从B 点运动到C 点,设BP=x ,四边形APCD 的面积为y . ⑴ 写出y 与x 之间的函数关系式及x 的取值范围;⑵ 说明是否存在点P ,使四边形APCD 的面积为1.5?A D P24. k在为何值时,直线2k+1=5x+4y与直线k=2x+3y的交点在第四象限?四、附加题(做对另加10分,若整卷总分超过100分以100分计算)25.有一条直线y=kx+b,它与直线132y x=+交点的纵坐标为5,而与直线y=3x-9的交点的横坐标也是5.求该直线与两坐标轴围成的三角形面积.八年级一次函数数学检测试卷班级_________ 姓名_________ 学号_________ 成绩_________一、选择题(每题3分,共30分)1.直线x y 39-=与x 轴交点的坐标是________,与y 轴交点的坐标是_______.2.把直线121-=x y 向上平移21个单位,可得到函数__________________. 3.若点P 1(–1,3)和P 2(1,b )关于y 轴对称,则b = .4.若一次函数y =mx -(m -2)过点(0,3),则m = .5.函数y =x 的取值范围是 .6.如果直线b ax y +=经过一、二、三象限,那么ab ____0 (“<”、“>”或“=”).7.若直线12-=x y 和直线x m y -=的交点在第三象限,则m 的取值范围是________.8.函数y = -x +2的图象与x 轴,y 轴围成的三角形面积为_________________.9.某单位为鼓励职工节约用水,作出了以下规定:每位职工每月用水不超过10立方米的,按每立方米m 元水费收费;用水超过10立方米的,超过部分加倍收费.某职工某月缴水费16m 元,则该职工这个月实际用水为___________立方米.10.有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2、3、4…的等边三角形(如图).根据图形推断每个等边三角形卡片总数S 与边长n 的关系式 .二、选择题(每题3分,共18分) 11.函数y =x-2x+2的自变量x 的取值范围是( ) A.x ≥-2 B.x >-2 C.x ≤-2 D.x <-212.一根弹簧原长12cm ,它所挂的重量不超过10kg ,并且挂重1kg 就伸长1.5cm ,写出挂重后弹簧长度y (cm )与挂重x (kg )之间的函数关系式是( ) A.y =1.5(x +12)(0≤x ≤10) B.y =1.5x +12 (0≤x ≤10) C.y =1.5x +10 (0≤x ) D.y =1.5(x -12) (0≤x ≤10) 13.无论m 为何实数,直线m x y 2+=与4+-=x y 的交点不可能在(A.第一象限B.第二象限C.第三象限D.第四象限14.某兴趣小组做实验,将一个装满水的啤酒瓶倒置(如图),高度h 随水流出的时间t 变化的图象大致是 ( )A. B. C. D. 15.已知函数122y x =-+,当-1<x ≤1时,y 的取值范围是( ) A.5322y -<≤ B.3522y << C.3522y <≤ D.3522y ≤<16.某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A 地后,宣传8分钟;然后下坡到B 地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A 地仍要宣传8分钟,那么他们从B 地返回学校用的时间是( ) A.45.2分钟 B.48分钟 C.46分钟 D.33分钟三、解答题(第17—20题每题10分,第21题12分,共52分)17.观察图,先填空,然后回答问题:(1)由上而下第n 行,白球有_______个;黑球有_______个. (2)若第n 行白球与黑球的总数记作y , 则请你用含n 的代数式表示y ,并指出其中n 的取值范围. 18.已知,直线y =2x +3与直线y =-2x -1.(1)求两直线与y 轴交点A ,B 的坐标; (2)求两直线交点C 的坐标;(3)求△ABC 的面积. h t O htO h t O h t O xy A BC)19. 旅客乘车按规定可以免费携带一定重量的行李.如果所带行李超过了规定的重量,就要按超重的千克收取超重行李费.已知旅客所付行李费y (元)可以看成他们携带的行李质量x (千克)的一次函数为561-=x y .画出这个函数的图象,并求旅客最多可以免费携带多少千克的行李?20.某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y 与时间t 之间近似满足如图所示曲线: (1)分别求出21≤t 和21≥t 时,y 与t 之间的函 数关系式;(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?21. 某军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油.在加油的过程中,设运输飞机的油箱余油量为Q 1吨,加油飞机的加油油箱的余油量为Q 2吨,加油时间为t 分钟,Q 1、Q 2与t 之间的函数关系如图.回答问题:(1) 加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需要多少分钟?(2) 求加油过程中,运输飞机的余油量Q 1(吨)与时间t (分钟)的函数关系式;(3) 运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?请通过计算 说明理由.四、附加题(做对另加10分,若整卷总分超过100分以100分计算)22.将长为30cm ,宽为10cm 的长方形白纸,按如图所示的方发粘合起来,粘合部分的宽为3cm .设x 张白纸粘合后的总长度为ycm ,写出y 与x 的函数关系式,并求出当x =20时, y 的值.3 10 30A 答案1. s 和t ;v2. x ≥53. 2,≠-14. >53-5. -26. 0,347. y =90°-0.5x8. I=32R,6.4 9. 8 10. 0.7, 2.2 11.D 12.D 13.B 14.B 15.D 16.D 17. B 18. C19.3y x =-+ 20. y =2x -5 21. y =0.9x +0.2,4.722.(1)A (0,1) (2)y =-2x +123.(1)上午9点;(2)30千米;(3)15千米/小时;(4)略24.(1)在直线上;(2)一次函数,210y x =-;(3)当y =40时,x =25 25. 143y x =-或331--=x yB 答案1.C 、r , 2π2. x ≥23.x =2或-24. 4133y x =-+ 5. 35=y x y x =--, 6. y=0.4x (x≥0) 7. y =15-x ( x <15) 8. y =x +5 9. -2,-1,0 10. 1611. D 12. B 13. C 14. B 15.A 16.C 17.D 18.B19.(1)自变量是地表以下的深度x ,因变量是所达深度的温度y ;(2)19.520.(1)y =2x +3;(2)2;(3)y =2x -521.y =0.3x +6 22. (1)60米;(2)300米,小强;(3)8分钟23. (1) y =4-x (0≤x ≤2) (2) 当y =4-x =1.5时,x =2.5不在0≤x ≤2,因此不存在点P 使四边形APCD的面积为1.524.由题意得⎩⎨⎧=++=+.32,1245k y x k y x 解得⎪⎪⎩⎪⎪⎨⎧-=+=.72,732k y k x 因为两直线交点在第四象限,所以x >0,y <0,即⎪⎪⎩⎪⎪⎨⎧<->+.072,0732k k 解得⎪⎨⎧->,23k 故223<<-k 时,两直线交点在第四象限.25.提示:先求出直线的解析式为y =x +1,再求出它与两坐标轴的交点,进而求得三角形的面积为0.5C 答案1. (3,0)(0,9)2.y =0.5x -0.53. 34.–15.x ≥56. >7. m <-1 8. 2 9. 13 10. 2s n =11. B 12. B 13. C 14. A 15. D 16. A17.(1) n ,2n -1; (2) y = 3n -1 (n 为正整数)18. (1) A (0,3),B (0,-1); (2) C(-1,1); △ABC 的面积=13+112⨯⨯()=2 19. (1)y =12x (0≤21≤t );y =-0.8x +6.4 (21≥t ) (2) 若y ≥4时, 则133x ≤≤,所以7:00服药后,7:20到10:00有效 20. 函数561-=x y (x ≥30)的图象如右图所示. 当y =0时,x =30.所以旅客最多可以免费携带30千克的行李.21.(1) 30吨油,需10分钟(2) 设Q 1=kt +b ,由于过(0,30)和(10,65)点,可求得:Q 1=2.9t +36(0≤t ≤10)(3) 根据图象可知运输飞机的耗油量为每分钟0.1吨,因此10小时耗油量为10×60×0.1=60(吨)<65(吨),所以油料够用22. y =27x +3, 当x =20时,y =543.19.(6分)如图,是一位护士统计一位病人 的体温变化图:根据统计图回答下列问题: ⑴病人的最高体温是达多少?⑵什么时间体温升得最快?⑶如果你是护士,你想对病人说:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学(上)周周清试卷(四)
命题人:宿丑云
班级姓名成绩.
一、填空:(每空2分)
1、直线y=-3x+6与x轴的交点坐标为__________,与y轴的交点坐标为________,经
过象限,图象与坐标轴所围成的三角形面积是.
2、直线l与y轴交于点(0,7),且与直线8
3+
-
=x
y平行,则直线l的解析式
为____________.
3、购买单价为30(元)的篮球,所花费用y(元)与购买数量x(个)之间的函数关系式为__________________,其中____________是自变量,__________是因变量.
4、一次函数y=5-x与y=2x-1图象的交点为(2,3), 则方程组
⎩
⎨
⎧
=
-
=
+
1
2
5
y
x
y
x
的解为.
5、弹簧挂上物体后会伸长,测得一弹簧长度y(cm)与所挂物体质量x(kg)有下面关系:那么弹簧总长y(cm)与所挂物体质量x(kg)之间关系式是________________.
6、写出同时具备下列两个条件的一次函数表达式(写出一个即可) . (1)y随着x的增大而减小。
(2)图象经过点(1,-3)
7、某人用IC卡从A地向B地打长途电话,按通话时间收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若此人第一次通话t分钟(t为整数且t>3),则通话费用y(元)与t(分)之间的关系式是 .
8、如图,已知B地在A地前方3千米处,甲、乙两人同时
分别从A、B两地出发匀速前进,他们离开A地的距离
S(千米)与所行的时间t(小时)之间的函数关系图象如
图所示的AC和BD。
当他们行走小时后,甲走在了乙
的前面.
二、选择题(每题3分)
1、下列函数关系式:①x
y-
=;②11
2+
=x
y③
1
2+
+
=x
x
y;④
x
y
1
=.其中一次函数的个数是
()
(A)1个(B)2个(C)3个(D)4个
2、如图,射线l甲、l乙分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的函数关系,则他们行进的速度关系是()
(A)甲比乙快(B)乙比甲快(C)甲、乙同速(D)不确定
3.已知一次函数y=kx+b的图象,当x<0时,y的取值范围是()(A)(C)
x 0 1 2 3 4 5 6 7 8
y 12 12.5 13 13.5 14 14.5 15 15.5 16
4、函数y =
x x 3
-的自变量的取值范围是( ) A .x ≥3 B .x >3 C .x ≠0且x ≠3
D .x ≠0 5、下列函数中,图象经过原点的有( )
①y =2x -2 ②y =-3x ③y =x 2 ④y =-7x+1
A .1个
B .2个
C .3个
D .4个
6、 直线a x y +=3经过),5(1y 和),2(2y -,则1y 与2y 的大小关系是 ( )
A. 21y y >
B. 21y y <
C.21y y =
D.无法确定
7、若函数y =2x +3与y =3x -2b 的图象交y 轴于同一点,则b 的值为( )
A.-3
B.23
C.23-
D.32
- 8、某厂今年前五个月生产某种产品的月产量Q (件)与时间t (月)的函数图象如图所示,则对这种产品来说,下列说法正确的是 ( )
(A) 1月至3月每月产量逐月增加,4、5两月 每月产量逐月减少
(B) 1月至3月每月产量逐月增加,4、5两月
每月产量逐月持平
(C) 1月至3月每月产量逐月增加,4、5两个
月停止生产
(D) 1月至3月每月产量不变,4、5两个月停止生产
三、解答题
1、(12分)已知某一次函数的图象经过点(0, -3),且与正比例函数y= 12
x 的图象相交于点 (2,a)。
(1)求a 的值。
(2)求这个一次函数的解析式。
(3)在同一直角坐标系中画出这两个函数
的图象。
(4)这两个函数图象与x 轴所围成的三角
形面积。
2、(10分)如图是某出租车单程收费y (元)与行驶路程x (千米)之间的函数关系图象,根据图象回答下列问题: Q (件)
t (月) 1 2 3 4 5 O
(1)当行使8千米时,收费应为 元。
(2)从图象上你能获得哪些信息?(请写出2条)
①
②
(3)求出收费y (元)与行使x (千米)(x ≥3)
之间的函数关系式
3、(本小题4分) 已知函数3)12(-++=m x m y
若这个函数是一次函数,且图象不经过第二象限, 求m 的取值范围.
4、(6分)旅客乘车按规定可携带一定重量的行李,如果超过规定则需购行李票,设行李费y (元)是行李重量x (千克)的一次函数,其图象如图所示。
(1)求y 与x 之间的函数关系式; (2)旅客最多可免费携带多少千克行李?
5.(10分)如图,l A 、l B 分别表示A 步行与B 骑车在
同一路上行驶的路程S 与时间t 的关系。
(1)B 出发时与A 相距 千米。
(2)B 走了一段路后,自行车发生故障,进行
修理,所用的时间是 小时。
(3)B 出发后 小时与A 相遇。
(4)若B 的自行车不发生故障,保持出发时 的速度前进, 小时与A 相遇,
相遇点离B 的出发点 千米。
6、(8分)某公司到果园基地购买某种优质水果,3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门。
乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元。
(1)分别写出该公司两种购买方案的付款y (元)与所购买的水果质量x (千克)之间的
t (时) O 0.5
函数关系式(x≥3000千克)。
(2)依据购买量判断,选择哪种购买方案付款优惠?并说明理由。
