初三《圆》知识点及定理

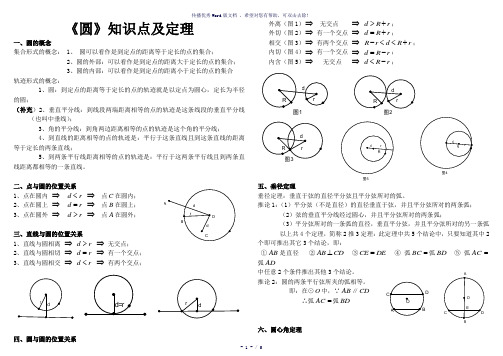
《圆》知识点及定理
一、圆的概念
集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；
2、圆的外部：可以看作是到定点的距离大于定长的点的集合；
3、圆的内部：可以看作是到定点的距离小于定长的点的集合
轨迹形式的概念：
1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；
（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；
3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；
4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；
5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系
1、点在圆内⇒d r
<⇒点C在圆内；
2、点在圆上⇒d r
=⇒点B在圆上；
3、点在圆外⇒d r
>⇒点A在圆外；
三、直线与圆的位置关系
1、直线与圆相离⇒d r
>⇒无交点；
2、直线与圆相切⇒d r
=⇒有一个交点；
3、直线与圆相交⇒d r
<⇒有两个交点；
四、圆与圆的位置关系
外离（图1）⇒无交点⇒d R r
>+；
外切（图2）⇒有一个交点⇒d R r
=+；
相交（图3）⇒有两个交点⇒R r d R r
-<<+；
内切（图4）⇒有一个交点⇒d R r
=-；
内含（图5）⇒无交点⇒d R r
<-；
图1
五、垂径定理
垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；
（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；
（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧
以上共4个定理，简称2推3
定理：此定理中共5个结论中，只要知道其中2
个即可推出其它3个结论，即：
①AB是直径②AB CD
⊥③CE DE
=④弧BC=弧BD
⑤弧AC=
弧AD
中任意2个条件推出其他3个结论。

推论2：圆的两条平行弦所夹的弧相等。

即：在⊙O中，∵AB∥CD
∴弧AC=弧BD
六、圆心角定理
圆心角定理：同圆或等圆中，相等的圆心角所对的弦相
等，所对的弧相等，弦心距相等。

此定理也称1推3定理，
即上述四个结论中，
A
图2
图4
图5
D
只要知道其中的1个相等，则可以推出其它的3个结论， 即：①AOB DOE ∠=∠；②AB DE =；
③OC OF =；④ 弧BA =弧BD
七、圆周角定理
1、圆周角定理：同弧所对的圆周角等于它所对的圆心的角的一半。

即：∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠
2、圆周角定理的推论：
推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧是等弧；
即：在⊙O 中，∵C ∠、D ∠都是所对的圆周角 ∴C D ∠=∠
推论2：半圆或直径所对的圆周角是直角；圆周角是直角所对的弧是半圆，所对的弦是直径。

即：在⊙O 中，∵AB 是直径 或∵90C ∠=︒ ∴90C ∠=︒ ∴AB 是直径
推论3：若三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

即：在△ABC 中，∵OC OA OB ==
∴△ABC 是直角三角形或90C ∠=︒
注：此推论实是初二年级几何中矩形的推论：在直角三角形中斜边上的中线等于斜边的一半的逆定理。

八、圆内接四边形
圆的内接四边形定理：圆的内接四边形的对角互补，外角等于它的内对角。

即：在⊙O 中， ∵四边形ABCD 是内接四边形
∴180C BAD ∠+∠=︒ 180B D ∠+∠=︒ DAE C ∠=∠
九、切线的性质与判定定理
（1）切线的判定定理：过半径外端且垂直于半径的直线是切
线；
两个条件：过半径外端且垂直半径，二者缺一不可 即：∵MN OA ⊥且MN 过半径OA 外端 ∴MN 是⊙O 的切线
（2）性质定理：切线垂直于过切点的半径（如上图） 推论1：过圆心垂直于切线的直线必过切点。

推论2：过切点垂直于切线的直线必过圆心。

以上三个定理及推论也称二推一定理：
即：①过圆心；②过切点；③垂直切线，三个条件中知道其中两个条件就能推出最后一个。

十、切线长定理
切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。

即：∵PA 、PB 是的两条切线 ∴PA PB = PO 平分BPA ∠
十一、圆幂定理
（1）相交弦定理：圆内两弦相交，交点分得的两
条线段的乘积相等。

即：在⊙O 中，∵弦AB 、CD 相交于点P ， ∴PA PB PC PD ⋅=⋅
（2）推论：如果弦与直径垂直相交，那么弦的一半是它分
直径所成的两条线段的比例中项。

即：在⊙O 中，∵直径AB CD ⊥，
∴2
CE AE BE =⋅
（3）切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长
的比例中项。

即：在⊙O 中，∵PA 是切线，PB 是割线
B
A
B
A
O
D
B
A
∴ 2
PA PC PB =⋅
（4）割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等（如上图）。

即：在⊙O 中，∵PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅
十二、两圆公共弦定理
圆公共弦定理：两圆圆心的连线垂直并且平分这两个圆的的公共弦。

如图：12O O 垂直平分AB 。

即：∵⊙1O 、⊙2O 相交于A 、B 两点 ∴12O O 垂直平分AB 十三、圆的公切线 两圆公切线长的计算公式：
（1）公切线长：12Rt O O C ∆
中，221AB CO = （2）外公切线长：2CO 是半径之差； 内公切线长：2CO 是半径之和 。

十四、圆内正多边形的计算 （1）正三角形
在⊙O 中△ABC 是正三角形，有关计算在Rt BOD ∆中进
行：::2OD BD OB =；
（2）正四边形
同理，四边形的有关计算在R t O A E ∆中进行
，::1:2O E A E O A =
（3）正六边形
同理，六边形的有关计算在Rt OAB ∆
中进行，::2AB OB OA =.
十五、扇形、圆柱和圆锥的相关计算公式 1、扇形：（1）弧长公式：180
n R
l π=
； （2）扇形面积公式： 2
1
3602
n R S lR π=
= n ：圆心角 R ：扇形多对应的圆的半径 l ：扇形弧长
S ：扇形面积
2、圆柱：
（1）圆柱侧面展开图
2S S S =+侧表底=2
22rh r ππ+
（2）圆柱的体积：2
V r h π=
（2）圆锥侧面展开图
（1）S S S =+侧表底=2
Rr r ππ+
（2）圆锥的体积：2
13
V r h π=
十六、圆中常见的辅助线
1）．作半径，利用同圆或等圆的半径相等．
2）．作弦心距，利用垂径定理进行证明或计算，或利用“圆心、弧、弦、弦心距”间的关系进行证明．
3）．作半径和弦心距，构造由“半径、半弦和弦心距”组成的直角三角形进行计算． 4）．作弦构造同弧或等弧所对的圆周角．
5)．作弦、直径等构造直径所对的圆周角——直角． 6)．遇到切线，作过切点的弦，构造弦切角．
7)．遇到切线，作过切点的半径，构造直角．
l
O
C 1
D 1B
A
8)．欲证直线为圆的切线时，分两种情况：(1)若知道直线和圆有公共点时，常连结公共点和圆心证明直线垂直；(2)不知道直线和圆有公共点时，常过圆心向直线作垂线，证明垂线段的长等于圆的半径．
9)．遇到三角形的外心常连结外心和三角形的各顶点．
10)．遇到三角形的内心，常作：(1)内心到三边的垂线；(2)连结内心和三角形的顶点．
11)．遇相交两圆，常作：(1)公共弦；(2)连心线．
12)．遇两圆相切，常过切点作两圆的公切线．
13)．求公切线时常过小圆圆心向大圆半径作垂线，将公切线平移成直角三角形的一条直角边．
十七、圆中较特殊的辅助线
1)．过圆外一点或圆上一点作圆的切线．
2)．将割线、相交弦补充完整．
3)．作辅助圆．
例1如图23-11，CA为⊙O的切线，切点为A，点B在⊙O上，如果∠CAB＝55°，那么∠AOB等于( )
A．35°B．90°
C．110°D．120°
例2如果圆柱的底面半径为4cm，母线长为5cm，那么侧面积等于( )
A ．
B ．
C ．
D ．
例3 如图23-12，在半径为4的⊙O中，AB、CD是两条直径，M
为OB的中点，延长CM交⊙O于E，且EM>MC，连结OE、DE ，．求：EM的长．
例4如图23-13，AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，PF分别交AB、BC于E、D，交⊙O于F、G，且BE、BD恰好是关于x 的方程
(其中m为实数)的两根．
(1)求证：BE＝BD；
(2)若，求∠A的度数．。