Reconstruction of wavelet coefficients using total variation minimization
函数功能解释(英文版)
tifs2seq
Create a MATLAB sequence from a multi-frame TIFF file.
Geometric Transformations
imtransf orm2
2-D image transformation with fixed output location.
Computes and displays the error between two matrices. Decodes a TIFS2CV compressed image sequence. Decodes a Huffman encoded matrix. Builds a variable-length Huffman code for a symbol source. Compresses an image using a JPEG approximation. Compresses an image using a JPEG 2000 approximation. Computes the ratio of the bytes in two images/variables. Decodes an IM2JPEG compressed image. Decodes an IM2JPEG2K compressed image. Decompresses a 1-D lossless predictive encoded matrix. Huffman encodes a matrix. Compresses a matrix using 1-D lossles predictive coding. Computes a first-order estimate of the entropy of a matrix. Quantizes the elements of a UINT8 matrix. Displays the motion vectors of a compressed image sequence. Compresses a multi-frame TIFF image sequence. Decodes a variable-length bit stream.
实验法求解汽车鼓式制动器对流换热系数

O.411 835
650
643.126 505
0.486 714
羹蚕曛。1~36……。蚤i蓁臣
时间/5 (a)转速1lO r/min
时间/S Co)转速170 r/min
时间/S (c)转速280 r/mm
p、巡躁 匕蚤蓬匕薹溪匕
如m∞加 O
60 120 180
0 30 60 90
0
30 60 90
V01.26 NO.4 Jul.2006
文章编号:1671—8879(2006)04—0092—03
实验法求解汽车鼓式制动器对流换热系数
郭应时,袁伟,付锐
(长安大学汽车学院,陕西西安710064)
摘 要:在传热学理论基础上,结合汽车鼓式制动器的结构和工作原理,建立了鼓式制动器热平衡
关系式,分析了影响对流换热系数的主要因素。依据对流换热过程的3个相似准则,进行鼓式制动
流换热系数的关系,则有描述无相变条件下鼓式制
动器对流换热一般性方程
h—f(p,Cp,叩,A,“,Z)
(5)
式中:p、孙“分别为外掠空气的密度、动力粘度和速
度;A、C。分别为制动鼓材料的导热系数和比热;z为
制动鼓外表面几何特性尺寸。
3量纲分析与相似分析
在式(5)中有6个参数影响换热系数,若在实验 过程中每个参数仅改变10次,就要做106次实验, 这个工作量是非常巨大的。同时为了使实验结果能 够推广应用到其他具有不同几何参数、物性参数和 运行环境的鼓式制动器,本文采用无量纲分析法和 相似理论来指导实验。通过量纲分析和相似分析, 可以得到对流换热的3个相似准则。
所以流体只有空气一种,即P,是常数,所以式(9)
简化后带入式(7)可以得到
小波分解英文缩写

小波分解英文缩写Title: Wavelet Decomposition: An In-Depth Analysis of its Principles and ApplicationsWavelet decomposition, abbreviated as WD, is a powerful tool in signal and image processing that allows for the analysis of data at multiple scales. It offers a more flexible and localized approach compared to traditional methods like Fourier analysis, making it suitable for non-stationary signals and images with complex features. Inthis article, we delve into the principles of wavelet decomposition, its mathematical foundations, and exploreits diverse applications across various fields.The core concept of wavelet decomposition lies in the use of wavelets, which are small, oscillating waveformsthat can be scaled and shifted to match different parts of a signal or image. These wavelets form a basis set that can be used to represent the original data in a sparse and efficient manner. By decomposing a signal or image into a series of wavelet coefficients, we can capture both the frequency and temporal or spatial localization of its features.The process of wavelet decomposition typically involves two main steps: wavelet transform and coefficient extraction. The wavelet transform applies a series of wavelet functions to the input data, resulting in a set of wavelet coefficients that represent the data in a new domain. These coefficients capture the contributions of different wavelet scales and shifts to the original signal or image. The coefficient extraction step involvesselecting and organizing these coefficients based on their significance, allowing for further analysis or compression. One of the key advantages of wavelet decomposition is its ability to handle non-stationary signals, which exhibit varying characteristics over time. Unlike Fourier analysis, which assumes stationarity and provides global frequency information, wavelet decomposition offers a localized analysis that can capture changes in frequency and amplitude over time. This makes it particularly useful in fields such as biomedical engineering, where signals often exhibit transient or periodic features that are criticalfor diagnosis and monitoring.In addition to signal processing, wavelet decomposition has found widespread applications in image processing and compression. By decomposing an image into wavelet coefficients, we can separate its various components suchas edges, textures, and smooth regions. This allows for targeted processing or compression based on the importanceof different image features. For example, wavelet-based image compression techniques can achieve high compression ratios while preserving important visual information, making them suitable for applications like remote sensing, medical imaging, and video conferencing.Furthermore, wavelet decomposition has been applied to various other fields including financial analysis, geophysics, and acoustics. In financial analysis, it can be used to detect patterns and trends in stock market data orto forecast future prices. In geophysics, wavelet decomposition can help in the interpretation of seismic signals for earthquake prediction or geological exploration. In acoustics, it can be employed to analyze sound signalsfor noise reduction or speech recognition tasks.In conclusion, wavelet decomposition is a powerful tool that offers a unique perspective on data analysis and processing. Its ability to capture both frequency and temporal or spatial localization makes it suitable for a wide range of applications across various fields. As research continues to advance in this area, we can expect to see more innovative applications and techniques emerging that further leverage the strengths of wavelet decomposition.。
数据挖掘顶级期刊简介

顶级会议第一KDD 第二SIAM ICDM中国计算机学会推荐国际学术刊物(数据库、数据挖掘与内容检索)序号刊物简称刊物全称出版社网址1 TODS ACM Transactions on Database Systems ACM /tods/2 TOIS ACM Transactions on Information andSystems ACM /pubs/tois/3 TKDE IEEE Transactions on Knowledge and Data Engineering IEEE Computer Society /tkde/4 VLDBJ VLDB Journal S pringer-Verlag/dblp/db/journals/vldb/index.html二、B类序号刊物简称刊物全称出版社网址1 TKDD ACM Transactions on Knowledge Discovery from Data ACM/pubs/tkdd/2 AEI Advanced Engineering Informatics Elsevier/wps/find/journaldescription.cws_home/622240/3 DKE Data and Knowledge Engineering Elsevier/science/journal/0169023X4 DMKD Data Mining and Knowledge DiscoverySpringer/content/100254/5 EJIS European Journal of Information Systems The OR Society/ejis/6 GeoInformatica Springer /content/1573-7624/7 IPM Information Processing and Management Elsevier/locate/infoproman8 Information Sciences Elsevier /locate/issn/002002559 IS Information Systems Elsevier/information-systems/10 JASIST Journal of the American Society for Information Science and TechnologyAmerican Society for Information Science and Technology /Publications/JASIS/jasis.html11 JWS Journal of Web Semantics Elsevier /locate/inca/67132212 KIS Knowledge and Information Systems Springer /journal/1011513 TWEB ACM Transactions on the Web ACM /三、C类序号刊物简称刊物全称出版社网址1 DPD Distributed and Parallel Databases Springer/content/1573-7578/2 I&M Information and Management E lsevier /locate/im/3 IPL Information Processing Letters Elsevier /locate/ipl4 Information Retrieval Springer /issn/1386-45645 IJCIS International Journal of Cooperative Information Systems World Scientific/ijcis6 IJGIS International Journal of Geographical Information Science Taylor & Francis/journals/tf/13658816.html7 IJIS International Journal of Intelligent Systems Wiley/jpages/0884-8173/8 IJKM International Journal of Knowledge Management IGI/journals/details.asp?id=42889 IJSWIS International Journal on Semantic Web and Information Systems IGI/10 JCIS J ournal of Computer Information Systems IACIS/web/journal.htm11 JDM Journal of Database Management IGI-Global/journals/details.asp?id=19812 JGITM Journal of Global Information Technology Management Ivy League Publishing/bae/jgitm/13 JIIS Journal of Intelligent Information Systems Springer/content/1573-7675/14 JSIS Journal of Strategic Information Systems Elsevier/locate/jsis中国计算机学会推荐国际学术刊物(数据库、数据挖掘与内容检索)一、A类序号刊物简称刊物全称出版社网址1 TODS ACM Transactions on Database Systems ACM /tods/2 TOIS ACM Transactions on Information andSystems ACM /pubs/tois/3 TKDE IEEE Transactions on Knowledge and Data Engineering IEEE Computer Society /tkde/4 VLDBJ VLDB Journal S pringer-Verlag/dblp/db/journals/vldb/index.html二、B类序号刊物简称刊物全称出版社网址1 TKDD ACM Transactions on Knowledge Discovery from Data ACM/pubs/tkdd/2 AEI Advanced Engineering Informatics Elsevier/wps/find/journaldescription.cws_home/622240/3 DKE Data and Knowledge Engineering Elsevier/science/journal/0169023X4 DMKD Data Mining and Knowledge DiscoverySpringer/content/100254/5 EJIS European Journal of Information Systems The OR Society/ejis/6 GeoInformatica Springer /content/1573-7624/7 IPM Information Processing and Management Elsevier/locate/infoproman8 Information Sciences Elsevier /locate/issn/002002559 IS Information Systems Elsevier/information-systems/10 JASIST Journal of the American Society for Information Science and TechnologyAmerican Society for Information Science and Technology /Publications/JASIS/jasis.html11 JWS Journal of Web Semantics Elsevier /locate/inca/67132212 KIS Knowledge and Information Systems Springer /journal/1011513 TWEB ACM Transactions on the Web ACM /三、C类序号刊物简称刊物全称出版社网址1 DPD Distributed and Parallel Databases Springer/content/1573-7578/2 I&M Information and Management E lsevier /locate/im/3 IPL Information Processing Letters Elsevier /locate/ipl4 Information Retrieval Springer /issn/1386-45645 IJCIS International Journal of Cooperative Information Systems World Scientific/ijcis6 IJGIS International Journal of Geographical Information Science Taylor & Francis/journals/tf/13658816.html7 IJIS International Journal of Intelligent Systems Wiley/jpages/0884-8173/8 IJKM International Journal of Knowledge Management IGI/journals/details.asp?id=42889 IJSWIS International Journal on Semantic Web and Information Systems IGI/10 JCIS J ournal of Computer Information Systems IACIS/web/journal.htm11 JDM Journal of Database Management IGI-Global/journals/details.asp?id=19812 JGITM Journal of Global Information Technology Management Ivy League Publishing/bae/jgitm/13 JIIS Journal of Intelligent Information Systems Springer/content/1573-7675/14 JSIS Journal of Strategic Information Systems Elsevier/locate/jsis一、以下是一些数据挖掘领域专家牛人的网站,有很多精华,能开阔研究者的思路,在此共享:1.Rakesh Agrawal主页:/en-us/people/rakesha/ 数据挖掘领域唯一独有的关联规则研究的创始人,其主要的Apriori算法开启了这一伟大的领域。
IEEESignalProcessingSociety:IEEE信号处理学会
Jerome N. Shapiro, for the paper entitled, "Embedded Image Coding Using Zerotrees of Wavelet Coefficients," published in the IEEE Transactions on Signal Processing, Volume 41, Number 12, December 1993.
Digital Signal Processing
Avideh Zakhor, for the paper co-authored with Søren Hein entitled, "Reconstruction of Oversampled Band-Limited Signals from Sigma-Delta Encoded Binary Sequences," published in the IEEE Transactions on Signal Processing, Volume 42, Number 4, April 1994.
小波去噪阈值的确定和分解层数的确定
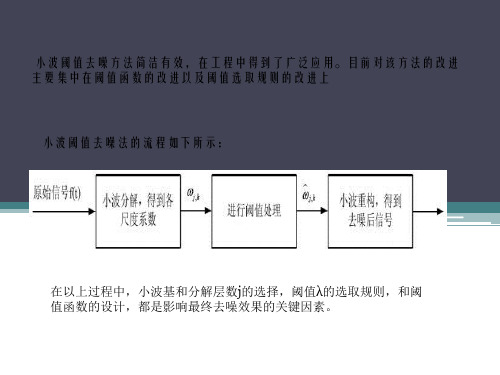
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.(根据计算后的小 波包系数重构原信号。)
1
0.5
0
-0.5
获得单个阈值,对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.(计算信号x在N层小波包分解的系数) 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.(以熵为准则,计算最佳树,当然 这一步是可选择的。) 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.(对于每一个小波包分解系数,选择阈值 并应用于去噪) The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.(工具箱会根据压缩量和剩余能量提供一个初始化的阈值,不过仍需要不 断测试来选择阈值优化去噪效果) a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
信号处理中英文对照外文翻译文献

信号处理中英文对照外文翻译文献(文档含英文原文和中文翻译)译文:一小波研究的意义与背景在实际应用中,针对不同性质的信号和干扰,寻找最佳的处理方法降低噪声,一直是信号处理领域广泛讨论的重要问题。
目前有很多方法可用于信号降噪,如中值滤波,低通滤波,傅立叶变换等,但它们都滤掉了信号细节中的有用部分。
传统的信号去噪方法以信号的平稳性为前提,仅从时域或频域分别给出统计平均结果。
根据有效信号的时域或频域特性去除噪声,而不能同时兼顾信号在时域和频域的局部和全貌。
更多的实践证明,经典的方法基于傅里叶变换的滤波,并不能对非平稳信号进行有效的分析和处理,去噪效果已不能很好地满足工程应用发展的要求。
常用的硬阈值法则和软阈值法则采用设置高频小波系数为零的方法从信号中滤除噪声。
实践证明,这些小波阈值去噪方法具有近似优化特性,在非平稳信号领域中具有良好表现。
小波理论是在傅立叶变换和短时傅立叶变换的基础上发展起来的,它具有多分辨分析的特点,在时域和频域上都具有表征信号局部特征的能力,是信号时频分析的优良工具。
小波变换具有多分辨性、时频局部化特性及计算的快速性等属性,这使得小波变换在地球物理领域有着广泛的应用。
随着技术的发展,小波包分析 (Wavelet Packet Analysis) 方法产生并发展起来,小波包分析是小波分析的拓展,具有十分广泛的应用价值。
它能够为信号提供一种更加精细的分析方法,它将频带进行多层次划分,对离散小波变换没有细分的高频部分进一步分析,并能够根据被分析信号的特征,自适应选择相应的频带,使之与信号匹配,从而提高了时频分辨率。
小波包分析 (wavelet packet analysis) 能够为信号提供一种更加精细的分析方法,它将频带进行多层次划分,对小波分析没有细分的高频部分进一步分解,并能够根据被分析信号的特征,自适应地选择相应频带 , 使之与信号频谱相匹配,因而小波包具有更广泛的应用价值。
利用小波包分析进行信号降噪,一种直观而有效的小波包去噪方法就是直接对小波包分解系数取阈值,选择相关的滤波因子,利用保留下来的系数进行信号的重构,最终达到降噪的目的。
适于硬件实现的无损图像压缩

适于硬件实现的无损图像压缩王建军;刘波【摘要】A hardware implementation method for lossless image compression is proposed to overcome the difficulties of embedded wavelet coding methods in hardware implementation and high costs. Firstly, the algorithm divides wavelet coefficients into a low frequency block and three high frequency blocks according to sub-band properties, and then uses different methods to code respectively. In the low frequency block coding method, the Difference Pulse coding Modulation(DPCM) is firstly used to reduce coefficients' dynamic range. Then, a modified bit plane coding method is used to output the bit stream. In the high frequency block coding method, the proposed modified Set Partitioning in Hierarchical trees(MSPIHT) algorithm is used to code three high frequency blocks respectively with their thresholds. The MSPIHT optimizes the outputted bit stream by using a type of A set judge, reduces memory requirement and avoids memory dynamic management by eliminating the lists of SPIHT algorithm. Moreover, the MSPIHT avoids repeated calculation in scanning process and enhances the coding efficiency by adopting MMVS. Experiment results show that the bit-rates of all international standard testing images have reduced more than 1.4 bit/pixel and the coding speed has increased more than three times as compared with that SPHIT. It is concludes that the proposed algorithm is super in realtime performance, low memory requirement and fit for hardwareimplementation.%针对常见嵌入式小波编码算法硬件实现困难、成本较高等问题,提出了一种适用于硬件实现的无损图像压缩算法.该算法根据子带属性的不同将小波系数分为1个低频子块和3个高频子块,然后使用不同的方法分别进行量化编码.对于低频子块,首先使用脉冲差分编码调制(DPCM)方法压缩其数据动态,然后使用改进的比特位平面编码算法编码输出对应码流;对于各高频子块,则使用提出的改进集合树分裂(SPIHT)算法分别进行量化编码.在改进的SPIHT算法中,通过加入A类集合的分类优化了码流输出;通过消除链表,降低了内存需求并避免了内存的动态管理;通过使用集合极值矩阵,避免了扫描过程中的重复判断,提高了编码效率.实验结果表明,与传统SPIHT算法相比,本文算法可使各国际标准测试图像的编码比特率均降低0.14 bit/pixel以上,而编码速度提高3倍以上.该算法具有实时性高、内存需求低、适于硬件实现的特点.【期刊名称】《光学精密工程》【年(卷),期】2011(019)004【总页数】7页(P922-928)【关键词】图像压缩;无损压缩;小波变换;SPIHT算法;硬件实现【作者】王建军;刘波【作者单位】中国人民武装警察部队工程学院,陕西西安710086;中国科学院空间科学与应用研究中心,北京1001909【正文语种】中文【中图分类】TP391.41 引言无损图像压缩在遥感图像与医学图像的获取、传输和存储等领域有着广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1754
RECONSTRUCTION OF WAVELET COEFFICIENTS
1755
In ψj,n , j is the index of scale and n the translation factor, taking values in the countable set Ψ. The term φJ,n denotes the scaling function on scale 2J translated by n, which is indexed to a finite set Φ. The family {φJ,n }n∈Φ is an orthonormal basis of a space VJ that belongs to a multiresolution approximation of L2 (I ). The hard thresholding operator τ is defined by (1.4) τ (x) = x if |x| ≥ λ, 0 if |x| < λ,
©2003 SIAM. SIAM Copyright Assignement Agreement gives the right to post an electronic version of the final SIAM file of the work on the author's current institutional Internet server for limited noncommercial distribution, provided that proper notice of SIAM's copyright is included and that no separate or additional fees are collected for access to or distribution of the work apart from Internet access fees which may be paid to an Internet access provider.
(j,n)∈Ψ
u ˜, ψj,n ψj,n +
n∈Φ
u ˜, φJ,n φJ,n ,
where for all u, v ∈ L2 (I ), (1.3) u, v = u(x) v (x) dx.
I
∗ Received by the editors November 12, 2001; accepted for publication (in revised form) October 18, 2002; published electronically April 15, 2003. /journals/sisc/24-5/39779.html † LAMFA, Universit´ e de Picardie-Jules Verne, 33 rue Saint Leu, 80039 Amiens cedex 1, France and CMLA, Ecole Normale Sup´ erieure de Cachan, 61 avenue du Pr´ esident Wilson, 94235 Cachan cedex, France (sdurand@cmla.ens-cachan.fr). ‡ LMAM, Universit´ e de Bretagne Sud, Centre Y. Coppens, campus de Tohannic, BP 573, 56017 Vannes, France (Jacques.Froment@univ-ubs.fr) and CMLA, Ecole Normale Sup´ erieure de Cachan, 61 avenue du Pr´ esident Wilson, 94235 Cachan cedex, France.
SIAM J. SCI. COMPUT. Vol. 24, No. 5, pp. 1754–1767
c 2003 Society for Industrial and Applied Mathematics
RECONSTRUCTION OF WAVELET COEFFICIENTS USING TOTAL VARIATION MINIMIZATION∗
(j,n)∈Ψ
τ( u ˜, ψj,n )ψj,n +
n∈Φ
u ˜, φJ,n φJ,n .
We will denote by M the map that records the indexes of retained coefficients: (1.7) M = {(j, n) ∈ Ψ : | u ˜, ψj,n | ≥ λ}.
1. Introduction. Let us consider the problem of denoising nearly piecewise smooth functions presenting sharp discontinuities, following the additive noise model (1.1) u ˜=u+ ,
Because of its simplicity, the algorithm sketched in (1.6) has been widely used by engineers since the beginning of wavelet in signal processing. It has been formalized by Donoho and Johnstone in [15], where they proved that the performance associated with the nonlinear thresholding estimator in orthogonal bases is close to an ideal coefficient selection and attenuation. In addition, among classical orthogonal bases, wavelet series outperform Fourier or cosine series in the representation of piecewise smooth functions (see, e.g., [7, 9]): the efficiency of the estimator depends on the rate of decay of the sorted decomposition coefficients and, thanks to the wavelets timelocalization, the decay of wavelet coefficients in the neighborhood of discontinuities is faster that the decay of Fourier coefficients. However, the wavelet thresholding method is still a regularization process and the estimator presents oscillations in the vicinity of the function’s discontinuities. Such oscillations are very close to the Gibbs phenomena exhibited by Fourier thresholding, although they are more local and of smaller amplitude. For this reason, they are called pseudo-Gibbs phenomena. These oscillations do not affect too much the L2 error between the original noiseless signal and the estimated one, but they do affect the visual quality of the result: it is often impossible to perform a complete denoising while keeping the threshold small enough to avoid the pseudo-Gibbs phenomena. If is a Gaussian white noise of standard deviation σ , the threshold should be set to (1.8) λ=σ 2 log N ,
