2016年春季新版青岛版八年级数学下学期8.1、不等式的基本性质导学案4
青岛版初中数学八年级下册 8.1 不等式的基本性质 导学案(无答案)

青岛版初中数学八年级下册8.1 不等式的基本性质导学案(无答案)第8章一元一次不等式8.1 不等式的基本性质一、导入激学的大小吗?你能比较265 12二、导标引学学习目标:1.会利用作差的方法比较两个实数的大小。
2.了解不等式的意义,发展学生的符号意识。
3.经历不等式基本性质的探索过程,能运用不等式的基本性质对不等式进行简单变形,会用有理数估计一个无理数的大致范围。
学习重点:不等式的基本性质及应用学习难点:不等式性质的探究三、学习过程(一)导预疑学(10分钟)(一)预学核心问题1.两个实数比较大小的方法。
2.不等式的定义3.不等式的基本性质。
(1)(2)(3)A. x -3>y -3B. -3x>-3yC.x+3>y+3 D. 33x y 3. 下列四个不等式:①ac>bc ②-ma<-mb ③ac 2>bc 2 ④-ac 2≤-bc 2中,能推出a>b 的有( )A. 1个B. 2个C. 3个D. 4个4.若x 是任意实数,则下列不等式中,恒成立的是( )A. 3x>2xB. 3x 2>2x 2C. 3+x>2D. 3+x 2>25.根据不等式的基本性质,用“<”或“>”填空.(1)若a -1>b -1,则a____b ;(2)若a+3>b+3,则a____b ;(3)若2a>2b ,则a____b ;(4)若-2a>-2b ,则a___b .四、导学慧学1.本节课你收获了哪些新知识?你认为特别注意什么问题?2.类比等式基本性质与不等式基本性质的区别与联系。
青岛版八下数学8.1《不等式的基本性质》教案

青岛版⼋下数学8.1《不等式的基本性质》教案不等式的基本性质【教材分析】不等式的基本性质是⼋年级下册第⼀章第⼀节内容。
不等式是现实世界中不等关系的⼀种数学表⽰形式,它不仅是现阶段学⽣学习的重点,⽽且也是后续学习的重要基础。
它是刻画现实世界中量与量之间关系的有效数学模型,在现实⽣活中有着⼴泛的应⽤,所以对不等式的学习有着重要的现实意义。
本节课是建⽴在学⽣认识了不等关系的基础上进⾏的,也是解不等式及应⽤不等式解决实际问题的重要依据,因此本节课内容在⼀元⼀次不等式这⼀章占据重要位置,本节课的教学指导思想是从学⽣实际认知⽔平及知识结构出发,让学⽣⾃主探究获取知识。
【教学⽬标】知识与技能⽬标:1.掌握不等式的三条基本性质;2. 能熟练的应⽤不等式的性质进⾏不等式的变形;3.理解不等式的基本性质与等式的基本性质之间的区别。
过程与⽅法⽬标:1.通过等式的性质,探索不等式的性质,初步体会“类⽐”的数学思想。
2. 经历探索不等式基本性质的过程,体会不等式的三条基本性质的作⽤和意义,培养学⽣发现探索数学问题的能⼒。
3.通过观察、探索、归纳等数学活动,感受数学思考过程的条理性,发展思维能⼒和语⾔表达能⼒。
情感态度与价值观⽬标:通过学⽣的⾃主探究、合作交流提⾼学⽣观察和归纳的能⼒,培养集体合作的意识。
【重点和难点】教学重点:不等式的性质掌握以及应⽤教学难点:不等式的性质探究与理解。
【学情分析】本节课的教学对象是初中⼆年级学⽣,他们特点是个性突出、爱说爱动,有较强的表现欲和⼀定的计算能⼒。
同时学⽣之前已经学过了等式及其基本性质,了解了不等关系,学习了作差法⽐较两个实数的⼤⼩,具有⼀定的观察、分析、解决问题的能⼒。
但是他们基础薄弱,学⽣差异⼤,同时,初⼆数学难度加⼤,部分学⽣已经开始对学习缺乏兴趣。
【教学⽅法】采⽤激趣—探究法进⾏教学,师⽣互动,共同探究不等式的性质1,学⽣⾃主探究性质2、3.通过知识类⽐、合理引导等突出学⽣主体地位,让教师成为学⽣学习的组织者、引导者、合作者,让学⽣亲⾃动⼿、动脑、动⼝参与数学活动,经历问题的发⽣、发展和解决过程,在解决问题的过程中完成教学⽬标。
青岛版八下数学8.1不等式的基本性质教学设计

青岛版八下数学8.1不等式的基本性质教学设计一. 教材分析《青岛版八下数学8.1不等式的基本性质》这一节内容,主要让学生掌握不等式的性质,包括不等式的两边同时加减同一个数或同一个整式,不等号的方向不变;不等式的两边同时乘除同一个正数,不等号的方向不变;不等式的两边同时乘除同一个负数,不等号的方向改变。
这些性质是解决不等式问题的基础,对于学生后续学习函数、方程等领域具有重要的意义。
二. 学情分析学生在学习这一节内容时,已具备了一定的代数基础,对不等式有一定的了解。
但是,对于不等式的性质,学生可能还比较陌生,需要通过具体的例子和操作来理解和掌握。
此外,学生可能对于一些概念理解不深,如“两边同时加减”、“两边同时乘除”等,需要教师在教学中进行引导和解释。
三. 教学目标1.让学生了解不等式的基本性质,能够运用不等式的性质解决简单的问题。
2.培养学生的逻辑思维能力和解决问题的能力。
3.提高学生的数学兴趣,增强学生的自信心。
四. 教学重难点1.教学重点:不等式的基本性质,如何运用不等式的性质解决简单的问题。
2.教学难点:对于一些概念的理解,如“两边同时加减”、“两边同时乘除”等,以及如何将这些性质运用到实际问题中。
五. 教学方法1.采用问题驱动的教学方法,让学生在解决问题的过程中,理解和掌握不等式的性质。
2.使用具体的例子和操作,让学生直观地感受不等式的性质。
3.采用小组合作学习的方式,让学生在讨论和交流中,进一步理解和掌握不等式的性质。
六. 教学准备1.PPT课件2.教学素材和例子3.小组合作学习的任务单七. 教学过程1.导入(5分钟)利用PPT课件,展示一些实际问题,让学生感受不等式的性质在日常生活中的应用。
例如,两人赛跑,一人跑得快,一人跑得慢,如何比较他们的速度。
通过这些问题,激发学生的学习兴趣,引出今天要学习的内容——不等式的基本性质。
2.呈现(15分钟)利用PPT课件,展示不等式的基本性质,引导学生理解和掌握这些性质。
青岛版数学八下8.1《不等式的基本性质》word学案

§8.1不等式的基本性质 导学案学习目标1.探索并掌握不等式的基本性质;2.理解不等式与等式性质的联系与区别.学习重点探索不等式的基本性质,并能灵活地掌握和应用.学习过程一、课前预习:1、我们学习了等式,并掌握了等式的基本性质,大家还记得等式的基本性质吗?等式的基本性质一:在等式的两边都 或( )同一个 ,等式仍然成立。
可用符号表示为: 若b a =,则c a ± c b ±等式的基本性质二:在等式的两边都 同一个 或( )同一个 ,等式仍然成立。
可用符号表示为: 若b a =,则c a ⨯ c b ⨯,c a c b (0≠c ) 2、不等式与等式只有一字之差,那么它们的性质是否也有相似之处呢?二、探究新知:(一)不等式基本性质的推导1、自主学习:填空:2 <3 2 < 3 2 < 32+3 3+3 2×5 3×5 2÷5 3÷52+5 3+5 2×21 3×21 2÷21 3÷21 2+8 3+8 2×(-1) 3×(-1) 2÷(-1) 3÷(-1)2-3 3-3 2×(-5) 3×(-5) 2÷(-5) 3÷(-5)2-5 3-5 2-8 3-8 2、合作交流:做完上面的填空,你发现了什么?请你再举几例试一试,还有类似的结论吗?与同学交流,归纳上题的结论,我们便得到了不等式的基本性质:不等式的基本性质一:不等式的两边都 或( )同一个 ,不等号的方向不变。
可用符号表示为: 若a >b ,则c a ± c b ±不等式的基本性质二:不等式的两边都 或( )同一个 ,不等号的方向 。
可用符号表示为: 若a >b ,c >0,则c a ⨯ c b ⨯,或c a cb 不等式的基本性质三:不等式的两边都 或( )同一个 ,不等号的方向 。
青岛版(新)数学八年级下册 8.1.1不等式的基本性质(导

8.1.1不等式的基本性质
【学习目标】
1、知道两个实数中存在的三种大小关系.
2.能利用做差的方法比较两个的大小.
【学习重难点】
能利用做差的方法比较两个的大小.
【学习过程】
一、课前准备
1.一般地,两个实数或两个相同单位的量a,b 在下列三种关系中,有且只有一种 成立,______________________________________.
二、学习新知
2.引入了减法运算后,对于两个实数a,b ,可以借助a-b 的符号来比较它们的大小. 对于两个实数a,b ,
如果a-b 是______,那么a____b ;如果a-b 是______,那么a____b ;
如果a-b 是______,那么a____b ;
3.不等关系的传递性(间接比较大小的理论依据)若a>b,b>c,则a___c.
练习:⑴比较1-2与1-3的大小.
⑵当x=22,3+3时,比较代数式3x-1的值与11的大小.
三、合作交流
例1:试比较(1)(5)x x ++与2
(3)x +的大小
四、课堂小结:
这节课你有什么收获?
1.差值比较法的一般步骤:⑴作差 ⑵变形(配方法和因式分解为代数变形的常用方法) ⑶定号 ⑷下结论
【当堂测试】
1、 比较
2
51+与261+的大小. 2、 比较)5)(3(-+a a 与)4)(2(-+a a 的大小
3、比较x x -2与2-x 的大小关系。
八年级数学下册 8.1 一元一次不等式的基本性质教案2 (新版)青岛版-(新版)青岛版初中八年级下册
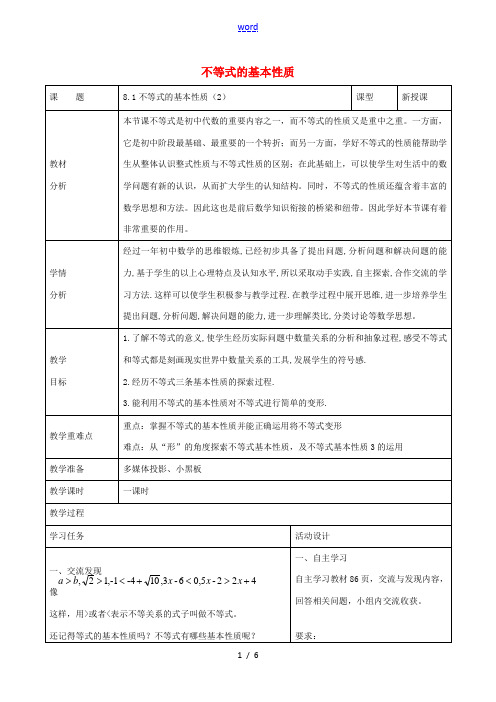
不等式的基本性质1.甲的年龄为a岁,乙的年龄为b岁,如果甲的年龄比乙大,则用不等式表示a与b的大小关系为;c年后,它们二人谁的年龄大?用不等式表示为;c年前,他们二人谁的年龄大?用不等式表示为。
2.在数轴上,点A与点B分别对应实数a、b,并且点A在点B 的右边,请你用不等式表示a、b之间的大小关系为;如果同时将点A、B向右(或向左)沿x轴移动c个单位长度,得到点A′、B′,用不等式表示点A′、B′所对应的数的大小关系为。
3.有1/2,你发现了有关不等式的什么结论?能不能用式子表示出来?二、不等式的基本性质由上面的探讨我们可以得出:不等式的性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.这个性质可以用数学语言表示为:2.仿照下表,分组探讨不等式不等式的两边都乘以(或除以)同一个正数结果与原不等式比较不等号的方向是否改变了7 > 4 乘以5 35>20 没有改变-8<4 除以4 -2<1 没有改变。
1.静心默读,并用红笔标出你认为重要的内容。
2.独立完成右面的问题(2mins)。
3.组内相互校对答案(1mins)。
4.教师个别指导。
二、合作探究(7mins)1.结合自主学习内容,总结不等式的基本性质;2.小组内交流。
3.互说:同桌结对,起立互说解题思路或过程;4.互帮,组际帮扶;5.互帮中不能解决的问题,由抄板手写到小黑板上;6.师生互帮(交流展示,精讲点拨).由上面的探讨我们可以继续得出: 不等式的基本性质 2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.这个性质可以用数学语言表示为:3.仿照下表,分组探讨不等式不等式的两边都乘以(或除以)同一个负数结 果 与原不等式比较不等号的方向是否改变了 7 > 4 乘以-5 -35<-20 改变了 -8<4 除以-4 2 >-1 改变了 …………由上面的探讨我们可以继续得出: 不等式的基本性质 3:不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变.这个性质可以用数学语言表示为:三、典例透析例3.三、例题透析老师针对教材的典型例题精讲点拨。
初中数学青岛版八年级下册高效课堂资料8.1 不等式的基本性质 教学设计

初中数学青岛版八年级下册高效课堂资料8.1 不等式的基本性质教学设计【教学目标】1. 掌握不等式的基本性质并会对不等式进行简单的变形;2.体会类比的思想;3.发展符号感.【教学重难点】重点:不等式的意义.难点:不等式的意义.【课时安排】1课时【教学过程】一、导入环节(3分钟)(一)导入新课,板书课题导入语:同学们,在七年级里我们学习了方程和等式,接下来的一周,我们要学习方程和等式关系比较密切的第九章:一元一次不等式.一共4大节.这节课我们学习第一节:不等式的基本性质的第一课时,请看学习目标.(二)出示学习目标课件展示教学目标,让一名学生读学习目标.过渡语:让我们带着目标、带着问题进入自主学习环节.二、自主学习(7分钟)认真阅读课本P84-P88,掌握不等式的基本性质,并完成以下问题.1.一般地,两个实数或相同单位的量a,b存在几种关系?2. 通过减法运算,如何借助a-b的符号比较两个实数a,b的大小?3.问题一:不等式与等式只有一字之差,那么它们的性质是否也有相似之处呢?用“>”,“<”或“=”填空:(1)7 4 (2)7+4 4+4(3)7+(-3)4+(-3)(4)7-9 4-9(5)7+a 4+a (6)7-b 4-b由此得出不等式的基本性质1可用符号表示为:若a>b,则ca±cb±问题二:如果不等式的两边都乘以(或除以)同一个不为零的数, 不等号的方向是否也不变呢?(1)7×3 ______4×3, (2)7×2 ______4×2 ,(3)7×(-1)______4×(-1), (4)7×(-5)______4×(-5),(5)7÷4______ 4÷4 (6)7÷(-3)______4÷(-3),由此得出不等式的基本性质2可用符号表示为:若a >b ,c >0,则c a ⨯ c b ⨯,或c a c b由此得出不等式的基本性质3___________________________________可用符号表示为: 若a >b ,c <0,则c a ⨯ c b ⨯,或c a c b三、合作探究(15分钟)首先组内交流自主学习中的疑惑问题,然后完成下列探究问题.例1.1.用作差法比较数的大小(1)-2与1-5(2)当x= 3,22时,分别比较代数式3x 2+5x-1的值与3x 2+2x+4的大小。
青岛版八年级下册8.1(1)导学案设计 不等式的基本性质学案设计(无答案)

8.1 不等式的基本性质(1)(预习导案)【学习目标】1.会比较两个实数的大小;2.掌握作差法比较两个实数大小的方法.3.了解不等式的意义,发展符号意识,能够判断算式是否为不等式.【相关链接】有理数的比较方法:(1)法则法:正数都大于,零大于一切,两个负数相比较,绝对值大的反而(2)数形结合法:在同一数轴上,右边的点表示的数总比左边的点表示的数.【预习导航】阅读课本84页到85页,完成相关内容.8.1 不等式的基本性质(1)(分层练习)★1.在空格处填写适当的不等号. (1)π 3.14 (2)223 530 (3)若a 是实数,则12+a 02.(1)如果02>a ,那么( )A.0≥a B.0>a C.0≠a D.a 是任意实数(2)如果a a -<,那么( )A.0<a B.0>a C.0≤a D.0≥a 3.110+与5的大小关系是( )A.5110>+ B.5110=+ C.5110<+ D.不能确定 4.有下列式子:①3>4 ②-5>0 ③32+x ④y 63x 2<+ ⑤))(22b a b a b a -+=-(其中不等式有()A.1个B.2个C.3个 D4个★★5.已知a,b,c (b<c)是△ABC 的三边长,则a 与b-c 的大小关系是 .6.若a 为实数,则3a 与2a 的大小关系是( )A.a a 23<B.a a 23=C.a a 23>D.不能确定8.用不等式表示下列问题中的数量关系 (1)5514的和小于倍与的x (2)21的差不大于的相反数与x (3)差的一半是正数与b a9.比较大小:(1)51-23与 (2)13-32-与★★★10.已知13422++=y x P ,1622-+-=x y x Q ,则代数式P ,Q 的大小关系是什么?【反思梳理】总结你的收获.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1不等式的基本性质一、自主学习1、一般地,两个实数或两个相同单位的量a 、b 在下列三种关系中,有且只有一种成立:_______________,________________,___________________。
2、在下面的空格处填上“>”或“<”:(1)在Rt △ABC 中,∠C=90°,那么∠C____∠A ,a_____c ;(2)π______3.1416;(3)3______2;(4)a 是实数,0____12+a 。
(5)如果a>b ,b>c ,那么a_____c3、(1)引入了减法运算后,由两个数的大小可以确定它们差的符号:如果a>b ,那么___________;如果a=b ,那么___________;如果a<b ,那么___________;(2)用作差法比较两个数的大小:如果a-b>0,那么________;如果a-b=0,那么________;如果a-b<0,那么________;二、 合作探究1、用适当的不等号表示下列数量关系:(1)数a 比它的倒数大;_______________________________(2)a 的3倍与5的和比20大;__________________________(3)a 的32与11的差不大于2;________________________________ (4)原价为a 元的商品,降价x%后仍不低于15元。
__________________2、用作差法比较两个数的大小:(1)67+与36+ (2)2-与54+-3、当x=22,4,33+时,分别比较代数式3x+1的值与11的大小。
三、达标检测1、用适当的不等式符号表示下列关系:(1) a 是负数; (2) a 是非负数;(3) a 与b 的和小于5; (4) x 与2的差大于-1;(5) x 的4倍不大于7; (6) y 的一半不小于3.2、如果a 2>0,那么( )A.a ≥0 B. a>0 C. a ≠0 D. a 是任意实数3、如果a <a -,那么( )A. a>0 B. a<0 C. a ≥0 D. a ≤04、用作差法比较两个数的大小:7311-与71四、作业(必做题:1、2、3(1)选做题:3(2)。
)1、用适当的不等号表示下列数量关系:(1) x 与y 同号______________. (2)x 与y 异号______________(3)a 的一半与4的差的绝对值不小于a ;(4)x 的2倍减去1不小于x 与3的和;(5)a 与b 的平方和是非负数;(6)y 的2倍加上3的和大于-2且小于4;2、有理数在数轴上的位置如图所示,则下列各式中成立的是( )A 、a+b >0B 、b -cC 、ab > 0D 、ba >0 3、用作差法比较两个数的大小:(1)251+与261+ (2)332+-与332--8.1《不等式的基本性质(2)》导学案一、自主学习1、用适当的不等符号表示下列关系:(1) a 是正数; (2) a 是非正数;(3) a 与b 的差小于5; (4) x 与2的差大于-1;(5) x 的4倍不小于7; (6) y 的一半不等于3.2、 ___________________________叫做不等式。
3、常用的不等号有: _________________4、判断下列各式中哪些是不等式,哪些不是。
(是打“√”不是打“×”)⑴ x+1=2 ( ) ⑵ 5x-3>1 ( ) ⑶ x-6 ( )⑷ 11x-4≤6( ) ⑸ 7>4 ( ) ⑹2x-y ≥0 ( )二、 合作探究1、(1)将不等式2>-1的两边加上2或都减去1,不等号是否改变?2+2______-1+2 2-1_____-1-1(2)如果a>b,试用作差法比较两个数的大小:(1)a+c 与b+c ,(2)a-c 与b-c我的发现:不等式性质1 如果a>b ,那么a+c b+c ,a-c b-c 。
不等式的两边都加上(或减去) ,不等号方向________。
2、(1)将不等式6>-3和-4<-2的两边都乘3或都除以2,不等号是否改变?6×3___(-3) ×3 (-4)×3____(-2)×3 6÷2___(-3)÷2 (-4)÷2___(-2)÷2(2)如果a>b, 并且c>0,试用作差法比较两个数的大小:(1)ac 与bc ,(2)c a 与cb我的发现:不等式性质2 如果a>b,并且c>0,那么ac bc ,c a ____cb . 不等式两边都乘以(或除以) ,不等号方向_________。
3、(1)将不等式6>-3和-4<-2的两边都乘-3或都除以-2,不等号是否改变?6×(-3)___(-3) ×(-3) (-4)×(-3)____(-2)×(-3)6÷(-2)___(-3)÷(-2) (-4)÷(-2)___(-2)÷(-2)(2)如果a>b, 并且c<0,试用作差法比较两数的大小:(1)ac 与bc ,(2)c a 与cb我的发现:不等式性质3 如果a>b,并且c<0,那么ac bc ,c a ____cb . 不等式两边都乘以(或除以) ,不等号方向________。
4、利用不等式的性质,用“<“,”>“号填空。
若a>b,那么a+2 b+2;a-5 b-5 若a<b,那么b-a 0;若x>-3,那么x-m -3-m; 若a<0,b<0, c<0,那么(a+b)c 0.5、你能根据3<2,利用不等式的基本性质,推出323-<0吗?6、你能根据3<2,利用不等式的基本性质,估计4323-与25.0-哪个大吗?三、达标检测1、指出下列各题中不等式变形的依据:(1)由3a>2,得a>32. _________(2)由a+3>0,得a>-3. _____(3)由-5a<1,得a>-51. __(4)由4a>3a+1,得a>1. _______________________2.如果10<<x ,则xx x 1,,2的大小关系是 < < , 如果01<<-x ,则xx x 1,,2的大小关系是 < < . 3、(1)若 x ﹥y , 则 x - z y - z ; (2) 若 x ﹤0, 则 3x 5x ; (3) 若 x ﹥y , 则 x z 2 y z 2 ;四、作业1、设a>b,用“<”或“>”填空.(1) a -3____b –3 (2.)- 4a____ - 4b (3) 2-3a______2-3b2、由x<y 得mx>my 的条件是 ( )A . m ≥0B . m ≤0 C. m >0 D. m <03、若mx<m,且x>1,则应为 ( )A. m<0B. m>0C. m ≤0D. m ≥04、若m 是有理数,则-7m 与3m 的大小关系应是 ( )A. -7m<3mB. -7m>3mC. -7m ≤3mD. 不能确定8.2《一元一次不等式(1)》导学案总第 课时 主备人 石在宏 使用人一、自主学习1、当x 的值分别取-1、0、2、3、3.5、5时,不等式x -3>0和x -4<0能分别成立吗?解:当x 取 时不等式x -3>0成立;当x 取 时不等式x -4<0成立2、(1)x =4,5,6,8能使不等式x +2>5成立吗?(2)你还能找出一些使不等式x+2>5成立的x 的值吗?例如 ________________________等。
如果不等式中含有未知数,__________________________,叫做这个不等式的解。
(3)由此看来,满足__________的任何一个实数都能使不等式x+2>5成立,所以不等式x+2>5的解有多少?一般地,_________________________________________叫做这个不等式的解集。
二、 合作探究1、我们知道实数可以用数轴上的点来表示,那么不等式的解集x >3是否也可以借助数轴直观地表示出来呢?2、将下列不等式的解集在数轴上表示出来,并写出(1)题不等式的所有正整数解和(2)题不等式的所有负整数解。
(1)x ﹤221 (2)x ≥-2 (3)x ≤-1我的发现:不等式的解集在数轴上可直观地表示出来,但应注意不等号的类型,小于在左边,大于在右边。
当不等号为“>”“<”时用 圆圈,当不等号为“≤”“≥”时用 圆圈。
3、如图,写出下列数轴上所表示的关于x 的不等式的解集:(1 (2) (3) (4)三、达标检测1.已知40<<x ,则x 可取的整数解有 。
2、不等式x <2有_____个整数解,有______个非负整数解。
3、已知不等式2x+3≥5.(1)写出它的五个整数解:_______________________;(2)写出它的三个无理数解:__________________________。
4、将下列不等式的解集在数轴上表示出来:(1)x>5 (2)x ≤0四、作业1x 的不等式的解集是______________。
2、如图,数轴上所表示的关于x 的不等式的解集是______________。
3、不等式x ≤3的非负数解是___________________________________。
4、在5,6,7,8,9,10中,使不等式2x+1≥15成立的数是____________________。
5、将不等式x>-4.5的解集在数轴上表示出来,并写出这个不等式的所有负整数解。
35353535-3 (2题)2(1。
