宁夏2013年高考试卷理科数学试题采用
宁夏银川市第二中学2023-2024学年高三下学期级适应性考试二(理科)数学试题

宁夏银川市第二中学2023-2024学年高三下学期级适应性考试二(理科)数学试题一、单选题1.2024年的高考数学将在6月7日下午进行,其中数学有12道单项选择题,如果每道选择题的答案是从A ,B ,C ,D 四个选项中随机生成,那么请你运用概率统计的知识,推断分析下列哪个选项最有可能成为2024年高考数学选择题的答案分布( ) A .AAAAAAAAAAAA B .ABCDABCDABCD C .CDABACADCBDBD .DBCCCDCDBDBD2.在复数集中,我们把实部与实部相等,虚部与虚部互为相反数的一对具有孪生关系的复数记为z 和z ,他们也是实系数一元二次方程(0a ≠)在判别式小于0时的两个复数根,我们将这种关系定义为共( ) A .额B .呃C .扼D .轭3.已知命题:,sin 1p x x ∃∈<R ﹔命题:q x ∀∈R ﹐||e 1x ≥,则下列命题中为真命题的是( ) A .p q ∧B .p q ⌝∧C .p q ∧⌝D .()p q ⌝∨4.设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ l ⊥于Q ,则线段FQ 的垂直平分线( ). A .经过点O B .经过点P C .平行于直线OPD .垂直于直线OP5.“实数a ,b ,c 成等比数列”是“2b ac =”的( ) A .充分不必要条件 B .充要条件C .必要不充分条件D .既不充分也不必要条件6.已知,x y R ∈,且0x y >>,则A .110x y ->B .sin sin 0x y ->C .11()()022x y -<D .ln ln 0x y +>7.今年两会期间,“新质生产力”被列为了2024年政府工作十大任务之首.某中学为了让高三同学对“新质生产力”有更多的了解,利用周五下午课外活动时间同时开设了四场有关“新质生产力”方面的公益讲座.已知甲、乙、丙、丁四位同学从中一共选择两场去学习,则甲、乙两人不参加同一个讲座的不同方法共有( ) A .48种B . 84种C .24种D .12种8.根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN最接近的是 (参考数据:lg3≈0.48) A .1033 B .1053 C .1073D .10939.从区间[]0,1随机抽取2n 个数1x ,2x ,…,n x ,1y ,2y ,…,n y ,构成n 个数对()11,x y ,()22,x y ,…,(),n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为 A .4n mB .2n mC .4mnD .2mn10.如图,已知12,F F 为双曲线22221x y a b-=的焦点,过2F 作垂直于x 轴的直线交双曲线于点P ,且1230PF F ∠=︒,则双曲线得渐近线方程为( )A .y x =±B .y =C .y =D .2y x =±11.已知数列{}n a 满足1214a a ==,,n 2134n n a a a +++=,则下列是等比数列的是( )A .{3}n a +B .{3}n a -C .{}n 1n a a ++D .{}n 1n a a +-12.袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则A .乙盒中黑球不多于丙盒中黑球B .乙盒中红球与丙盒中黑球一样多C .乙盒中红球不多于丙盒中红球D .乙盒中黑球与丙盒中红球一样多二、填空题13.设,a b r r 为单位向量,且||1a b +=r r ,则||a b -=rr .14.tan20tan40tan40︒+︒︒︒= 15.若()1ln 1f x a b x++-=是奇函数,则b =. 16.函数()log (1)x a f x a x a =->有两个零点,求a 的范围三、解答题17.如图,在山脚A 测得山顶P 的仰角为α,沿倾斜角为β的斜坡向上走a 米到B ,在B 出测得山顶P 得仰角为γ,(1)若15β︒=,求坡面的坡比.(坡比是坡面的垂直高度与水平宽度的比值) (2)求证;山高sin sin()sin()a h αγβγα-=-18.一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n .如果n =3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n =4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为12,且各件产品是否为优质品相互独立(1)求这批产品通过检验的概率;(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X (单位:元),求X 的分布列.19.如图,菱形ABCD 的对角线AC 与BD 交于点,5,6O AB AC ==,点,E F 分别在,AD CD 上,5,4AE CF EF ==交BD 于点H ,将DEF ∆沿EF 折到D EF '∆位置,OD '(1)证明:D H '⊥平面ABCD ; (2)求二面角B D A C '--的正弦值.20.已知函数2()12f x x =-.(Ⅰ)求曲线()y f x =的斜率等于2-的切线方程;(Ⅱ)设曲线()y f x =在点(,())t f t 处的切线与坐标轴围成的三角形的面积为()S t ,求()S t 的最小值.21.已知椭圆2222:1x y C a b+=过点(2,1)A --,且2a b =.(Ⅰ)求椭圆C 的方程:(Ⅱ)过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q .求||||PB BQ 的值. 22.在直角坐标系xOy 中,曲线C 的参数方程为22223x t t y t t ⎧=--⎨=-+⎩(t 为参数且t ≠1),C 与坐标轴交于A ,B 两点. (1)求|AB |:(2)以坐标原点O 为极点,x 轴正半轴为极轴建立极坐标系,求分别以OA ,OB 为直径的圆的极坐标方程.23.已知a ,b ,c 为正数,且满足abc =1.证明:(1)222111a b c a b c++≤++;(2)333()()()24a b b c c a +++≥++.。
新课标高考理科数学试卷分析

新课标高考理科数学试卷分析一.题型、题量全卷包括第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷为选择题。
第Ⅱ卷为非选择题。
考试时间为120分钟,总分为150分。
试题分选择题、填空题和解答题.其中,选择题有12个小题,每题5分,共计60分;填空题有4个小题,每题5分,共计20分;解答题有8个题,其中第17题~21题各12分,第22~24题(各10分)选考一题内容分别为选修4—1(几何选讲)、选修4-4(坐标系与参数方程)、4-5(不等式选讲),共计70分.全部试题都要求在答题卡上作答.题型、题量同教育部考试中心近几年命制的新高考数学理科卷相同。
二。
试题考查内容试题内容与考试要求都与2012年新课程高考《考试大纲》的考试内容与要求相吻合,考查的知识内容与方法分布与高中数学新课标和考试大纲所规定的相同.三.试题考查的知识和方法四. 2012年新课标高考理科数学试卷分析2012年全国新课标理科数学试卷突出主干、强化综合;突出应用、体现创新;强化思想、能力立意。
总体难度高于近几年全国新课标卷,平均分将明显下降,对2012年首次参加新课标高考的省份是一个不小的打击,试卷是否会是新课标卷的一个分水岭,值得思考。
(一)、小题综合、难度上升。
相比近几年新课标卷,小题更趋综合,难度提升,基本没有送分题,没有稳定情绪的题目.1、选择题部分。
第1题考查集合,就有一定难度,要求学生对集合语言有一定的理解,更要求学生具有一定的实际操作能力;第2题考查排列组合分配问题,这是教学的一个难点,学生多有恐惧心理,位置太靠前,造成学生一定心理负担,影响全卷解答,试题排列顺序值得商榷;第3题考查复数,结合命题真假命制,题目简单,有创新;第5题考查等比数例性质与运算,要求学生运算能力强、有方程思想;第六题考查程序框图,字母较多、结构复杂,难度相比往年上升一档;第8题考查解析几何,双曲线与抛物线综合,要求学生概念清楚,综合能力强;第11题考查立体几何,三棱锥外接球问题,空间想象能力要求非常高,难度高于往年相同位置的题目;第12题考查指对函数,可结合反函数的思想,利用导数的几何意义进行求解,显然,这部分超出了课标与考纲对反函数知识的要求;2、填空题部分。
宁夏2013年高考试卷理科数学试题

绝密★启用前宁夏2013年高考试卷理科数学试题采用:新课标卷I2013年普通高等学校招生全国统一考试(新课标Ⅰ卷)数学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x+1)2 < 4,x∈R},N={-1,0,1,2,3},则M∩N=()(A){0,1,2}(B){-1,0,1,2}(C){-1,0,2,3} (D){0,1,2,3}(2)设复数z满足(1-i)z=2 i,则z= ()(A)-1+i (B)-1-i (C)1+i (D)1-i(3)等比数列{a n}的前n项和为S n,已知S3= a2 +10a1 ,a5 = 9,则a1= ()(A)(B)-(C)(D)-(4)已知m,n为异面直线,m⊥平面α,n⊥平面β。
直线l满足l ⊥m,l ⊥n,l β,则()(A)α∥β且l ∥α(B)α⊥β且l⊥β(C)α与β相交,且交线垂直于l (D)α与β相交,且交线平行于l(5)已知(1+ɑx)(1+x)5的展开式中x2的系数为5,则ɑ=(A)-4 (B)-3 (C)-2 (D)-1(7)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(1,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为搞影面,则得到正视图可以为(8)设ɑ=log36,b=log510,c=log714,则(A)c>b>a (B)b>c>ax≥1,x+y≤3,y≥a(x-3).{(C)a>c>b (D)a>b>c(10)已知函数f(x)=x2+αx2+bx+,下列结论中错误的是(A)∑xα∈R f(xα)=0(B)函数y=f(x)的图像是中心对称图形(C)若xα是f(x)的极小值点,则f(x)在区间(-∞,xα)单调递减(D)若xn是f(x)的极值点,则f1(xα)=0(11)设抛物线y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5若以MF为直径的园过点(0,3),则C的方程为(A)y2=4x或y2=8x (B)y2=2x或y2=8x(C)y2=4x或y2=16x (D)y2=2x或y2=16x(12)已知点A(-1,0);B(1,0);C(0,1),直线y=ax+b(a> 0)将△ABC分割为面积相等的两部分,则b的取值范围是(A)(0,1)(B)(1- ,1/2)( C)(1- ,1/3)(D)[ 1/3, 1/2)第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2024年宁夏高考语文试题及答案

2024年宁夏高考语文试题及答案本试卷满分150分,考试时间150分钟。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成下面小题。
2019年4月23日,习近平主席在会见应邀出席中国人民解放军海军成立70周年多国海军活动的外方代表团团长时指出:“海洋对于人类社会生存和发展具有重要意义。
海洋孕育了生命、联通了世界、促进了发展。
我们人类居住的这个蓝色星球,不是被海洋分割成了各个孤岛,而是被海洋连结成了命运共同体,各国人民安危与共。
”作为“人类命运共同体”的重要组成部分,海洋命运共同体的建设目标是打造一个持久和平、普遍安全、共同繁荣、开放包容、清洁美丽的海洋环境。
要实现海洋的持久和平与普遍安全,各国必须摒弃传统的大国争霸思路,充分照顾彼此的安全关切和合理利益,联合起来打击海盗、人口走私、贩毒等海上犯罪行为,在涉及海洋权益争端时通过友好协商的方式来解决问题,短期内无法协商的问题可以考虑搁置争议。
共同繁荣、开放包容和清洁美丽的愿景意味着,我们要坚持开放的自由贸易体系,同时共同应对气候变化、海洋环境保护等问题,发挥海洋作为国际贸易大通道的积极作用,关注发展中国家的发展诉求。
随着人类技术水平的提升和各国经济发展对资源需求的日益增加,各国都希望开发利用更多的海洋资源。
如何才能在更好地利用海洋资源的同时又促进可持续发展、构建海洋命运共同体?习近平总书记提出海洋发展的“四个转变”:“要提高海洋资源开发能力,着力推动海洋经济向质量效益型转变”;“要保护海洋生态环境,着力推动海洋开发方式向循环利用型转变”;“要发展海洋科学技术,着力推动海洋科技向创新引领型转变”;“要维护国家海洋权益,着力推动海洋维权向统筹兼顾型转变”。
这为海洋开发利用指明了方向。
具体到全球、地区和双边层面,构建海洋命运共同体应该着眼于不同的路径,这样才更具有可行性。
在全球层面,构建海洋命运共同体主要着眼于涉海全球公共问题的治理,各国应致力于构建更加公正合理、稳定有效的国际法和国际规则体系。
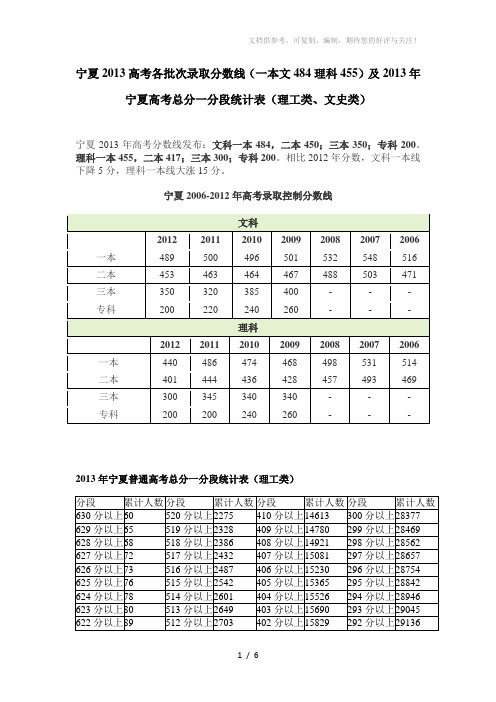
宁夏2013高考各批次录取分数线(一本文484理科455)及2013年宁夏高考总分一分段统计表(理工
427分以上
12057
317分以上
26696
207分以上
34741
536分以上
1598
426分以上
12201
316分以上
26798
206分以上
34773
535分以上
1636
425分以上
12338
315分以上
26889
205分以上
34797
534分以上
1682
424分以上
12474
314分以上
622分以上
89
512分以上
2703
402分以上
15829
292分以上
29136
621分以上
97
511分以上
2755
401分以上
15962
291分以上
29240
620分以上
104
510分以上
2807
400分以上
16097
290分以上
29338
619分以上
109
509分以上
2878
399分以上
16272
306分以上
27812
525分以上
2044
415分以上
13861
305分以上
27896
524分以上
2083
414分以上
14027
304分以上
27999
523分以上
2121
413分以上
14164
303分以上
28098
522分以上
2167
412分以上
14288
302分以上
28189
521分以上
宁夏中卫市(新版)2024高考数学部编版测试(综合卷)完整试卷

宁夏中卫市(新版)2024高考数学部编版测试(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知关于的方程且有两个不等实根,则实数的取值范围是()A.B.C.D.第(2)题已知等差数列的前n项和为,且,,若对于任意的,不等式恒成立,则实数x可能为()A.B.0C.1D.2第(3)题已知函数()在区间上单调递增,若存在唯一的实数,使得,则的取值范围是()A.B.C.D.第(4)题设,则()A.B.C.2D.5第(5)题北宋科学家沈括在《梦溪笔谈》中记载了“隙积术”,提出长方台形垛积的一般求和公式.如图,由大小相同的小球堆成的一个长方台形垛积的第一层有个小球,第二层有个小球,第三层有个小球……依此类推,最底层有个小球,共有层,由“隙积术”可得这些小球的总个数为若由小球堆成的某个长方台形垛积共8层,小球总个数为240,则该垛积的第一层的小球个数为()A.1B.2C.3D.4第(6)题角为第三象限角的充要条件是()A.B.C.D.第(7)题已知,记表示不超过的最大整数,如,则的值域为()A.B.C.D.第(8)题将函数的图象向右平移个单位长度,再将图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到的图象,则()A.B.是图象的一条对称轴,C .是图象的一个对称中心D.在上的最大值为二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题如图,在四棱锥中,底面是边长为2的正方形,底面交于点O,M是棱上的动点,则()A.三棱锥体积的最大值为B.存在点M,使平面C.点M到平面的距离与点M到平面的距离之和为定值D.存在点M,使直线与所成的角为第(2)题将一组数据从小到大排列为:,中位数和平均数均为a,方差为,从中去掉第6项,从小到大排列为:,方差为,则下列说法中一定正确的是()A.B.的中位数为aC.的平均数为a D.第(3)题已知函数的定义域为,且,,则()A.B.为奇函数C.3是函数的周期D.三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题在平面四边形中,,,,,,,若点M为边上的动点,则的最小值为________.第(2)题斜率为的直线过抛物线的焦点,且与交于,两点,若,则______,为坐标原点)的面积为_______.第(3)题已知满足,则的最小值为____________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知函数.(1)求不等式的解集;(2)若对任意的实数,都有成立,求的取值取值范围;第(2)题如图,在四棱锥中,底面是直角梯形,,平面,点是线段上靠近的三等分点,.(1)求证:是直角三角形;(2)若,与平面所成角的正弦值为,求的值.第(3)题已知动点在上,过作轴的垂线,垂足为,若为中点.(1)求点的轨迹方程;(2)过作直线交的轨迹于、两点,并且交轴于点.若,,求证:为定值.第(4)题在中,,,分别是角,,所对的边,点在边上,且满足,.(1)求的值;(2)若,求.第(5)题已知函数.(1)记函数,求函数的极大值点;(2)记函数,讨论函数的零点个数.。
新课标全国统考区(宁夏、吉林、黑龙江)高三数学 名校最新试题精选(一)分类汇编6 不等式 理

一、选择题 1 .(宁夏银川一中2013届高三第二次模拟数学(理)试题)已知函数y =f (x )是定义在R 上的增函数,函数y =f (x -1)的图象关于点(1,0)对称,若任意的x ,y ∈R ,不等式f (x 2-6x +21)+f (y 2-8y )<0恒成立,则当x >3时,x 2+y 2的取值范围是 ( ) A .(3,7) B .(9,25) C .(13,49) D .(9,49) 2 .(宁夏银川一中2013届高三第二次模拟数学(理)试题)已知正数x ,y 满足⎩⎨⎧≥+-≤-05302y x y x ,则y x z )21(4⋅=-的最小值为( )A .1B .3241C .161 D .3213 .(宁夏银川市育才中学2013届高三第五次月考数学(理)试题 )△ABC 满足23AB AC ⋅=,∠BAC=30°,设M 是△ABC 内的一点(不在边界上),定义f(M)=(x,y,z),其中x,y,z 分别表示△MBC,△MCA,△MAB 的面积,若f(M)=(x,y,12),则14x y +的最小值为( )A .9B .8C .18D .164 .(宁夏银川二中2013届高三第六次月考数学(理)试题)设两个正数满足1x y +=,则49x y+的最小值为( )A .24B .26C .25D .15 .(吉林省实验中学2013年高三下学期第一次模拟考试数学(理)试题)已知32()69f x x x x abc =-+-,a b c <<,且()()()0f a f b f c ===. 现给出如下结论:①(0)(1)0f f >; ②(0)(1)0f f <; ③(0)(3)0f f >; ④(0)(3)0f f <; ⑤4abc <; ⑥4abc >.其中正确结论的序号是 ( )A .①③⑤B .①④⑥C .②③⑤D .②④⑥6 .(吉林省吉林市普通中学2013届高三下学期期中复习检测数学(理)试题)不等式2log 0a x x -<在1(0,)2x ∈时恒成立,则a 的取值范围是( )A .1116a ≤< B .01a << C .1a > D .1016a <≤7 .(吉林省2013年高三复习质量监测数学(理)试题)设x,y 满足约束条件⎪⎩⎪⎨⎧≥≥-≤--,0,0,023y y x y x 则z=-2x+y的最小值为( )A .-34B .-1C .0D .18 .(黑龙江省教研联合体2013届高三第一次模拟考试数学(理)试题 )设函数1()f x x x=-,对任意[1,),()()0x f mx mf x ∈+∞+<恒成立,则实数m 的取值范围是( )A .(1,1)-B .,0m R m ∈≠C .--∞(,1)D .--∞(,1)或+∞(1,)9 .(黑龙江省哈尔滨市六校2013届高三第一次联考理科数学试题 )实数对(x,y)满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩则目标函数z=kx-y 当且仅当x=3,y=1时取最大值,则k 的取值范围是 ( ) A .[)1,1,2⎛⎫-∞-+∞ ⎪⎝⎭B .1,|2⎛⎫-+∞ ⎪⎝⎭C .1.12⎛⎫- ⎪⎝⎭D .(],1-∞-10.(黑龙江哈尔滨市九中2013届高三第五次月考数学(理)试题)若()224ln f x x x x =--,不等式()'0f x >的解集为p ,关于x 的不等式2(1)0x a x a +-->的解集记为q ,已知p 是q 的充分不必要条件,则实数a 的取值范围是 ( )A .(]2,1--B .[]2,1--C .φD .[)2,-+∞二、填空题11.(宁夏育才中学2013届高三第一次模拟考试数学(理)试题)当实数,x y 满足约束条件{220x y x x y a ≥≤++≤ (a 为常数)时3z x y =+有最大值为12,则实数a 的值为___12.(吉林省延边州2013届高三高考复习质量检测数学(理)试题)设函数b ax x x f ++=2)(,且方程0)(=x f 在区间()1,0和()2,1上各有一解,则b a -2的取值范围用区间表示为________________.13.(吉林省实验中学2013年高三下学期第一次模拟考试数学(理)试题)已知x ,y 为正实数 ,且满足3x y xy ++=,若对任意满足条件的x ,y ,都有2()()10x y a x y +-++≥恒成立,则实数a 的取值范围为_______________.14.(吉林省实验中学2013年高三下学期第一次模拟考试数学(理)试题)设x ,y 满足约束条件112210x y x x y ⎧⎪⎪⎨⎪+⎪⎩≥≥≤,向量(2)(11)a b y x m =-=-,,,,且a ∥b ,则m 的最小值为_________________.15.(黑龙江省教研联合体2013届高三第二次模拟考试数学(理)试题(word 版,含答案) )“求方程34()()155x x +=的解”有如下解题思路:设34()()()55x x f x =+,则()f x 在R 上单调递减,且(2)1f =,所以原方程有唯一解2x =.类比上述解题思路,不等式632(2)(2)x x x x -+>+-的解集为____ 16.(黑龙江省哈三中等四校联考2012届四校联考第三次高考模拟考试数学(理)试题)已知y x ,满足条件⎪⎩⎪⎨⎧≤-+≥+-≥.052,02,0y x y x x 则y x z 3+=的最大值是____________ 17.(黑龙江省大庆实验中学2013届高三下学期开学考试数学(理)试题)若A 为不等式组002x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域,则当a 从-2连续变化到1时,动直线x y a += 扫过A 中的那部分区域的面积为 ____________.18.(黑龙江哈尔滨市九中2013届高三第五次月考数学(理)试题)若在不等式组02y x x x y ≥⎧⎪≥⎨⎪+≤⎩所确定的平面区域内任取一点(),P x y ,则点P 的坐标满足221x y +≤的概率是__________________.19.(2013年宁夏回族自治区石嘴山市高三第一次联考理科数学试题)已知变量x 、y 满足202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则41log (24)2u x y =+++的最大值为__________.【精品推荐】新课标全国统考区(宁夏、吉林、黑龙江)2013届高三名校理科最新试题精选(一)分类汇编6:不等式参考答案一、选择题 1. C 2. C3. C4. C5. C6. A7. A8. C9. C 10. D二、填空题 11. -12 12. ()2,8-- 13. 37(,]6-∞ 14. -615. ),2()1,(+∞⋃--∞ 16. 10 17.7418.;8π19. 2。
宁夏2013年高考语文试题及答案

2013年普通高等学校招生全国统一考试语文注意事项:1. 本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
第Ⅰ卷1至8页,第Ⅱ卷9至10页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题老子其人其书的时代,自司马迁《史记》以来只有异说,清代学者崇尚考据,对此议论纷纷,如汪中作《老子考异》,力主老子为战国时人,益启争端。
钱穆先生说:“老子伪迹不彰,真相大白,则先秦诸子学术思想之系统条贯始终不明,其源流派别终无可言.”大家都期待这个问题有新的解决线索.过去对于古书真伪及年代的讨论,只能以材料证明纸上材料,没有其它的衡量标准,因而难有定论。
用来印证《老子》的古书,大多收到辨伪家的怀疑,年代确不可移的,恐怕要数到《林非子》。
《吕氏春秋》和《淮南子》,但这几木书戍书太晚,没有多少作用.近年战国秦汉简帛侠籍大黄出上,为学术界提供了许多前所未见的地下材料,这使我们有可能重新考虑《老子》的时代问题。
1973牛长沙马王堆三亏汉基出土的串书,内有《老子》两种版本,甲本字体比较早,不避汉高祖讳,应抄写于高祖即帝位前,乙本避高祖讳,可以抄写于文帝初。
这两本《老子》抄写年代都晚,无益于《老子》著作年代的推定,但乙本前面有《黄帝书》四篇,系。
黄”、“老”合抄之本,则从根本上改变了学术界对早期道家的认识。
郭沐若先生曾指出,道家都是以“发明黄老道德意”为其指归,故也可称之为黄老学派.《老子》和《黄帝书》是道家的经典,在汉初被妙写在《老子》前面的《黄帝书》显然在当时公众心目中已据有崇高位置,不会是刚刚撰就的作品。
同时,《黄帝书》与《申子》、《慎子》、《韩非子》等有许多共通文句,而申不害、慎到、韩非二人均曾学黄老之术,这些共通之处可认作对《皇帝书》的引用阐发。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁夏2013年高考试卷理科数学试题采用:新课标卷I
数学(理科)
第Ⅰ卷(选择题共50分)
一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x+1)2 < 4,x∈R},N={-1,0,1,2,3},则M∩N= ()
(A){0,1,2}(B){-1,0,1,2}(C){-1,0,2,3} (D){0,1,2,3} (2)设复数z满足(1-i)z=2 i,则z= ()
(A)-1+i (B)-1-i (C)1+i (D)1-i (3)等比数列{a n}的前n项和为S n,已知S3 = a2 +10a1 ,a5 = 9,则a1= ()
(A)(B)- (C)(D)-
(4)已知m,n为异面直线,m⊥平面α,n⊥平面β。
直线l满足l ⊥m,l ⊥n,l β,则()
(A)α∥β且l ∥α(B)α⊥β且l⊥β
(C)α与β相交,且交线垂直于l (D)α与β相交,且交线平行于l
(5)已知(1+ɑx)(1+x)5的展开式中x2的系数为5,则ɑ=(A)-4 (B)-3 (C)-2 (D)-1
(7)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(1,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为搞影面,则得到正视图可以为
(8)设ɑ=log36,b=log510,c=log714,则
(A)c>b>a (B)b>c>a
x≥1,
x+y≤3,
y≥a(x-3).
{
(C)a>c>b (D)a>b>c
(10)已知函数f(x)=x2+αx2+bx+,下列结论中错误的是(A)∑xα∈R f(xα)=0
(B)函数y=f(x)的图像是中心对称图形
(C)若xα是f(x)的极小值点,则f(x)在区间(-∞,xα)单调递减
(D)若xn是f(x)的极值点,则f1(xα)=0
(11)设抛物线y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5若以MF为直径的园过点(0,3),则C的方程为
(A)y2=4x或y2=8x (B)y2=2x或y2=8x
(C)y2=4x或y2=16x (D)y2=2x或y2=16x
(12)已知点A(-1,0);B(1,0);C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是(A)(0,1)(B)(1- ,1/2)( C)(1- ,1/3)(D)[ 1/3, 1/2)
二、填空题:本大题共4小题,每小题5分。
(13)已知正方形ABCD的边长为2,E为CD的中点,则
=_______.
(14)从n个正整数1,2,…,n中任意取出两个不同的数,若取出的两数之和等于5的概率为,则n=________. (15)设θ为第二象限角,若tan(θ+ )= ,则
sinθ+conθ=_________.
(16)等差数列{a n}的前n
项和为S n ,已知S10=0,S15
=25,则nS n 的最小值为
________.
三.解答题:解答应写出文
字说明,证明过程或演算步
骤。
(17)(本小题满分12分)
△ABC在内角A、B、C的对边分别为a,b,c,已知
a=bcosC+csinB。
(Ⅰ)求B;
(Ⅱ)若b=2,求△ABC面积的最大值。
(18)如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB= /2AB。
(Ⅰ)证明:BC1//平面A1CD1
(Ⅱ)求二面角D-A1C-E的正弦值
(19)(本小题满分12分)
经销商经销某种农产品,在一个销售季
度内,每售出1t该产品获利润500元,未售
出的产品,没1t亏损300元。
根据历史资料,
得到销售季度内市场需求量的频率分布直方
图,如有图所示。
经销商为下一个销售季度
购进了130t该农产品。
以x(单位:t,
100≤x≤150)表示下一个销售季度内经销该
农产品的利润。
(Ⅰ)将T表示为x的函数
(Ⅱ)根据直方图的需求量分组中,以各组的区间中点值代表改组的各个值求量落入该区间的频率作为需求量取
该区间中点值的概率(例如:若x )则取x=105,且x=105的概率等于需求量落入[100,110]的T的数学期望。
(20)(本小题满分12分)
平面直角坐标系xOy中,过椭圆M:x2/a2+y2/b2=1(a>b>0)
右焦点y- =0交m,f ,A,B两点,P为Ab的中点,且OP的斜率为1/2
(Ι)求M的方程
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形的最大值
(21)(本小题满分12分)
已知函数f(x)=ex-ln(x+m)
(Ι)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(Ⅱ)当m≤2时,证明f(x)>0
请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一部分,做答时请写清题号。
(22)(本小题满分10分)选修4-1几何证明选讲
如图,CD为△ABC外接圆的切线,AB的延长线教直线CD
于点 D,E、F分别为弦AB与弦AC上的点,
且BC-AE=DC-AF,B、E、F、C四点共圆。
(1)证明:CA是△ABC外接
圆的直径;
(2)若DB=BE=EA,求过B、E、
F、C四点的圆
的面积与△ABC外接圆面积
的比值。
(23)(本小题满分10分)选修4——4;坐标系与参数方程已知动点p,Q都在曲线c
x=2cosβ(β为参数)上,对应参数分别为β=α
y=2sinβ
与α=2πM为(①<α<2π)M为PQ的中点。
(Ⅰ)求M的轨迹的参数方程
(Ⅱ)将M到坐标原点的距离d表示为a的函数,并判断M 的轨迹是否过坐标原点。
(24)(本小题满分10分)选修4——5;不等式选讲
设a,b,c均为正数,且a+b+c=Ⅱ,证明:
(Ⅰ)ab+bc+ac小于等于1/3
(Ⅱ)a2/a-b2/b-c/c2≥1。
