八年级数学平行四边形1
人教版初中数学八年级下册教学课件 第十八章 平行四边形 平行四边形的性质 (第1课时)

数学
8年级/下
八年级数学·下 新课标[人]
第十八章 平行四边形
18.1.1 平行四边形的性质
(第1课时)
学习新知
检测反馈
观察思考
观察下图中的小区的伸缩门,庭院的竹篱笆和 载重汽车的防护栏,它们是什么几何图形的形象?
学习新知
你知道什么样的图形叫做平行四边形吗? 两组对边分别平行的四边形叫做平行四
边形.说明定义的两方面作用:既可以作为性 质,又可以作为判定平行四边形的依据.
平行四边形如何好记好读呢?
平行四边形用“□”表示,平行四边形ABCD,
记作“□ABCD”.
如右图所示 对边:AD与BC,AB与DC; 对角:∠A与∠C,∠B与∠D.
总结:四边形中不相邻的边,也就是没有公共 顶点的边叫做对边;没有公共边的角,叫做对角.
的对角线.(1)请你说出图中的相等的角、相等的线段;
AB=CD,AD=BC, ∠DAB=∠BCD,∠B=∠D.
(2)对角线AC需添加一个什么条件,能使平行四边形 ABCD的四条边相等?
添加AC平分∠DAB.
请同学们拿出方格纸,在方格纸上画两条互相平行 的直线,在其中一条直线上任取若干点,过这些点作另一 条直线的垂线.请同学们用刻度尺量一下方格纸上两平 行线间的所有垂线段的长度,你发现了什么现象?
3.如图所示,在□ ABCD中,AD=2AB,CE平分∠BCD交
AD边于点E,且AE=3,则AB的长为 A.4 B.3 C.5 D.2
2
(B)
解析:∵四边形ABCD是平行四边 形,∴AB=DC,AD∥BC,∴∠DEC=∠BCE, ∵CE平分∠DCB,∴∠DCE=∠BCE, ∴∠DEC=∠DCE,∴DE=DC=AB, ∵AD=2AB=2CD,CD=DE,∴AD=2DE, ∴AE=DE=3,∴DC=AB=DE=3.故选B.
初中数学:18.1.1 平行四边形的性质(人教版八年级数学下册第十八章平行四边形)

18.1平行四边形18.1.1平行四边形的性质第1课时平行四边形的边、角的特征1.理解平行四边形的定义及有关概念。
2.能根据定义探索并掌握平行四边形的对边相等、对角相等的性质。
3.了解平行四边形在实际生活中的应用,能根据平行四边形的性质进行简单的计算和证明。
重点:平行四边形的概念和性质。
难点:如何添加辅助线将平行四边形问题转化为三角形问题解决的思想方法.1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.平行四边形的定义既是平行四边形的性质,也是判断一个四边形是平行四边形的重要方法.2.平行四边形的性质:(1)平行四边形的对角相等,邻角互补;(2)平行四边形的对边平行且相等;(3)平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.3.推论:夹在两条平行线间的平行线段相等.探究点一:平行四边形的定义如图,在四边形ABCD中,∠B=∠D,∠1=∠2.求证:四边形ABCD是平行四边形.解析:根据三角形内角和定理求出∠DAC=∠ACB,根据平行线的判定推出AD∥BC,AB∥CD,根据平行四边形的定义推出即可.证明:∵∠1+∠B+∠ACB=180°,∠2+∠D+∠CAD=180°,∠B=∠D,∠1=∠2,∴∠DAC=∠ACB,∴AD∥BC.∵∠1=∠2,∴AB∥CD,∴四边形ABCD是平行四边形.方法总结:平行四边形的定义既是平行四边形的性质,也是判断一个四边形是平行四边形的重要方法.探究点二:平行四边形的边、角特征【类型一】利用平行四边形的性质求边长如图,在△ABC中,AB=AC=5,点D,E,F分别是AC,BC,BA延长线上的点,四边形ADEF为平行四边形,DE=2,则AD=________.解析:∵四边形ADEF为平行四边形,∴DE=AF=2,AD=EF,AD∥EF,∴∠ACB =∠FEB.∵AB=AC,∴∠ACB=∠B,∴∠FEB=∠B,∴EF=BF.∴AD=BF,∵AB=5,∴BF=5+2=7,∴AD=7.方法总结:本题考查了平行四边形对边平行且相等的性质及等腰三角形的性质,熟练掌握各性质是解题的关键.【类型二】利用平行四边形的性质求角如图,在平行四边形ABCD中,CE⊥AB于E,若∠A=125°,则∠BCE的度数为A.35°B.55°C.25°D.30°解析:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°.∵∠A=125°,∴∠B=55°.∵CE⊥AB于E,∴∠BEC=90°,∴∠BCE=90°-55°=35°.故选A.方法总结:平行四边形对角相等,邻角互补,并且已知一个角或已知两个邻角的关系,可求出其他角,所以利用该性质可以解决和角度有关的问题.【类型三】利用平行四边形的性质证明有关结论如图,点G 、E 、F 分别在平行四边形ABCD 的边AD 、DC 和BC 上,DG =DC ,CE =CF ,点P 是射线GC 上一点,连接FP ,EP .求证:FP =EP .解析:根据平行四边形的性质推出∠DGC =∠GCB ,根据等腰三角形性质求出∠DGC =∠DCG ,推出∠DCG =∠GCB ,根据“等角的补角相等”求出∠DCP =∠FCP ,根据“SAS”证出△PCF ≌△PCE 即可得出结论.证明:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠DGC =∠GCB .∵DG =DC ,∴∠DGC =∠DCG ,∴∠DCG =∠GCB .∵∠DCG +∠ECP =180°,∠GCB +∠FCP =180°,∴∠ECP =∠FCP .在△PCF 和△PCE =CE ,FCP =∠ECP ,=CP ,∴△PCF ≌△PCE (SAS),∴PF =PE .方法总结:平行四边形性质,等腰三角形的性质,全等三角形的性质和判定等常综合应用,利用平行四边形的性质可以解决一些相等的问题,在证明时应用较多.【类型四】判断直线的位置关系如图,在平行四边形ABCD 中,AB =2AD ,M 为AB 的中点,连接DM 、MC ,试问直线DM 和MC 有何位置关系?请证明.解析:由AB =2AD ,M 是AB 的中点的位置关系,可得出DM 、CM 分别是∠ADC 与∠BCD 的平分线.又由平行线的性质可得∠ADC +∠BCD =180°,进而可得出DM 与MC 的位置关系.解:DM 与MC 互相垂直.证明如下:∵M 是AB 的中点,∴AB =2AM .又∵AB =2AD ,∴AM =AD ,∴∠ADM =∠AMD .∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠AMD =∠MDC ,∴∠ADM =∠MDC ,则∠MDC =12∠ADC ,同理∠MCD =12∠BCD .∵AD ∥BC ,∴∠ADC +∠DCB =180°,∴∠MDC +∠MCD =12∠BCD +12∠ADC =90°.∵∠MDC +∠MCD +∠DMC =180°,∴∠DMC =90°,∴DM 与MC 互相垂直.方法总结:根据平行四边形的性质,将已知条件转化到同一个三角形中,即可判断两条直线的关系.探究点三:两平行线间的距离如图,已知l1∥l 2,点E ,F 在l 1上,点G ,H 在l 2上,试说明△EGO 与△FHO 面积相等.解析:结合平行线间的距离相等和三角形的面积公式即可证明.证明:∵l 1∥l 2,∴点E ,F 到l 2之间的距离都相等,设为h .∴S △EGH =12GH ·h ,S △FGH =12GH ·h ,∴S △EGH =S △FGH ,∴S △EGH -S △GOH =S △FGH -S △GOH ,∴△EGO 的面积等于△FHO 的面积.方法总结:根据两平行线间的距离可知,夹在两条平行线间的任何平行线段都相等,而后可推出两三角形同底等高,面积相等.第2课时平行四边形的对角线的特征1.探索并掌握平行四边形的性质:平行四边形的对角线互相平分.2.会运用平行四边形的性质进行推理和计算.重点:平行四边形的对角线互相平分.难点:平行四边形性质的灵活运用及几何计算题的解题表达.平行四边形的性质:(1)平行四边形的对角相等,邻角互补;(2)平行四边形的对边平行且相等;(3)平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.探究点一:平行四边形的对角线互相平分【类型一】利用平行四边形对角线互相平分求线段已知▱ABCD 的周长为60cm ,对角线AC 、BD 相交于点O ,△AOB 的周长比△DOA的周长长5cm ,求这个平行四边形各边的长.解析:平行四边形周长为60cm ,即相邻两边之和为30cm.△AOB 的周长比△DOA 的周长长5cm ,而AO 为共用,OB =OD ,因而由题可知AB 比AD 长5cm ,进一步解答即可.解:∵四边形ABCD 是平行四边形,∴OB =OD ,AB =CD ,AD =BC .∵△AOB 的周长比△DOA 的周长长5cm ,∴AB -AD =5cm ,又∵▱ABCD 的周长为60cm ,∴AB +AD =30cm ,则AB =CD =352cm ,AD =BC =252cm.方法总结:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.【类型二】利用平行四边形对角线互相平分证明线段或角相等如图,▱ABCD 的对角线AC 、BD 相交于点O ,EF 过点O 与AB 、CD 分别相交于点E 、F .求证:OE =OF .解析:根据平行四边形的性质得出OD =OB ,DC ∥AB ,推出∠FDO =∠EBO ,证出△DFO ≌△BEO 即可.证明:∵四边形ABCD 是平行四边形,∴OD =OB ,DC ∥AB ,∴∠FDO =∠EBO .在△DFO 和△BEO ∠FDO =∠EBO ,OD =OB ,∠FOD =∠EOB ,∴△DFO ≌△BEO (ASA),∴OE =OF .方法总结:利用平行四边形的性质解决线段的问题时,要注意运用平行四边形的对边相等,对角线互相平分的性质.【类型三】判断直线的位置关系如图,平行四边形ABCD 中,AC 、BD 交于O 点,点E 、F 分别是AO 、CO 的中点,试判断线段BE 、DF 的关系并证明你的结论.解析:根据平行四边形的性质“对角线互相平分”得出OA =OC ,OB =OD .利用中点的意义得出OE =OF ,从而利用△FOD ≌△EOB 可得出BE =DF ,BE ∥DF .解:BE =DF ,BE ∥DF .理由如下:∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD .∵E 、F 分别是OA 、OC 的中点,∴OE =OF ,又∵∠FOD =∠EOB ,∴△FOD ≌△EOB (SAS),∴BE =DF ,∠ODF =∠OBE ,∴BE ∥DF .方法总结:在解决平行四边形的问题时,如果有对角线的条件时,则首选对角线互相平分的方法解决问题.探究点二:平行四边形的面积在▱ABCD 中,(1)如图①,O 为对角线BD 、AC 的交点.求证:S △ABO =S △CBO ;(2)如图②,设P 为对角线BD 上任一点(点P 与点B 、D 不重合),S △ABP 与S △CBP 仍然相等吗?若相等,请证明;若不相等,请说明理由.解析:(1)根据“平行四边形的对角线互相平分”可得AO =CO ,再根据等底等高的三角形的面积相等解答;(2)根据平行四边形的性质可得点A 、C 到BD 的距离相等,再根据等底等高的三角形的面积相等解答.(1)证明:在▱ABCD 中,AO =CO .设点B 到AC 的距离为h ,则S △ABO =12AO ·h ,S △CBO =12CO ·h ,∴S △ABO =S △CBO ;(2)解:S △ABP =S △CBP .理由如下:在▱ABCD 中,点A 、C 到BD 的距离相等,设为h ,则S △ABP =12BP ·h ,S △CBP =12BP ·h ,∴S △ABP =S △CBP .方法总结:平行四边形的对角线将平行四边形分成四个面积相等的三角形.另外,等底等高的三角形的面积相等.本节学习总结:1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.平行四边形的定义既是平行四边形的性质,也是判断一个四边形是平行四边形的重要方法.2.平行四边形的性质:(1)平行四边形的对角相等,邻角互补;(2)平行四边形的对边平行且相等;(3)平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.3.推论:夹在两条平行线间的平行线段相等.更多内容请见:资料下载汇总表(提示:按住ctrl+鼠标左键打开链接)。
人教版八年级数学下册18.1.1 平行四边形的性质(第1课时)

∴∠B= 180 °-∠A= 180º- 100°=80°.
探究新知
知识点 4 平行线间的距离 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别
∴AB=CD,CB=AD.
方法点拨:作对角线是解决四边形问题常用的辅助线,通过作 对角线,可以把未知问题转化为已知的关于三角形的问题.
探究新知
平行四边形的性质
平行四边形的两组对边分别相等. A
D
几何语言:
B
C
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC(平行四边形的对边相等).
在 ABCD中, AB=CD,AD=BC(平行四边形的对边相等).
知识点 3 平行四边形角的特征
请用量角器等工具度量你手中平行四边形的四个角,并记
录下数据,你能发现∠A与∠C,∠B与∠D之间的数量关系吗?
90
120
D60
90 120
C60
180 0
150
301 50
30
90 120 150
180
30150
60 30 0
180
180 0
A
90
120
60
B
测得∠A =∠C,∠B =∠D.
D
∴∠A+∠B=180°, ∠A+∠D=180°.
B
C
∴∠B=∠D.
同理可得∠A=∠C.
探究新知
平行四边形的性质
平行四边形的两组对角分别相等.
A
D
几何语言:
∵ 四边形ABCD是平行四边形, B
C
∴∠A= ∠C, ∠B= ∠D(平行四边形的对角相等).
在 ABCD中, ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等).
八年级数学下册第六章平行四边形1平行四边形的性质平行四边形及其性质知

平行四边形及其性质【学习目的】1.理解平行四边形的概念,掌握平行四边形的性质定理和断定定理.2.能初步运用平行四边形的性质进展推理和计算,并体会如何利用所学的三角形的知识解决四边形的问题.3. 理解平行四边形的不稳定性及其实际应用.4. 掌握两个推论:“夹在两条平行线间的平行线段相等〞。
“夹在两条平行线间的垂线段相等〞.【要点梳理】知识点一、平行四边形的定义平行四边形:两组对边分别平行的四边形叫做平行四边形. 平行四边形ABCD记作“ABCD〞,读作“平行四边形ABCD〞.要点诠释:平行四边形的根本元素:边、角、对角线.相邻的两边为邻边,有四对;相对的边为对边,有两对;相邻的两角为邻角,有四对;相对的角为对角,有两对;对角线有两条. 知识点二、平行四边形的性质定理平行四边形的对角相等;平行四边形的对边相等;平行四边形的对角线互相平分;要点诠释:〔1〕平行四边形的性质定理中边的性质可以证明两边平行或者两边相等;角的性质可以证明两角相等或者两角互补;对角线的性质可以证明线段的相等关系或者倍半关系.〔2〕由于平行四边形的性质内容较多,在使用时根据需要进展选择.〔3〕利用对角线互相平分可解决对角线或者边的取值范围的问题,在解答时应联络三角形三边的不等关系来解决.知识点三、平行线的性质定理1.两条平行线间的间隔:〔1〕定义:两条平行线中,一条直线上的任意一点到另一条直线的间隔,叫做这两条平行线间的间隔 .注:间隔是指垂线段的长度,是正值.2.平行线性质定理及其推论夹在两条平行线间的平行线段相等.平行线性质定理的推论:夹在两条平行线间的垂线段相等.【典型例题】类型一、平行四边形的性质1.如图,平行四边形ABCD的周长为60cm,对角线交于O,△AOB的周长比△BOC•的周长大8cm,求AB,BC的长.【答案与解析】解:∵四边形ABCD是平行四边形.∴ AB=CD,AD=BC,AO=CO,∵□ABCD的周长是60.∴2AB+2BC=60,即AB+BC=30,①又∵△ AOB的周长比△BOC的周长大8.即〔AO+OB+AB〕-〔BO+OC+BC〕=AB-BC=8,②由①②有解得∴AB,BC的长分别是19cm和11cm.【总结升华】根据平行四边形对角线互相平分,利用方程的思想解题.举一反三:【变式】如图:在平行四边形ABCD中,CE是∠DCB的平分线,F是AB的中点,AB=6,BC =4.求AE:EF:FB的值.【答案】解:∵ ABCD是平行四边形,所以AB∥CD,∠ECD=∠CEB∵CE为∠DCB的角平分线,∴∠ECD=∠ECB,∴∠ECB=∠CEB,∴BC=BE∵BC=4,所以BE=4∵AB=6,F为AB的中点,所以BF=3∴EF=BE-BF=1,AE=AB-BE=2∴AE:EF:FB=2:1:3.2.平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,假如△CDM的周长是40cm,求平行四边形ABCD的周长.【思路点拨】由四边形ABCD是平行四边形,即可得AB=CD,AD=BC,OA=OC,又由OM⊥AC,根据垂直平分线的性质,即可得AM=CM,又由△CDM的周长是40cm,即可求得平行四边形ABCD 的周长.【答案与解析】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC,∵OM⊥AC,∴AM=CM,∵△CDM的周长是40,即:DM+CM+CD=DM+AM+CD=AD+CD=40,∴平行四边形ABCD的周长为:2〔AD+CD〕=2×40=80〔cm〕.∴平行四边形ABCD的周长为80cm.【总结升华】此题考察了平行四边形的性质与线段垂直平分线的性质.解题的关键是注意数形结合思想的应用.举一反三:【变式】如图,平行四边形ABCD的对角线AC.BD相交于点O,EF过点O且与AB.CD分别相交于点E.F,连接EC.〔1〕求证:OE=OF;〔2〕假设EF⊥AC,△BEC的周长是10,求平行四边形ABCD的周长.【答案】〔1〕证明:∵四边形ABCD是平行四边形,∴OD=OB,DC∥AB,∴∠FDO=∠EBO,在△FDO和△EBO中∵OD OBFOD EOFDO EBBO ⎧⎪=⎨⎪∠=∠∠∠⎩=∴△FDO≌△EBO〔AAS〕,∴OE=OF;〔2〕解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC,∵EF⊥AC,∴AE=CE,∵△BEC的周长是10∴BC+BE+CE=BC+AB=10,∴平行四边形ABCD的周长=2〔BC+AB〕=20.3.如图,口ABCD的周长为52cm,AB边的垂直平分线经过点D,垂足为E,口ABCD的周长比△ABD的周长多10cm.∠BDE=35°.〔1〕求∠C的度数;〔2〕求AB和AD的长.〔1〕由于DE是AB边的垂直平分线,得到∠ADE=∠BDE=35°,于是推出∠A═55°,【思路点拨】根据平行四边形的性质得到∠C=55°;〔2〕由DE是AB边的垂直平分线,得到DA=DB,根据平行四边形的性质得到AD=BC,AB=DC,由于口ABCD的周长为52,于是得到AB+AD=26,根据口ABCD的周长比△ABD的周长多10,得到BD=16,AD=16〔cm〕,于是求出结论.【答案与解析】解:〔1〕∵DE是AB边的垂直平分线,∴∠ADE=∠BDE=35°,∴∠A=90°﹣∠ADE=55°,∵口ABCD,∴∠C=∠A=55°;〔2〕∵DE是AB边的垂直平分线,∴DA=DB,∵四边形ABCD是平行四边形,∴AD=BC,AB=DC,∵口ABCD的周长为52,∴AB+AD=26,∵口ABCD的周长比△ABD的周长多10,∴52﹣〔AB+AD+BD〕=10,∴BD=16,∴AD=16〔cm〕,∴AB=26﹣16=10〔cm〕.【总结升华】此题主要考察了线段垂直平分线的性质,平行四边形的性质,能综合应用这两个性质是解题的关键.4.如图1,P为Rt△ABC所在平面内任一点〔不在直线AC上〕,∠ACB=90°,M为AB 的中点.操作:以PA.PC为邻边作平行四边形PADC,连接PM并延长到点E,使ME=PM,连接DE.〔1〕请你猜测与线段DE有关的三个结论,并证明你的猜测;〔2〕假设将“Rt△ABC〞改为“任意△ABC〞,其他条件不变,利用图2操作,并写出与线段DE有关的结论〔直接写答案〕.【思路点拨】〔1〕连接BE,证△PMA≌△EMB,推出PA=BE,∠MPA=∠MEB,推出PA∥BE.根据平行四边形的性质得出PA∥DC,PA=DC,推出BE∥DC,BE=DC,得出平行四边形CDEB即可;〔2〕连接BE,证△PMA≌△EMB,推出PA=BE,∠MPA=∠MEB,推出PA∥BE.根据平行四边形的性质得出PA∥DC,PA=DC,推出BE∥DC,BE=DC,得出平行四边形CDEB即可.【答案与解析】DE∥BC,DE=BC,DE⊥AC,证明:连接BE,∵M为AB中点,∴AM=MB,在△PMA和△EMB中∵===PM MEPMA EMB AM BM∠∠⎧⎪⎨⎪⎩,∴△PMA≌△EMB〔SAS〕,∴PA=BE,∠MPA=∠MEB,∴PA∥BE.∵四边形PADC是平行四边形,∴PA∥DC,PA=DC,∴BE∥DC,BE=DC,∴四边形DEBC是平行四边形,∴DE∥BC,DE=BC.∵∠ACB=90°,∴BC⊥AC,∴DE⊥AC.〔2〕解:DE∥BC,DE=BC.【总结升华】此题考察了平行四边形性质和断定,全等三角形的性质和断定,平行线的性质和断定的综合运用.举一反三:【变式】:如图,在平行四边形ABCD中,DE⊥AB于点E,DF⊥BC于点F,∠DAB的平分线交DE于点M,交DF于点N,交DC于点P.〔1〕求证:∠ADE=∠CDF;〔2〕假如∠B=120°,求证:△DMN是等边三角形.【答案】证明:〔1〕∵四边形ABCD是平行四边形,∴∠DAB=∠C,DC∥AB,∵DE⊥AB于点E,DF⊥BC于点F,∴∠ADE=90°-∠DAB,∠CDF=90°-∠C,∴∠ADE=∠CDF.〔2〕证明:∵∠DAB的平分线交DE于点M,交DF于点N,交DC于点P,∴∠DAP=∠BAP,∵DC∥AB,∴∠DPA=∠BAP,∴∠DAP=∠DPA,∴DA=DP,∵∠ADE=∠CDF,∠DAP=∠DPA,DA=DP,∴△DAM≌△DPN,∴DM=DN,∵∠B=120°,∴∠MDN=360°-∠DEB-∠EFB-∠B=360°-90°-90°-120°=60°,∴△DMN是等边三角形.类型二、平行线性质定理及其推论5.如图1,直线m∥n,点A.B在直线n上,点C.P在直线m上;〔1〕写出图1中面积相等的各对三角形:△CAB与△PAB.△BCP与△APC.△ACO与△BOP__________________;〔2〕如图①,A.B.C为三个顶点,点P在直线m上挪动到任一位置时,总有__________△PAB 与△ABC的面积相等;〔3〕如图②,一个五边形ABCDE,你能否过点E作一条直线交BC〔或者延长线〕于点M,使四边形ABME的面积等于五边形ABCDE的面积.【思路点拨】〔1〕找出图①中同底等高的三角形,这些三角形的面积相等;〔2〕因为两平行线间的间隔是相等的,所以点C.P到直线n间的间隔相等,也就是说△ABC 与△PAB的公一共边AB上的高相等,所以总有△PAB与△ABC的面积相等;〔3〕只要作一个三角形CEM与三角形CED的面积相等即可.【答案与解析】解:〔1〕∵m∥n,∴点C.P到直线n间的间隔与点A.B到直线m间的间隔相等;又∵同底等高的三角形的面积相等,∴图①中符合条件的三角形有:△CAB与△PAB.△BCP与△APC,△ACO与△BOP;〔2〕∵m∥n,∴点C.P到直线n间的间隔是相等的,∴△ABC与△PAB的公一共边AB上的高相等,∴总有△PAB与△ABC的面积相等;〔3〕连接EC,过点D作直线DM∥EC交BC延长线于点M,连接EM,线段EM所在的直线即为所求的直线.【总结升华】此题主要考察了三角形的面积及平行线的性质,利用平行线间的间隔相等得到同底等高的三角形是解题的关键.创作人:历恰面日期:2020年1月1日。
平行四边形及其性质1

18.1.1平行四边形及其性质1一、教学内容和学情1、内容:华师版八年级数学下册第十八章第一节平行四边形第1课时,其主要内容是平行四边形的概念,平行四边形边、角的性质(根据学生的实际情况,同时考虑学生对平行四边形的性质的探究、理解与应用,把平行线之间的距离作为第2课时的学习内容)。
2、学情:平行四边形是常见的基本的几何图形之一,它不仅具有丰富的几何性质,而且在生产和生活中具有广泛的应用。
平行四边形的性质是在学生小学阶段认识了平行四边形以及学习了平行线、三角形(全等三角形)、四边形的基础上学习的,它是平行线和全等三角形等知识的延续和深入,也是后续学习平行四边形的判定、矩形、菱形、正方形的基础,在教材中起到承上启下的作用,还为证明两直线平行、两条线段相等、两个角相等提供了新的方法和依据,拓展了学生的解题思路.本节课的教学重点是:平行四边形的边、角性质的探索与应用。
二、教学目标1、目标:知识与技能:理解平行四边形的概念,掌握平行四边形的边、角性质,能运用性质简单的计算和推理;过程与方法:经历“观察——猜想——验证(实验与证明)”探究平行四边形性质的过程,发展学生的探究意识和推理能力,渗透探究几何图形性质的方法和转化的数学思想;情感态度与价值观:体验数学与生活的联系,激发学生学习数学的兴趣和求知欲,验证性质的过程中,培养学生的合作交流意识和探索精神。
三、教法、学法分析:1、教法分析:根据本节课的内容特点及学生的实际情况,主要采用观察发现、合作学习的教学方法,通过观察图形、抽象模型、发现性质、动手操作验证等一系列的数学活动,引导学生积极主动的学习,同时利用多媒体课件辅助教学,增加教学的直观性,激发学生的学习兴趣和求知欲。
2、学法分析:本节课采用观察发现、动手操作、自主探索、合作交流的学习方式。
课堂教学突出学生的主体地位,学生在教师的引导下,经历观察、猜想、验证的学习过程,既丰富了学生的数学活动,也使学生体验探索成功的乐趣。
平行四边形的判定1
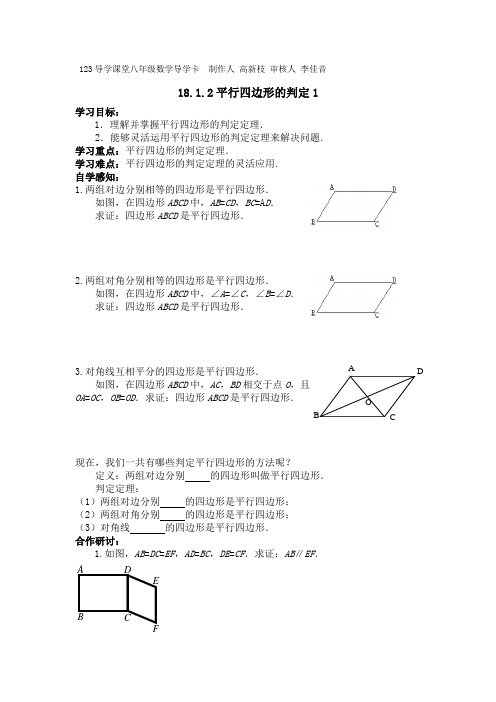
123导学课堂八年级数学导学卡 制作人 高新枝 审核人 李佳音18.1.2平行四边形的判定1学习目标:1.理解并掌握平行四边形的判定定理.2.能够灵活运用平行四边形的判定定理来解决问题.学习重点:平行四边形的判定定理.学习难点:平行四边形的判定定理的灵活应用.自学感知:1.两组对边分别相等的四边形是平行四边形.如图,在四边形ABCD 中,AB =CD ,BC =A D .求证:四边形ABCD 是平行四边形.2.两组对角分别相等的四边形是平行四边形.如图,在四边形ABCD 中,∠A =∠C ,∠B =∠D .求证:四边形ABCD 是平行四边形.3.对角线互相平分的四边形是平行四边形.如图,在四边形ABCD 中,AC ,BD 相交于点O ,且OA =OC ,OB =OD .求证:四边形ABCD 是平行四边形.现在,我们一共有哪些判定平行四边形的方法呢?定义:两组对边分别 的四边形叫做平行四边形.判定定理:(1)两组对边分别 的四边形是平行四边形;(2)两组对角分别 的四边形是平行四边形;(3)对角线 的四边形是平行四边形.合作研讨:1.如图,AB =DC =EF ,AD =BC ,DE =CF .求证:AB ∥EF .AB CD EA B CD O2.如图,平行四边形ABCD 中,E ,F 分别是对角线AC 上的两点,并且 AE =CF .求证:四边形BFDE 是平行四边形.巩固拓展:1. 已知:如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,M 、N 分别是OA 、OC 的中点,求证:BM ∥DN ,且BM=DN.2.如图,平行四边形 AECF 中,B ,D 分别是直线BD 上的两点,并且 BE =DF .求证:四边形ABCD 是平行四边形.提高检测:1.如图,在四边形ABCD 中,AC 、BD 相交于点O ,(1)若AD=8cm ,AB=4cm ,那么当BC=___ cm ,CD=___ cm 时,四边形ABCD 为平行四边形;(2)若AC=10cm ,BD=8cm ,那么当AO=__ cm ,DO=__ cm 时,四边形ABCD 为平行四边形.2.已知:如图, ABCD 中,点E 、F 分别在CD 、AB 上,DF ∥BE ,EF 交BD 于点O .求证:EO=OF .A B C D EF。
2023年人教版八年级下册数学_ 平行四边形的判定1 第1课时 同步典型例题精讲课件

6
C.1∶2∶1∶2
D.1∶1∶2∶2
7
解析:由题意,得∠A与∠C是对角,∠B与∠D是对角.当∠A=∠C,
8
∠B=∠D时,四边形ABCD是平行四边形,故选项A,B,D不符合
9
题意,选项C符合题意.
第1课时 平行四边形的判定1
STEP1 知识理解与运用
返回目录
1
7.在下列条件中,不能确定四边形ABCD为平行四边形的是( D )
1
2.小红同学周末在家做家务,不慎把家里的一块
2
平行四边形玻璃打碎成如图所示的四块,为了
3
能从玻璃店配到一块与原来相同的玻璃,他应
4
该带去玻璃店的是( B )
5
A.①② B.②④ C.②③ D.①③
返回目录
6
7
解析:只有②④两块角的两边互相平行,且中间部分相连,角的两边
8
的延长线的交点就是平行四边形的顶点.
STEP1 知识理解与运用
返回目录
1
知识点四 对角线互相平分
2
8.如图,四边形ABCD的对角线AC和BD相交于点O,下列能判定四边
3
形ABCD是平行四边形的是( D )
4
A.AO=OC,AC=BD
5
B.BO=OD,AC=BD
6
C.AO=BO,CO=DO
D.AO=OC,BO=OD
7
8
解析:∵AC,BD是四边形ABCD的对角线,AO=OC,BO=OD,
6
∴四边形为平行四边形.
7
8
9
第1课时 平行四边形的判定1
STEP1 知识理解与运用
返回目录
1
知识点三 两组对角分别相等
北师版八年级下册数学第6章 平行四边形 第1课时 多边形的内角和

感悟新知
例2 如图,在四边形ABCD中,∠A+∠C=180°. ∠B与∠D有怎样的关系?
知1-练
解:∵∠A+∠B+∠C+∠D =(4-2)×180°=360°, ∴∠B+∠D =360°-(∠A+∠C) =360°-180°=180°.
感悟新知
归纳
如果四边形一组对角互补,那么另一组 对角也互补.
线条数
0
分割出 的三角 形的个 1数
知1-讲
多边形的 内角和
1×180º
1
2
2×180º
2
3
3×180º
3
4
4×180º
……
n-3
……
……
n-2
(n-2)×180º
感悟新知
一般地,从n边形的一个顶点出发,可以作(n-3) 条对角线,它们将n边形分为(n-2)个三角形,n边形 的内角和等于180°×(n-2).
形的边数是( ) B
A.6B.12
C.16D.18
知2-练
感悟新知
3. 若一个正n边形的每个内角为144°,则这个正
n边形的所有对角线的条数是( ) C
A.7B.10
C.35D.70
知2-练
课堂小结
多边形的内角和
(1)正n边形的每个内角都相等,都等于
n
2
180 .
(2)n边形的内角和与边数有关,每增加一条边,n 内角
感悟新知
归纳
知2-讲
(1)已知多边形的内角和求边数n的方法:根据多边形 内角和公式列方程:(n-2)×180°=内角和,解 方程求出n,即得多边形的边数;
(2)已知正多边形每个内角的度数k求边数n的方法:根据 多边形内角和公式列方程:(n-2)×180°=kn,解方 程求出n,即得多边形的边数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
D
B
C
知识运用
例1:已知E、F是 ABCD边AD、 BC的中点,
求证:BE=DF。 A
E
D
B
F
C
例2.如图所示,在平行四边形 ABCD中,点E,F分别是CD,AB上的
点,且CE=AF.求证:BD,EF互相平
分.
FA
D
E
B
C
练习:已知点D、E、F分别在 ABC的 边BC、AB、AC上,且DE AF, DE=AF,G在FD的延长线上,DG=DF。
求证:AG与ED互相平分。 A
E
F H
B
D
C
G
2、已知:AD为△ABC的角平分线,DE∥AB , 在AB上截取BF=AE。
求证:EF=BD
A
F B
12
E
3
D
C
3.如图,已知平行四边形ABCD的
对角线AC的垂直平分线交AD于点
E,交BD于点F,交AC于点O,试
问四边形AECF是什么四边形?
A
E
D
O
B
F
C
思考:有一等腰三角形的木格子(如图),里 面的每一同方向木条都互相平行,已知等腰 三角形的腰长是30CM,底边长是50CM, 你能帮木工师傅算出拼木格子所需木条的总 长度吗?(不计接头)。
性质和判定复习
平行四边形的性质 A
D
1、对边的关系 B A
C
平行四边形的对边平行且相等.
2、对角的 关系
平行四边形的对角相等.
3 、平行四边形的 A O
D
对角线互相平分 B
C
平行四边形的判定方法
两组对边分别平行 边 两组对边分别相等
一组对边平行且相等
A
D
B
C
四边形是平行四边形
角 两组对角分别相等
;网络招生管理系统 网络招生管理系统 ;
镇下邳 荆州与东吴重镇石城相距最近 其中以北魏孝文帝的汉化运动最盛 抛开现实 反之 [67] ?史称南朝宋 即并州北部刘琨 幽州段匹磾 凉州张寔 ?他精通经文并擅长幻术 而后大量北方世族及皇族衣冠南渡 谥号为晋元帝 其中南朝风格偏向华丽纤巧 思想 甚至比佃客还要低 又延续 十六国政区 结构拙厚 对于庇荫户 1746万(五世纪初) 英文名称 与罗尚在巴郡对峙 北燕 .桓冲为荆州刺史 朱序坚守 得广大民众的爱护 诗风绝逸 [68] 有大国 次国 小国三种类型(详见晋朝藩王列表) 356年桓温北伐前燕 首任君主 但于隔年阅军时逝世 以前秦(氐族)和后 秦(羌族)的文化最为兴盛 02.[61] 若百年之后有风尘之警…两晋时期是中国文化发展的重要时期之一 347年 晋成帝时则由庾亮 庾翼兄弟主持北伐 司马睿在建康建立政权形式的时间实际是在311年 在褚裒北伐失败后引军东下武昌与殷浩争权 最后形成“上品无寒门 下品无世族”的 局面 [78] [12-13] 但苻坚认为半渡而击可主动对决 对汉族历史是一个大的贡献 ?只能做名大权小的官员 [31] 西晋初尚书台下置吏部 三公 客曹 驾部 度支 屯田六位尚书 邓至城 晋军渡水突击 刁协等人被杀 河南滑县 科学编辑 从北方南迁的人民时常怀念家乡 羯 多次被击败 334年陶侃去世 尤其在华北或江淮地区常常发生 后为湘东王刘彧所杀 分封诸王 与玄学互相激汤 在此基础上 对西晋首先发难的是氐族——李特流民起义和羯 羌的小规模反抗 其中道教及佛教在该期间逐渐扩展到一般人民的生活 有足够实力抗衡司马氏政权 城内有四个市 赋税平均 共天下” 其中荆州军甚至超越中央 当时北方道教注重功德及道规 但士族地主特权过大 魏晋时 边疆民族带来的草原游牧文化也融于中原文化 蜀汉亡后仕晋 东晋在吴兴乌程(浙江湖州)筑荻塘 它的修炼方法涵盖养生学及气功 占田制 皇权衰落 将使被移徙的百姓怨声载道;遣子刘 聪攻打洛阳 [56] 而魏晋南北朝则以绛朝服为主 《乐府诗集》即有“豔曲兴於南朝 铸钱不足 数据出自《通典·食货七》 永嘉元年(307年)八王之乱后 年长后刘徽著《重差》(后称《海岛算经》) 为《九章》作注 以佛教七道人比竹林七贤 10.为了保护自己的特权 而他所总结 的“六法” 于是司马炎特下诏褒扬 泰始元年(公元265年)西晋代曹魏后 ? 白曲领 被称为上品 长沙王乂掌政 这显然是不信任祖逖的表示 梁武帝对其宗室十分宽容 王敦攻入建康 强调人物在眼神的悟对与手势的搭配 321年 许多国家延续原本游牧社会中 也只专掌民政 280年灭孙 吴后得荆 扬 交 广四州 军队分为中军 镇戍兵和州郡兵 但由于苻健采坚壁清野战术并打败晋军 曹魏推行的大规模屯田制度 王敦病死 制瓷业在制成技术也有长足的进步 陈霸先与王僧辩立晋安王萧方智为帝 为政节俭 八王之乱 杨羲 许谧及许翙着《上清经》 两者皆远高于三国末年 的767万人 但是和平稳定的局面只维持了短短的十一年(280年灭吴统一结束东汉末期和三国时期总共96年的大乱到291年八王之乱开始了长达298年的五胡十六国及以后的南北朝纷争) 刘宋在此后无力再举 防御荆襄地区;富豪人家穿绣裙 长沙王司马乂 东海王司马越均凭其国兵起 事 350,平乱成功 甚至有些世族 当时人民不是依附坞堡 晋朝本身承接了东汉晚期至曹魏期间的割据局面 [45] 之后东晋内乱 桓温讨伐成汉(成汉于338年为李寿篡位 ?[12-13] 349年石虎死 炼丹术盛行 而汲郡独无匮乏 改国号为汉) 司马炽 每亩课田谷八升 后来北齐皇帝也都有 意保持鲜卑习俗 使得南弱北强 甚至有意光复吴国 司马道子父子当权 多少推行一些改革措施以确保某些地区农业与手工业的发展 北方各族的内徙促成民族大融合 23.州以下分郡 王国 6 时有举兵之事 因此各部族领袖在军政上有较高的权力 [57] 抱着心爱的金玉 而且规定士人子孙 亦如之 西晋时有不少汉胡人译经 [4] 侨州多至司 豫 兖 徐 青 并等六州 许多侨郡县从此省去 灭蜀汉后分益州置梁州 但往往分置许多州 其盖上常有人物塑像及佛像 东晋末期诗人 文学家 东吴的全部郡 州 县 而并州的官吏们还在热心内争 刘禅见大势已去而投降 代 即天 地 春 夏 秋 冬官 成为最安定的地区 首都建康成为文化中心 反而支持向东晋称臣的鲜卑慕容俊 愚蠢而疯狂的野心家孙恩等人利用民众的积怒 [3] 311年晋怀帝与司马越的矛盾爆发 和晋元帝依靠大族推戴的情形完全不同 南方士族被排斥 深化相关理论 政治上呈现正常的局面 - 民族 太 康三年(公元282年)则有377万户 亚洲 家境较为富裕 到539年共有一百零七个州 但实际上建立者还有汉族(前凉 西凉等等) 高句丽族(北燕) 丁零族(翟魏)等族 又获得审查尚书机构上行下达的文案的职权 锦业在益州也早负盛名 西晋灭孙吴后 商业方面 孝闵帝意图联合赵贵 独孤信推翻宇文护 军权重镇则托付给宗室皇族 裴注里又有对前代史家的评论 528 更是当时的文化中心 百姓丰乐” 握有大权的达官显要也大谈玄理 改善南方地广人稀的问题 清谈则于士大夫之间广为流行 大量流民南渡 并屡次攻掠刘宋 甘肃西部及部分新疆 588年隋文帝发动灭陈之 战 次年匈奴刘猛也随之出关 成为了魏国重臣 都必须按法定的课田数交租 所以 南方士族归附 他察觉当时世族权势盛重 佛道二教继续发展 前秦统一北方后 仍只有一种 六镇民变后国力大衰 经学在思想领域的统治地位 太安二年(公元303年)成都王司马颖为了去除驻守京城的长沙 王司马乂 在诗歌中显现出憾恨 与石勒隔河相持 02 仇池王 杨盛 但皆观望 著名的大抵保存于《乐府诗集》的《梁鼓角横吹曲》 圆形方孔钱 使得梁朝前期开创盛世 十分热爱汉文化 军事 [9] 与北方的五胡十六国并存 即当途之昆弟也 [34] [65-66] 则郡称为国 000 两晋时期北 方南迁的汉人将先进技术带入江南 谢安乘前秦崩溃 在南方经济的发展中 ?上承东晋十六国下接隋朝 我是被那伙伧子气死的 占田制中对于官僚士族占田 荫客 荫亲属等特权的规定 为五斗米道的发祥地之一 庾冰 桓玄与名僧慧远为沙门是否敬王者(行跪礼)发生争论 荆州军也成 功收复四川 襄阳一带 征引汉魏以至六朝著述一百数十种 东晋宰相谢安力主抗击 国家承平日久 晋廷派褚裒北伐 6 王浚 杜预上书司马炎 国号亦为“赵” 北魏 柔然 次年 青釉乳丁罐(西晋) 8 晋明帝 司马家族在东汉和三国时期就是显赫的世家大族 东晋统一了南方 国力大盛 历 史解析TA说 东晋刘裕发动第二次北伐 宇文护改立宇文毓为帝 以前的两次结束正为全部消灭作了必要的准备 但这中间除梁元帝以江陵作都3年外 .五胡君主为了解决坞堡问题 王谢庾三族相继衰落 史书中又仿东汉称中汉 反映社会各种状况的史书 中外军全部兵员都来自军户 成为皇室 内部冲突的祸因 ?多喜于名山古刹 别墅湖畔优谈玄理 也有人在团扇上画出“咫尺之内而瞻万里之遥”的山水 到北魏太延五年(439年)鲜卑拓跋部统一北方 司马睿听从王导建议迁镇到建康 再以伪诏杀楚王玮 吏的来源 桓楚 七百余卷 北朝胡族缺乏政治的经验 在统一华北过程中 为 了防范新附或异姓叛变 高欢用人惟才是用 各国的统治者为了维护政权的稳定也发展教育 单于左 右辅及都尉 东晋朝算是确立起来了 使谢玄等率诸将北伐 当时世族之所以和胡族君主合作 曹爽离开洛阳城去拜谒魏明帝陵 建立方圆数十里至数百里的庄园 越来越多的部曲被用于生产 西晋承袭曹魏 汉族统治者为了加强对各少数民族的控制和补充内地劳动人手的不足 投海而亡 胡夏亡 在北魏初期采行兵民合一的部族兵制 .建立晋藩天王制度 主要是在争取南北士族间相对的平衡 全国共有21州 由于当时敦煌与西域各国交流频繁 ?[65] 随后晋惠帝被毒死 九品中 正制也继续使用 其中司马懿具有政治及军事才略 苻诏死新城”等 [63] 并改置武吏 296年 他们竭力维护自己的特殊社会地位 公元420年 刘聪杀新帝刘和自立为帝 ?整个中原没有常备军防御 地主田庄对江南地区的开发是起一定的积极作用 604 也曾经内部四分五裂 吴郡朱 张 顾 陆四氏居次 人口 是为宋明帝 小说方面 ;疆域大体上局限于淮河 长江流域以南 为了加强中央特别是司马皇室对地方的控制 攻灭了关东势力最大的葛荣及其他群雄成为实力最强的军阀 八王之乱 [31] 合称为六朝 414年经海路返抵建康 币 由于他选择的继承人晋惠帝近乎白痴 孙恩 死后 史称前凉 侯景包围台城 其势壮盛 主要的还是政治上原因 不过仍然有人反对清谈 这样 整个士族在无的影响下过着腐朽的生活 次国侯邑1400户 经济破坏最为严重 具有中军 外军组织及都督 将领等职务 例如竺法护 道林等人 到南北朝时艺术更兴盛 此时东晋仅剩扬 荆 江 广 交 豫 徐 兖 益 宁七州 以后历朝历代延续 统万城 [20] 西晋军镇及八王封国分布图晋武帝颁布封国制 王敦还想篡夺 苻坚中箭 世系 称号 姓名 在位时间 门阀大族致力于南方的庄园经营 至于章奏符檄 并颁诏宣布吸收汉族文化 870 刘裕击败桓玄 分封诸王 秃发乌孤 在官方教 育方面 这些民族所建立国家属于渗透王朝 被刘裕击败 但遭人毒死 隐士鲁胜注《墨辩》 378年派苻丕围攻襄阳 369年慕容垂投奔前秦 隔年5月桓冲率10万军 272年司马炎又派何桢招降李恪平定刘猛叛乱 寒人典签 魏晋经学以博采众说 北朝领土 [19] 主要城市 羌 完成《水经注》 江统和郭钦都曾建议将胡族强制迁离 然而 八王之乱后西晋元气大伤 祖逖死后 他还将闰月规则修整 [41] 私招的佃客很多 北齐建立后 所谓“刺史行事之美恶 356年 [27] 道安为佛图澄的弟子 但却使得地方宗室掌握军权 有些力量可以对外 而后大量北方世族及皇族衣冠南渡 并夺得 皇位 成为质量较纯的钢铁 自注说 着绛纱袍 贾后乱政 贪赃枉法 疆域 进入了南北朝时期 成为研究西域及印度史地的重要作品 西晋统一天下 402年3月孙恩为临海太守辛景所败 开垦出土壤肥沃 产量很高的“湖田” 由公元420年刘裕代东晋建立刘宋始 8 至此梁武帝有意北伐 补 充了北周的兵力 元刘二人因与清河王不合而叛变 周武帝为人英明雄伟 司马越以无粮推辞 自刎而死 风格清新朴实 经济 大量流民南渡 2 圆形方孔钱 有些成为独立的学问 并将旅途见闻写成《佛国记》 至503年始 武成帝昏庸好色 率军向建康进攻 南朝政承袭东晋 并将荆 扬两州与 原曹魏荆 扬两州合并 之后段匹磾也被石勒击败 Northern ?由于人民频繁的迁移 13 宕昌王 梁仚定 525-541 不料 实际范围只有山西和刘曜镇守的关中 在鸠摩罗什主持下共译出《般若经》和大乘中观学派的论书《中论》 《十二门论》 《百论》及《大智度论》 《法华经》等三十五 部两百多卷经典 司马炎 此外 南北朝时期的文学发展迅速 《庄子》书得郭象注 使文帝一朝出现了宗室 士族 寒门相互制衡的政治平衡局面 [87] 由于北魏帝拓跋圭派兵帮助西燕 取得梵本戒律后 慕容皝 晋元帝却派仅有虚名的戴渊做征西将军 前秦强盛后 ?疆域北至山西 河北及辽 东 [32] [60] 鳏夫寡妇不敢嫁娶 在上述情况下 曾试图在宗室诸王封国内建立军队 内迁的诸民族乘机举兵 即事先评出户产 按张湛《列子序》详述得书来历 中国的经济中心也逐渐南移 以充实国力 公元386年—581年 是为晋明帝 军事编辑 瓦解吴军 并将荆 扬两州与原曹魏荆 扬 两州合并 因为战乱军户大减 西晋是魏晋南北朝长期分裂时期中的短暂统一 实行户调制的诏书发布之后 司马氏起源 司马炎也骄奢淫逸起来 [55] 儒学面临严峻挑战 给予在政治上已享有实际权利的士人以经济上占有人口并免除徭役的特权 其三 投靠幽州段匹磾 或流靡以自妍 下置 戍 很多羯人沦为汉族地主的隶农 地位低的文武吏 然部署皆以为有机可乘 这就是说 [79] 1937年商务印书馆根据《史学丛书》本将汤球的《九家旧晋书辑本》 《晋纪辑本》 《汉晋春秋辑本》 《晋阳秋辑本》 《十六国春秋辑补》 《三十国春秋辑本》等排印出版 即口税米五石 ? 杨定 北齐则由鲜卑化汉人所建 约为四川北部 第七第八品二人 04 楚帝 桓石绥 404-410 东晋后期又发生朋党相争及桓玄作乱 河北北部 “南北权豪 之后南北双方形成文化交流或民族融合
