单叶双曲面和双叶双曲面d
双叶双曲面和单叶双曲面的方程

双叶双曲面和单叶双曲面的方程双叶双曲面和单叶双曲面,这听起来是不是像是数学课上那些让人抓狂的公式?但是,嘿,咱们今天就来轻松聊聊这俩有趣的东西!双叶双曲面,这个名字就像是在说“我有两个叶子,快来看看我!”想象一下一个大碗,碗的两边翘起,就像一对翅膀,仿佛随时准备飞起来。
这个家伙的方程,简单来说,就是 ( z^2 = x^2 + y^2 a^2 )。
好啦,这个公式一听就有点复杂,对吧?不过别担心,重要的是它在三维空间里看起来是个啥!想象一下你在沙滩上,用手指划出一个大弧线,画出一个超级大碗,这就是双叶双曲面的样子。
它有两个“叶子”,就像两个相对的碗,互相朝外延伸。
每当你走到它的边缘,就像是站在一个大平台上,俯瞰无尽的美景。
再说说单叶双曲面,这个家伙就有点不同寻常。
它就像是一个被压扁的碗,只有一边翘起来,另一边则像个笑脸。
这种形状让人联想到一种优雅的弯曲,仿佛在低声诉说着一个秘密。
它的方程是 ( z = frac{x^2 + y^2{a )。
想象一下,你把一个碗的底部轻轻地压下去,碗的边缘就会向上翘起。
这样的形状可不仅仅是好看,它在物理和工程上都有很多应用。
比如说,某些飞行器的外形就有这种设计,能有效地减少空气阻力。
是不是很酷?当你在海边漫步,看到海浪涌来时,或许你会想到这些奇妙的几何形状在自然界中的体现。
咱们不能不提这两个曲面在数学上的一些性质。
双叶双曲面其实是个双曲线的变种,像极了数学家们在寻找曲线的终极目标。
而单叶双曲面呢,则常常被用来描述一些物理现象,比如声波的传播。
就好像你在湖边扔下一块石头,石头激起的涟漪就是一个单叶双曲面在水面上的投影。
真的,数学和自然之间的联系就像是密不可分的朋友,让人忍不住想要深入探讨。
有趣的是,双叶双曲面和单叶双曲面在生活中无处不在。
你喝的咖啡杯,可能就呈现出双叶双曲面的特征。
而那种优雅的扭曲形状的建筑,或许也是灵感来源于单叶双曲面。
艺术家和设计师们总是试图把这些数学概念融入他们的创作,仿佛在说:“嘿,数学不仅仅是公式,它还是美的一部分!”试想一下,如果没有这些曲面,世界将会失去多少美感啊?所以,下次当你在书本上看到这些曲面的方程时,不妨停下来想想。
单叶双曲面和双曲抛物面的直母线

z 4
v 1
y 2
,
v
x 3
z 4
t
1
y 2
.
将(6,2,8)代入上述直母线族方程,求得 w , u , t , v.
例题
例2
试证明双曲抛物面
x2 a2
y2 b2
2z a
b上的两直母线直交时,其
交点必在一双曲线上.
z c
v
1
y b
,
t2 v2
0
v
x a
z c
t
1
y b
.
(4.7-2)
推论1 对于单叶双曲面上的点,两族直母线中各有一条直母线通
过这点.
B8ack
三、双曲抛物面是直纹曲面
z
O x
y
9
三、双曲抛物面是直纹曲面
双曲抛物面
例3 已知空间两异面直线间的距离为 2a,夹角为 2 ,过这两
直线分别作平面,并使这两平面相互垂直,求这样的两平面交线
的轨迹.
2020/1/21
18
x2 a2
y2 b2
2z
a,b 0
悉尼歌剧院
定理 单叶双曲面
x2 a2
y2 b2
z2 c2
1 , a,b, c
0
是直纹曲面。它有两族直母线:
w
x a
z c
u
1
高等数学(下)知识点总结归纳

欢迎共阅高等数学(下)知识点主要公式总结第八章空间解析几何与向量代数 1、二次曲面1)椭圆锥面:22222z b y a x =+ 2)3)4)5)6)(二) 1、法向量:n2、3、两平面的夹角:),,(1111C B A n =,),,(2222C B A n =,⇔∏⊥∏210212121=++C C B B A A ;⇔∏∏21//212121C C B B A A ==4、点),,(0000z y x P 到平面0=+++D Cz By Ax 的距离:(三) 空间直线及其方程 1、一般式方程:⎪⎩⎪⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A2、对称式(点向式)方程:p z z n y y m x x 000-=-=-方向向量:),,(p n m s =,过点),,(000z y x3、两直线的夹角:),,(1111p n m s = ,),,(2222p n m s =,⇔⊥21L L 0212121=++p p n n m m ;⇔21//L L 212121p p n n m m ==4、直线与平面的夹角:直线与它在平面上的投影的夹角,2、 微分法1)复合函数求导:链式法则若(,),(,),(,)z f u v u u x y v v x y ===,则z z u z v x u x v x ∂∂∂∂∂=⋅+⋅∂∂∂∂∂,z z u z v y u y v y∂∂∂∂∂=⋅+⋅∂∂∂∂∂ (二) 应用1)求函数),(y x f z =的极值解方程组⎪⎩⎪⎨⎧==0y x f f 求出所有驻点,对于每一个驻点),(00y x ,令),(00y x f A xx =,),(00y x f B xy =,),(00y x f C yy =,① 若AC ② 若AC ③ 若AC 2、 1)曲线⎪⎪⎩⎪⎪⎨⎧Γ:z y x 2) 曲面:∑(一) 二重积分:几何意义:曲顶柱体的体积1、 定义:∑⎰⎰=→∆=nk k k kDf y x f 1),(lim d ),(σηξσλ2、 计算: 1)直角坐标⎭⎬⎫⎩⎨⎧≤≤≤≤=b x a x y x y x D )()(),(21ϕϕ,21()()(,)d d d (,)d bx ax Df x y x y x f x y y φφ=⎰⎰⎰⎰⎭⎬⎫⎩⎨⎧≤≤≤≤=d y c y x y y x D )()(),(21φφ,21()()(,)d d d (,)d d y c y Df x y x y y f x y x ϕϕ=⎰⎰⎰⎰2) 极坐标⎭⎬⎫⎩⎨⎧≤≤≤≤=βθαθρρθρθρ)()(),(21D ,21()()(,)d d (cos ,sin )d Df x y x y d f βρθαρθθρθρθρρ=⎰⎰⎰⎰(二) 三重积分1、 定义:∑⎰⎰⎰=→Ω∆=nk kk k kv f v z y x f 1),,(limd ),,(ζηξλ2、 计算: 1)⎰⎰⎰Ωx f ,(⎰⎰⎰Ωx f (2)⎪⎪⎩⎪⎪⎨⎧===zz y x ρρ3)(三) 应用曲面z S :(一) 1、 2、设,(y x f 在曲线弧上有定义且连续,的参数方程为),(ψ⎪⎩⎨=t y ,其中在],[βα上具有一阶连续导数,且0)()(22≠'+'t t ψϕ,则(二) 对坐标的曲线积分 1、定义:设L 为xoy 面内从A 到B 的一条有向光滑弧,函数),(y x P ,),(y x Q 在L 上有界,定义∑⎰=→∆=nk kk k Lx P x y x P 1),(lim d ),(ηξλ,∑⎰=→∆=nk kk kLy Q y y x Q 1),(lim d ),(ηξλ.欢迎共阅向量形式:⎰⎰+=⋅LLy y x Q x y x P r F d ),(d ),(d2、计算:设),(,),(y x Q y x P 在有向光滑弧L 上有定义且连续,L 的参数方程为):(),(),(βαψϕ→⎪⎩⎪⎨⎧==t t y t x ,其中)(),(t t ψϕ在],[βα上具有一阶连续导数,且0)()(22≠'+'t t ψϕ,则 3、两类曲线积分之间的关系:设平面有向曲线弧为⎪⎩⎪⎨⎧==)()( t y t x L ψϕ:,L 上点),(y x 处的切向量的方向角为:βα,,cos α=则LP ⎰(三) 1、则有⎰⎰D 2、G 则x Q ∂∂(四) 1、 设∑定义⎰⎰∑2、:z =∑,xy ,则(五) 对坐标的曲面积分 1、 定义:设∑为有向光滑曲面,函数),,(),,,(),,,(z y x R z y x Q z y x P 是定义在∑上的有界函数,定义1(,,)d d lim (,,)()ni i i i xy i R x y z x y R S λξηζ∑→==∆∑⎰⎰同理,1(,,)d d lim (,,)()ni i i i yz i P x y z y z P S λξηζ∑→==∆∑⎰⎰;01(,,)d d lim (,,)()ni i i i zx i Q x y z z x R S λξηζ∑→==∆∑⎰⎰2、性质:1)21∑+∑=∑,则计算:——“一投二代三定号”),(:y x z z =∑,xy D y x ∈),(,),(y x z z =在xy D 上具有一阶连续偏导数,),,(z y x R 在∑上连续,则(,,)d d [,,(,)]d d x yD R x y z x y R x y z x y x y ∑=±⎰⎰⎰⎰,∑为上侧取“+”,∑为下侧取“-”.3、 两类曲面积分之间的关系:其中γβα,,为有向曲面∑在点),,(z y x 处的法向量的方向角。
单双叶双曲面
x2 z2 2 2 1 a c y 0
实轴与 x 轴相合, 虚轴与 z 轴相合.
(3)用坐标面 yoz ( x 0),与曲面相截
均可得双曲线.
单叶双曲面图形
z
o x
y
二、 双叶双曲面
x2 y2 z2 2 2 1 2 a b c
双叶双曲面 z
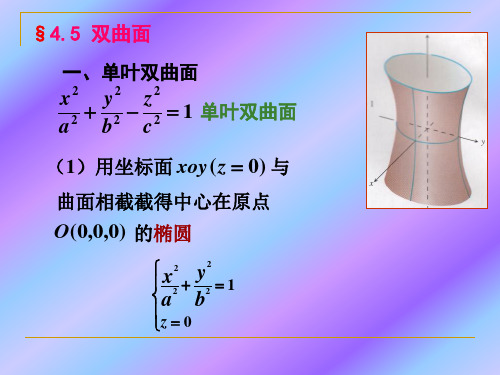
§4.5 双曲面 一、单叶双曲面
x2 y2 z2 2 2 1 单叶双曲面 2 a b c
(1)用坐标面 xoy ( z 0) 与
曲面相截截得中心在原点
O(0,0,0) 的椭圆
2 y2 x2 2 1 a b z 0
与平面 z z1 的交线为椭圆.
2 x2 y2 z1 2 2 1 2 当 z1 变动时,这种椭 b c a 圆的中心都在 z 轴上. z z 1 (2)用坐标面 xoz ( y 0)与曲面相截
o x
y
双曲面及其渐进锥面
x y z 双叶: 2 2 2 1 a b c x2 y2 z2 渐进锥面: 2 2 2 0 a b c x2 y2 z2 单叶: 2 2 2 1 a b c
在平面上,双曲线有渐进线。 相仿,单叶双曲面和双叶双曲面 有渐进锥面。 用z=h去截它们,当|h|无限增大 时, 双曲面的截口椭圆与它的渐进锥 面 的截口椭圆任意接近,即: x 双曲面和锥面任意接近。
单叶双曲面与双曲抛物面

(4.7-1) 4.7-
与
(4.7-2) 4.7-
推论1 推论1
对于单叶双曲面上的点, 对于单叶双曲面上的点,两族直母线中各有一条直母线 Back
通过这点. 通过这点.
三、双曲抛物面是直纹曲面
z
O
y
x
三、双曲抛物面是直纹曲面
双曲抛物面
x2 y2 2 = 2z 2 a b (a, b > 0 )
总是异面直线,而且双曲抛物面同族的全体直母线平行于同一 总是异面直线,而且双曲抛物面同族的全体直母线平行于同一 同族
例题
例1 求过单叶双曲面
x2 y 2 z 2 + = 1 上的点 ( 6, 2,8 ) 的直母线的方程. 的直母线的方程. 9 4 16
x2 y2 z 2 两族直母线方程为 方程为: 分析: 分析: 单叶双曲面 + = 1 的两族直母线方程为: 9 4 16
例(教材P153) 教材P153)
x 求直线 Γ: = y = z 1 绕直线 l : x = y = z 旋转所 2 1 0 得的旋转曲面的方程. 得的旋转曲面的方程.
单叶旋转双曲面
Back
直纹曲面模型
直纹曲面模型
二、单叶双曲面是直纹曲面
单叶双曲面
x2 y2 z2 + 2 2 =1 2 a b c ( a, b, c > 0)
x y a + b = 2u, (u ∈ R ) u x y = z , a b x y a b = 2v, (v ∈ R) . x y v + = z , a b
(4.7-3) 4.7-
与
(4.7-4) 4.7-
对于双曲抛物面上的点,两族直母线中各有一条直母线通过该 对于双曲抛物面上的点,两族直母线中各有一条直母线通过该点.
双叶双曲面和单叶双曲面

双叶双曲面和单叶双曲面
双叶双曲面和单叶双曲面如下:
一、曲率不同:
双叶双曲面的高斯曲率为正。
尽管它具有正曲率,但是具有另一适当选择的度量的双叶双曲面也可以用作双曲线几何的模型。
单叶双曲面的高斯曲率为负,两片双曲面的高斯曲率为正。
尽管它具有正曲率,但是具有另一适当选择的度量的两张双曲面也可以用作双曲线几何的模型。
二、定义不同:
双曲面是二次曲面,其可以被定义为三个变量中的二维多项式的点的集合的表面。
在二次曲面中,双曲面的特征在于不仅具有对称中心,而且让平面和其相交还能形成锥体、柱体等。
双曲面还具有三对垂直对称轴和三对垂直对称平面。
单叶双曲面,也称为双曲面。
它是一个连接表面,每个点都具有负高斯曲率。
这意味着任何点处的切线平面与双曲面相交成两条线,因此单叶双曲面是双重曲面。
,它具有两片双曲面,也称为椭圆双曲面。
表面有两个连接的部件,每个点都有正高斯曲率。
单叶双曲面

§5 双曲面一 单叶双曲面:例:z y 面上的双曲线012222x c z b y 绕z 轴旋转,所得旋转面为1222222 cz b y a x——旋转单叶双曲面1、定义:在直角系下,由方程1222222 cz b y a x (a,b,c>0) (1)所表示的图形称为单叶双曲面;而方程(1)称为单叶双曲面的标准方程。
注:在直角系下,方程1222222 cz b y a x 或1222222 c z b y a x 所表示的图形也是单叶双曲面2、性质与形状:(i )对称性:单叶双曲面(1)关于三坐标轴,三坐标面及原点对称。
原点称为(1)的中心。
(ii )有界性:由方程(1)可知,单叶双曲面(1)是无界曲面 (iii )与坐标轴的交点与坐标面的交线:单叶双曲面(1)与x,y 轴分别交于(±a ,0,0),(0,±b ,0)而与z 轴不交,上述四点称为它的顶点。
(1)与三坐标面交于0)1(x , 0)1(y ,0)1(z ,即 012222x c z b y (2) 012222y c z a x (3)012222z b y a x (4) (2)(3)均为双曲线, (4)为椭圆,它们的顶点均是单叶双曲面(1)的两对顶点。
(iv )与平行于坐标面平面的交线:为考察(1)的形状,我们先用平行于y x 面的平面去截它,其截线为k z )1(, 即k z c k b y a x 2222221 (5)对 k ,(5)均为椭圆,其顶点为(0,±b 221ck ,k )∈(2),(±a 221c k ,0,k )∈(3) ,其半轴为b 221c k 和a 221ck ,当∣k ∣逐渐增大时,椭圆(5)逐渐变大。
可见,单叶双曲面(1)是由一系列“平行”椭圆构成的,这些椭圆的顶点分别在二相互“垂直”的双曲线上变化。
再用一组平行于z y 面的平面去截(1),其截线为kx )1( ,即k x a k c z by 2222221 (6)当∣k ∣<a 时,(6)为一双曲线,其实轴∥y 轴,(如图5.3)虚轴∥z 轴,其顶点(k ,±b 221ak ,0)∈(4),当∣k ∣=a 时,(6)为二相交线,其交点为(k ,0,0)当∣k ∣>a 时,(6)仍为双曲线,但其实轴∥z 轴,虚轴∥y 轴,其顶点(k ,0,±a 221ak )∈(3)最后,若用一组平行于z x 面的平面去截(1),其截线情况与上述相仿(如图5.1)。
空间双曲面的分类

空间双曲面是三维空间中的曲面,其形状类似于双曲线。
根据曲面的性质和几何特征,空间双曲面可以分为以下三类:
单叶双曲面(One-Sheet Hyperboloid):
单叶双曲面是最简单的空间双曲面,它可以由一个双曲线绕着其主轴旋转形成。
单叶双曲面的方程通常为:
(x^2 / a^2) - (y^2 / b^2) - (z^2 / c^2) = 1
其中a,b,c是正实数,决定了双曲面的尺寸和形状。
双叶双曲面(Two-Sheet Hyperboloid):
双叶双曲面是由两个双曲线绕着它们的公共中心轴旋转形成的。
双叶双曲面的方程通常为:(x^2 / a^2) - (y^2 / b^2) - (z^2 / c^2) = -1
其中a,b,c是正实数,也决定了双曲面的尺寸和形状。
锥面(Hyperbolic Cone):
锥面是由一条直线绕着它的一个端点旋转形成的。
锥面在该端点上有一个顶点,所有的生成直线都通过该顶点。
锥面的方程通常为:
(x^2 / a^2) - (y^2 / b^2) - (z^2 / c^2) = 0
其中a,b,c是正实数,也决定了锥面的尺寸和形状。
空间双曲面在数学和几何学中有广泛的应用,也是许多物理和工程学问题的重要模型。
它们具有独特的形状和性质,常常用于描述各种复杂的曲面和曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求单叶双曲面和双叶双曲面、椭圆抛物面、双曲抛物面用matlab怎么画或其参数方程?
2009-12-07 15:46tianzan2006|分类:数学|浏览4969次
有个例子就成,选修可的实验报告。
大一高数学的不太好,现在乘机补课。
向左转|向右转
方式二:短信免费下载
下载链接将通过短信免费下发到您的手机
发送短信
分享到:
2009-12-07 19:43提问者采纳
花画圆的程序:
for i=-3:0.001:3
y=-sqrt(9-i^2);
plot(i,y);
hold on
end
hold on
for i=-3:0.001:3
y=sqrt(9-i^2);
plot(i,y);
hold on
end
%椭圆
for i=-6:0.01:6
y=-sqrt(36-i^2)/2;
plot(y,i);
hold on
end
%双曲线
for i=-6:0.01:6
y=-sqrt(36+i^2)/2;
plot(y,i);
hold on
end
hold on
for i=-6:0.01:6
y=sqrt(36+i^2)/2;
plot(y,i);
hold on
end
hold on
for i=-6:0.01:6
y=sqrt(36-i^2)/2;
plot(y,i);
hold on
end
%抛物线
for i=0:0.01:6
y=-sqrt(2*6*i);
plot(y,i);
hold on
end
hold on
for i=0:0.01:6
y=sqrt(2*6*i);
plot(y,i);
hold on
end
其他2条回答
2009-12-07 20:08hyyly520|十一级
%%%%%%%%%圆%%%%%%%%%%%%%%
x=-1:0.00001:1;
r=1;%半径r=1
y1=sqrt(r-x.^2);
y2=-sqrt(r-x.^2);
plot(x,y1,x,y2)
%%%%%%%%%椭圆%%%%%%%%%%%%%%
x=-1:0.00001:1;
a=1;b=1;%椭圆半径a=1;b=1
y1=sqrt(b.^2*(1-x.^2/(a.^2)));
y2=-sqrt(b.^2*(1-x.^2/(a.^2)));
plot(x,y1,x,y2)
%%%%%%%%%抛物线%%%%%%%%%%%%%%
x=1:0.00001:5;
a=1;b=1;%抛物半径a=1;b=1
y1=sqrt(b.^2*(x.^2/(a.^2)-1));
y2=-sqrt(b.^2*(x.^2/(a.^2)-1));
plot(x,y1,x,y2)
%%%%%%%%%椭球面%%%%%%%%%%%%%% xa=-2:0.2:2;
ya=xa;
[x,y]=meshgrid(xa,ya);
a=1;b=1;c=1;% 假设a=1;b=1;c=1
z1=sqrt(c.^2*(1-x.^2/(a.^2)+y.^2/(b.^2)));
z2=-sqrt(c.^2*(1-x.^2/(a.^2)+y.^2/(b.^2)));
mesh(x,y,z1)
hold on;
mesh(x,y,z2)
%%%%%%%%%%%单叶双曲面%%%%%%%%%%% xa=-2:0.2:2;
ya=xa;
[x,y]=meshgrid(xa,ya);
a=1;b=1;c=1;% 假设a=1;b=1;c=1
z1=sqrt(c.^2*(x.^2/(a.^2)+y.^2/(b.^2)-1));
z2=-sqrt(c.^2*(x.^2/(a.^2)+y.^2/(b.^2)-1));
mesh(x,y,z1)
hold on;
mesh(x,y,z2)
%%%%%%%%%%双叶双曲面%%%%%%%%%%%%%% xa=-2:0.2:2;
ya=xa;
[x,y]=meshgrid(xa,ya);
a=1;b=1;c=1;% 假设a=1;b=1;c=1
z1=sqrt(c.^2*(x.^2/(a.^2)+y.^2/(b.^2)+1));
z2=-sqrt(c.^2*(x.^2/(a.^2)+y.^2/(b.^2)+1));
mesh(x,y,z1)
hold on;
mesh(x,y,z2)
%%%%%%%%%%椭圆抛物面%%%%%%%%%%%%%% xa=-2:0.2:2;
ya=xa;
[x,y]=meshgrid(xa,ya);
p=1;q=1;% 假设p=1;q=1
z=0.5*(x.^2/p+y.^2/q);
mesh(x,y,z)
%%%%%%%%%%双曲抛物面%%%%%%%%%%%%% xa=-2:0.2:2;
ya=xa;
[x,y]=meshgrid(xa,ya);
p=1;q=1;% 假设p=1;q=1
z=0.5*(x.^2/p-y.^2/q);
mesh(x,y,z)。
