振动习题课 PPT
合集下载
2024年物理 必修第一册(配人教版)PPT课件:第二章 习题课一 匀变速直线运动的推论

()
A.子弹在每个水球中运动的时间相同 B.由题干信息可以确定子弹穿过每个水球的时间之比 C.子弹在每个水球中速度变化相同 D.子弹穿出第三个水球的瞬时速度与全程的平均速度相等 答案:BD
典例4 (多选)如图所示,在水平面上固定着三个完全相同的木块,一 颗子弹以水平速度v射入。若子弹在木块中做匀减速直线运动,当穿透第 三个木块时速度恰好为零,则子弹依次穿入每个木块时的速度之比和穿过
每个木块所用时间之比分别为
()
A.v1∶v2∶v3=3∶2∶1 B.v1∶v2∶v3= 3∶ 2∶1 C.t1∶t2∶t3=1∶ 2∶ 3 D.t1∶t2∶t3=( 3- 2)∶( 2-1)∶1
通过 x0、2x0、3x0、…、nx0 所用时间之比,由 x=12at2 得 t= 2ax0,
可推得:
按位移等 t1∶t2∶t3∶…∶tn=1∶ 2∶ 3∶…∶ n 分(设相 通过第一个 x0、第二个 x0、第三个 x0、…、第 N 个 x0 所用时间 等的位移 之比,由 tⅠ=t1,tⅡ=t2-t1,tⅢ=t3-t2,…可推得:tⅠ∶tⅡ∶tⅢ∶…∶
经历的时间为t,则下列说法不正确的是
()
A.物体运动全过程中的平均速度是Lt
B.物体在2t 时的瞬时速度是2tL
C.物体运动到斜面中点时瞬时速度是
2L t
D.物体从顶端运动到斜面中点所需的时间是
2t 2
答案:B
综合提能(三) 逐差相等公式的理解及应用
【知识贯通】 1.逐差相等公式:Δx=xⅡ-xⅠ=xⅢ-xⅡ=…=aT2 做匀变速直线运动的物体,如果在各个连续相等的时间T内的位移分 别为xⅠ、xⅡ、xⅢ、…、xN,则匀变速直线运动中任意两个连续相等的时 间间隔内的位移差都相等。
2021学年高二上学期物理人教版教材选择性必修第一册习题PPT-2.2简谐运动的描述

答案 (1)10 cm 0.2 s 5 Hz (2)0.05 s (3)1 000 cm 10 cm 解析 (1)从题图可知,振子振动的振幅为 10 cm,t=0.1 s =T2,所以 T=0.2 s.由 f=T1得 f=5 Hz. (2)根据简谐运动的对称性可知,振子由 A 到 O 的时间与振 子由 O 到 B 的时间相等,均为 0.05 s.
(1)求振子的振幅和周期; (2)在图中作出该振子的位移—时间图像; (3)写出振子的振动方程.
答案 (1)10 cm 0.2 s (2)图见解析 (3)y=-10sin(10πt) cm 解析 (1)振幅 A=10 cm,T=120 s=0.2 s. (2)四分之一周期时具有正的最大加速度,故有 负向最大位移,如图所示. (3)设振动方程为 y=Asin(ωt+φ),当 t=0 时,y=0,则 sin φ=0,得 φ=0 或 φ=π,当再过14周期后,y 为负值,所以 φ =π,所以振动方程为 y=10sin(10πt+π) cm=-10sin(10πt) cm.
6.相位差:如果两个简谐运动的频率相同,其初相分别是 φ1 和 φ2,当 φ2>φ1 时,它们的相位差是Δφ=φ2-φ1.
对点训练
考点一 描述简谐运动的物理量 1.关于振幅,下列说法正确的是( C ) A.振幅是矢量,方向是从平衡位置指向最大位移处 B.振幅描述的是物体振动的快慢 C.振动物体离开平衡位置的最大距离叫作振幅,是标量 D.做简谐运动的振子在振动的过程中振幅是不断变化的
若 C 对应 t1 时刻,C′对应 t2 时刻,则 t2-t1=nT+Δt(n= 0,1,2,3,…).
其中Δt 为 t2-t1 的最小值,对应的运动过程是 C→O→C′, 由图所示:0<Δt<T2,根据题意有,t2-t1<T,即 0<t2-t1<T2.进 一步观察:C、C′可无限靠近 0,因此Δt 可无限短,即Δt 可 小于14T,也可大于14T,故 A、B 两项正确.
机械振动基础课后习题解答_第3章习题
m
0
0 m
u1 u2
3k k
k 3k
u1 u2
2ku0
sin 0
t
K
2M
3k
2m
k
k
3k 2m
H11 ( )
3k 2m ()
H 21 ( )
k ()
u1(t) u2 (t)
H11 ( ) H21()
2ku0
sin
t
3k 为反共振频率 m
P140,3-9: 图示系统初始静止,求左端基础产生阶跃位移u0后系统的响应。
ml2 1 0 M 3 0 7 /16
K
l2k 16
9 9
9
13
| K 2M | 0
1 0.65
k m
2 2.62
k m
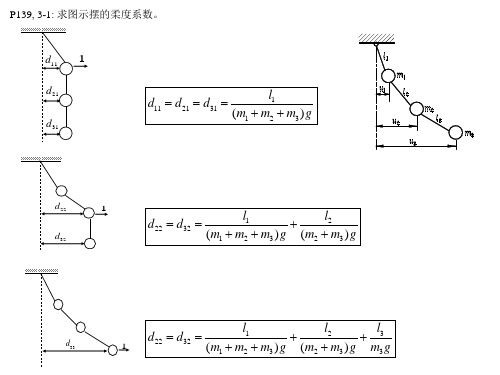
P139,3-3: 建立图示系统的运动微分方程,并求当ki k,i 1, 6, m1 m, m2 2m, m3 m时的固有 频率和固有振型。
m1
M
m2
u2
c
3c
2c
u2
k
3k
2k
u2
0
m u3 0 2c 2c u3 0 2k 2k u3 f0
1 0,2
k m
, 3
2k m
1 1 1
φ1
1 , φ2
0
, φ3
1
1
1/ 2
1
u1 1
u2
1
u3 1
1 0 1/ 2
1 q1
1
q2
1 q3
)d
u0 2
(1 cos1t)
q2
(t)
u0 2
(1
cos 2t )
振动与波习题课

b
c
O
a
.
b
c X t
a 0
b
2
3 c 2
10.如图(a)为t=0时的波形曲线,经0.5s后波形变为(b) 求(1)波动方程 Y (a) (b) u
(2)P点的振动方程
解:O处的振动方程为 0.1
yo A cos(t )
由图得A=0.1 =/2 =4m
( 2k 1) 2 2 1 1 2 ( 2k 1) 4 r1 [ ] 2 ( 2k 1) 2 ( 2k 1)
Y
u=0.08m/s P . 0.02
X yo A cos(t ) -0.04 0.04 P点的振动方程 2 1 T u 0.08 令x=0.02 u 2 2 3 4 y P 0.04 cos(4t ) T 2 x y 0.04 cos[4 ( t ) ] 0.08 2
A A A 2 A1 A2 cos( 2 1 ) A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2 2 1 B.同方向不同频率:拍 拍频为:
A. 同方向同频率:
2 1 2 2
C.两个相互垂直同频率的振动:椭圆 D.两个相互垂直不同频率的振动:李萨如图 5.平面简谐波波动方程:
u 0.84m / s 取 /3
故得波动方程为
17 / 3
O a b
u
X
x y 0.1cos[7 ( t ) ]( m ) 0.84 3
13.题中图a表示一水平轻绳,左端D为振动器,右端 固定于B点。t0时刻振动器激起的简谐波传到O点。其 波形如图b所示。已知OB=2.4m,u=0.8m/s. 求:(1) 以为计时零点,写出O点的谐振动方程;(2)取O 点 为原点,写出向右传播的波动方程;(3)若B 处有 半波损失,写出反射波的波动方程(不计能量损失)。 2 D O 解:(1)由 B u 2 2 y(cm) 得 u 80 4 40 4
振动和波动习题课(改)

x)
yBP
Acos[ t
2
(30 x)]
l
两波同频率,同振幅,同方向振动,所以相干静止的点满足:
(t 2 x) [t 2 (30 x)]
l
l
(2k 1)
k 0,1,2,...
化简后 30 2x kl
30 2x kl O x
X
因为: l u 4m
x 15 k 2
1
3
x 3 102 sin(4t 1 ) (SI)
2
6
画出两振动的旋转矢量图,并求合振动的振动
方程.
x1
5
102
cos(4t
1 3
)
x2
3
102
sin(4t
1 6
)
3
102
cos(4t
1 6
1 2
)
3 102 cos(4t 2 ) 3
x x1 x2
1
2 102 cos(4t 1 )
7.一简谐振动曲线如图所示,试由图确
定在t=2s时刻质点的位移为
,速
度为
。
t=2s, x=0
Vm
A
2 A
T
3
102
8.已知两个简谐振动 曲线如图所示,
X1的位相比X2的位相
A) 落后 1
2
C) 落后
B) 超前 1 √
2
D) 超前
9.一简谐振动的振动曲线如图,求此振动的 周期。
解: =/3+ /2=5/6 t=5= 5/6 = /6
2
之间)
(1)2 1 2k k 0,1,2,
A A1 A2 振动加强; 此时有= 1= 2
A1
振动与波动习题课

A
(1) B处质元的振动动能减小 处质元的振动动能减小, 则其弹性势能必增大; 则其弹性势能必增大 错 答:质元的振动动能和弹 质元的振动动能和弹 性势能是同相位的 ,同 时增大,同时减少. 时增大,同时减少.
B
o
C
x
(2) A处质元回到平衡位置的过程中 它把自己的能量 处质元回到平衡位置的过程中,它把自己的能量 传给相邻的质元,其能量逐渐减小 其能量逐渐减小; 传给相邻的质元 其能量逐渐减小 错 在平衡位置质元的振动动能和弹性势能是最大, 答:在平衡位置质元的振动动能和弹性势能是最大,所 质元回到平衡位置的过程中能量应该逐渐增大 能量应该逐渐增大. 以A处质元回到平衡位置的过程中能量应该逐渐增大.
关于干涉条件的讨论
y1 = A1 cos( ω t + 10
y2 = A2 cos( ω t + 20
P点的合振动为 点的合振动为
2π r1
2π r2
λ
)
注意: 为正值! 注意:r1, r2为正值! P
r1
λ
)
S1 r2 S2
y = y1 + y2 = A cos( ω t + 0 )
2 1 2
波动学基础
教学要求
1 . 掌握平面简谐波波动方程的物理意义 掌握由质点 掌握平面简谐波波动方程的物理意义.掌握由质点 的谐振动方程或某时刻的简谐波波形曲线等已知条件建 立简谐波波动方程的方法. 立简谐波波动方程的方法 2 .理解波长,周期,频率,波速等概念的含意 并掌 理解波长, 理解波长 周期,频率,波速等概念的含意,并掌 握它们之间的关系. 握它们之间的关系 3 .理解波的干涉现象 掌握波的相干条件 能运用相位 理解波的干涉现象.掌握波的相干条件 理解波的干涉现象 掌握波的相干条件.能运用相位 差或波程差来确定相干波叠加后加强或减弱的条件. 差或波程差来确定相干波叠加后加强或减弱的条件 4 .理解驻波的特性及其形成条件 了解驻波与行波的 理解驻波的特性及其形成条件.了解驻波与行波的 理解驻波的特性及其形成条件 区别. 区别 5 .理解波的能量传播特征以及能流,能流密度等概念 理解波的能量传播特征以及能流, 理解波的能量传播特征以及能流 能流密度等概念. 6.掌握多普勒效应 6.掌握多普勒效应
(1) B处质元的振动动能减小 处质元的振动动能减小, 则其弹性势能必增大; 则其弹性势能必增大 错 答:质元的振动动能和弹 质元的振动动能和弹 性势能是同相位的 ,同 时增大,同时减少. 时增大,同时减少.
B
o
C
x
(2) A处质元回到平衡位置的过程中 它把自己的能量 处质元回到平衡位置的过程中,它把自己的能量 传给相邻的质元,其能量逐渐减小 其能量逐渐减小; 传给相邻的质元 其能量逐渐减小 错 在平衡位置质元的振动动能和弹性势能是最大, 答:在平衡位置质元的振动动能和弹性势能是最大,所 质元回到平衡位置的过程中能量应该逐渐增大 能量应该逐渐增大. 以A处质元回到平衡位置的过程中能量应该逐渐增大.
关于干涉条件的讨论
y1 = A1 cos( ω t + 10
y2 = A2 cos( ω t + 20
P点的合振动为 点的合振动为
2π r1
2π r2
λ
)
注意: 为正值! 注意:r1, r2为正值! P
r1
λ
)
S1 r2 S2
y = y1 + y2 = A cos( ω t + 0 )
2 1 2
波动学基础
教学要求
1 . 掌握平面简谐波波动方程的物理意义 掌握由质点 掌握平面简谐波波动方程的物理意义.掌握由质点 的谐振动方程或某时刻的简谐波波形曲线等已知条件建 立简谐波波动方程的方法. 立简谐波波动方程的方法 2 .理解波长,周期,频率,波速等概念的含意 并掌 理解波长, 理解波长 周期,频率,波速等概念的含意,并掌 握它们之间的关系. 握它们之间的关系 3 .理解波的干涉现象 掌握波的相干条件 能运用相位 理解波的干涉现象.掌握波的相干条件 理解波的干涉现象 掌握波的相干条件.能运用相位 差或波程差来确定相干波叠加后加强或减弱的条件. 差或波程差来确定相干波叠加后加强或减弱的条件 4 .理解驻波的特性及其形成条件 了解驻波与行波的 理解驻波的特性及其形成条件.了解驻波与行波的 理解驻波的特性及其形成条件 区别. 区别 5 .理解波的能量传播特征以及能流,能流密度等概念 理解波的能量传播特征以及能流, 理解波的能量传播特征以及能流 能流密度等概念. 6.掌握多普勒效应 6.掌握多普勒效应
大学物理《光的偏振、衍射》习题课课件

( AC BD) (a b)(sin sin ) k (2).
水平线下方的角度取负号即可。
11
6. 以波长为 = 500 nm (1 nm = 10-9 m)的单色平行光斜入射在光栅常数为
d = 2.10 mm、缝宽为a = 0.700 mm的光栅上,入射角为i = 30.0°,求能看
成的半波带数目为
(A) 2 个. (B) 4 个. (C) 6 个. (D) 8 个.
答案:(B)
根据半波带法讨论,单缝处波阵面可分成的半波带数
目取决于asin 的大小,本题中
ቤተ መጻሕፍቲ ባይዱ
a 4, 300.
a sin 2 4 ,
2
满足单缝衍射暗条纹的公式: a sin 2k , (k 1,2...)
到哪几级光谱线.
解:(1) 斜入射时的光栅方程
光栅 透镜
屏
G L2
C
d sin i
d sin d sin i k k = 0,±1,±2,…n
第k 级谱线
n
i
分析在900 < < 900 之间,可呈现的主极大:
i = 30°,设 = 90°, k = kmax1,则有
d sin
kmax1 (d / )(sin 90 d sin 30) 2.10
解: a b 1 mm 3.33μm 300
(1) (a + b) siny =k, ∴ k= (a + b) sin24.46°= 1.38 mm
∵ R=0.63─0.76 mm, B=0.43─0.49 mm,第二级开始会有谱线重叠。
对于红光,取k=2 , 则 R=0.69 mm; 对于蓝光,取k=3, 则 B=0.46 mm.
振动与波动习题课修

4 4
A = 5 / cos α = 5 2 cm
2
πt 3π t= 0 t= 2 s (1) x = 5 2 × 10 cos( )( SI ) 4 4 3 π 2 (2) v = ω A sin = 5 2 × 10 sin( π ) 4 4 = 3 . 93 × 10 2 m / s
v A1
O X O
v A1
X O
A2
v A1
X
v A2
反相 同相
振动2比振动 超前 振动 比振动1超前 比振动
四、谐振动的合成 1。同方向、同频率的谐振动的合成: 。同方向、同频率的谐振动的合成:
A=
2 A12 + A2 + 2 A1 A2 cos( 2 1
A1 sin 1 + A2 sin 2 tg = A1 cos 1 + A2 cos 2
v0 tg = ω x0
两同频率的谐振动在任意时刻的相位差: 两同频率的谐振动在任意时刻的相位差:
= 2 1
振动2比振动1超前 > 0 LLLLL 落后 < 0 = = 2 kπ ( k = 0 ,1L ) 振动2和振动1同相 = ( 2 k + 1 )π ( k = 0 ,1L ) LLL反相
8. 一系统作简谐振动,周期为 ,以余弦函数 一系统作简谐振动,周期为T,
1 表达振动时,初相位为零。 表达振动时,初相位为零。在 0 ≤ t ≤ T范围 2 T/8或3T/8 时动能和势能相等 系统在t=_________时动能和势能相等。 时动能和势能相等。 内,系统在
解: x = Acosωt
x = 2cos(ωt + )
O t=0
5 Vm = ωA = 5 ω = 2 5 π x = 2cos( t )cm 2 2
A = 5 / cos α = 5 2 cm
2
πt 3π t= 0 t= 2 s (1) x = 5 2 × 10 cos( )( SI ) 4 4 3 π 2 (2) v = ω A sin = 5 2 × 10 sin( π ) 4 4 = 3 . 93 × 10 2 m / s
v A1
O X O
v A1
X O
A2
v A1
X
v A2
反相 同相
振动2比振动 超前 振动 比振动1超前 比振动
四、谐振动的合成 1。同方向、同频率的谐振动的合成: 。同方向、同频率的谐振动的合成:
A=
2 A12 + A2 + 2 A1 A2 cos( 2 1
A1 sin 1 + A2 sin 2 tg = A1 cos 1 + A2 cos 2
v0 tg = ω x0
两同频率的谐振动在任意时刻的相位差: 两同频率的谐振动在任意时刻的相位差:
= 2 1
振动2比振动1超前 > 0 LLLLL 落后 < 0 = = 2 kπ ( k = 0 ,1L ) 振动2和振动1同相 = ( 2 k + 1 )π ( k = 0 ,1L ) LLL反相
8. 一系统作简谐振动,周期为 ,以余弦函数 一系统作简谐振动,周期为T,
1 表达振动时,初相位为零。 表达振动时,初相位为零。在 0 ≤ t ≤ T范围 2 T/8或3T/8 时动能和势能相等 系统在t=_________时动能和势能相等。 时动能和势能相等。 内,系统在
解: x = Acosωt
x = 2cos(ωt + )
O t=0
5 Vm = ωA = 5 ω = 2 5 π x = 2cos( t )cm 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、描写谐振动的几个物理量
1. 振幅 A x02 v0 2
2. 初相 cos x0
A
和v0正负确定。
3. 圆频率
弹簧振子
k m
单摆 g
l
周期、频率 T 2 1
三、旋转矢量
物理模型与数学模型比较
谐振动
旋转矢量
A
t+
T
振幅 初相 位相 圆频率 谐振动周期
半径 初始角坐标
角坐标 角速度 圆周运动周期
(1)物体的振动方程(自选坐标系); (2)物体在平衡位置上方 5cm 时弹簧对物体的 拉力; (3)物体从第一次越过平衡位置时刻起到它运 动到上方 5cm 处所需要的最短时间。
解: k/m7.0r7as d 1
(1)选坐标系如图
A0.1m , 0
x 0 .1 co 7 .0 s t7
A
ox
ox
ox
4. 已知某质点作简谐运动,振动曲线如图, 试根据图中数据写出振动表达式。
解 xAc ots ()
由图,A=2m, π
4
x(m )
2
2
3 S 1
0
1
t(s)
4
-2
x2c o3st() m
44
5.已知一简谐振动曲线如图所示,由图确定振子: (1) 在_t___k__1___k__0_,_1,_2___ s时速度为零. (2) 在______2__________ s时动能最大.
旋转矢量
由旋转矢量 法,任意时 刻 t, 谐振动 物体的速度 方向的判定:
参考圆
x<0 x>0
v <0
v <0
o x < 0 x > 0
x
v >0 v >0
由此可判断位相或初位相所在的象限。
四、同方向同频率谐振动合成
合成后仍为谐振动,角频率不变。
大家有疑问的,可以询问和交流
可以互相讨论下,但要小
图中哪一图?
x A
(A)
A/2
O -A/2
x
A
A/2
(C)
O
-A/2
x
t
A
(B) A/2
O
-A/2
x
t
(D)
A/2
O
-A/2
-A
tt
t
[A]
10. 两个同方向的简谐振动曲线如图所示,
合振动的振幅为 AA2A1 ,
合振动的振动方程为
(A2A1)c
o2s(t)
T2
.
A2 x A1
x1(t) t
O
T/2
(A)
A
O
A/2
x
(B)
A/2
O
x
A
A
(C )
O
A/2
x
(D)
A/2
O
x
A
3.一单摆,把它从平衡位置拉开,使摆线与竖
如用余弦函数表 示其运动方程,则该单摆振动的初位相为:
(A); (B);
l
l
(C)0;
(D)/2
A
A
[ B,C ]
(A) xA= at + bcost; (B) xB= asint + bcost; (C) xC= asint + bcos2t; (D) xD= asint cost 其中 a、b、 均为大于零的常量,则其中
作谐振动的质点为:
[ B,D ]
2.一物体做谐振动,振幅为 A,在起始时刻质点 的位移为 A/2 且向 x 轴的正方向运动,代表此 谐振动的旋转矢量图为: [ D ]
t k k 0,1,2
(3) 在__t___2_k___1___ s时加速度取正的最大值.
2x (cm)
t (s) O 12
6.如图所示,M静止地放置在光滑的水平面上,质量 为m的子弹以水平速度v1射入M中,与之一起运动。选 m、M开始共同运动的时刻为 t = 0,求固有频率、振 幅和初相位。
解: k
M m
碰撞过程中动量守恒:
k
M
V1 m
v0
mv1 M m
12(Mm)v02
1k 2
A 2
A
m2 k(Mm)
v1
或A
x02
v0
2
m2 k(M m)
v1
初始条件 t 0 x0 0 v0 0
2
k
M
V1 m
0
x
A
ox
7. 两个弹簧串联构成弹簧系统,劲度系数 分别为k1、k2 ,求弹簧系统的k。
解: m位移x,两弹簧伸 长各为x1、x2,
k1
k2
m
x
k1x1k2x2k x k k1k2
xx1x2
k1 k2
讨论:如图
k ?
k1
k k1k2 k1 k2
k2
如果一根弹簧被剪成n段,取其中一段,则 m
k? knk
x
讨论:如图
k ?
k xk1xk2x
kk1k2
k1
k2
m
8.一轻弹簧k=200N·m1,质量 4kg 的物体悬挂在 下端,使其在平衡位置下方 0.1m 处由静止开始 运动,若由此时刻开始计时,求:
o
0.1m
x
(2)物体在平衡位置上方 5cm时,弹簧对物体的拉力
mgf k x
f 29.2N
(3)物体从第一次越过平衡
位置时刻起到它运动到上方
5cm 处所需要的最短时间。
A
t
t 0 6
ox t0.07s4
o
0.1m
x
9.用余弦函数描述一简谐振动,已知振幅为
A,周期为T,初位相 = -/3,则振动曲线为
T
x2(t)
《振动》
小结 习题课
一、谐振动的基本规律
1. 动力学特征:
Fk x
2. 运动学特征:
d2x dt2
2x
0
x A co t s )(
v A si tn ) (
a A 2co t s( )
3. 能量特征
动能 Ek1 2kA 2si2n (t)
势能 Ep1 2kA 2co 2( st)
机械能 E 1 kA2 2
9
同方向同频率谐振动合成
xAc ots()
A A 1 2 A 2 2 2 A 1 A 2 co 2 s 1 )(
tgA A1 1scio n1 1s A A2 2scio n2 2s
21 2 k AA1A2
2 1 (2 k 1 ) A|A1A2|
1.若A、B、C、D四质点的运动方程分别为:
