2017年高考数学文黄金易错点:专题15-椭圆、双曲线、抛物线含答案
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)
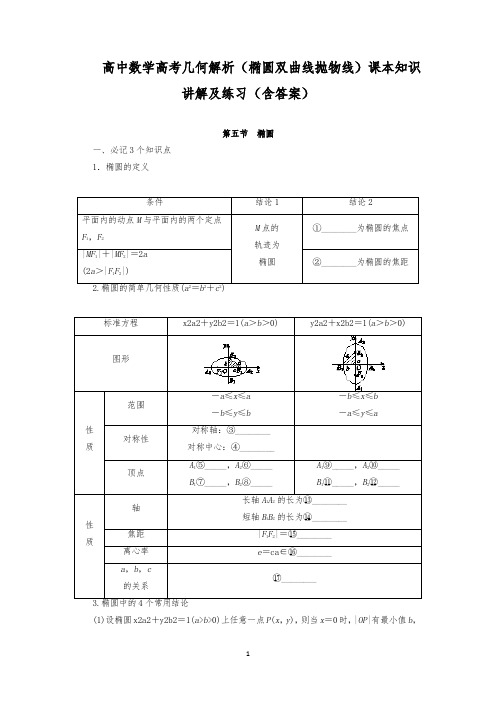
高中数学高考几何解析(椭圆双曲线抛物线)课本知识讲解及练习(含答案)第五节椭圆一、必记3个知识点1.椭圆的定义(1)设椭圆x2a2+y2b2=1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最小值b,这时,P在短轴端点处;当x=±a时,|OP|有最大值a,这时,P在长轴端点处.(2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a是斜边长,a2=b2+c2.(3)已知过焦点F1的弦AB,则△ABF2的周长为4a.(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c.二、必明3个易误点1.椭圆的定义中易忽视2a>|F1F2|这一条件,当2a=|F1F2|其轨迹为线段F1F2,当2a<|F1F2|不存在轨迹.2.求椭圆的标准方程时易忽视判断焦点的位置,而直接设方程为x2a2+y2b2=1(a>b>0).3.注意椭圆的范围,在设椭圆x2a2+y2b2=1(a>b>0)上点的坐标为P(x,y)时,则|x|≤a,这往往在求与点P有关的最值问题中特别有用,也是容易被忽略而导致求最值错误的原因.三、技法1.求椭圆标准方程的2种常用方法(1)直接求出a,c来求解e.通过已知条件列方程组,解出a,c的值.(2)构造a,c的齐次式,解出e.由已知条件得出关于a,c的二元齐次方程,然后转化为关于离心率e的一元二次方程求解.(3)通过取特殊值或特殊位置,求出离心率.提醒:在解关于离心率e的二次方程时,要注意利用椭圆的离心率e∈(0,1)进行根的取舍,否则将产生增根.3.求解最值、取值范围问题的技巧(1)与椭圆几何性质有关的问题要结合图形进行分析,即使画不出图形,思考时也要联想到一个图形.(2)椭圆的范围或最值问题常常涉及一些不等式.例如,-a≤x≤a,-b≤y≤b,0<e<1,在求椭圆的相关量的范围时,要注意应用这些不等关系.(3)最值问题,将所求列出表达式,构造基本不等式或利用函数单调性求解.4.判断直线与椭圆位置关系的四个步骤第一步:确定直线与椭圆的方程.第二步:联立直线方程与椭圆方程.第三步:消元得出关于x(或y)的一元二次方程.第四步:当Δ>0时,直线与椭圆相交;当Δ=0时,直线与椭圆相切;当Δ<0时,直线与椭圆相离.5.直线被椭圆截得的弦长公式设直线与椭圆的交点坐标为A(x1,y1),B(x2,y2),则|AB|=(1+k2)[(x1+x2)2-4x1x2])=(y1+y2)2-4y1y2])(k为直线斜率).参考答案①F1,F2②|F1F2|③x轴,y轴④坐标原点⑤(-a,0)⑥(a,0)⑦(0,-b)⑧(0,b)⑨(0,-a)⑩(0,a)⑪(-b,0)⑫(b,0)⑬2a⑭2b⑮2c⑯(0,1)⑰c2=a2-b2第六节双曲线一、必记3个知识点1.双曲线的定义(1)平面内与两个定点F1、F2(|F1F2|=2c>0)的距离①________________为非零常数2a(2a<2c)的点的轨迹叫做双曲线.这两个定点叫做双曲线的②________,两焦点间的距离叫做③________.(2)集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a,c为常数且a>0,c>0.(ⅰ)当④________________时,M点的轨迹是双曲线;(ⅱ)当⑤________________时,M点的轨迹是两条射线;(ⅲ)当⑥________________时,M点不存在.2.双曲线的标准方程和几何性质⑧________x ∈对称轴:⑪________对称中心:⑫________顶点坐标:A 1⑮______,A 2⑯________⑱____________c =⑳________|=21________;线段________;a 叫做双曲线的虚半轴长>b >0)(1)双曲线为等轴双曲线⇔双曲线的离心率e =2⇔双曲线的两条渐近线互相垂直.(2)渐近线的斜率与双曲线的焦点位置的关系:当焦点在x 轴上时,渐近线斜率为±ba,当焦点在y 轴上时,渐近线斜率为±ab.(3)渐近线与离心率.x2a2-y2b2=1(a >0,b >0)的一条渐近线的斜率为ba=e2-1.(4)若P 为双曲线上一点,F 为其对应焦点,则|PF |≥c -a .二、必明4个易误点1.双曲线的定义中易忽视2a <|F 1F 2|这一条件.若2a =|F 1F 2|,则轨迹是以F 1,F 2为端点的两条射线,若2a >|F 1F 2|则轨迹不存在.2.双曲线的标准方程中对a ,b 的要求只是a >0,b >0,易误认为与椭圆标准方程中a ,b 的要求相同.若a >b >0,则双曲线的离心率e ∈(1,2);若a =b >0,则双曲线的离心率e =2;若0<a <b ,则双曲线的离心率e >2.3.注意区分双曲线中的a ,b ,c 大小关系与椭圆a ,b ,c 关系,在椭圆中a 2=b 2+c 2,而在双曲线中c2=a2+b2.4.易忽视渐近线的斜率与双曲线的焦点位置关系.当焦点在x轴上,渐近线斜率为±ba,当焦点在y轴上,渐近线斜率为±ab.三、技法1.双曲线定义的应用(1)判定满足某条件的平面内动点的轨迹是否为双曲线,进而根据要求可求出曲线方程;(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合||PF1|-|PF2||=2a,运用平方的方法,建立|PF1|与|PF2|的关系.[注意]在应用双曲线定义时,要注意定义中的条件,搞清所求轨迹是双曲线,还是双曲线的一支,若是双曲线的一支,则需确定是哪一支.2.求双曲线标准方程的一般方法(1)待定系数法:设出双曲线方程的标准形式,根据已知条件,列出参数a,b,c的方程并求出a,b,c的值.与双曲线x2a2-y2b2=1有相同渐近线时,可设所求双曲线方程为:x2a2-y2b2=λ(λ≠0).(2)定义法:依定义得出距离之差的等量关系式,求出a的值,由定点位置确定c的值.3.求双曲线离心率或其范围的方法(1)求a,b,c的值,由c2a2=a2+b2a2=1+b2a2直接求e.(2)列出含有a,b,c的齐次方程(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.4.求双曲线的渐近线方程的方法求双曲线x2a2-y2b2=1(a>0,b>0)的渐近线的方法是令x2a2-y2b2=0,即得两渐近线方程为:xa±yb=0.参考答案①之差的绝对值②焦点③焦距④2a<|F1F2|⑤2a=|F1F2|⑥2a>|F1F2|⑦x≥a或x≤-a⑧y≥a或y≤-a⑨x轴,y轴⑩坐标原点⑪x轴,y轴⑫坐标原点⑬(-a,0)⑭(a,0)⑮(0,-a)⑯(0,a)⑰y=±ba x⑱y=±ab x⑲ca⑳a2+b2212a222b23a2+b2第七节抛物线一、必记2个知识点1.抛物线定义、标准方程及几何性质x轴⑤________y轴⑥________O(0,0)O(0,0)O(0,0)O(0,0)F⑦________⑧________⑨________设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),则(1)x1x2=p24,y1y2=-p2.(2)弦长|AB|=x1+x2+p=2psin2α(α为弦AB的倾斜角).(3)以弦AB为直径的圆与准线相切.(4)通径:过焦点且垂直于对称轴的弦,长等于2p.二、必明2个易误点1.抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与直线垂直的直线.2.抛物线标准方程中参数p易忽视,只有p>0,才能证明其几何意义是焦点F到准线l 的距离,否则无几何意义.三、技法1.应用抛物线定义的2个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P(x,y)到焦点F的距离|PF|=|x|+p2或|PF|=|y|+p2.2.求抛物线的标准方程的方法(1)求抛物线的标准方程常用待定系数法,因为未知数只有p,所以只需一个条件确定p值即可.(2)因为抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量.3.确定及应用抛物线性质的技巧(1)利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化为标准方程.(2)要结合图形分析,灵活运用平面几何的性质以图助解.4.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.提醒:涉及弦的中点、斜率时,一般用“点差法”求解.参考答案①相等②y2=-2px(p>0)③x2=-2py(p>0)④x2=2py(p>0)⑤x轴⑥y轴⑦F(-p2,0)⑧F(0,-p2)⑨F(0,p2)⑩e=1⑪x=-p2⑫y=-p2⑬-y0+p2⑭y0+p2⑮y≤0⑯y≥0。
椭圆-双曲线-抛物线练习题及答案

1、已知椭圆方程为2212332x y +=,则这个椭圆的焦距为〔 〕A .6B .3C .D .2、椭圆22421xy +=的焦点坐标是〔 〕A .(B .(0,C .11(0,),(0,)22-D .(22- 3、12F F ,是定点,且12FF =6,动点M 满足12MF +MF 6=,则M 点的轨迹方程是〔 〕A .椭圆B .直线C .圆D .线段 4、已知方程221xmy +=表示焦点在y 轴上的椭圆,则m 的取值X 围是〔 〕A .m <1B .-1<m <1C .m >1D .0<m <1 5、过点〔3,-2〕且与椭圆224936xy +=有相同焦点的椭圆方程是〔 〕A .2211510x y += B .222211510x y += C .2211015x y += D .222211015x y += 6、若直线1y mx =+与椭圆2241x y +=只有一个公共点,那么2m 的值是〔 〕A .12 B .34 C .23 D .457、已知椭圆C :22192x y +=,直线l :110xy +=,点P 〔2,-1〕,则〔 〕 A .点P 在C 内部,l 与C 相交 B .点P 在C 外部,l 与C 相交 C .点P 在C 内部,l 与C 相离 D .点P 在C 外部,l 与C 相离8、过椭圆C :22221x y a b+=的焦点引垂直于x 轴的弦,则弦长为〔 〕A .22b aB .2b aC .b a D .2b a9、抛物线220xy +=的准线方程是〔 〕A .18x =B .18x =-C .14x =-D .14x = 10、抛物线22(0)y px p =>上一点M 与焦点F 的距离MF =2p ,则点M 的坐标是〔 〕A .3()2p B .3(,)2p C .3,)2p D .3(,)2p 11、若抛物线214y x =上一点P 到焦点F 的距离为5,则P 点的坐标是〔 〕A .(4,4)±B .(4,4)±C .79(168±, D .79()816±, 12、已知抛物线24xy =,过焦点F,倾斜角为4π的直线交抛物线于A,B 两点,则线段AB 的长为〔 〕A .8B .C .6D .13、抛物线260x ay-=的准线方程是34x =-,则a 等于〔 〕 A .2 B .-2 C .3 D .-314、以抛物线的焦点弦为直径的圆与抛物线的准线的位置关系是〔 〕A .相离B .相切C .相交D .不能确定15、已知直线l 是抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A,B 两点,12AB =,P 为C 准线上一点,则ABPS=〔 〕A .18B .24C .36D .48 16、已知抛物线C :24y x =的焦点为F,直线24y x =-与C 相交于A 、B 两点,则cos AFB ∠=〔 〕A .115 B .35 C .45- D .35- 17、设抛物线28y x =的焦点为F,准线为l ,P 为抛物线上一点,PA ⊥l ,A 为垂足,如果直线AF 的斜率为则PF =〔 〕A .B .8C .D .1618、设斜率为2的直线l 过抛物线2(0)y ax a =≠的焦点F,且和y 轴交于点A,若△OAF 〔O 为坐标原点〕的面积为4,则抛物线方程为〔 〕 A .24y x =± B .28y x =± C .24y x = D .28y x =19、若点O 和点F 〔-2,0〕分别是双曲线2221(0)x y a a-=>的中心和左焦点,点P 为双曲线右支上任意一点,则OP FP ⋅的取值X 围是〔 〕A .)3⎡-+∞⎣B .)3⎡++∞⎣ C .7,4⎡⎫-+∞⎪⎢⎣⎭ D .7,4⎡⎫+∞⎪⎢⎣⎭20、已知椭圆22221(0)x y a b a b+=>>,斜率为1的直线l 与椭圆相交,截得的弦长为正整数的直线l 恰有3条,则b 的值为〔 〕A B C D 21、已知方程2213+2x y k k+=-表示椭圆,则k 的取值X 围为〔 〕 22、22112x y m m+=--表示焦点在y 轴上的椭圆,则m 的取值X 围是〔 〕23、若椭圆2215x y m+=的离心率5e =,则m 的值是〔 〕24、已知直线1y x =-+与椭圆22221x y a b+=〔0a b >>〕相交于A 、B 两点,且线段AB 的中点在直线L :20x y-=上,则此椭圆的离心率为〔 〕25、若椭圆221369x y +=的弦被点A 〔4,2〕平分,那么这条弦所在的直线方程是〔 〕 26、以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为〔 〕 27、若,x y R ∈,且22326xy +=,则x y +的最大值是〔 〕,22x y +的最小值是〔 〕答案:1~5:ACDDA 6~10:BAAAB 11~15:BAABC 16~20:CBBBC21、11(3,)(,2)22k ∈--⋃-22、3(,1)(1,)2-∞-⋃-23、3或25324225、x+2y-8=026、27;2双曲线习题1、在平面直角坐标系中,已知双曲线221412x y -=上一点M 的横坐标为3,则点M 到此双曲线的右焦点距离为〔〕2、设12,F F 为双曲线2214x y -=的两个焦点,点P 在双曲线上,且满足12120F PF ∠=,则12F PF S △=〔〕3、双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为〔〕4、过双曲线22221(00)x y a b a b-=>,>的右顶点A 作斜率为-1的直线,该直线与双曲线两渐近线的交点分别为B,C,若1AB=BC 2,则双曲线的离心率是〔〕 5、已知1F :2210240xy x +++=,2F :221090x y x +-+=,动圆M 与定圆12,F F 都外切,求动圆圆心M 的轨迹方程.6、已知点B 〔6,0〕,C 〔-6,0〕,过B 的直线l 与过点C 的直线m 相交于点A,设l 的斜率为1k ,直线m 的斜率为2k 〔1〕若1249k k =,求点A 的轨迹方程,并说明此轨迹是何种曲线? 〔2〕若12k k a =,其中0a ≠,求点A 的轨迹方程,并根据a 的取值讨论此轨迹是何种轨迹?7、中心在原点,焦点在x 轴上的一个椭圆与双曲线有共同的焦点12,F F ,且12F F =,椭圆的长半轴与双曲线的实半轴之差为4,离心率之比为3:7 〔1〕求两曲线方程〔2〕若P 为这两双曲线的一个交点,求12cos F PF ∠的值8、已知双曲线的中心在原点,焦点12,F F 在坐标轴上,,且过点(4,〔1〕求双曲线方程;〔2〕若点M 〔3,m 〕在双曲线上,求证:12MF MF ⊥ 〔3〕求2F MF S △9、若一个椭圆长轴长,短轴长和焦距成等差数列,则椭圆离心率为e =〔〕10、椭圆中心在原点,左右焦点12,F F 在x 轴上,A,B 是椭圆顶点,P 是椭圆上一点<点P 在第二象限>,且1PF x ⊥轴,2PF ∥AB,则e =〔 〕11、已知椭圆22221(00)x y a b a b+=>,>的左右焦点分别为12-c,0,(,0)F F c ().椭圆上存在点P 〔异于长轴的端点〕,使得1221sin sin c PF F a PF F ⋅∠=∠,则该椭圆的离心率X 围是〔〕12、已知P 是以12,F F 为焦点的椭圆22221(00)x y a b a b +=>,>上一点,若120PF PF ⋅=,121tan 2PF F ∠=,则离心率e =〔〕 13、已知P 为椭圆2214x y +=上任意一点,12,F F 是椭圆的两个焦点,求 〔1〕12PF PF ⋅的最大值〔2〕2212PF +PF 的最小值答案:1、4 2 3、3 4 5、22441(0)991x y x -=< 6、略7、〔1〕椭圆:2214936x y +=双曲线:221494x y -=〔2〕458、〔1〕22166x y -=〔2〕略〔3〕6 9、3510 1 1、1,1) 1213、4;8。
易错点17 双曲线答案-备战2023年高考数学易错题

易错点17 双曲线易错点1:焦点位置不确定导致漏解 要注意根据焦点的位置选择双曲线方程的标准形式,知道,,a b c 之间的大小关系和等量关系:易错点2:双曲线的几何性质,渐近线、离心率、焦半经、通径; 易错点3:直线与双曲线的位置关系(1)忽视直线斜率与渐近线平行的情况;(2)在用椭圆与直线联立求解时,消元后得到的方程中要注意:二次项的系数是否为零?判别式的限制.(求交点,弦长,中点,斜率,对称,存在性问题都在下进行).题组一:定义与标准方程1.(2015福建理)若双曲线22:1916x y E -= 的左、右焦点分别为12,F F ,点P 在双曲线E 上,且13PF =,则2PF 等于( )A .11B .9C .5D .3 【答案】B【解析】由双曲线定义得,即,解得,故选B . 2.(2019年新课标1卷)已知椭圆C 的焦点为1(1,0)F -,2(1,0)F ,过2F 的直线与C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为( ) A .2212x y +=B .22132x y +=C .22143x y +=D .22154x y +=【答案】B【解答】∵22||2||AF F B =,∴23AB BF =, 又1||||AB BF =,∴|BF 1|=3|BF 2|, 又|BF 1|+|BF 2|=2a ,∴|BF 2|=2a , ∴|AF 2|=a ,|BF 1|=32a , 在Rt △AF 2O 中,cos ∠AF 2O =1a, 1226PF PF a -==236PF -=29PF =在△BF 1F 2中,由余弦定理可得cos ∠BF 2F 1=223422222a a a ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭⨯⨯, 根据cos∠AF 2O +cos∠BF 2F 1=0,可得214202a a a-+=,解得a 2=3,∠a =b 2=a 2﹣c 2=3﹣1=2.所以椭圆C 的方程为22132x y +=故选:B .3.(2017新课标Ⅲ理)已知双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线方程为2y x =,且与椭圆221123x y +=有公共焦点,则C 的方程为 A .221810x y -= B .22145x y -= C .22154x y -= D .22143x y -= 【答案】B【解析】由题意可得:b a =3c =,又222a b c +=,解得24a =,25b =, 则C 的方程为2145x y 2-=,故选B . 4.(2016年新课标1卷)已知方程132222=--+nm y n m x 表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是( ) A.(-1,3) B.(-1,3) C.(0,3) D.(0,3) 【答案】A【解析】由题意知c=2,()()2224=3,1m n m n m ++-=解得,因为方程132222=--+nm y n m x 表示双曲线, 所以()()()()2230,130m n m n n n +->+->可得 解得-1<n<3,故选A.题组二:焦点三角形5.(2020·新课标∠文)设12,F F 是双曲线22:13y C x -=的两个焦点,O 为坐标原点,点P在C 上且||2OP =,则12PF F △的面积为( ) A .72B .3C .52D .2【答案】B【解析】由已知,不妨设12(2,0),(2,0)F F -, 则1,2a c ==,∵121||1||2OP F F ==,∴点P 在以12F F 为直径的圆上, 即12F F P 是以P 为直角顶点的直角三角形,故2221212||||||PF PF F F +=, 即2212||||16PF PF +=,又12||||22PF PF a -==,∴2124||||PF PF =-=2212||||2PF PF +-12||||162PF PF =-12||||PF PF ,解得12||||6PF PF =,∴12F F P S =△121||||32PF PF =,故选B . 6.【2020年高考全国Ⅲ卷理数11】已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点12,F F ,离心率为5.P 是C 上的一点,且P F P F 21⊥.若21F PF ∆的面积为4,则=a ( )A .1B .2C .4D .8 【答案】A 【解析】解法一:5ca=,c ∴=,根据双曲线的定义可得122PF PF a -=, 12121||42PF F PF F S P =⋅=△,即12||8PF PF ⋅=, 12F P F P ⊥,()22212||2PF PF c ∴+=,()22121224PF PF PF PF c ∴-+⋅=,即22540a a -+=,解得1a =,故选A .解法二:由题意知,双曲线的焦点三角形面积为2tan 221θb S F PF =.∴︒45tan 2b =4,则2=b , 又∵5==ace ,∴1=a . 解法三:设n PF m PF ==21,,则421==mn S F PF ,a n m 2=-,5,4222===+ace c n m ,求的1=a .7.(2015全国1卷)已知00(,)M x y 是双曲线22:12x C y -=上的一点,12,F F 是C 上的两个焦点,若120MF MF <,则0y 的取值范围是( )A.⎛⎝⎭B.⎛ ⎝⎭C.⎛ ⎝⎭D.⎛ ⎝⎭【答案】A【解析】法1:根据题意12,F F的坐标分别为()),,所以()()1002003,,3,,MF x y MF xy =---=--所以()()2221200000003,,3310MF MF x y x y x y y ⋅=-⋅-=-+=-<所以033y -<<.故选A. 秒杀法2:012==90F MF θ∠当 当由等面积得:33y ⇒y 212tan00212===F F b S θ 因为120MF MF <,所以12F MF ∠为钝角,根据变化规律,可得3333-0<<y 故选A.8.(2016全国II 理)已知1F ,2F 是双曲线E :22221x y a b-=的左、右焦点,点M 在E 上,1MF 与x 轴垂直,211sin 3MF F ∠=,则E 的离心率为( )AB .32C D .2 【答案】A【解析】设1(,0)F c -,将x c =-代入双曲线方程,得22221c y a b -=,化简得2by a=±,因为211sin 3MF F ∠=,所以222212112||tan ||222b MF b c a a MF F F F c ac ac -∠=====12222c a e a c e -=-=,所以210e --=,所以e =A . 题组三:渐进线9.(2019全国3卷)双曲线的右焦点为,点在的一条渐近线上,为22:142x y C -=F P C O坐标原点,若,则的面积为ABC.D.【答案】A【解析】双曲线的右焦点为,渐近线方程为:,不妨设点在第一象限,可得,,所以的面积为:,故选A.10.(2018全国2卷)双曲线22221(0,0)-=>>x ya ba bA.=y B.=yC.2=±y x D.=y x【答案】A【解析】解法一由题意知,==cea,所以=c,所以==b,所以=ba=±=by xa,故选A .解法二由===cea,得=ba,所以该双曲线的渐近线方程为=±=by xa.故选A.11.(2017天津理)已知双曲线22221(0,0)x ya ba b-=>>的左焦点为F,.若经过F和(0,4)P两点的直线平行于双曲线的一条渐近线,则双曲线的方程为A.22144x y-=B.22188x y-=C.22148x y-=D.22184x y-=【答案】B【解析】设(,0)F c-,双曲线的渐近线方程为by xa=±,由44PFkc c-==-,由题意有4bc a=,又ca=222c a b=+,得b=,a=,故选B.12.(2015新课标1文)已知双曲线过点,且渐近线方程为,则该双曲||||PO PF=PFO∆()22:142x yC-=F2y x=±P tan2POF∠=P PFO△124=)3,4(xy21±=线的标准方程为 .【答案】2214x y -=【解析】∵双曲线的渐近线方程为,故可设双曲线的方程为22(0)4x y λλ-=>,又双曲线过点,∴2244λ-=,∴1λ=,故双曲线的方程为2214x y -=. 题组四:离心率13.(2021年高考全国甲卷理科)已知12,F F 是双曲线C 的两个焦点,P 为C 上一点,且121260,3F PF PF PF ∠=︒=,则C 的离心率为 ( )A.2B.2CD【答案】A 【解析】因为213PF PF =,由双曲线的定义可得12222PF PF PF a -==,所以2PF a =,13PF a =;因为1260F PF ∠=︒,由余弦定理可得2224923cos60c a a a a =+-⨯⋅⋅︒,整理可得2247c a =,所以22274a c e ==,即2e =.故选:A14.(2021全国乙卷理科)设B 是椭圆2222:1(0)x y C a b a b+=>>的上顶点,若C 上的任意一点P 都满足||2PB b ≤,则C 的离心率的取值范围是( )A.2⎫⎪⎢⎪⎣⎭B .1,12⎡⎫⎪⎢⎣⎭ C.0,2⎛ ⎝⎦D .10,2⎛⎤ ⎥⎝⎦【答案】C【解析】设()00,P x y ,由()0,B b ,因为2200221x y a b+=,222a b c =+,所以()()2223422222220000022221y c b b PB x y b a y b y a b b b c c ⎛⎫⎛⎫=+-=-+-=-++++ ⎪ ⎪⎝⎭⎝⎭,因为0b y b -≤≤,当32bb c-≤-,即22b c ≥时,22max 4PB b =,即max 2PB b =,符合x y 21±=)3,4(题意,由22b c ≥可得222a c ≥,即202e <≤; 当32b b c->-,即22b c <时,42222max b PB a b c =++,即422224b a b b c ++≤,化简得,()2220cb-≤,显然该不等式不成立.故选:C .15.(2019全国1卷)已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1F ,2F ,过1F 的直线与C 的两条渐近线分别交于A ,B 两点.若1F A AB =,120F B F B =,则C 的离心率为 . 【答案】2【解析】如图,1F A AB =,120F B F B =,∴OA ⊥F1B , 则F 1B :()a y x c b =+①,渐近线OB 为by x a=② 联立①②,解得B 22222,a c abc b a b a ⎛⎫⎪--⎝⎭, 则222212222a c abc F B c b a b a ⎛⎫⎛⎫=++ ⎪ ⎪--⎝⎭⎝⎭, 222222222a c abc F B c b a b a ⎛⎫⎛⎫=-+ ⎪ ⎪--⎝⎭⎝⎭, 又2221212F B F B F F +=,所以2222222222222224a c abc a c abc c c c b a b a b a b a ⎛⎫⎛⎫⎛⎫⎛⎫+++-+= ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭⎝⎭ 整理得:22222223,3,4b a a a a c 所以c 即=-==,故C 的离心率为2ce a== 16.(2019全国2卷)设为双曲线的右焦点,为坐标原点,以为直径的圆与圆交于,两点,若,则的离心率为( ). A .B .C .2D .【答案】AF 2222:1(0,0)x y C a b a b-=>>O OF 222x y a +=P Q ||||PQ OF =C【解析】法1:由题意,把代入,得,再由,得,即,所以,解得.故选A .法2:如图所示,由可知为以 为直径圆的另一条直径, 所以,代入得, 所以,解得.故选A .法3:由可知为以为直径圆的另一条直径,则,.故选A . 题组五:距离17.【2020年高考北京卷12】已知双曲线22:163x y C -=,则C 的右焦点的坐标为________;C 的焦点到其渐近线的距离是__________.【答案】(3,0),3【解析】∵双曲线22163x y -=,∴26a =,23b =,222639c a b =+=+=,∴3c =,∴右焦点坐标为(3,0),∵双曲线中焦点到渐近线距离为b ,∴3b =.18.【2018·全国Ⅲ文】已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2,则点(4,0)到C 的渐近线的距离为 A .2B .2C .322D .22【答案】D 【解析】21()2c b e a a==+=,1b a ∴=,∴双曲线C 的渐近线方程为0x y ±=,∴2c x =222x y a +=2224c PQ a =-PQ OF =2224ca c -=222a c =222c a=2c e a ==PQ OF =PQ OF ,22cc P ⎛⎫±⎪⎝⎭222x y a +=222a c =222c a=2c e a ==PQ OF =PQ OF 12222OP a OF c==⋅=2c e a ==点(4,0)到渐近线的距离d ==,故选D . 19.(2018全国1卷)已知双曲线C :x 23 - y 2=1,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐近线的交点分别为M 、N.若ΔOMN 为直角三角形,则|MN|=____. 【答案】3【解析】因为双曲线2213-=x y的渐近线方程为=±y x ,所以60∠=MON .不妨设过点F 的直线与直线3=y x 交于点M ,由∆OMN 为直角三角形,不妨设90∠=OMN ,则60∠=MFO ,又直线MN 过点(2,0)F ,所以直线MN的方程为2)=-y x ,由2)⎧=-⎪⎨=⎪⎩y x y x,得322⎧=⎪⎪⎨⎪=⎪⎩x y,所以3(2M ,所以||==OM|||3==MN OM . 20.【2020年高考浙江卷8】已知点()()()0,0,2,0,2,0O A B -.设点P 满足–2PA PB =,且P为函数y =OP =( )A.2 B.5CD【答案】D【解析】由条件可知点P 在以,A B 为焦点的双曲线的右支上,并且2,1c a ==,∴23b =,方程为()22103y x x -=> 且点P 为函数y =上的点,联立方程()22103y x x y ⎧-=>⎪⎨⎪=⎩,解得:2134x =,2274y =,OP ∴==,故选D .1.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,AB =C 的实轴长为( )B. 4 D.8 【答案】C【解析】设等轴双曲线C:2220x y a a ,x y 162=的准线:4l x因为C 与抛物线x y 162=的准线交于,A B 两点,AB = 所以4,23,4,23AB ,将A 点代入双曲线方程得2224234,2,24a a a 所以,故选C.2.双曲线的渐进线方程为x y 21±=,且焦距为10,则双曲线方程为( ) A.152022=-y x B.120522=-y x 或152022=-y x C.120522=-y x D.1|520|22=-y x 【答案】D【解析】当焦点在x 轴时,渐进线方程为x y 21±=, 所以2221,210,2b c a b c a 又,解得25,5a b,所以双曲线的方程为221205x y .焦点在y 轴时,渐进线方程为x y 21±=, 所以2221,210,2a c abc b 又,解得5,25a b,所以双曲线的方程为221205x y .故选D.3.已知双曲线E 的中心为原点,(3,0)F 是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为(12,15)N --,则E 的方程式为( )A.22136x y -=B.22145x y -=C.22163x y -= D.22154x y -= 【答案】B【解析】由双曲线E 的中心为原点,(3,0)P 是E 的焦点可设双曲线的方程为2222221(9)x y a b a b -=+=,设1122(,),(,)A x y B x y ,即 2222112222221,1x y x y a b a b -=-= 则22121222121212015115312y y x x b b x x a y y a -+-+=⋅=⋅==-+-+,则22225,5,44b b a a ===,故E 的方程式为22145x y -=.应选B . 4. 已知双曲线C :)0,0(12222>>=-b a by a x 的离心率为25,则C 的渐近线方程为( )A.x y 41±=B.x y 31±=C.x y 21±= D.x y ±= 【答案】C【解析】由题意22511,22c b b e a a a 得==+==,所以C 的渐近线方程为,21x a b y ±=±=故选C. 5. 已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为( )A.3B.3C.3mD.3m 【答案】A【解析】由C:223(0)x my m m -=>得2221,33,33,33x y c m c m m -==+=+ ()33,0,Fm 设+33y x m一条渐近线为=即0x m y -=, 则点F 到C 得一条渐近线得距离333,1m d m+==+故选A.6.P 是双曲线右支上的一点,F 1、F 2分别是左、右焦点,且焦距为2c ,则的内切圆的圆心的横坐标为 . 【答案】x=a【解析】如图所示:()()12,0,,0F c F c -,设内切圆与x 轴的切点是点H ,PF 1,PF 2与内切圆的切点分别为M 、N ,由双曲线定义有|PF 1|-|PF 2|=2a ,由圆的切线长定理知, |PM|=|PN|,所以|MF 1|-|NF 2|=2a ,即|HF 1|-|HF 2|=2a,设内切圆的圆心横坐标为x ,)0,0(12222>>=-b a by a x 21F PF ∆则点H 的横坐标为x ,所以(x+c)-(c -x)=2a ,得x=a.7.已知F 1、F 2为双曲线C :122=-y x 的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则P 到x 轴的距离为________.【解析】法1:设12,,PF m PF n m n 不妨设==>,可知1,1,a b c ===,根据双曲线定义222,24m n a m n mn 即-=+-=①, 在ΔPF 1F 2中,根据余弦定理22201212122cos60,F F PF PF PF PF =+-228m n mn 即+-=②联立①②得4mn =,设P 到x 轴得距离为h ,则011sin 60,22h mn h ⨯==所有秒杀法2:由等面积得:4⇒3πsin 2132θtan 21212====PF PF PF PF b S设P 到x 轴得距离为h ,01211sin 60,22h PF PF h 所有⨯==8.已知A ,B 为双曲线E 的左,右顶点,点M 在E 上,∆ABM 为等腰三角形,且顶角为120°,则E 的离心率为_____.【解析】根据题意,设双曲线()222210,0x y a b a b-=>>,不妨设点M 在第一象限,所以|AB|=|BM|=2a,∠MBA=1200,作MH ⊥x 轴于点H ,则∠MBH=600,故|BH|=a,(),2,MH M a =将点M 代入()222210,0x y a b a b-=>>得a=b,所以e =9.若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为___.【答案】2【解析】双曲线C 的渐近线方程为0bx ay ±=,圆心(2,0)到渐近线的距离为2bd c==,圆心(2,0)到弦的距离也为d ==所以2b c =222c a b =+,所以得2c a =,所以离心率2ce a== 10.设F 1,F 2是双曲线C: x 2a 2-y2b 2=1(a >0,b >0)的左,右焦点,O 是坐标原点.过F 2作C的一条渐近线的垂线,垂足为P .若|PF 1|=6|OP|,则C 的离心率为_____.【解析】法1:不妨设一条渐近线的方程为by x a=, 则2F 到by x a =的距离d b ==, 在2Rt F PO ∆中,2||F O c =,所以||PO a =,所以1||PF =,又1||F O c =,所以在1F PO ∆与2Rt F PO ∆中,根据余弦定理得22212)cos cos 2a c aPOF POF ac c+-∠==-∠=-,即2223)0a c +-=,得223a c =.所以ce a==. 法2:选C 设P(t,- b a t),∵PF 2与y=- ba x 垂直,∴-bt a(t-c)=a b ,解得t=a 2c 即P(a 2c ,- abc ) ∴|OP|=(a 2c )2+(-ab c)2=a ,|PF 1|=(a 2c +c)2+(-ab c)2,依题有(a 2c +c)2+(- ab c )2=6a 2,化简得c 2=3a 2,即c e a ==。
椭圆、双曲线(含答案)

2017-11-11【双曲线】1.双曲线方程为,则它的右焦点坐标为 ( )CA 、B 、C 、D 、【解析】双曲线的,,,所以右焦点为. 【误区警示】本题考查双曲线的交点,把双曲线方程先转化为标准方程,然后利用求出c 即可得出交点坐标.但因方程不是标准形式,很多学生会误认为或,从而得出错误结论.2.已知直线l 过双曲线C 的一个焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,||AB 为C 的实轴长的2倍,C 的离心率为 (B ) (A(B(C ) 2 (D ) 33.若双曲线-=1(b>0)的渐近线方程式为y=,则b等于 。
【答案】1 【解析】由题意知,解得b=1。
【命题意图】本小题考查双曲线的几何性质、待定系数法,属基础题。
4.已知双曲线的离心率为2,焦点与椭圆221259x y +=的焦点相同,那么双曲线的焦点坐标为 ;渐近线方程为 。
答案:(,0)【提高】5.已知、为双曲线C:的左、右焦点,点P 在C 上,∠=,则( ) (A)2 (B)4 (C) 6 (D) 8B 【命题意图】本小题主要考查双曲线定义、几何性质、余弦定理,考查转化的数学思想,通过本题可以有效地考查考生的综合运用能力及运算能力. 【解析1】.由余弦定理得cos ∠P =4【解析2】由焦点三角形面积公式得:46.已知椭圆22122:1(0)x y C a b a b +=>>与双曲线222:14y C x -=有公共的焦点,2C 的一条渐近线与以1C 的长轴为直径的圆相交于,A B 两点,若1C 恰好将线段AB 三等分,则(C )A .2132a =B .213a =C .212b = D .22b =7.设、分别为双曲线的左、右焦点.若在双曲线右支上存在点,满足,且到直线的距离等于双曲线的实轴长,则该双曲线的渐近线方程为(A ) (B ) (C ) (D )解析:利用题设条件和双曲线性质在三角形中寻找等量关系,得出a 与b 之间的等量关系,可知答案选C ,本题主2221x y -=2⎛⎫ ⎪ ⎪⎝⎭2⎛⎫⎪ ⎪⎝⎭2⎛⎫⎪ ⎪⎝⎭)2211,2a b ==232c =2c =⎫⎪⎪⎝⎭222c a b =+21b =22b =22y b 2x 41x 2±122b =22221x y a b-=4±0y =1F 2F 221x y -=1F P 2F 06012||||PF PF =1F 2F 222121212||||||2||||PF PF F F PF PF +-()(22221212121212122221cos60222PF PF PF PF PF PF F F PF PF PF PF +--+-⇒=⇒=12||||PF PF = 1202201216011cot 1cot sin 602222F PF S b PF PF PF PF θ∆====12||||PF PF = 1F 2F 22221(0,0)x y a b a b-=>>P 212PF FF =2F 1PF 340x y ±=350x y ±=430x y ±=540x y ±=要考察三角与双曲线的相关知识点,突出了对计算能力和综合运用知识能力的考察,属中档题 8.设双曲线的一个焦点为,虚轴的一个端点为,如果直线与该双曲线的一条渐近线垂直,那么此双曲线的离心率为 ( )(A(B(C(D 解析:选D.不妨设双曲线的焦点在轴上,设其方程为:,则一个焦点为一条渐近线斜率为:,直线的斜率为:,, ,解得. 9.设O 为坐标原点,,是双曲线(a >0,b >0)的焦点,若在双曲线上存在点P ,满足∠P =60°,∣OP ∣,则该双曲线的渐近线方程为()(A )(B y=0 (C )=0 (D ±y=0解析:选D ,本题将解析几何与三角知识相结合,主要考察了双曲线的定义、标准方程,几何图形、几何性质、渐近线方程,以及斜三角形的解法,属中档题 【椭圆】10.已知椭圆x y +=221169的左、右焦点分别为F 1、F 2,点P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为 9411.已知椭圆C 的方程x y +=22143,试确定m 的取值范围,使得对于直线yx m =+4,椭圆C 上有不同两点关于直线对称.分析:椭圆上两点(,)x y 11,(,)x y 22,代入方程,相减得31212()()x x x x +-+412()y y +()y y 120-=又x x x +=122,y yy +=122,y y k x x -==--121214,代入得y x =3。
专题15 椭圆、双曲线、抛物线易错练兵-2018年高考数学文备考黄金易错点 含解析 精品

1.已知k <4,则曲线x 29+y 24=1和x 29-k +y 24-k =1有( )A .相同的准线B .相同的焦点C .相同的离心率D .相同的长轴 解析:∵k <4,∴曲线x 29+y 24=1和x 29-k +y 24-k =1都是椭圆.又9-4=9-k -(4-k ),∴两曲线的半焦距相等,故两个椭圆有相同的焦点. 答案:B2.双曲线x 24-y 2=1的顶点到其渐近线的距离等于( ) A.25 B.45 C.255 D.455解析:双曲线x 24-y 2=1的渐近线方程为y =±x2,即x ±2y =0,所以双曲线的顶点(±2,0)到其渐近线距离为25=255.答案:C3.以抛物线y 2=4x 的焦点为圆心,且与抛物线的准线相切的圆的方程是( ) A .(x -2)2+y 2=4 B .(x -1)2+y 2=4 C .(x -2)2+y 2=2 D .(x -1)2+y 2=24.若双曲线x 2a 2-y 2b2=1的离心率为3,则其渐近线方程为( )A .y =±2xB .y =±2xC .y =±12xD .y =±22x解析:双曲线的离心率e =ca=1+⎝ ⎛⎭⎪⎫b a2=3,可得b a=2,故所求的双曲线的渐近线方程是y =±2x .答案:B5.已知实数4,m,9构成一个等比数列,则圆锥曲线x 2+y 2m=1的离心率为( )A.306B.7C.306或7 D.56或76.已知直线l 与双曲线C :x 2-y 2=2的两条渐近线分别交于A ,B 两点,若AB 的中点在该双曲线上,O 为坐标原点,则△AOB 的面积为( ) A.12 B .1 C .2 D .4解析:由题意得,双曲线的两条渐近线方程为y =±x ,设A (x 1,x 1)、B (x 2,-x 2),∴AB 中点坐标为⎝ ⎛⎭⎪⎫x 1+x 22,x 1-x 22,∴⎝ ⎛⎭⎪⎫x 1+x 222-⎝ ⎛⎭⎪⎫x 1-x 222=2,即x 1x 2=2,∴S △AOB =12|OA |·|OB |=12|2x 1|·|2x 2|=x 1x 2=2,故选C. 答案:C7.已知F 1,F 2分别是椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点,若椭圆C 上存在点P ,使得线段PF 1的中垂线恰好经过焦点F 2,则椭圆C 离心率的取值范围是( ) A.⎣⎢⎡⎭⎪⎫23,1 B.⎣⎢⎡⎦⎥⎤13,22C.⎣⎢⎡⎭⎪⎫13,1D.⎝ ⎛⎦⎥⎤0,138.点F 为椭圆x 2a 2+y 2b2=1(a >b >0)的一个焦点,若椭圆上存在点A 使△AOF 为正三角形,那么椭圆的离心率为( ) A.22 B.32C.2-12D.3-1答案 D解析 如图所示,设F 为椭圆的右焦点,点A 在第一象限,由已知得直线OA 的斜率为k=tan60°=3,∴点A 的坐标为⎝ ⎛⎭⎪⎫c2,32c .∵点A 在椭圆上,∴c 24a 2+34c2b2=1,即c 24a 2+3c 24b2=1. ∴b 2c 2+3a 2c 2=4a 2b 2,又∵b 2=a 2-c 2,∴4a 4-8a 2c 2+c 4=0, ∴e 4-8e 2+4=0,∴e 2=4±23, 又∵e ∈(0,1),∴e =3-1.故选D.9.已知椭圆C 1:x 2m 2+y 2=1(m >0)与双曲线C 2:x 2n2-y 2=1(n >0)的焦点重合,e 1,e 2分别为C 1,C 2的离心率,则( ) A .m >n 且e 1e 2>1 B .m >n 且e 1e 2<1 C .m <n 且e 1e 2>1 D .m <n 且e 1e 2<1答案 A解析 由题意可得:m 2-1=n 2+1,即m 2=n 2+2, 又∵m >0,n >0,故m >n .又∵e 21·e 22=m 2-1m 2·n 2+1n 2=n 2+1n 2+2·n 2+1n2=n 4+2n 2+1n 4+2n 2=1+1n 4+2n 2>1,∴e 1·e 2>1. 10.已知双曲线C :x 23-y 2=1的左,右焦点分别为F 1,F 2,过点F 2的直线与双曲线C 的右支相交于P ,Q两点,且点P 的横坐标为2,则△PF 1Q 的周长为( ) A.1633 B .5 3 C.1433D .4 311.设抛物线E :y 2=2px (p >0)的焦点为F ,点M 为抛物线E 上一点,|MF |的最小值为3,若点P 为抛物线E 上任意一点,A (4,1),则|PA |+|PF |的最小值为( ) A .4+32B .7C .4+2 3D .1012.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)与抛物线y 2=8x 有一个共同的焦点F ,两曲线的一个交点为P ,若|PF |=5,则点F 到双曲线的渐近线的距离为( ) A. 3 B .2 C. 6 D .3答案 A解析 ∵抛物线y 2=8x 的焦点为F (2,0),∴双曲线x 2a 2-y 2b2=1(a >0,b >0)的一个焦点F 的坐标为(2,0),∴c 2=a 2+b 2=4.①∵P 是两曲线的一个交点,且|PF |=5, ∴x p +2=5,∴x p =3,∴y 2p =24.∵P (x p ,y p )在双曲线x 2a 2-y 2b2=1上,∴9a 2-24b2=1.②联立⎩⎪⎨⎪⎧a 2+b 2=4,9a 2-24b2=1, 解得a 2=1,b 2=3.∴双曲线的方程为x 2-y 23=1.又双曲线的渐近线方程为y =±3x , ∴点F (2,0)到渐近线的距离为 3.13.已知点A (2,4)在抛物线y 2=2px (p >0)上,且抛物线的准线过双曲线x 2a 2-y 2b2=1(a >0,b >0)的一个焦点,若双曲线的离心率为2,则该双曲线的方程为____________. 答案 x 2-y 23=1解析 ∵点A (2,4)在抛物线y 2=2px (p >0)上, ∴16=4p ,解得p =4. ∴抛物线的准线方程为x =-2.又抛物线的准线过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点,∴c =2,又e =ca=2,∴a =1,则b 2=c 2-a 2=4-1=3, ∴双曲线的方程为x 2-y 23=1. 14.一动圆与已知圆O 1:(x +3)2+y 2=1外切,与圆O 2:(x -3)2+y 2=81内切,则动圆圆心的轨迹方程为__________.答案x 225+y 216=115.过椭圆x25+y24=1的右焦点作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,则△AOB的面积为________. 答案 53解析 由已知得直线方程为y =2(x -1).由⎩⎪⎨⎪⎧y =2x -2,4x 2+5y 2-20=0,得3y 2+2y -8=0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=-23,y 1y 2=-83,∴|y 1-y 2|=y 1+y 22-4y 1y 2=49+323=103, ∴S △AOB =12×1×103=53.16.已知椭圆C :x 2a +y 2b =1(a >b >0)的离心率为12,椭圆的短轴端点与双曲线y 22-x 2=1的焦点重合,过点P (4,0)且不垂直于x 轴的直线l 与椭圆C 相交于A ,B 两点.(1)求椭圆C 的方程; (2)求OA →·OB →的取值范围.解 (1)由双曲线y 22-x 2=1得其焦点为(0,±3),∴b = 3.又由e =c a =12,a 2=b 2+c 2,得a 2=4,c =1.故椭圆C 的方程为x 24+y 23=1.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=32k 24k 2+3,x 1x 2=64k 2-124k 2+3,∴y 1y 2=k 2(x 1-4)(x 2-4) =k 2x 1x 2-4k 2(x 1+x 2)+16k 2,∴OA →·OB →=x 1x 2+y 1y 2=(1+k 2)·64k 2-124k 2+3-4k 2·32k 24k 2+3+16k 2=25-874k 2+3. ∵0≤k 2<14,∴-29≤-874k 2+3<-874,∴OA →·OB →∈[-4,134).故OA →·OB →的取值范围为[-4,134).17.如图所示,抛物线y 2=4x 的焦点为F ,动点T (-1,m ),过F 作TF 的垂线交抛物线于P ,Q 两点,弦PQ 的中点为N .(1)证明:线段NT 平行于x 轴(或在x 轴上); (2)若m >0且|NF |=|TF |,求m 的值及点N 的坐标.(2)解 已知|NF |=|TF |,在△TFN 中,tan ∠NTF =|NF ||TF |=1⇒∠NTF =45°,设A 是准线与x 轴的交点,则△TFA 是等腰直角三角形,所以|TA |=|AF |=2, 又动点T (-1,m ),其中m >0,则m =2.因为∠NTF =45°,所以k PQ =tan45°=1,又焦点F (1,0),可得直线PQ 的方程为y =x -1,由m =2得T (-1,2),由(1)知线段NT 平行于x 轴,设N (x 0,y 0),则y 0=2,代入y =x -1,得x 0=3,所以N (3,2).18.如图所示,已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A 、B 两点.(1)若线段AB 的中点在直线y =2上,求直线l 的方程; (2)若线段|AB |=20,求直线l 的方程.解析:(1)由已知得抛物线的焦点为F (1,0).因为线段AB 的中点在直线y =2上,所以直线l 的斜率存在,设直线l 的斜率为k ,A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),则⎩⎪⎨⎪⎧x 0=x 1+x22,y 0=y 1+y22.由⎩⎪⎨⎪⎧y 21=4x 1,y 22=4x 2,得(y 1+y 2)(y 1-y 2)=4(x 1-x 2),所以2y 0k =4. 又y 0=2,所以k =1,故直线l 的方程是y =x -1.19.已知椭圆与抛物线y 2=42x 有一个相同的焦点,且该椭圆的离心率为22. (1)求椭圆的标准方程;(2)过点P (0,1)的直线与该椭圆交于A ,B 两点,O 为坐标原点,若AP →=2PB →,求△AOB 的面积.解析:(1)依题意,设椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0),由题意可得c =2,又e =ca =22,∴a =2. ∴b 2=a 2-c 2=2,∴椭圆的标准方程为x 24+y 22=1.(2)设A (x 1,y 1),B (x 2,y 2),由AP →=2PB →,得⎩⎪⎨⎪⎧-x 1=2x 21-y 1=y 2-.设直线AB 的方程为y =kx +1,代入椭圆方程整理,得(2k 2+1)x 2+4kx -2=0,∴x 1+x 2=-4k 2k 2+1,x 1·x 2=-22k 2+1. 将x 1=-2x 2代入上式可得,(4k 2k 2+1)2=12k 2+1, 解得k 2=114.∴△AOB 的面积S =12|OP |·|x 1-x 2|=x 1+x 22-4x 1x 22=12·28k 2+22k 2+1=3148. 20.已知椭圆C 1的方程为x 24+y 2=1,双曲线C 2的左、右焦点分别是C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点,O 为坐标原点.(1)求双曲线C 2的方程;(2)若直线l :y =kx +2与双曲线C 2恒有两个不同的交点A 和B ,且OA →·OB →>2,求k 的取值范围.(2)将y =kx +2代入x 23-y 2=1, 得(1-3k 2)x 2-62kx -9=0. 由直线l 与双曲线C 2交于不同的两点, 得⎩⎨⎧ 1-3k 2≠0,Δ=-62k2+-3k 2=-k 2,∴k 2<1且k 2≠13.① 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=62k 1-3k 2,x 1x 2=-91-3k2. ∴x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2) =(k 2+1)x 1x 2+2k (x 1+x 2)+2 =3k 2+73k 2-1.。
2017年高考数学(四海八荒易错集)专题15椭圆、双曲线、抛物线理

联立①②,解得 a= 2, c= 1,
所以 b2= 1,
故椭圆
C 的标准方程为
x2 2+
y2=
1.
因为点 P,N在椭圆上, 所以 x21+ 2y21=2, x22+ 2y22= 2,⑥
x2 y2
1
3
8.已知椭圆 C: a2 +b2= 1( a>b>0) 的离心率为 2,且点 (1 , 2) 在该椭圆上.
(1) 求椭圆 C的方程;
62
(2) 过椭圆 C的左焦点 F1 的直线 l 与椭圆 C相交于 A, B 两点,若△ AOB的面积为
,求圆心在原点 O
7
且与直线 l 相切的圆的方程.
a- c
b2
b2
+ a,
【名师点睛】
(1) 明确圆锥曲线中 a, b,c, e 各量之间的关系是求解问题的关键.
F1、 F2,过 F1 作圆 x2+ y2= a2 的切线分别交双曲线的左、
右两支于点 B、 C,且 | BC| =| CF2| ,则双曲线的渐近线方程为 (
)
A. y=±3x
B. y=±2 2x
C. y=±( 3+ 1) x D. y=±( 3- 1) x
答案 (1) 3- 1 (2)C
a
b
易得直线 BC的斜率为 b,cos∠ CF1F2= c,
设△ MF1F2 的内切圆的半径为 r , 3
由题意可得 2π r =3π ,解得 r = 2.
5.已知圆 x2+y2= a2 上点 E 处的一条切线 16
例析椭圆、双曲线、抛物线解题误区

椭圆、双曲线与抛物线是高考考查平面解析几何的重点内容,在每年的高考中都占有较大的比例,初学者容易在它们定义的理解、焦点的位置及性质运用等方面出现错误,有的错误还不易察觉。
下面对几个常见错误进行错因分析,帮助学生少犯错误,提高解题的准确率。
误区一、忽视了圆锥曲线的严格定义而致误例1已知动点P与定点(11)F,和直线:340l x y+-=的距离相等,则点P的轨迹是()A.椭圆B.双曲线C.抛物线D.直线【错解】由抛物线的定义可知选(C)。
【错因分析】抛物线的定义中,定点一定不在定直线上,而本题中的定点(11)F,在定直线:340l x y+-=上.【正解】设动点P的坐标为()x y,,则。
整理,得320x y-+=.所以动点P的轨迹为直线,选(D)。
误区二、忽视了焦点的多种情况而致误例2求以原点为顶点,坐标轴为对称轴,并且经过点(24)P--,的抛物线的标准方程.【错解】设抛物线22(0)y p x p=>,将点(24)P--,代入得4p=.故抛物线的标准方程为28y x=-.【错因分析】错解只考虑了抛物线方程的焦点在x的正半轴这一种情况,焦点也可能在y轴的负半轴上。
【正解】当抛物线焦点在x的正半轴时,设抛物线为22(0)y px p=>,将(24)P--,代入得4p=.得标准方程为28y x=-.当抛物线焦点在y轴的负半轴时,设抛物线为)0(22>-=ppyx,则可得标准方程为2x y=-.故满足条件的抛物线的标准方程为28y x=-或2x y=-。
误区三、忽视了参数的取值范围而致误例3已知双曲线方程为221x y-=,双曲线左支上一点(,)P a b到直线y x=试求a b+的值。
【错解】由于点(,)P a b到直线y x=的距离是,故=,则2a b-=±,又因为221a b-=,则()()1a b a b+-=,故12a b+=±。
【错因分析】错解忽视了条件点(,)P a b在双曲线的左支上,当点(,)P a b在双曲线的左支上时,有0a b-<=2a b-=-。
圆锥曲线椭圆双曲线抛物线知识点总结例题习题精讲详细答案

【椭圆】 一、椭圆的定义1、椭圆的第一定义:平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆。
这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距。
注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ;若)(2121F F PF PF <+,则动点P 的轨迹无图形。
二、椭圆的方程1、椭圆的标准方程(端点为a 、b ,焦点为c )(1)当焦点在x 轴上时,椭圆的标准方程:12222=+b y a x )0(>>b a ,其中222b a c -=;(2)当焦点在y 轴上时,椭圆的标准方程:12222=+b x a y )0(>>b a ,其中222b a c -=;2、两种标准方程可用一般形式表示:221x y m n += 或者 mx 2+ny 2=1 三、椭圆的性质(以12222=+by a x )0(>>b a 为例)知能梳理1、对称性:对于椭圆标准方程12222=+by a x )0(>>b a :是以x 轴、y 轴为对称轴的轴对称图形;并且是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。
2、范围:椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内,所以椭圆上点的坐标满足a x ≤,b y ≤。
3、顶点:①椭圆的对称轴与椭圆的交点称为椭圆的顶点。
②椭圆12222=+by a x )0(>>b a 与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为)0,(1a A -,)0,(2a A ,),0(1b B -,),0(2b B 。
③线段21A A ,21B B 分别叫做椭圆的长轴和短轴,a A A 221=,b B B 221=。
a 和b 分别叫做椭圆的长半轴长和短半轴长。
