数学建模作业:多元统计
数学建模多元统计分析引论

数学建模多元统计分析引论数学建模与多元统计分析是现代统计学中的重要分支,广泛应用于各个领域。
本文将介绍数学建模的基本概念和方法,以及多元统计分析的基本原理和应用。
一、数学建模数学建模是指将实际问题转化为数学问题,并通过数学模型进行分析和求解的过程。
数学建模的目的是通过数学模型来描述和模拟实际问题,从而得出有关问题的一些结论和解决方案。
数学建模的过程通常包括以下几个步骤:1.问题的描述和分析:首先要对实际问题进行准确的描述和分析,明确问题的目标和约束条件。
2.模型的建立:根据问题的特点和需求,选择适当的数学模型来描述问题。
常用的数学模型包括线性模型、非线性模型和随机模型等。
3.模型的求解:根据模型的类型和性质,选择合适的方法和算法来求解模型。
常用的方法包括数值求解、优化算法和随机模拟等。
4.模型的验证和分析:对求解结果进行验证和分析,评价模型的可靠性和适用性。
如果需要,可以对模型进行修正和改进。
数学建模的核心是数学模型的建立和求解。
数学模型是对实际问题的抽象和简化,通过数学模型的求解,可以获得有关问题的一些重要信息和结论。
数学建模在工程、经济、生物、环境等领域都有广泛的应用。
二、多元统计分析多元统计分析是指对多个变量之间的关系和差异进行统计分析的方法。
它将统计学的基本概念和原理扩展到多个维度,并通过数学模型和统计方法来研究和解释这些多元数据。
多元统计分析的主要内容包括多元数据的描述、多元数据的降维和多元数据的分类与聚类等。
具体包括以下几个方面的内容:1.多元数据的描述:对多元数据进行统计描述,包括均值、方差、协方差、相关系数等。
通过描述统计,可以了解多元数据的分布和变化情况。
2.多元数据的降维:通过主成分分析、因子分析等方法将多元数据降维,提取出主要信息和特征。
降维可以简化多元数据的分析和处理过程,并通过降维后的数据进行可视化和解释。
3.多元数据的分类与聚类:根据多元数据的特征,将数据进行分类和聚类,找出数据中的规律和结构。
数学建模-多元统计

逐步判别法
在判别问题中,当判别变量个数较多时, 如果不加选择地一概采用来建立判别函数,不 仅计算量大,还由于变量之间的相关性,可能 使求解逆矩阵的计算精度下降,建立的判别函 数不稳定。因此适当地筛选变量的问题就成为 一个很重要的事情。凡具有筛选变量能力的判 别分析方法就统称为逐步判别法。
逐步判别法其基本思路类似于逐步回归分析,按 照变量是否重要逐步引入变量,每引入一个“最重要” 的变量进入判别式,同时要考虑较早引入的变量是否 由于其后的新变量的引入使之丧失了重要性变得不再 显著了(例如其作用被后引入地某几个变量的组合所 代替),应及时从判别式中把它剔除,直到判别式中 没有不重要的变量需要剔除,剩下来的变量也没有重 要的变量可引入判别式时,逐步筛选结束。也就是说 每步引入或剔除变量,都作相应的统计检验,使最后 的判别函数仅保留“重要”的变量。
数 学 建 模
华中农业大学数学建模基地系列课件
聚类分析
聚类分析又称群分析,它是研究分类问题的一 种多元统计方法。所谓类,通俗地说,就是指相似 元素的集合。那么要将相似元素聚为一类,通常选 取元素的许多共同指标,然后通过分析元素的指标 值来分辨元素间的差距,从而达到分类的目的。 聚类分析可以分为:Q型(样品分类)分类、 R型(指标分类)分类。这里介绍的是Q型(样 品分类)分类。
Cluster History表示聚类的具体过程,NCL表示 当前系统存在类的总个数,Clusters Joined表示当前 加入的编号,例如NCL等于20时,是类1,2聚为一类, FREQ表示新类的元素个数。SPRSQ表示类与类间最 2 短规格化最短距离,RSQ表示R 统计量,ERSQ表示半 2 偏R 统计量,CCC统计量值。PSF为伪F统计量,PST2 2 为伪t 统计量。Tie表示“节”,是指当前类间最小距离 不止一个的时候,此时可以任意选择一对最短距离进 行聚类,在计算其他类与新类的距离。从CCC统计量 的结果可以看出,最大值对应的类数为4。从四类合并 2 为三类时,伪t 统计量显著的增加,伪F统计量下降显 著,综合各方面的结果,因此分4类最为合适。
多元统计分析(数学建模)

2022/1/31
30
目录 上页 下页 返回 结束
其他变量(A)对内生变量(B)的影响有两种情况 :若A直接通过单向箭头对B具有因果影响,称A 对B有 直接作用(direct effect);若A 对B的作用是间接地通 过其他变量(C)起作用,称A 对B有间接作用( indirect effect),称C为中间变量(mediator variable) 。变量间的间接作用常常由多种路径最终总合而成。图 10-2中,四个外生变量耐用性、操作的简单性、通话效 果和价格既对忠诚度有直接作用,同时通过感知价值对 忠诚度具有间接作用。
(2)统计关系:(如:收入和消费;身高的遗传.)
事物间的关系不是确定性的.即:当一个变量x取 一定值时,另一变量y的取值可能有几个.一个变 量的值不能由另一个变量唯一确定
概述
统计关系的常见类型:
线性相关:正线性相关、负线性相关 非线性相关
统计关系不象函数关系那样直接,但却普遍 存在,且有强有弱.如何测度?
需求量和价格之间的相关关系包含了消费者收入对商品需 求量的影响;收入对价格也产生影响,并通过价格变动传 递到对商品需求量的影响中。 又如:粮食产量与平均气温、月降水量、平均日照时间、 温度之间的关系的研究。
偏相关分析
(2)计算方法:
ry1.2
ry1 ry2r1 2 (1ry22)(1r122)
y: 2 3 1 4 5
一致对:(2,3) (2,4)(2,5)(3,4)(3,5)(1,4)(1,5)(4,5)
非一致对:(2,1)(3,1)
然若后两计变算量K存en在d强all相相关关系性数,则. V较小,秩序相关系数较大T;若两(U变量V存)在n强(n2负1关)
性,则V较大,秩序相关系数为负,绝对值较大
数学建模作业:多元统计
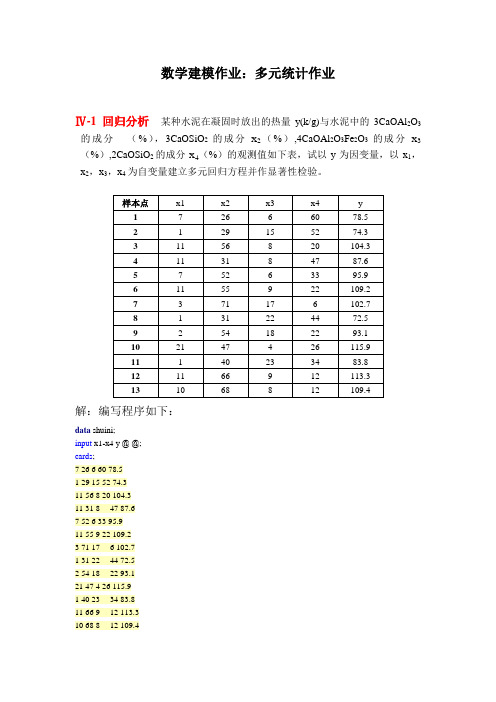
数学建模作业:多元统计作业Ⅳ-1 回归分析某种水泥在凝固时放出的热量y(k/g)与水泥中的3CaOAl2O3的成分(%),3CaOSiO2的成分x2(%),4CaOAl2O3Fe2O3的成分x3(%),2CaOSiO2的成分x4(%)的观测值如下表,试以y为因变量,以x1,x2,x3,x4为自变量建立多元回归方程并作显著性检验。
解:编写程序如下:data shuini;input x1-x4 y @ @;cards;7 26 6 60 78.51 29 15 52 74.311 56 8 20 104.311 31 8 47 87.67 52 6 33 95.911 55 9 22 109.23 71 17 6 102.71 31 22 44 72.52 54 18 22 93.121 47 4 26 115.91 40 23 34 83.811 66 9 12 113.310 68 8 12 109.4; proc reg ;model y=x1 x2 x3 x4/selection =stepwise; run ;运行结果如下:(1) 回归方程显著性检验:Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > FModel 2 2657.85859 1328.92930 229.50 <.0001 Error 10 57.90448 5.79045 Corrected Total 12 2715.76308由Analysis of Variance 表可知:F Value=229.50,Pr > F 远小于0.05,故回归方程的线性性及各参数的显著性检验均通过。
(2) 参数显著性检验Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 52.57735 2.28617 3062.60416 528.91 <.0001 x1 1.46831 0.12130 848.43186 146.52 <.0001 x2 0.66225 0.04585 1207.78227 208.58 <.0001由结果可知,X1,X2均通过检验。
多元统计分析及r语言建模答案

多元统计分析及r语言建模真题及答案多元统计分析是研究从实验观察和测量获得的不同变量之间相互关系的一种统计学方法,有助于用户综合考虑多个变量影响因素。
r语言是一种便于多元分析和建模的编程语言,下面我们将介绍一个多元统计分析和r语言建模真题,以及答案。
题目:分析某elPharmaceutical Company的股票价格。
此多元统计分析和R语言建模真题考察的是某elPharmaceutical 公司的股票价格,要求完成以下工作:1. 使用R语言建立回归模型来分析该公司股票价格。
2. 使用R语言建立股票价格的统计图表和预测图表,以及相关统计模型分析。
3. 对模型的结果进行评估,并对预测的数据进行可视化展示。
答案:r语言可以使用多元线性回归分析模型,来分析该elPharmaceutical公司的股票价格。
回归模型的代码如下:lm1<-lm(price~x1+x2+x3+x4) #建立多元线性回归模型summary(lm1) #查看回归分析汇总结果plot(lm1) #绘制回归模型图然后可以使用r语言进行以下工作:1. 使用R语言绘制统计图表来分析:ggplot(data=data,aes(x=x1,y=price))+geom_point()+scale_x_ discrete+xlab("因素1")+ylab("股票价格")2. 使用R语言计算Spearman相关系数:(data$x1,data$price)3. 使用R语言建立预测图表:<-predict(lm1)plot(data$x1,data$price)lines(data$x1,,col=”red”) 4. 对模型的结果进行评估:rsq<-summary(lm1)$r.squared<-summary(lm1)$adj.r.squared fstat<-summary(lm1)$fstatistic 5. 可视化展示预测结果:ggplot(data=data,aes(x=x1,y=price))+geom_point()+scale_x_ discrete+xlab("因素1")+ylab("股票价格")lines(data$x1,,col=”red”)+scale_y_continuous+geom_text( aes(,x=x1+0.2,),data=data)本题用r语言完成多元统计分析和建模任务,可以评估模型的拟合情况,并可视化展示预测结果。
数学建模-多元统计模型专题(最新版)

(16)
ˆ 3 ˆ 3 ˆ bx ˆ , y2 a ˆ bx ˆ y1 a 1 2
分别求出 x1 和 x2 ,从而确定变量 x 值的控制范围。
(17)
2. 多元线性回归
经典的多元线性回归模型为
yi b0 b1 xi1 b2 xi 2
ˆ y y
i 1 i i n 2
(22)
其中 SSR 立时,
ˆ y y
i 1 i
2
为回归平方和, SSE
为残差平方和。 当原假设 H 0 成
F ~ F m, n m 1 。
(23)
对于给定的显著性水平 0 1 ,由 P F F m, n m 1 ,查表确定临界值
n i 1
(5)
其中 SSR
2
2 ˆ2l bl ˆ 为回归平方和, SSE y y b i ˆi 为残差平方和。 xx xy
当原假设 H 0 成立时,
F ~ F 1, n 2 。
(6)
对于给 定的 显著 性水 平 0 1 ,由 P F F 1, n 2 ,查表 确定 临界值
2 x x SSE 1 ˆ 0 F 1, n 2 n 0 y0 y 2 n 2 n xi x i 1 2 x x SSE 1 ˆ 0 F 1, n 2 n 0 , y 2 n 2 n xi x i 1
多元统计模型——数模竞赛辅导专题
河南科技大学数学与统计学院 (2010-07-23) 武新乾
一、前言
24 年前(1986 年) ,美国出现了大学生数学建模竞赛。随着改革开放的进程,数模竞赛 逐渐传入我国。1992 年,开始国内第一届大学生数学建模比赛。数模竞赛一经传入,便受 到了全国高校的普遍关注,引起了大学生的广泛兴趣。特别是近年来,虽然试题难度不断增 大,但是,参赛的学生规模空前膨胀,获奖的组队也日益增加,论文质量不断提高。 综观 18 年的竞赛试题,问题广泛,解决方案多种多样,其中基于统计分析的问题屡见 不鲜。比如:1992 年 A 题(简单记为 1992A,下同) “施肥方案对作物、蔬菜的影响” ,采 用多元二次回归、全回归、逐步回归和二次响应面回归;1993A“非线性交调的频率设计” , 采用最小二乘方法(简单记为 LS) ;1998A“资产投资收益与风险模型”和 2000A“DNA 序 列的分类” ,都采用多元分析方法;2001A“血管管道的三维重建”和“血管切片的三维重 建” ,分别采用 LS 方法和非线性拟合;2001B“公交车调度的规划数学模型” ,采用聚类分 析、 平滑方法和随机过程的有关知识; 2003A “SARS 传播的数学原理及预测与控制” 和 “SARS 传播的研究” ,均考虑了时间序列的应用;2003A“SARS 传播预测的数学模型” ,采用非线 性拟合,建立了指数模型;2004A“ MS 网点的合理布局”采用了聚类分析, “基于利润最大 化的实运商业网点分布微观经济模型”采用多元统计分析方法,另外, “临时超市网点的规 划模型研究”考虑了经验分布的应用;2004B“电力市场的输电阻塞优化管理(指导教师: 肖华勇) ”和“电力市场输电阻塞管理模型” ,均使用了多元线性回归;2005A“长江水质的 评价和预测” 、 “长江水质的评价预测模型” (二元线性回归预测) 、 “基于回归分析的长江水 质预测与控制” ,均考虑了回归分析,此外, “长江水质评价和预测的研究” 、 “水质的评价和 预测模型” ,均考虑了时间序列分析方法和多元线性回归模型;2005B“DVD 在线租赁系统 的优化设计”应用了抽样统计和随机服务模型, “DVD 在线租赁问题”和“DVD 租赁优化 方案(指导教师:孙浩) ”考虑了二项分布和随机模拟;2005B“DVD 在线租赁问题研究” 和 2005C“雨量预报方法的评价模型”考虑了均值的应用;2006B“艾滋病疗法评价及疗效 预测模型”使用了二次曲线和多元方差分析, “艾滋病疗法评价及疗效的预测模型”使用了 逐步回归方法, “艾滋病疗法的评价及疗效的预测模型”应用了假设检验和方差分析, “艾滋 病疗法的评价及疗效的预测”使用了线性拟合、二次和三次曲线拟合与非线性回归, “基于 数据统计分析的艾滋病疗效评价方法”采用了 F-检验和二次多项式回归;2007A“中国人口 区域结构向量模型”采用了倒数曲线模型拟合, “基于 Les lie 模型的中国人口预测及蒙特卡 罗仿真(指导教师:梅长林) ”应用了概率方法;2008A“数码相机定位”应用了多元线性 回归分析;2008B“高等教育学费标准探讨(华南农业大学,编号 1910) ”应用了因子分析、 主成分分析和聚类分析, “高等教育学费标准的探讨(华南农业大学,编号 1920) ”采用了 多元回归分析、数据挖掘和模拟退火算法, “关于高等教育学费标准的评价及建议(编号 cumcm0849) ”和“高校学费合理性研究(编号 cumcm0860) ”分别考虑了回归分析和曲线 拟合。 由是可知, 多元统计分析是常见的解决数模竞赛的主要工具之一, 务必给以充分的重视 和加强训练指导。
多元统计分析习题与答案

多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法,它通过同时考虑多个变量之间的关系,帮助研究者更全面地理解和解释现象。
在本文中,我将分享一些多元统计分析的习题和答案,希望能够帮助读者更好地掌握这一方法。
习题一:相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。
你收集了100个学生的数据,学习成绩用分数表示,学习时间用小时表示。
以下是你的数据:学习成绩(X):75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间(Y):5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数,并解释其含义。
答案一:首先,我们需要计算学习成绩和学习时间之间的协方差和标准差。
根据公式,协方差可以通过以下公式计算:协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中,X和Y分别表示学习成绩和学习时间,X平均和Y平均表示它们的平均值,n表示样本数量。
标准差可以通过以下公式计算:标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式,我们可以得出学习成绩和学习时间之间的协方差为-22.5,标准差分别为18.03和2.87。
然后,我们可以通过以下公式计算相关系数:相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式,我们可以得出相关系数为-0.93。
由于相关系数接近于-1,可以得出结论:学习成绩和学习时间之间存在强烈的负相关关系,即学习时间越长,学习成绩越低。
习题二:多元线性回归假设你正在研究一个人的身高(X1)、体重(X2)和年龄(X3)对其收入(Y)的影响。
你收集了50个人的数据,以下是你的数据:身高(X1):160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重(X2):50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄(X3):20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入(Y):5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析,建立一个预测人的收入的模型,并解释模型的结果。
数学建模多元统计分析报告

.. ..实验报告一、实验名称多元统计分析作业题。
二、实验目的(一)了解并掌握主成分分析与因子分析的基本原理和简单解法。
(二)学会使用matlab编写程序进行因子分析,求得特征值、特征向量、载荷矩阵等值。
(三)学会使用排序、元胞数组、图像表示最后的结果,使结果更加直观。
三、实验容与要求四、实验原理与步骤(一)第一题:1、实验原理:因子分析简介:(1)1.1 基本因子分析模型设p维总体x=(x1,x2,....,xp)'的均值为u=(u1,u2,....,u3)',因子分析的一般模型为x1=u1+a11f1+a12f2+........+a1mfm+ε1x2=u2+a21f1+a22f2+........+a2mfm+ε2.........xp=up+ap1f1+fp2f2+..........+apmfm+εp其中,f1,f2,.....,fm为m个公共因子;εi是变量xi(i=1,2,.....,p)所独有的特殊因子,他们都是不可观测的隐变量。
称aij(i=1,2,.....,p;j=1,2,.....,m)为变量xi的公共因子fi上的载荷,它反映了公共因子对变量的重要程度,对解释公共因子具有重要的作用。
上式可以写为矩阵形式x=u+Af+ε其中A=(aij)pxm 称为因子载荷矩阵;f=(f1,f2,....,fm)'为公共因子向量;ε=(ε1,ε2,.....εp)称为特殊因子向量(2)1.2 共性方差与特殊方差xi的方差var(xi)由两部分组成,一个是公共因子对xi方差的贡献,称为共性方差;一个是特殊因子对xi方差的贡献,称为特殊方差。
每个原始变量的方差都被分成了共性方差和特殊方差两部分。
(3)1.3 因子旋转因子分析的主要目的是对公共因子给出符合实际意义的合理解释,解释的依据就是因子载荷阵的个列元素的取值。
当因子载荷阵某一列上各元素的绝对值差距较大时,并且绝对值大的元素较少时,则该公共因子就易于解释,反之,公共因子的解释就比较困难。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模作业:多元统计作业Ⅳ-1 回归分析某种水泥在凝固时放出的热量y(k/g)与水泥中的3CaOAl2O3的成分(%),3CaOSiO2的成分x2(%),4CaOAl2O3Fe2O3的成分x3(%),2CaOSiO2的成分x4(%)的观测值如下表,试以y为因变量,以x1,x2,x3,x4为自变量建立多元回归方程并作显著性检验。
解:编写程序如下:data shuini;input x1-x4 y @ @;cards;7 26 6 60 78.51 29 15 52 74.311 56 8 20 104.311 31 8 47 87.67 52 6 33 95.911 55 9 22 109.23 71 17 6 102.71 31 22 44 72.52 54 18 22 93.121 47 4 26 115.91 40 23 34 83.811 66 9 12 113.310 68 8 12 109.4; proc reg ;model y=x1 x2 x3 x4/selection =stepwise; run ;运行结果如下:(1) 回归方程显著性检验:Analysis of VarianceSum of MeanSource DF Squares Square F Value Pr > FModel 2 2657.85859 1328.92930 229.50 <.0001 Error 10 57.90448 5.79045 Corrected Total 12 2715.76308由Analysis of Variance 表可知:F Value=229.50,Pr > F 远小于0.05,故回归方程的线性性及各参数的显著性检验均通过。
(2) 参数显著性检验Parameter StandardVariable Estimate Error Type II SS F Value Pr > FIntercept 52.57735 2.28617 3062.60416 528.91 <.0001 x1 1.46831 0.12130 848.43186 146.52 <.0001 x2 0.66225 0.04585 1207.78227 208.58 <.0001由结果可知,X1,X2均通过检验。
(3) 建立线性回归方程为:2166.047.158.52x x y ++=,且拟合优度达到R2=0.9787。
可知,方程拟合效果很好。
Ⅳ-2 聚类分析 DNA 是由A ,T ,C ,G 这4种碱基按一定顺序排成的序列,长短不一,其中碱基含量的百分比不同通常能揭示该序列的一些规律,试根据下表所给出的20条DNA 序列的碱基含量百分比对其20条DNA 序列进行分类。
(注,计算式下面的数据需要转置)解:编写代码如下:data ex;input a t c g@@;cards;0.2973 0.1351 0.1712 0.39640.2703 0.1532 0.1622 0.41440.2703 0.0631 0.2162 0.45050.4234 0.2883 0.1081 0.18020.2342 0.1081 0.2342 0.42340.3514 0.1261 0.1261 0.39640.3514 0.1892 0.0991 0.36040.2793 0.1892 0.1622 0.36940.2072 0.1532 0.2072 0.43240.1818 0.1364 0.2727 0.40910.3545 0.5000 0.0455 0.10000.3273 0.5000 0.0273 0.14550.2545 0.5182 0.1000 0.12730.3000 0.5000 0.0818 0.11820.2909 0.6455 0 0.06360.3636 0.4636 0.0818 0.09090.3545 0.2636 0.2455 0.13640.2909 0.5000 0.1182 0.09090.2182 0.5636 0.1455 0.07270.2000 0.5636 0.1727 0.0636;proc cluster method=single ccc;proc tree;run;聚类图如下,根据动态聚类图可以看出,此处20个DNA序列分成三类较为合适,具体情况如下:观察SPRSQ,发现分三类最好第一类:4,17;第二类:1,2,3,5,6,7,8,9,10;第三类:11,12,13,14,15,16,18,19,20Ⅳ-4 主成分分析某市为全面分析机械类各企业的经济效益,选择了8个不同的利润指标,14个企业关于这8个指标的统计数据如下表,试进行主成分分析并将14个企业的经济效益进行排序。
解:编写主成分分析的程序如下:data ex;input x1-x8;cards;40.4 24.7 7.2 6.1 8.3 8.7 2.442 20.025.0 12.7 11.2 11.0 12.9 20.2 3.542 9.113.2 3.3 3.9 4.3 4.4 5.5 0.578 3.622.3 6.7 5.6 3.7 6.0 7.4 0.176 7.334.3 11.8 7.1 7.1 8.0 8.9 1.726 27.535.6 12.5 16.4 16.7 22.8 29.3 3.017 26.622.0 7.8 9.9 10.2 12.6 17.6 0.847 10.648.4 13.4 10.9 9.9 10.9 13.9 1.772 17.840.6 19.1 19.8 19.0 29.7 39.6 2.449 35.824.8 8.0 9.8 8.9 11.9 16.2 0.789 13.712.5 9.7 4.2 4.2 4.6 6.5 0.874 3.91.8 0.6 0.7 0.7 0.8 1.1 0.056 1.032.3 13.9 9.4 8.3 9.8 13.3 2.126 17.138.5 9.1 11.3 9.5 12.2 16.4 1.327 11.6;proc princomp out=prin;var x1-x8;run;proc print data=prin;var prin1-prin13;run;根据运行结果,以累积贡献率超过90%为标准,可选择三个主成分Eigenvalues of the Correlation MatrixEigenvalue Difference Proportion Cumulative1 6.13662351 5.09449321 0.7671 0.76712 1.04213030 0.60617666 0.1303 0.89733 0.43595365 0.21558158 0.0545 0.95184 0.22037207 0.06846521 0.0275 0.97945 0.15190686 0.14307942 0.0190 0.99846 0.00882744 0.00586506 0.0011 0.99957 0.00296238 0.00173859 0.0004 0.99988 0.00122379 0.0002 1.0000 根据特征向量可以写出主成分表达式:根据特征向量可以写出主成分表达式:如第一主成分可写为如下,其它类似:8765432136.032.037.038.038.039.030.032.01x x x x x x x x prin +++++++=由变量前的系数大小可见,第一主成分主要是反映总产值利润率、销售收入利润率和产品成本利润率的,是用来衡量企业经营状况的一个综合指标,其它可类似分析。
另外,还可进行主成分得分分析,主成分得分的结果如下:可见,在第一主成分上得分最高的是企业9,在第二主成分上得分最高的是企业1,在第三主成分上得分最高的是企业2。
Ⅳ-5 因子分析 有10例患者的4项肝功能指标的观测数据如下表,试作这4项指标的因子分析并对病人进行病情分析。
患者 转氨酶量 肝大指数 硫酸锌浊度胎甲球 1 40 2.0 5 20 2 10 1.5 5 30 3 120 3.0 13 50 4 250 4.5 18 0 5 120 3.5 9 50 6 10 1.5 12 50 7 40 1.0 19 40 8 270 4.0 13 60 9 170 3.0 9 60 101302.03050解:编写因子分析程序如下:data ex; input a b c d; cards ; 40 2.0 5 20 10 1.5 530120 3.0 13 50 250 4.5 18 0 120 3.5 95010 1.5 12 50 40 1.0 19 40 270 4.0 13 60 170 3.0 9 60130 2.0 30 50;proc corr out=ex1;proc factor data =ex1 outstat =ex2 method =prin priors=one rotate =orthomax score ; proc score data =ex score =ex2 out =ex3; proc print ;run ;根据程序结果,按累积贡献率超过90%,选择三个公因子:为了便于解释,旋转过后的因子模式为:由此可写出:3211.022.096.0F F F a ++=,其它类似。
标准化因子得分系数如下:由此有d c b a F 02.007.054.050.01+-+=,其它类似。
根据上式有因子得分结果如下:在三个公因子上得分最高的患者依次是:4,10,8。
Ⅳ-6 典型相关分析棉花红铃虫第一代发蛾高峰日y1、第一代累计百株卵量y2、发蛾高峰日百株卵量y3及2月下旬至3月中旬的平均气温x1(℃)、1月下旬至3月上旬的日照小时累计数的常用对数x2的16组观测数据如下表,试作气象指标x1、x2与y1、y2、y3的典型相关分析。
x1 x2 y1 y2 y31 9.200 2.014 186 46.3 14.32 9.100 2.170 169 30.7 14.03 8.600 2.258 171 144.6 69.34 10.233 2.206 171 69.2 22.75 5.600 2.067 181 16.0 7.36 5.367 2.197 171 12.3 8.07 6.133 2.170 174 2.7 1.38 8.200 2.100 172 26.3 7.99 8.800 1.983 186 247.1 85.210 7.600 2.146 176 47.7 12.711 9.700 2.074 176 536. 25.312 8.367 2.102 172 137.6 58.013 12.167 2.284 176 118.9 43.314 10.267 2.242 161 62.7 29.315 8.900 2.283 171 26.2 8.316 8.233 2.068 172 123.9 32.7答案仅供参考假设:x1、x2服从二元正态分布;y1、y2、y3服从三元正态分布与多元线性回归揭示一个变量与一组变量的相关关系不同的是,典型相关分析是用于揭示了两组多元随机变量之间的相关关系。
