2016-2017学年浙江省宁波市北仑中学高二(下)期中数学试卷
浙江省宁波市北仑中学2016-2017学年高二下学期期中考试数学试题

绝密★启用前浙江省宁波市北仑中学2016-2017学年高二下学期期中考试数学试题试卷副标题考试范围:xxx ;考试时间:66分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、设函数,若存在唯一的整数使得,则的取值范围是( )A .B .C .D .2、某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两人至少有一人参加.当甲、乙同时参加时,他们两人的发言不能相邻,那么不同的发言顺序的种数( )A .360B .520C .600D .7203、已知可导函数满足,则当时,和大小关系为A .B .C .D .4、某五所大学进行自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是( ) A . B .C .D .5、已知,若~,则和分别是( )A .6和2.4B .2和2.4C .2和5.6D .6和5.66、设函数在定义域内可导,它的图象如图所示,则它的导函数图象可能为( )B.C.D.7、2017年5月30日是我国的传统节日端午节,这天小明的妈妈为小明煮了5个粽子,其中两个大枣馅三个豆沙馅,小明随机取出两个,事件“取到的两个为同一种馅”,事件取到的两个都是豆沙馅”,则=()8、二项式的展开式中的有理项共有()A.4项 B.5项 C.6项 D.7项9、从一批产品中取出三件,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是()A.A与C互斥 B.B与C互斥 C.任两个均互斥 D.任两个均不互斥10、已知函数,则的值为()A.-20 B.-10 C.10 D.20第II卷(非选择题)二、填空题(题型注释)11、如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有_____个.12、关于二项式(x-1)2005有下列命题:①该二项展开式中非常数项的系数和是1;②该二项展开式中第六项为x1999;③该二项展开式中系数最大的项是第1002项;④当x=2006时,(x-1)2005除以2006的余数是2005。
浙江省宁波市北仑中学2016-2017学年高一下学期期中考试数学试题

绝密★启用前浙江省宁波市北仑中学2016-2017学年高一下学期期中考试数学试题试卷副标题考试范围:xxx ;考试时间:60分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、关于x 的不等式的解集为非空数集,则实数的取值范围是( )A .B .C .或D .或2、一船沿北偏西方向航行,正东有两个灯塔A,B,海里,航行半小时后,看见一灯塔在船的南偏东,另一灯塔在船的南偏东,则这艘船的速度是每小时 ( ) A .5海里 B .海里 C .10海里 D .海里A. B.16 C.20 D.104、数列{a n}满足a1=0,,则()A.0 B. C.1 D.25、等差数列{a n}中,a2+a8=16,则{a n}的前9项和为()A.56 B.96 C.80 D.726、数列,,,,…的一个通项公式为()A. B.C. D.7、已知则是=()A. B. C. D.8、已知正数满足,则的最小值为( )A.3 B. C.4 D.第II 卷(非选择题)二、填空题(题型注释)9、在非等腰直角△ABC 中,已知C=90°,D 是BC 的一个三等分点,若cos ∠BAD=,则sin ∠BAC=_________.10、设实数满足,则的最大值是_______.11、正项数列{a n },a 1=1,前n 项和S n 满足,则________________.12、等差数列{a n }中,,公差,则使前n 项和S n 取得最大值的正整数n的值是 ________,使前n 项和S n >0的正整数n 的最大值是________.13、已知实数x, y 满足且,则不等式围成的区域面积为______,则的取值范围是________.14、已知,,m 的最小值为:_______,则m, n之间的大小关系为___________.15、△ABC 中,.则______________,______ .三、解答题(题型注释)16、已知数列{a n }的前n 项和S n 满足,(1)求数列{a n }的通项公式;(2)求证:数列{a n }中的任意三项不可能成等差数列;(3)设,T n 为{b n }的前n 项和,求证.17、对于函数,若存在区间,使得,则称函数为“可等域函数”,区间为函数的一个“可等域区间”,已知函数.(1)若,,是“可等域函数”,求函数的“可等域区间”;(2)若区间为的“可等域区间”,求,的值.18、数列{a n }中,前n 项和为,(1)求数列{a n }通项公式;(2)若数列{b n }满足,求数列{b n }的前n 项和.19、在中,(1)求的值;(2)设,求的面积.20、设函数,已知不等式的解集为.(1)若不等式的解集为,求实数的取值范围;(2)若对任意的实数都成立,求实数的取值范围.参考答案1、B2、B3、A4、B5、D6、D7、C8、C9、10、2711、12、 5或6 1113、14、 415、 4:5:6 , 12:9:216、(1)数列{a n}的通项公式为;(2)证明过程详见试题解析;(3)证明过程详见试题解析.17、(1),;(2)或.18、(1) (2).19、(1)(2)20、(1);(2).【解析】1、关于x的不等式|x−1|−|x−3|>a2−3a的解集为非空数集,则a2−3a<(|x−1|−|x−3|)max即可,而|x−1|−|x−3|的最大值是2,∴只需a2−3a−2<0,解得:,本题选择B选项.2、如图所示,∠COA=135°,∠ACO=∠ACB=∠ABC=15°,∠OAC=30°,AB=10,∴AC=10. △AOC中,由正弦定理可得,∴,∴,∴这艘船的速度是每小时海里,本题选择D选项.3、由,当且仅当x=y=4取等号。
浙江宁波市北仑中学高二下学期期中考试数学1-2班试题 word版含答案

北仑中学2015学年第二学期高二年级期中考试数学试卷(供高二(1)、(2)班用)命题:王加白审题:高一琦一、选择题(每小题5分,共40分)1、函数在点(1,1)处的切线方程为()A.x﹣y﹣2=0 B.x+y﹣2=0 C.x+4y﹣5=0 D.x﹣4y+3=02、现有12张不同的卡片,其中红色、黄色、蓝色、绿色卡片各三张,从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张,不同的取法种数()A.135 B.172 C.189 D.1623、已知(1+x)10=a0+ a1(1-x)+ a2(1- x)2+…+ a10(1- x)10,则a8等于()A.-5 B.5 C.90 D.1804、一种团体竞技比赛的积分规则是:每队胜、平、负分别得2分、1分、0分。
已知甲球队已赛4场,积4分,在这4场比赛中,甲球队胜、平、负(包括顺序)的情况共有()A.7种B.13种C.18种D. 19种5、若函数存在与直线2x-y=0平行的切线,则实数a的取值范围是()A. B. C. D.6、对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′(x)是函数y=f(x)的导数,f″(x)是f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.探究发现:任何一个三次函数都有“拐点”,任何一个三次函数都有对称中心,且“拐点”就是对称中心,设函数g(x)= x3﹣ x2+3x﹣,则g()+g()+…+g()=()A.2 013 B.2 014 C.2 015 D.20167、已知一函数满足x>0时,有g′(x)=2x2>,则下列结论一定成立的是( ) A.﹣g(1)≤3 B.﹣g(1)≥2C.﹣g(1)<4 D.﹣g(1)≥48、若函数()22ln (0)f x x a x a x=+->有唯一零点x 0,且m<x 0<n(m ,n 为相邻整数),则m+n 的值为( )A.1B.3C.5D.7二、填空题(每小题5分,共35分)9、若曲线y=x 2+ax+b 在点(0,b )处的切线方程是x ﹣y+1=0,则a 的值为 . 10、已知f (x )=x 2+3xf′(2),则f′(2)= .11、如图所示22⨯方格,在每一个方格中填入一个数字,数字可以是1、2、3中的任何一个, 允许重复.若填入A 方格的数字大于B 方格的 数字,则不同的填法共有_______种(用数字作答).12、在平面直角坐标系xOy 中,若曲线xb x a y 222-=(a ,b 为常数)过点P (1,y 0),且该曲线在点P 处的切线与直线2x ﹣y+3=0平行,则22228ba ab +取最小时=0y . 13、用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性 不同,且1和2相邻,这样的六位数的个数是 (用数字作答). 14、若(a+x )(1+x)4展开式中x 的奇数次幂项的系数和为32,则展开式中x 3的系数为. 15、设函数()fx 在R 上存在导数()f x ',对任意实数x 有()()22f x f x x+-=,当x (,0∈-∞⎤⎦时()12,f x x '+<若()()222f m f m m +--≤+,则实数m 的取值范围是________.三、解答题(每小题15分,共75分) 16、求曲线y=x 3的过(1,1)的切线方程.17、已知函数12()ln .x xe f x e x x-=+ (1)求曲线y =f (x )在x =1处的切线方程; (2)证明:f (x )>1.18、2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源是中国古代数学家祖冲之的圆周率,为庆祝该节日,某校举办的数学嘉年华活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得5个学豆、10个学豆、20个学豆的奖励,游戏还规定,当选手闯过一关后,可以选择带走相应的学豆,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部学豆归零,游戏结束。
浙江省宁波市北仑中学高二数学下学期期中试题(310班)

北仑中学2015学年第二学期高二年级期中考试数学试卷(供高二(3)-(10)班用)一、选择题(每小题5分,共40分) 1、若(12)n x +的展开式中仅第5项二项式系数最大,则n 的值是( )(A )6; (B) 7; (C)8 ; (D) 9.2、已知函数2()(2)f x x π=,则/()f x = ( )(A )4x π; (B) 8x π; (C) 24x π ; (D) 28x π.3、在电话号码中后四个数全不相同的概率为( )(A )44410A(B)410410A(C)441A(D)44410A A4、有两条平行直线a 和b ,在直线a 上取4个点,直线b 上取5个点,以这些点为顶点作 三角形,这样的三角形共有( )(A)70; (B) 78; (C)80; (D)84.5、如果函数()()y f x x R =∈在R 上处处可导,P :函数()()y f x x R =∈是偶函数,q :函数/()()y f x x R =∈是奇函数.则P 是q 的( )(A )充分不必要条件;(B) 必要不充分条件;(C)充要条件;(D) 既不充分也不必要条件.6、有5列火车停在某车站并排的五条轨道上,若快车A 不能停在第三条轨道上,货车B 不 能停在第一条轨道上,则五列火车的停车方法有( )种. (A )72; (B) 78; (C)96 ; (D)120.7、已知c 是椭圆)0(12222>>=+b a b y a x 的半焦距,则acb +的取值范围是 ( )(A )(1, +∞) ; (B)),2(∞+; (C) )2,1(; (D)]2,1(.8、设函数()()()()()222,2,0,8x e e f x x f x xf x f x f x x '+==>满足则时, ( ) (A )有极大值,无极小值; (B )有极小值,无极大值 ; (C )既有极大值又有极小值 ; (D )既无极大值也无极小值. 二、填空题(9、10、11题每空3分,12、13、14、15每空5分,共38分)9、双曲线22184x y -=的渐近线方程为____ ___,离心率为 . 10、()732x x-的展开式的第4项的二项式系数是 ,所有项的系数和是 .11、四个标有1、2、3、4号码的小球都放入四个标有1、2、3、4号码的盒中,恰有一个空 盒有 种不同的放法,每盒一球且仅一组球盒同号有 种不同的放法.12、设函数()f x 在(0,)+∞内可导,且()xxf e x e =+,则/(1)f = .13、在一次口试中,要从10道题中随机抽出3道题进行回答,答对了其中2道题就获得及格,某考生会回答10道题中的6 道题,那么他获得及格的概率是 . 14、用0到5这6个数字,可以组成 个同时满足以下两个条件的五位数:(1)有 重复数字;(2)偶数字在奇数位,奇数字在偶数位.15、函数f (x )=2ln x 的图像与函数g (x )=x 2-4x +5的图像的交点个数为 .三、解答题(18、19、20、21题每题14分,22题16分,共72分) 16、(14分)从5名语文老师、6名数学老师和5名英语老师中,(I )每科安排2名老师,承担期中考试的命题和审题工作,有多少种不同的安排方法?(II )每科各选2名老师排成一排,数学老师都不相邻,且英语老师都排在一起的概率是多少? (Ⅲ)选派6名老师参加一个座谈会,至少有2名语文老师的概率是多少?17、(14分)已知曲线3:8C y ax a =+经过定点P .(I )若(1,3)M 在曲线C 上,求/x ay =的值;(II )求曲线C 经过点P 的切线方程.18、(14分)已知22()nx x的展开式中,第五项与第三项的二项式系数之比为14:3, (I )求n 的值;(II )求展开式的常数项; (Ⅲ)求展开式系数最大的项.19、(14分)如图,点A 是椭圆2222:1(0)x y C a b a b+=>>的短轴位于x 轴下方的端点,过A 作斜率为k 的直线交椭圆于另一点B .(I )若1k =,点P (0,1)满足//BP x 轴,9AP AB ⋅=u u u r u u u r,求椭圆的方程;(II )求OAB ∆(O 为坐标原点)面积的最大值及此时斜率k 的值.20、(16分)已知函数()ln af x x x x=++. (I )当2a =时,求函数()f x 在区间1,42⎡⎤⎢⎥⎣⎦上的最大值和最小值;(II )讨论函数()f x 的单调性;(Ⅲ)若对于21,2a e e⎡⎤∀∈⎢⎥⎣⎦,函数()f x 满足对于[]1,x e ∀∈都有()f x m <成立.求实数m 的取值范围.北仑中学2015学年第二学期高二年级期中考试数学答题卷(供高二(3——10)班使用)题号 1 2 3 4 5 6 7 8答案二.填空题(共7题,每小题4分,共28分)9. 、; 10. 、;11. 、; 12. ;13. ; 14. ;15. .三.解答题(共5题,72分)16(14分)17.(14分)18. (14分)19 (14分)20(16分)答案:1---8CDBAC BDD 9、22y x =±,离心率为62. 10、35,1-. 11、144; 8 12、 2 13、2314、138 15、 2 16、(I )22256512000A A A =种(II )2223325653422226565625C C C A A A p C C C A == (Ⅲ)61511511616917112626C C C p C +=-=-= 17、(I )若(1,3)M 在曲线C 上,则13a =,则/2y x =,/19x ay ==已知曲线3:8C y ax a =+经过定点P .求/x ay=的值;(II )定点P 的坐标为(2,0)-,/23y ax =若P 为切点,则12k a =,切线方程为12240ax y a -+=; 若P 不是切点,设切点为00(,)Q x y ,则有200032y k ax x ==+,3008y ax a =+,解得 01x =或02x =-(舍去),3k a =,切线方程为360ax y a -+=综上,曲线C 经过点P 的切线方程为12240ax y a -+=和360ax y a -+=.18、已知:已知22()nx x的展开式中,第五项与第三项的二项式系数之比为14;3, (I )10n =;(II )展开式的常数项为3180T =;(Ⅲ)展开式系数最大的项为10713440T x -=.19、(I )若1k =,点P (0,1)满足//BP x 轴,9AP AB •=u u u r u u u r,椭圆的方程为 22:1124x y C += (II )设直线AB :y kx b =-,11(,)B x y ,将y kx b =-与22221x y a b +=联立解得212222kba x a k b =+,则2222221kba AB k a k b=++,原点到直线AB 的距离21b d k-=+,2222212OABb a k S AB d a k b∆==+222212b a ab b a k k=≤+,当且仅当1k =±是取等号.所以OAB ∆(O 为坐标原点)的面积得最大值为12ab ,此时1k =±. 20、已知函数()ln af x x x x=++.(I )当2a =时,2/22212()10x x f x x x x +-=-+==得1x =或2x =-(舍去),显然当1(,1)2x ∈时,函数()f x 递减,当(1,4)x ∈时,函数()f x 递增,所以()f x 得最小值为(1)3f =;而1(4)()02f f ->,()f x 最大值为9(4)2ln 22f =+求函数()f x 在区间1,42⎡⎤⎢⎥⎣⎦上的最大值和最小值;(II )2/221()1a x x af x x x x+-=-+=(0x >) 当0a ≤时,/()0f x >,()f x 在(0,)+∞递增;当0a >时,由/()0f x =得1142ax -++=或1142a x --+=(舍去),()f x 在114(0,)2a -++递减,()f x 在114(,)2a-+++∞递增. (Ⅲ)对于21,2a e e ⎡⎤∀∈⎢⎥⎣⎦, ()ln af x x x m x =++<,(0x >)恒成立,则22ln e x x m x ++<.设22()ln e g x x x x =++,又对于[]1,x e ∀∈都有()f x m <恒成立,则2max1()max (),(2)g x f f e m e ⎡⎤=<⎢⎥⎣⎦,即有(1)()g m g e m <⎧⎨<⎩ ⇔ 21231e m e m⎧+<⎨+<⎩,因为22131e e +>+,所以221m e >+,即所求实数m 的取值范围是2(21,)e ++∞.。
浙江宁波市北仑区2016-2017学年高二数学上学期期中试题(4班,无答案)

浙江省宁波市北仑区2016-2017学年高二数学上学期期中试题(4班,无答案)一、选择题:本题共10小题,每小题5分,共50分。
1抛物线24x ay=的准线方程为------------------------------------------------------------------------[ ] (A )x a =- (B ) x a = (C )y a =- (D )y a =2.椭圆221925x y +=的焦点为12,F F ,AB 是过焦点1F 的弦,则2ABF ∆的周长为----------[ ] (A )20 (B ) 12 (C )10 (D )6 3.双曲线22149x y -=的渐近线方程是-------------------------------------------------------------------[ ](A) 23y x =±(B) 49y x =±(C) 32y x =±(D) 94y x =±4.设,αβ是方程20x ax b -+=的两个实根,则“2,1a b >>”是“,αβ均大于1”的-----[ ] (A)充分非必要条件. (B)必要非充分条件 (C)充要条件 (D)非充分又非必要条件 5.如果方程222=+ky x 表示焦点在y 轴上的椭圆,那么实数k 的取值范围是-------------[ ] (A )()+∞,0 (B )()2,0 (C )()+∞,1 (D )()1,06.双曲线)0(122≠=-mn ny m x 离心率为2,有一个焦点与抛物线x y 42=的焦点重合,则mn的值为--------------------------------------------------------------------------------------------[ ] (A)163 (B)83 (C)316 (D)38 7.设F 为抛物线C :23y x =的焦点,过F 且倾斜角为30°的直线交C 于,A B 两点,O 为坐 标原点,则OAB∆的面积为-------------------------------------------------------------------------[ ](C) 6332 (D) 948.已知命题,:R x p ∈∀总有02>x;命题:q “1>x ”是“2>x ”的充分不必要条件,则下 列命题中为真命题的是---------------------------------------------------------------------------------[ ] (A) q p ∧ (B) q p ⌝∧⌝ (C) q p ∧⌝ (D)q p ⌝∧ 9.设Q P ,分别为()2622=-+y x 和椭圆11022=+y x 上的点,则Q P ,两点间的最大距离[ ](A)25 (B)246+ (C)27+ (D)2610直线143x y+=与椭圆221169x y +=相交于,A B 两点,P 为椭圆上的点,且PAB ∆的面积等于3,则这样的点P共有-------------------------------------------------------------------------------[ ] (A)1个 (B)2个 (C)3个 (D) 4个二、填空题:本题共6小题,每小题5分,共30分。
浙江省宁波市北仑中学2016-2017学年高一下学期期中数学试卷Word版含解析

2016-2017学年浙江省宁波市北仑中学高一(下)期中数学试卷一、单项选择题:本大题共8小题,每小题5分,共40分.1.已知A={x|x2﹣3x+2≤0},B={﹣2,﹣1,0,1,2},则A∩B=()A.{﹣1,0} B.{0,1} C.{1,2} D.∅2.数列,﹣,,﹣,…的一个通项公式为()A.a n=(﹣1)n B.a n=(﹣1)nC.a n=(﹣1)n+1D.a n=(﹣1)n+13.等差数列{a n}中,a2+a8=16,则{a n}的前9项和为()A.56 B.96 C.80 D.724.数列{a n}满足a1=0,a n+1=,则a2015=()A.0 B.C.1 D.25.已知0<x≤3,则的最小值为()A.B.16 C.20 D.106.一船沿北偏西45°方向航行,看见正东方向有两个灯塔A,B,AB=10海里,航行半小时后,看见一灯塔在船的南偏东60°,另一灯塔在船的南偏东75°,则这艘船的速度是每小时()A.5海里B.5海里 C.10海里D.10海里7.关于x的不等式|x﹣1|﹣|x﹣3|>a2﹣3a的解集为非空数集,则实数a的取值范围是()A.1<a<2 B.C.a<1或a>2 D.a≤1或a≥28.已知正数x、y、z满足x2+y2+z2=1,则S=的最小值为()A.3 B.C.4 D.2(+1)二、填空题:本大题共7小题,前四题每空3分,后三题每空4分9.△ABC中,sinA:sinB:sinC=4:5:6,.则a:b:c= ,cosA:cosB:cosC= .10.已知,,m的最小值为:,则m,n之间的大小关系为.11.已知实数x,y满足﹣1≤x+y≤4且2≤x﹣y≤3,则不等式围成的区域面积为,则2x﹣3y的取值范围是.12.等差数列{a n}中,|a3|=|a9|,公差d<0,则使前n项和S n取得最大值的正整数n的值是,使前n项和S n>0的正整数n的最大值是.13.正项数列{a n},a1=1,前n项和S n满足,则s n= .14.设实数x,y满足3≤xy2≤8,4≤≤9,则的最大值是.15.△ABC中,sin(A﹣B)=sinC﹣sinB,D是边BC的一个三等分点(靠近点B),记,则当λ取最大值时,tan∠ACD= .三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤16.设函数f(x)=x2+ax+b,已知不等式f(x)<0的解集为{x|1<x<3},(1)若不等式f(x)≥m的解集为R,求实数m的取值范围;(2)若f(x)≥mx对任意的实数x≥2都成立,求实数m的取值范围.17.在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.18.设数列{a n}的前n项和为S n,已知2S n=3n+3.(1)求数列{a n}的通项公式;(2)若数列{b n}满足a n•b n=log3a n,求{b n}的前n项和T n.19.对于函数f(x),若存在区间A=(m<n),使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”,已知函数f(x)=x2﹣2ax+b (a,b∈R).(I)若b=0,a=1,g(x)=|f(x)|是“可等域函数”,求函数g(x)的“可等域区间”;(Ⅱ)若区间为f(x)的“可等域区间”,求a、b的值.20.已知数列{a n}的前n项和S n满足S n=a n﹣1.(1)求数列{a n}的通项公式;(2)求证:数列{a n}中的任意三项不可能成等差数列;(3)设b n=,T n为{b n}的前n项和,求证:T n<3.2016-2017学年浙江省宁波市北仑中学高一(下)期中数学试卷参考答案与试题解析一、单项选择题:本大题共8小题,每小题5分,共40分.1.已知A={x|x2﹣3x+2≤0},B={﹣2,﹣1,0,1,2},则A∩B=()A.{﹣1,0} B.{0,1} C.{1,2} D.∅【考点】1E:交集及其运算.【分析】求出A的等价条件,结合集合交集的定义进行求解即可.【解答】解:A={x|x2﹣3x+2≤0}={x|1≤x≤2},则A∩B={1,2},故选:C2.数列,﹣,,﹣,…的一个通项公式为()A.a n=(﹣1)n B.a n=(﹣1)nC.a n=(﹣1)n+1D.a n=(﹣1)n+1【考点】81:数列的概念及简单表示法.【分析】根据已知中数列各项的符号是一个摆动数列,我们可以用(﹣1)n+1来控制各项的符号,再由各项的分母为一等比数列,分子2n+1,由此可得数列的通项公式.【解答】解:由已知中数列,﹣,,﹣,…可得数列各项的分母为一等比数列{2n},分子2n+1,又∵数列所有的奇数项为正,偶数项为负故可用(﹣1)n+1来控制各项的符号,故数列的一个通项公式为a n=(﹣1)n+1故答案为:D.3.等差数列{a n}中,a2+a8=16,则{a n}的前9项和为()A.56 B.96 C.80 D.72【考点】84:等差数列的通项公式.【分析】由已知结合等差数列的性质求得a5,再由S9=9a5得答案.【解答】解:在等差数列{a n}中,由a2+a8=16,得2a5=16,∴a5=8,则{a n}的前9项和S9=9a5=9×8=72.故选:D.4.数列{a n}满足a1=0,a n+1=,则a2015=()A.0 B.C.1 D.2【考点】8H:数列递推式.【分析】通过计算出前几项的值确定周期,进而可得结论.【解答】解:∵a n+1==,a1=0,∴a2==1,a3==,a4==2,a5==0,∴数列{a n}是以4为周期的周期数列,又∵2015=503×4+3,∴a2015=a3=,故选:B.5.已知0<x≤3,则的最小值为()A.B.16 C.20 D.10【考点】7F:基本不等式.【分析】根据勾勾函数性质,可得在(0,4)单调性递减,即可得答案.【解答】解:由,当且仅当x=y=4取等号.根据勾勾函数性质,可得在(0,4)单调性递减,∵0<x≤3,∴当x=3时,y取得最小值为.故选:A.6.一船沿北偏西45°方向航行,看见正东方向有两个灯塔A,B,AB=10海里,航行半小时后,看见一灯塔在船的南偏东60°,另一灯塔在船的南偏东75°,则这艘船的速度是每小时()A.5海里B.5海里C.10海里D.10海里【考点】HU:解三角形的实际应用.【分析】根据题意作出对应的三角形,结合三角形的边角关系即可得到结论.【解答】解:如图所示,∠COA=135°,∠AOC=∠ACB=∠ABC=15°,∠OAC=30°,AB=10,∴AC=10.△AOC中,由正弦定理可得,∴OC=5,∴v==10,∴这艘船的速度是每小时10海里,故选:D.7.关于x的不等式|x﹣1|﹣|x﹣3|>a2﹣3a的解集为非空数集,则实数a的取值范围是()A.1<a<2 B.C.a<1或a>2 D.a≤1或a≥2【考点】R4:绝对值三角不等式.【分析】由题意可得|x﹣1|﹣|x﹣3|>a2﹣3a的解集非空,根据绝对值的意义求得|x﹣1|﹣|x﹣3|的最大值为2,可得2>a2﹣3a,由此求得实数a的取值范围.【解答】解:关于x的不等式|x﹣1|﹣|x﹣3|>a2﹣3a的解集为非空数集,则a2﹣3a<(|x﹣1|﹣|x﹣3|)max即可,而|x﹣1|﹣|x﹣3|的最大值是2,∴只需a2﹣3a﹣2<0,解得:<a<,故选:B.8.已知正数x、y、z满足x2+y2+z2=1,则S=的最小值为()A.3 B.C.4 D.2(+1)【考点】7F:基本不等式;RA:二维形式的柯西不等式.【分析】由题意可得1﹣z2=x2+y2≥2xy,从而可得≥,由基本不等式和不等式的性质可得≥≥4【解答】解:由题意可得0<z<1,0<1﹣z<1,∴z(1﹣z)≤()2=,当且仅当z=(1﹣z)即z=时取等号,又∵x2+y2+z2=1,∴1﹣z2=x2+y2≥2xy,当且仅当x=y时取等号,∴≥1,∴≥1,∴≥,∴≥≥4,当且仅当x=y=且z=时取等号,∴S=的最小值为4故选:C二、填空题:本大题共7小题,前四题每空3分,后三题每空4分9.△ABC中,sinA:sinB:sinC=4:5:6,.则a:b:c= 4:5:6 ,cosA:cosB:cosC=12:9:2 .【考点】HR:余弦定理;HP:正弦定理.【分析】由正弦定理得出sinA:sinB:sinC=a:b:c;设a=4k,b=5k,c=6k,由余弦定理求得cosA、cosB和cosC的值.【解答】解:△ABC中,由正弦定理知,sinA:sinB:sinC=a:b:c=4:5:6;设a=4k:b=5k:c=6k,(其中k≠0),由余弦定理得cosA==,cosB==,cosC==,∴cosA:cosB:cosC=:: =12:9:2.故答案为:4:5:6,12:9:2.10.已知,,m的最小值为: 4 ,则m,n之间的大小关系为m>n .【考点】7F:基本不等式.【分析】利用基本不等式的性质、指数函数的单调性即可得出.【解答】解:∵,∴m=a﹣2++2≥2+2=4,当且仅当a=4时取等号.∵,∴n<22=4.故答案为:4,m>n.11.已知实数x,y满足﹣1≤x+y≤4且2≤x﹣y≤3,则不等式围成的区域面积为,则2x﹣3y的取值范围是.【考点】7F:基本不等式.【分析】实数x,y满足﹣1≤x+y≤4且2≤x﹣y≤3,如图所示,求出矩形ABCD的顶点坐标可得面积,令2x﹣3y=t,则直线经过点A时,t取得最大值.直线经过点C时,t取得最小值.【解答】解:实数x,y满足﹣1≤x+y≤4且2≤x﹣y≤3,如图所示,A(1,﹣2),B,C(3,1),D.|AB|==,|BC|==.则不等式围成的区域面积==.令2x﹣3y=t,则直线经过点A时,t取得最大值t=2×1﹣3×(﹣2)=8.直线经过点C时,t取得最小值t=2×3﹣3×1=3.则2x﹣3y的取值范围是.故答案为:,.12.等差数列{a n}中,|a3|=|a9|,公差d<0,则使前n项和S n取得最大值的正整数n的值是5或6 ,使前n项和S n>0的正整数n的最大值是10 .【考点】85:等差数列的前n项和.【分析】由题意,公差d<0,等差数列{a n}是递减数列,|a3|=|a9|,即a3=﹣a9,可得a3+a9=0,即可前n项和S n取得最大值的正整数n的值和前n项和S n>0的正整数n的值.【解答】解:由题意,公差d<0,等差数列{a n}是递减数列,|a3|=|a9|,即a3=﹣a9,可得a3+a9=0,∵a3+a9=2a6,∴a6=0,∴等差数列{a n}的前5项是正项,第6项为0.则前n项和S n取得最大值的正整数n的值为:5或6.又∵=0,∴使前n项和S n>0的正整数n的最大值是:10.13.正项数列{a n},a1=1,前n项和S n满足,则s n= .【考点】8E:数列的求和.【分析】正项数列{a n},a1=1,前n项和S n满足,可得:﹣=2,利用等差数列的通项公式即可得出.【解答】解:∵正项数列{a n},a1=1,前n项和S n满足,∴﹣=2,∴数列是等差数列,首项为1,公差为2.∴=1+2(n﹣1)=2n﹣1.∴S n=.故答案为:.14.设实数x,y满足3≤xy2≤8,4≤≤9,则的最大值是27 .【考点】7G:基本不等式在最值问题中的应用.【分析】首先分析题目由实数x,y满足条件3≤xy2≤8,4≤≤9.求的最大值的问题.根据不等式的等价转换思想可得到:,,代入求解最大值即可得到答案.【解答】解:因为实数x,y满足3≤xy2≤8,4≤≤9,则有:,,再根据,即当且仅当x=3,y=1取得等号,即有的最大值是27.故答案为:27.15.△ABC中,sin(A﹣B)=sinC﹣sinB,D是边BC的一个三等分点(靠近点B),记,则当λ取最大值时,tan∠ACD= 2+.【考点】HP:正弦定理.【分析】由sin(A﹣B)=sinC﹣sinB,得sinB=2cosAsinB,cosA=,可得:A=,由已知得,利用和a2=b2+c2﹣bc可得λ取最值时,a、b、c间的数量关系.【解答】解:∵sin(A﹣B)=sinC﹣sinB,∴sinAcosB﹣cosAsinB=sinC﹣sinB=sinAcosB+cosAsinB﹣sinB,∴sinB=2cosAsinB,∵sinB≠0,∴cosA=,由A∈(0,π),可得:A=,在△ADB中,由正弦定理可将,变形为则,∵=∴即a2λ2=4c2+b2+2bc…①在△ACB中,由余弦定理得:a2=b2+c2﹣bc…②由①②得令,,f′(t)=,令f′(t)=0,得t=,即时,λ最大.结合②可得b=,a= c在△ACB中,由正弦定理得⇒,⇒tanC=2+故答案为:2+.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤16.设函数f(x)=x2+ax+b,已知不等式f(x)<0的解集为{x|1<x<3},(1)若不等式f(x)≥m的解集为R,求实数m的取值范围;(2)若f(x)≥mx对任意的实数x≥2都成立,求实数m的取值范围.【考点】3W:二次函数的性质;74:一元二次不等式的解法.【分析】(1)由不等式f(x)<0的解集为{x|1<x<3},可以确定f(x),不等式f(x)≥m的解集为R,等价于m≤f(x)min(2)由恒成立问题转化为根的个数以及对称轴和端点值问题.【解答】解:(1)∵函数f(x)=x2+ax+b,且f(x)<0的解集为{x|1<x<3},∴a=﹣4,b=3∴f(x)=x2﹣4x+3,∴f(x)=(x﹣2)2﹣1,∴f(x)最小值为﹣1∴不等式f(x)≥m的解集为R,实数m的取值范围为m≤﹣1(2)∵f(x)≥mx对任意的实数x≥2都成立,即x2﹣4x+3≥mx对任意的实数x≥2都成立,两边同时除以x得到:x+﹣4≥m对任意的实数x≥2都成立,x≥2时,x+﹣4≥﹣,∴m≤﹣,综上所述,m≤﹣.17.在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.【考点】HX:解三角形.【分析】(I)利用sin(C﹣A)=1,求出A,C关系,通过三角形内角和结合sinB=,求出sinA的值;(II)通过正弦定理,利用(I)及AC=,求出BC,求出sinC,然后求△ABC的面积.【解答】解:(Ⅰ)因为sin (C ﹣A )=1,所以,且C+A=π﹣B ,∴,∴,∴,又sinA >0,∴(Ⅱ)如图,由正弦定理得∴,又sinC=sin (A+B)=sinAcosB+cosAsinB=∴18.设数列{a n }的前n 项和为S n ,已知2S n =3n+3. (1)求数列{a n }的通项公式;(2)若数列{b n }满足a n •b n =log 3a n ,求{b n }的前n 项和T n . 【考点】8H :数列递推式;8E :数列的求和.【分析】(1)通过可知,化简可知,进而验证当n=1时是否成立即可; (2)通过(1)即a nb n =log 3a n可知当n>1时,利用错位相减法计算可知,进而检验当n=1时是否成立即可.【解答】解:(1)因为,所以,2a1=3+3,故a1=3,当n>1时,,此时,,即,所以,.(2)因为a n b n=log3a n,所以,当n>1时,,所以,当n>1时,.所以,两式相减,得,所以,经检验,n=1时也适合,综上可得:.19.对于函数f(x),若存在区间A=(m<n),使得{y|y=f(x),x∈A}=A,则称函数f(x)为“可等域函数”,区间A为函数f(x)的一个“可等域区间”,已知函数f(x)=x2﹣2ax+b(a,b∈R).(I)若b=0,a=1,g(x)=|f(x)|是“可等域函数”,求函数g(x)的“可等域区间”;(Ⅱ)若区间为f(x)的“可等域区间”,求a、b的值.【考点】34:函数的值域.【分析】(Ⅰ)根据题意可知,函数y=x和y=f(x)交点的横坐标便是m,n的值,而b=0,a=1时,可以得到g(x)=|x2﹣2x|,从而解x=|x2﹣2x|便可得出函数g(x)的“可等域区间”;(Ⅱ)据题意可知,方程x=x2﹣2ax+b的两实根为x=1,或a+1,这样将x=1,和x=a+1分别带入方程便可得出关于a,b的方程组,解方程组即可得出a,b的值.【解答】解:(Ⅰ)b=0,a=1时,g(x)=|x2﹣2x|,设y=g(x);解x=|x2﹣2x|得,x=0,1,或3;∴函数g(x)的“可等域区间”为,,或;(Ⅱ)据题意知,方程x=x2﹣2ax+b的解为x=1或a+1;∴;解得,或(舍去);即a=1,b=2.20.已知数列{a n}的前n项和S n满足S n=a n﹣1.(1)求数列{a n}的通项公式;(2)求证:数列{a n}中的任意三项不可能成等差数列;(3)设b n=,T n为{b n}的前n项和,求证:T n<3.【考点】8E:数列的求和;8H:数列递推式.【分析】(1)运用数列的通项和前n项和的关系,结合等比数列的通项公式,即可得到所求;(2)运用反证法,假设数列{a n}中的任意三项成等差数列,由(1)的结论,推出矛盾,即可得证;(3)把数列的通项公式放大,然后利用等比数列的求和公式求和后再放大得答案.【解答】(1)解:n=1时, S1=a1﹣1=a1,可得a1=2,n>1时, S n﹣1=a n﹣1﹣1,与S n=a n﹣1,相减可得, a n=a n﹣a n﹣1,即为a n=2a n﹣1,即有数列{a n}为等比数列,且a n=2n;(2)证明:假设数列{a n}中的任意三项成等差数列,由它们构成等比数列,则它们为公比为1的常数列,这与公比为2的等比数列矛盾,故假设错误,则数列{a n}中的任意三项不可能成等差数列;(3)证明:b n===<(n≥2),∴T n=b1+b2+…+b n<b1+=2+1﹣=3﹣<3.2017年6月22日。
2016-2017学年浙江省宁波市九校联考高二(下)期中数学试卷

一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合A ={x|−1≤x ≤3},B ={x|x 2−3x +2<0},则A ∩(∁R B )=( )A 、[−1,1)∪(2,3)B 、[−1,1]∪[2,3]C 、(1,2)D 、R2.i 是虚数单位,计算ii -+11=( ) A 、−1 B 、1 C 、i D 、−i3.已知曲线f (x )=lnx 在点(2,f (2))处的切线与直线ax +y +1=0垂直,则实数a 的值为( )A 、21B 、−2C 、2D 、−21 4.下面四个条件中,使a >b 成立的必要而不充分条件是( )A 、a −1>bB 、a +1>bC 、|a|>|b|D 、a 3>b 35.已知函数f (x )=1ln 1--x x ,则y =f (x )的图象大致为( ) A 、 B 、C 、D 、6.从1,2,3,…,9这九个整数中同时取四个不同的数,其和为偶数,则不同取法共有( )A 、62B 、64C 、65D 、667.已知1<a <b ,m =a 1-b ,n =b 1-a ,则m ,n 的大小关系为( )A 、m <nB 、m =nC 、m >nD 、m ,n 的大小关系不确定,与a ,b 的取值有关8.已知下列各式:①f (|x|+1)=x 2+1; ②f(112+x )=x ;③f (x 2−2x )=|x|; ④f (|x|)=3x +3x -.其中存在函数f (x )对任意的x ∈R 都成立的是( )A 、①④B 、③④C 、①②D 、①③9.设函数f (x )=log 2x +ax +b (a >0),若存在实数b ,使得对任意的x ∈[t ,t +2](t >0)都有|f (x )|≤1+a ,则t 的最小值是( )A 、2B 、1C 、43D 、32 10.定义在R 上的可导函数f (x )满足f (x )−f (−x )=2x 3,当x ∈(−∞,0]时f'(x )<3x 2,实数a 满足f (1−a )−f (a )≥−2a 3+3a 2−3a +1,则a 的取值范围是( ) A 、[23,+∞) B 、(−∞,23] C 、[21,+∞) D 、(−∞,21] 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.已知log a 2=m ,log a 3=n ,则an m +2=__________,用m ,n 表示log 46为_________. 12.已知(2x −x21)n 的展开式中二项式系数和为64,则n =________,该展开式中常数项为__________.13.已知函数f (x )=⎩⎨⎧>++≤+-2,122,4x a a x x x ,其中a >0且a ≠1.若a =21时方程f (x )=b 有两个不同的实根,则实数b 的取值范围是 ;若f (x )的值域为[2,+∞),则实数a 的取值范围是_________.14.函数f (x )=x 3−2x +e x −e x -的奇偶性为_________,在R 上的增减性为_________(填“单调递增”、“单调递减”或“有增有减”).15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与小明相邻,则不同的坐法总数为________.16.已知f(x)=|x +x 1−a|+|x −x 1−a|+2x −2a (x >0)的最小值为23.则实数a =_________. 17.已知函数f (x )=x 2+ax +b (a ,b ∈R )在区间(0,1]上有零点x 0,则ab(40x +091x −31)的最大值是__________. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.已知n ∈N*,S n =(n +1)(n +2)…(n +n ),T n =2n×1×3×…×(2n −1). (Ⅰ)求 S 1,S 2,S 3,T 1,T 2,T 3;(Ⅱ)猜想S n 与T n 的关系,并用数学归纳法证明.19.(Ⅰ)已知(2x−1)10=a0+a1(x−1)+a2(x−1)2+…+a10(x−1)10,其中ai∈R,i=1,2,…10.(i)求a0+a1+a2+…+a10;(ii)求a7.(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位,每个岗位至少有一人参加,且五人均能胜任这四个岗位.(i)若每人不准兼职,则不同的分配方案有几种?(ii)若甲乙被抽调去别的地方,剩下三人要求每人必兼两职,则不同的分配方案有几种?20.已知a∈R,函数f(x)满足f(2x)=x2−2ax+a2−1.(Ⅰ)求f(x)的解析式,并写出f(x)的定义域;(Ⅱ)若f(x)在[21 a,2]上的值域为[−1,0],求实数a的取值范围.21.已知函数f (x )=e x -−x+11. (Ⅰ)证明:当x ∈[0,3]时,e x -≥x911+. (Ⅱ)证明:当x ∈[2,3]时,−72<f(x)<0.22.已知a <−1,函数f (x )=|x 3−1|+x 3+ax (x ∈R ). (Ⅰ)求函数f (x )的最小值;(Ⅱ)已知存在实数m ,n (m <n ≤1),对任意t 0∈(m ,n ),总存在两个不同的t 1,t 2∈(1,+∞),使得f (t 0)−2=f (t 1)=f (t 2),求证:n −m ≤274.。
2016-2017学年高二上学期期中考试数学试题Word版含答案
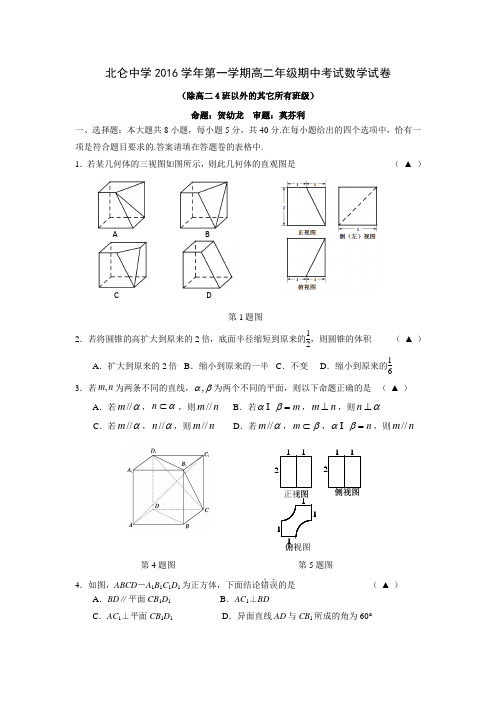
北仑中学2016学年第一学期高二年级期中考试数学试卷(除高二4班以外的其它所有班级) 命题:贺幼龙 审题:莫芬利一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,恰有一项是符合题目要求的.答案请填在答题卷的表格中.1.若某几何体的三视图如图所示,则此几何体的直观图是 ( ▲ )第1题图2.若将圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积 ( ▲ )A .扩大到原来的2倍B .缩小到原来的一半C .不变D .缩小到原来的163.若,m n 为两条不同的直线,,αβ为两个不同的平面,则以下命题正确的是 ( ▲ ) A .若α//m ,α⊂n ,则n m // B .若m =βα ,n m ⊥,则α⊥nC .若α//m ,α//n ,则n m //D .若α//m ,β⊂m ,n =βα ,则n m //第4题图 第5题图4.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是 ( ▲ )A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1所成的角为60°A BC D5.某几何体三视图如图所示,则该几何体的体积为 ( ▲ ) A .82π- B .8π- C .82π- D .84π-6.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是 ( ▲ )A .2+2 B.1+22 C.2+22D .1+ 27.下列四个命题中正确的命题有 ( ▲ ) ①过空间任何一点P 可以作无数条直线与已知的异面直线b a ,都相交; ②三个平面两两相交,有三条交线,则此三条交线或交于一点,或互相平行;③直线a α⊥平面,直线b β⊥平面,则直线b a ,所成角与平面βα,所成角相等或互补; ④αβ⊥平面平面,,,m n m n αβ⊂⊂⊥,则β⊥m 或α⊥n .A.1个B.2个C.3个D.4个8.如图,正方体1111ABCD A B C D -的棱长为1,点A 在平面α内,点E 是底面ABCD 的中心.若1C E ⊥平面α,则1C AB ∆在平面α内的射影的面积为 ( ▲ )ABCD第8题图 第11题图 第12题图二、填空题:本大题共7小题,前4题每空3分,后3题每空4分,共36分.将正确答案填在答题卷的横线上.9.正方体1111ABCD A B C D -的棱长为1,则其表面积为 ▲ ,其内切球的体积为 ▲ . 10.将一个边长分别是2 cm 和3 cm ,两邻边夹角为60°的平行四边形绕其3 cm 边上的高所在直线旋转一周形成的简单几何体是 ▲ ,其体积为 ▲ cm 3.11.如图,P 是正方形ABCD 外一点,且PA ABCD ⊥平面,则此几何体的5个面中互相垂直的面有 ▲ 对;若PA AB =,则直线PC 与平面PAB 所成角的正切值为 ▲ .1C 1A 1D 1B CDABαE12.一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体体积为 ▲ ,表面积为 ▲ .第13题图 第15题图13.如图,已知正三棱锥A —BCD 侧面的顶角为45°,侧棱长为a ,动点E 在侧棱AC 上运动,则线段BE 、ED 长度和的最小值为 ▲ .14,a b ,则a,b 所满足的等量关系式是 ▲ .15.如图,已知平面⊥α平面β,、A B 是平面α与β的交线上的两个定点,β⊂DA ,β⊂CB ,且6,8,4,,===⊥⊥AB BC AD CB DA αα,在平面α上有一个动点P ,使得BPC APD ∠=∠,则PAB ∆的面积的最大值为 ▲ .三、解答题:本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分14的正四棱锥P -ABCD 中,侧棱与底面所成角的大小为60°. (1)求侧棱的长度;(2)求正四棱锥P -ABCD 的外接球的表面积.第16题图 第17题图17.(本题满分15分)如图所示,在直三棱柱ABC -A 1B 1C 1中,AB =BC =AA 1=1,∠ABC=PDCBABCDAE90°. 点E 、F 分别是棱AB 、BB 1的中点. (1)求三棱锥B -AFC 的体积; (2)求异面直线EF 和BC 1所成的角.18.(本题满分15分)如图1,平面四边形 ABCD 关于直线AC 对称,2=CD ,60,90,A C ︒︒∠=∠=把ABD ∆沿BD 折 起(如图2)使二面角C BD A --的余弦值 为33.对于图2 (1)求AC 的长;(2)证明:⊥AC 平面BCD ;(3)求直线AC 与平面ABD 所成角的正弦值.第18题图19.(本题满分15分)如图,两矩形ABCD ,ABEF 所在平面互相垂直,DE 与平面ABCD 及平面ABEF 所成角分别为0030,45,N M ,分别为DB DE 、的中点,且1=MN . (1)求证:⊥MN 平面ABCD ; (2)求二面角B DE A --的正弦值.第19题图 第20题图20.(本题满分15分)如图,矩形ABCD 所在的半平面和直角梯形CDEF 所在的半平面 成60的二面角,.45,6,23,2,,// =∠===⊥CFE CF EF AD DE CD CF DE (1)求证:BF ∥平面ADE ;A CDB图1CABD图2FACB ED(2)试问在线段CF 上是否存在一点G ,使锐二面角D EG B --的余弦值为41.若存在,请求出CG 的值;若不存在,请说明理由.北仑中学2016学年第一学期高二年级期中考试数学参考答案(除高二4班以外的其它所有班级)一.选择题二.填空题9._____6______ ___6π____ 10.__圆台_____ ___3319π__ 11.______5_____ ____22___ 12.___ 31____ ____32+__13. 14. 822=+b a15. 12三.解答题16.(本题满分14分) (1)2 (2)316π17. (本题满分15分)PDCBA(1)1/12(2)318.(本题满分15分)解:(Ⅰ)取的中点,连接,由,得:就是二面角的平面角,在中,(Ⅱ)由,,又平面(Ⅲ)方法一:由(Ⅰ)知平面平面∴平面平面平面平面,作交于,则平面,就是与平面所成的角方法二:设点到平面的距离为,∵于是与平面所成角的正弦为.19. (本题满分15分)(1)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB ⊥AB,∴EB⊥平面ABCD,又MN∥EB,∴MN⊥面ABCD.(2)解:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,∵AD⊥平面ABEF,BO面ABEF,∴BO⊥平面ADE,∴OH为BH在平面ADE内的射影,∴BH⊥DE,即∠BHO为所求二面角的平面角,在Rt△ABE中,BO=,在Rt△DBE中,由BH·DE=DB·OE得BH=,∴sin∠BHO= .MOGFACBEDHOH20. (本题满分15分)证明:(1)∵在矩形ABCD 中BC ∥AD , AD ⊂平面ADE BC ⊄平面ADE , ∴BC ∥平面ADE , 同理CF ∥平面ADE , 又∵BC∩CF=C , ∴平面BCF ∥平面ADE , 而BF ⊂平面BCF , ∴BF ∥平面ADE . (2)∵CD ⊥AD ,CD ⊥DE∴∠ADE 即为二面角A-CD-F 的平面角, ∴∠ADE=60° 又∵AD∩DE=D , ∴CD ⊥平面ADE , 又∵CD ⊂平面CDEF ∴平面CDEF ⊥平面ADE ,作AO ⊥DE 于O ,则AO ⊥平面CDEF .过O 作EH OH ⊥于H,连接BH,易得BHO ∠是锐二面角D EG B --的平面角 因为3=BO ,易求得55=OH 取CF 中点M,易知OHG ∆与EMG ∆相似,设x OG =(x>0),则EGEMOG OH =,即2)2(9355x x -+=,解得21=x 或2213-=x (舍)因此存在符合题意的点G,使得CG=23.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年浙江省宁波市北仑中学高二(下)期中数学试卷一.选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)已知函数f(x)=2ln3x+8x,则的值为()A.﹣20 B.﹣10 C.10 D.202.(4分)从一批产品中取出三件,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是()A.A与C是对立事件B.B与C互斥C.任两个均互斥D.任两个均不互斥3.(4分)二项式的展开式中的有理项共有()A.4项 B.5项 C.6项 D.7项4.(4分)2015年6月20日是我们的传统节日﹣﹣”端午节”,这天小明的妈妈为小明煮了5个粽子,其中两个腊肉馅三个豆沙馅,小明随机取出两个,事件A=“取到的两个为同一种馅”,事件B=“取到的两个都是豆沙馅”,则P(B|A)=()A.B.C.D.5.(4分)设函数y=f(x)在定义域内可导,它的图象如下图所示,则它的导函数y=f'(x)图象可能为()A.B.C.D.6.(4分)已知随机变量ξ+η=8,若ξ~B(10,0.6),则Eη,Dη分别是()A.6和2.4 B.2和2.4 C.2和5.6 D.6和5.67.(4分)某五所大学进行自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是()A.B. C. D.8.(4分)已知可导函数f(x)(x∈R)满足f′(x)>f(x),则当a>0时,f(a)和e a f(0)大小关系为()A.f(a)<e a f(0)B.f(a)>e a f(0)C.f(a)=e a f(0) D.f(a)≤e a f(0)9.(4分)某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两名同学至少有一人参加,且若甲乙同时参加,则他们发言时不能相邻.那么不同的发言顺序种数为()A.360 B.520 C.600 D.72010.(4分)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)二.填空题:本大题共7小题,多空每空3分,单空每题4分,共36分.把答案填在答题卷的相应位置.11.(6分)在一次招聘中,主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.甲能正确完成其中的4道题,乙能正确完成每道题的概率为,且每道题完成与否互不影响.(1)记所抽取的3道题中,甲答对的题数为X,则X的分布列为;(2)记乙能答对的题数为Y,则Y的期望为.12.(6分)若函数f(x)=x3+3ax﹣1在x=1处的切线与直线y=6x+6平行,则实数a=;当a≤0时,若方程f(x)=15有且只有一个实根,则实数a的取值范围为.13.(6分)若,其中a2=﹣6,则实数m=;a1+a3+a5=.14.(6分)甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率;②求第4次由甲射击的概率.15.(4分)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有种(用数字作答).16.(4分)关于二项式(x﹣1)2005,有下列命题:①该二项展开式中非常数项的系数之和是1;②该二项展开式中第六项为C x1999;③该二项展开式中系数最大的项为第1002项;④当x=2006时,(x﹣1)2005除以2006的余数是2005.其中正确命题的序号是.(注:把你认为正确的命题序号都填上)17.(4分)如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有个.三.解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(14分)有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,求分别符合下列条件的选法数:(1)有女生但人数必须少于男生;(2)男生甲必须包括在内,但不担任数学课代表;(3)女生乙一定要担任语文课代表,男生丙只想担任数学课代表或物理课代表.19.(15分)已知f(x)=ax﹣lnx,其中x∈(0,e](e是自然对数的底数),(1)当a=1时,求f(x)的单调区间、极值;(2)是否存在a∈R,使f(x)的最小值是3,若存在求出a的值,若不存在,说明理由.20.(15分)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;(Ⅱ)记X为比赛决胜出胜负时的总局数,求X的分布列和均值(数学期望).21.(15分)已知的展开式中第五项的系数与第三项的系数的比是10:1.(1)求展开式中各项系数的和;(2)求展开式中含x的项;(3)求展开式中系数最大的项和二项式系数最大的项.22.(15分)已知函数.(Ⅰ)若p=2,求曲线f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;(Ⅲ)设函数,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.2016-2017学年浙江省宁波市北仑中学高二(下)期中数学试卷参考答案与试题解析一.选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)(2017春•北仑区校级期中)已知函数f(x)=2ln3x+8x,则的值为()A.﹣20 B.﹣10 C.10 D.20【解答】解:∵函数f(x)=2ln3x+8x,∴f′(x)=+8,∴f′(1)=10.∴=2=2f′(1)=20.故选:D.2.(4分)(2013•西湖区校级模拟)从一批产品中取出三件,设A=“三件产品全不是次品”,B=“三件产品全是次品”,C=“三件产品不全是次品”,则下列结论正确的是()A.A与C是对立事件B.B与C互斥C.任两个均互斥D.任两个均不互斥【解答】解:由题意知事件C包括三种情况,一是有两个次品一个正品,二是有一个次品两个正品,三是三件都是正品,∴事件C中不包含B事件,事件C和事件B不能同时发生,∴B与C互斥,故选B.3.(4分)(2015秋•荆州校级期末)二项式的展开式中的有理项共有()A.4项 B.5项 C.6项 D.7项=•2r•,【解答】解:二项式的展开式中通项公式为T r+1令20﹣为整数,可得r=0,2,4,6,8,10,共计6项,故选:C.4.(4分)(2016春•南城县校级期末)2015年6月20日是我们的传统节日﹣﹣”端午节”,这天小明的妈妈为小明煮了5个粽子,其中两个腊肉馅三个豆沙馅,小明随机取出两个,事件A=“取到的两个为同一种馅”,事件B=“取到的两个都是豆沙馅”,则P(B|A)=()A.B.C.D.【解答】解:由题意,P(A)==,P(AB)==,∴P(B|A)==,故选:A.5.(4分)(2017春•北仑区校级期中)设函数y=f(x)在定义域内可导,它的图象如下图所示,则它的导函数y=f'(x)图象可能为()A.B.C.D.【解答】解:函数的图象可知,x<0时,函数是增函数,f′(x)>0,函数f(x)有两个极值点,导函数的图象与x轴有2个交点,排除A,C;x>0的极大值前是增函数,导函数为正值,排除B.故选:D.6.(4分)(2015春•四平校级期末)已知随机变量ξ+η=8,若ξ~B(10,0.6),则Eη,Dη分别是()A.6和2.4 B.2和2.4 C.2和5.6 D.6和5.6【解答】解:∵ξ~B(10,0.6),∴Eξ=10×0.6=6,Dξ=10×0.6×0.4=2.4,∵ξ+η=8,∴Eη=E(8﹣ξ)=2,Dη=D(8﹣ξ)=2.4故选B.7.(4分)(2012•永新县校级二模)某五所大学进行自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是()A.B. C. D.【解答】解:五位同学到五所大学就读的所有就读方式有55=3125仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)就读方式有5×C52A43=1200仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是P==故选D8.(4分)(2014•陈仓区校级三模)已知可导函数f(x)(x∈R)满足f′(x)>f (x),则当a>0时,f(a)和e a f(0)大小关系为()A.f(a)<e a f(0)B.f(a)>e a f(0)C.f(a)=e a f(0) D.f(a)≤e a f(0)【解答】解:由题意知,可设函数f(x)=e2x,则导函数f′(x)=2•e2x,显然满足f'(x)>f(x),f(a)=e2a,e a f(0)=e a,当a>0时,显然e2a>e a ,即f(a)>e a f(0),故选B.9.(4分)(2016•衡水万卷模拟)某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两名同学至少有一人参加,且若甲乙同时参加,则他们发言时不能相邻.那么不同的发言顺序种数为()A.360 B.520 C.600 D.720【解答】解:根据题意,分2种情况讨论,若只有甲乙其中一人参加,有C21•C53•A44=480种情况;若甲乙两人都参加,有C22•C52•A44=240种情况,其中甲乙相邻的有C22•C52•A33•A22=120种情况;则不同的发言顺序种数480+240﹣120=600种,故选C.10.(4分)(2015•新课标Ⅰ)设函数f(x)=e x(2x﹣1)﹣ax+a,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a的取值范围是()A.[)B.[)C.[)D.[)【解答】解:设g(x)=e x(2x﹣1),y=ax﹣a,由题意知存在唯一的整数x0使得g(x0)在直线y=ax﹣a的下方,∵g′(x)=e x(2x﹣1)+2e x=e x(2x+1),∴当x<﹣时,g′(x)<0,当x>﹣时,g′(x)>0,∴当x=﹣时,g(x)取最小值﹣2,当x=0时,g(0)=﹣1,当x=1时,g(1)=e>0,直线y=ax﹣a恒过定点(1,0)且斜率为a,故﹣a>g(0)=﹣1且g(﹣1)=﹣3e﹣1≥﹣a﹣a,解得≤a<1故选:D二.填空题:本大题共7小题,多空每空3分,单空每题4分,共36分.把答案填在答题卷的相应位置.11.(6分)(2017春•北仑区校级期中)在一次招聘中,主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.甲能正确完成其中的4道题,乙能正确完成每道题的概率为,且每道题完成与否互不影响.(1)记所抽取的3道题中,甲答对的题数为X,则X的分布列为X123P0.20.60.2;(2)记乙能答对的题数为Y,则Y的期望为E(Y)=2.【解答】解:(1)主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题;甲能正确完成其中的4题,所抽取的3道题中,甲答对的题数为X,由题意得X的可能取值为1,2,3,P(X=1)==,P(X=2)==,P(X=3)==,∴X的分布列为:(2)主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题,乙能正确完成每道题的概率为,且每道题完成与否互不影响,由题意Y的可能取值为0,1,2,3,且Y~B(3,),P(Y=0)==,P(Y=1)=••=,P(Y=2)=••=,P(Y=3)=•=,∴Y的分布列为:数学期望为E(Y)=0×+1×+2×+3×=2.(或E(Y)=3×=2).故答案为:(1)(2)E(Y)=2.12.(6分)(2017春•北仑区校级期中)若函数f(x)=x3+3ax﹣1在x=1处的切线与直线y=6x+6平行,则实数a=1;当a≤0时,若方程f(x)=15有且只有一个实根,则实数a的取值范围为﹣<a≤0.【解答】解:(1)由f(x)=x3+3ax﹣1,得到f′(x)=3x2+3a,因为曲线在x=1处的切线与y=6x+6平行,而y=6x+6的斜率为6,所以f′(1)=6,即3+3a=6,解得a=1;(2)令g(x)=x3+3ax﹣16,g′(x)=3x2+3a=3(x2+a),a=0时,g′(x)≥0,g(x)在R递增,而x→﹣∞时,g(x)→﹣∞,x→+∞时,g(x)→+∞,故函数g(x)有且只有一个零点,即方程f(x)=15有且只有一个实根,a<0时,令g′(x)>0,解得:x>或x<﹣,令g′(x)<0,解得:﹣<x<,则g(x)在(﹣∞,﹣)递增,在(﹣,)递减,在(,+∞)递增,故g(x)极大值=g(﹣)=a+3a﹣16<0,解得:a>﹣,综上:﹣<a≤0,故答案为:1,﹣<a≤0.13.(6分)(2017春•北仑区校级期中)若,其中a2=﹣6,则实数m=;a1+a3+a5=.【解答】解:,则x(1﹣mx)4=x,则﹣4m=a2=﹣6,解得m=.对:,令x=1时,=a1+a2+a3+a4+a5,x=﹣1时,﹣=﹣a1+a2﹣a3+a4﹣a5,∴2(a1+a3+a5)=+,解得a1+a3+a5=.故答案为:,.14.(6分)(2017春•北仑区校级期中)甲、乙二人做射击游戏,甲、乙射击击中与否是相互独立事件.规则如下:若射击一次击中,则原射击人继续射击;若射击一次不中,就由对方接替射击.已知甲、乙二人射击一次击中的概率均为,且第一次由甲开始射击.①求前3次射击中甲恰好击中2次的概率;②求第4次由甲射击的概率.【解答】解:①由题意,前3次射击中甲恰好击中2次,即前2次甲都击中目标,但第三次没有击中目标,故它的概率为••=.②第4次由甲射击包括甲连续射击3次且都击中;第一次甲射击击中,但第二次没有击中,第三次由乙射击没有击中;第一次甲射击没有击中,且乙射击第二次击中,但第三次没有击中;第一次甲射击没有击中,且乙射击第二次没有击中,第三次甲射击击中;故这件事的概率为++•+=,故答案为:;.15.(4分)(2007•天津)如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色,要求相邻的两个格子颜色不同,且两端的格子的颜色也不同,则不同的涂色方法共有630种(用数字作答).【解答】解:根据题意,分为三类:第一类是只用两种颜色则为:C62A22=30种,第二类是用三种颜色则为:C63C31C21C21=240种,第三类是用四种颜色则为:C64A44=360种,由分类计数原理,共计为30+240+360=630种,故答案为630.16.(4分)(2008•宁波校级模拟)关于二项式(x﹣1)2005,有下列命题:①该二项展开式中非常数项的系数之和是1;②该二项展开式中第六项为C x1999;③该二项展开式中系数最大的项为第1002项;④当x=2006时,(x﹣1)2005除以2006的余数是2005.其中正确命题的序号是①④.(注:把你认为正确的命题序号都填上)【解答】解:令x=1求出二项式(x﹣1)2005所有项的系数和为0,令x=0求出常数项为﹣l,非常数项的系数和是1,即得①正确;二项展开式的第六项为C20055x2000,即得②错误;二项展开式中系数绝对值最大的项为=C20051002,﹣=﹣C20051003,得系数最大的项是第1003项C20051002•x1003,即③错误;当x=2006时,(x﹣1)2005除以2 006的余数是2006﹣l=2005,即④正确.故答案为:①④.17.(4分)(2017春•北仑区校级期中)如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.【解答】解:根据题意,分3种情况讨论:①、取出的3个点都在圆内,有C43=4种取法,即有4种取法,②、在圆内取2点,圆外12点中取1点,有C42C101=60种,即有60种取法,③、在圆内取1点,圆外12点中取2点,有C41(C122﹣4)=248种,即有248种取法,则至少有一个顶点在圆内的三角形有4+60+248=312个,故答案为:312.三.解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(14分)(2017春•北仑区校级期中)有5个男生和3个女生,从中选出5人担任5门不同学科的课代表,求分别符合下列条件的选法数:(1)有女生但人数必须少于男生;(2)男生甲必须包括在内,但不担任数学课代表;(3)女生乙一定要担任语文课代表,男生丙只想担任数学课代表或物理课代表.【解答】解:(1)根据题意,分2步进行分析:①、在8个人中选出5人,有3男2女和4男1女2种情况,则有(C53C32+C54C31)种取法,②、将取出的5人全排列,有A55种情况,则共有(C53C32+C54C31)A55=5400种选法;(2)分2步进行分析:①、由于男生甲不担任数学课代表,在除数学课代表之外的4门不同学科的课代表选出1门,由甲担任,则男生甲有C41种选择情况,②、在除男生甲之外的7人中任选4人,有C74种情况,将4人全排列,对应其他4门不同学科的课代表,有C74•A44种情况,则C74C41A44=3360种符合条件的选法;(3)根据题意,女生乙一定在选出的5人中,对于男生丙分2种情况讨论:①、男生丙也在选出的5人中,则男生丙担任数学课代表或物理课代表,男生丙有C21种情况,在其余6人中任选3人,担任剩下3门不同学科的课代表,有A63种情况,此时有C21•A63种选法,②、男生丙不在选出的5人中,则在其余6人中任选4人,担任剩下4门不同学科的课代表,有A64种情况,此时有A44种选法,则一共有种符合条件的选法.19.(15分)(2017春•北仑区校级期中)已知f(x)=ax﹣lnx,其中x∈(0,e](e是自然对数的底数),(1)当a=1时,求f(x)的单调区间、极值;(2)是否存在a∈R,使f(x)的最小值是3,若存在求出a的值,若不存在,说明理由.【解答】解:(1)∵f(x)=ax﹣lnx,(x∈(0,e]),∴f′(x)=a﹣,a=1时,f′(x)=1﹣=,∴当0<x<1时,f′(x)<0,此时f(x)单调递减.当1<x<e时,f′(x)>0,此时f(x)单调递增.∴f(x)的极小值为f(1)=1.(2)假设存在实数a,使f(x)=ax﹣lnx(x∈(0,e])有最小值3,f′(x)=.①当a≤0时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae﹣1=3,解得a=(舍去),∴此时f(x)无最小值.②当<e时,f(x)在上单调递减,在上单调递增.f(x)min=f=1+lna=3,a=e2,满足条件.③当≥e时,f(x)在(0,e]上单调递减,f(x)min=f(e)=ae﹣1=3,解得a=(舍去)∴此时f(e)无最小值.综上,存在实数a=e2,使得当x∈(0,e]时,f(x)有最小值3.20.(15分)(2014•安徽)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立.(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;(Ⅱ)记X为比赛决胜出胜负时的总局数,求X的分布列和均值(数学期望).【解答】解:用A表示甲在4局以内(含4局)赢得比赛的是事件,A k表示第k 局甲获胜,B k表示第k局乙获胜,则P(A k)=,P(B k)=,k=1,2,3,4,5(Ⅰ)P(A)=P(A1A2)+P(B1A2A3)+P(A1B2A3A4)=()2+×()2+××()2=.(Ⅱ)X的可能取值为2,3,4,5.P(X=2)=P(A1A2)+P(B1B2)=,P(X=3)=P(B1A2A3)+P(A1B2B3)=,P(X=4)=P(A1B2A3A4)+P(B1A2B3B4)=,P(X=5)=P(A1B2A3B4A5)+P(B1A2B3A4B5)+P(B1A2B3A4A5)+P(A1B2A3B4B5)==,或者P(X=5)=1﹣P(X=2)﹣P(X=3)﹣P(X=4)=,故分布列为:E(X)=2×+3×+4×+5×=.21.(15分)(2017春•北仑区校级期中)已知的展开式中第五项的系数与第三项的系数的比是10:1.(1)求展开式中各项系数的和;(2)求展开式中含x的项;(3)求展开式中系数最大的项和二项式系数最大的项.【解答】解:由题意知,第五项系数为,第三项的系数为,则有,化简得n2﹣5n﹣24=0,解得n=8或n=﹣3(舍去).(1)令x=1得各项系数的和为(1﹣2)8=1.==.(2)通项公式T k+1令﹣2k=,则k=1,可得:==.故展开式中含x的项为﹣16x.(3)设展开式中的第k项,第k+1项,第k+2项的系数绝对值分别为,,,若第k+1项的系数绝对值最大,则解得5≤k≤6.又T6的系数为负,∴系数最大的项为T7=1792x﹣11.由n=8知第5项二项式系数最大,此时T5=1120x﹣6.22.(15分)(2012•桂林二模)已知函数.(Ⅰ)若p=2,求曲线f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数f(x)在其定义域内为增函数,求正实数p的取值范围;(Ⅲ)设函数,若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求实数p的取值范围.【解答】解:(I)当p=2时,函数,f(1)=2﹣2﹣2ln1=0.,曲线f(x)在点(1,f(1))处的切线的斜率为f'(1)=2+2﹣2=2.从而曲线f(x)在点(1,f(1))处的切线方程为y﹣0=2(x﹣1)即y=2x﹣2.(II).令h(x)=px2﹣2x+p,要使f(x)在定义域(0,+∞)内是增函数,只需h(x)≥0在(0,+∞)内恒成立.由题意p>0,h(x)=px2﹣2x+p的图象为开口向上的抛物线,对称轴方程为,∴,只需,即p≥1时,h(x)≥0,f'(x)≥0∴f(x)在(0,+∞)内为增函数,正实数p的取值范围是[1,+∞).(III)∵在[1,e]上是减函数,∴x=e时,g(x)min=2;x=1时,g(x)max=2e,即g(x)∈[2,2e],当p<0时,h(x)=px2﹣2x+p,其图象为开口向下的抛物线,对称轴在y 轴的左侧,且h(0)<0,所以f(x)在x∈[1,e]内是减函数.当p=0时,h(x)=﹣2x,因为x∈[1,e],所以h(x)<0,,此时,f(x)在x∈[1,e]内是减函数.∴当p≤0时,f(x)在[1,e]上单调递减⇒f(x)max=f(1)=0<2,不合题意;当0<p<1时,由,所以.又由(2)知当p=1时,f(x)在[1,e]上是增函数,∴,不合题意;当p≥1时,由(2)知f(x)在[1,e]上是增函数,f(1)=0<2,又g(x)在[1,e]上是减函数,故只需f(x)max>g(x)min,x∈[1,e],而,g(x)=2,即,解得min综上所述,实数p的取值范围是.参与本试卷答题和审题的老师有:沂蒙松;涨停;caoqz;刘长柏;qiss;wdnah;minqi5;danbo7801;lincy;742048;刘老师;若尘;maths;左杰(排名不分先后)菁优网2017年6月23日。
