第二章 电阻电路的等效变换.
第二章 电阻电路的等效变换
i
+
… i
+ -
u
-
K=1,2 , i
+ -
u
Reg
u
G1
in Gn
u
-
Geg
分流公式: 分流公式:ik=Gku=Gk/Geg i n=2时,Reg=R1R2/(R1+R2) 时 ( i1=R2/(R1+R2), 2=R1/(R1+R2)×i ),i ( ( *混联:有串,又有并 混联:有串, 混联 1 R1 R2 R3 R4
对于△ 对于△形,各电阻中电流为:i12=u12/R12 i23=u23/R23 i31=u31/R31 各电阻中电流为:
i ′ =i12-i31=u12/R12-u31/R31 1
i ′2 =u23/R23-u12/R12
i ′3 =u31/R31-u23/R23
i1 + i 2 + i 3 = 0
③
2
2 i31 1 i12
④
2
⑤
i′2
1
1
R2
3
自已补充:R 自已补充 4与1串,R3与2串,然 串 串然 后再并 i2
R4 R3 2
3
i3 2
1
1
2-5
电压源和电流源的串联和并联
+
1、n个电压源串联:us=∑usk--------等效电压源 、 个电压源串联: 等效电压源 个电压源串联 + - + ○ ○ -○ us1 us2 usn。 。 注:正、负号取 。 。 。 2、n个电流源的并联: 个电流源的并联: 、 个电流源的并联 is1 is=is1+is2+…is=∑isk 。 。
αi
+ uS - i +
第二章电阻电路的等效变换

ab
20 100 60
120 60
ab 20 100
100 Rab=70
ab
20 100 60
40
例2 求: Rab
5
15 6
a 20
b
缩短无
电阻支路
7
6
Rab=10
4 a b
15
10
20
5
a
15 b
7 6 6 4 a
b
15 7
3
例6
求: Rab c
对称电路 c、d等电位
R
R
R
c R
a R
断路 a
+a
2 +
U
6V –
(a)
b
3 9V +
(b)
解: a
+
+a U b
a +
3A 2 U
3A 3 U
b
(a)
b
(b)
例1: 求下列各电源等效变换
+a
3A 1 U
解:
(c)
b
a
+
1 +
U
3V –
(c)
b
+a
2A 5 U
(d) b
a
+
5 -
U
10V +
(d)
b
例2: 试用电压源与电流源等效变换的方法,计算2
2.1 概述
1 一些概念
1)电阻电路 仅由电源和线性电阻构成的电路。
2)等效的概念:
若结构、元件参数不相同的两部分电路N1、N2,具 有相同的电压、电流关系,则称它们彼此等效。
i
高等教育出版社第六版《电路》第2章_电阻电路的等效变换课件

n
顺之者正,逆之者负。
2、串联: is1 is2
isn
is = is1= is2 = isn is
(1)电流相同的电流源能串联,但每个电源中的电压不确定。 (2)电流不相等,则不能串联,否则,违背KCL。 3、电流源is 和R、 us的串联: us is + – + u1 – R 注意:电压变化了。
第二章 电阻电路的等效变换
§2-1 引言
线性电路:由线性无源元件(R、L、C·)、线性受控 · · 源和独立电源组成。 线性电阻电路:由线性电阻、线性受控源和独立电源组成。 直流电路:独立电源为直流电源的线性电阻电路。
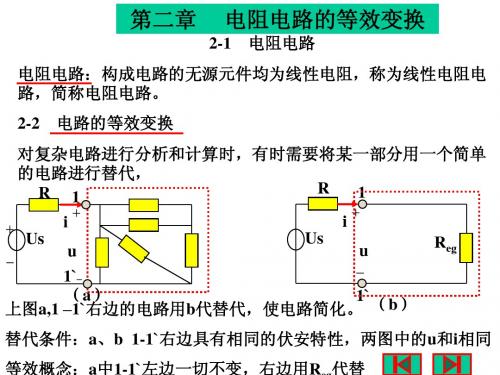
§2-2 电路的等效变换
一、等效的概念:
R R R1 §2-2 电路的等效变换 1 1 R2 i + R4 u R _ 3 ,
解:用电源变换法。受控源和独立源一样可以进行电源转换。 R i R _ + uR_ i R + uR + + ic + uc _ uS R _uS _
uc Ric 2 2 uR 4uR
Ri + Ri + uc = us
2uR 4uR us us uR 2V 6 在进行电源变换时,为避免出错控制量一般不要转换掉!
i2
i3
i3
u31 u23 R31 R23
R1u23 R3u12 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
R2u31 R1u23 R1R2 R2 R3 R3 R1 R1R2 R2 R3 R3 R1
由Y : R R R2 R3 R3 R1 R12 1 2 R3 R1R2 R2 R3 R3 R1 R23 R1 R R R2 R3 R3 R1 R31 1 2 R2
第02章电阻电路的等效变换(丘关源)

(6)恒压源并联任何元件其两端电压不变;
恒流源串联任何元件其流出电流不变;
a a
+ us
-
+ +
-
对外等效
us
-
b
c
b c
对外等效
is
+
-
d
is
d
(1-30)
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解:
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS=+uS1 …-uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件:uS=uS1=uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
(1-21)
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS=+uS1-uS2
R=R1 + R2
(1-22)
二、理想电流源的串联和并联
第二章 电阻电路的等效变换

注意: 注意: 上的电压; (1)变换后 0是两个元件上的电压; )变换后u 两个元件上的电压 控制变量所在支路不能动 (2)受控源的控制变量所在支路不能动。 )受控源的控制变量所在支路不能动。 2. 利用两类约束找关系 利用两类约束 两类约束找关系
1 对回路列KVL: (1 + R 3 + R 4 )i + 2 R 4 u 3 = u S 对回路列 : 2 受控源的控制量: 受控源的控制量: u 3 = R3 i
2、并联等效电阻 、并联等效电阻
(1)等效条件: )等效条件: (2)分流公式: )分流公式:
G
等
=
∑
G
并
Gk ik = G k u = i G等
i1
i2 G2 iS
特殊: 特殊:
G
k
= ∞ ,即 R
k
=
0 ,
i
k
=
i
,
短路处电流 电流源电流 其它电导电流 电流= 电流, 电导电流= ) (短路处电流=电流源电流,其它电导电流=0)
§2-1 引言 -
由时不变线性无源元件、线性受控源和独立电源 时不变线性无源元件 线性受控源和 元件、 组成的电路,称为时不变线性电路,简称线性电 组成的电路,称为时不变线性电路,简称线性电 路。 如果构成电路的无源元件均为线性电阻,则称为 如果构成电路的无源元件均为线性电阻, 构成电路的无源元件均为线性电阻 线性电阻性电路。 线性电阻性电路。电路中电压源的电压或电流源 的电流,可以是直流, 的电流,可以是直流,也可以随时间按某种规律 变化;当电路中的独立电源均为直流电源 直流电源时 变化;当电路中的独立电源均为直流电源时,称 直流电路。 为直流电路。 简单电阻电路的分析与计算 本章为简单电阻电路的分析与计算,着重介绍 本章为简单电阻电路的分析与计算, 等效变换的概念 的概念。 等效变换的概念。
第二章 电阻电路的等效变换

Ib Ic
c
将Y形联接等效变换为∆形联结时 形联接等效变换为∆ 3R 若 Ra=Rb=Rc=RY 时,有Rab=Rbc=Rca= R∆ = 3RY; 将∆形联接等效变换为Y形联结时 形联接等效变换为Y 若 Rab=Rbc=Rca=R∆ 时,有Ra=Rb=Rc=RY =R∆/3
总目录 章目录 返回 上一页 下一页
总目录 章目录 返回 上一页 下一页
+ U –
2.3.2 电阻的并联
I + I1 U – I2 R1 R2 特点: 特点: (1)各电阻联接在两个公共的结点之间; (1)各电阻联接在两个公共的结点之间 各电阻联接在两个公共的结点之间; (2)各电阻两端的电压相同; (2)各电阻两端的电压相同; 各电阻两端的电压相同 (3)等效电阻的倒数等于各电阻倒数之和; (3)等效电阻的倒数等于各电阻倒数之和; 等效电阻的倒数等于各电阻倒数之和 1 1 1 = + Req R1 R2 (4)并联电阻上电流的分配与电阻成反比。 (4)并联电阻上电流的分配与电阻成反比 并联电阻上电流的分配与电阻成反比。 两电阻并联时的分流公式: 两电阻并联时的分流公式: Req
R R ab ca R = a R +R +R ab bc ca R R bc ab R = b R +R +R ab bc ca R R ca bc R = c R +R +R ab bc ca
总目录 章目录 返回 上一页 下一页
Ia a Ra Ib Ic b Rb Rc c 等效变换
Ia
a Rab RbcRca b
第2章 电阻电路的等效变换 章
2.1 引言 2.2 电路的等效变换 2.3 电阻的串联和并联 2.4 电阻星型联结与三角型联结的等效变换 电阻星型联结与三角型联结的等效变换 2.5 电压源、电流源的串联和并联 电压源、 2.6 实际电源的两种模型及其等效变换 实际电源的两种模型及其等效变换 2.7 输入电阻
02第二章电阻电路的等效变换

如果它们彼此等效,那么流入对应端子的电流必须分别相
等。应当有:
i1
i' 1
,
i2
i' 2
,
i3
i' 3
i' 2
2
对,各个电阻的电流分别为:
R31
'
i ' 31
i3 3
1 i'
1
i' 12
u '
12
i 12
R12
R 12
R23
i' 23
i' 2
2
u '
23
i 23
R23
按KCL,端子处 的电流分别为:
§2-1电阻的串联、并联和混联
线性电路:
由时不变线性无源元件、线性受控源和独立电源 组成的电路,称为时不变线性电路,简称线性电 路。
线性电阻电路:
如果构成电路的无源元件均为线性电阻,则称为 线性电阻电路。
直流电路:
当电路中的独立电源都是直流电源时,这类电 路简称直流电路。
等效变换: 对电路进行分析和计算时,有时可以把电路中某一 部分简化,即用一个较简单的电路替代原电路,但端口的电压电 流关系保持不变。
1. 电路特点:
i 1 R1
R2
Rn
u
u1
u2
un
1' (a) 各电阻顺序连接,流过同一电流 (KCL);
(b) 总电压等于各串联电阻的电压之和 (KVL)。
2. 等效电阻Req
i1
R 1
R2
u
u1
u 2
Rn
i R 1
eq
u n
u
1'
第2章电阻电路的等效变换

总电流
U S 18 I= = A = 6A R 3
由分流公式得
6 I1 = I = × 6A = 4A 4× 4 9 6 + (1 + ) 4+4
再分流得
6
1 I x = I 1 = 2A 2
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.4 Y形电路和Δ形电路之间 的等效变换
返回
电路分析基础
如何等效化简电桥测温电路? 如何等效化简电桥测温电路?
返回
电路分析基础
第2章 电阻电路的等效变换
2.1 等效变换
电阻电路
线性电阻电路
非线性电阻电路
简化线性电阻电路的主要依据是等效变换
返回
电路分析基础
第2章 电阻电路的等效变换
2.1.1 一端口网络的定义
二端网络
一端口网络
流入一个端子的电流必定等于流出另一端子的电流
Ig =
Rp Rg + R p
× 10 × 10 −3 = 1 × 10 −3 mA
解之得应并联的电阻为
0.1RG 2 × 10 3 Rp = = Ω ≈ 222.22Ω 0.9 9
返回
电路分析基础
第2章 电阻电路的等效变换
2.2.3 电阻的混联
判别电路的串并联关系根据以下原则: 判别电路的串并联关系根据以下原则: (1)看电路的结构特点。 看电路的结构特点。 (2)看电压、电流关系。 看电压、电流关系。 (3)对电路作变形等效。 对电路作变形等效。 (4)找出等电位点。 找出等电位点。
R4 R5 R2(R3 + ) R4+R5 R = R1 + R4 R5 R2 + (R3 + ) R4 + R5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 电阻电路的等效变换§ 2-1 引言§ 2-2电阻的等效变换 § 2-3 电阻串联和并联§ 2-4 星三角变换(一)教学目标1、 要求掌握电路等效的概念;2、 要求掌握电阻串并联电路的计算方法及分压分流公式;3、要求掌握星形三角形的等效变换。
(二)教学难点星三角变换为难点(三)教学思路对于简单电路的分析,常常采用的是等效化简的方法,首先让同学理解等效的概念,在此基础上,再接下来介绍串并联等效化简及其他变换。
(四)教学内容和要点2.2等效变换的概念(二端网络)i =i ’c(二端网络)若两个二端网络N 1和N 2,当它们与同一个外部电路相接,在相接端点处的电压、电流关系完全相同时,则称N 1和N 2为相互等效的二端网络.2.3 电阻的串联、并联和混联一. 电阻的串联+ + _ _ u u u R 3 i R eq1.特征:流过同一电流(用于以后判断是否为串联) 2.KVL:iR u u u u u k R k ⋅==++∑3213.等效电阻:∑=keq RR4.分压公式:u R R u eqkk =5.功率:2i R P k k = ∑=kPP二. 电阻的并联特征:1.承受同一个电压2.KCL:∑=++k i i i i 321分流不分压,分流电路u GR ui k kk ==u G i k )(∑= ∑=k eq G G3.等效电阻:∑=keq GG4.分压公式:i G G u G i eqkk k == 5.功率:2u G P k k =∑=kP P并联串联↔↔↔,,i u G RR 1 G 1i 1(R eq)G eq三.电阻的混联串联 串并联13232R R R R R R eq++=321321)(R RR R R R R eq ++⋅+=求R ab . R ab =4Ω+6Ω=10Ω 例:桥式电路 具有四个节点 每个节点联接三条支路求R ab .平衡电桥:R 1﹒R 4=R 2﹒R 3例:R 1c 6Ω3Ω4Ω4Ω2Ω1Ω3R 4求R ab =2R a00804080804031603a ab R R ⨯==Ω+=Ω 例:无限长梯形网络,求R ab =?(R=5Ω) R cd ≈R ab 近似解法22205250ab ab abab ab abab ab R R R R R R R R R R R R R ⋅=++--⋅=--=∴==R ab2.4 电阻的Y —⊿等效变换1、三端网络的等效概念若两个三端网络的电压u 13、u 23与电流i 1、i 2之间的关系完全相同时,则称这两个三端网络对外互为等效。
2、等效互换的公式:Y 形:u 13=R 1i 1+R 3(i 1+i 2)=(R 1+R 3)i 1+R 3i 2u 23=R 2i 2+R 3(i 1+i 2)=R 3i 1+(R 2+R 3)i 2⊿形:⎪⎪⎩⎪⎪⎨⎧-+=-+=1213232323212231313131R u u R u i R u u R u i⎪⎪⎩⎪⎪⎨⎧++++++=++++++=23123122331231213123123123232312312312313123123123311213i R R R R R R R i R R R R R u i R R R R R i R R R R R R R u⊿—Y :31231231121R R R R R R ++=31231223122R R R R R R ++= 31231231233R R R R R R ++=分母为⊿形中三个电阻之和。
分子为⊿形中与之对应节点相联的电阻之积Y 313322112R R = 113322123R R R R R R R R ++=213322131R R R R R R R R ++=分子为Y 形电阻的两两乘积之和12 3 Y 23 - u 23分母为Y 形与之对应两节点无关的电阻例:求R ab =? 4131911++=ab R Ω(五)教学方法和手段教学方法:讲述法教学手段:普通教学手段和多媒体教学手段相结合§ 2-5电压源和电流源的串并联§ 2-6实际电源的两种模型及其等效变换 § 2-7输入电阻(一) 教学目标1、要求掌握独立电源串并联的概念及计算方法;2、要求掌握实际电源的模型和等效变换;3、要求掌握输入电阻的概念。
(二) 教学难点确定实际电压源和实际电流源变换时的方向为难点。
(三) 教学思路1、充分掌握电压源和电流源的性质,这样对于独立电源的串并联的化简和计算的理解有很大帮助。
2、引入实际电源的电路模型有两种,在分析电路的时候,为了简化计算,可以采用相互间的等效变换。
3、无源电阻网络可以用一个电阻来等效,这就是等效电阻。
引入输入电阻,数值上等于等效电阻,但概念不同。
Ω(四) 教学内容和要点2.5 (理想的) 电压源、电流源的串联和并联 1、∑=+-=sk s s s s u u u u u 321u sk 方向与u s 方向一致时取正u sk 方向与u s方向不一致时取负2、 并联同极性、同数值并联二、电流源的并联与串联1、 并联:要承受同一个电压∑=+-=sks s s s ii i i i 321i sk 方向与i s 方向一致取正 i sk 方向与i s 方向不一致取负2、 串联:同方向、同数值串联 2.6 实际电源的等效互换N 1:u =u s -R s u iN 2:sis R ui i -=i R i R u si s si -=(四)教学内容和要点2.5 (理想的) 电压源、电流源的串联和并联 3、 串联i iu s2u∑=+-=skssssuuuuu321u sk方向与u s方向一致时取正u sk方向与u s方向不一致时取负4、并联同极性、同数值并联二、电流源的并联与串联3、并联:要承受同一个电压∑=+-=skssssiiiii321i sk方向与i s方向一致取正i sk方向与i s方向不一致取负4、串联:同方向、同数值串联2.6 实际电源的等效互换N1:u=u s-R s u iN2:sis Ruii-=iRiRu sissi-=一、等效互换条件()ss s s sssu si suu R i iRR R R⎧==⎪⎨⎪==⎩二、注意1、两个条件必须同时满足iiu s2u2、 保持变换前后参考方向一致3、 等效是对外部而言,对内不等效4、 与理想电压源并联的元件(支路)对外电路不起作用;当对外电路讨论时,并联的元件(支路)可断开处理5、 与理想电流源串联的元件(支路)对外电路讨论时可以短接。
例:V u 5.62424=+⨯= V u 5.144485'-=⨯+-=例:Ω 5V Ω 8VI6Ω23I 8I 35=⨯+⨯ I=1A2.7 利用等效变换的概念分析含受控源电路 一、求输入电阻输入电阻 i uR in =825.12111=⨯+==u u u i u R Ω 025.0111)2(=⨯-==u u u i u R0=in R85.0411==u u R in Ω 二、 利用等效变换方法分析含受控源电路注意:等效变换中控制支路不能变动,应予以保留 例:求I 329.05.0333=-+I I IA I 3103=4Ω8ΩI8ΩI R ab a b-uu 1 u 1 2u 1 4Ω+ -u u 1 u 1 2u 1 -4Ω 6ΩI 3例: 解: u u u 5.11=+⇒u u 5.01= 535.01=-u u ⇒u=6V )5(965.131i i -⨯=⨯+⇒31=i A i u i 311=-= w i u p 275.1=⨯=求受控电压源的发出功率(电桥平衡只是相对于无源电路而言)(五)教学方法和手段教学方法:讲述法教学手段:普通教学手段和多媒体教学手段相结合。
