平面曲线弧长的概念(精)
定积分之几何应用-弧长曲率
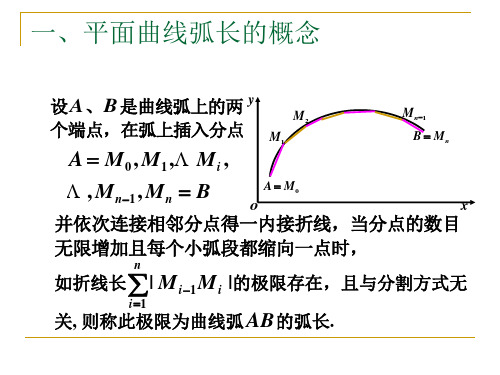
x y
r( r(
)cos )sin
( )
ds (dx)2 (dy)2 r 2( ) r2( )d ,
弧长 s r 2( ) r2( )d .
例 5 求极坐标系下曲线r a sin 3的长.
3
(a 0) (0 3)
解
r
3a sin
2
cos
1
3 3 3
2
2
0
a2 2 a2d a 0
2 1d
a 2 1 42 ln( 2 1 42 ) . 2
五、小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
曲率
一、曲率及其计算公式
1.曲率的定义
曲率是描述曲线局部性质(弯曲程度)的量。
1
2
M2 S2 M3
所求弧长为
a
b
s
b
1
xdx
2
[(1
3
b)2
(1
3
a)2 ].
a
3
x
例 2 计算曲线 y n n sin d 的弧长(0 x n). 0
解 y n sin x 1 sin x ,
nn
n
s
b a
1 y2dx
n nt
0
1 sin t ndt
0
0
6a.
例 4 证明正弦线 y a sin x (0 x 2) 的弧长
x cos t
等于椭圆 y
1 a 2 sin t
(0 t 2) 的周长.
证 设正弦线的弧长等于s1
s1
2 0
1 y2dx
平面曲线的弧长与曲率

§3 平面曲线的弧长与曲率教学目标:掌握平面曲线的弧长与曲率教学内容:平面曲线的弧长与曲率的计算公式.(1) 基本要求:掌握平面曲线的弧长计算公式. (2) 较高要求:掌握平面曲线的曲率计算公式. 教学建议:(1) 要求学生必须熟记平面曲线的弧长计算公式. (2) 对较好学生可要求他们掌握平面曲线的曲率计算公式. 教学过程:一、曲线弧长的概念设平面曲线),(B A C ,在其上从A 到B 依次取分点得曲线的一个分割T :B P P PP A n ==,,,,210 用线段联结相邻的点得:n i P P i i ,,2,1,1 =-。
记∑=--≤≤==ni ii T i i ni P P s P P T 1111,max分别表示最长弦的长度和折线的总长度。
定义1 对于平面曲线C 的无论怎样的分割T ,若极限ss T T =→0lim存在,则称曲线C 是可求长的,并称s 为曲线C 的弧长。
二、参数形曲线的弧长的计算公式定义2 设平面曲线].,[),(),(:βα∈==t t y y t x x C 若)(t x 与)(t y 在],[βα上连续可微,且)('t x 与)('t y 不同时为零,则称C 为一条光滑曲线。
定理1 设平面曲线],[),(),(:βα∈==t t y y t x x C 为一光滑曲线,则C 是可求长的,且弧长为.)(')('22dt t y t x s ⎰βα+=证: 对C 作任意分割T : B P P PP A n ==,,,,210 ,并设n P P ,0分别对应α=t 与β=x ,且.1,2,1)),(),((),(-==n i t y t x y x P i i i i i 于是与T 对应地得到区间],[βα的一个分割.:'110β=<<<<=α-n n t t t t T 在],[1i i i x x -=∆上应用微分中值定理得;,)(')()(1i i i i i i i t x t x t x x ∆∈ξ∆ξ=-=∆- .,)(')()(1i i i i i i i t y t y t y y ∆∈η∆η=-=∆- 从而有.)(')('122122i ni i i ni i i T t y x y x s ∆η+ξ=∆+∆=∑∑==由C 为一光滑曲线知,0→T 与0'→T 是等价的。
7-2平面曲线的弧长及旋转体的侧面积

2 2
2
π
1
1
周所得的旋转面的面积为
2 0
1 5 S 2= ∫ 2π ⋅ x ⋅ dx = 5π . 2 2
因此, 因此,所求旋转体的表面积为
练习题答案
a 2 1 3 5 3 2、 3、 一、1、1 + ln ; 2、 π ; 3、 + ln . 2 2 12 2 2 3 8 5 二、 [( ) 2 − 1]. 9 2 三、6a . 四、8a .
2 3 3 )a, a ) . 六、(( π − 3 2 2
2 2
= n∫
0
sin t + cos t + 2 sin t cos t dt 2 2 2 2
sin t + cos t dt = n∫ = 4n. 0 2 2
π
三、参数方程情形
曲线弧为
x = ϕ (t ) , y = ψ (t )
= r (θ ) + r ′ (θ )dθ ,
2 2
故弧长 s = ∫α r (θ ) + r ′ (θ )dθ .
β
2 2
例 4 求阿基米德螺线 r = aθ (a > 0)上相应
的弧长. 于 θ 从 0 到 2π 的弧长. 解Q
r′ = a,
β α
2π
∴ s=∫
′ 2 (θ )dθ r (θ ) + r
第二节 平面曲线的弧长与 旋转体的侧面积
一、 平面曲线弧长的概念 二、 直角坐标系情况 三、 参数方程情况 四、 极坐标情况 五、旋转体的侧面积 六、 小结
《微积分》第八节 平面曲线的弧长
小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b]上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
作业
P236习题3_8 1(单),2(2),3,4(2), 5,7(1、4),8,10(单)
三、平面曲线的弧长
直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a, b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
曲线弧为 ( ) ( )
其中 ( ) 在[ , ]上具有连续导数.
x y
( (
)cos )sin
( )
dx [()cos ()sin]d,
dy [()sin ()cos]d,
ds (dx)2 (dy)2 2( ) 2( )d,
弧长
s
2( ) 2( )d .
例5
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
解
r
3a
sin
3
2
cos
3
1 3
a sin
2
cos
,
3 3
s
r 2( ) r2( )d
3 0
a2
sin
3
数学分析10.3平面曲线的弧长与曲率

第十章 定积分的应用 3 平面曲线的弧长与曲率一、平面曲线的弧长设平面曲线C=⌒AB. 如图所示,在C 上从A 到B 依次取分点: A=P 0,P 1,P 2,…,P n-1,P n =B ,它们成为曲线C 的一个分割,记为T. 用线段联结T 中每相邻两点,得到C 的n 条弦P i-1P i (i=1,2,…,n),这n 条弦又成为C 的一条内接折线,记:T =ni 1max ≤≤|P i-1P i |,s T =∑=n1i i 1-i |P P |,分别表示最长弦的长度和折线的总长度。
定义1:对于曲线C 的无论怎样的分割T , 如果存在有限极限:0T lim →s T =s ,则称曲线C 是可求长的, 并把极限s 定义为曲线C 的弧长.定义2:设平面曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 如果x(t)与y(t)在[α,β]上连续可微,且x ’(t)与y ’(t)不同时为零 (即x ’2(t)+y ’2(t)≠0, t ∈[α,β]),则称C 为一条光滑曲线.定理:设曲线C 由参数方程x=x(t), y=y(t), t ∈[α,β]给出. 若C 为一光滑曲线,则C 是可求长的,且弧长为:s=⎰'+'βα22(t)y (t)x dt.证:对C 作任意分割T={P 0,P 1,…,P n },并设P 0与P n 分别对应t=α与t=β, 且P i (x i ,y i )=(x(t i ),y(t i )), i=1,2,…,n-1.于是,与T 对应得到区间[α,β]的一个分割T ’: α=t 0< t 1<t 2<…t n-1<t n =β.在T ’所属的每个小区间△i =[t i-1,t i ]上,由微分中值定理得△x i =x(t i )-x(t i-1)=x ’(ξi )△t i , ξi ∈△i ;△y i =y(t i )-y(t i-1)=y ’(ηi )△t i , ηi ∈△i . 从而C 的内接折线总长为s T =∑=∆+∆n1i 2i 2i y x =∑='+'n1i i 2i 2)(ηy )(ξx △t i .记σi =)(ηy )(ξx i 2i 2'+'-)(ξy )(ξx i 2i 2'+',则s T =[]∑=+'+'n1i i i 2i 2σ)(ηy )(ξx △t i .又由三角形不等式可得:|σi |≤||y ’(ηi )|-|y ’(ξi )||≤|y ’(ηi )-y ’(ξi )|. 由y ’(t)在[α,β]上连续,从而一致连续,∴对任给的ε>0, 存在δ>0, 当T '<δ时,只要ηi , ξi ∈△i ,就有|σi |≤|y ’(ηi )-y ’(ξi )|<α-βε, i=1,2,…,n. ∴|s T -∑='+'n1i i 2i 2)(ξy )(ξx △t i |=|∑=n1i i σ△t i |≤∑=n1i i |σ|△t i <ε,∴0T lim →s T =∑=→''+'n1i i 2i 20T )(ξy )(ξx lim △t i ,即s=⎰'+'βα22(t)y (t)x dt.注:1、若曲线C 由直线坐标方程y=f(x), x ∈[a,b]表示,则看作参数方程:x=x, y=f(x), x ∈[a,b]. 因此,当f(x)在[a,b]上连续可微时,此曲线即为一光滑曲线,其弧长公式为:s=⎰'+ba 2(x )f 1dx. 2、若曲线C 由极坐标方程r=r(θ), θ∈[α,β]表示,则 化为参数方程:x=r(θ)cos θ, y=r(θ)sin θ, θ∈[α,β]. 由x ’(θ)=r ’(θ)cos θ-r(θ)sin θ, y ’(θ)=r ’(θ)sin θ+r(θ)cos θ, 得:x ’2(θ)+y ’2(θ)=r 2(θ)+r ’2(θ),∴当r ’(θ)在[α,β]连续,且r(θ)与r ’(θ)不同时为零时,此极坐标曲线为一光滑曲线, 其弧长公式为:s=⎰'+βα22 )(θr )(θr d θ.例1:求摆线x=a(t-sint), y=a(1-cost)(a>0)一拱的孤长.解:∵x’(t)=a-acost; y’(t)=asint. ∴x’2(t)+y’2(t)=2a2(1-cost)=4a2sin22t.其弧长为s=⎰2π222tsin4a dt=4a⎰2π02tsin d⎪⎭⎫⎝⎛2t=8a.例2:求悬链线y=2ee-xx+从x=0到x=a>0那一段的弧长.解:∵y’=2ee-xx-. ∴1+y’2=2x-x2ee⎪⎪⎭⎫⎝⎛+.其弧长为s=⎰+a-xx2ee dx=2ee-aa-.例3:求心形线r=a(1+cosθ) (a>0)的周长.解:∵r’(θ)=-asinθ. ∴r2(θ)+r’2(θ)=4a2cos22θ.其周长为s=⎰2π02θacos2dθ=4a⎰2π02θcos d⎪⎭⎫⎝⎛2θ=8a.注:∵s(t)=⎰'+'tα22(t)y(t)x dt连续,∴dtds=22dtdydtdx⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛,即有ds=22dydx+. 特别称s(t)的微分dx为弧微分. (如左下图)PR为曲线在点P处的切线,在Rt△PQR中,PQ为dx,QR为dy,PR则为dx,这个三角形称为微分三角形。
史上最详细的平面曲线的弧长公式计算(微积分)[优质PPT]
![史上最详细的平面曲线的弧长公式计算(微积分)[优质PPT]](https://img.taocdn.com/s3/m/b2ec775455270722182ef728.png)
1 33
asi
n
2
co
s
3 3
10
7.4 平面曲线的弧长
例 求阿基米德螺线 ra(a0)上相应于
从0到2π的弧. 长
2πa
解
o
x
s
r2()r2()d
2π
2π
a22a2da
21d
0
0
a [2 π1 4 π 2 ln 2 π (1 4 π 2)]. 2
x2 a2dx x x2 a2 a2 ln | x x2 a2 | C
2
2
11
7.4 平面曲线的弧长
四、小结
平面曲线弧长的概念
直角坐标系下 求弧长的公式 参数方程情形下
极坐标系下
12
7.4 平面曲线的弧长
思考题
闭区间[a, b]上的连续曲线 y = f (x)是否
一定可求长?
解答
不一定. 仅仅有曲线连续还不够, 必须保证曲线光滑才可求长.
等于椭圆 y x c1o tas2sitn (0t2π)的周长.
证 设正弦线的弧长等于s1 对称性
π
s120
1y2dx2π 0
1a2co2xsdx
设椭圆的周长为s2
π
s220
(x)2(y)2dt2π 0
(st)i2 n (1a2)(c t)2d o t s
x
s b 1 y2dx a
例 计算曲线 y n n sind的弧长 (0xnπ). 0
解 y n sin x 1 sin x ,
nn
n
s nπ 0
1sinnxdxdnxx0π
大一高数课件第六章 6-4-1

a
3
0
3 sin d a . 3 2
2
五、小结
平面曲线弧长的概念
弧微分的概念 直角坐标系下
求弧长的公式 参数方程情形下 极坐标系下
思考题
闭区间[a , b] 上的连续曲线 y f ( x ) 是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
的面积;
2 2 2
s a 0
1 2 d 1 2 ln 1 2 a 1 2 2
2
2 0
例6
解
r 3a sin cos a sin cos , 3 3 3 3 3
s r 2 ( ) r 2 ( )d
一、填空题: 1、曲线 y ln x 上相应于 3 x 8 的一段弧长为 ____________; 2、渐 伸 线 x a (cos t t sin t ) , y a (sin t t cos t ) 上相应于 t 从 0 变到 的一段弧长为______; r 1 自 3 至 4 一 段 弧 长 为 3、曲 线 4 3 ____________ .
设曲线弧为 y f ( x )
( a x b) ,
o a
b
x
其中 f (x )在[a , b]上有一阶连续导数
取积分变量为 x ,在[a , b]上 任取小区间[ x, x dx],
以对应小切线段的长代替小 弧段的长, 小切线段的长
y
dy
(dx )2 (dy )2 1 y 2 dx
弧长 s
r 2 ( ) r 2 ( )d .
§3 平面曲线的弧长概要

(2)曲线C由极坐标方程
r r ( ), [ , ]
表示, 把它化为参数方程: 由于 x r cos r sin
x r cos , y r sin , ,
,
y' r sin r cos ,
2
d 8a .
e x e x 例2 求悬链线y= 从x=0到x=a>0那一段的弧长. 2
解 y′=
e x e x 2
a 2
2 , 1 y =
a
e x e x
4
2
,由公式(4)得
s=0
例3 解
1 y dx
0
e x e x ea ea dx . 2 2
其中f(x)在[a,b]上连续可微时,弧长公式为
s = a
b
1 f 2 x dx
(4)
r r ( ), [ , ] 表示, (2)若曲线C由极坐标方程
其中 r '( ) 在 [ , ]上连续,且 r ( ) 与 r '( )不同时 为零时,弧长公式为 s=
i 1
利用三角形不等式易证
i y i y i y i y i
' 由 y ( t ) 在 [ , ] 上连续,从而一致连续,
首页
×
故对任给的 0, 存在 0, 当 就有,
T'
时,只要 i ,i i,
首页
×
设平面曲线C.如图10—14所示,在C 上从A到B依次取分点: A=P0,P1,P2…,Pn-1,Pn=B,它们 成为对曲线C的一个分割,记为T.然 后用线段联结T中每相邻两点,
