整式的加减(教案)
七年级上册数学《整式的加减》教案优秀

七年级上册数学《整式的加减》教案优秀整式的加减篇一整式的加减篇二教学目的:1.经历及字母表示数量关系的过程,发展符号感;2.会进行整式加减的运算,并能说明其中的算理,发展有条理的思考及语言表达能力。
教学重点:会进行整式加减的运算,并能说明其中的算理。
教学难点:正确地去括号、合并同类项,及符号的正确处理。
教学过程:一、课前练习: 1.填空:整式包括_____________和_______________2.单项式的系数是___________、次数是__________3.多项式3m3-2m-5+m2是_____次______项式,其中二次项系数是______,一次项是__________,常数项是____________.4.下列各式,是同类项的一组是()(a)22x2y 与 yx2(b)2m2n与2mn2(c) ab与abc5.去括号后合并同类项:(3a-b)+(5a+2b)-(7a+4b).二、探索练习:1.如果用a、b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为_____________交换这个两位数的十位数字和个位数字后得到的两位数为__________________,这两个两位数的和为_________________________________.2.如果用a、b、c分别表示一个三位数的百位数字、十位数字和个位数字,那么这个三位数可以表示为___________,交换这个三位数的百位数字和个位数字后得到的三位数为______________,这两个三位数的差为___________________________.●议一议:在上面的两个问题中,分别涉及到了整式的什么运算?说说你是如何运算的?▲整式的加减运算实质就是____________________________,运算的结果是一个多项式或单项式。
三、巩固练习:1.填空:(1)2a-b与a-b的差是__________________________;(2)单项式、、、的和为___________;(3)如图所示,下面为由棋子所组成的三角形,一个三角形需六个棋子,三个三角形需_______个棋子,n个三角形需__________个棋子。
七年级数学第2章整式的加减2.2整式的加减课时2去括号教案

第二章整式的加减2。
2 整式的加减课时2 去括号【知识与技能】能运用运算律探究去括号法则,并能运用去括号法则将整式化简.【过程与方法】经过类比带括号的有理数的运算,发现去括号时的符号变化的规律,归纳去括号法则,培养学生观察、分析、归纳的能力。
【情感态度与价值观】让学生逐渐养成运用旧知识探索新知识的习惯,培养学生独立思考、勇于探索的精神。
去括号法则,运用法则将整式化简.括号前是“—”的去括号法则.多媒体课件情境(投影仪展示)如图2—2.2-1,要计算这个图形的面积.你有几种不同的方法?请计算结果,分小组讨论.总结出两个结果:3(x+3)和3x+9。
问题:一个图形的面积怎么会有两个结果呢?你们从中发现了什么?小组继续讨论,得出两个结果实际上是一样的,即3(x+3)=3x+9。
那分配律是否同样适用于整式的运算呢?(引入新课,板书课题)一、思考探究,获取新知问题:在格尔木到拉萨路段,如果列车通过冻土地段要t (1<t<3)h,那么它通过非冻土地段的时间为(t—0。
5)h,列车在冻土地段、非冻土地段的行驶速度分别是100 km/h和120 km/h。
于是,冻土地段的路程为100t km,非冻土地段的路程为120(t-0.5) km.因此,这段铁路的全长为[100t+120(t—0.5)] km①,冻土地段与非冻土地段相差[100t—120(t—0.5)]km②.上面的①②式子都带有括号,它们应如何化简?100t+120(t-0.5)=100t+=;100t—120(t—0.5)=100t+=。
我们知道,化简带有括号的整式,应先去括号.上面两个式子去括号部分的变形分别为+120(t—0。
5)=120t—60;③-120(t—0。
5)=—120t+60。
④比较③④两式,你能发现去括号时符号变化的规律吗?教师引导学生总结去括号法则:法则1:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;法则2:如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.特别地,形如+(x—3)与—(x—3)可以分别看作1乘(x—3)与-1乘(x-3)。
七年级上册数学《整式的加减》教案精选范文五篇

七年级上册数学《整式的加减》教案精选范文五篇教育是石,撞击生命的火花。
教育是灯,照亮夜行者踽踽独行的路。
教育是路,引领人类走向黎明。
因为有教育,一切才都那么美好,因为有教育,人类才有无穷的希望。
下面是小编给大家准备的七年级上册数学《整式的加减》教案精选范文,供大家阅读参考。
七年级上册数学《整式的加减》教案精选范文一教学目标和要求:1.理解同类项的概念,在具体情景中,认识同类项。
2.通过小组讨论、合作学习等方式,经历概念的形成过程,培养学生自主探索知识和合作交流的能力。
3.初步体会数学与人类生活的密切联系。
教学重点和难点:重点:理解同类项的概念。
难点:根据同类项的概念在多项式中找同类项。
教学方法:分层次教学,讲授、练习相结合。
教学过程:一、复习引入:1、创设问题情境⑴5个人+8个人=⑵5只羊+8只羊=⑶5个人+8只羊=(数学教学要紧密联系学生的生活实际、学习实际,这是新课程标准所赋予的任务。
学生尝试按种类、颜色等多种方法进行分类,一方面可提供学生主动参与的机会,把学生的注意力和思维活动调节到积极状态;另一方面可培养学生思维的灵活性,同时体现分类的思想方法。
)2、观察下列各单项式,把你认为相同类型的式子归为一类。
8x2y,-mn2,5a,-x2y,7mn2,,9a,-,0,0.4mn2,,2xy2。
由学生小组讨论后,按不同标准进行多种分类,教师巡视后把不同的分类方法投影显示。
要求学生观察归为一类的式子,思考它们有什么共同的特征?请学生说出各自的分类标准,并且肯定每一位学生按不同标准进行的分类。
(充分让学生自己观察、自己发现、自己描述,进行自主学习和合作交流,可极大的激发学生学习的积极性和主动性,满足学生的表现欲和探究欲,使学生学得轻松愉快,充分体现课堂教学的开放性。
)二、讲授新课:1.同类项的定义:我们常常把具有相同特征的事物归为一类。
8x2y与-x2y可以归为一类,2xy2与-可以归为一类,-mn2、7mn2与0.4mn2可以归为一类,5a与9a可以归为一类,还有、0与也可以归为一类。
整式的加减(教案)
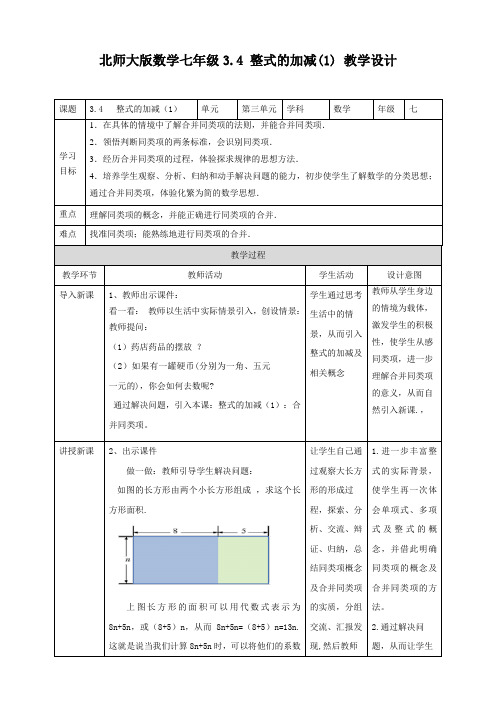
北师大版数学七年级3.4 整式的加减(1) 教学设计课题 3.4 整式的加减(1)单元第三单元学科数学年级七学习目标1.在具体的情境中了解合并同类项的法则,并能合并同类项.2.领悟判断同类项的两条标准,会识别同类项.3.经历合并同类项的过程,体验探求规律的思想方法.4.培养学生观察、分析、归纳和动手解决问题的能力,初步使学生了解数学的分类思想;通过合并同类项,体验化繁为简的数学思想.重点理解同类项的概念,并能正确进行同类项的合并.难点找准同类项;能熟练地进行同类项的合并.教学过程教学环节教师活动学生活动设计意图导入新课1、教师出示课件:看一看:教师以生活中实际情景引入,创设情景:教师提问:(1)药店药品的摆放?(2)如果有一罐硬币(分别为一角、五元一元的),你会如何去数呢?通过解决问题,引入本课:整式的加减(1):合并同类项。
学生通过思考生活中的情景,从而引入整式的加减及相关概念教师从学生身边的情境为载体,激发学生的积极性,使学生从感同类项,进一步理解合并同类项的意义,从而自然引入新课.,讲授新课2、出示课件做一做:教师引导学生解决问题:如图的长方形由两个小长方形组成,求这个长方形面积.上图长方形的面积可以用代数式表示为8n+5n,或(8+5)n,从而8n+5n=(8+5)n=13n.这就是说当我们计算8n+5n时,可以将他们的系数让学生自己通过观察大长方形的形成过程,探索、分析、交流、辩证、归纳,总结同类项概念及合并同类项的实质,分组交流、汇报发现,然后教师1.进一步丰富整式的实际背景,使学生再一次体会单项式、多项式及整式的概念,并借此明确同类项的概念及合并同类项的方法。
2.通过解决问题,从而让学生合并同类项时,把同类项的系数相加,字母和字母的指数不变. 例3 合并同类项:归纳总结“合并同类项”的方法:一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;三合,将同一括号内的同类项相加即可. 3.出示课件 试一试 :鼓励学生尝试用第二种方法解得出方法一,先化简再求值会更简便例3. 求代数式-3x ²y+1.5x-1.5x ²y+3.5x ²y-7的值, 其中x=1,y=0师:试试用两种方法去解该题,你又发现了什么?总结提高学生对同类项及合并同类项的认知。
3.4整式的加减第2课时去括号(教案)

举例解释:
(1)对于表达式-2(3x - 4y + 5),学生需注意去括号后变为-6x + 8y - 10,括号内每一项都要乘以括号前的“-2”。
(2)对于多层括号的情况如-3{(2x - [4 - (1 - 2y)])},需要先去最内层括号,然后依次向外进行,注意每层括号前的符号对括号内项的影响。
本节课通过讲解和练习,使学生熟练掌握去括号的方法,并能将其应用于整式的加减运算中,提高学生的运算能力和解决问题的能力。
二、核心素养目标
1.培养学生的逻辑推理能力:通过去括号法则的学习,让学生掌握从特殊到一般、从具体到抽象的逻辑推理方法,提高学生分析问题和解决问题的能力。
2.培养学生的数学运算能力:使学生能够熟练运用去括号法则进行整式的加减运算,提高运算速度和准确性。
3.4整式的加减第2课时去括号(教案)
一、教学内容
本节课选自七年级数学上册第三章“整式的加减”中的3.4节,第2课时“去括号”。主要内容包括以下两点:
1.掌握去括号的方法:在整式的加减运算中,根据括号前的符号,去掉括号,并注意括号内各项符号的变化。
2.应用去括号法则解决实际问题:运用去括号的方,解决生活中的数学问题,如购物时计算总价等。
(2)对于表达式4 - (2x - 3y + 5),当括号前为“-”号时,去掉括号后,括号内各项符号取反,即4 - 2x + 3y - 5。
2.教学难点
-括号前“-”号时去括号后括号内各项符号的取反:学生容易在这一步出错,忘记改变括号内各项的符号。
-多个括号嵌套时的去括号顺序:在多层括号的情况下,学生可能不知道从哪一层开始去括号,导致运算错误。
2.2整式的加减去括号(教案)

此外,学生小组讨论环节,我发现学生们在分享自己的观点和成果时,能够主动思考并尝试解决问题。这表明他们具备了较强的自主学习能力。但在讨论过程中,我也观察到一些学生对去括号法则的应用仍不够熟练。因此,我计划在接下来的课程中,增加一些有针对性的练习,帮助学生巩固所学知识。
3.重点难点解析:在讲授过程中,我会特别强调分配律的运用和正负号的处理这两个重点。对于难点部分,比如多层括号嵌套的情况,我会通过举例和步骤分解来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与去括号相关的实际问题,如购物时计算折扣后的价格。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。通过实际运算,演示去括号的基本原理。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了去括号的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对去括号法则的理解。我希望大家能够掌握这些知识点,并在数学运算中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解去括号的基本概念。去括号是指在整式的加减运算中,根据分配律将括号内的项与括号外的系数相乘,从而去掉括号的过程。这一步骤是解决整式运算问题的关键。
2.案例分析:接下来,我们来看一个具体的案例:2(a+b)-3(a-b)。这个案例将展示如何运用去括号法则简化整式,以及它如何帮助我们解决问题。
整式的加减(去括号)教案)

整式的加减(去括号)教案一、教学目标1、知识与技能:理解去括号时符号的规律,会用去括号法则进行计算。
2、通过类比,让学生经历去括号法则的探索过程,掌握去括号的方法。
3、情感与态度:通过观察、猜想、整理,培养学生的归纳能力;通过合作学习、讨论,培养学生学会与他人交流的意识和能力。
二、重点难点。
1、重点:去括号法则,准确应用法则将整式化解。
2、难点:括号前面是“_”号,去括号时,括号内各项变号容易产生错误。
三、教学准备多媒体课件.四、教学方法分层教学,讲练结合。
五、教学过程(一)、复习导入1、师:同学们还记得乘法分配律吗?用字母怎样表示?学生回答,教师补充。
然后在ppt 上展示成法分配律。
一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把和相加。
用字母表示为: ()a b c ab ac +=+2、利用乘法分配律计算:12(1)12+=2+86311(2)-12-=-3+443⎛⎫⨯ ⎪⎝⎭⎛⎫⨯ ⎪⎝⎭教师强调项数、各项的符号的变化。
3、师:这是有理数的运算中有括号的,我们可以应用乘法分配律进行计算,那么如果是多项试的化简中有括号的我们又该怎么化简呢?(二)讲授新课1、用类比的方法计算下列各式:(1)2()(2)3(34)912(3)7(75)4935x x x x y y +=+-+=----=-+28216注意项数和符号2、小组讨论:通过刚才的3个例子,你能够发现去括号时符号的变化规律?项数呢?你明白它们变化的依据吗?教师鼓励学生通过观察,试用自己的语言叙述去括号法则。
符号变化规律:如果括号外面是“+”,去掉括号和它前面的“+”号,括号内的各项都不变号。
如果括号外面是“—”,去掉括号和它前面的“—”号,括号内的各项都要变号。
括号内的项数都没变变化的依据是乘法分配律3、课堂练习1、计算探求并讨论下列两个式子 (3)(3)?(4)(3)?x x ++=--=引导学生可以把(3)x ++看做1 乘(3)x +,把(3)x --看做1-乘(3)x -。
3.2 整式的加减(教案)北师大版(2024)数学七年级上册

3.2整式的加减第1课时合并同类项1.在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律;2.了解合并同类项的法则,能进行同类项的合并.重点了解同类项的定义以及合并同类项的法则.难点准确理解合并同类项法则并进行计算.一、导入新课课件出示生活中各种水果的图片,让学生根据其本身具有的不同特征对其进行分类.教师:我们常常把具有相同特征的事物归为一类.今天我们要将生活中的分类思想应用到数学中.二、探究新知1.同类项的概念课件出示问题:图3-6中的长方形由两个小长方形组成.(1)利用图3-6化简8n+5n,并用运算律解释你的化简结果.(2)你能用类似的方法化简2xy+3xy及-7a2b+2a2b吗?根据乘法对加法的分配律可得8n+5n=(8+5)n=13n,2xy+3xy=(2+3)xy=5xy,-7a2b+2a2b=(-7+2)a2b=-5a2b.把你认为类型相同的式子归为同一类,并说出分类依据.8n与5n,2xy与3xy,-7a2b与2a2b先让学生自己独立思考,再在小组内讨论说出分类的依据.教师点评并进一步讲解:所含字母相同,并且相同字母的指数也相同的项,叫做同类项.强调判断同类项的方法:①两相同:字母相同,相同字母的指数也相同;②两无关:与系数无关,与字母顺序无关;③所有的常数项都是同类项.2.合并同类项教师:同类项之间能否进行运算呢?课件出示教材第90页图3-8,提出问题:图3-8的长方形由两个小长方形组成,求这个长方形的面积.学生独立完成后汇报答案,教师进一步讲解:长方形的面积可用代数式表示为8n+5n,或(8+5)n,从而8n+5n=(8+5)n=13n.引导学生说明:同类项之间能进行运算,把同类项合并成一项,叫做合并同类项.让学生进一步观察:在合并同类项的过程中,它们的系数、字母和字母的指数有什么变化?学生归纳出合并同类项的方法,教师进一步说明:合并同类项的法则:同类项的系数相加,字母和字母的指数不变. 课件出示例1:(1)-xy 2+3xy 2;(2)7a +3a 2+2a -a 2+3.学生独立完成后,小组讨论合并同类项的步骤:(1)发现同类项(找);(2)确定各同类项系数(移);(3)合并同类项(并).课件出示例2:例2 合并同类项:(1)3a +2b -5a -b ;(2)-4ab +13 b 2-9ab -12 b 2课件出示练习:求代数式-3x 2y +5x -0.5x 2y +3.5x 2y -2的值,其中x =15 ,y =7.说说你是怎么做的,并与同伴进行交流.三、举例分析例1 (课件出示教材第90页例1)例2 (课件出示教材第91页例2)学生独立完成后汇报答案,教师点评.四、课堂练习1.合并同类项:6xy-10x2-5yx+7x2.2.求x2+2x-2y2-y-x2+2y2的值,其中x=1,y=2.3.教材第89页“随堂练习”第1~3题.【答案】1.-3x2+xy 2.原式=2x-y,当x=1,y=2时,原式=2×1-2=0五、课堂小结1.什么是同类项?其判定方法是什么?2.合并同类项的定义及法则分别是什么?3.怎样合并同类项?六、课后作业教材第93页第1,2题.本节课的内容是合并同类项,是本章的一个重点知识,是以后学习解方程、解不等式的基础.课堂中,用生活中的事例导入新课,充分调动了学生学习的积极性,激发了学生的求知欲.随后,通过教师的引导,让学生一步步总结出了同类项的定义、合并同类项的定义及法则.本节课充分尊重学生的主体地位,积极鼓励学生独立思考,自主探索,合作交流,让同学们体验和经历知识的发生、发展、形成和应用的过程,学会获取新知识的方法.第2课时去括号1.掌握去括号的法则,并能根据去括号的法则进行运算;2.培养学生观察、类比、归纳的能力.重点运用去括号的法则进行化简.难点正确进行括号前面是“-”号的运算.一、导入新课问题1:什么叫同类项?问题2:若149xm y4和34x5y2n是同类项,则m=________,n=________,它们的和为________.指名学生回答,教师点评.二、探究新知1.去括号法则课件出示:(1)13+2×(7-5);(2)13-2×(7-5).教师:谁能用两种方法分别解这两题?学生回答,教师进一步提出:运用分配律可以去括号.教师:若将数换成代数式,又会怎么样呢?课件出示:在上一节用小棒拼摆正方形时,我们得到了几个不同的代数式:x+x+(x+1),4+3(x-1),4x-(x-1),3x+1,它们都表示拼摆x个正方形所需小棒的根数,因此应该相等.对此,你能用运算律加以解释吗?与同伴进行交流.利用乘法分配律去括号,可得x+x+(x+1)=x+x+x+1=3x+1;4+3(x-1)=4+3x-3=3x+1;4x-(x-1)=4x+(-1)(x-1)=4x+(-1)x+(-1)(-1)=4x-x+1=3x+1.三个代数式都可化为3x+1的形式,因此,这四个代数式是相等的.教师:仿照刚才的两种方法,分别化简这两道题.利用乘法分配律将下列各式去括号.去括号前后,括号里各项的符号有什么变化?与同伴进行交流.(1)a+(b+c);(2)a-(b+c);(3)a+(b-c);(4)a-(b-c).学生完成后汇报答案,教师点评,引导学生思考:(1)我们是怎么得到多项式去括号的方法的?(2)这两道题中的第(1)小题与第(2)小题的去括号有何不同?(3)你能总结去括号的法则吗?学生讨论后回答,教师讲评并课件出示:括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.为了便于记忆,教师引导学生共同完成下面的顺口溜:去括号,看符号:是“+”号,不变号;是“-”号,要变号.课件出示例3:化简下列各式:(1)4a-(a-3b);(2)a+(5a-3b)-(a-2b)(3)3(2xy-y)-2xy;(4)5x-y-2(x-y)你认为去括号时要注意什么?与同伴进行交流.三、课堂练习1.教材第91页“随堂练习”第1,2题.2.(1)9a+2(6a-a);(2)9a-2(6a-a).【答案】(1)原式=9a+10a=19a(2)原式=9a-10a=-a四、课堂小结1.去括号的法则是什么?五、课后作业教材第93页第5,6,7题.本节课的内容是去括号,是本章的一个重点知识,是以后学习解方程、解不等式的基础.去括号看似容易,实际上是最容易出错的地方.课堂中,用自然数去括号的计算导入代数式去括号的问题.随后,让学生通过比较归纳得出去括号时符号的变化规律,将新知识转化为已经学过的知识,从而构建新的知识体系,在此基础上要求学生用自己的语言叙述这个规律,有利于提高学生数学语言的表达能力.第3课时整式的加减1.让同学们从实际背景中去体会进行整式加减的必要性,会进行整式的加减运算;2.经历探索整式加减运算法则的过程,进一步培养学生观察、归纳、运算的能力.重、难点掌握去括号法则.一、导入新课课件出示问题:(1)任意写一个两位数;(2)交换这个两位数的十位数字和个位数字,又得到一个数;(3)求这两个数的和.二、探究新知1.整式的加减教师:再写几个两位数重复上面的过程.这些和有没有规律?如果有规律,这个规律对任意一个两位数都成立吗?如果用字母表示两位数,结果会怎样?学生小组讨论完毕后,派代表回答,教师点评.课件出示问题:(1)任意写一个三位数;(2)交换它的百位数字与个位数字,又得到一个三位数;(3)两个数相减.教师:两个数相减后的结果有什么规律?这个规律对任意一个三位数都成立吗?如果用字母表示三位数,结果会怎样?在上面的两个问题中,分别涉及整式的什么运算?说一说你是如何运算的,并与同伴进行交流.学生小组讨论完毕后,派代表回答,教师点评,进一步引导学生总结归纳:整式的加减实质上就是去括号后合并同类项,运算的结果是一个单项式或一个多项式.课件出示例4计算:(1)2x 2-3x +1与-3x 2+5x -7的和;(2)-x 2+3x -12 y 2与-12 x 2+4xy -32 y 2的差.学生独立完成后汇报答案,教师点评,进一步引导学生得出:进行整式加减运算时,如果遇到括号要先去括号,再合并同类项.三、课堂练习计算:(1)(4k 2+7k )+(-k 2+3k -1);(2)(5y +3x -15z 2)-(12y +7x +z 2);(3)7(p 3+p 2-p -1)-2(p 3+p );(4)-(13 +m 2n +m 3)-(23 -m 2n -m 3).【答案】(1)原式=3k 2+10k -1 (2)原式=-16z 2-4x -7y (3)原式=5p 3+7p 2-9p -7 (4)原式=-1四、课堂小结1.整式加减运算的实质及步骤是什么?五、课后作业教材P93~P94第6、7、9题.其实整式的加减本质上就是合并同类项的问题,重点是让学生较好的记住法则,依据法则去解决问题.只是学生的基本计算能力有待加强,计算出现的错误比较多,说明学生计算的基本功有待加强.有理数的学习不够优秀是本章学习的一大难题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整式的加减(一)
问题1:
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶
速度是100千米/小时,在非冻土地段的行驶速度可以达到120千米/小时,而列车通过
非冻土地段的时间是通过冻土地段的时间的2.1倍,如果通过冻土地段需要t小时,请用
含t的式子表示这段铁路的全长:________________________________。 练习1:运用有理数的运算律计算: ⑴ 100 × 2 + 252 ×2 =______________________=________ ⑵ 100 × (-2) + 252 × (-2) =___________________________=________ 问题1中的字母表示的是一个数字,故问题1中的结果可进一步写成 (______+_____)t =________ 练习2: 填空: ⑴ 100t- 252t =___________ ⑵ 23x +22x =_______________ ⑶ 23ab - 24ab =______________ 讨论 : 练习2中各小题的项分别是什么? 这些项有什么共同点? ⑴式的项是_______和_________,共同点是_________________________________; ⑵式的项是_______和_________,共同点是_________________________________; ⑶式的项是_______和_________,共同点是_________________________________。 像这样,___________________________叫做同类项。 思考:下列各组是不是同类项: (1) 20.5yx和20.2xy (2)4abc和 3ab (3) 23ab和 ba (4) 235mn和322nm 判断同类项要注意两点:①字母要求相同;②相同的字母其指数也要求相同。 范例:多项式中的字母表示数字,所以我们可以运用交换律、结合律、分配律把多项式中的同 类项进行合并。 例如 :22427382xxxx ( 找出多项式中的同类项 ) 解:原式=24x 28x 2x 3x 7 2( 运用交换律把同类项放在一起 注意 ,交换位置时符号也要同时进行交换)
=2(48)x (23)x (72) ( 运用结合律和分配律 )
=24x 5x 5
把多项式中的同类项合并成一项,叫做合并同类项。
观察并讨论:
合并同类项后,所得项的系数、字母以及字母的指数与合并前各项的系数、字
母及字母的指数有什么联系?
___________________________________________________________________________。
注意
:多项式中只有同类项才能合并,不是同类项不能合并。
练习3:
合并下列各式的同类项:
⑴ 2215xyxy
(2) 22223232yyxyxyxx
(3) 222243244ababab
课堂小结:
(1) 什么叫同类项?字母相同,次数也相同的项是同类项吗?举例说明。
(2) 什么叫合并同类项?合并前后同类项的系数,字母及字母的指数有什么关系? 课堂练习: 一.填空题: 1.如果25yx与 12nmyx是同类项,那么m=_________ n=________ 2.合并同类项: ⑴ 2aaa_____________ ⑵ 56xyxyyx=_____________ ⑶ 2220.80.2ababab _______________ 二.选择题: 3.下列各组是同类项的是( )。 A. 2a 与 2a B. 22ab 与 23ab C. 25abc 与 2bac D. 217ab 与 24abc 4.下列运算正确的是( )。 A. 22321aa B.232xxx C.2233xx D.22232aaa 三.合并下列各式中的同类项。 5.75mnmnmn 6.22251623xxx
7.2222345274abababab
作业:
P71 1.
