用几何画板巧作分段函数的图像
在几何画板中绘制分段函数图象的方法之探究
在几何画板中绘制分段函数图象的方法之探究作者：陈峰来源：《新课程·下旬》2018年第11期摘要：几何画板是高中数学备课和课堂教学中不可或缺的一款教学软件，在几何画板中，不仅可以利用根号和对数函数作出连续型或限定定义域的初等函数的图象，还能借助符号函数构造出分段函数各段上的所乘函数，进而绘制出分段函数的图象，达到为教学研究服务的目的。
关键词：几何画板；分段函数；图象几何画板（The Geomter’s Sketchpad，简称GSP）是一款适用于数学、物理等学科，可以进行矢量分析、作图、函数作图等操作的动态几何工具.由于它能够动态地展现出函数图象和几何对象的位置关系及运行变化规律，深受广大教师的青睐，也是不少数学教师在备课、上课中不可或缺的教学软件之一.然而，即便是功能如此强大的几何画板，仍旧在绘制分段函数这一方面显得不够“体贴”和“人性化”，这也或多或少地限制了教师对它的开发与使用.因此，本文基于5.04版的几何画板，针对如何在几何画板中绘制分段函数的图象进行研究.一、在几何画板中作限定定义域的初等函数的图象类型1 初等函数在定义域内连续例1 作函数f（x）=x2-2x+，x∈[0，3]的图象.操作步骤：（1）在“绘图”——“绘制新函数”的对话框中直接输入函数表达式x^2-2*x+1/2得到函数f （x）=x2-2x+在R上的图象.（2）点击函数图象选中，右击选择“属性”（如图1），可在栏目“绘图”内设置函数的定义域边界的数值（如图2），点击确定可得到函数f（x）=x2-2x+，x∈[0，3]的图象.上述操作步骤的优势在于操作比较便捷，只要在几何画板内对函数图象进行简单设置便可实现，主要适用于在定义域上连续的初等函数.类型2 初等函数在定义域内不连续例2 作函数f（x）=x2-2x+，x∈[0，1]∪[2，3]的图象.操作步骤：（1）构造函数F（x）=x2-2x++0·.（2）在“绘图”——“绘制新函数”的对话框中输入函数表达式x^2-2*x+1/2+0*sqrt[-x*（x-1）*（x-2）*（x-3）]，点击确定可得到函数f（x）=x2-2x+，x∈[0，1]∪[2，3]的图象（如图3）.虽然函数F（x）中0·的值恒为0，但要使得其有意义，即解不等式-x（x-1）（x-2）（x-3）≥0，可解得x∈[0，1]∪[2，3]，这恰好为所画函数f（x）的定义域.因此，函数f（x）与函数F（x）本质上是相同函数.一般地，对于限定定义域的初等函数f（x），通过构造得到函数f（x）的相同函数F （x）的方式有下列8种情况：1.函数f（x）的定义域为[a，b]，可构造函数：F（x）=f（x）+0·.2.函数f（x）的定义域为（a，b]，可构造函数：F（x）=f（x）+0·.3.函数f（x）的定义域为[a，b），可构造函数：F（x）=f（x）+0·.4.函数f（x）的定义域为（a，b），可构造函数：F（x）=f（x）+0·ln[-（x-a）（x-b）]或F（x）=f（x）·.5.函数f（x）的定义域为（a，+∞），可构造函数：F（x）=f（x）+0·ln（x-a）或F（x）=f（x）·.6.函数f（x）的定义域为[a，+∞]，可构造函数：F（x）=f（x）+0·.7.函数f（x）的定义域为（-∞，b），可构造函数：F（x）=f（x）+0·ln（b-x）或F（x）=f（x）·.8.函数f（x）的定义域为（-∞，b]，可构造函数：F（x）=f（x）+0·.二、在几何画板中作分段函数的图象例3 作分段函数f（x）=2x-1，x≤13-x，x>1 的图象.方法1 先将分段函数f（x）拆分为两个函数，即f1（x）=2x-1（x≤1）和f2（x）=3-x （x>1），然后再分别作上述两个函数的图象.操作步骤：（1）构造以下两个函数，F1（x）=2x-1+0·和F2（x）=3-x+0·ln（x-1）.（2）在几何画板的同一文档页面内的“绘图”——“绘制新函数”的对话框中分别输入函数表达式2^x-1+0*sqrt（1-x）和3-x+0*ln（x-1），分别点击确定后可得到函数f1（x）和f2（x）的图象，两者可组成函数f（x）=2x-1，x≤13-x，x>1 的图象（如图4）.方法1的本质是拼接了函数f1（x）和f2（x）的图象，虽然可以使人在视觉上感觉在同一坐标系下作出了f（x）的图象，但其缺陷也是显而易见的，比如说函数f（x）图象并非一次成图，函数图象也不能被整体选中，并且在图象上任取的一点更不可以在分段函数f（x）各段的图象上自由移动.因此，方法1所绘制的函数图象有较大的局限性，不适合用以研究函数f （x）的性质.方法2 利用符号函数sgn（x）=1，x>0，0，x=0，-1，x操作步骤：（1）构造函数F（x）=（2x-1）+（3-x）.（2）在“绘图”——“绘制新函数”的对话框中输入函数表达式（2^x-1）*[1+sgn（1-x）]/2+（3-x）*[1+sgn（x-1）]/2，点击确定后可得到函数f（x）=2x-1，x≤13-x，x>1 的图象.方法2巧妙地利用了分段函数的特点，弥补了方法1中不能一次成图、无法整体选中、取点无法自由移动等缺陷.函数F（x）中所构造的和用于匹配其所乘函数的定义域的范围.具体地，当x1时，F（x）=3-x.因而，类似地，对于分段函数g（x）=g1（x），x≤a，g2（x），ab.（a=g1（x）·+g2（x）·+g3（x）·.较之方法1，方法2已有明显的改进，弥补了方法1的诸多缺陷，同时也是目前较为普遍的一种处理方式.但即便如此，方法2仍存在不完美之处.对于函数f（x）=2x-1，x≤13-x，x>1 ，当取x=1时，f（1）=0，而对于函数F（x）=（2x-1）+（3-x），当取x=1时，F（1）=0·+2·=1≠f（1）.由于几何画板中孤立的点不被显示，这使得上述问题常常被忽略.其实通过观察和分析不难发现，造成上述偏差的主要原因是函数y=虽然可以在x>1和x方法3 对方法2进行改进，重新构造2x-1和3-x的所乘函数，分别为k1（x）=sgn[1+sgn （1-x）]和k2（x）=sgn[1+sgn（x-1）]·sgn|x-1|.操作步骤：（1）构造函数F（x）=（2x-1）·sgn[1+sgn（1-x）]+（3-x）·sgn[1+sgn（x-1）]·sgn|x-1|.（2）在“绘图”——“绘制新函数”的对话框中输入函数表达式，（2^x-1）*sgn[1+sgn（1-x）]+（3-x）*sgn[1+sgn（x-1）]*sgn[abs（x-1）]点击确定后可得到函数f（x）=2x-1，x≤13-x，x>1 的图象.方法3构造了y=k1（x）和y=k2（x）两个函数，当x>1时，由于1+sgn（x-1）=0，所以k1（x）恒等于0，由于1+sgn（x-1）>0，|x-1|>0，k2（x）恒等于1；同理可得，当x0，|x-1|=0，仍能保证k1（x）恒等于1，k2（x）恒等于0.类似地，利用相同的原理，根据不同定义域下的函数，可构造出其所对应的不同的所乘函数k（x），具体如下：1.当x≤a时，构造k（x）=sgn[1+sgn（a-x）].2.当x3.当x≥b时，构造k（x）=sgn[1+sgn（x-b）].4.当x>b时，构造k（x）=sgn[1+sgn（x-b）]·sgn|x-b|.5.当a≤x≤b时，构造k（x）=sgn[1+sgn（x-a）（b-x）].6.当a7.当a≤x8.当a对于一个含有n（n∈N*）段的分段函数f（x），其每一段所对应的解析式为fi（x）（1≤i≤n，i∈N*），根据上述方法，可以构造出fi（x）所对应的所乘函数ki（x），再令F （x）=[fi（x）·ki（x）]，则f（x）与F（x）为相同函数.因此，只需在几何画板“绘图”——“绘制新函数”的对话框中输入函数表达式后再点击确定，即可得到函数f（x）的图象.至此，在几何画板中绘制分段函数图象这一问题才最终得以真正解决.？誗编辑赵飞飞。
怎样用几何画板画分段函数
怎样用几何画板画分段函数要有清晰的步骤，注明怎样标明每一个分段函数的定义域；例如：f(x)=3^(x-1)+1 (X<=1)=3^(1-x)+1(x>1)这个分段函数方法这样：（1）在图表菜单下，建立网格，再按住shitf键，在x轴点（1，0）上向左画一条水平向左的射线，并选中射线，点击作图菜单下“射线上的点”设为点A，再隐藏射线；（2）选中点A，右键单击“横坐标”，出现“X A＝**”，再点“图表”菜单下，计算命令，输入3^(x-1)+1（输X时只需点一下“X A＝**”），出现“3^(X A-1)+1＝**”；（3）分别选中“X A =**”和“3^( X A -1)+1＝**”，单击“图表”菜单，“绘制点”命令，即出现一点，——有时候，你要仔细找找，才能找到；（4）选中点A和上一步的点，再单击作图菜单下的“轨迹”命令；（5）此时即作出来f(x)=3^(x-1)+1 (X<=1) 部分；（6）f(x)=3^(x-1)+1 (X>1) ,如法炮制。
《几何画板》：绘制某区间内的函数图像第1步，启动几何画板，依次单击“图表”→“定义坐标系”菜单命令，在操作区建立直角坐标系。
然后依次单击“图表”→“隐藏网格”菜单命令，隐藏坐标系中的网格。
单击工具箱上的“文本”工具，移动光标至圆点，当变成一只小黑手时，单击鼠标左键，然后再双击鼠标左键，将标签修改为“O”。
同法，给单位点加注标签为“1”。
第2步，单击工具箱上的“选择箭头”工具，单击操作区空白处，释放所选对象。
依次单击“图表”→“绘制点”菜单命令，弹出“绘制点”对话框，按照图143所示输入数据，单击“绘制”按钮，操作区显示一点。
继续在对话框中输入数据，如图144所示，单击“确定”操作区中又显示一点。
单击工具箱上的“文本”工具，移动光标至绘制的第一点上，当光标变成小黑手时，双击鼠标左键，弹出如图145所示的对话框，按照图所示，在标签栏里输入“π”，然后单击“确定”按钮。
关于几何画板分段函数的处理
几何画板中函数和分段函数定义域处理郑 明 淮(福建尤溪文公高级中学，365100)几何画板是数学新课程推荐使用信息技术软件。
它作出的几何图形、函数图象非常精确，运算功能也十分强大，更重要的是它拥有用动态方式揭示几何图形中的元素间关系保持不变的特点。
这些特点对于学生认清问题的本质，弥补空间想像力不足，对相关问题进行验证、探索提供了易于操作的平台。
正因为如此，几何画板相对于其他常用软件倍受数学教师的青睐。
当然，任何一款软件都不可能做到十全十美，几何画板也是如此。
虽然它的版本已经升级到5.0，我们在使用过程中仍然发现有许多方面不尽如人意。
例如：新建一个函数后，利用绘制函数图象功能画出来的是其完整定义域上的图象。
而在高中数学中很多函数是限定定义域的，而几何画板不具备直接限定定义域的作图像功能，我们只能另想方法以达到这一目的。
这一问题以及分段函数是高中数学中的重点内容，在使用几何画板辅助教学中必需突破这一瓶颈。
本文就此两个问题在几何画板环境下做一个探索，希望能有效地、可操作地解决这一问题。
一、几何画板中限定定义域函数的图像处理方案例1、作函数822--=x x y(53≤≤-x )的图像分析：822--=x x y 的定义域是R ，要去掉 53≤≤-x 之外的图像只能改变原函数的表达式，使其对应关系与原函数相同，但定义域为53≤≤-x 。
构造如下：)5)(3(082)(2x x x x x f -+⋅+--=然后绘制函数f(x) 效果如图。
函数f(x) 中的)5)(3(0x x -+⋅把函数定义域限定在53≤≤-x ，并且在定义域范围内其值恒为0，因此不改变原函数的值。
一般地，限定函数定义域的构造有以下八种情况：1、限定函数f(x)定义域为[a ，b]构造函数：))((0)(x b a x x f y --⋅+=2、限定函数f(x)定义域为(a ，b]构造函数：ax x b x f y --⋅+=0)( 3、限定函数f(x)定义域为[a ，b)构造函数：xb a x x f y --⋅+=0)( 4、限定函数f(x)定义域为(a ，b)构造函数：)))(log((0)(x b a x x f y --⋅+=5、限定函数f(x)定义域为(a ，+∞)构造函数：)log(0)(a x x f y -⋅+=6、限定函数f(x)定义域为[a ，+∞)构造函数：a x x f y -⋅+=0)(7、限定函数f(x)定义域为(-∞，b)构造函数：)log(0)(x b x f y -⋅+=8、限定函数f(x)定义域为(-∞，b]构造函数：x b x f y -⋅+=0)(二、几何画板中分段函数的图像处理例2．作分段函数⎪⎩⎪⎨⎧≥+-<≤--<+=)4........(63)42.....(..........)2.........(83)(2x x x x x x x f 的图像。
用_几何画板_画分段函数图像的简单方法
・ ２００８ ０４
用*几何画板+画分段函数图像的简单方法
☆
黎凤仁
先 来 看 例 题 ： 在《 几 何 画 板 》中 画 出 分 段 函 数 Ｆ （ ｘ）＝ 点 １、 ０ ， 点 击 绘 制 得 点 Ａ（ １ ， ０ ） ， 输 入 － １ ， ０ 得 点 Ｂ（ － １ ，
ｆ１ （ｘ），ｘ＜ １ " ｆ２ （ｘ），１＜ ｘ＜ ２ # $ ｆ３ （ｘ），ｘ＞ ２ %
１，ｘ＞ ０ 借 助 函 数 ｓｇｎ （ｘ） ＝ ０，ｘ＝ ０ 可 以 将 Ｆ （ｘ） ＝ － １，ｘ＜ ０
!
２
２
ｘ２＋ ｓｇｎ（ｘ－ ２）＋ １ ×１ ， 点 击“ 确 定 ”即 可 画 出 此 分 段 函 数 ２ ｘ
的图像。 显 然 方 法 二 非 常 简 单 。 对 于 ｎ 段 分 段 函 数 Ｆ （ｘ） ＝
ｆ３ （ｘ）＝ １ （ ｘ＞ ２ ） 。 ｘ＜ ２ ） 、 ｘ
对 于 此 题 ， 可 以 有 两 种 方 法 画 出 其 函 数 图 像 。分 别 介 绍如下： 方 法 一（ 复 杂 ） ： 逐 段 画 图 像 ， 再“ 拼 ”成 一 个 分 段 函 数图像。 作法如下： 第 一 步 ， 打 开《 几 何 画 板 》， 点 击“ 编 辑 ”→“ 参 数 选 项 ”→“ 文 本 ”→ ， 在 “ 所 有 新 建 的 点 ”、 “度量过的对
义时， 对应的端点所处位置要依据原分段函数来确定。 第二， 形 式 统 一 后 定 义 域 会 变 化 。 如 ： Ｆ （ｘ） ＝ 定 义 域 为 Ｒ， 而 Ｆ （ｘ） ＝ １－ ｓｇｎ（ｘ－ １） ・ｘ２ ＋
得 ａ １ ＝ １－ ｓｇｎ（ｘ－ １） ，ａ ２
２
＝ ｓｇｎ（ｘ－ １）－ ｓｇｎ（ｘ－ ２） ，ａ ２ ２
如何用几何画板画出函数图象
如何用几何画板画出函数图象在解析几何中，抛物线是平面内到定点和到定直线的距离相等的动点的轨迹，我们可通过尺规作图在平面内很容易找到这样的点，在用几何画板的轨迹工具就可画出抛物线。
1、新建一个绘图，选择菜单里的“图表”，鼠标单击“建立坐标轴”。
2、选择X轴，右击鼠标显示快捷菜单，选择作图，对象上的点；确保该点处在被选中状态，选择工具栏里的“标出文本&标签”工具，鼠标单击刚画出的点，将显示出该点的“标签”（假设为“M”）。
选择工具栏里的“选择&平移”工具，鼠标单击M点，按住Shift键，鼠标单击X轴，右击鼠标显示快捷菜单，选择作图，作垂线。
准线作好了。
3、选择X轴，右击鼠标显示快捷菜单，选择作图，对象上的点；确保该点处在被选中状态，选择工具栏里的“标出文本&标签”工具，鼠标单击刚画出的点，将显示出该点的“标签”（假设为“F”）。
点F为抛物线的焦点。
4、选择垂线，右击鼠标显示快捷菜单，选择作图，对象上的点。
确保该点处在被选中状态，选择工具栏里的“标出文本&标签”工具，鼠标单击刚画出的点，将显示出该点的“标签”（假设为“N”）。
选择点N，按住Shift键，鼠标单击直线。
右击鼠标显示快捷菜单，选择作图，作垂线。
选择点N和点F，右击鼠标显示快捷菜单，选择作图，线段NF，选择线段NF，右击鼠标显示快捷菜单，选择作图，中点A。
选择点A和线段NF，右击鼠标显示快捷菜单，选择作图，垂线。
选择直线和直线，右击鼠标显示快捷菜单，选择作图，交点。
鼠标单击刚画出的点，将显示出该点的“标签”（假设为“P”）。
5、选择点N和点P，右击鼠标显示快捷菜单，选择作图，轨迹。
抛物线作好了，可适当调整准线和焦点F的位置，则可以得到不同的抛物线。
在几何画板中通过作图可以对函数的代数形式和几何特征都可得到实质性的了解。
既可增加学生学习兴趣，又可更深刻地了解函数的实质。
几何画板5,0画分段函数的图象的方法
法二：几何构造法借助在不同范围上相应的几何对应关系构造分段函数的图像。
例3．四边形OBCD是正方形，边长为定值。
点P自B沿边BC、CD、DO移动到O，△POB 的面积为S，绘出S与P移动的距离x关系的图像（图四）。
图四制作过程分析：①先制作点P自B沿边BC、CD、DO移动到O的动画，同时△POB的位置也作相应变化；②再制作S与P移动的距离x关系的分段函数图像.①的制作过程：（1）画线段OB，以O为旋转中心，把点B旋转90°度到D，再以以B为旋转中心，把点O旋转－90°度到C，连接相应线段得到正方形OBCD；（2）在平面上任意画一点P，依次选中点P，B，选择【编辑】→【操作类按钮】→【移动】，弹出对话框如图五所示，选“高速”，单击“确定”按钮；图五（3）单击按钮，则点P高速运动到B；（4）单击点B处，屏幕左下方出现提示，再单击点C，选择【编辑】→【操作类按钮】→【移动】，选“中速”；单击“确定”按钮，单击按钮“从P→C移动”；（5）单击点C处，屏幕左下方出现提示，再单击点D，选择【编辑】→【操作类按钮】→【移动】，选“中速”；单击“确定”按钮,单击按钮“从P→D移动”；(6) 单击点D处，屏幕左下方出现提示，再单击点O，选择【编辑】→【操作类按钮】→【移动】，选“中速”；单击“确定”按钮,单击按钮“从P→O移动”；(7) 单击按钮“从P→C移动”，当点P还没移动到点C时，再次单击该按钮，同时选中点P，B，C，构造“三角形内部”，再次同时选中这三点，构造“线段”；（8）依次选中按钮“从P→B移动”, 按钮“从P→C移动”, 按钮“从P→D移动”, 按钮“从P→O移动”,选择【编辑】→【操作类按钮】→【系列】，选“依序执行”，单击“确定”；单击按钮“序列4动作”，则点P自B沿边BC、CD、DO移动到O时，△POB的位置也作相应变化。
②的制作过程：（1）在线段BC上任取点Q，度量QB的长度，度量△QOB的面积，依次选中长度，面积，单击【图表】→【绘制（x,y）】,选中点Q，构造轨迹；（2）在线段CD上任取点R，度量RC的长度，度量△ROB的面积，计算RC+OB的长度和，依次选中长度和，面积，单击【图表】→【绘制（x,y）】,选中点R，构造轨迹；（3）在线段DO上任取点S，度量SD的长度，度量△SOB的面积，计算SD+2*OB的长度和，依次选中长度和，面积，单击【图表】→【绘制（x,y）】,选中点S，构造轨迹；S与P移动的距离x关系的分段函数图像制作完成。
用几何画板绘制函数图象的基本技法
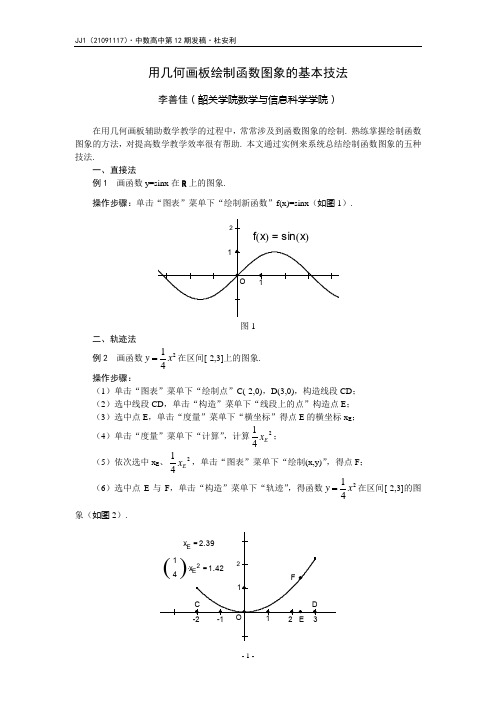
用几何画板绘制函数图象的基本技法李善佳（韶关学院数学与信息科学学院）（4）单击“度量”菜单下“计算”，计算214E x ； 21图2三、参数法例3 绘制二次函数y=-x 2+2x+3的图象. 操作步骤：例4 画函数223(1),1()4,1312,33x x r x x x x x ⎪--<⎪=-≤<⎨⎪⎪-≥⎩，，的图象。
操作步骤：（1）单击“图表”菜单下“新建参数”a=1，b=3（设定区间分界点）； （2）单击“图表”菜单下“新建函数”f(x)=3-(x-1)2，g(x)=4-x ，h(x)=2123x -； （3）单击“图表”菜单下“绘制新函数”1sgn()1sgn(()())1sgn()()()()()()()()222a x x ab x x b r x f x g x h x +-+--+-=⋅+⋅+⋅（如图4）.()h x =. 因此，最后画出的只是区间[a,b]上的图象.五、变换法 1. 平移一个平移就是一个向量，对于函数图象的平移，采取“标记向量”较为简单. 例7 绘制与214y x =，x ∈[-2,3]图象相同，而位置可任意改变的函数图象. 操作步骤：（1）用轨迹法绘制214y x =，x ∈[-2,3]图象（同例2）； （2）用“点工具”任作两个点A 、B ；JJ1（21091117）·中数高中第12期发稿·杜安利说明：拖动点A 或点B ，就可以把图象按向量AB 任意平移. 2. 反射 例8 绘制与214y x =，x ∈[-2,3]图象关于任意直线对称的图象.3. 旋转 例9 绘制与214y x =，x ∈[-2,3]图象绕任意点旋转任意角度的图象. 操作步骤：（1）用轨迹法绘制214y x =，x ∈[-2,3]图象（例2）； （2）用“点工具”任作点A ，选中点A ，单击“变换”菜单下“标记中心”； （3）单击“图表”菜单下“新建参数”，设置参数t ，单位设置为“弧度”，选中t ，单击“变换”菜单下“标记角度”；（4）选中点F ，单击“变换”菜单下“旋转”，在“旋转参数”中选择“标记角度”，按“确定”得到点'F ；（5）选中点E 与'F ，单击“构造”菜单下“轨迹”，得到原函数图象绕点A 旋转t 角度的图象（如图9）.。
《几何画板》：绘制分段函数的图像
《几何画板》：绘制分段函数的图像第1步，启动几何画板，依次单击“图表”→“定义坐标系”菜单命令，在操作区建立直角坐标系。
单击工具箱上的“文本”工具，移动光标至圆点，当变成一只小黑手时，单击鼠标左键，然后再双击鼠标左键，将标签修改为“O”，同样方法，给单位点加注标签为“A”。
第2步，单击工具箱上的“选择箭头”工具，然后依次选中点A和点O，依次单击“构造”→“射线”菜单命令，在操作区中绘制出射线AO，即为区间X≤1。
然后单击工具箱上的“点”工具，移动光标至X轴上，当X轴呈现高亮度时，在点A右边作出任意一点B，按照上述方法，绘制出射线AB。
然后再用“点”工具，分别在X轴上，点A的左边和右边分别绘制出点C 和点D，如图163所示。
第3步，单击工具箱上的“选择箭头”工具，单击操作区空白处，释放所选对象，然后选中点C，依次单击“度量”→“横坐标”菜单命令，度量值显示在操作区中。
选中操作区中显示的度量值，依次单击“数值”→“计算”菜单命令，弹出“计算器”对话框，依次单击“数值”下拉列表中的“Xc”、计算器上的平方号、数字“2”，对话框中显示计算式，如图164所示，单击“确定”按钮，操作区中显示计算式及结果。
单击操作区空白处，释放所选对象，然后依次选中度量值“Xc=-1.75”和操作中显示的另外一个计算值，依次单击“图表”→“绘制（X,y）”菜单命令，在操作区绘制出一点，并用“文本”工具加注标签为“E”。
依次选择点C和点E，单击“构造”→“轨迹”菜单命令，绘制出区间函数图像，如图165所示。
第4步，单击操作区空白处，释放所选择对象，按照上述方法，度量出点D的横坐标值，依次单击“度量”→“计算”菜单命令，单击“数值”菜单的下拉列表中的“Xd”，然后单击“确定”按钮，操作区中显示计算值。
依次选中操作区中的两个“Xd=2.22”，单击“图表”→“绘制（x,y）”菜单命令，绘制出一点，并用“文本”工具加注标签为“F”。
用几何画板制作函数图象
用几何画板制作函数图象
几何画板应该是每个数学教师必备的工具之一，有很多老师问我如何用几何画板制作函数图象，只需要最简单的方法，不需要那些套套。
对于老师来说，假如我们构造函数f(x)=2^x+3x-6的图象，可以使用下面的方法（我用的是4.07中文版）：
一、单击“图表”菜单，选择第一个命令“定义坐标系”；
二、选定横坐标系，单击“构造”菜单，选择第一个命令“轴上的点”，这时在横坐标上构造了一个点A；
三、单击“度量”菜单，选择“横坐标”，这时在画板上出现了刚才我们在轴上生成的点的横坐标xA的值；
四、在”度量“菜单中继续选择“计算”，在输入框中输入“2^xA+3*xA-6”（注意xA是单击“数值(V)”选择的），输入完成以后，单击“确定”按钮，这时在画板上生成另一个文本。
五、依次选定这两个文本（刚才的横坐标和现在生成的文本），单击“图表”菜单，选择“绘制(x,y)”命令，这时绘制了点B；
六、依次选择A，B两点，单击“构造”菜单，选择“轨迹”命令，这时就生成了函数的图象。
如何用几何画板画函数图像？
如何用几何画板画函数图像？函数的定义域是函数定义的基础，是制约函数图像的重要因素，同一解析式在不同定义域下的图像不同，具体表现在其范围的大小。
本节就来学习几何画板中不同定义域下函数图像的作图方法。
比如定义域是区间形式的函数图像，可按以下步骤操作：步骤一选取定义域1.打开几何画板，单击上方菜单栏“绘图”菜单中的“定义坐标系”命令建立直角坐标系；2.构造x轴上的线段代表定义域区间。
使用左侧工具栏“移动工具”选中x轴，然后点击“构造”菜单中“对象上的点”，再重复一次这一操作，则在x轴上取到两点，选种这两点，单击“构造”菜单中的“线段”，这条线段就可以代表一个定义域区间，如果作端点为（a，0），右端点为（b，0），则定义域区间为（a ，b）。
在x轴上构造定义域区间示例步骤二在定义域上建立自变量选中表示定义域线段，然后单击“构造”菜单中的“对象上的点”，再点击“度量”菜单中的“横坐标”，出现“x C=-2.79”即为我们要选择的自变量。
构造线段上的点作为自变量示例步骤三计算自变量的函数值单击“度量”菜单中的“计算”命令，在弹出的对话框利用“x C=-2.79”计算出如下图所示的函数值。
利用计算命令计算函数值示例步骤四构造函数图像上的点使用移动工具选中上面得到的自变量值和函数值，然后单击“绘图”菜单中的“绘制（x，y）”命令，就可以构造出函数图像上的点P。
构造函数图像上的点P示例步骤五绘制函数图像使用移动工具选中上面图像上的点P和定义域上C点，单击上方菜单栏“构造”菜单中“轨迹”命令，就可以画出如下图所示的函数图像。
构造轨迹绘制函数图像示例步骤六任意调整函数的定义域区间用移动工具选中“a”和“b”点任意拖动，可以看到函数图像随a、b的变化而变化的情形，比如如下图所示的效果。
调整函数的定义域观看图像变化示例看了以上教程，就掌握了用几何画板画指定定义域函数图像的方法，主要运用了几何画板构造轨迹功能，通过拖动线段上的“a”和“b”点，就可以改变定义域，观察函数图像的不同。
在几何画板中绘制分段函数图象的方法之探究
教学篇•教育技术几何画板（The Geomter ’s Sketchpad ，简称GSP ）是一款适用于数学、物理等学科，可以进行矢量分析、作图、函数作图等操作的动态几何工具.由于它能够动态地展现出函数图象和几何对象的位置关系及运行变化规律，深受广大教师的青睐，也是不少数学教师在备课、上课中不可或缺的教学软件之一.然而，即便是功能如此强大的几何画板，仍旧在绘制分段函数这一方面显得不够“体贴”和“人性化”，这也或多或少地限制了教师对它的开发与使用.因此，本文基于5.04版的几何画板，针对如何在几何画板中绘制分段函数的图象进行研究.一、在几何画板中作限定定义域的初等函数的图象类型1初等函数在定义域内连续例1作函数f （x ）=x 2-2x +12，x ∈［0，3］的图象.操作步骤：（1）在“绘图”———“绘制新函数”的对话框中直接输入函数表达式x ^2-2*x +1/2得到函数f （x ）=x 2-2x +12在R 上的图象.（2）点击函数图象选中，右击选择“属性”（如图1），可在栏目“绘图”内设置函数的定义域边界的数值（如图2），点击确定可得到函数f （x ）=x 2-2x +12，x ∈［0，3］的图象.上述操作步骤的优势在于操作比较便捷，只要在几何画板内对函数图象进行简单设置便可实现，主要适用于在定义域上连续的初等函数.图1图2类型2初等函数在定义域内不连续例2作函数f （x ）=x 2-2x +12，x ∈［0，1］∪［2，3］的图象.操作步骤：（1）构造函数F （x ）=x 2-2x +12+0·-x（x -1）（x -2）（x -3）√.（2）在“绘图”———“绘制新函数”的对话框中输入函数表达式x ^2-2*x +1/2+0*sqrt ［-x*（x -1）*（x -2）*（x -3）］，点击确定可得到函数f （x ）=x 2-2x +12，x ∈［0，1］∪［2，3］的图象（如图3）.4321-12图3虽然函数F （x ）中0·-x （x -1）（x -2）（x -3）√的值恒为0，但要使得其有意义，即解不等式-x （x -1）（x -2）（x -3）≥0，可解得x ∈［0，1］∪［2，3］，这恰好为所画函数f （x ）的定义域.因此，函数f （x ）与函数F （x ）本质上是相同函数.一般地，对于限定定义域的初等函数f （x ），通过构造得到函数f （x ）的相同函数F （x ）的方式有下列8种情况：1.函数f （x ）的定义域为［a ，b ］，可构造函数：F （x ）=f （x ）+0·-（x -a ）（x -b ）√.2.函数f （x ）的定义域为（a ，b ］，可构造函数：F （x ）=f （x ）+0·-x-b x-a √.3.函数f （x ）的定义域为［a ，b ），可构造函数：F （x ）=f （x ）+0·-x-a x-b√.4.函数f （x ）的定义域为（a ，b ），可构造函数：F （x ）=f （x ）+0·ln［-（x-a ）（x-b ）］或F （x ）=f （x ）·-（x -a ）（x -b ）√-（x -a ）（x -b ）√.5.函数f （x ）的定义域为（a ，+∞），可构造函数：F （x ）=f （x ）+0·ln （x-a ）或F （x ）=f （x ）·x -a √x -a √.6.函数f （x ）的定义域为［a ，+∞］，可构造函数：F （x ）=f （x ）+0·x -a √.7.函数f （x ）的定义域为（-∞，b ），可构造函数：F （x ）=f （x ）+0·ln （b-x ）或F （x ）=f （x ）·b-x √b-x√.在几何画板中绘制分段函数图象的方法之探究陈峰（江苏省苏州市苏州大学附属中学，江苏苏州）摘要：几何画板是高中数学备课和课堂教学中不可或缺的一款教学软件，在几何画板中，不仅可以利用根号和对数函数作出连续型或限定定义域的初等函数的图象，还能借助符号函数构造出分段函数各段上的所乘函数，进而绘制出分段函数的图象，达到为教学研究服务的目的。
利用几何画板绘制分段函数图像
利用<几何画板>绘制分段的图像东北育才双语学校 王海涛就像社会体制有“一国两制”，即不同的地域实行不同的社会制度一样，函数中有分段函数，即在不同的区间上有不同的规则，但它确实是一个函数。
在命题及其解题时都要求绘制这类函数的图像。
目前用<几何画板>绘制单一函数图像没有任何问题，但是分段函数的绘制还是需要有一定的技巧的。
另外有时我们需要绘制曲线的部分或不同部分不同的要求，也需要掌握绘制方法，针对这些，笔者认真思考后在利用<几何画板>绘制分段图像问题上有一点点心得，下面记录下来与读者分享。
一、分段函数绘制方法 （一）两段函数绘制原理：()11()()()()f x x x F xg x x x <⎧=⎨≥⎩⇔ ()11()()()()22x x f x g x f x g x F x x x -+-=+⋅-…………（*） 显然，1x x < 时，111x x x x -=- ，此时（*）式为()()()()()()1=22f xg x f x g x F x f x +-=+⋅； 1x x ≥ 时，111x x x x -=--，此时（*）式为()()()()()()()1=22f xg x f x g x F x g x +-=+-⋅. 例1.绘制函数()()()2200xx F x x x ⎧<⎪=⎨≥⎪⎩ 的图像. 解：打开<几何画板>，在绘制新函数对话框中输入函数解析式，如图按下确定键，就可以得到函数的图像了，如图——2这样绘制出来的函数图像，在上面取一点，该点是可以在两段上自由运动的，这是分段绘制所得图像不能做到的。
注意：为了更好体现图像的精确性,我们可以再绘制点(0,1),将该点的颜色选择为白色,以表示空心点.（二）三段函数绘制()1122()()()()()()f x x x F xg x x x xh x x x <⎧⎪=≤<⎨⎪≥⎩,令()112()()()()f x x x p x g x x x x <⎧=⎨≤<⎩则由(一)得, ()11()()()()22x x f x g x f x g x p x x x -+-=+⋅-.而()22()()()()p x x x F x h x x x <⎧=⎨≥⎩()22()()()()22x x p x h x p x h x F x x x -+-=+⋅-………………（△）即两次使用在（一）中使用过的原理.而我们在“绘制新函数”中输入解析式（△）即可得到所求函数的图像，这里要求我们要有很好的层次逻辑就行；例2. 绘制函数()()()()22002sin 2x x F x x x x x ⎧<⎪⎪=≤<⎨⎪≥⎪⎩的图像.解：打开<几何画板>，在绘制新函数对话框中输入函数解析式，如图第3页按下确定键，就可以得到函数的图像了，如图——xyf x () =2x + x 22+x x()∙2x x 2()2()+sin x ()2+2 x 2 x∙2x+ x 22+x∙2x x 2()2() sin x ()2()()O 1同样，为了更好体现图像的精确性，我们可以再绘制点(0,1)，将该点的颜色选择为白色，以表示空心点.像上一个例题中的函数图像一样，由一个解析式绘制出来的函数图像，在任何一段上取一点，该点是可以在三段上自由运动的。
用几何画板巧作分段函数的图像
用几何画板巧作分段函数的图像教学应用分段函数的复杂性表现在两个方面：一是定义域被分成多个区间，二是在各个区间上的解析式又函数”的功能来绘制分段函数的图像，是不能直接解决这两方面问题的。
利用“０构造法”和“降段”待定系数法，以及几何画板中内置的符号函数，可以巧妙地把分段函数复杂多段的解析式转化为“一”个的解析式，从而就可以把分段函数的图像轻易地用几何画板绘制出来。
１．作指定区间的函数图像２］的图像。
假若在新建函数的对话框中直接输入表达式得到指定的多个区间上的函数图像，我们得用“０构造法”来确定函数的定义域，本题就可构造为如下的形式：ｆ（ｘ）＝ｘ＋１＋０×－（ｘ＋１）ｘ（ｘ－１）（ｘ－２），虽然式子０×－（ｘ＋１）ｘ（ｘ－１）（ｘ－２）的值是０，但要使根式有意义，则被开方式－（ｘ＋１）ｘ（ｘ－１）（ｘ－２）≥０，解得ｘ∈［－１，０］∪［１，２］，这正符合原具体制作操作时，只要在编辑函数对话框中输入ｆ（ｘ）＝ｘ＋１＋０×－（ｘ＋１）ｘ（ｘ－１）（ｘ－２）而不是ｆ（ｘ）＝ｘ＋１，即可得到指定区间上的函数图像（如图１）。
２．分段函数段的处理方法个重要的符号函数，用几何画板巧作分段函数的图像解：这里０是分段的关键点，设ｆ（ｘ）＝ｋ１ｓｇｎ（ｘ）１２ｋ１＋ｋ２＝２ｘ＋１，解得ｋ１＝ｘ，ｋ２＝ｘ＋１，于是得到ｆ（ｘ）＝ｘｓｇｎ（ｘ）＋ｘ＋１…………①当ｘ＝０时，①式的值是１，仍符合原分段函数（１），数。
对话框中输入①式就可绘出所求的分段函数（如图２）。
例３．作分段函数阳际国何画板不能直接绘制的分段函数。
图１图２键点时，设ｆ（ｘ）＝ｋ１ｓｇｎ（ｘ）＋ｋ２＋０×ｘ（ｘ－２）当ｘ＜０时，有－ｋ１＋ｋ２＋０×ｘ（ｘ－２）＝２，当ｘ≥２时，有ｋ１＋ｋ２＋０×ｘ（ｘ－２）＝２ｘ，解得ｋ１＝ｘ－１，ｋ２＝ｘ＋１－０×ｘ（ｘ－２）＝ｘ＋１（这里由于０×ｘ（ｘ－２）是用来控制自变量ｘ取值范围的，因此可以把ｋ２化简为ｋ２＝ｘ＋１），于是得到：验证当ｘ＝０时，②式的值是１，而不是原分段函数（２）的值２，但由于几何画板绘制函数图像时，无法显示出来），因此②式与原分段函数（２）除了一个点的差别，显示出来的图像是“完全”一样的！因此我们仍可用②来绘制所求的分段函数（２）的图像例２．作分段函数……（１）的图像……（２）的图像就是一个分段函数，利用此函数，我们可以构造出几教学应用设为：ｆ（ｘ）＝ｋ１ｓｇｎ（ｘ－２）＋ｋ２＋０×ｘ（ｘ－２），当ｘ＜２时，有－ｋ＋ｋ＋０×ｘ（ｘ－２）＝２，当ｘ＞１２１１，ｋ２＝ｘ＋１－０×ｘ（ｘ－２）＝ｘ＋１，于是得到：ｘ（ｘ－２）……③验证当ｘ＝２时，③式的值是３，而不是原分段函数（２）的值４，同前面说到的一样，显示出来的图像还是“完全”一样的！一般地，若形如样的方法，这里５是分段的关键点，因此可以设ｆ（ｘ）＋ｔ２＋０×－ｘ（ｘ－６）的，同上说到的理由，计算时可以省略，只要在最后的解析式中加上控制函数ｆ（ｘ）时，ｔ１＋ｔ２＝４＋４（５－ｘ），解得设，这里２是分段的关键点，数，仿例２和例３我们可以类似地加以一般化的讨论，这里不再赘述了。
用《几何画板》画分段函数图像
用《几何画板》画分段函数的图像 用《几何画板》软件能比较容易的画出基本初等函数及其复合函数的图像。
比如用《几何画板》5.03版的“绘图”菜单—“绘制新函数”命令绘制函数图像。
《几何画板》能识别函数定义域，即能自动识别使输入函数解析式有意义的自变量的范围，并画出这个范围内的图像。
比如画出xy 1=的图像是两支，不会与y 轴相交。
画11-=x y 的图像也是两支，不会与x=1相交。
但是画分段函数图像时，由于分段函数的定义域不仅是使函数解析式有意义，还要考虑实际意义，往往各段（区间）比较小而零碎，各段函数图像也不是同一类型。
如果还是用上面的命令来画各段图像时，《几何画板》还是按使输入函数解析式有意义来判定自变量的范围，画出的图像就会超出区间，且各段函数图像的连接也不美观。
按《几何画板》现有版本的功能，解决办法是不用“绘图”菜单—“绘制新函数”命令绘制分段函数图像，而用“构造”菜单“轨迹命令”，来绘制。
具体方法我用一例来详细说明。
人教版高一数学必修教材中一道函数应用题（p113）原题：如图，三角形OAB 是边长为2的正三角形，记三角形OAB位于直线x=t （t>0）左侧的图形面积为f(t),试求函数f(t)的解析式，并画出函数图像。
经分析函数解析式为()()()⎪⎪⎩⎪⎪⎨⎧≤<--≤<=212233)10(2322t t t t t f 画出的分段函数图像：图像是有两段二次函数图像拼接而成，在点（1，23）连接。
连接处有显示。
可见每段二次函数图像没有超出相应区间，在衔接处实现无缝衔接。
具体画法如下。
启动《几何画板》5.03，打开绘图菜单，单击显示网格命令，显示坐标网格，适当调长网格单位长，使之便于观察。
1、分别用“绘制线段”工具在x 轴上绘制线段(0，0）--（1,0）；（1,0）--(2,0),再用“绘制点”工具分别在两连线段上绘制自由点A 、B ，A 、B 各自线段上可自由移动，但不能移出各自线段。
用几何画板绘制函数图像技巧三例
图 0 从" 坐 标 平 移 ( 的 角 度 看 ! 函 数 !+! 45A8&:& 4; 在 以 点
8& 4> ! 4; 为 原 点 的 直 角 坐 标 系 中 的 图 像 与 函 数 !+A8&; 在 原
坐标系中的图像形状是相同的’
三 ! 分段函数的图像
设 分 段 函 数 为 B8&;+
"
&
0
8C & ,;
-"-T22(
!""#$ %
!"
软件研制
经 过 系 统 计 算 器 的 计 算 ! 化 为" 数 对 # $ 代 数 % ! 再 把 数 对 用 点$ 几 何 % 表 示 ! 通 过 主 动 点 与 被 动 点 之 间 的 制 约 关 系 作 出 点 的 运 动 轨 迹& && 函 数 的 图 像 ’
第 七 步 ! 先 后 选 择 度 量 值 & B+,<,3 * B8&;+2<J2 ! 并 选 择 ) 图 表 ! 绘 制 8&> !; # 命 令 ! 绘 制 出 点 K8& H> H8&;; ’ 第 八 步 ! 同 时 选 择 点 H * L ! 并 选 择) 构 造 ! 轨 迹 # 命 令 ! 得 到 函 数 B 8&; +
34 ( " 再 选 择& 构 造 # 线 段 上 的 点 $ 命 令 %
第 四 步 " 选 中 点 5 " 并 选 择& 度 量 # 横 坐 标 $ 命 令 " 得
“几何画板”作分段函数图像
“几何画板”作分段函数图像
陈永胜;董达
【期刊名称】《衡水学院学报》
【年(卷),期】2011(013)004
【摘要】The Geometer＇s Sketchpad is outstanding specialized discipline platform software.It takes mathematics as the basis,＂the dynamic geometry＂ as the characteristic to show dynamically the designer＇s thoughts,and provides a new tool to explore the geometry mys%几何画板是一个优秀的专业学科平台软件,它以数学为根本,以＂动态几何＂为特色来动态表现设计者的思想,为探索几何奥秘提供一个新的工具.本文研究了使用＂几何画板＂画分段函数图像,给出详细的制作步骤.
【总页数】4页(P30-33)
【作者】陈永胜;董达
【作者单位】吉林师范大学数学学院,吉林四平136000;吉林师范大学数学学院,吉林四平136000
【正文语种】中文
【中图分类】O17;G633.6
【相关文献】
1.用几何画板巧作分段函数的图像 [J], 阳际国
2.也谈用《几何画板》作二次函数图像 [J], 周灵
3.利用几何画板探究函数的图像及其性质——以反比例函数为例 [J], 许滨
4.利用几何画板的内置函数作复杂的函数图象——符号函数sgn(x)的应用 [J], 李天红
5.利用几何画板作反比例函数y=k/x的图像 [J], 王青生
因版权原因，仅展示原文概要，查看原文内容请购买。
教程“分段函数”图像生成
教程“分段函数”图像生成
'
今天的话题是应一位同行对函数做图的要求而成的，顺便录了个教程，以供初识玲珑者学习，相信应该会有一定帮助，更希望大家能提些意见。
'
话题出处：
玲珑画板
《玲珑画板》是由成都高仲富老师开发的，一款好用、实用、灵活、方便的动态数学教学软件。
能够动态展示几何、函数图形，极具创新性和实用性。
朴素应该是玲珑画板的最大特点，对于没有任何画板基础的老师来说，一般情况下熟练掌握也只需几天时间即可，它非常适合高中、初中和小学数学的教与学。
利用玲珑画板工具可以做到：
一、备课授课画图：能实现即画即讲的效果，方便灵活；
二、探究解题思路：通过做图过程的思考，便于引导探究解题思路；
三、数学教学教研：适合学科组进行教学研讨活动，增强教学研讨的趣味性。
感谢高仲富老师的倾心付出！
欢迎访问玲珑官网：
欢迎入群在线学习交流：
142671406（玲珑画板学习群2）
温馨提示。
ggb画分段函数
ggb画分段函数
许多函数在数学中扮演着重要的角色，分段函数也是如此。
分段函数指在特定的范围内定义的一系列函数，其中各个函数段之间通过离散点连接。
因此，分段函数的图像具有可读性，很容易理解，因此使用geogebra具有更强的可视化性，很容易画出ppt形式的分段函数图形。
在geogebra中，分段函数可以通过几个步骤很容易绘制。
首先，创建标尺，并设置XY轴的范围，以此来指定函数的定义域和值域。
其次，给出不同的段，每个段的函数可以由参数的关系建模，以及通过几何对象，如点、线、圆等来进行定义。
最后，通过调节参数可以得到不同类型的分段函数图像，如线性、二次、三次以及更高阶分段函数图形。
由于geogebra中分段函数的可视化性，示例函数可以非常清晰地显示出来。
比如，二次函数f (x) = ax2 + bx + c，它是一个由三个参数确定的函数，在geogebra中，它可以很容易地表示出来，用几何对象绘制它的方程，并可以灵活调整参数，以便得到不同的形状的函数图像，甚至是分段的函数图像。
总之，geogebra的强大功能尤其在于可视化的分段函数，经过几次简单的操作，就可以创建出精美的函数图形，使数学更具有吸引力，进而更有动力更深入地探索数学世界。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图４ 下面讨论一般的情况。设分段函数表达式为：
（ａ ＜ ｂ ＜ ｃ ＜ ｄ） ，
解：对于三段或三段以上的分段函数，我们可以 “先降段”，同时像前面的例题一样，利用待定系数
法，把此分段函数写成一个新的解析式。
这里 ｂ，ｃ 是关键点，考虑关键点 ｂ 时，我们可以设 ｆ （ ｘ ）
＝ｋ１ｓｇｎ（ｘ－ｂ）＋ｋ２＋０ × －（ｘ－ａ）（ｘ－ｂ）（ｘ－ｃ）（ｘ－ｄ），当
＋ ｋ ，下面我们来求待定系数 ｋ 和 ｋ 。
２
１
２
当 ｘ ＜ ０ 时，有 － ｋ ＋ ｋ ＝ １ ，当 ｘ ＞ ０ 时，有
１
２
ｋ ＋ ｋ ＝ ２ ｘ ＋ １ ，解得 ｋ ＝ ｘ ， ｋ ＝ ｘ ＋ １ ， 于是得到 ｆ （ ｘ ）
１
２
１
２
＝ ｘ ｓ ｇ ｎ （ ｘ ） ＋ ｘ ＋ １ …………①
当 ｘ＝０ 时，①式的值是
例 ４．作分段函数 …（３）的图像
……④ 验证知，当 ｘ＝５ 时，④式值是 ４，适合（４ ），也 适合（３ ），因此绘制图像时，只要在编辑函数的对话 框中输入④式就可绘出所求的分段函数（ 如图 ４ ） 。
……⑤ 如果考虑的是关键点 ｃ 时，同样可以得到： ……⑥ 不论 ｂ ＝ ｃ ，还是 ｂ ≠ ｃ ，⑤式的值和⑥式的值的 差别最多只是一个点的问题。 通过上面介绍的例题与论述，利用“０ 构造法”、 “降段”待定系数法，以及内置的符号函数 ，我 们可以将分段函数复杂多段的解析式化为“一”个的 解析式，虽然新的解析式与原分段函数有个别点的 差别，但绘制后所显示出来的图像与原分段函数的 图像是“完全”一样的。
１
２
１
２
１
ｘ ，ｋ ＝ ｘ ＋ ２ ，于是得到 ｆ （ ｘ ） ＝ （ ２ － ｘ ） ｓ ｇ ｎ （ ｘ － ２ ） ＋
２
１
（ ｘ ＋ ２ ） ，验证 ｘ ＝ ２ 时 ｆ １ （ ｘ ） ＝ ４ ，也符合原分段函数
（３ ），从而得到：
……（４）
ｆ（ｘ）＝（ｘ－１）ｓｇｎ（ｘ－２）＋（ｘ＋１）＋０ ×源自ｘ （ ｘ － ２ ） ……③
验证当 ｘ ＝ ２ 时，③式的值是 ３ ，而不是原分段
函数（２ ）的值 ４ ，同前面说到的一样， 显示出来的
图像还是“完全”一样的！
一般地，若形如 的分段函
数，仿例２和例３我们可以类似地加以一般化的讨 论，这里不再赘述了。
这是一个“降段”的分段函数，我们再次应用同
（作者单位：广东佛山顺德区杏坛中学）
中小学信息技术教育
２ ０ ０ ４ ． ０９
６７
＝ ｔ ｓ ｇ ｎ （ ｘ － ５ ） ＋ ｔ （本来应设为 ｆ （ ｘ ） ＝ ｔ ｓ ｇ ｎ （ ｘ － ５ ）
１
２
１
＋ ｔ ＋ ０ × － ｘ （ ｘ － ６ ） 的，同上说到的理由，计算时 ２
可以省略，只要在最后的解析式中加上控制函数 ｆ（ｘ）
的自变量 ｘ 的取值范围 ０ × －ｘ（ｘ－６） 就行），当 ｘ ＜ ５
２
只是用来控制函数 ｆ （ ｘ ） 自变量 ｘ 的取值范围，并且 １
它的值是 ０ ，对中间计算不起关键作用，因此可简化
设为 ｆ １（ ｘ ） ＝ ｋ １ ｓ ｇ ｎ （ ｘ － ２ ） ＋ ｋ ２ ，当 ｘ ＜ ２ 时，－
ｋ ＋ ｋ ＝ ２ ｘ ，当 ｘ ＞ ２ 时，ｋ ＋ ｋ ＝ ４ ，解得 ｋ ＝ ２ －
ｘ ＜ ｂ 时，－ｋ ＋ｋ ＝ｆ （ｘ），当 ｘ ＞ ｂ 时，有 ｋ ＋ｋ ＝ｆ （ｘ），
１２１
１ ２２
解得 ，
设 ，这里 ２ 是分段的关键点， 于是得到：
设 ｆ １（ ｘ ） ＝ ｋ １ｓ ｇ ｎ （ ｘ － ２ ） ｋ ２，本来应设为 ｆ １（ ｘ ） ＝ ｋ １ｓ ｇ ｎ （ ｘ － ２ ） ＋ ｋ ＋ ０ × － ｘ （ ｘ － ５ ） ，但由于 ０ × － ｘ （ ｘ － ５ ）
１，仍符合原分段函数（１ ），
因此①与（１ ）是相同的函
数。
用几何画板绘制此图
像时，只要在编辑函数的
对话框中输入①式就可绘
出所求的分段函数（如图
２）。
图２
例 ３ ．作分段函数
……（２） 的图像
解：这里 ０ 和 ２ 是分段的关键点，考虑 ０ 这一关
键点时，设 ｆ （ ｘ ） ＝ ｋ ｓ ｇ ｎ （ ｘ ） ＋ ｋ ＋ ０ × ｘ （ ｘ － ２ ） 当
１
２
ｘ ＜ ０ 时，有 － ｋ １＋ ｋ ２＋ ０ × ｘ （ ｘ － ２ ） ＝ ２ ，当 ｘ ≥
２ 时，有 ｋ １＋ ｋ ２＋ ０ × ｘ （ ｘ － ２ ） ＝ ２ ｘ ，解得 ｋ １＝ ｘ －
１ ，ｋ ＝ ｘ ＋ １ － ０ × ｘ （ ｘ － ２ ） ＝ ｘ ＋ １ （ 这里由于 ０ × ２
１
２
ｘ ＜ ２ 时，有 － ｋ ＋ ｋ ＋ ０ × ｘ （ ｘ － ２ ） ＝ ２ ，当 ｘ ＞
１
２
２ 时，有 ｋ １＋ ｋ ２＋ ０ × ｘ （ ｘ － ２ ） ＝ ２ ｘ ，解得 ｋ １＝ ｘ －
１ ，ｋ ＝ ｘ ＋ １ － ０ × ｘ （ ｘ － ２ ） ＝ ｘ ＋ １ ，于是得到： ２
是不能绘制孤立的“点”的（实际上是由于点太小而
无法显示出来），因此②式与原分段函数（２ ）除了一
个点的差别，显示出来的图像是“完全”一样的！因
此我们仍可用②来绘制所求的分段函数（２ ）的图像
中小学信息技术教育
６６
２ ０ ０ ４ ． ０９
教学应用
技术与应用
（如图 ３） 。
样的方法，这里 ５ 是分段的关键点，因此可以设 ｆ（ｘ）
ｘ （ ｘ － ２ ） 是用来控制自变量 ｘ 取值范围的，因此可以
把 ｋ ２ 化简为 ｋ ２ ＝ ｘ ＋ １ ） ，于是得到： ｆ（ｘ）＝（ｘ－１）ｓｇｎ（ｘ）＋（ｘ＋１）＋０ × ｘ （ ｘ － ２ ）…②
验证当 ｘ ＝ ０ 时，②式的值是 １ ，而不是原分段
函数（２ ）的值 ２ ，但由于几何画板绘制函数图像时，
时，－ ｔ ＋ ｔ ＝ （ ２ － ｘ ） ｓ ｇ ｎ （ ｘ － ２ ） ＋ （ ｘ ＋ ２ ） ，当 ｘ ＞ ５
１
２
时，ｔ １ ＋ ｔ ２ ＝ ４ ＋ ４ （ ５ － ｘ ） ，解得
于是得到：
图３
如果考虑的是关键点 ２ ，而不是 ０ ，此时可把它
设为：ｆ （ ｘ ） ＝ ｋ ｓ ｇ ｎ （ ｘ － ２ ） ＋ ｋ ＋ ０ × ｘ （ ｘ － ２ ） ， 当
２． 分段函数段的处理 方法
几何画板中内置了一 个重要的符号函数 ，
本身
图１ 就是一个分段函数，利用此函数，我们可以构造出几
何画板不能直接绘制的分段函数。 例２．作分段函数 ……（１）的图像
解：这里 ０ 是分段的关键点，设 ｆ（ｘ）＝ｋ１ｓｇｎ（ｘ）
技术与应用
教学应用
用几何画板巧作分段函数的图像
阳际国
分段函数的复杂性表现在两个方面：一是定义 域被分成多个区间，二是在各个区间上的解析式又 各不相同。仅用几何画板（４．０３ 及以上版本）“绘制新 函数”的功能来绘制分段函数的图像，是不能直接解 决这两方面问题的。利用“０ 构造法”和“降段”待 定系数法，以及几何画板中内置的符号函数 ，可 以巧妙地把分段函数复杂多段的解析式转化为“一” 个的解析式，从而就可以把分段函数的图像轻易地 用几何画板绘制出来。