立体几何中垂直地证明
立体几何第五讲 垂直的性质和证明学生
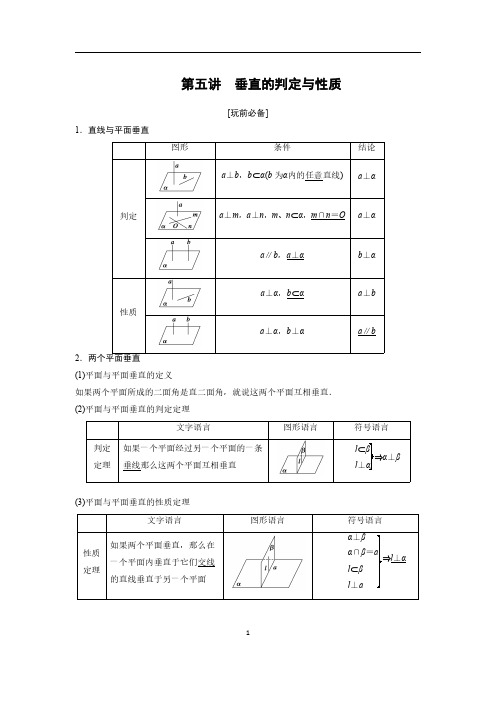
(2)平面与平面垂直的判定定理
文字语言
图形语言
符号语言
判定 如果一个平面经过另一个平面的一条 定理 垂线那么这两个平面互相垂直
l⊂β ⇒α⊥β
l⊥α
(3)平面与平面垂直的性质定理 文字语言
性质 定理
如果两个平面垂直，那么在 一个平面内垂直于它们交线 的直线垂直于另一个平面
图形语言
符号语言
α⊥β α∩β＝a ⇒l⊥α l⊂β l⊥a
A．4 B．3 C．2 D．1 6．如图，正方体 ABCD－A1B1C1D1 的棱长为 1，过 A 点作平面 A1BD 的垂线，垂足为点 H， 有下列三个结论：
①点 H 是△A1BD 的中心； ②AH 垂直于平面 CB1D1； ③AC1 与 B1C 所成的角是 90°. 其中正确结论的序号是________． 7. 如图，AB 为⊙O 的直径，PA 垂直于⊙O 所在的平面，M 为圆周上任意一点，AN⊥PM， N 为垂足．
6
(1)求证：AN⊥平面 PBM. (2)若 AQ⊥PB，垂足为 Q， 求证 NQ⊥PB.
8. 如图，在直三棱柱 ABC—A1B1C1 中，E、F 分别是 A1B、A1C 的中点，点 D 在 B1C1 上， A1D⊥B1C1. 求证：(1)EF∥平面 ABC；
(2)平面 A1FD⊥平面 BB1C1C.
3 积．
2
[玩转跟踪] 1．(2018·江苏高考)在平行六面体 ABCDA1B1C1D1 中，AA1＝AB，AB1⊥B1C1. 求证：(1)AB∥平面 A1B1C； (2)平面 ABB1A1⊥平面 A1BC.
2.(2020·安徽淮北一中模拟)如图，四棱锥 PABCD 的底面是矩形，PA⊥ 平面 ABCD，E，F 分别是 AB，PD 的中点，且 PA＝AD. 求证：(1)AF∥平面 PEC； (2)平面 PEC⊥平面 PCD.
高考指南立体几何垂直证明的六大绝招秒懂
高考指南立体几何垂直证明的六大绝招秒懂！类型一AD⊥SC，求证:AD⊥面SBC证明：∵SA⊥面ABC ∴SA⊥BC又∠ACB=90°∴AC⊥BC又AC，SA⊆面SAC ∴BC ⊥面SAC∴BC⊥AD又AD⊥SC且BC，SC⊆面SBC∴AD⊥面SBC变式：如图，在三棱锥A-BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，求证：AD⊥AC类型二利用等腰三角形中线证垂直例题：在三棱锥P-ABC中，AC=BC，AP=BP，求证PC⊥AB证明：取AB的中点M，连接PM，CM∵AC=BC，M是AB的中点，∴AB⊥CM∵AP=BP，M是AB的中点，∴AB⊥PM∴AB⊥面PCM∴AB⊥PC变式：四棱锥P-ABCD，底面ABCD是正方形，PA=AD，求证面PAD⊥面PCD类型三利用勾股定理逆定理证垂直例题：如图，四棱锥P-ABCD的底面是边成为3的正方形，PA⊥CD，PA=4，PD=5，求证：PA⊥面ABCD证明：∵PA=4，AB=3，PD=5∴PA2+AB2=PD2，∴三角形PAD是直角三角形，∴PA⊥AD又PA ⊥CD，∴PA⊥面ABCD变式：如果，在三棱台ABC-DEF中，平面BDEF⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3，求证：BF⊥面ACFD类型四利用三角形全等证垂直例题：如图，三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°，求证：AB⊥PC证明：取AB的中点M，连接CM，∵△PAB是等边三角形，∴PB=PA又PC=PC，∠PAC=∠PBC=90°∴△PBC≌△PAC，∴BC=AC∴△ACB是等腰三角形，M是AB的中点，∴CM⊥AB又在等边△PAB中，M是AB的中点，∴PM⊥AB∴AB⊥面PMC∴AB⊥PC变式：如图，在以A、B、C、D、E、F为顶点的五面体中，平面CDEF⊥平面ABCD，FC=FB，四边形ABCD为平行四边形，且∠BCD=45°，求证：CD⊥BF类型五利用平行关系证明垂直例题：如图四棱锥P-ABCD，底面是正方形，PA⊥底面ABCD，∠PDA=45°，E是棱AB的中点，求证：面PCE⊥面PCD证明：分别做PC，PD的中点M，N两点，连接EM，MN，NA∵MN为△PCD的中位线，∴MN∥CD且MN=1/2CD又∵E是AB的中点，∴AE∥CD且AE=1/2CD ∴四边形AEMN是平行四边形，则EM∥AN，∵PA⊥面ABCD，∴PA⊥AD，且∠PDA=45°，∴△PAD 是等腰直角三角形又N是PD中点，∴AN⊥PD∵四边ABCD是正方形，∴CD⊥AD，又PA⊥CD，∴CD⊥面PAD，∴CD⊥AN，又上面已求PD⊥AN，∴AN⊥面PCD又∵EM∥AN，∴EM⊥面PCD∵EM ⊂面PEC，∴面PEC⊥面PCD变式：如图1，在直角梯形ABCD中，AD∥BC，∠BAD=90°，AB=BC=1，AD=2，E是AD的中点，O是AC与BE的交点，将△ABE沿BE折起到△A1BE的位置，如图2，证明CD⊥面A1OC.类型六梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2CD，侧面PBC⊥底面ABCD，证明：PA⊥BD。
立体几何中垂直的证明
高。 （1）证明：； （2）若求三棱锥的体积；
（3）证明：.
同步练习二 如图所示, 四棱锥PABCD底面是直角梯形底面ABCD, E为PC的中点,
PA＝AD。
证明: ;
利用等腰三角形底边上的中线的性质 例3、在三棱锥 中， ， ， 。
（1）三棱锥的体积
如图，四棱锥 中，底面 为平行四边形。 底面 ，证明：
A C B P
（Ⅰ）求证： ；
同步练习三
（1）如图，在长方体中，，，则四棱锥的体积为 cm3． （2）已知直三棱柱中，，，为的中点。（Ⅰ）求异面直线和的距离。
利用勾股定理
例4、如图，四棱锥的底面是边长为1的正方形，
_ D _ C _ B _ A _ P
求证:平面
同步练习四
如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2+MC取得最小值时，求证：B1M⊥平面MAC。
如图1，在直角梯形中，，，且． 现以为一边向形外作正方形，然后沿边将正方形翻折，使平面与平面垂 直，为的中点，如图2．
（1）求证：∥平面 （2）求证：平面
如图，三棱柱ABC－A1B1C1中，侧棱垂直底面，∠ACB=90°，
AC=BC=AA1，D是棱AA1的中点 (Ｉ)证明：平面BDC1⊥平面BDC （Ⅱ）平面BDC1分此棱柱为两部分，求这两部分体积的比.
典型例题剖析
通过“平移”证明垂直根据若 例1、在四棱锥P-ABCD中，△PBC为正三角形，AB⊥平面PBC， AB∥CD，AB=DC，.求证：AE⊥平面PDC.
P E D C B A
同步练习一 （1）如图，在正方体中，、分别是、的中点，则异面直线与所成的角 的大小是____________。
高中数学必修立体几何专题线面垂直方法总结
棱
柱
A
B
C
D－
A1
B1C
1
D
中
1
，
侧
棱
A
A1＝
6，
底 面 A B C D 是 菱 形 ， A B＝ 2， A B C＝ 60， P为 侧 棱
B B1上 的 动 点 ．
1求 证 ： D1P AC；
2 设 AC BD＝ O，
求 当 B1P 等 于 多 少 时 ， PB
PO 平 面 D1AC ?
【 解 析 】1 证 明 ：
因为E是PC的中点，所以AE⊥PC. 由(1)知，AE⊥CD，且PC∩CD＝C， 所以AE⊥平面PCD. 而PD 平面PCD，所以AE⊥PD. 又因为PA⊥底面ABCD，所以PA⊥AB. 由已知得AB⊥AD，且PA∩AD＝A，所以AB⊥ 平面PAD. 又PD 平面PAD，所以AB⊥PD. 因为AB∩AE＝A，所以PD⊥平面ABE.
【证明】(1)连结AC，取其 中点O，连结NO、MO，并 延长MO交CD于R. 因为N为PC的中点， 所以NO为△PAC的中位线，所以NO∥PA. 而PA⊥平面ABCD，所以NO⊥平面ABCD，所 以NO⊥CD. 又四边形ABCD是矩形，M为AB的中点，O为 AC的中点，所以MO⊥CD. 而MO∩NO＝O， 所以CD⊥平面MNO，所 以 CD⊥MN.
BB1C1C.
【
证
明
】
直
棱
柱
A
B
C
D－
A1 B 1C
1
D
中
1
，
BB1 平 面 ABC D， 所 以 BB1 AC .
又 因 为 B A D＝ A D C ＝ 9 0 ， A B
＝ 2AD＝ 2C D＝ 2，
立体几何中的向量方法——证明平行及垂直
立体几何中的向量方法(一)——证明平行与垂直1．直线的方向向量与平面的法向量确实定(1)直线的方向向量：在直线上任取一非零向量作为它的方向向量．(2)平面的法向量可利用方程组求出：设a ，b 是平面α两不共线向量，n 为平面α的法向量，则求法向量的方程组为⎩⎨⎧n ·a ＝0，n ·b ＝0.2．用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1∥l 2(或l 1与l 2重合)⇔v 1∥v 2.(2)设直线l 的方向向量为v ，与平面α共面的两个不共线向量v 1和v 2，则l ∥α或l ⊂α⇔存在两个实数*，y ，使v ＝*v 1＋y v 2.(3)设直线l 的方向向量为v ，平面α的法向量为u ，则l ∥α或l ⊂α⇔v ⊥u .(4)设平面α和β的法向量分别为u 1，u 2，则α∥β⇔u 1∥u 2.3．用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2，则l 1⊥l 2⇔v 1⊥v 2⇔v 1·v 2＝0.(2)设直线l 的方向向量为v ，平面α的法向量为u ，则l ⊥α⇔v ∥u .(3)设平面α和β的法向量分别为u 1和u 2，则α⊥β⇔u 1⊥u 2⇔u 1·u 2＝0.【思考辨析】判断下面结论是否正确(请在括号中打"√〞或"×〞)(1)直线的方向向量是唯一确定的．()(2)平面的单位法向量是唯一确定的．()(3)假设两平面的法向量平行，则两平面平行．()(4)假设两直线的方向向量不平行，则两直线不平行．()(5)假设a ∥b ，则a 所在直线与b 所在直线平行．()(6)假设空间向量a 平行于平面α，则a 所在直线与平面α平行．()1．以下各组向量中不平行的是()A ．a ＝(1,2，－2)，b ＝(－2，－4,4)B ．c ＝(1,0,0)，d ＝(－3,0,0)C ．e ＝(2,3,0)，f ＝(0,0,0)D ．g ＝(－2,3,5)，h ＝(16,24,40)2．平面α有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则以下点P 中，在平面α的是()A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．AB →＝(1,5，－2)，BC →＝(3,1，z )，假设AB →⊥BC →，BP →＝(*－1，y ，－3)，且BP ⊥平面ABC ，则实数*，y ，z 分别为______________．4．假设A (0,2，198)，B (1，－1，58)，C (－2,1，58)是平面α的三点，设平面α的法向量n ＝(*，y ，z )，则*∶y ∶z ＝________.题型一 证明平行问题例1(2013·改编)如图，在四面体A －BCD 中，AD ⊥平面BCD ，BC ⊥CD ，AD ＝2，BD ＝22，M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且AQ ＝3QC .证明：PQ ∥平面BCD .如图，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ ；(2)是否存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角？假设存在，求出λ的值；假设不存在，说明理由．题型二 证明垂直问题例2 如下图，正三棱柱(底面为正三角形的直三棱柱)ABC —A 1B 1C 1的所有棱长都为2，D 为CC 1的中点．求证：AB 1⊥平面A 1BD .如下图，在四棱锥P －ABCD 中，PC ⊥平面ABCD ，PC ＝2，在四边形ABCD 中，∠B ＝∠C ＝90°，AB ＝4，CD ＝1，点M 在PB 上，PB ＝4PM ，PB 与平面ABCD 成30°角．(1)求证：CM ∥平面PAD ；(2)求证：平面PAB ⊥平面PAD .题型三 解决探索性问题例3 如图，棱柱ABCD－A1B1C1D1的所有棱长都等于2，∠ABC和∠A1AC均为60°，平面AA1C1C⊥平面ABCD.(1)求证：BD⊥AA1；(2)求二面角D－A1A－C的余弦值；(3)在直线CC1上是否存在点P，使BP∥平面DA1C1，假设存在，求出点P的位置，假设不存在，请说明理由．如下图，四棱锥S—ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点．(1)求证：AC⊥SD.(2)假设SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC.假设存在，求SE∶EC的值；假设不存在，试说明理由．利用向量法解决立体几何问题典例：如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB∥平面AEC；(2)设二面角D－AE－C为60°，AP＝1，AD＝3，求三棱锥E－ACD的体积．A组专项根底训练1．假设直线l的方向向量为a＝(1,0,2)，平面α的法向量为n＝(－2,0，－4)，则()A．l∥αB．l⊥αC．l⊂αD．l与α相交2．假设AB→＝λCD→＋μCE→，则直线AB与平面CDE的位置关系是()A．相交B．平行C．在平面D．平行或在平面3．A(4,1,3)，B(2，－5,1)，C(3,7，－5)，则平行四边形ABCD的顶点D的坐标是() A．(2,4，－1) B．(2,3,1)C．(－3,1,5) D．(5,13，－3)4．a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，假设a，b，c三向量共面，则实数λ等于()A.627B.637C.607D.6575．如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝2，AA 1＝3，AD ＝22，P 为C 1D 1的中点，M 为BC 的中点．则AM 与PM 所成的角为()A ．60°B ．45°C ．90°D ．以上都不正确6．平面α的三点A (0,0,1)，B (0,1,0)，C (1,0,0)，平面β的一个法向量n ＝(－1，－1，－1)，则不重合的两个平面α与β的位置关系是________．7．设点C (2a ＋1，a ＋1,2)在点P (2,0,0)、A (1，－3,2)、B (8，－1，4)确定的平面上，则a ＝________.8．如图，在正方体ABCD —A 1B 1C 1D 1中，棱长为a ，M 、N 分别为A 1B 和AC 上的点，A 1M ＝AN ＝2a 3，则MN 与平面BB 1C 1C 的位置关系是________． 9．如图，四边形ABCD 为正方形，PD ⊥平面ABCD ，PD ∥QA ，QA ＝AB＝12PD .证明：平面PQC ⊥平面DCQ . 10．如图，在底面是矩形的四棱锥P －ABCD 中，PA ⊥底面ABCD ，E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2.(1)求证：EF ∥平面PAB ；(2)求证：平面PAD ⊥平面PDC .B 组 专项能力提升11．如图，正方形ABCD 与矩形ACEF 所在平面互相垂直，AB ＝2，AF ＝1，M 在EF 上，且AM ∥平面BDE ，则M 点的坐标为()A ．(1,1,1)B ．(23，23，1) C ．(22，22，1) D ．(24，24，1)12．设u ＝(－2,2，t )，v ＝(6，－4,4)分别是平面α，β的法向量，假设α⊥β，则t 等于()A ．3B ．4C ．5D ．613．在正方体ABCD —A 1B 1C 1D 1中，P 为正方形A 1B 1C 1D 1四边上的动点，O 为底面正方形ABCD 的中心，M ，N 分别为AB ，BC 的中点，点Q 为平面ABCD 一点，线段D 1Q 与OP 互相平分，则满足MQ →＝λMN→的实数λ有________个．14．如下图，直三棱柱ABC —A 1B 1C 1中，△ABC 为等腰直角三角形，∠BAC ＝90°，且AB ＝AA 1，D 、E 、F 分别为B 1A 、C 1C 、BC 的中点．求证：(1)DE ∥平面ABC ；(2)B 1F ⊥平面AEF .15．在四棱锥P —ABCD 中，PD ⊥底面ABCD ，底面ABCD 为正方形，PD ＝DC ，E 、F 分别是AB 、PB 的中点．(1)求证：EF ⊥CD ；(2)在平面PAD 求一点G ，使GF ⊥平面PCB ，并证明你的结论．。
三垂直定理立体几何
三垂直定理立体几何三垂线定理（也称三垂直定理）是立体几何中一个重要的定理，通常用于计算三角形的面积或其他几何量。
在三维空间中，如果一个点P在三角形ABC所在平面上，那么它到三角形的三个顶点的连线所在的直线都与三角形的平面垂直。
换句话说，点P到三角形的三个边AB、BC、CA 所在平面的距离都是垂直距离。
证明：设点P在平面ABC上，向量a、b、c分别表示边向量AB、BC、CA，则向量n=a×b表示平面ABC的法向量（叉积）。
点P到平面ABC的距离（设为h）满足n·OP=h|n|，其中OP 为点P到原点O的向量。
考虑向量PA在向量n上的投影PA'，即PA'=(PA·n/|n|)n/|n|。
根据余弦公式，PA·PB=PA^2+PB^2-AB^2/2，因此PA·n=PA·(a×b)=PA·c^2/2SABC。
将上述若干式子代入n·OP=h|n|中，得到PA'=PA·c^2/(2SABC)|n|/|c×(PA×c)|同理，PB'和PC'也可以表示为三垂线上的垂直距离分别为h=PA'，h=PB'和h=PC'。
应用：利用三垂线定理，可以方便地计算三角形的面积。
设三角形ABC的三边长分别为a、b、c，其半周长为s=(a+b+c)/2，则三角形的面积S可以表示为S=abc/4R=1/2absinC=1/2crsinA=1/2basinC其中R为三角形外接圆半径，A、B、C为三角形的角度。
由于三条垂线的长度都可以用三条边的长度表示，因此可以通过这些式子计算出三角形的面积。
三垂线还可以用于计算三角形垂心（三条垂线交点）、oktane棱锥的体积等相关几何量。
需要注意的是，在三维空间中绝大多数点不在三角形所在平面上，因此计算其垂距要用到点到平面的距离公式。
立体几何线线垂直的证明方法
立体几何线线垂直的证明方法在立体几何中，线线垂直是一种非常重要的关系，它在很多问题中都有着重要的应用。
本文将介绍几种线线垂直的证明方法，希望能够帮助读者更好地理解和运用这一关系。
一、垂线段的垂线段垂直首先介绍的是垂线段的垂线段垂直的证明方法。
具体来说，如果有两个垂直于同一个平面的线段AB和CD，且它们之间有一条垂线段EF，则EF和CD垂直。
证明如下：1、连接AE和CF，得到平面ACEF。
2、由于AB和CD垂直于平面ACEF，所以它们的交点O在平面ACEF 内。
3、由于EF垂直于平面ACEF，所以它与平面ACEF的任意一条交线都垂直，特别地，它与CF垂直。
4、因此，EF和CD垂直。
二、平面的法线和平面内的任意直线垂直接下来介绍的是平面的法线和平面内的任意直线垂直的证明方法。
具体来说，如果有一个平面P和一条直线L在平面P内，且L与P垂直，则L与P的法线垂直。
证明如下：1、连接L和P的交点O。
2、在平面P内任意取一点A，连接OA。
3、由于L与P垂直，所以OA与L垂直，即OA和L在点O处垂直。
4、由于P的法线垂直于P，所以它与P内任意一条直线都垂直，特别地，它与OA垂直。
5、因此，L与P的法线垂直。
三、垂线段和平面的法线垂直最后介绍的是垂线段和平面的法线垂直的证明方法。
具体来说，如果有一条垂直于平面P的直线L，且L与平面P上的一条线段AB相交于点O，则OA和OB的中垂线与P的法线垂直。
证明如下：1、连接OA和OB，得到线段AB的中垂线CD。
2、连接CO和DO，得到平面COD。
3、由于L垂直于平面P，所以L和P的法线在平面P内的交点O 处垂直。
4、由于OA和OB在点O处相交，所以它们的中垂线CD也经过点O。
5、因此，CD与P的法线垂直。
以上就是三种线线垂直的证明方法，它们都非常简单易懂，但是能够解决很多实际问题。
在实际应用中，我们可以根据具体情况选择不同的证明方法，以便更好地解决问题。
立体几何平面垂直的判定定理
立体几何平面垂直的判定定理一、定义在立体几何中，平面垂直的判定定理是指：如果两个平面的法线向量互相垂直，则这两个平面是垂直的。
二、判定方法根据平面的法线向量的定义，我们知道平面的法线向量是与该平面垂直的向量。
因此，要判断两个平面是否垂直，只需判断它们的法线向量是否互相垂直即可。
具体而言，设平面P1的法线向量为n1，平面P2的法线向量为n2，如果n1·n2 = 0，其中"·"表示向量的点积运算，那么平面P1与平面P2垂直；反之，如果n1·n2 ≠ 0，则两个平面不垂直。
三、相关应用平面垂直的判定定理在实际问题中有着广泛的应用。
以下是一些常见的应用场景：1. 建筑工程中的搭建在建筑工程中，平面垂直的判定定理被广泛应用于搭建建筑物的过程中。
例如，当建筑物的墙壁需要与地面垂直时，可以利用该定理判断墙壁的法线向量与地面的法线向量是否垂直，从而保证墙壁的竖直性。
2. 三维模型的设计在三维模型的设计过程中，平面垂直的判定定理常用于判断不同部位的平面是否垂直。
例如，当设计一个立方体时，可以利用该定理判断立方体的各个面是否相互垂直，从而确保模型的准确性。
3. 几何证明中的推理在几何证明中，平面垂直的判定定理是一种常用的推理方法。
通过运用该定理，可以推导出两个平面垂直的结论，然后应用于其他几何证明中。
四、总结立体几何平面垂直的判定定理是立体几何中的重要概念，能够帮助我们判断平面是否垂直。
通过判断两个平面的法线向量是否互相垂直，可以准确地判定平面的垂直性。
该定理在建筑工程、三维模型设计以及几何证明等领域都有着广泛的应用。
因此，掌握平面垂直的判定定理对于学习和应用立体几何都具有重要意义。
立体几何证垂直的方法
立体几何证垂直的方法垂直是立体几何中一个非常重要的概念，常常用于判断两个直线、两个平面或者一个直线和一个平面之间的关系。
本文将介绍几种常见的方法来证明两个线段、两个直线、两个平面或者一个线段和一个平面之间的垂直关系。
1. 定义证明法：垂直可以通过定义来证明。
垂直的定义是：两条直线相交，互相垂直。
这个定义可以用来判断两条直线之间是否垂直。
如果已知两条直线相交，并且相交角度为90度，则可以得出两条直线垂直的结论。
2. 重叠线证明法：当两个线段的一个端点重合，并且两个线段的另一个端点也重合时，可以得出这两个线段垂直的结论。
这是因为，当两个线段垂直时，它们的端点将构成一个直角，而直角的两条边重合时，会得到一个重叠的线段，从而可以推出两个线段垂直。
3. 垂直性质证明法：根据垂直性质来证明两个直线或者平面之间的垂直关系。
例如，两个直线垂直的性质之一是：直线的斜率相乘为-1。
如果已知两个直线的斜率，且斜率的乘积等于-1，则可以得出这两条直线垂直的结论。
类似地，两个平面之间垂直的性质之一是：平面上两个垂直的直线在平面上的投影线也垂直。
如果已知两个平面上的直线的投影线垂直，则可以得出这两个平面垂直的结论。
4. 垂直线性等式证明法：当两个线段、直线或平面上的点坐标可以满足垂直线性等式时，可以证明它们之间的垂直关系。
例如，对于两个直线L1:y = a1x + b1和L2:y = a2x + b2，如果它们的斜率满足a1 * a2 = -1，则可以得出这两条直线垂直的结论。
5. 三角形几何证明法：在三角形中，垂直性质也可以用来证明两个线段或直线之间的垂直关系。
例如，如果一条线段平分了一个角，并且与另一条线段垂直相交，那么可以得出这两个线段垂直的结论。
同样地，如果一个直角三角形中的两条边互相垂直，那么可以得出这两条边垂直的结论。
总结起来，证明垂直关系的方法有很多种，包括基于定义、重叠线、垂直性质、线性等式和三角形几何的方法。
立体几何中不易建系的用空间向量证明垂直问题。
立体几何中不易建系的用空间向量证明垂直问题。
1. 引言1.1 概述立体几何是数学中的一个重要分支，研究空间中的图形和特定关系。
建系问题是立体几何中一个常见的难题，它涉及到如何确定或构建一个合适的坐标系来描述和表示空间中的元素和关系。
在解决建系问题时，传统的方法存在一定局限性和困难，例如难以应对复杂的几何结构、缺乏普适性等。
1.2 文章结构本文将通过引入空间向量理论来探讨解决立体几何中不易建系的问题。
文章分为以下几个部分：- 引言：介绍本文的背景和论文结构。
- 立体几何中的建系问题：阐述建系定义与重要性、传统方法的局限性与困难，以及空间向量在解决建系问题中的优势。
- 空间向量证明垂直问题的基本原理与方法：讨论垂直关系的定义与特征、空间向量表示垂直关系的有效途径，以及应用空间向量证明垂直性质时需要考虑的因素。
- 实例分析：通过一个具体案例来说明使用空间向量证明垂直问题的步骤和推理过程，并对结果进行分析和讨论。
- 结论与展望：总结研究成果并得出结论，同时提出未来研究方向和进一步工作的展望。
1.3 目的本文的目的是介绍空间向量在解决立体几何中不易建系的问题中所起到的作用和优势，并通过实例分析来验证其有效性。
通过本文的研究，读者将能够理解空间向量在解决建系问题中的重要性，并了解使用空间向量证明垂直问题的基本原理与方法。
最终，本文希望为立体几何领域中建系问题的解决提供一种新思路和有价值的参考。
2. 立体几何中的建系问题：2.1 建系的定义与重要性：在立体几何中，建系是指通过选取适当的点或向量作为参照，构建坐标系或基底来描述和表示空间中的几何事物或运动。
建系是解决立体几何问题和进行进一步分析的基础，它可以帮助我们确定方向、测量距离和角度，从而推导出更多关于空间图形、运动和变换的性质。
2.2 建系方法的局限性与困难：传统的建系方法主要包括平行四边形法、角平分线法、垂直线法等。
然而，这些方法在实际应用中存在一定的局限性和困难。
立体几何垂直判定定理
立体几何垂直判定定理立体几何垂直判定定理一、前言在立体几何中，垂直是一个非常重要的概念。
垂直关系不仅存在于平面内，也存在于空间中。
本文将介绍立体几何中的垂直判定定理。
二、定义在三维空间中，两条直线或两个平面互相垂直，当且仅当它们的方向向量互相垂直。
三、证明1. 两条直线的垂直判定对于两条不共面的直线l1和l2，它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件：l1·l2=0（点乘为0）其中，“·”表示向量点乘运算。
证明如下：设l1的方向向量为a=(x1,y1,z1)，l2的方向向量为b=(x2,y2,z2)。
则有：a·b=x1x2+y1y2+z1z2若a·b=0，则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
反之，若a与b互相垂直，则有a·b=0。
因此，两条不共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
对于两条共面的直线，它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件：l1·l2=0（点乘为0），且l1和l2不共线其中，“·”表示向量点乘运算。
证明如下：设l1的方向向量为a=(x1,y1,z1)，l2的方向向量为b=(x2,y2,z2)。
则有：a·b=x1x2+y1y2+z1z2若a·b=0，则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
但是，如果a和b共线，则它们不可能互相垂直。
因此，我们需要加上一个限制条件：l1和l2不共线。
反之，若a与b互相垂直，且l1和l2不共线，则有a·b=0。
因此，两条共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
综上所述，两条直线互相垂直当且仅当它们的方向向量满足上述条件。
2. 两个平面的垂直判定对于两个平面P1和P2，它们互相垂直当且仅当它们的法向量n1和n2满足以下条件：n1·n2=0（点乘为0）其中，“·”表示向量点乘运算。
立体几何中平行和垂直问题的证明
摇生"攵浬化知识篇科学备考新指向高考数学2021年2月立"#何％&行直问题的证明■江苏省华罗庚中学李普红平行与垂直关系的证明是高考考查立体几何的高频考点，大部分问题都可以用传统的几何方法解决，有一部分问题需要建立空间直角坐标系利用空间向量解决。
用传统法解题时，应注重线线平行、线线垂直、线面平行、线面垂直、面面平行、面面垂直等问题的性质定理和判定定理的灵活应用。
用向量法解题时，应建立恰当的空间直角坐标系，准确表示各点与相关向量的坐标。
考向一：证明线面平行!!如图1,已知空间几何体BACDE中，&BCD与&CDE均是边长为2的等边三角形,&ABC是腰长为3,底边为BC的等腰三角形，平面CDE丄平面BCD，平面ABC丄平面BCD"(1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；(2)求三棱锥E-ABC的体积。
解析：(1)如图2所示，取DC的中点为N,BD的中点为/，连接MN，则MN即为所求。
连接EM，EN，取BC的中点4，连接AH"因为&ABC是腰长为3的等腰三角形，H为BC的中点，所以AH丄BC。
又平面ABC丄平面BCD，平面ABC'平面BCD$BC，AH U平面ABC，所以AH 丄平面BCD"同理可证EN丄平面BCD"所以EN/AH"因为EN1平面ABC，AH U平面ABC，所以EN/平面ABC"又M，N分别为BD，DC的中点，所以MN/BC"因为MN1平面ABC，BC U平面ABC，所以MN/平面ABC"又MN'EN$N，MN U平面EMN，EN U平面EMN，所以平面EMN/平面ABC"又EF U平面EMN，所以EF/平面ABC，即直线MN上任意一点F与E的连线EF均与平面ABC平行°(2)连接DH，取CH的中点为G，连接NG，则NG/DH"由(1)可知EN/平面ABC，所以点E到平面ABC的距离与点N到平面ABC的距离相等°又&BCD是边长为2的等边三角形，所以DH丄BC。
立体几何垂直证明
立体几何垂直证明方法技巧类型一：线线垂直证明（共面垂直、异面垂直）（1） 共面垂直：掌握几种模型①等腰（等边）三角形中的中线 ②菱形（正方形）的对角线互相垂直 ③勾股定理中的三角形 ④ 直角梯形⑤利用相似或全等证明直角。
例：在正方体1111ABCD A B C D -中，O 为底面ABCD 的中心， E 为1CC 中点,求证： (1) 1A O OE ⊥ (2) 1A O BDE ⊥平面（2） 异面垂直（利用线面垂直来证明）例1 在正四面体ABCD 中， 求证：AC BD ⊥变式1 如图，在四棱锥ABCD P -中，底面ABCD 是矩形，已知ο60,22,2,2,3=∠====PAB PD PA AD AB ．证明：AD PB ⊥；变式2 如图，在边长为2的正方形ABCD中，点E是AB的中点，点F是BC的中点，将△AED,△DCF分别沿,DE DF折起，使,A C两点重合于'A.求证:'A D EF⊥；变式3如图，在三棱锥P ABC-中，⊿PAB是等边三角形，∠P AC=∠PBC=90 º证明：AB⊥PC类型二：直线与平面垂直证明BE'ADFG方法○1利用线面垂直的判断定理例：在正方体1111ABCD A B C D -中，,求证：11AC BDC ⊥平面变式1：如图：直三棱柱ABC －A 1B 1C 1中， AC =BC =AA 1=2，∠ACB =90︒.E 为BB 1的中点，D 点在AB 上且DE = 3 . 求证：CD ⊥平面A 1ABB 1；变式2：如图，在四面体ABCD 中，O 、E 分别是BD 、BC 的P中点，2,CA CB CD BD AB AD ====== 求证：AO ⊥平面BCD ；变式3 如图，在底面为直角梯形的四棱锥P ABCD -中，(1) 求证：//AF 平面BCE ；(2) 求证：平面BCE ⊥平面CDE ；例2 如图，在四棱锥P ABCD -中，PA ⊥底面ABCD ，60AB AD AC CD ABC ⊥⊥∠=，，°，PA AB BC ==，FADPEE是PC的中点．⊥；（2）证明PD⊥平面ABE；（1）证明CD AE变式1已知直四棱柱ABCD—A′B′C′D′的底面是菱形，∠60ABC，E、F分别是棱CC′与BB′上的点，=︒且EC=BC=2FB=2．（1）求证：平面AEF⊥平面AA′C′C；类型三：平面与平面垂直证明1.AB是圆O的直径，PA垂直于圆O所在的平面，M是圆周上任意一点，AN⊥PM，点N为垂足，求证：平面PAM⊥平面PBM2．如图，在空间四边形ABCD中，AB=BC，CD=DA，E，F，Ｇ分别为ＣＤ，ＤＡ和对角线ＡＣ的中点。
证明两线互相垂直的常用方法
证明两线互相垂直的常用方法我们学习了平面与直线垂直的定义、判定定理和性质定理，大家可以体会线线垂直在证明线面垂直时的重要性，将“三维”问题转化为“二维”解决是一种重要的立体几何数学思想方法.在处理实际问题过程中，可以先从题设条件入手，分析已有的垂直关系，再从结论入手分析所要证明的重要垂直关系，从而架起已知与未知的“桥梁”，同学们下面欣赏常见的线面垂直证明方法.一、利用定义垂直的定义：如果两条直线相交成直角，那么这两条直线互相垂直。
从定义可以看出，只要说明两条直线相交的角是直角，就可以说明两条直线互相垂直。
例1：如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.求证：PC是⊙O的切线；分析：因为点C在圆上，只要说明OC⊥CP即可。
解：∵OA=OC,∴∠A=∠ACO∵∠COB=2∠ A ,∠COB=2∠PCB∴∠A=∠ACO=∠PCB∵AB是⊙O的直径∴∠ACO+∠OCB=90°∴∠PCB+∠OCB=90°,即OC⊥CP∵OC是⊙O的半径∴PC是⊙O的切线例2：（1）把两个含有45°角的直角三角板如图1放置，点D在BC上，连结BE，AD，AD的延长线交BE于点F．求证：AF⊥BE．分析：线段之间的垂直，只要说明∠BFD=90°，直接计算不出来，通过三角形全等，间接证明角度为90°。
证明：在△ACD和△BCE中，AC＝BC，∠DCA＝∠ECB＝90°，DC＝EC，∴ △ACD≌△BCE（SAS）∴ ∠DAC＝∠EBC．∵ ∠ADC＝∠BDF，∴ ∠EBC＋∠BDF＝∠DAC＋∠ADC=90°．∴ ∠BFD=90°∴ AF⊥BE．（2）把两个含有30°角的直角三角板如图2放置，点D在BC上，连结BE，AD，AD的延长线交BE于点F．问AF与BE是否垂直？并说明理由．分析：题目同（1）类似，类比（1）思路，这里△ACD和△BCE，显然不全等，考虑相似即可。
高中数学立体几何证垂直公式
高中数学立体几何证垂直公式垂直公式是高中数学立体几何中的一个重要概念。
在几何学中，我们经常遇到需要判断两个线段是否垂直的情况。
垂直公式提供了一种简便的方法来验证两个线段是否垂直。
垂直公式的表达方式是：若两条线段的斜率乘积为-1，则这两条线段垂直。
我们来回顾一下斜率的定义。
在平面直角坐标系中，给定两个点A(x1, y1)和B(x2, y2)，线段AB的斜率可以通过以下公式计算：斜率 k = (y2 - y1) / (x2 - x1)接下来，我们将使用垂直公式来证明两个线段的垂直关系。
假设有两条线段AB和CD，我们需要验证这两条线段是否垂直。
首先，我们计算线段AB和线段CD的斜率分别为k1和k2。
如果k1 * k2 = -1，那么根据垂直公式，可以得出线段AB和线段CD垂直。
现在，让我们通过一个具体的例子来演示如何使用垂直公式。
假设有两个点A(2, 3)和B(4, -1)，以及两个点C(1, 2)和D(3, 0)。
我们需要验证线段AB和线段CD是否垂直。
我们计算线段AB的斜率。
k1 = (-1 - 3) / (4 - 2) = -4 / 2 = -2接下来，我们计算线段CD的斜率。
k2 = (0 - 2) / (3 - 1) = -2 / 2 = -1然后，我们计算斜率的乘积。
k1 * k2 = -2 * -1 = 2由于k1 * k2不等于-1，所以线段AB和线段CD不垂直。
通过这个例子，我们可以看到垂直公式的应用。
它提供了一种简单快捷的验证两个线段是否垂直的方法，通过计算斜率的乘积，我们可以得出结论。
需要注意的是，垂直公式只是一种判断两个线段是否垂直的方法，它并不提供线段的具体垂直方向信息。
如果我们想要确定两个线段的垂直方向，可以通过计算线段的方向向量来实现。
垂直公式是高中数学立体几何中的一个重要概念。
通过计算两个线段的斜率乘积，我们可以判断这两个线段是否垂直。
垂直公式提供了一种简便的方法来验证两个线段的垂直关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
全方位教学辅导教案
线面垂直的判定及其性质
●知识要点 1.线面垂直 （1）定义：
如果直线l 与平面α的任意一条直线都垂直，则直线l 与平面α互相垂直，记作l α⊥. l －平面α的垂线，α－直线l 的垂面，它们的唯一公共点P 叫做垂足. （2）判定定理：（线线垂直→线面垂直）
一条直线与一个平面的两条相交直线都垂直，则这条直线与该平面垂直. ☆ 符号语言：若l ⊥m ，l ⊥n ，m ∩n ＝B ，m α，n α，则l ⊥α. （3）性质定理：（线面垂直→线线平行） 垂直于同一个平面的两条直线平行. 2.二面角 （1）定义：
从一条直线出发的两个半平面所组成的图形叫二面角. 这条直线叫做二面角的棱，这两个半平面叫做二面角的面. 记作二面角AB αβ－－. （简记P AB Q －－） （2）二面角的平面角：
在二面角αβ－l －的棱l 上任取一点O ，以点O 为垂足，在半平面,αβ分别作垂直于棱l 的射线OA 和OB ，则射线OA 和OB 构成的AOB ∠叫做二面角的平面角. 围：000180θ<<. 3.面面垂直
（1）定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直. 记作αβ⊥.
（2）判定定理：（线面垂直→面面垂直）
一个平面过另一个平面的垂线，则这两个平面垂直. （3）性质定理：（面面垂直→线面垂直）
两个平面垂直，则一个平面垂直于交线的直线与另一个平面垂直.
“垂直关系”常见证明方法
（一）直线与直线垂直的证明
1) 利用某些平面图形的特性：如直角三角形的两条直角边互相垂直等。
6、如图，在四棱锥P－ABCD中， PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝
AB＝BC，E是PC的中点．
(1)求证：CD⊥AE；(2)求证：PD⊥面ABE.
题型二、面面垂直的判定与性质
1、如图AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任意一点，求证：平面PAC垂直平面PBC。
2、如图，棱柱111
ABC A B C
-
的侧面11
BCC B
是菱形，
11
B C A B
⊥
证明：平面
1
AB C⊥平面
11
A BC；
3、已知：如图，将矩形ABCD沿对角线BD将BCD折起，使点C移到点
1
C，且1
C AB
D O AB
在平面上的射影恰好在上。
1
1
(2).
BDC
⊥
⊥
1
1
（）求证：AD BC
求证：面ADC面
4、如图所示，在长方体
1111
ABCD A B C D
-中，AB=AD=1，AA1=2，M是棱CC1的中点
（Ⅰ）求异面直线A1M和C1D1所成的角的正切值；
（Ⅱ）证明：平面ABM⊥平面A1B1M1
5、已知四面体ABCD中，CD
BD
AC
AB=
=,,平面⊥
ABC平面BCD,E为棱BC的中点。
（1）求证：⊥
AE平面BCD;
（2）求证：BC
AD⊥;
6、S是△ABC所在平面外一点，SA⊥平面ABC,平面SAB⊥平面SBC,求证AB⊥BC.
S
A
C
B
O
B
C1
A
D
C
7、在四棱锥中，底面ABCD 是正方形，侧面VAD 是正三角形，平面VAD ⊥底面ABCD 证明:AB ⊥平面VAD
8、如图所示，在四棱锥P —ABCD 中，底面ABCD 是∠DAB=60°且边长为a 的菱形，侧面PAD 为正三角形，其所在平面垂直于底面ABCD ，若G 为AD 边的中点， （1）求证：BG ⊥平面PAD ； （2）求证：AD ⊥PB ；
（3）若E 为BC 边的中点，能否在棱PC 上找到一点F ，使平面DEF ⊥平面ABCD ，并证明你
的结论.
V
D C
B
A
题型三、平行与垂直的综合题
(2)PDA=45.
PA ABCD CD
MN PCD ⊥⊥∠⊥。
1、已知矩形所在的平面，M,N 分别是AB,PC 的中点。
（1）求证：MN 若，求证：平面
2、如图所示，直三棱柱ABC —A 1B 1C 1中，B 1C 1=A 1C 1，AC 1⊥A 1B ，M 、N 分别是A 1B 1、AB 的中点.
（1）求证：C 1M ⊥平面A 1ABB 1； （2）求证：A 1B ⊥AM ；
（3）求证：平面AMC 1∥平面NB 1C ；
3、如图，在四棱锥ABCD P -中，平面PAD ⊥平面ABCD ， AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点
求证：（1）直线EF ‖平面PCD ；
（2）平面BEF ⊥平面PAD
4.如图5所示，在四棱锥P-ABCD 中,AB ⊥平面PAD,AB CD,PD=AD,E 是PB 的中点，F 是DC 上的点且DF=
2
1
AB,PH 为∆PAD 中AD 边上的高． （1） 证明：PH ⊥平面ABCD ；
（2） 若PH=1，AD=2,FC=1，求三棱锥E-BCF 的体积； 证明：EF ⊥平面PAB ．
课堂检测： 课后作业:
签字 教研组长： 教学主任： 学生： 教务老师： 家长：
老师 课后 评价 下节课的计划：
学生的状况、接受情况和配合程度： 给家长的建议：。