重庆大学工程力学作业解答
大学《工程力学》课后习题解答-精品
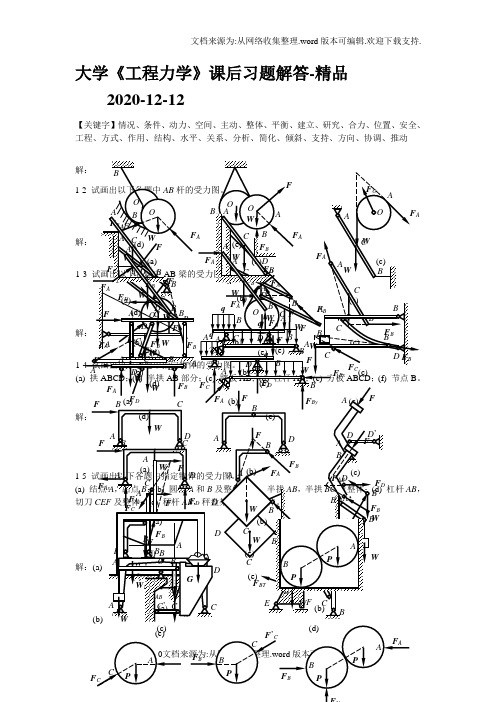
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
重庆大学工程力学(一)复习题及答案
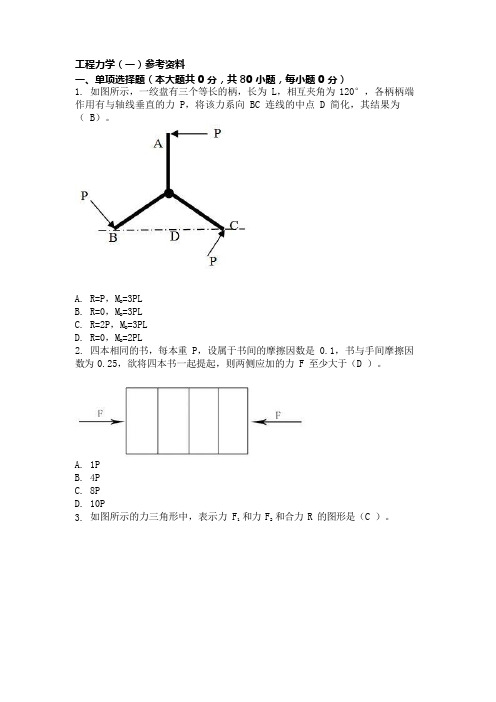
工程力学(一)参考资料一、单项选择题(本大题共 0 分,共 80 小题,每小题 0 分)1.如图所示,一绞盘有三个等长的柄,长为 L,相互夹角为120°,各柄柄端作用有与轴线垂直的力 P,将该力系向 BC 连线的中点 D 简化,其结果为( B)。
=3PLA.R=P,MDB.R=0,M=3PLD=3PLC.R=2P,MDD.R=0,M=2PLD2.四本相同的书,每本重 P,设属于书间的摩擦因数是 0.1,书与手间摩擦因数为 0.25,欲将四本书一起提起,则两侧应加的力 F 至少大于(D )。
A.1PB.4PC.8PD.10P3.如图所示的力三角形中,表示力 F1 和力 F2 和合力 R 的图形是(C )。
A.图1B.图2C.图3D.图44.如图所示某种材料的σ-ε曲线,若在 k 点时将荷载慢慢卸掉,则σ-ε曲线将沿着与 Oa 平行的直线 kA 回落到 A 点,从图可以看出( B)。
A.OA 段是弹性变形,AB 段是塑性变形B.OA 段是塑性变形,AB 段是弹性变形C.如果在重新加载,σ-ε曲线将沿着 Oa 上升到 k 点D.如果在重新加载,σ-ε曲线将沿着 Bk 上升到 k 点5.图示简支梁,已知 C 点的挠度为 y,在其他条件不变的情况下,若将荷载 F 增大一倍,则 C 点的挠度为( C)。
A. 0.5y;B.y;C.2y;D.4y。
6.简支梁受力如图,下列说法正确的是(B )。
A.1-1 截面的弯矩为零,3-3 截面的弯矩为零;B.1-1 截面的弯矩为-12kN.m,3-3 截面的弯矩为零;C.1-1 截面的弯矩为 12kN.m,3-3 截面的弯矩为零;D.3-3 截面的弯矩不为零;7.图示悬臂梁拟用(a)(b)两种方式搁置,则两种情况下的最大应力(σmax)a/(σmax)b 为之比为(A )。
A. 1/4B. 1/16C. 1/64D. 48. 冲床如图所示,若要在厚度为δ的钢板上冲出直径为 d 的圆孔,则冲头的冲压力 F 必须不小于(D )。
重庆大学工程力学作业解答

工程力学课后解答5、9 题图5、9所示中段开槽得杆件,两端受轴向载荷P 得作用,试计算截面1-1与2-2上得应力。
已知:P = 140kN,b = 200mm,b 0 = 100mm,t = 4mm 。
题图5、9解:(1) 计算杆得轴力 kN 14021===P N N (2) 计算横截面得面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题得目得就是说明在一段轴力相同得杆件内,横截面面积小得截面为该段得危险截面)5、10 横截面面积A=2cm 2得杆受轴向拉伸,力P=10kN,求其法线与轴向成30°得及45°斜截面上得应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆得轴力kN 10==P N(2) 计算横截面上得正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上得应力MPa 5.37235030cos 2230=⎪⎪⎭⎫ ⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生得截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°得截面上。
(注:本题得结果告诉我们,如果拉压杆处横截面得正应力,就可以计算该处任意方向截面得正应力与剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°得截面上,最大正应力发生在横截面上,横截面上剪应力为零) 5、17 题图2、17所示阶梯直杆AC ,P =10kN,l 1=l 2=400mm,A 1=2A 2=100mm 2,E =200GPa 。
重庆大学2020年春季学期课程作业工程力学(一)

答案+我名字2020年春季学期课程作业工程力学(一)第1次工程力学(一)题号一二合计已做/题量20 / 2020 / 2040 / 40得分/分值48 / 6030 / 4078 / 100一、单项选择题(共20 题、48 / 60 分)1、有主次之分的物体系统,关于其荷载传递规律的论述不正确的是()正确!收藏该题展开该题2、如果梁上某段承受梯形分布荷载,那么该梁段的挠曲线是()。
正确!收藏该题展开该题3、关于铰链约束,以下说法不正确的是()。
正确!收藏该题展开该题4、图示四根细长压杆,其材料、截面相同,它们在纸平面内失稳的先后次序正确的是()。
正确!收藏该题展开该题5、如图所示,插销穿过水平位置的平板上的圆孔,在其下端受有一拉力F,该插销的剪切面面积和挤压面面积分别等于()。
正确!收藏该题展开该题6、图示梁,弯矩图发生突变的截面是:正确!收藏该题展开该题7、铸铁试件压缩时沿与轴线约为45o的斜截面断裂,产生破坏的主要原因是()。
正确!收藏该题展开该题8、如图所示等直杆,抗拉刚度为EA,则杆段AB的轴向线变形为()。
正确!收藏该题展开该题9、如图所示,结构在D点作用一水平力F,大小为F=2kN,不计杆ABC的自重,则支座B 的约束反力为()。
A、RB<2kNB、RB=2kNC、RB>2kND、RB=0收藏该题10、边长为a的正方形截面对其对称轴的回转半径为()正确!收藏该题展开该题11、图示T字形截面,要使y、z轴始终为该截面的主惯性轴,则下述正确的是()正确!收藏该题展开该题12、矩形截面细长压杆如题11.4图所示,其两端约束情况为:在纸平面内为两端铰支,在出平面内一端固定、一端夹支(不能水平移动与转动)。
其横截面高度b和宽度a的合理比值为()。
正确!收藏该题展开该题13、梁的转角出现极值的截面为()正确!收藏该题展开该题14、图示矩形截面梁采用两种放置方式, 从弯曲正应力强度观点, (b)的承载能力是(a)的多少倍?()。
重庆大学工程力学作业解答

工程力学课后解答5.9 题图5.9所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图5.9解:(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)5.10 横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ (3) 计算斜截面上的应力MPa 5.37235030cos 2230=⎪⎪⎭⎫⎝⎛⨯==σσMPa 6.2123250)302sin(230=⨯=⨯=στ MPa 25225045cos 2245=⎪⎪⎭⎫⎝⎛⨯==σσMPa 251250)452sin(245=⨯=⨯=στ (4) m ax τ发生的截面 ∵0)2cos(==ασαταd d 取得极值 ∴ 0)2cos(=α 因此:22πα=, 454==πα故:m ax τ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)5.17 题图2.17所示阶梯直杆AC ,P =10kN ,l 1=l 2=400mm ,A 1=2A 2=100mm 2,E =200GPa 。
工程力学知到章节答案智慧树2023年重庆大学

工程力学知到章节测试答案智慧树2023年最新重庆大学第一章测试1.变形固体的基本假设是()。
参考答案:连续、均匀性假设和各向同性假设;2.要使构件安全、正常地工作,必须满足()。
参考答案:强度要求、刚度要求、稳定性要求第二章测试1.平衡是指物体相对于惯性参考系保持静止或作匀速转动的状态。
()参考答案:错2.根据力的平行四边形法,作用于同一物体上的两个力都可以合成为一个合力。
()参考答案:错3.变形体在两个大小相等、方向相反、作用线沿同一直线的力作用下不一定能维持平衡。
()参考答案:对4.受力图中各约束反力的作用线方位及指向(除柔索和光滑接触面约束外)一般自己假定。
()参考答案:对5.下列关于刚体的描述,不正确的是()。
参考答案:变形极小的物体就可视为刚体6.下列关于约束反力的表述中,不正确的是()。
参考答案:约束反力的大小和方向由约束构造特点确定7.如题图所示体系,构件自重不计,则支座A处约束反力作用线方位正确的是()。
参考答案:沿AE8.如题图所示体系,构件自重不计,则受力分析图不正确的是()。
参考答案:第三章测试1.在任何坐标系中,力都可以用其在坐标轴上的投影解析表示。
()参考答案:错2.力对某轴之矩等于力对轴上任一点之矩在该轴上的投影。
()参考答案:对3.只要保持力偶矩不变,力偶可在其作用面内任意移动和转动,都不会改变原力偶对物体的作用效应。
()参考答案:错4.力系向某点简化,其主矢和主矩都不为零,且主矢和主矩正交,则该力系可以继续简化为一合力。
()参考答案:错5.作用在一个刚体上的两力,满足的条件,则该二力可能是()。
参考答案:一对平衡的力或一个力偶6.某平面力系向其平面内A点简化的结果为:,则该力系向其平面内任选的另一点B简化的结果为()。
参考答案:7.下列关于力平移的表述中,正确的是()。
参考答案:作用在刚体上的力可以沿其作用线平移到该刚体上任一点,其作用效应不变8.各力作用位置如图所示的平面力系中,已:F1=4kN,F2=3kN,q=2kN/m,M1=100N·m,M2=200N·m。
工程力学课后习题答案
工程力学课后习题答案工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC 或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第一章静力学基础 9第二章平面力系2-1 电动机重P=5000N,放在水平梁AC 的中央,如图所示。
梁的A端以铰链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F F F F FB A y A B x 30sin 30sin ,0030cos 30cos ,0 解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F F P F F FBC y BC AB x解得:P F P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交N F NF F F F F F FC A GA y C A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
重庆大学2019年秋季学期课程作业工程力学(一)
答案+名字2019年秋季学期课程作业工程力学(一)第1次工程力学(一)题号一二三四五合计已做/题量0 / 10 0 / 10 0 / 6 0 / 2 0 / 2 0 / 30得分/分值0 / 30 0 / 20 0 / 18 0 / 16 0 / 16 0 / 100一、单项选择题(共10 题、0 / 30 分)1、简支梁受力如图,下列说法正确的是()。
A、1-1截面的弯矩为零,3-3截面的弯矩为零;B、1-1截面的弯矩为-12kN.m,3-3截面的弯矩为零;C、1-1截面的弯矩为12kN.m,3-3截面的弯矩为零;D、3-3截面的弯矩不为零;收藏该题2、冲床如图所示,若要在厚度为δ的钢板上冲出直径为d的圆孔,则冲头的冲压力F必须不小于()。
已知钢板的屈服应力τs和强度极限应力τb。
B、C、D、收藏该题3、以下说法错误的是()。
A、对形心轴的静矩一定为零B、对形心轴的静矩不一定为零C、静矩为零的轴一定是形心轴D、静矩可能为正、可能为负、可能为零收藏该题4、平面一般力系的最后可能简化结果情形有()A、1种;2种;C、3种;D、4种。
收藏该题5、直径为d的实心圆截面等直梁的抗弯截面模量是()。
A、;B、;C、;D、。
收藏该题6、图示四根细长压杆,其材料、截面相同,它们在纸平面内失稳的先后次序正确的是()。
A、(a)(b)(c)(d);B、(d)(a)(b)(c);C、(c)(d)(a)(b);D、(b)(c)(d)(a)。
收藏该题7、图示梁,弯矩图发生突变的截面是:A、B截面B、C截面C、D截面D、C截面和D截面收藏该题8、直径为d的圆形截面对其形心轴的回转半径为()A、B、C、D、收藏该题9、均质杆AB重P=6KN,A端置于粗糙地面上,静滑动摩擦因数fs=0.3,B端靠在光滑墙上,杆在图示位置保持平衡,则杆在A端所受的摩擦力Fs为()。
A、Fs = 2kNB、Fs = 1.8kNC、D、Fs=1.5kN收藏该题10、作用在一个刚体上的两力,满足的条件,则该二力可能是()A、作用力和反作用力或一对平衡的力;B、一对平衡的力或一个力偶;C、一对平衡的力或一个力或一个力偶;D、作用力和反作用力或一个力偶。
重庆大学2021年秋季学期课程作业《工程力学(二)》
一、判断题(共20题、共40分)1.使用单位荷载法计算计算位移时,是适用了虚力原理。
正确错误2.两端同支等截面直杆的转角位移方程表达的是三个独立的杆端位移和三个杆端力之间的函数变换关系。
正确错误3.力法基本方程实质是静力平衡方程。
正确错误4.频率方程,为关于w的一元n次方程(n为体系的动力自由度)。
正确错误5.图示体系中的I、II两部分为较结三角形。
正确荷载作用下的梁和刚架中,位移的主要贡献是弯曲变形,通常剪切变形和轴向变形可以忽略不i+o正确错误7.平面一般力系的平衡方程一定可以求解出三个未知量。
正确错误8.两个弯矩图都是非直线图形时,图形相乘法无法直接适用。
正确错误9.图示两弯矩图(对应日为常数),图乘结果为。
正确错误10.力法基本方程中,主系数可能等于零。
正确钱结点可以承受和传递所有类型的内力。
正确错误12.构件抗侧刚度系数越大,其承受的剪力值也就相对越大。
正确错误13.虚位移原理等价于体系的真实平衡条件。
正确错误14.刚体或刚片也可以写作钢体或钢片,是指用钢材制成的物体。
正确错误15.若已知体系运动的初速度(初位移为零),质点的运动规则应表达为正弦函数。
正确错误16.几何瞬变体系不能用作结构的原因是,这类体系在有限的外力作用下可能产生极大的内力。
错误17.钢筋混凝土现浇结点在计算简图中一定都简化成刚结点。
正确错误18.虚功互等定理表明:一个线弹性结构,第一状态的外力在第二状态的位移上所做的外力虚功(W12),等于第二状态的外力在第一状态的位移上所做的外力虚功(W21)。
正确错误19.若解耦成功,在每一广义自由度上,体系作单频振动。
正确错误20.位移计算公式5.4.1-1只适用于小变形状态。
正确错误二、单项选择题(共20题、共60分)1.下列关于三钱拱或相当简支梁说法中,正确的是()。
A、任意荷载作用下,三钱拱的弯矩都等于相当简支梁对应截面弯矩减去水平反力与该截面高之三钱拱与相当简支梁相比,具有弯矩和剪力减小,而轴力增大的特点c、三钱拱的内力与相当简支梁的轴力相关D、三较拱的水平推力与其自身(或相当简支梁)的跨度成反比2.国家大剧院(北京)属于()结构。
大学《工程力学》课后习题解答
1-1试画出以下各题中圆柱或圆盘的受力图,与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
解:(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程力学课后解答5.9 题图5.9所示中段开槽的杆件,两端受轴向载荷P 的作用,试计算截面1-1和2-2上的应力。
已知:P = 140kN ,b = 200mm ,b 0 = 100mm ,t = 4mm 。
题图5.9解:(1) 计算杆的轴力 kN 14021===P N N (2) 计算横截面的面积21m m 8004200=⨯=⨯=t b A202mm 4004)100200()(=⨯-=⨯-=t b b A (3) 计算正应力MPa 1758001000140111=⨯==A N σ MPa 3504001000140222=⨯==A N σ (注:本题的目的是说明在一段轴力相同的杆件内,横截面面积小的截面为该段的危险截面)5.10 横截面面积A=2cm 2的杆受轴向拉伸,力P=10kN ,求其法线与轴向成30°的及45°斜截面上的应力ασ及ατ,并问m ax τ发生在哪一个截面? 解:(1) 计算杆的轴力kN 10==P N(2) 计算横截面上的正应力MPa 501002100010=⨯⨯==A N σ(3) 计算斜截面上的应力MPa5.37235030cos 22 30=⎪⎪⎭⎫⎝⎛⨯==οοσσMPa6.2123250)302sin(230=⨯=⨯=οοστMPa25225045cos2245=⎪⎪⎭⎫⎝⎛⨯==οοσσMPa251250)452sin(245=⨯=⨯=οοστ(4)m axτ发生的截面∵0)2cos(==ασαταdd取得极值∴0)2cos(=α因此:22πα=,ο454==πα故:m axτ发生在其法线与轴向成45°的截面上。
(注:本题的结果告诉我们,如果拉压杆处横截面的正应力,就可以计算该处任意方向截面的正应力和剪应力。
对于拉压杆而言,最大剪应力发生在其法线与轴向成45°的截面上,最大正应力发生在横截面上,横截面上剪应力为零)5.17 题图2.17所示阶梯直杆AC,P=10kN,l1=l2=400mm,A1=2A2=100mm2,E=200GPa。
试计算杆AC的轴向变形Δl。
题图5.17解:(1) 计算直杆各段的轴力及画轴力图kN101==PN(拉)kN102-=-=PN(压)(2) 计算直杆各段的轴向变形mm 2.010010002004001000101111=⨯⨯⨯⨯==∆EA l N l (伸长) mm 4.05010002004001000102222-=⨯⨯⨯⨯-==∆EA l N l (缩短) (3) 直杆AC 的轴向变形m m 2.021-=∆+∆=∆l l l (缩短)(注:本题的结果告诉我们,直杆总的轴向变形等于各段轴向变形的代数和)5.20 题图5.20所示结构,各杆抗拉(压)刚度EA 相同,试求节点A 的水平和垂直位移。
( a) (b)题图5.20(a) 解:(1) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,P N =2( 拉 ) 0=∑Y ,01=N(2) 计算各杆的变形01=∆lEAPl EA Pl EA l N l 245cos /222===∆ο(3) 计算A 点位移以切线代弧线,A 点的位移为:EA Pll x A 245cos 2=∆=∆ο0=∆A y(b) 解:(1) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,P N 21= ( 拉 )0=∑Y ,P N-=2( 压 )(2) 计算各杆的变形EAPaEA a P EAl N l 222111=⨯==∆ ( 伸长 )EAPa EA a P EA l N l =⨯==∆222 ( 缩短 )(3) 计算A 点位移以切线代弧线,A 点的位移为:EA PaEA Pa EA Pa l l A C AB x A )122(2245cos 21+=+=∆+∆='+=∆οEAPal y A -=∆-=∆2 [注:①本题计算是基于小变形假设(材料力学的理论和方法都是基于这个假设),在此假设下,所有杆件的力和变形都是沿未变形的方向。
②计算位移的关键是以切线代弧线。
)5.15 如题图5.15所示桁架,α =30°,在A 点受载荷P = 350kN ,杆AB 由两根槽钢构成,杆AC 由一根工字钢构成,设钢的许用拉应力MPa 160][=t σ,许用压应力MPa 100][=c σ。
试为两根杆选择型钢号码。
题图5.15解:(1) 计算杆的轴力以A点为研究对象,如上图所示,由平衡方程可得=∑X,0coscos12=-ααNN=∑Y,0sinsin21=-+PNNαα∴kN3501==PN (拉)kN35012==NN (压)(2) 计算横截面的面积根据强度条件:][maxσσ≤=AN,有211mm5.21871601000350][2=⨯=≥tNAσ,21m m75.1093≥A222mm35001001000350][=⨯=≥cNAσ(3) 选择型钢通过查表,杆AB为No.10槽钢,杆BC为No.20a工字钢。
(注:本题说明,对于某些材料,也许它的拉、压许用应力是不同的,需要根据杆的拉、压状态,使用相应得许用应力)5.25 题图5.25所示结构,AB为刚体,载荷P可在其上任意移动。
试求使CD杆重量最轻时,夹角α应取何值?题图5.25解:(1) 计算杆的轴力载荷P 在B 点时为最危险工况,如下图所示。
以刚性杆AB 为研究对象0=∑AM, 02sin =⋅-⋅l P l N CD ααsin 2PN CD =(2) 计算杆CD 横截面的面积设杆CD 的许用应力为][σ,由强度条件,有ασσσsin ][2][][PN N A CD ===(3) 计算夹角α设杆CD 的密度为ρ,则它的重量为ασραασραρρρ2cos ][cos sin ][2cos PlPl l A CD A V W ==⋅=⋅== 从上式可知,当ο45=α时,杆CD 的重量W 最小。
(注:本题需要注意的是:①载荷P 在AB 上可以任意移动,取最危险的工作状况(工况);② 杆的重量最轻,即体积最小。
)5.34 题图5.34所示结构,AB 为刚性梁,1杆横截面面积A 1=1cm 2,2杆A 2=2cm 2,a=1m ,两杆的长度相同,E =200GPa ,许用应力[σt ]=160MPa ,[σb ]=100MPa ,试确定许可载荷[P ]。
题图5.34解:(1) 计算杆的轴力以刚性杆AB 为研究对象,如下图所示。
0=∑AM, 03221=⋅-⋅+⋅a P a N a N即:P N N 3221=+ (1) 该问题为一次静不定,需要补充一个方程。
(2) 变形协调条件如上图所示,变形协调关系为2Δl 1 =Δl 2 (2)(3) 计算杆的变形 由胡克定理,有 111EA a N l =∆; 222EA aN l =∆ 代入式(2)得:22112EA a N EA a N = 即:22112A N A N = (3) (4) 计算载荷与内力之间关系由式(1)和(3),解得: 112134N A A A P += (4) 或 222164N A A A P +=(5) (5) 计算许可载荷如果由许用压应力[σb ]决定许可载荷,有:])[4(31][34][34][2111211121b b b A A A A A A N A A A P σσ+=⋅+=+=)(30)(30000100)2004100(31kN N ==⨯⨯+= 如果由许用拉应力[σt ]决定许可载荷,有:])[4(61][64][64][2122212221t t t A A A A A A N A A A P σσ+=⋅+=+=)(24)(24000160)2004100(61kN N ==⨯⨯+=比较两个许可载荷,取较小的值,即{})(24][,][m in ][kN P P P t b == (注:本题需要比较由杆1和杆2决定的许可载荷,取较小的一个值,即整个结构中,最薄弱的部位决定整个结构的许可载荷。
)5.42 题图5.42所示正方形结构,四周边用铝杆(E a =70GPa ,αa =21.6×10-6 ℃-1);对角线是钢丝(E s =70GPa ,αs =21.6×10-6 ℃-1),铝杆和钢丝的横截面面积之比为2:1。
若温度升高ΔT=45℃时,试求钢丝内的应力。
题图5.42解:(1) 利用对称条件对结构进行简化 由于结构具有横向和纵向对称性,取原结构的1/4作为研究的结构如下图所示,(2) 计算各杆的轴力以A 点为研究对象,如右图所示,由平衡方程可得0=∑X ,045cos =-a sN Nο即: a s N N 2= ①(3) 变形协调关系如上图所示,铝杆与钢丝的变形协调关系为: a s l l ∆=∆2 ② 钢丝的伸长量为:(设钢丝的截面积为A ) )(22AE l N l T A E l N l T l s s s s s s s s s s +∆=+∆=∆αα ③ 铝杆的伸长量为: )2(41AE l N l T A E l N l T l a a a a a a a a a a -∆=-∆=∆αα ④ 由①②③④式,可解得: A T E E E E N s a sa s a s ⋅∆-+=)(2222αα(4) 计算钢丝的应力 T E E E E A N s a sa sa s ∆-+==)(2222αασ )(3.4445)107.11106.21(1020010702210200107022663333MPa =⨯⨯-⨯⨯+⨯⨯⨯⨯⨯⨯=-- 3.8题图6.8所示夹剪,销钉B 的直径d=5mm,销钉与被剪钢丝的材料相同,剪切极限应力u τ=200Mpa ,销钉的安全系数n=4,试求在C 处能剪断多大直径的钢丝。
解:设B,C 两点受力分别为1F , 2F 。
剪切许用应力为:[]unττ==50Mpa 对B 点,有力矩和为零可知:B M ∑=0,即:1F =4P 由力平衡知:1F +P=2F∴2F =541F 其中:2F =[]τ⋅A=12.52d π 故: 1F =102d π 又由强度要求可知:uτ≤11F A 即: d ≤114uF πτ56.11车床的转动光杆装有安全联轴器,当超过一定载荷时,安全销即被剪断。
已知安全销的平均直径为5mm ,其剪切强度极限b τ=370Mpa ,求安全联轴器所能.传递的力偶矩m.解:设安全销承受的最大力为,则:F = b τ ⨯214d π 那么安全联轴器所能传递的力偶矩为:m = F ⋅D 其中b τ=370Mpa ,b=5mm ,D=20mm , 代入数据得:力偶矩 m=145.2N m ⋅7.7求题图7.7中各个图形对形心轴z 的惯性矩z I 。
