《材料力学》课件2-4拉(压杆的变形.胡克定律.
合集下载
西南交大 材料力学 龚晖 拉压变形
分段累加
100kN
75kN 50kN
A
BC
D
1.75m 1.25m 1.50m
75kN
100kN (1)
50kN
(2)
(3)
lAC lAC1 lAC2 lAC3 lAB1 lAC2 lAC3
=
(-100)×103 ×1.75×103 70×103×800
75×103 ×3.0×103 + 70×103×800
l 1 FN l EA
E
称为单轴应力状态下的胡克定律
例 求各段的线应变。
100kN
A
B
75kN 50kN
C
D
1.75m 1.25m 1.50m
解:lAB 0.78mm
lBC 2.79mm
lCD 2.14mm
AB
l AB lAB
0.78 1.75103
5.2104
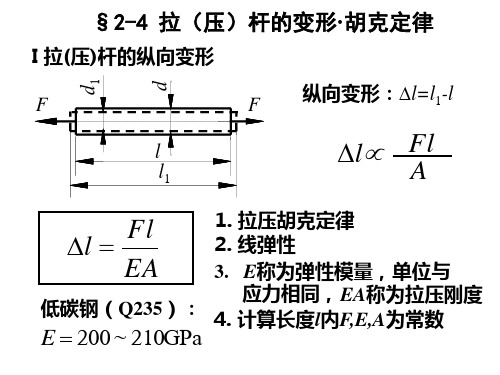
§2-4 拉(压)杆的变形·胡克定律
I 拉(压)杆的纵向变形
d1 d
F
F
纵向变形:l=l1-l
l l1
l
Fl A
l Fl
1. 拉压胡克定律 2. 线弹性
EA
3. E称为弹性模量,单位与
低碳钢(Q235):
4.
应力相同, EA称为拉压刚度 计算长度l内F,E,A为常数
E 200 ~ 210GPa
-ν
520106
520με
II 拉(压)杆的横向变形
d1 d
F
F
l l1
绝对变形 d d1 - d
相对变形
ν
' d
材料力学之四大基本变形 ppt课件

1.轴力:拉正压负。轴力图
2.横截面上的应力: N 或 = FN
A
A
3.变形公式:l Nl 或l FNl
EA
EA
4.强度条件: max [ ]
5.材料的力学性能: ~ 曲线
两个强度指标,两个塑性指标
ppt课件
3
例1-1 图示为一悬臂吊车, BC为
C
实心圆管,横截面积A1 = 100mm2, AB为矩形截面,横截面积 A2 = 200mm2,假设起吊物重为 Q = 10KN,求各杆的应力。
内径d=15mm,承受轴向载荷F=20kN作用, 材料的屈服应力σs=235MPa,安全因数ns= 1.5。试校核杆的强度。
ppt课件
8
解:杆件横截面上的正应力为
N
A
(
4F D2
d
2
)
4(20103 N )
[(0.020m)2 (0.015m)2]
1.45108 Pa 145MPa
76.4Nm
mB
9550 NB n
9550 10 500
191Nm
mC
9550 NC n
9550 6 500
114.6 Nm
计算扭矩:
mA
x
T1
MX 0
MX 0
T1 mA 0
mc T2
AB段 BC段
T1设为正的 T2设为正的
T1 mA 76.4Nm
86.6 MPa
ppt课件
5
例1-2:图示杆,1段为直径 d1=20mm的圆 杆,2段为边长a=25mm的方杆,3段为直径 d3=12mm的圆杆。已知2段杆内的应力σ 2=30MPa,E=210GPa,求整个杆的伸长△l
《材料力学》课件2-4拉(压)杆的变形.胡克定律

拉(压)杆的综合变形
综合变形
杆件在受到拉力或压力作用时,不仅会发生轴向变形和横向变形,还可能发生弯曲变形 等其他形式的变形。
胡克定律的应用
胡克定律只适用于描述杆件的轴向变形,对于其他形式的变形,需要使用更复杂的力学 公式来描述。
Part
02
胡克定律
胡克定律的表述
总结词
胡克定律是材料力学中一个重要的基本定律,它表述了材料 在拉伸或压缩过程中所遵循的应力和应变之间的关系。
胡克定律的局限性
总结词
胡克定律的应用有一定的局限性,它仅适用于线弹性材料,且只考虑了单向受力的情况。
详细描述
胡克定律的应用范围仅限于线弹性材料,对于非线性材料或塑性材料,胡克定律不再适用。此外,胡克定律只考 虑了单向拉伸或压缩受力的情况,对于剪切、弯曲等复杂受力情况,需要引入更复杂的力学模型进行分析。
详细描述
胡克定律指出,在弹性范围内,材料所受的应力与产生的应变 之间成正比,即应力与应变之比为常数,这个常数称为材料的 弹性模量或杨氏模量,用符号E表示。数学表达式为:σ=E*ε, 其中σ为应力,ε为应变。
胡克定律的应用
总结词
胡克定律在工程实践中广泛应用于材料的强度分析、结构设计等方面。
详细描述
通过胡克定律,可以计算出材料在受到拉伸或压缩力时的应力和应变,从而评估 材料的承载能力和安全性。在结构设计时,可以利用胡克定律进行受力分析和优 化设计,以确保结构的稳定性和可靠性。
详细描述
均匀性假设意味着材料在各个部分都 具有相同的性质,如密度、弹性模量 等。这一假设使得我们能够将材料的 性质视为空间位置的常数,从而简化 分析过程。
各向同性假设
总结词
各向同性假设认为材料在各个方向上都 具有相同的性质。
材料力学(全套483页PPT课件)-精选全文

三、构件应有足够的稳定性
稳定性(stability)—构件承受外力时, 保持原有平衡状态的能力
4
材料力学的任务: 在满足强度、刚度和稳定性的要
求下,为设计既经济又安全的构件提 供必要的理论基础和计算方法。
5
1.2 变形固体的基本假设
1.连续性假设
假设在变形体所占有的空间内毫无空隙地充满了物质。即认 为材料是密实的。这样,构件内的一些力学量(如各点的位 移)可用坐标的连续函数表示,并可采用无限小的数学分析 方法。
2、横向变形、泊松比
横向线应变: b b1 b
bb
称为泊松比
32
是谁首先提出弹性定律? 弹性定律是材料力学中一个非常重要的基础定
律。一般认为它是由英国科学家胡克(1635一1703) 首先提出来的,所以通常叫做胡克定律。其实,在 胡克之前1500年,我国早就有了关于力和变形成正 比关系的记载。
1-1截面
A
X 0 N1 40 30 20 0 N1 N1 50kN(拉)
2-2截面
X 0 N 2 30 20 0
1 B 2C 3D 40 kN 30 kN 20 kN
N2
30 kN 20 kN
N2 10kN(拉)
3-3截面
N 50 kN
N3
20 kN
X 0
N 3 20 0 N 3 20 kN(压)
10 103 100 103 500 106
10 103 100 103 200 106
mm
0.015mm
计算结果为负,说明整根杆发生了缩短
35
静定汇交杆的位移计算,以例题说明。 例3 图示结构由两杆组成,两杆长度均为 l,B 点受垂直荷 载 P 作用。(1) 杆①为刚性杆,杆②刚度为 EA ,求节点 B 的位移;(2) 杆①、杆②刚度均为 EA,求节点 B 的位 移。
稳定性(stability)—构件承受外力时, 保持原有平衡状态的能力
4
材料力学的任务: 在满足强度、刚度和稳定性的要
求下,为设计既经济又安全的构件提 供必要的理论基础和计算方法。
5
1.2 变形固体的基本假设
1.连续性假设
假设在变形体所占有的空间内毫无空隙地充满了物质。即认 为材料是密实的。这样,构件内的一些力学量(如各点的位 移)可用坐标的连续函数表示,并可采用无限小的数学分析 方法。
2、横向变形、泊松比
横向线应变: b b1 b
bb
称为泊松比
32
是谁首先提出弹性定律? 弹性定律是材料力学中一个非常重要的基础定
律。一般认为它是由英国科学家胡克(1635一1703) 首先提出来的,所以通常叫做胡克定律。其实,在 胡克之前1500年,我国早就有了关于力和变形成正 比关系的记载。
1-1截面
A
X 0 N1 40 30 20 0 N1 N1 50kN(拉)
2-2截面
X 0 N 2 30 20 0
1 B 2C 3D 40 kN 30 kN 20 kN
N2
30 kN 20 kN
N2 10kN(拉)
3-3截面
N 50 kN
N3
20 kN
X 0
N 3 20 0 N 3 20 kN(压)
10 103 100 103 500 106
10 103 100 103 200 106
mm
0.015mm
计算结果为负,说明整根杆发生了缩短
35
静定汇交杆的位移计算,以例题说明。 例3 图示结构由两杆组成,两杆长度均为 l,B 点受垂直荷 载 P 作用。(1) 杆①为刚性杆,杆②刚度为 EA ,求节点 B 的位移;(2) 杆①、杆②刚度均为 EA,求节点 B 的位 移。
材料力学2-4

300
A A2 l 2 P
C
2
ቤተ መጻሕፍቲ ባይዱl 1
A1
A2 A A2 A3 0 tg 30 l 2 l 1 0 tg 30 sin 300
2 2 AA3 ( AA2) ( A2 A3)
A2
A
A’
l 2
l1
300
A1
300
3.78mm
A3
补充题 : 一等直杆受自重及集中力P作用。杆的长度为l,横
截面面积为A,材料的容重为,弹性模量为E,许用应力 为[]。试分析杆的自重对强度的影响,并求杆的伸长。 解: N(x)=P+ Ax Nmax=P+ Al
m m
N(x)
P+ Al
l
m Ax m
+
x
P
P P
P+ Ax
Nmax=P+ Al
N(x)
强度条件为
m
m
l
m Ax m
+
x
P γ l [σ ] A
(1) 1—1,11—11,111—111截面的轴力,作轴力图 (2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
111
11
1
P3 C
111
P2
11
P1 A
1
D
B
l3
111
l2
11
l1
1
R
P3 C
111
P2
11
P1 A
1
D
B
l3
l2
l1
解:求支座反力
R = -50KN
111
11
1
A A2 l 2 P
C
2
ቤተ መጻሕፍቲ ባይዱl 1
A1
A2 A A2 A3 0 tg 30 l 2 l 1 0 tg 30 sin 300
2 2 AA3 ( AA2) ( A2 A3)
A2
A
A’
l 2
l1
300
A1
300
3.78mm
A3
补充题 : 一等直杆受自重及集中力P作用。杆的长度为l,横
截面面积为A,材料的容重为,弹性模量为E,许用应力 为[]。试分析杆的自重对强度的影响,并求杆的伸长。 解: N(x)=P+ Ax Nmax=P+ Al
m m
N(x)
P+ Al
l
m Ax m
+
x
P
P P
P+ Ax
Nmax=P+ Al
N(x)
强度条件为
m
m
l
m Ax m
+
x
P γ l [σ ] A
(1) 1—1,11—11,111—111截面的轴力,作轴力图 (2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
111
11
1
P3 C
111
P2
11
P1 A
1
D
B
l3
111
l2
11
l1
1
R
P3 C
111
P2
11
P1 A
1
D
B
l3
l2
l1
解:求支座反力
R = -50KN
111
11
1
材料力学第2章 PPT课件

NAB
P
4
BC
N BC ABC
26 103 142 106
133106 N
/ m2
133MPa
30
NBC
B
P
2.5 拉(压)杆斜截面上的应力
沿斜截面kk(如图), p
k
p
将杆截分为二。
(a)
k
研究左段杆的平衡, p k
得到斜截面kk上内力 (b)
p
k
P P
(a)
量时才能应用。
对于阶梯杆或轴力分段变化的杆件:
l
N i li EAi
(2-9)
当轴力 N x和横截面积 A x沿杆轴线x方
向连续变化时,有
l
l
N (x)dx EA( x)
(2-10)
二、横向变形 泊松比
设杆件变形前的横向尺寸为b,变形后为b1, 则杆的横向线应变为
p
p b1 b
圣维南原理 —— 虽然力作用于杆端的 方式不同,只要它们是静力等效的,则杆件 中应力分布仅在作用点附近不大的范围内(不 大于杆的横向尺寸)有明显影响。
P
P
应力等效
P/2
PP//2AP
PP//A2
P/2
例2-2 图所示铰接支架,AB为圆截面杆,
直径为d=16mm,BC为正方形截面杆,边长为
a=14mm。若载荷P=15kN,试计算各杆横截面
p
p
sin
0
2
sin 2
(2-5) (2-6)
2.当 90o时(纵截面) 90 90 0
即与轴线平行的纵截面上的正应力为0。
材料力学课件

例 一阶梯形立柱受力如图a所示,F1=120kN,F2= 60kN,柱的上、中、下三段的横截面面积分别为A1 =2×104 mm2,A2=2.4×104 mm2, A3= 4×104 mm2。 试求立柱的最大工作正应力(不计自重)。 解 作立柱的轴力图如图b 所示,分三段计算工作 正应力
〖颈撑弦张,柱哑弦吟〗小提琴和竖琴
1. 弦振动梅逊定律
1 F f 2L m
式中,f ——弦振动频率(1/s) L ——弦的长度(m) F ——弦受到的拉力(N) m——单位长度弦的质量(kg/m) 2. 弦、索等构件只能承受拉力。
〖观察思考〗 图示各杆件的BC 段是否轴向拉伸(压缩)?
F5=F
F1=4F F2=5.5F F3=2.5F
F4= 2F
A
B
C
D
E
〖远距相吸,近距相斥〗内力概念
有诗曰:
轴向拉压杆变形Байду номын сангаас固体粒子引斥生;
微观平均宏观力,截面一侧取平衡。
固体受外力作用而变形时,其内部相邻粒子 间的距离将发生变化。内力则是相邻粒子抵抗这 种变化的相互作用力:引力抵抗距离增大;斥力 抵抗距离减小。
B点处沿s方向的平均线应变
d s em s d s dd s e lim s 0 s ds
B点处沿s方向的线应变
s B
s
s
ds
s
B
二、横截面上的正应力及其分布 〖合纵连横、一统“应立”〗横截面上的正应力 有诗曰: 横平截面纵线连,伸展收缩共长短。 应力分布保常量,连续均匀是关键。 已知:轴力FN和静力学条件 求解:横截面上正应力s 分析:须先确定横截面上分布内力的变化规律
F F
(压)杆的变形· 胡克定律 - 材料力学

内力。
第二章 轴向拉伸和压缩
Ⅱ. 截面法· 轴力及轴力图
步骤: (1)断开 (2)代替 (3)平衡
解得:轴力FN=F ,方向:拉为正,压为负。
第二章 轴向拉伸和压缩
思考题 静力学中力的可传递性原理,在用截面法求内力的 过程中是否可用?
轴力图:平行于杆轴线的坐标表示横截面的位置。 垂直于杆轴线的坐标表示横截面轴力的数值。
3
第二章 轴向拉伸和压缩
例题2-5 如图所示杆系,荷载 P = 100 kN,试求结点A 的位移ΔA。已知: = 30° ,l = 2 m,d = 25 mm,杆的材
料(钢)的弹性模量为E = 210 GPa。
第二章 轴向拉伸和压缩
解:结点A的位移ΔA系由两杆的伸长变形引起,故需先
求两杆的伸长。 1. 求杆的轴力及伸长 由结点 A 的平衡(如图)有
说,拉杆在其任意两个横截面之间的纵向线段的伸长是均
匀的。
第二章 轴向拉伸和压缩
FN s A
推论:横截面上各点处的正应力s 都相等
第二章 轴向拉伸和压缩
注意: 由于杆端连接方式的不同,等直杆在外力作用点附近, 横截面上的应力情况复杂。圣维南原理:“力作用于杆端方
式的不同,只会使与杆端距离不大于杆的横向尺寸的范围内
受到影响”。
第二章 轴向拉伸和压缩
例题2-2 试求此正
方形砖柱由于荷载引起
的横截面上的最大工作 应力。已知F = 50 kN。
第二章 轴向拉伸和压缩
解:Ⅰ段柱横截面上的正应力
FN1 50 103 N s1 A1 (0.24 m) (0.24 m) 0.87 106 P a 0.87 MP a (压应力)
化阶段中,Δl=Δle+Δlp。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B b e
A
a
c
d
ae. 因各条纵向纤维的应变相等,所以上边纤维长,伸长量也大。
例:图示直杆,其抗拉刚度为 EA ,试 例题 求杆件的轴向变形△L,B点的位移 2.10 δB和C点的位移δC
F A
F
B LAB
C
FL EA
B
L
L
FL C B EA
例题
2.11
图示结构,横梁AB是刚性杆,吊杆CD是等截面直杆, B点受荷载P作用,试在下面两种情况下分别计算B点的位 移δB。1、已经测出CD杆的轴向应变ε;2、已知CD杆 的抗拉刚度EA. 1. 已知ε D
F
LAC
A
FL LAC A AA 2 EA cos 2 cos 1.3mm 100 103 2
LAB
2 2.1105 106
4
252 10 6 cos 300
A
图所示结构,刚性横梁AB由斜杆CD吊在水 例题 平位置上,斜杆CD的抗拉刚度为EA,B点 2.13 处受荷载F作用,试求B点的位移δB。
α
A
C
D F B B1 a
BB1 B 2CC1
C LC CD CC1 cos cos
C
FNCD
C1
L/2 L/2
4 Fa B EA cos 3
2F FNCD mA 0 cos 1 F LF L cos FCD NCD LCD LCD 2 EA 2 F a EA cos 2
FNCD
LCD a
LCD a
B 2LCD 2a
刚杆
A
L 2
C C1
F
B
a
2. 已知EA
LCD
FNCD a EA
m
A
0
FNCD 2 F
L 2
B1
B
L 4 Fa F 2LCD FL 0 NCD 2 EA
例题
2.12
图示的杆系是由两根圆截面钢杆铰接而成。已知 α=300,杆长L=2m,杆的直径d=25mm,材 料的弹性模量E=2.1×105MPa,设在结点A处悬 挂一重物F=100kN,试求结点A的位移δA。
EA L L
FNi Li L i EAi 在计算ΔL的L长度内,F ,E,A均 N
为常数。
FN EA L E A AL
在材料的线弹性范围内,正应力与线应变呈正比关系。
例题 2.9
图示为一端固定的橡胶板条,若在加力前在 板表面划条斜直线AB,那么加轴向拉力后 AB线所在位置是?(其中ab∥AB∥ce)
1 α α 2
ห้องสมุดไป่ตู้
B
FNAB FNAC
C
X 0 Y 0
FNAC sin FNAB sin F 0 FNAC FNAB 2 cos FNAC cos FNAB cos F 0
FNAC L FL EA 2 EA cos
LAB LAC
A
A
拉(压)杆的变形.胡克定律`
杆件在轴向拉压时:
沿轴线方向产生伸长或缩短——纵向变形
横向尺寸也相应地发生改变——横向变形
L L
实验表明:在材料的线弹性范围内,△L与外力F
和杆长L成正比,与横截面面积A成反比。
FN L L EA
胡克定律
EA :拉抗(压)刚度
当拉(压)杆有两个以上的外力作用时,需要先画出轴力图,然后 分段计算各段的变形,各段变形的代数和即为杆的总伸长量。
