最新人教版高中数学必修5第一章应用举例
高中数学新人教B版必修5课件:第一章解三角形1.2应用举例

面内),求两目标A,B之间的距离.
分析:要求出A,B之间的距离,可在△ABC(或△ADB)中去找关系,
但不管在哪个三角形中,AC,BC这些量都是未知的,需要在三角形中
找出合适的关系式,求出它们的值,然后解斜三角形即可.
Z 知识梳理 Z 重难聚焦
目标导航
题型一
题型二
题型三
题型四
HISHISHULI
HONGNANJUJIAO
,
,
∴a=CD=BC-BD=tan ∠ − tan ∠ .
目标导航
Z 知识梳理 Z 重难聚焦
HISHISHULI
D典例透析 S随堂演练
HONGNANJUJIAO
IANLITOUXI
UITANGLIANXI
∴a=CD=BC-BD=tan ∠ − tan ∠ .
∵AC=BC,
∴∠A=∠ABC=
180°-80°
2
=50°.
∴∠ABG=180°-∠CBH-∠CBA=180°-120°-50°=10°.故选B.
答案:B
Z 知识梳理 Z 重难聚焦
目标导航
HISHISHULI
HONGNANJUJIAO
2.三角形中的有关公式和结论
(1)直角三角形中各元素间的关系.
在△ABC中,若∠C=90°,AB=c,AC=b,BC=a,则有:
HISHISHULI
D典例透析 S随堂演练
HONGNANJUJIAO
IANLITOUXI
UITANGLIANXI
(2)斜三角形中各元素间的关系.
在△ABC中,若∠A,∠B,∠C为其内角,a,b,c分别表示∠A, ∠B,
最新人教版高中数学必修5第一章《应用举例(二)》自我检测
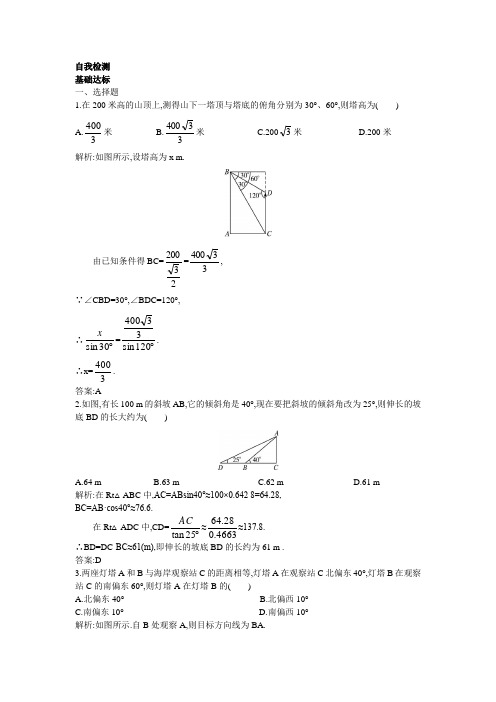
自我检测 基础达标 一、选择题1.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( ) A.3400米 B.33400米 C.2003米 D.200米 解析:如图所示,设塔高为x m.由已知条件得BC=23200=33400,∵∠CBD=30°,∠BDC=120°,∴︒30sin x =︒120sin 33400. ∴x=3400. 答案:A2.如图,有长100 m 的斜坡AB,它的倾斜角是40°,现在要把斜坡的倾斜角改为25°,则伸长的坡底BD 的长大约为( )A.64 mB.63 mC.62 mD.61 m 解析:在Rt △ABC 中,AC=ABsin40°≈100×0.642 8=64.28, BC=AB·cos40°≈76.6. 在Rt △ADC 中,CD=︒25tan AC ≈4663.028.64≈137.8.∴BD=DC-BC≈61(m),即伸长的坡底BD 的长约为61 m . 答案:D3.两座灯塔A 和B 与海岸观察站C 的距离相等,灯塔A 在观察站C 北偏东40°,灯塔B 在观察站C 的南偏东60°,则灯塔A 在灯塔B 的( ) A.北偏东40° B.北偏西10° C.南偏东10° D.南偏西10° 解析:如图所示.自B 处观察A,则目标方向线为BA.由已知可得A 在灯塔B 的北偏西10°. 答案:B4.如图,在山脚A 处测得山顶S 的仰角为45°,沿倾斜角为15°的斜坡向上走100米到B,又测得S 的仰角为75°,则山高为__________________米.( )A.50B.502C.503D.506 解析:在△ABS 中,由条件得∠BAS=30°,∠SBA=120°. 由正弦定理得︒120sin SA =︒30sin 100,∴SA=1003.在Rt △ADS 中,SD=sin45°×SA=22×1003=506. 答案:D5.某人先向正东方向走了x km,然后他向右转150°,向新的方向走了3 km,结果他离出发点恰好为3 km,那么x 的值为( )A.3B.23C.23或3D.3 解析:画出示意图后,由余弦定理有(3)2=x 2+32-2·x·3·cos30°, 解得x=23或x=3.答案:C6.在一座20 m 高的观测台顶测得对面一水塔塔顶的仰角为60°,塔底的俯角为45°,那么这座水塔的高是( ) A.20(1+33) m B.20(1+3) m C.10(6+2) m D.20(6+2) m 解析:h=20+20·tan60°=20(1+3).答案:B7.一船自西向东航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船航行的速度为________________海里/时.( ) A.2617 B.346 C.2217 D.342 解析:如图所示,由题意知∠APM=75°,∠APN=45°,∠ANP=45°,在△MPN 中,︒45sin 68=)4575sin(︒+︒MN ,∴MN=346(海里),这只船航行的速度为4634=2617(海里/时). 答案:A8.如图,B 、C 、D 三点在地面同一直线上,DC=a,从C 、D 两点测得A 点的仰角分别为β、α(α<β),则A 点离地面的高AB 等于()A.)sin(sin sin αββα-a B.)cos(sin sin αββα-aC.)sin(cos sin αββα-a D.)cos(cos cos αββα-a解析:tanα=BC a AB +,tanβ=BCAB,联立两式解得AB=αββαtan tan tan tan -a=ααβββαβαcos sin cos sin cos cos sin sin -a -αβαββαsin cos cos sin sin sin -a =)sin(sin sin αββα-a . 答案:A 二、填空题9.有一长为1 km 的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要加长______km..解析:如图,AC=ABsin20°=sin20°,BC=AB·cos20°=cos20°,DC=︒10tan AC=2cos 210°.∴DB=DC-BC=1. 答案:110.外国船只除特许外,不得进入离我国海岸线d 海里以内的区域,如图所示,设A 及B 是我们的观测站,A 与B 之间的距离为s 海里,海岸线是过A 、B 的直线,一外国船只在P 点,在A 站测得∠BAP=α,同时在B 站测得∠ABP=β,则α与β满足的三角不等式为_____________时,就应当向此未经特许的外国船只发出警告,命令其退出我国海域.解析:在△ABC 中,)sin(βαπ--s =βsin AP .AP=)sin(sin βαβ+∙s .在Rt △APM 中,h=sinα·AP=sinα·)sin(sin βαβ+∙s =)sin(sin sin βαβα+∙s . 答案:d≥)sin(sin sin βαβα+∙s三、解答题11.一舰艇在海上巡逻,沿岸自西向东航行,在A 处见岸边一灯塔C 在船的北偏东60°,一小时后在B 处见灯塔在船的北偏东30°.若舰艇每小时航行30海里.当舰艇至D 点处,可见灯塔在船的西北方向,求舰艇从A 到D 的航行距离.解法一:在△ABC 中, ∠CAB=30°,∠ABC=90°+30°=120°, ∴∠ACB=180°-120°-30°=30°. ∵AB=30×1=30,∴BC=AB=30. 在△BDC 中,∠CBD=90°-30°=60°, ∴∠BCD=180°-60°-45°=75°. 由正弦定理有︒45sin BC =︒75sin BD.∴BD=2sin75°·BC=302·sin75°≈40.98. ∴AD=AB+DB=30+40.98=70.98(海里). 解法二:在△ACD 中,易知AC=303,∠ACD=180°-30°-45°=105°, 由正弦定理,得︒105sin AD =︒45sin AC,∴AD=2×303sin105° =306sin105°≈70.98(海里).答:A 、D 两地相距约70.98海里.12.如图,在一个山坡上的一点A,测得山顶上一个微波塔顶端C 对于山坡的坡度的斜度为20°,向山顶前进80米后的B 点,又测得斜度为40°,设塔高为60米,求此山对于地面的倾角θ的余弦值.解:在△ABC 中,∠BAC=20°,∠ABC=180°-40°=140°,AB=80, ∴∠ACB=20°. 由正弦定理,得︒20sin 80=︒20sin BC,∴BC=80.在△BDC 中,∠BDC=90°+θ,∠DBC=40°, ∴由正弦定理,得︒40sin 60=)90sin(80θ+︒.∴cosθ=68sin40°≈0.857.答:此山对于地面的倾角θ的余弦值约为0.857.更上一层1.在海岸A 处,发现北偏东45°方向,距A 为(3-1)海里的B 处有一艘走私船,在A 处北偏西75°方向,距A 为2海里的C 处的缉私船奉命以103海里/时的速度追截走私船,此时走私船正以10海里/时的速度从B 处向北偏东30°方向逃窜,问缉私船沿什么方向可最快追上走私船?并求出所需要的时间.解:如图所示,设缉私船追上走私船的时间为t h,则有CD=103t,BD=10t,在△ABC 中,∵AB=3-1,AC=2,∠BAC=45°+75°=120°.∴BC=︒-∙∙-+-120cos )13(222)13(22=6. 根据正弦定理可得sin ∠ABC=BC AC ︒∙120sin =22.∴∠ABC=45°,而∠CBD=90°+30°=120°. 又sin ∠BCD=CD CBD BD ∠∙sin =21.∴∠BCD=30°,∠BDC=30°. ∴BD=BC=6,则有10t=6,t=106=0.245(h)=14.7(min). ∴缉私船沿北偏东60°方向,需14.7 min 能追上走私船.2.在一大河边上高a m 处的A 点,测得对岸一铁塔顶点M 的仰角为θ,而在河中铁塔倒影的俯角为φ,求铁塔的高度.解:如图所示,设直线A′M′在河面上,点N 是塔顶点M 在水中的倒影,M′是MN 与A′M′的交点,由于塔顶点M 与它在河中的倒影关于河面对称,故MN ⊥A′M′,且MM′=M′N. 由点A 向MN 作垂线,设垂足为B,且设AB=x, 则由题设条件知∠MAB=θ,∠BAN=φ. 于是在Rt △ABM 中,MB=xtanθ, 由于A′A=a,且MM′=M′N,∴由BN-MB=2a,可得xtanφ-xtanθ=2a. ∴x=θϕαtan tan 2-.∴MB=xtanθ=θϕθαtan tan tan 2-.∴BN=xtanφ=θϕϕαtan tan tan 2-.∴塔高M′M=2BNMB + =)sin()sin(θϕϕθ-+a .。
高中数学新人教A版必修5课件:第一章解三角形1.2应用举例第二课时正、余弦定理在三角形中的应用

3 ,则∠BDC= π 或 2π .
62
33
3
又由 DA=DC,则 A= π 或 π . 63
(2)若△BCD的面积为 1 ,求边AB的长.
6
解:(2)由于 B= π ,BC=1,△BCD 的面积为 1 ,
4
6
则 1 BC·BD·sin π = 1 ,解得 BD= 2 .
2
46
3
由余弦定理得 CD2=BC2+BD2-2BC·BD·cos π =1+ 2 -2× 2 × 2 = 5 ,故 CD= 5 .
2
2
2
关系,又由正弦值还可求出余弦值,这就可以与余弦定理建立关系,另外面积公式中有两边
的乘积,在余弦定理中也有,所以面积公式、正弦定理和余弦定理之间可以相互变换,关键是
根据题中的条件选择正确的变换方向.
即时训练 1-1:在△ABC 中,已知 AB=2,AC=2 2 ,cos B= 1 . 3
(1)求sin C的值;
3
3
3
所以 sin(B+C)= 2 10 + 2 , 99
所以 sin A= 2 10 + 2 , 99
因为 AB=2,AC=2 2 ,
因为 S= 1 AB·AC·sin A,所以 S= 8 5 4 2 .
2
9
题型二 平面图形中线段长度的计算
【例2】 如图,在平面四边形ABCD中,AD=1,CD=2,AC= 7 . (1)求cos∠CAD的值;
49
3 29
3
又 AB=AD+BD=CD+BD= 5 + 2 = 2 5 ,
33
3
故边 AB 的长为 2 5 . 3
高一数学人教A必修5课件:1.2 应用举例(一)

规律方法
解决实际测量问题的过程一般要充分认真理
解题意,正确做出图形,把实际问题里的条件和所求转 换成三角形中的已知和未知的边、角,通过建立数学模 型来求解.
跟踪演练1 如图,在相距2千米的A、B两点处 测量目标点C,若∠CAB=75°,∠CBA=60°, 则A、C两点之间的距离为________千米.
6
解析 由题意知C=180°-A-B=45°,
AC 2 2 3 由正弦定理得sin 60° =sin 45° ,∴AC= ·2 = 6. 2 2
要点二 测量两个不可到达点间的距离
例2 在某次军事演习中,红方为了准确分 析战场形势,在两个相距为
3a 的军事基 2 地C和D测得蓝方两支精锐部队分别在 A处
把求不可到达的两点 A, B之间的距离转化为应用余弦定 理求三角形的边长问题,然后在相关三角形中利用正弦定 理计算其他边.
跟踪演练 2
如下图, A 、 B 两点都在河的对岸 ( 不可到达 ) ,
若在河岸选取相距40米的C、D两点,测得∠BCA=60°, ∠ACD=30°,∠CDB=45°,∠BDA =60°,那么此时A、 B两点间的距离是多少?
在△ABC中,由余弦定理得
AB2=AC2+BC2-2AC· BC· cos 45°
32 32 3 6 2 32 = a + a -2× a× a× = a . 4 8 2 4 2 8
6 ∴AB= 4 a.
∴蓝方这两支精锐部队之间的距离为
6 a . 4
规律方法
测量两个不可到达的点之间的距离问题 . 首先
第一章——
1.2
应用举例(一)
[学习目标]
1.利用正、余弦定理解决生产实践中的有关距离的测量问题. 2.利用正、余弦定理解决生产实践中的有关高度的测量问题.
最新人教版高中数学必修5第一章《解三角形》

数学人教B 必修5第一章解三角形知识建构综合应用专题一判断三角形的形状正弦定理、余弦定理是反映三角形中边角关系的重要定理,是处理有关三角形问题的有力工具,要注意两定理的变形运用及实际应用.判断三角形的形状,其常用方法是:将已知式子都化为角的式子或边的式子再判断.通常利用正弦定理的变形如a =2R ·sin A 将边化角,b 2+c 2-a 2a 利用余弦定理的推论如cos A =把角的余弦化边,或利用sin A =把角的正弦化2bc 2R边,然后利用三角形的有关知识,三角恒等变形方法、代数恒等变形方法进行转化、化简,从而得出结论.常见结论有:设a ,b ,c 是△ABC 的角∠A ,∠B ,∠C 的对边,①若a 2+b 2=c 2,则∠C =90°;②若a 2+b 2>c 2,则∠C <90°;③若a 2+b 2<c 2,则∠C >90°;π④若sin 2A =sin 2B ,则∠A =∠B 或∠A +∠B =.2应用1在△ABC 中,若sin A ∶sin B ∶sin C =2∶3∶4,则该三角形是__________三角形.提示:考虑到已知条件是三个角正弦的比值,可用正弦定理得出三边的关系,再利用余弦定理判断最大角的大小即可.应用2在△ABC 中,若∠B =60°,2b =a +c ,试判断△ABC 的形状.提示:已知条件中等式只有边,故结合其特点,可选择利用正弦定理化边为角,再结合三角函数关系化简求解;本题也可利用∠B =60°这一条件,用余弦定理,找出边之间的关系来判断.专题二恒等式的证明证明有关三角形中边角关系的恒等式,若出现边角混合关系式,通常情况下,有两种方法:化边为角,将已知条件统一用角表示;化角为边,将已知条件用边表示,然后利用角的关系或边的关系进行求解,从而使问题得到解决.应用1在△ABC 中,求证:a 2+b 2sin 2A +sin 2B (1)2=;c sin 2C(2)a 2+b 2+c 2=2(bc cos A +ca cos B +ab cos C ).提示:本题(1)可从左边证到右边,利用正弦定理将边的关系转化为角的关系;本题(2)可从右边证到左边,利用余弦定理将角的关系转化为边的关系.应用2已知在△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,△ABC 的面积为S .a 2+b 2+c 2求证:cot A +cot B +cot C =.4S提示:解本题的关键是化切为弦,再结合余弦定理变形.专题三三角形的面积问题求三角形面积与正弦定理、余弦定理、三角函数、函数的有关知识紧密地联系在一起,是高考中的常见题型.常用三角形面积公式:111(1)S △ABC =ah a =bh b =ch c .222111(2)S △ABC =ab sin C =bc sin A =ac sin B .222a +b +c (3)S =p (p -a )(p -b )(p -c )(其中p =).2应用在△ABC 中,sin A +cos A =2,AC =2,AB =3,求tan A 的值和△ABC 的面积.2提示:由已知可把角A 算出来,再求tan A ,并求出sin A ,直接代入面积公式即可求面积.专题四正、余弦定理的综合应用以三角形为载体,以正、余弦定理为工具,以三角恒等变换为手段来考查解三角形问题是近几年高考中一类热点题型.在具体解题中,除了熟练使用正弦、余弦定理这个工具外,也要根据条件,合理选用三角函数公式,达到简化解题的目的.cos C 2a -c 应用1在△ABC 中,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,且=.cos B b(1)求cos B 的值;(2)若b =7,a +c =4,求△ABC 的面积.提示:(1)先利用正弦定理化简,再用三角变换整理即得.(2)利用余弦定理及面积公式,再注意整体求ac 的技巧.应用2在锐角△ABC 中,a ,b ,c 分别为角A ,B ,C 所对的边,且3a =2c sin A .(1)确定角C 的大小;33(2)若c =7,且△ABC 的面积为,求a +b 的值.2提示:(1)利用正弦定理将边转化为角即可;(2)利用余弦定理和面积公式列出关于a ,b 的方程求解,注意整体技巧.专题五正、余弦定理在实际问题中的应用解决有关三角形的应用问题时,首先要认真分析题意,找出各量之间的关系,根据题意画出示意图,将要求的问题抽象为三角形模型,然后利用正弦定理、余弦定理求解,最后将结果还原为实际问题,这一程序可用框图表示为:实际问题――→解三角形问题――→三角形问题的解――→实际问题的解概括演算应用1如图所示,一辆汽车在一条水平的公路上向正西行驶,到A 处时测得公路北侧抽象推理还原远处一山顶D 在西偏北15°的方向上,行驶5 km 后到达B 处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高度CD .提示:要测出高CD ,只要测出高所在的直角三角形的另一条直角边或斜边的长即可.根据已知条件,可以计算出BC 的长.应用2如图,某巡逻艇在A 处发现北偏东45°相距9海里的C 处有一艘走私船,正沿南偏东75°的方向以10海里/时的速度向我海岸行驶,巡逻艇立即以14海里/时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才能追赶上该走私船?提示:在求解三角形中,可以根据正弦函数的定义得到两个解,但作为有关现实生活的应用题,必须检验上述所求的解是否符合实际意义,从而得出实际问题的解.真题放送1.(2011·天津高考)如图,在△ABC 中,D 是边AC 上的点,且AB =AD,2AB =3BD ,BC =2BD ,则sin C 的值为().A .3366B .C .D .36362.(2011·福建高考)若△ABC 的面积为3,BC =2,∠C =60°,则边AB 的长度等于__________.→→3.(2011·上海高考)在正三角形ABC 中,D 是BC 上的点.若AB =3,BD =1,则AB ·AD=______.4.(2011·湖南高考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足c sin A =a cos C .(1)求角C 的大小;π(2)求3sin A -cos(B +)的最大值,并求取得最大值时角A ,B 的大小.45.(2011·湖北高考)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知a =1,b1=2,cos C =.4(1)求△ABC 的周长;(2)求cos(A -C )的值.6.(2011·辽宁高考)△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,a sin A sin B +b cos 2A =2a .b (1)求;a(2)若c 2=b 2+3a 2,求∠B .7.(2011·浙江高考)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知sin A +sin C1=p sin B (p ∈R ),且ac =b 2.45(1)当p =,b =1时,求a ,c 的值;4(2)若角B 为锐角,求p 的取值范围.答案:综合应用专题一应用1:钝角∵sin A ∶sin B ∶sin C =2∶3∶4,根据正弦定理,得a ∶b ∶c =2∶3∶4.设a =2m ,b =3m ,c =4m (m >0),∵c >b >a ,∴∠C >∠B >∠A .a 2+b 2-c 24m 2+9m 2-16m 21∴cos C ===-<0.2ab 42×2m ×3m∴∠C 是钝角.∴△ABC 是钝角三角形.应用2:解:解法一:由正弦定理,得2sin B =sin A +sin C .∵∠B =60°,∴∠A +∠C =120°.∴∠A =120°-∠C ,代入上式,得2sin 60°=sin (120°-C )+sin C ,31展开,整理得sin C +cos C =1.22∴sin(C +30°)=1.∴∠C +30°=90°.∴∠C =60°.故∠A =60°.∴△ABC 为等边三角形.解法二:由余弦定理,得b 2=a 2+c 2-2ac cos B .a +c ∵∠B =60°,b =,2a +c 2∴()=a 2+c 2-2ac cos 60°.2整理,得(a -c )2=0,∴a =c .从而a =b =c .∴△ABC 为等边三角形.专题二a b c 应用1:证明:(1)由正弦定理,设===k ,sin A sin B sin Ck 2sin 2A +k 2sin 2B sin 2A +sin 2B 显然k ≠0,所以,左边===右边,即原等式成立.k 2sin 2C sin 2Cb 2+c 2-a 2c 2+a 2-b 2a 2+b 2-c 2(2)根据余弦定理,右边=2(bc ·+ca ·+ab ·)=(b 2+c 2-a 2)2bc 2ca 2ab222222222+(c +a -b )+(a +b -c )=a +b +c =左边,即原等式成立.222b 2+c 2-a 2cos A b +c -a 应用2:证明:由余弦定理,得cos A =,所以cot A ===2bc sin A 2bc sin Ab 2+c 2-a 2a 2+c 2-b 2a 2+b 2-c 2,同理可得cot B =,cot C =,所以cot A +cot B +cot C =4S 4S 4Sb 2+c 2-a 2a 2+c 2-b 2a 2+b 2-c 2a 2+b 2+c 2++=.4S 4S 4S 4S专题三2应用:解:∵sin A +cos A =2cos (A -45°)=,21∴cos (A -45°)=.2又∵0°<∠A <180°,∴∠A =105°.tan 45°+tan 60°∴tan A =tan (45°+60°)==-2-3,1-tan 45°tan 60°2+6sin A =sin (45°+60°)=sin 45°cos 60°+cos 45°sin 60°=.4又∵AC =2,AB =3,2+6311∴S △ABC =AC ·AB ·sin A =×2×3×=(2+6).2244专题四cos C 2a -c 2sin A -sin C 应用1:解:(1)由==,得cos B b sin Bcos C ·sin B =2sin A ·cos B -cos B ·sin C .∴2sin A ·cos B =sin B ·cos C +cos B ·sin C=sin (B +C )=sin (π-A )=sin A .1∵sin A ≠0,∴cos B =.2(2)∵b 2=a 2+c 2-2ac cos B =a 2+c 2-ac =7,又a +c =4,∴(a +c )2-3ac =7.∴ac =3.11333∴S △ABC =ac sin B =×3×=.2224应用2:解:(1)由3a =2c sin A 及正弦定理,得a 2sin A sin A ==.c sin C 33∵sin A ≠0,∴sin C =.2∵△ABC 是锐角三角形,π∴∠C =.3π(2)∵c =7,∠C =.由面积公式,得31π33ab sin =,∴ab =6.①232π由余弦定理,得c 2=a 2+b 2-2ab cos =7,即a 2+b 2-ab =7.②3由①②,得(a +b )2=25,故a +b =5.专题五应用1:解:在△ABC 中,∠BAC =15°,∠ACB =25°-15°=10°.根据正弦定理,AB sin ∠BAC 5sin 15°得BC ==≈7.452 4(km),sin 10°sin ∠ACBCD =BC tan ∠DBC =BC ×tan 8°≈1.047 (km).答:山的高度约为1.047 km.应用2:解:设该巡逻艇沿AB 方向经过x 小时后在B 处追上走私船,则CB =10x ,AB =14x ,AC =9,∠ACB =75°+45°=120°,222∴(14x )=9+(10x )-2×9×10x cos 120°,2化简,得32x -30x -27=0.39解得x =或x =-(舍去).216∴BC =10x =15,AB =14x =21.BC sin 120°15353又∵sin ∠BAC ==×=,AB 21214∴∠BAC =38°13′或∠BAC =141°47′(钝角不合题意,舍去).∴38°13′+45°=83°13′.答:巡逻艇应该沿北偏东83°13′方向去追,经过1.5小时才能追赶上该走私船.真题放送31.D 设BD =a ,则BC =2a ,AB =AD =a .2在△ABD 中,由余弦定理,得33(a )2+(a )2-a 222222AB +AD -BD 1cos A ===.2AB ·AD 3332×a ·a 2222又∵∠A 为△ABC 的内角,∴sin A =.3BC AB 在△ABC 中,由正弦定理,得=.sin A sin C3a 222AB 6∴sin C =·sin A =·=.BC 2a 361132.2在△ABC 中,由面积公式得S =BC ·CA ·sin C =×2·AC ·sin60°=AC =3,∴AC 2221=2.再由余弦定理,得AB 2=BC 2+AC 2-2·AC ·BC ·cos C =22+22-2×2×2×=4.∴AB =2.23.15如图,在△ABD 中,由余弦定理得2AD 2=AB 2+BD 2-2AB ·BD ·cos 60°=9+1-2×3×cos 60°=7,∴AD =7,AB 2+AD 2-BD 29+7-15∴cos ∠BAD ===.2AB ·AD 2×3×727515于是,AB ·AD =|AB ||AD |cos ∠BAD =3×7×=.2724.解:(1)因为c sin A =a cos C ,由正弦定理,得sin C sin A =sin A cos C .因为0<A <π,所以sin A >0.从而sin C =cos C .π又cos C ≠0,所以tan C =1,则∠C =.43π(2)由(1)知,B =-A .于是4π3sin A -cos(B +)4=3sin A -cos(π-A )=3sin A +cos Aπ=2sin(A +).63πππ11π因为0<A <,所以<A +<.46612ππππ从而当A +=,即A =时,2sin(A +)取最大值2.6236ππ5π综上所述,3sin A -cos(B +)的最大值为2,此时∠A =,∠B =.431215.解:(1)∵c 2=a 2+b 2-2ab cos C =1+4-4×=4,4∴c =2.∴△ABC 的周长为a +b +c =1+2+2=5.1(2)∵cos C =,4115∴sin C =1-cos 2C =1-()2=.44154a sin C 15∴sin A ===.c 28∵a <c ,∴∠A <∠C .故∠A 为锐角.1527)=.88∴cos(A -C )=cos A cos C +sin A sin C71151511=×+×=.8484166.解:(1)由正弦定理得,sin 2A sin B +sin B cos 2A =2sin A ,即sin B (sin 2A +cos 2A )=2sin A .b 故sin B =2sin A ,所以= 2.a(2)由余弦定理和c 2=b 2+3a 2,(1+3)a 得cos B =.2c由(1)知b 2=2a 2,故c 2=(2+3)a 2.12可得cos 2B =,又cos B >0,故cos B =,22所以∠B =45°.5a +c =,47.解:(1)由题设和正弦定理,得1ac =,4∴cos A =1-sin 2A =1-(⎧⎨⎩1a =1,⎧⎧⎪⎪a =4,解得⎨1或⎨c =,⎪⎪⎩4⎩c =1.11(2)由余弦定理,b 2=a 2+c 2-2ac cos B =(a +c )2-2ac -2ac cos B =p 2b 2-b 2-b 2cos B ,2231即p2=+cos B,223因为0<cos B<1,得p2∈(,2).2由题设知p>0,所以6<p< 2. 2。
高中数学必修5:1.2应用举例( 人教版高中数学必修5第一章解三角形 )

分析
在△AOP中,OA
OP tan 30
3h
在△BOP中,OB
OP tan 45
h
在△ABO中,AB2 OA2 OB2 2OAOB cos60
即 400 4h2 3h2
解得 h 400 4 3
题型四 求角度问题
例4 如图,在海岸A处发现北偏东45o方向,距A处 ( 3 1) 海里的B处有 一艘走私船. 在A处北偏西75o方向,距A处2海里的C处的我方缉私船,奉 命以 10 3 海里/时的速度追截走私船,此时走私船正以10海里/时的速度, 从B处向北偏东30o方向逃窜. 问:缉私船沿什么方向行驶才能最快截获走 私船?并求出所需时间.
2. 方位角:指以观测者为中心,从正北方向线顺时针旋转到目标方向线所 形成的水平角.如图所示的θ1、θ2即表示点A和点B的方位角.故方位角的范 围是[0o,360o).
测量中的有关概念、名词、术语
3. 方向角:以观测者为中心,指北或指南的方向线与目标方向线所成的小 于90°的水平角,它是方位角的另一种表示形式. 如图,左图中表示北偏 东30°,右图中表示南偏西60°.
6. 坡角、坡比:坡面与水平面的夹角称为坡角,坡面的竖直高度与水平宽 度的比称为坡比.
解三角形应用题
解三角形应用题时,通常都要根据题意,从实际问题中抽象出一个或几 个三角形,然后通过解三角形,得到实际问题的解,求解的关键是将实 际问题转化为解三角形问题.
题型一 测量一个不可到达点的距离
例1 海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角, 从B岛望C岛和A岛成75°的视角,则B,C间的距离是( )
ABC 45
题型四 求角度问题
分析 设缉私船应沿CD方向行驶 t 小时,才能最快 截获(在D点)走私船,则CD=10 3t ,BD=10t.
人教版高中数学必修5第一章解三角形 1.2 应用举例

(3)求解:利用正弦定理或余弦定理有序地解出三角形, 求得数学模型的解.
(4)检验:检验上述所求的解是否符合实际意义,从而得 出实际问题的解.
第2课时 解三角形的实际应用举例 —高度、角度问题
1.能够运用正弦定理、余弦定理等知识和方法解决一些有 关底部不可到达的物体高度测量的问题; 2.能够运用正弦定理、余弦定理等知识和方法解决一些有 关计算角度的实际问题.
1.现实生活中,人们是怎样测量底部不可到达的建筑物高 度呢?又怎样在水平飞行的飞机上测量飞机下方山顶的 海拔高度呢?
2.在实际的航海生活中,人们又会遇到新的问题:在浩瀚 无垠的海面上如何确保轮船不迷失方向,保持一定的航 速和航向呢?
今天我们就来共同探讨这些方面的问题.
探究一、测量底部不可到达的建筑物高度
4.自动卸货汽车的车厢采用液压机构.设计时需要计算油泵 顶杆BC的长度.已知车厢的最大仰角是60°,油泵顶点B与 车厢支点A之间的距离为1.95m,AB与水平线之间的夹角为 6°20′,AC长为1.40m,计算BC的长(精确到0.01m).
(1)什么是最大仰角?
(2)例题中涉及一个怎样的三角形?
答:三角形的面积为 3
3 或 3-
3 .
2
2
1.三角形面积公式:
2.确定三角形的形状 利用正弦定理或余弦定理,“化边为角”或“化角
为边”.
1.利用正弦定理和余弦定理来解题时,要学会审题及根据 题意画方位图,要懂得从所给的背景资料中进行加工、抽 取主要因素,进行适当的简化.
2.实际问题处理 实际问题
实际问题的解
抽象概括 示意图
还原说明
数学模型 推演 理算 数学模型的解
第3课时 三角形中的几何计算
最新高中数学必修5《应用举例》教案

最新高中数学必修5《应用举例》教案高中数学必修5《应用举例》教案【一】教学准备教学目标解三角形及应用举例教学重难点解三角形及应用举例教学过程一. 基础知识精讲掌握三角形有关的定理利用正弦定理,可以解决以下两类问题:(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他的边和角);利用余弦定理,可以解决以下两类问题:(1)已知三边,求三角;(2)已知两边和它们的夹角,求第三边和其他两角。
掌握正弦定理、余弦定理及其变形形式,利用三角公式解一些有关三角形中的三角函数问题.二.问题讨论思维点拨:已知两边和其中一边的对角解三角形问题,用正弦定理解,但需注意解的情况的讨论.思维点拨::三角形中的三角变换,应灵活运用正、余弦定理.在求值时,要利用三角函数的有关性质.例6:在某海滨城市附近海面有一台风,据检测,当前台风中心位于城市O(如图)的东偏南方向300 km的海面P处,并以20 km / h的速度向西偏北的方向移动,台风侵袭的范围为圆形区域,当前半径为60 km ,并以10 km / h的速度不断增加,问几小时后该城市开始受到台风的侵袭。
一. 小结:1.利用正弦定理,可以解决以下两类问题:(1)已知两角和任一边,求其他两边和一角;(2)已知两边和其中一边的对角,求另一边的对角(从而进一步求出其他的边和角);2。
利用余弦定理,可以解决以下两类问题:(1) 已知三边,求三角;(2)已知两边和它们的夹角,求第三边和其他两角。
3.边角互化是解三角形问题常用的手段.三.作业:P80 闯关训练高中数学必修5《应用举例》教案【二】教学准备教学目标1、应用正弦余弦定理解斜三角形应用题的一般步骤及基本思路(1)分析,(2)建模,(3)求解,(4)检验;2、实际问题中的有关术语、名称:(1)仰角与俯角:均是指视线与水平线所成的角;(2)方位角:是指从正北方向顺时针转到目标方向线的夹角;(3)方向角:常见的如:正东方向、东南方向、北偏东、南偏西等;3、用正弦余弦定理解实际问题的常见题型有:.com测量距离、测量高度、测量角度、计算面积、航海问题、物理问题等;教学重难点1、应用正弦余弦定理解斜三角形应用题的一般步骤及基本思路(1)分析,(2)建模,(3)求解,(4)检验;2、实际问题中的有关术语、名称:(1)仰角与俯角:均是指视线与水平线所成的角;(2)方位角:是指从正北方向顺时针转到目标方向线的夹角;(3)方向角:常见的如:正东方向、东南方向、北偏东、南偏西等;3、用正弦余弦定理解实际问题的常见题型有:测量距离、测量高度、测量角度、计算面积、航海问题、物理问题等;教学过程一、知识归纳1、应用正弦余弦定理解斜三角形应用题的一般步骤及基本思路(1)分析,(2)建模,(3)求解,(4)检验;2、实际问题中的有关术语、名称:(1)仰角与俯角:均是指视线与水平线所成的角;(2)方位角:是指从正北方向顺时针转到目标方向线的夹角;(3)方向角:常见的如:正东方向、东南方向、北偏东、南偏西等;3、用正弦余弦定理解实际问题的常见题型有:测量距离、测量高度、测量角度、计算面积、航海问题、物理问题等;二、例题讨论一)利用方向角构造三角形四)测量角度问题例4、在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.如图,设A、B两点在河的两岸,要测量 两点之间的距离,测量者在A的同侧,在所在 的河岸边选定一点C,测出AC的距离是55m, o o ∠BAC=51 ,∠ACB=75 . 求A、B两点的距 离.(精确到0.1m)
B
A
C
两灯塔A、B与海洋观察站C的距离都等
于a km,灯塔A在观察站C的北偏东30 ,
3. 什么是余弦定理?
3. 什么是余弦定理? 三角形中任何一边的平方等于其他两边 的平方的和减去这两边与它们的夹角的余弦 的积的两倍. 即:
a = b + c - 2bccosA
b = a + c - 2accosB c = a + b - 2abcosC
2 2 2 2 2 2
2
2
2
4. 运用余弦定理能解怎样的三角形? ①已知三边求三角;
o
灯塔B在观察站C南偏东60 ,则A、B之
间的距离为多少?
o
例2. 如图,A、B两点都在河的对岸(不
可到达),设计一种测量A、B两点间距
离的方法.
A B
可见,在研究三角形时,灵活根据 两个定理可以寻找到多种解决问题的方 案,但有些过程较繁复,如何找到最优 的方法,最主要的还是分析两个定理的 特点,结合题目条件来选择最佳的计算 方式.
②已知两边及它们的夹角,求第三边.
例1.如图,设A、B两点在河的两岸,要测量 两点之间的距离,测量者在A的同侧,在所在 的河岸边选定一点C,测出AC的距离是55m, ∠BAC=51o,∠ACB=75o. 求A、B两点的距 离(精确到0.1m)
B
A
C
1. 在△ABC中,根据已知的边和对应角, 运用哪个定理比较适当? 2. 运用该定理解题还需要哪些边和角呢?
1. 什么是正弦定理?
A C
B
1. 什么是正弦定理?
在一个三角形中,各边和它所对 角的正弦的比相等,即
A
a b c = = sin的三角形?
2. 运用正弦定理能解怎样的三角形?
①已知三角形的任意两角及其一边; ②已知三角形的任意两边与其中一边 的对角.
解斜三角形应用题的一般步骤: (1)分析:理解题意,分清已知与未知,画出示意图. (2)建模:根据已知条件与求解目标,把已知量与求 解量尽量集中在有关的三角形中,建立一个解斜 三角形的数学模型. (3)求解:利用正弦定理或余弦定理有序地解出三角 形,求得数学模型的解. (4)检验:检验上述所求的解是否符合实际意义,从 而得出实际问题的解.
课本对应习题
