初中数学中考模拟数学总复习 投影与视图经典考试题及答案2 .docx
初三数学投影与视图试题答案及解析

初三数学投影与视图试题答案及解析1.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是()A.3B.4C.5D.6【答案】B【解析】根据左视图和主视图,这个几何体的底层最少有1+1+1=3个小正方体,第二层最少有1个小正方体,因此组成这个几何体的小正方体最少有3+1=4个.故选B.【考点】三视图2.如图,该几何体的左视图是()A.B.C.D.【答案】D【解析】左视图有2列,从左往右依次有2,1个正方形,其左视图为:.【考点】简单组合体的三视图.3.如下左图是由五个小正方体搭成的几何体,它的左视图是()【答案】A.【解析】从左面可看到从左往右2列小正方形的个数为:2,1,故选A.【考点】简单组合体的三视图.4.如图是由四个小正方体叠成的一个立体图形,那么它的左视图是()【答案】D.【解析】从左面可看到第一列有2个正方形,第一列有一个正方形.故选D.【考点】简单组合体的三视图.5.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底面边长分别为()A.3,2B.2,2C.3,2D.2,3【答案】C【解析】设底面边长为x,则x2+x2=(2)2,解得x=2,即底面边长为2,根据图形,这个长方体的高是3,根据求出的底面边长是2.【考点】1.由三视图判断几何体;2.简单几何体的三视图.6.如图所示的几何体中,俯视图形状相同的是()A.①④B.②④C.①②④D.②③④【答案】B.【解析】找到从上面看所得到的图形比较即可:①的俯视图是圆加中间一点;②的俯视图是一个圆;③的俯视图是一个圆环;④的俯视图是一个圆. 因此,俯视图形状相同的是②④. 故选B.【考点】简单几何体的三视图.7.如图是由相同的小正方体组成的几何体,它的俯视图为()【答案】B【解析】根据几何体的三视图可知,主视图是从正面看到的图形,左视图是从左面看到的图形,俯视图是从上面看到的图形,由图可得它的为俯视图第二个,故选B【考点】几何体的三视图.8.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是()【答案】A【解析】从几何体上面看,是左边2个,右边1个正方形.故选A.【考点】简单组合体的三视图.9.一个几何体的三视图如图所示,则这个几何体是()【答案】D.【解析】如图,俯视图为三角形,故可排除A、B.主视图以及左视图都是矩形,可排除C,故选D.【考点】由三视图判断几何体.10.下列四个水平放置的几何体中,三视图如右图所示的是()【答案】D【解析】三视图是指分别从物体的前面、左面、上面看到的平面图形.故选D.11.一个几何体的三视图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【答案】D【解析】根据主视图和左视图可以确定该物体是棱柱,根据俯视图可以确定该物体的底面是三角形,满足上述条件的只有三棱柱,故选D.12.如图所示零件的左视图是()A. B. C. D.【答案】D.【解析】:零件的左视图是两个竖叠的矩形.中间有2条横着的虚线.故选D.【考点】三视图.13.如图是由五个相同的小正方体组成的几何体,则下列说法正确的是( )A.左视图面积最大B.左视图面积和主视图面积相等C.俯视图面积最小D.俯视图面积和主视图面积相等【答案】D.【解析】观察图形可知,几何体的主视图由4个正方形组成,俯视图由4个正方形组成,左视图由3个正方形组成,所以左视图的面积最小,俯视图面积和正视图面积相等.故选D.考点: 简单组合体的三视图.14.某几何体的三视图如下图所示,则该几何体可能为()【答案】D.【解析】试题分析:由主视图和左视图可以得到该几何体是圆柱和小圆锥的复合体,由俯视图可以得到小圆锥位于圆柱的正中间.故选D.考点:三视图判断几何体.15.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是()A.4个B.5个C.6个D.7个【答案】A.【解析】根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.故选A.【考点】三视图.16.如图所示是小红在某天四个时刻看到一个棒及其影子的情况,那么她看到的先后顺序是.【答案】④③①②.【解析】根据平行投影中影子的变化规律:就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.可知先后顺序是④③①②.故答案是④③①②.【考点】平行投影.17.如图下面几何体的左视图是A.B.C.D.【答案】B【解析】左视图即从物体左面看到的图形,从左面看易得三个竖直排列的长方形,且上下两个长方形的长大于高,比较小,中间的长方形的高大于长,比较大。
九年级数学投影与视图测试题(后附答案)
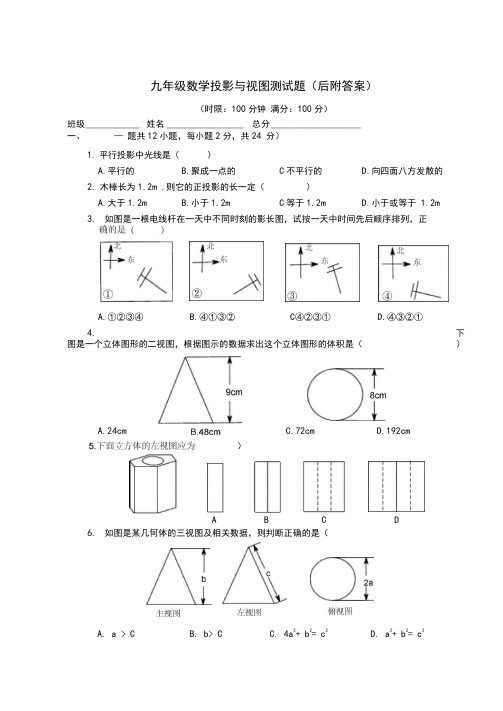
九年级数学投影与视图测试题(后附答案)(时限:100分钟 满分:100分)班级 ____________ 姓名 _________________ 总分 ____________________ 一、 — 题共12小题,每小题2分,共24 分)1. 平行投影中光线是( )A.平行的B.聚成一点的 C 不平行的D.向四面八方发散的 2. 木棒长为1.2m ,则它的正投影的长一定()A.大于1.2mB.小于1.2mC 等于1.2mD.小于或等于 1.2m3. 如图是一根电线杆在一天中不同时刻的影长图,试按一天中时间先后顺序排列,正A.①②③④B.④①③② C ④②③① D.④③②①4.下图是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是()6. 如图是某几何体的三视图及相关数据,则判断正确的是(C.72cmD.192cmA. a >C B. b >C C. 4a 2+ b 2= c 2D. a 2+ b 2= c 2)A.24cmAB C D7. 如图是由一些相同的小正方体构成的几何体的三视图,则这个几何体的小正方体的 个数是(9•一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底边长10.下列投影一定不会改变厶 ABC 的形状和大小的是( )A.中心投影B.平行投影 C 正投影。
.当厶ABC 平行投影面时的平行投影主视图 B. 5左视图 C. 6A. 4个8.将一个几何体放在桌子上,它的三视图如下,这个几何体是(俯视图D. 7个主视图A.三棱体B ∙长方体C 正方体D 球体A. 3,2√B. 2,2√C. 3, 2D. 2,311.已知一个物体由X 个相同的正方体堆成,值是()它的主视图和左视图如图, 那么X 的最大A. 13B. 12C. 11D.1012.下面左图表示一个由相同小立方块搭成的几何体的俯视图,位置上小立方块的个数,则该几何体的主视图为(小正方形中的数字表示 )俯视图 分别为(主视图左视图俯视图A B C D2420.如图,水平放置的长方体的底面是边长为则长方体的体积等于 __________ .2和4的矩形,它的左视图的面积为 6,、填空题:(本大题共8小题,每小题3分,共24分)13. 在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 _________.(填序号)14. 由一些大小相同的小正方体组成的几何体三视图如图所示,那么,组成这个几何体的小正方体有 ____________ 块•主视图左视图 俯视图15. 正方形ABCD 的边长为3,以直线AB 为轴旋转一周,所得几何体的左视图的周长 是 ___________ .16. 如图是一个几何体的三视图,其中主视图、左视图、都是腰为13cm ,底为IOcm的等腰三角形,则这个几何体的表面积为 ____________ .17. 一个圆锥的轴截面平行于投影面, 已知圆锥的正投影是边长为a 的等边三角形,则圆锥的体积是 __________ .18. 某一时刻,身高为165cm 的小丽影长是55cm ,此时,小玲在同一地点测得旗杆的 影长为5m ,则该旗杆的高度为 ____________ m. 19. 如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是 ________________ (把下图中正确和立体图形的序号都填在横线上)③ ④三、解答题:(本大题共52分)21. ( 7分)圆形餐桌正上方有一个灯泡 A ,灯泡A 照射到餐桌后在地面上形成阴影已知餐桌的半径为 0∙4m 、高为1m ,灯泡距地面2.5m,求地面上阴影部分的面积A22. ( 7分)一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积∙23. (8分)某班一位学生要过生日了,为了筹备生日聚会,班主任准备让学生自己动 手制作生日礼帽.如图所示,是礼帽的三视图,请计算制作一个这样的生日礼帽需 要纸板的面积为多少?30cm4 20cm *一24. ( 8分)求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度 之和是一个定值.俯视图25. (8分)如图,花丛中有一路灯杆 AB ,在灯光下,小丽在D 点处的影长DE = 3米, 沿BD 方向行走到达 G 点,DG = 5米,这时小丽的影长 GH = 5米.如果小丽的身高 为1.7米,求路灯杆 AB 的高度(精确到0.1米)26. ( 7分)八年级美术老师在课堂上进行立体模型素描教学时,把14个棱长为10的正方体摆成如图所示的形式,然后他把露出的表面都涂上不同的颜色,求被他涂 上颜色部分的面积.27. ( 7分)观察下列由棱长为 1的小立方体摆成的图形•寻找规律,如图①中共有 1个小立方体,其中1个看得见,0个看不见;如图②共有 8个立方体,其中7个看 得见,1个看不见;如图③中,共有 27个小立方体,其中19个看得见,8个看不照此规律,请你判断第⑥个图中有多少个小立方块,有多少个看不见?③a同理BN = b -^FB.a• MB + BN = (DB + FB)=常数(定值) b-a、选择题:参考答案:1.A ;2.D ;3.B ;4.B ;5.B ;6.D ;7.B ;8.A ;9.C ; 二、填空题:10.D ; 11.C ; 12.C ;13.②;14.5; 15.18 π; 16.90 ∏cm2; 17. n ;18.15 ; 19.①、②、 ④;20.24 ;三、解答题:21.解:如图所示, DE// BC 设底面半径为 可得22.解: 23.解:0.4 =1.5=解得•••底面面积为:该几何体的形状是直四棱柱 .由三视图可知:棱柱底面菱形的对角线长分别为5•菱形的边长为-Cm5•棱柱的测面积=2× 8× 4 = 80 (cm 2)由三视图可知,该几何体是圆锥体 其中,底面直径是 20cm ,高为 30cm. 则圆锥的母线长为 圆锥的表面积为1S=1× 20 π× 4cm 、3cm ,=100 π√10 ( cm 2)•制作生日礼帽需要纸板 100 ∏√0 (cm 2).24.解:如图所示,CD EF 为路灯高度,BM 、BN 为该人前后的两个影子 AB 为该人高度,∙∙∙ AB // CDMB a DM = bMB _ a DB b-aa即MB=b-TDB.F√102+ 302= 10√∣0cm25. 解:如图所示,∙∙∙ CD// AB26. 解:从前、后、左、右看该物体均为 6个正方形,从上面看有9个正方形,所以被涂上颜色部分的面积为6 × 100 × 4+ 900= 3300.27. 解:照此规律,第⑥个图形中有 216个小立方块,有125个小立方块看不见CD 3 X BE1.7 3 x-1.7BD 1.75 x-1.7BG ②得3BD1.7 3—C C 1.7—3—2 1∙75E G15∙∙∙.∙. X ≈ 6.①5 同理BD + 55 BD + 5x-1.72。
初中数学中考模拟模拟考试题分类投影与视图考试卷及答案.docx
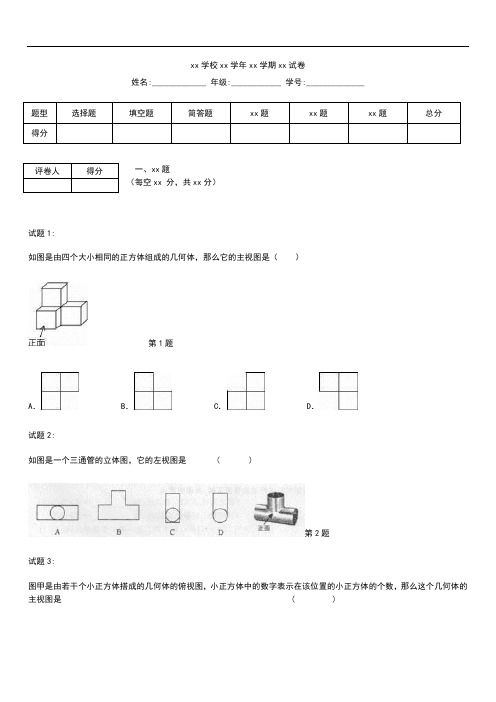
xx学校xx学年xx学期xx 试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:如图是由四个大小相同的正方体组成的几何体,那么它的主视图是()第1题A. B. C. D.试题2:如图是一个三通管的立体图,它的左视图是 ( )第2题试题3:图甲是由若干个小正方体搭成的几何体的俯视图,小正方体中的数字表示在该位置的小正方体的个数,那么这个几何体的主视图是( )第3题ABCD试题4:一个几何体是由一些大小相同的小正方体摆成的,其俯视图与主视图如图所示,则组成这个几何体的小正方体最多有:() A.4个 B.5个 C. 6个 D. 7个试题5:如图1所示的几何体的主视图是【】试题6:如图,几个完全相同的小正方体组成一个几何体,这个几何体的三视图中面积最大的是()A.主视图B.左视图C.俯视图D.主视图和左视图试题7:图中的两个长方体底面相同而高度不同,关于这两个长方体的视图说法正确的是()A.主视图相同B.俯视图相同C.左视图相同D.主视图、俯视图、左视图都相同试题8:如图是由5个大小相同的正方体摆成的立体图形,它的主视图是()A. B. C. D.试题9:从正面观察下图的两个物体,看到的是()A. B. C. D.试题10:用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )A. B. C. D.试题11:如图是几何体的三视图,该几何体是()A.正三棱柱 B.正三棱锥 C.圆锥 D.圆柱试题12:)下图所示几何体的左视图为(如右图是某个几何体的三视图,则该几何体的形状是()A.长方体 B.圆锥C.三棱锥 D.直三棱柱试题14:如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为()A. B. C. D.试题15:如图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的)主视图为(试题16:右图是由5个相同的正方体组成的立体图形,它的主视图是()试题17:由5个相同的立方体搭成的几何体如图所示,则它的主视图是()第17题A.B.C.D.考点:几何体的三视图试题18:如图所示的几何体的主视图是()A. B. C.D.【考点】简单组合体的三视图.【专题】常规题型.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:几何体的主视图是:试题19:由六个小正方体搭成的几何体如图所示,则它的主视图是()A. B. C. D.试题20:如图所示的几何体是由4个相同的小正方体组成.其主视图为()A .B .C . D.试题21:如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是()A.主视图B.主视图和左视图C.主视图和俯视图 D.左视图和俯视图试题22:一个立体图形三视图如图所示,那么这个立体图形的名称是三棱锥四棱锥三棱柱四棱柱试题23:如图所示,该几何体的主视图是()A .B .C .D .【分析】主视图是从物体前面看所得到的图形,依此即可求解.【解答】解:观察图形可知,该几何体的主视图是.试题24:如图是一个几何体的三视图,则这个几何体是()A.正方体 B.长方体 C.三棱柱 D.三棱锥试题25:如图是几何体的三视图,该几何体是()A.圆锥 B.圆柱 C.正三棱柱 D.正三棱锥试题26:如图,由4个大小相同的正方体组合而成的几何体,其俯视图是()A. B. C. D.试题27:有一种圆柱体茶叶筒如图所示,则它的左视图是试题28:下面四个几何体中,俯视图为四边形的是()A. B. C. D.试题29:如图是一个螺母的示意图,它的俯视图是()A. B. C. D.试题30:)用个完全相同的小正方体组成如图所示的立体图形,它的俯视图是试题31:下列几何体的主视图既是中心对称图形又是轴对称图形的是()A.B.C. D.试题32:如图是一个几何体的俯视图,则该几何体可能是A. B. C. D.试题33:由几个小正方体搭成的几何体,其主视图、左视图相同,均如图所示,则搭成这个几何体最少需要________个小正方体.试题34:一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8,则a的值为.试题35:由一些完全相同的小正方形搭成的几何体的左视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是.试题1答案:B试题2答案:D试题3答案:B试题4答案:C试题5答案::D试题6答案:C试题7答案:B【考点】简单组合体的三视图.【分析】根据从正面看得到的视图是主视图,从左边看得到的图形是左视图,从上面看得到的图形是俯视图,可得答案.【解答】解:A、主视图的高不同,故A错误;B、俯视图是两个相等的正方形,故B正确;C、左视图的高不同,故C错误;D、主视图、俯视图不相同,故D错误;故选:B.【点评】本题考查了简单组合体的三视图,从正面看得到的视图是主视图,从左边看得到的图形是左视图,从上面看得到的图形是俯视图.试题8答案:D【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可.【解答】解:从物体正面看,左边1个正方形,中间2个正方形,右边1个正方形,故选D.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.试题9答案:C试题10答案:C试题11答案:A试题12答案:A试题13答案:D试题14答案:C试题15答案:C【考点】由三视图判断几何体.【分析】从正面看可看到每列正方体的最多个数分别为2,2,1,表示为平面图形即可,【解答】解:俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得主视图有3列,从左到右的列数分别是2,2,1.故选C.试题16答案:C试题17答案:C试题解析:从正面可看到从左往右三列小正方形的个数为:1,1,2.故选C.试题18答案::A.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.试题19答案:B【考点】简单组合体的三视图.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.【解答】解:从正面看易得第一层有3个正方形,第二层最左边有一个正方形.故选B.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.试题20答案:D【考点】简单组合体的三视图.【分析】根据主视图定义,得到从几何体正面看得到的平面图形即可.【解答】解:从正面看得到2列正方形的个数依次为2,1,故选:D.【点评】此题主要考查了几何体的三视图;掌握主视图是从几何体正面看得到的平面图形是解决本题的关键.试题21答案:D试题22答案:B试题23答案:D.试题24答案:B【考点】由三视图判断几何体.【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:根据主视图和左视图为矩形是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体.故选:B.【点评】本题考查由三视图判断几何体,由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.试题25答案:C【考点】由三视图判断几何体.【分析】如图:该几何体的俯视图与左视图均为矩形,主视图为三角形,易得出该几何体的形状.【解答】解:该几何体的左视图为矩形,俯视图亦为矩形,主视图是一个三角形,则可得出该几何体为三棱柱.故选:C.【点评】本题是个简单题,主要考查的是三视图的相关知识,解得此题时要有丰富的空间想象力.试题26答案:C【考点】简单组合体的三视图.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【解答】解:几何体的俯视图是横着的“目”字.故选C.【点评】本题考查了三视图的知识,俯视图是从物体的上面看得到的视图.试题27答案:D试题28答案:D【考点】简单几何体的三视图.【分析】俯视图是指从物体上面看,所得到的图形.【解答】解:A、圆柱的俯视图是圆;B、三棱锥的俯视图是三角形;C、三棱柱的俯视图是三角形;D、正方体的俯视图是四边形.故选D.【点评】本题考查了几何体的三种视图,掌握定义是关键.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.试题29答案:B试题30答案::D试题31答案:试题32答案:B试题33答案:3试题34答案:【考点】由三视图判断几何体.【分析】根据左视图中的a就是俯视图等边三角形的高,由此根据侧面积列出方程即可解决.【解答】解:由题意:3×a×=8,解得a=.故答案为.【点评】本题考查三视图的有关知识,解题关键是理解左视图中的a就是俯视图等边三角形的高,学会用方程的思想解决问题,属于中考常考题型.试题35答案:6或7或8【考点】由三视图判断几何体.【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层立方体的可能的个数,相加即可.【解答】解:由题中所给出的俯视图知,底层有5个小正方体;由左视图可知,第2层有1个或2个或3个个小正方体.所以组成这个几何体的小正方体的个数可能是6或7或8个.故答案为:6或7或8.【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.。
初三数学投影与视图试题答案及解析

初三数学投影与视图试题答案及解析1.如图,由三个小立方块搭成的俯视图是()【答案】A.【解析】从上面看可得到两个相邻的正方形.故选A.【考点】简单组合体的三视图.2.下左图是由八个相同小正方体组合而成的几何体,则其主视图是()【答案】C【解析】主视图是从正面观察所看到的平面图形.根据小正方体的摆放方法,画出图形即可.故选C【考点】简单组合体的三视图的画法.3.如图是由相同的小正方体组成的几何体,它的俯视图为()A.B.C.D.【答案】B.【解析】找到从上面看所得到的图形即可:此几何体的俯视图有4列,从左往右小正方形的个数分别是2,2,1,2. 故选B.【考点】简单组合体的三视图.4.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是A.①②B.②③C.②④D.③④【答案】B【解析】正方体主视图、左视图、俯视图都是正方形;圆柱主视图和左视图是长方形,俯视图是圆;圆锥主视图和左视图是三角形、俯视图是带圆心的圆;球主视图、左视图、俯视图都是圆,故选:B.【考点】简单几何体的三视图.5.下列四个立体图形中,主视图为圆的是()A.B.C.D.【答案】B.【解析】A、主视图是正方形,故此选项错误;B、主视图是圆,故此选项正确;C、主视图是三角形,故此选项错误;D、主视图是长方形,故此选项错误;故选B.考点: 简单几何体的三视图.6.如图所示几何体的左视图是【答案】C.【解析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.从左面看可看到一个矩形里有上下两条虚线.故选C.考点: 简单组合体的三视图.7.如图所示的几何体的主视图是【答案】C.【解析】试题分析:主视图是从立体图形的正面看所得到的图形,找到从正面看所得到的图形即可.注意所有的看到的棱都应表现在主视图中.从正面看,此图形的主视图有3列组成,从左到右小正方形的个数是:1,2,1.故选C.考点:简单组合体的三视图.8.如图所示,快下降到地面的某伞兵在灯光下的影子为AB.试确定灯源P的位置,并画出竖立在地面上木桩的影子EF.(保留作图痕迹,不要求写作法)【答案】作图见解析.【解析】先连接伞兵的头和脚与对应的影子的直线,两直线的交点即为点P,过点P作过木桩顶端的直线与地面的交点即为F.试题解析:作图如下:【考点】1.作图题;2.中心投影.9.下面几何体的左视图是A.B.C.D.【答案】A【解析】左视图是从图形的左面看到的图形,从左面看,是一个等腰三角形。
初中数学投影与视图经典测试题含答案

一、选择题
1.如图是某几何体的三视图,则这个几何体可能是()
A. B. C. D.
【答案】B
【解析】
【分析】
根据主视图和左视图判断是柱体,再结合俯视图即可得出答案.
【详解】
解:由主视图和左视图可以得到该几何体是柱体,由俯视图是圆环,可知是空心圆柱.
故答案选:B.
【点睛】
12.一个由16个完全相同的小立方块搭成的几何体,它的主视图和左视图如图所示,其最下层放了9个小立方块,那么这个几何体的搭法共有( )种.
A.8种B.9种C.10种D.11种
【答案】C
【解析】
【分析】
先根据主视图、左视图以及最下层放了9个小立方块,确定每一列最大个数分别为 ,每一行最大个数分别为 ,画出俯视图.进而根据总和为16,分析即可.
考点:三视图.
7.如图所示,该几何体的主视图是( )
A. B. C. D.
【答案】D
【解析】
【分析】
从前往后看到一个矩形,后面的轮廓线用虚线表示.
【பைடு நூலகம்解】
该几何体为三棱柱,它的主视图是由1个矩形,中间的轮廓线用虚线表示.
故选D.
【点睛】
本题考查了简单几何体的三视图:画物体的主视图的口诀为:主、俯:长对正;主、左:高平齐;俯、左:宽相等.掌握常见的几何体的三视图的画法.
10.如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
A.从前面看到的形状图的面积为5B.从左面看到的形状图的面积为3
C.从上面看到的形状图的面积为3D.三种视图的面积都是4
【答案】B
【解析】
A.从正面看第一层是三个小正方形,第二层中间一个小正方形,主视图的面积是4,故A错误;
中考数学总复习《投影与视图》专项测试卷带答案
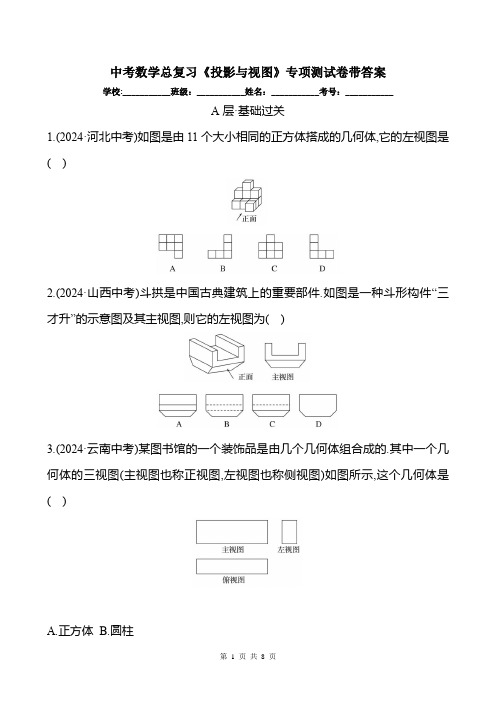
中考数学总复习《投影与视图》专项测试卷带答案学校:___________班级:___________姓名:___________考号:___________A层·基础过关1.(2024·河北中考)如图是由11个大小相同的正方体搭成的几何体,它的左视图是( )2.(2024·山西中考)斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )3.(2024·云南中考)某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图(主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是( )A.正方体B.圆柱C.圆锥D.长方体4.(2024·乐山中考)下列文物中,俯视图是四边形的是( )5.某几何体的三视图如图所示,这个几何体是( )6.(2024·自贡中考)下列几何体中,俯视图与主视图形状相同的是( )7.(2024·河南中考)信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )8.(2024·齐齐哈尔中考)如图,若几何体是由5个棱长为1的小正方体组合而成的,则该几何体左视图与俯视图的面积和是( )A.6B.7C.8D.9B层·能力提升9.(2024·吉林中考)葫芦在我国古代被看作吉祥之物.下图是—个工艺葫芦的示意图,关于它的三视图说法正确的是( )A.主视图与左视图相同B.主视图与俯视图相同C.左视图与俯视图相同D.主视图、左视图与俯视图都相同10.(2024·呼伦贝尔、兴安盟中考)如图是由七个完全相同的小正方体组成的立体图形,选项给出的四个平面图形中不属于其三视图的是( )11.(2024·包头中考)如图,正方形ABCD边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为( )A.8B.4C.8πD.4π12.(2024·济南历下区模拟)由6个同样的立方体摆出从正面看是的几何体,下面摆法正确的是( )C层·素养挑战13.(2024·绥化中考)某几何体是由完全相同的小正方体组合而成,下图是这个几何体的三视图,那么构成这个几何体的小正方体的个数是( )A.5B.6C.7D.8参考答案A层·基础过关1.(2024·河北中考)如图是由11个大小相同的正方体搭成的几何体,它的左视图是(D)2.(2024·山西中考)斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为(C)3.(2024·云南中考)某图书馆的一个装饰品是由几个几何体组合成的.其中一个几何体的三视图(主视图也称正视图,左视图也称侧视图)如图所示,这个几何体是(D)A.正方体B.圆柱C.圆锥D.长方体4.(2024·乐山中考)下列文物中,俯视图是四边形的是(D)5.某几何体的三视图如图所示,这个几何体是(C)6.(2024·自贡中考)下列几何体中,俯视图与主视图形状相同的是(C)7.(2024·河南中考)信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为(A)8.(2024·齐齐哈尔中考)如图,若几何体是由5个棱长为1的小正方体组合而成的,则该几何体左视图与俯视图的面积和是(B)A.6B.7C.8D.9B层·能力提升9.(2024·吉林中考)葫芦在我国古代被看作吉祥之物.下图是—个工艺葫芦的示意图,关于它的三视图说法正确的是(A)A.主视图与左视图相同B.主视图与俯视图相同C.左视图与俯视图相同D.主视图、左视图与俯视图都相同10.(2024·呼伦贝尔、兴安盟中考)如图是由七个完全相同的小正方体组成的立体图形,选项给出的四个平面图形中不属于其三视图的是(C)11.(2024·包头中考)如图,正方形ABCD边长为2,以AB所在直线为轴,将正方形ABCD旋转一周,所得圆柱的主视图的面积为(A)A.8B.4C.8πD.4π12.(2024·济南历下区模拟)由6个同样的立方体摆出从正面看是的几何体,下面摆法正确的是(B)C层·素养挑战13.(2024·绥化中考)某几何体是由完全相同的小正方体组合而成,下图是这个几何体的三视图,那么构成这个几何体的小正方体的个数是(A)A.5B.6C.7D.8。
初三数学中考复习 视图与投影 专项复习练习题 含答案

初三数学中考复习视图与投影专项复习练习题1.如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( B )2.如图是一个空心圆柱体,它的左视图是( B )3.中国讲究五谷丰登,六畜兴旺,如图是一个正方体展开图,图中的六个正方形内分别标有六畜:“猪”“牛”“羊”“马”“鸡”“狗”.将其围成一个正方体后,则与“牛”相对的是( C )A.羊 B.马 C.鸡 D.狗4.如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( B ),A) ,B) ,C) ,D)5.经过圆锥顶点的截面的形状可能是( B )6.某几何体的左视图如图所示,则该几何体不可能是( D )7.七巧板是我国祖先的一项卓越创造.下列四幅图中有三幅是小明用如图所示的七巧板拼成的,则不是小明拼成的那副图是( C )8.如图,是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是( D )A.5或6 B.5或7 C.4或5或6 D.5或6或79.不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( D )A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥10.有一个正方体,A,B,C的对面分别是x,y,z三个字母,如图所示,将这个正方体从现有位置依次翻到第1,2,3,4,5,6格,当正方体翻到第3格时正方体向上一面的字母是__x__.11.太阳光形成的投影是__平行__投影,灯光形成的投影是__中心__投影,身高相同的两名同学站在同一路灯下,影子长的离路灯__远__.12.已知,如图所示,木棒AB在投影面P上的正投影为A1B1,且AB=20 cm,∠BAA1=120°,则正投影A1B1=__103__cm.13.三棱柱的三视图如图所示,在△EFG中,EF=8 cm,EG=12 cm,∠EGF=30°,则AB的长为__6__cm.14.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是__4或5__.15.如图,小军、小珠之间的距离为2.7 m,他们在同一盏路灯下的影长分别为1.8 m,1.5 m,已知小军、小珠的身高分别为1.8 m,1.5 m,则路灯的高为__3__m. 16.画出如图所示立体图形的三视图.解:如图所示:17.如图①所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图②所示,已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出最长线段的长度,这样的线段可画几条?(2)试比较立体图形中∠BAC与平面展开图中∠B′A′C′的大小关系.解:(1)最长线段为10,有4条.(2)连结B′C′.由勾股定理得A′B′=5,B′C′=5,A′C′=10.∴A′B′2+B′C′2=A′C′2.∴∠A′B′C′=90°.∴∠C′A′B′=45°.又∠CAB=45°,∴∠BAC=∠B′A′C′.18.如图是一个几何体的三视图.(1)这个几何体的名称为__圆锥__;(2)根据所示数据计算这个几何体的表面积;(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程.解:(2)16π cm 2.(3)如图,将圆锥侧面展开,得到扇形ABB′,则线段BD 为所求最短路程.设∠BAB′=n °,∵n π×6180=4π,∴n =120,即∠BAB′=120°.∵C 为BB′︵的中点,∴∠ADB =90°,∠BAD =60°,∴BD =AB·sin ∠BAD =33cm ,∴线路的最短路程为3 3 cm.19.如图,在一间黑屋子里用一盏白炽灯照一个球.(1)球在地面上的阴影是什么形状?(2)当球沿铅垂方向下落时,阴影的大小会怎样变化?(3)若白炽灯到球心的距离是1 m ,到地面的距离是3 m ,球的半径是0.2 m ,求球在地面上留下的阴影的面积.解:(1)圆.(2)变小.(3)设如图所示各点,连结点O 与切点B ,由题意得△OAB∽△DAC.∵OB =0.2 m ,AO =1 m ,∴AB =256 m ,∴2563=0.2CD ,∴CD =64 m .∴S 阴影=(64)2π=38π m 2.。
中考数学专题复习题投影与视图(含解析)
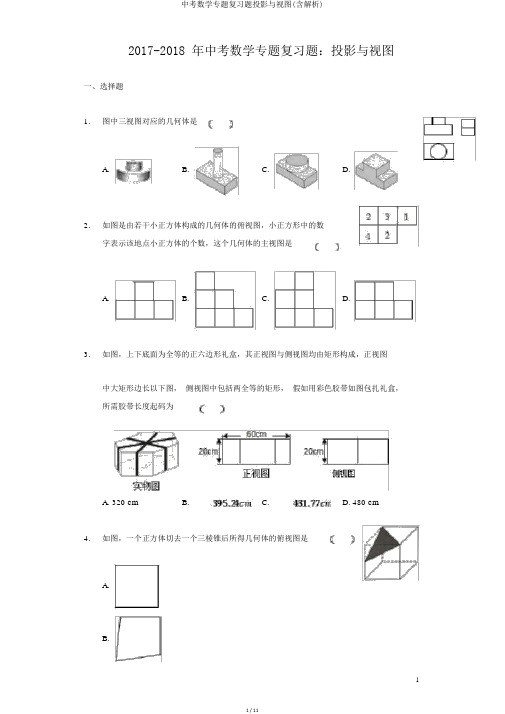
2017-2018 年中考数学专题复习题:投影与视图一、选择题1.图中三视图对应的几何体是A. B. C. D.2.如图是由若干小正方体构成的几何体的俯视图,小正方形中的数字表示该地点小正方体的个数,这个几何体的主视图是A. B. C. D.3.如图,上下底面为全等的正六边形礼盒,其正视图与侧视图均由矩形构成,正视图中大矩形边长以下图,侧视图中包括两全等的矩形,假如用彩色胶带如图包扎礼盒,所需胶带长度起码为A. 320 cmB.C.D. 480 cm4.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是A.B.C.D.5. 有一圆柱形的水池,已知水池的底面直径为 4 米,水面离池口 2 米,水池内有一小青蛙,它每日夜晚都会浮在水面上观月,则它能察看到的最大视角为A. B. C. D.6.以下图,在房屋外的屋檐 E 处安有一台监督器,房屋前有一面落地的广告牌,那么监督器的盲区在A. B. C. 四边形BCED D.7.如图,直立于地面上的电线杆AB,在阳光着落在水平地面和坡面上的影子分别是BC、CD,测得米,米,,在 D处测得电线杆顶端 A的仰角为,则电线杆AB的高度为A.B.C.D.8. 在阳光下,一名同学测得一根长为 1 米的垂直地面的竹竿的影长为米,同时另一名同学丈量树的高度时,发现树的影测得此影子长为米,一级台阶高为 米,以下图,若此时落在地面上的影长为米,则树高为A.米米C.米米9.以下图,右边水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是A. B. C. D.10. 圆桌面 桌面中间有一个直径为 的圆洞 正上方的灯泡 看作一个点 发出的光芒照耀平行于地面的桌面后,在地面上形成如图所示的圆环形暗影已知桌面直径为 ,桌面离地面 1m ,若灯泡离地面 3m ,则地面圆环形暗影的面积是A. B.C. D.二、填空题11. 如图,光源 P 在横杆 AB 的正上方, AB 在灯光下的影子为 CD ,,,,点 P 到 的距离是,CD则 AB 离地面的距离为 ______12. 如图,圆桌面正上方的灯泡发出的光芒照耀桌面后,在地面上形成暗影 圆形 已知灯泡距离地面,桌面距离地面的暗影面积是 ______.13. 如图是某几何体的三视图,依据图中数据,求得该几何体的表面积为 ______ .14. 如图,正三棱柱的底面周长为 15,截去一个底面周长为 6 的正三棱柱,所得几何体的俯视图的周长是 ______,面积是 ______.15. 如图, AB 和 DE 是直立在地面上的两根立柱,米,某一时辰 AB 在阳光下的投影 米,在丈量 AB 的投影时, 同时丈量出 DE 在阳光下的投影长为 6 米,则DE 的长为 ______.16. 如图,在一面与地面垂直的围墙的同侧有一根高13 米的旗杆 AB 和一根高度未知的电线杆 CD ,它们都与地面垂直,为了侧得电线杆的高度,数学兴趣小组的同学进行了以下丈量 某一时辰,在太阳光照耀下,旗杆落在围墙上的影子 EF 的长度为 3米,落在地面上的影子BF 的长为 8 米,而电信杆落在围墙上的影子的长度为GH米,落在地面上的银子 DH 的长为 6 米,依照这些数据,该小组的同学计算出了电线杆的高度是 ______米17.如图是王芳同学某一天察看到的一棵树在不一样时辰的影子,请你把它们准时间先后次序进行摆列是______ .18.墙壁 D处有一盏灯如图,小明站在 A处测得他的影长与身长相等都为,小明向墙壁走1m到B处发现影子恰好落在A点,则灯泡与地面的距离______.19.桌面上放两件物体,它们的三视图图,则这两个物体分别是______ ,它们的地点是 ______ .20.桌上放着一个三棱锥和一个圆柱体,如图的三幅图分别是从哪个方向看的?按图填写次序 ______正面、左面、上边三、计算题21.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次丈量它在地面上的影子,第一次是阳光与地面成角时,第二次是阳光与地面成角时,两次丈量的影长相差8 米,求树高AB多少米结果保存根号22.如图,是住所区内的两幢楼,它们的高,两楼间的距离,现需认识甲楼对乙楼的采光的影响状况.当太阳光与水平线的夹角为角时,求甲楼的影子在乙楼上有多高精准到,;若要甲楼的影子恰好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?23. 某兴趣小组展开课外活动如图,小明从点 M 出发以米 秒的速度,沿射线 MN 方向匀速行进, 2 秒后抵达点 B ,此时他 在某一灯光下的影长为 MB ,持续按原速行走 2 秒抵达点 D ,此时他在同一灯光下的影子 GD 仍落在其身后,并测得这个影长 GD 为 米,而后他将速度提升到本来的 倍,再行走 2 秒抵达点 F ,此时点 , , E 三点共线.A C请在图中画出光源 O 点的地点,并画出小明位于点 F 时在这个灯光下的影长不写画法 ;求小明抵达点 F 时的影长 FH 的长.24. 如图是一个密封纸盒的三视图, 请你依据图中数据计算这个密封纸盒的表面积 结果保存根号【答案】1. C2. C3. C4. D5. C6. D7. B8. B9. D 10. D11.12.13.14.13;15.10m16.1117.B、A、C、D18.19.长方体和圆柱;圆柱在前,长方体在后20.左面、上边、正面21.解:在中,,,在中,,,,,.答:树高 AB为米22. 解:如图,延伸交于,作,交于,OB DC E AB F,,.设,则 .依据勾股定理知,,负值舍去 ,.所以,.当甲幢楼的影子恰好落在点 C 处时, 为等腰三角形,所以,当太阳光与水平线夹角为 时,甲楼的影子恰好不落在乙楼的墙上. 23. 解:如图,点O 和为所作;FH,, ,设,作于 K ,如图,,∽,,即,,中考数学专题复习题投影与视图(含解析),即,由得,解得,,,,∽,,即,.答:小明抵达点 F 时的影长 FH的长为.24.解:依据该密封纸盒的三视图知道它是一个六棱柱,其高为 12cm,底面边长为 5cm,其侧面积为,密封纸盒的上、下底面的面积和为:,其表面积为.1111 / 11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xx学校xx学年xx 学期xx试卷
姓名:_____________ 年级:____________ 学号:______________
题型选择题填空题简答题xx 题xx题xx题总分
得分
一、xx题
(每空xx 分,共xx分)
试题1:
如图,在一水平面上摆放两个几何体,它的主视图是()
A. B.C. D.
试题2:
如图是由三个小正方体叠成的一个几何体,它的左视图是()
A. B. C. D.
试题3:
如图,从左面观察这个立体图形,能得到的平面图形是()
评卷人得分
A. B. C. D.
试题4:
如图,由4个相同的小立方块组成一个立体图形,它的主视图是()
A. B. C. D.
试题5:
如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是()
A.主视图的面积为5 B.左视图的面积为3 C.俯视图的面积为3 D.三种视图的面积都是4 试题6:
某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的主视图可以是()
A. B. C. D.
试题7:
如图的几何体的俯视图是()
A. B. C. D.
试题8:
如图是由几个小立方体快所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是()
A. B. C. D.
试题9:
某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为()
A. 3π B.2π C.π D. 12
试题10:
由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是.
试题11:
如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是.
试题12:
由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能
是.
试题13:
一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的底面边长是.
试题14:
一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有个碟子.
试题15:
若干桶方便面摆放在桌子上.实物图片左边所给的是它的三视图.则这一堆方便面共有桶.
试题16:
如图的三视图表示的物体的形状是.
试题17:
某物体的三视图如图:
(1)此物体是什么体;
(2)求此物体的全面积.
试题18:
如图假设一座大楼高30米,观众坐在距大楼500米处,魔术师只需做一个屏障,屏障上的图画和没有大楼以后的景物一样,将屏障立在大楼前100米处,这样观众看上去好像大楼突然消失了.若要完全挡住大楼,请你找到一个方法计算出屏障至少要多高?(人身高忽略不计)
试题19:
如图是某几何体的展开图.
(1)这个几何体的名称是;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(π取3.14)
试题20:
如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
试题21:
如图,是住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=30m,现需了解甲楼对乙楼的采光的影响情况.(1)当太阳光与水平线的夹角为30°角时,求甲楼的影子在乙楼上有多高(精确到0.1m,=1.73);
(2)若要甲楼的影子刚好不落在乙楼的墙上,此时太阳与水平线的夹角为多少度?
试题22:
如图是由几个棱长为1cm的小立方块搭成的几何体从上往下看的平面图形,小立方块中的数字表示该位置上小立方块的个数,求出这个几何体的体积.
试题23:
如图,左边的楼高AB=60m,右边的楼高CD=24m,且BC=30m,地面上的目标P位于距C点15m处.
(1)请画出从A处看地面上距点C最近的点,这个点与点C之间的距离是多少?
(2)从A处能看见目标P吗,为什么?
试题1答案:
B.
试题2答案:
C.
试题3答案:
A.
试题4答案:
C.
试题5答案:
B 解:A、从正面看,可以看到4个正方形,面积为4,故A选项错误;
B、从左面看,可以看到3个正方形,面积为3,故B选项正确;
C、从上面看,可以看到4个正方形,面积为4,故C选项错误;
D、三种视图的面积不相同,故D选项错误.
试题6答案:
B 解:从几何体的正面看可得,
试题7答案:
D 解:从上面看得到右下角少了一部分的正方形,并且右边的边少的与剩下的差不多.
试题8答案:
B 解:由俯视图可得主视图有2列组成,左边一列由4个小正方体组成,右边一列由2个小正方体组成.
试题9答案:
A 解:根据三视图可以判断该几何体为圆柱,圆柱的底面半径为1,高为3,
故体积为:πr2h=π×1×3=3π,
试题10答案:
4或5 解:由题中所给出的主视图知物体共三列,且左侧一列高两层,右侧一列最高一层;
由左视图可知左侧两行,右侧一行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,出可能两行都是两层.
所以图中的小正方体最少4块,最多5块.
试题11答案:
72 解:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,
∴设高为h,则6×2×h=36,
解得:h=3,
∴它的表面积是:2×3×2+2×6×2+3×6×2=72.
试题12答案:
4或5或6或7 解:由题中所给出的主视图知物体共三列,且左侧一列高两层,右侧一列最高一层;
由左视图可知左侧两行,右侧一行,于是,可确定左侧只有一个小正方体,而右侧可能是一行单层一行两层,出可能两行都是两层.
所以图中的小正方体最少4块,最多7块.
试题13答案:
2 解:
设底面边长为x,则x2+x2=(2)2,
解得x=2,即底面边长为2.
试题14答案:
12 解:易得三摞碟子数分别为3,4,5则这个桌子上共有12个碟子.
试题15答案:
6 解:三摞方便面是桶数之和为:3+1+2=6.
试题16答案:
圆锥解:由于主视图和左视图为三角形可得此几何体为锥体,
由俯视图为圆形可得为圆锥体.
试题17答案:
解:(1)根据三视图的知识,主视图以及左视图都为矩形,俯视图是一个圆,故可判断出该几何体为圆柱.(2分)
(2)根据圆柱的全面积公式可得,20π×40+2×π×102=1000π(6分).
试题18答案:
解:连接OA,交CD于E,
由题意知AB⊥OB,CD⊥OB,∠EOD=∠AOB=90°.
则,
故,
解得:ED=24(m).
答:屏障至少是24m.
试题19答案:
解:(1)圆柱;(2分)
(2)三视图为:
(5分)
(3)体积为:πr2h=3.14×52×20=1570.(7分)
试题20答案:
解:(1)连接PA并延长交地面于点C,线段BC就是小亮在照明灯(P)照射下的影子.(2分)
(2)在△CAB和△CPO中,
∵∠C=∠C,∠ABC=∠POC=90°
∴△CAB∽△CPO
∴(5分)
∴
∴BC=2m,
∴小亮影子的长度为2m(7分)
试题21答案:
解:(1)如图,延长OB交DC于E,作EF⊥AB,交AB于F,
在Rt△BEF中,
∵EF=AC=30m,∠FEB=30°,
∴BE=2BF.
设BF=x,则BE=2x.
根据勾股定理知BE2=BF2+EF2,
∴(2x)2=x2+302,
∴(负值舍去),
∴x≈17.3(m).
因此,EC=30﹣17.3=12.7(m).
(2)当甲幢楼的影子刚好落在点C处时,△ABC为等腰三角形,
因此,当太阳光与水平线夹角为45°时,甲楼的影子刚好不落在乙楼的墙上.
试题22答案:
解:(1×1×1)×(3+4+2+1)
=1×10
=10(cm3)
答:这个几何体的体积是10cm3.
试题23答案:
解:(1)如图,连接AD并延长,与地面相交于点E,
则点E即为从A处看地面上距点C最近的点,
∵AB、CD都与地面垂直,
∴AB∥CD,
∴△ABE∽△DCE,
∴=,
即=,
解得CE=20,
答:这个点与点C之间的距离是20米;(2)∵目标P位于距C点15m处,
∴CE>PC,
∴从A处不能看见目标P.。
