七年级上册第四章代数式及代数式求值(4.1-4.3)
2019年度浙教版七年级上册数学单元试卷 第四章 代数式04644

2018-2019年度浙教版七年级上册数学单元测试试卷第四章 代数式满分:100分;考试时间:120分钟学校:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息一、选择题1.一根绳子弯曲成如图2(1)所示的形状. 当用剪刀像图 2(2)那样沿虚线a 把绳子剪断时,绳子被剪为5段;当用剪刀像图2(3)那样沿虚线b (b ∥a )把绳子再剪一次时,绳子就被剪为 9段. 若用剪刀在虚线a 、b 之间把绳子再剪(1n -)次(剪刀的方向与a 平行),这时绳子的段数是( )A .41n +B . 42n +C .43n +D .45n +答案:D2.若k 为自然数,25k p p x y +与3312k x y +-是同类项,则满足条件的k 的值有( ) A .1 个 B .2 个 C .3个 D .无数个答案:D3.如果237m n -=,那么823m n -+等于( )A .15B .1C .7D .8答案:B4.a 表示一个一位数,b 表示一个两位数,把a 放到b 的左边组成一个三位数,则这个三位数可以表示为( )A .abB .10a b +C .100a b +D .a b +答案:C5.七年级 (1)班有 y 个学生,其中女生占55%,那么女生人数为( )A .55%yB .(1-55%)yC .155%y -D .55%y 答案:A6.甲、乙两地相距m 千米,原计划火车每小时行x 千米. 若火车实际每小时行50千米,则火车从甲地到乙地所需时间比原来减少( )A .50m 小时B .m x 小时C .(50m m x -)小时D .(50m m x -) 小时 答案:C二、填空题7.买 5 斤桔子需5a 元钱,则字母a 表示 .8.一盒铅笔12支,n 盒铅笔共有 支.9.当 x= 5,y= -2 时,232x y -+= .10.10 个小女孩去采花,其中 2个采到 x 朵花,其余每人都采到 12 朵花,则 10 个小女孩共采到 朵花.11.p-2[q-2p-3(-p-q)]= .12. 填表:13.有这样一道题:“计算322323323(232)(2)(3)x x y xy x xy y x x y y ----++-+-的值,其中12x =,1y =-.” 甲同学把“12x =”错抄成“12x =-”, 但他计算的结果也是正确的,你能说出这是什么原因?14.观代营养学家用身体质量指数判断人体健康状况,这个指数等于人体质量(kg)与人体身高(m)平方的商,一个健康人的身体质量指数在20~25之间,身体质量指数高于30,属于不健康的胖.。
7年级上册数学第四章《代数式1》讲义

第四章《代数式》讲义考点一:代数式的有关概念:(1)代数式:代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子.单独的一个数或者一个字母也是代数式.带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式。
② 书写代数式时,a ×b 通常写作ab ;1÷a 通常写作a1;数字通常写在字母的前面,带分数要先化成 假分数;数字与数字相乘仍用“×”号。
③ 当实际问题中含有单位时,若运算结果是和的形式时,则要把整个的代数式括起来再写单位。
(2)代数式的值:用数值代替代数式里的字母,计算后所得的结果p 叫做代数式的值.求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.(3)用代数式表达简单的数量关系:1、应特别注意数学语言中的关键词语。
2、要分清代数式中数量关系的运算层次和顺序,必要时要正确地添加括号。
3、有多种运算关系时,一般按“先读先写”的原则进行列式。
4、分清代数式、等式和不等式。
【典型例题】类型一:若正方形的边长为a ,则4a 表示的实际意义为类型二: ① 甲,乙两地相距15km ,小刚骑自行车从甲地用了t h ,那么他骑车的速度是每小时 千米。
② 某村去年梨的产量是a kg ,今年比去年增产30%,那么今年梨的产量是 千克。
类型三:如图所示,搭一个正方形需要4根火柴棒,按图中方式: ...... n=1 n=2 n=31、搭2个正方形需要 根火柴棒;2、搭3个正方形需要 根火柴棒;3、搭100个正方形需要 根火柴棒;4、若用n 表示所搭正方形的个数,则搭n 个正方形需要 根火柴棒;5、用2011根火柴棒能搭 个正方形 类型四:下列各式中哪些是代数式,哪些不是代数式2x -1 a =1 π a 0.5 S =πr 0.5>0.3类型五:当的值。
时,求代数式,)23)(32(43n m n m n m +-=-=【课堂练习题】1、某校学生总数是m 人,其中男生占52%,则女生人数为 。
七年级数学上册第4章代数式4.3代数式的值说课稿(新版浙教版)

七年级数学上册第4章代数式4.3代数式的值说课稿(新版浙教版)一. 教材分析《浙教版七年级数学上册》第4章介绍了代数式,而4.3节着重讲解了代数式的值。
这部分内容是学生在掌握了代数式的基本概念和运算法则后,进一步深化对代数式理解的重要环节。
通过本节课的学习,学生将能够求解各种代数式的值,从而为后续的方程和不等式学习打下基础。
二. 学情分析七年级的学生已经具备了一定的数学基础,对代数式有一定的认识。
但是,他们在处理复杂的代数式求值问题时,可能会感到困惑,特别是对于含有多个未知数的代数式。
因此,在教学过程中,我需要关注学生的认知水平,针对性地进行教学。
三. 说教学目标1.知识与技能目标:学生会求解简单代数式的值,并能运用所学知识解决实际问题。
2.过程与方法目标:学生通过自主学习、合作交流,培养观察、分析和解决问题的能力。
3.情感态度与价值观目标:学生体会数学与生活的联系,增强学习数学的兴趣和自信心。
四. 说教学重难点1.教学重点:求解代数式的值,熟练运用代数式的运算法则。
2.教学难点:对于含有多个未知数的代数式,如何正确求解其值。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和合作学习法。
2.教学手段:利用多媒体课件、黑板和教学卡片等辅助教学。
六. 说教学过程1.导入新课:通过一个实际问题,引入代数式的值的概念。
2.自主学习:学生根据导学案,独立探索代数式的值求解方法。
3.合作交流:学生分组讨论,分享解题心得,互相答疑。
4.课堂讲解:教师针对学生遇到的问题,进行讲解和示范。
5.练习巩固:学生完成课后练习,巩固所学知识。
6.课堂小结:教师引导学生总结本节课的主要内容和收获。
7.课后作业:布置适量的课后作业,巩固所学知识。
七. 说板书设计板书设计要清晰、简洁,能够突出本节课的重点内容。
主要包括以下几个部分:1.代数式的值的概念;2.代数式的运算法则;3.求解代数式的值的步骤;4.实例分析。
新浙教版七年级上册数学第四章《代数式》知识点及典型例题
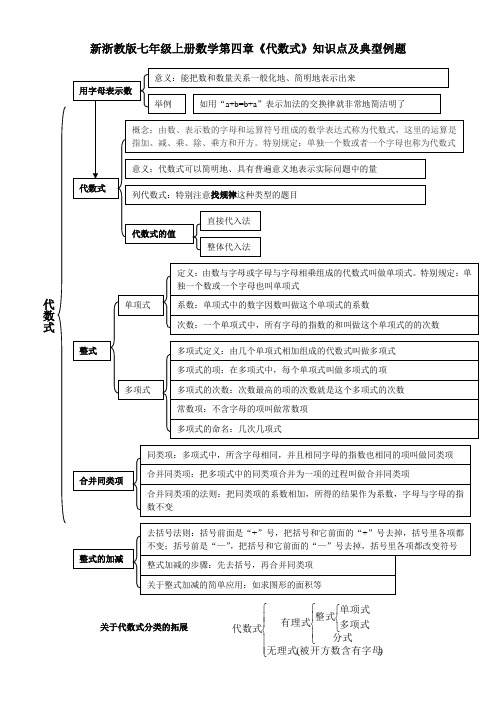
新浙教版七年级上册数学第四章《代数式》知识点及典型例题关于代数式分类的拓展⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧)(被开方数含有字母无理式分式多项式单项式整式有理式代数式将考点与相应习题联系起来考点一、关于代数式的书写是否正确的问题 1、下列代数式书写规范的是( ) A .512ab 2 B .a b ÷c C .a-cbD .m ·3 2、下列代数式书写规范的是( ) A .a ÷3 B .8×a C .5a D .212a 考点二、关于去括号的问题 1、下列运算正确的是( )A .-3(x-1)=-3x-1B .-3(x-1)=-3x+1C .-3(x-1)=-3x-3D .-3(x-1)=-3x+3 2、下列去括号中错误的是( ) A .2x 2-(x-3y)= 2x 2-x+3y B .13x 2+(3y 2-2xy)=13x 2-2xy +3y 2 C .a 2-4(-a+1)= a 2-4a-4 D .- (b-2a)-(-a 2+b 2)= - b+2a+a 2-b 23、下列去括号,错误的有( )个① x 2+(2x-1)= x 2+2x-1,② a 2-(2a-1)= a 2-2a-1,③ m-2(n-1)=m-2n-2,④ a-2(b-c)=a-2b+c A. 0 B. 1 C. 2 D. 34、去括号:-[-(1-a)-(1-b )]=考点三、关于代数式中与概念有直接关系的题目1、单项式中-27πa 2b 的系数和次数分别是( ) A .-27,4 B .27,4 C .-27π,3 D .27π,32.下列代数式中,不是整式的是( ) A.13a 2+12a+1 B. a 2+1b C. m+12 D. 2006x +y 3.下列说法正确的是( ) A. x 2-3x 的项是x 2,3x B.3a b 是单项式 C. 12,πa ,a 2+1都是整式 D. 3a 2bc-2是二次二项式 4、若m ,n 为自然数,则多项式x m-y n-2m+n的次数是( )A. mB. nC. m+nD. m ,n 中较大的数 5、下列各项式子中,是同类项的有( )组 ① -2xy 3与5y 3x ,② -2abc 与5xyz ,③ 0与136,④ x 2y 与xy 2,⑤ -2mn 2与mn 2,⑥ 3x 与-3x 2A. 2B. 3C. 4D. 56、若A 和B 都是三次多项式,则A+B 一定是( )A. 六次多项式B. 次数不高于三次的多项式或单项式C. 三次多项式D. 次数不低于三次的多项式或单项式0或27、已知-6a 9b 4和5a 4m b n是同类项,则代数式12m+n-10的值为 8、多项式2b-14ab 2-5ab-1中次数最高的项是 ,这个多项式是 次 项式 9、若2a 2m-5b 与mab 3n-2的和是单项式,则m 2n 2=考点四、关于代数式求值的问题,主要有先化简再直接代入、整体代入、稍作变形后再代入(把整式的加减也归入这一类)1、若代数式x2+3x-3的值为9,则代数式3x2+9x-2的值为()A、0B、24C、34D、442、已知a-b=2,a-c=12,则代数式(b-c)2+3(b-c)+94的值为()A、-32B、32C、0D、973、若a+b=3,ab=-2,则(4a-5b-3ab)-(3a-6b+ab)=4、已知a2-ab=15,b2-ab=10,则代数式3a2-3b2的值为5、先化简,再求值-12a-3(2a-23a2) -6(32a+13a2) -1,其中a=-26、先化简,再求值(1)3a2-5b2+12ab-5a2-b2-12ab+4a2,其中a=112,b= -12(2)5(x-y)3-3(x-y)2+7(x-y)-5(x-y)3+(x-7)2-5(x-y),其中x-y=1 37、有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=12,y=-1,小明把x=12错抄成x= -12,但他的计算结果也是正确的,请你帮他找出原因。
代数式化简求值的三种考法—2023-2024学年七年级数学上册(人教版)(解析版)

代数式化简求值的三种考法类型一、整体代入求值【答案】【分析】根据一元一次方程的解的定义,将3x =代入2mx n −=,得出32n m −=−,代入代数式,即可求解.【详解】解:∵3x =是关于x 的一元一次方程2mx n −=的解, ∴32m n −=,即32n m −=− ∴265n m −+=()()2352251n m −+=⨯−+=,故答案为:1.【点睛】本题考查了一元一次方程解的定义,代数式求值,整体代入解题的关键. 例2.已知代数式232a b −+的值为4,则代数式 2628b a −+的值为( ) A .4 B .8−C .12D .4−【答案】A【分析】由代数式232a b −+的值为4,可知23a b −的值,再观察题中的两个代数式23a b −和2628b a −+,可以发现226282(3)8b a a b −+=−−+,代入即可求解.【详解】解:∵代数式232a b −+的值为4,∴2324a b −+=,即232a b −=,∴2628b a −+22(3)8a b =−−+228=−⨯+4=,故选:A .【点睛】此题主要考查了代数式求值,代数式中的字母没有明确告知,而是隐含在题设中,首先应从题设入手,寻找要求的代数式与题设之间的关系,然后利用“整体代入法”求代数式的值.例3.已知535y ax bx cx =++−,当3x =时,7y =,那么3x =−时,y =( ) A .-3 B .-7 C .-17 D .7【答案】C【分析】把3x =,7y =代入计算得5333312a b c ++=,然后把3x =−代入原式化简,利用整体代入法即可得到答案.【详解】解:∵535y ax bx cx =++−中,当3x =时,7y =,∴5333357a b c ++−=, ∴5333312a b c ++=,把3x =−代入535y ax bx cx =++−,得 533335y b c a =−−−−, 53(333)5a b c =−++−125=−− 17=−;故选择:C.【点睛】本题考查了求代数式的值,解题的关键是利用整体代入法进行解题.【分析】根据绝对值的性质,求出,a b 可能取得值,根据0a b −<确定,a b 的值,再代数求值. 【详解】解:5a =,18b −=,5a ∴=±,18b −=±, 5a ∴=±,9b =或7−, 0a b −<Q ,∴当5a =,9b =时,5914a b +=+=;当5a =−,9b =时,594a b +=−+=. 故a b +的值为4或14.【点睛】本题考查了绝对值与代数式求值,解决本题的关键在于根据绝对值的性质求出,a b 的值,然后分情况讨论.【分析】先根据多项式乘以多项式运算法则,将括号展开,再将2a b −=,5ab =代入进行计算即可. 【详解】解:()()()444416416a b ab a b ab a b −+=+−−=+−−,∵2a b −=,5ab =, ∴原式5421619=−⨯−=−.故答案为:19−.【点睛】本题主要考查了多项式乘以多项式,解题的关键是掌握多项式乘以多项式,把前面一个多项式的每一项分别乘以后面一个多项式的每一项. 【变式训练3】已知a +b =2ab ,那么232a ab ba ab b++−+=( )A .6B .7C .9D .10【答案】B【详解】解:∵2a b ab +=,∴232a ab b a ab b ++−+=2()3a b ab a b ab +++−=2232ab ab ab ab ⨯+−=43ab ab ab +=7abab =7,故选:B .类型二、特殊值法代入求值例1.已知关于x 的多项式4323ax bx cx dx e ++++,其中a ,b ,c ,d 为互不相等的整数. (1)若4abcd =,求+++a b c d 的值;(2)在(1)的条件下,当1x =时,这个多项式的值为27,求e 的值;(3)在(1)、(2)条件下,若=1x −时,这个多项式4323ax bx cx dx e ++++的值是14,求a c +的值. 【答案】(1)0 (2)3e = (3) 6.5−【分析】(1)由a b c d 、、、是互不相等的整数,4abcd =可得这四个数由1−,1,2−,2组成,再进行计算即可得到答案;(2)把1x =代入432327ax bx cx dx e ++++=,即可求出e 的值;(3)把=1x −代入432314ax bx cx dx e ++++=,再根据0a b c d +++=,即可求出a c +的值.【详解】(1)解:4abcd =,且a b c d 、、、是互不相等的整数, ∴a b c d 、、、为1−,1,2−,2,0a b c d ∴+++=;(2)解:当1x =时,4323ax bx cx dx e ++++ 43231111a b c d e =⨯+⨯+⨯+⨯+ 3a b c d e =++++ 30e =+27=,3e ∴=;(3)解:当=1x −时,4323ax bx cx dx e ++++()()()()43231111a b c d e =⨯−+⨯−+⨯−+⨯−+3a b c d e =−+−+14=,13a b c d ∴−+−=−, 0a b c d +++=, 6.5a c ∴+=−.【点睛】本题主要考查了求代数式的值,解题的关键是得出a b c d 、、、这四个数以及a b c d 、、、之间的关系.【变式训练1】已知()20211232021012320211x a a x a x a x a x +=++++⋅⋅⋅+,则20212020201920181a a a a a −+−+⋅⋅⋅+的值为 .【答案】1【分析】分别令=1x −、0x =代入,求得对应代数式的值,求解即可.【详解】解:令=1x −,则()202101232020202110x a a a a a a +=−+−+⋅⋅⋅−=+,令0x =,则()2021011x a +==,∴2021202020192018100a a a a a a −+−+⋅⋅⋅+−=, ∴2021202020192018101a a a a a a −+−+⋅⋅⋅+==.故答案为:1.【点睛】此题考查了求代数式的值,解题的关键是给x 赋值,得到对应代数式的值. 【变式训练2】若()665432654321021x a x a x a x a x a x a x a −=++++++,则5310a a a a ++−=______. 【答案】365−【详解】解:令x=0,代入等式中得到:()61−=a ,∴0=1a , 令x=1,代入等式中得到:65432101①=++++++a a a a a a a , 令x=-1,代入等式中得到:66543210(3)②−−−−=+++a a a a a a a ,将①式减去②式,得到:65311(3)2()−−+=+a a a ,∴536113)3642(−+=+=−a a a ,∴53103641365++−=−−=−a a a a , 故答案为:365−.【变式训练3】特殊值法,又叫特值法,是数学中通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.例如:已知:432432106a x a x a x a x a x ++++=,则(1)取0x =时,直接可以得到00a =;(2)取1x =时,可以得到432106a a a a a ++++=; (3)取1x =−时,可以得到432106a a a a a −+−+=−;(4)把(2),(3)的结论相加,就可以得到4222a a +020+=a ,结合(1)00a =的结论,从而得出420a a +=.请类比上例,解决下面的问题:已知654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x −+−+−+−+−+−+=.求:(1)0a 的值;(2) 6543210++++++a a a a a a a 的值; (3) 642a a a ++的值. 【答案】(1)4;(2)8;(3)0 【解析】(1)解:当1x =时, ∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x−+−+−+−+−+−+=,∴0414a =⨯=;(2)解:当2x =时, ∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x−+−+−+−+−+−+=,∴65432108a a a a a a a +++++=+;(3)解:当2x =时, ∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x−+−+−+−+−+−+=,∴65432108a a a a a a a +++++=+①;当0x =时, ∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x−+−+−+−+−+−+=,∴65432100+−++=−−a a a a a a a ②;用①+②得:406282222++=+a a a a ,∴642040a a a a ++=−=. 类型三、降幂思想求值例.若2230x x −+=,则3227122020x x x −++=_____; 【答案】2029【详解】解:∵2230x x −+=, ∴223x x −=−,∴3227122020x x x −++=x(2x2-4x -3x+12)+2020=x[2(x2-2x)-3x+12]+2020= x[2×(-3)-3x+12]+2020=x(-3x+6)+2020=-3(x2-2x)+2020=-3×(-3)+2020=9+2020=2029 故答案为:2029.【分析】根据已知得到2232022x x −=,再将所求式子变形为()()22232320222020x x x x x x =−+−−−,整体代入计算即可.【详解】解:∵22320220x x −−=, ∴2232022x x −=, ∴32220252020x x x −−−322232*********x x x x x =−+−−−()()22232320222020x x x x x x =−+−−−2022202220222020x x =+−−2=故答案为:2.【点睛】本题主要考查了代数式求值,利用整体代入的思想求解是解题的关键. 【变式训练2】如果2233x x −+的值为5,则2695x x −−的值为______. 【答案】1【详解】∵22335x x −+=,∴2232x x −=∴2695x x −−()23235x x =−−325=⨯−1=,故答案为:1. 【变式训练3】已知21x x +=,求43222023x x x x +−−+的值. 【答案】2022【分析】把所求式子变形成含已知的代数式,结合整体代入的思想解答即可.【详解】解:∵21x x +=, ∴43222023x x x x +−−+()22222023x x x x x =+−−+2222023x x x =−−+ 22023x x =−−+()22023x x =−++12023=−+2022=.【点睛】本题考查了代数式求值和整式的乘法,正确变形,灵活应用整体思想是解题的关键. 【变式训练4】已知210x x −−=,则3222021x x −++的值是______. 【答案】2022【详解】解:∵210x x −−=,∴230x x x −−=, ∴32210x x −+−=,∴3221x x −+=,∴3222021120212022x x −++=+=,故答案为:2022.课后训练1.已知2|1|(2)0x y −++=,a 与b 互为倒数,c 与d 互为相反数,求32()()33x y ab c d +−−++的值. 【答案】-2 【详解】解:()2120x y −++=,()21020x y −≥+≥,.10x ∴−=,20y += 1x ∴=,2y =−因为a 与b 互为倒数,所以1ab = 因为c 与d 互为相反数,所以0c d += ∴原式()()()321213c d =−−−++()311=−−=-2.2.已知23a bc +=,222b bc −=−.则22543a b bc +−的值是( ) A .23− B .7C .13D .23【答案】B【分析】将所求式子变形为()()22542a bc b bc ++−,再整体代入计算.【详解】解:∵23a bc +=,222b bc −=−, ∴22543a b bc +−225548a bc b bc =+−+()()22254a bc b bc =+−+()5342=⨯+⨯−158=−7=故选B .【点睛】本题考查了整式的加减,代数式求值,解题的关键是掌握整体思想的灵活运用. 3.已知21a a +=,那么3222023a a ++的值是( ) A .2021 B .2022 C .2023 D .2024【答案】D【分析】先将3a 降次为2a a −+,然后代入代数式,再根据已知条件即可求解. 【详解】解:∵21a a +=,∴21a a =−+,则32a a a =−+,∴3222023a a ++2222023a a a =−+++ 22023a a =++12023=+2024=,故选:D .【点睛】本题考查了已知代数式的值求代数式的值,解决本题的关键是要将未知代数式进行降幂.【分析】根据2330a a −−=得出233a a ∴−=,然后整体代入求解;【详解】2330a a −−=Q ,233a a ∴−=,∴()222021262320212320212015a a a a −+=−−+=−⨯+=,故答案为:2015.【点睛】本题考查了求代数式的值,根据已有的等式整体代入求值是解题的关键.【分析】根据互为相反数的两个数的和为零,得到0m n +=,2c 与d 互为倒数得到21c d ⋅=,b 是最大的负整数得1b =-,代入求值.【详解】解:由题意可知,互为相反数的两个数的和为零,得到0m n +=,2c 与d 互为倒数得到21c d ⋅=,b 是最大的负整数得1b =-,故原式20200(11)=−−.0=.故答案为:0.【点睛】本题考查相反数的性质,倒数的性质以及最大的负整数,熟练掌握知识点是解题的关键.【答案】【分析】先把1x =代入531ax bx cx +++,可得a b c ++的值,再把1x =−代入531ax bx cx +++得1a b c −−−+,变形后再次把a b c ++的值代入计算即可.【详解】把1x =代入531ax bx cx +++得,12023a b c +++=∴2022a b c ++=,再把1x =−代入531ax bx cx +++得()11a b c a b c −−−+=−+++20221=−+ 2021=−.【点睛】此题考查代数式求值,解题关键在于把x 的值代入和整体思想的应用.【答案】(1)37;17;(2)2n+【分析】(1)根据题意代入求值即可;(2)分别计算1(),()f n f n 的值,找到规律再求解【详解】(1)()2263661637f ==+; 221114417114f ⎛⎫⎪⎛⎫⎝⎭== ⎪⎝⎭⎛⎫+ ⎪⎝⎭;(2)22222111(),()1111n n f n f n n n n ===+++1()()1f n f n \+=∴()()()()1111231231f f f f f f n f n ⎛⎫⎛⎫⎛⎫+++++⋅⋅⋅+++ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭()()()()1111231231f f f f f f n f n ⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=+++++⋅⋅⋅+++ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦11122n n =+⨯=+.【点睛】本题考查了代数式求值,分式的计算,理解题意,找到1()()1f n f n +=是解题的关键.【答案】【分析】把2x x +当整体代入求值,通过两次代入即可得出最后结果.【详解】解:230+−=x x ,23∴+=x x ,32225x x x +−+ 32225x x x x =++−+()2225x x x x x =++−+23x x +=,∴原式2325x x x =+−+25x x =++ 35=+8=,故答案为:8.【点睛】本题考查分解因式的应用,同时也要熟练运用整体代入的方法,快速分析出所需代入的整体是解题的关键.9.已知24a +=,()214b −=,且0ab <,则a b +=______.【答案】1或-3【详解】∵24a +=,()214b −=,∴a+2=±4,b−1=±2,∴a=2或a=−6,b=3或b=−1;∵0ab <,∴a=2,b=−1或a=−6,b=3,当a=2,b=−1时,则2(1)1a b +=+−=;当a=−6,b=3时,则633a b +=−+=−;故答案为:1或-3.。
2019年度浙教版七年级上册数学单元试卷 第四章 代数式01714

2018-2019年度浙教版七年级上册数学单元测试试卷第四章 代数式满分:100分;考试时间:120分钟学校:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息一、选择题1.如图,为做一个试管架,在 a (cm )长的木条上钻了 4 个圆孔,每个孔的直径为 2 cm ,则图中x 等于( )A .85a + cmB .165a -cmC .45a -cmD .85a -cm答案:D2.若代数式2231a a ++的值是 6,则代数式2695a a ++的值是( )3.A .18B .16C .15D .20答案:D 3.当a=8,b=4时,代数式22b ab a -的值是( ) A .62 B .63 C .126 D .1022答案:C4.下列各组代数式中,不是同类项的一组是( )A .12-和0B .213ab c -和2cabC .2xy 和2x yD .3xy 和xy - 答案:C5.a 的32大1的数”用代数式表示是( ) A .32a +1 B .23a +1 C .52a D .32a -1 答案:A6.当x=-1时,代数式122++x x 的值是( )A .-2B .-1C .0D .4答案:C7.下列说法中,正确的是( )A .a -是负数B .a 一定是非负数C .不论a 是什么数,都有11a a ⋅=D .7a 一定是分数 答案:B8.下列各选项中,两个单项式不是同类项的是( )A .23x y 和213yx -B .1与-2C .2m n 和22310nm ⨯D .213a b 与213b a 答案:D二、填空题9.当m= ,n= 时,32m x y 与33n xy -是同类项.10.已知 9×l+0=9,9×2+1=19,9×3+2=29,9×4+3=39,……. 根据前面式子构成的规律写出第n 个式子是 (n 是正整数)11.对有理数x 、y 定义运算 *,使x *y =1axy b ++,若-1 * 2=869 , 2* 3=883 , 则2*9= .三、解答题12.先化简,再求值.(1)222963()3x x x x +--,其中2x =-; (2)222222(53)()(53)a b a b a b -++-+,其中1a =-,1b =.13.一个三角形一边长为a b +,另一边长比这条边大2a b +,第三边长比这条边小3a b -,求这个三角形的周长 C .。
浙教版七年级数学上册第四章代数式单元测试题(含解析)

第四章代数式单元测试题一、单选题(共10题;共30分)1、某厂去年产值是x万元,今年比去年增产40%,今年的产值是()A、40%x万元B、(1+40%)x万元C、万元D、1+40%x万元2、下列各式符合代数式书写规范的是( )A、 B、a×3 C、3x-1个 D、2n3、下列语句中错误的是()A、数字0也是单项式B、xy是二次单项式C、单项式-a的系数与次数都是1D、- 的系数是—4、下列各式中,不是代数式的是()A、x—yB、xC、2x﹣1=6D、05、若代数式2x2+3x的值是5,则代数式4x2+6x﹣9的值是(A、10B、1C、—4D、—86、已知代数式m2+m+1=0,那么代数式2018﹣2m2﹣2m的值是()A、2016B、-2016C、2020D、—20207、已知﹣2x m+1y3与x2y n﹣1是同类项,则m,n的值分别为()A、m=1,n=4B、m=1,n=3C、m=2,n=4D、m=2,n=38、为了解决老百姓看病难的问题,卫生部门决定大幅度降低药品的价格,某种常用药品降价40%后的价格为a元,则降价前此药品价格为()A、元B、元C、40%元D、60%元9、如果A和B都是5次多项式,则下面说法正确的是()A、A﹣B一定是多项式B、A﹣B是次数不低于5的整式C、A+B一定是单项式D、A+B是次数不高于5的整式10、下列各式中运算错误的是()A、5x﹣2x=3xB、5ab﹣5ba=0C、4x2y﹣5xy2=﹣x2yD、3x2+2x2=5x2二、填空题(共10题;共36分)11、若a﹣2b=3,则9﹣2a+4b的值为 ________12、一个三位数,个位上的数为,十位上的数比个位上的数大2,百位上的数是个位上数的5倍,则这个三位数是________,当时,它是________13、若已知x+y=3,xy=﹣4,则(1+3x)﹣(4xy﹣3y)的值为________14、单项式﹣的系数是________ ,次数是________15、若3a3b n c2﹣5a m b4c2所得的差是单项式,则这个单项式为________16、若a x﹣3b3与﹣3ab2y﹣1是同类项,则x y=________.17、观察下列单项式:x,﹣3x2, 5x3,﹣7x4, 9x5,…按此规律,可以得到第2016个单项式是________.18、按照如图所示的操作步骤,若输入的值为3,则输出的值为________.19、当x=2017时,代数式(x﹣1)(3x+2)﹣3x(x+3)+10x的值为________.20、﹣的系数为________.三、解答题(共5题;共35分)21、某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2。
浙教版七年级上册数学第4章 4.3代数式的值 基础知识、课后巩固练习(包含答案)

4.3 代数式的值学习指要知识要点1.代数式的值:一般地,用数值代替代数式里的字母,计算后所得的结果叫做代数式的值2.利用代数式求值推断代数式所反映的规律3.解释代数式的值的实际意义重要提示1.求代数式的值是由一般的式子到特殊的数的问题,代数式里的字母取值要使代数式有意义如:代数式中要保证分母x-2≠0,即x不能取22.求代数式的值的步骤:(1)代人:代入时要注意:①如果代数式中省略乘号,代入后必须添上乘号.②如果字母给出的值是负数或分数,并作乘方或乘法运算,代入时都必须添上括号.③代人数值时,要“对号入座”,谨防混淆.④当题目按常规方法不能求解时,要充分利用“整体思想”将某一代数式作为一个整体,用“整体代入法”求解,解答此类问题的关键是确定合适的整体.(2)计算:计算时要注意运算顺序,同时考虑运用运算律简化运算.课后巩固之夯实基础一、选择题1.(2018·湖州长兴县期中)当x =-1时,代数式3x +1的值是( ) A .-1B .-2C .4D .-42.当x =-1时,下列代数式:①1-x ,②1-x 2,③-12x ,④1+x 3中,值为零的有( )A .1个B .2个C .3个D .4个3.(2018·杭州萧山区戴村片期中)当a =3,b =-1时,代数式0.5(a -2b)的值是( ) A .1B .0.5C .-2.5D .2.54.(2018·温州龙港镇期中)若2x -y =-3,则代数式1-4x +2y 的值等于( ) A .7B .-5C .5D .-45.若x =y =-1,a ,b 互为倒数,则代数式12(x +y)+3ab 的值是( )A .2B .3C .4D .3.56.下列代数式中,值一定为正数的是( ) A .(x +2)2 B .|x +1| C .(-x)2+2D .1-x 27.(2017·杭州大江东期中)如图K -23-1是一个数值运算程序,当输入x 的值为-2时,输出的结果为( )图K -23-1A .3B .8C .64D .638.图K-23-2中的图形都是由若干个灰色和白色的正方形按一定规律组成的,图①中有2个灰色正方形,图②中有5个灰色正方形,图③中有8个灰色正方形,图④中有11个灰色正方形……按此规律,图⑩中灰色正方形的个数是()图K-23-2A.32 B.29 C.28 D.26二、填空题9.当a=1,b=2时,代数式a2-ab的值是________.10.同一时刻北京的时间为7:00时,悉尼的时间是9:00.若北京时间用a表示,则悉尼时间为________,当北京时间为23:00时,悉尼时间为__________.11.(2017·湖州长兴县期末)已知实数x,y满足|x-4|+y+11=0,则代数式x-y 的值为________.12.(2018·绍兴嵊州期末)若a-b=2,则代数式5-2a+2b的值是________.13.某市出租车收费标准为起步价10元,3千米后每千米加收2元,那么乘坐出租车x(x>3)千米的收费y(元)的计算公式是y=__________,如果某人乘坐出租车5千米,那么应收费______元.14.(2018·杭州开发区期末)如图K-23-3是一种数值转换机的运算程序.若第一次输入的数为7,则第2018次输出的数是________;若第一次输入的数为x,使第2次输出的数也是x,则x=__________.图K-23-3三、解答题15.(2018·湖州长兴县期中)当a=2,b=-1时,求下列代数式的值:(1)2a+5b;(2)a2-2ab+b2.16.(2018·宁波余姚期末)已知2x-y=5,求-2(y-2x)2+3y-6x的值.17.若将一个棱长为8 cm的立方体的体积减小V cm3,而保持立方体形状不变,则棱长应减小多少厘米?若V=504,则棱长应减小多少厘米?18.(2018·衢州期中)“囧”(jiǒng)是一个风靡网络的流行词,像一个人脸郁闷的神情.如图K-23-4所示,一张边长为20 cm的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形的长和宽分别为x cm,y cm,剪去的两个小直角三角形的两直角边长也分别为x cm,y cm.(1)用含有x,y的代数式表示图中“囧”字图案(阴影部分)的面积;(2)当x=8,y=6时,求此时“囧”字图案(阴影部分)的面积.图K-23-419.(2018·湖州长兴县期中)某农户承包果树若干亩,收获水果总产量为20000千克,此水果可以在果园直接销售,也可以运去市场销售.已知在果园直接销售每千克售a元;在市场上每千克售b元,农户将水果运到市场销售平均每天售出1000千克,且在运到市场的过程中,需每天开支400元.(1)分别用含a,b的代数式表示两种方式销售水果的收入;(2)若a=4,b=4.5,且两种销售水果的方式都在规定的时间内售完全部水果,请你通过计算说明选择哪种销售方式较好.课后巩固之能力提升20.探索发现(2018·温州龙港镇期中)填写下表,观察下列两个代数式的值的变化情况:用代入检验的方法说明哪个代数式的值先超过100.21.新学期,两摞规格相同的数学课本整齐地叠放在课桌上,请根据图K-23-5(示意图)中所给出的数据信息,解答下列问题:(1)每本课本的厚度为________cm,课桌的高度为________cm;(2)若将x本同样规格的数学课本整齐地叠放在课桌上,则桌面上的课本距地面的高度为________cm(用含x的代数式表示);(3)桌面上有55本与(1)中规格相同的数学课本,它们整齐地叠放成一摞,若18名同学每人从中取走1本,则余下的数学课本距地面的高度是多少?图K-23-5详解详析1.[答案] B2.[答案] B3.[答案] D4.[答案] A5.[答案] A6.[答案] C7.[解析] D当x=-2时,输出(-2)2-1=3,再把x=3代入x2-1中,得x2-1=32-1=8,再把x=8代入x2-1中,得x2-1=82-1=63.∵63>50,∴输出的结果是63.故选D.8.[解析] B因为图①中有2个灰色正方形,2=3-1=3×1-1,图②中有5个灰色正方形,5=6-1=3×2-1,图③中有8个灰色正方形,8=9-1=3×3-1(3n -1)个灰色正方形,所以图⑩中灰色正方形的个数是3×10-1=29.故选B.9.[答案] -1[解析] a2-ab=12-1×2=-1.10.[答案] a+2次日1:00[解析] 悉尼与北京的时间差为2小时,所以当北京时间为a时,悉尼时间为a+2,当a=23时,a+2=25,即次日1:00.11.[答案] 15[解析] 因为|x-4|+y+11=0,所以x-4=0,y+11=0,所以x=4,y=-11,所以x-y=15.12.[答案] 113.[答案] 10+2(x -3) 14 14.[答案] 2 6或0或3 15.[答案] (1)-1 (2)9 16.[答案] -6517.解:棱长应减小⎝⎛⎭⎫8-383-V cm. 当V =504时, 棱长应减小8-383-504=6(cm).18.[解析] (1)直接利用正方形面积-2×三角形面积-长方形面积即可得出答案;(2)利用(1)中所求,将x ,y 的值代入,得出答案.解:(1)“囧”字图案阴影部分的面积=20×20-12xy×2-xy =(400-2xy)cm 2.(2)当x =8,y =6时,原式=400-2×8×6=304.故当x =8,y =6时,“囧”字图案(阴影部分)的面积为304 cm 2. 19.解:(1)在果园直接销售收入为20000a 元; 将这批水果运到市场上销售收入为(20000b -8000)元. (2)当a =4时,在果园直接销售收入为20000×4=80000(元);当b =4.5时,将这批水果运到市场上销售收入为20000×4.5-8000=82000(元). 因为82000>80000,所以选择运到市场上销售较好. [素养提升] 20.解:填表如下:因为当x =15时,12x 2=2252>100,6x -8=82,所以12x 2的值先超过100.21解:(1)每本课本的厚度为(88-86.5)÷(6-3)=0.5(cm); 课桌的高度为86.5-3×0.5=85(cm).故答案为0.5,85. (2)因为x 本课本的高度为0.5x cm ,课桌的高度为85 cm , 所以这些课本距地面的高度为(85+0.5x )cm. 故答案为(85+0.5x ).(3)当x =55-18=37时,85+0.5x =103.5. 故余下的数学课本距地面的高度为103.5 cm.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级第四章代数式及代数式求值(4.1-4.3)一.选择题(共1小题)1.代数式3(1﹣x)的意义是()A.1与x的相反数的和的3倍B.1与x的相反数的差的3倍C.1减去x的3倍D.1与x的相反数乘3的积二.填空题(共2小题)2.某商店举办促销活动,促销的方法是将原价x元的衣服以(x﹣10)元出售,则下列说法:(1)原价减去10元后再打8折;(2)原价打8折后再减去10元;(3)原价减去10元后再打2折;(4)原价打2折后再减去10元;其中能正确表达该商店促销方法的应该是.3.已知,如图为一日历的一部分,粗线所在的框刚好框住了9个数,设中间的一个数为x,那么这9个数的和为,右下角的数y用含x的代数式表示为.三.解答题(共37小题)4.某种杯子的高度是15cm,两个以及三个这样的杯子叠放时高度如图,(1)n个这样的杯子叠放在一起高度是(用含n的式子表示).(2)n个这样的杯子叠放在一起高度可以是35cm吗?为什么?5.在平阳县某住房小区建设中,为了提高业主的宜居环境,某小区规划修建一个广场(平面图如图所示).(1)用含m、n的代数式表示该广场的面积S;(2)若m、n满足(m﹣6)2+|n﹣8|=0,求出该广场的面积.6.“囧”(jiong)是最近时期网络流行语,想一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.(1)用含有x、y的代数式表示图中“囧”的面积;(2)若|x﹣6|+(y﹣3)2=0时,求此时“囧”的面积.7.每家乐超市出售一种商品,其原价a元,现有三种调价方案:(1)先提价20%,再降价20%;(2)先降价20%,再提价20%;(3)先提价15%,再降价15%.问这三种方案调价结果是否一样?最后是不是都恢复了原价?8.如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度忽略不计,单位:米),房子的主人计划把卧室以外的地面都铺上地砖,如果他选用的地砖价格是a元/米2,则买地砖只是要用多少元?(用含有a,x,y的代数式表示)9.一个两位数,若用a表示十位上的数,用b表示个位上的数.(1)用含a、b的式子表示这个两位数;(2)若把这个两位数个位上的数字与十位上的数字交换位置,所得新数与原数的差是多少?(3)若原数个位上的数是十位上的数的3倍,且新数与原数的差是36,求原来的两位数是多少?10.(1)各线段长度如图标记,请用含m,n的式子表示阴影部分的面积;(2)若(1)中的m,n满足|m﹣3|+(n﹣2)2=0,请计算阴影部分的面积.11.某校七年级组织学生为灾区捐款,甲班有x名同学,每人捐款3元;乙班人数比甲班的2倍少20人,每人捐款2.5元,丙班人数比乙班的一半多15人,每人捐款2元.(1)甲、乙、丙三个班共有多少人?(用含x的代数式表示);(2)若甲班捐款90元,则甲、乙、丙三个班共捐款多少元?12.如图,用整式表示图中阴影部分的面积,并计算当a=4cm,b=8cm时的阴影部分的面积(结果保留π)13.一种商品每件成本a元,原来按成本增加25%定出价格,现在由于库存积压减价,按原价的90%出售,现售价多少元?每件还能盈利多少元?14.为了节约用水,某市决定调整居民用水收费方法,规定如果每户每月用水不超过10吨,每吨水收费2元,如果每户每月用水超过10吨,则超过部分每吨水收费2.5元;小红看到这种收费方法后,想算算她家每月的水费:(1)如果小红家每月用水8吨,则水费是元;如果小红家每月用水20吨,则水费是元.(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费该如何用x的代数式表示呢?15.杭州微公交公司有20辆微公交纯电动汽车(K10车型).单日租金120元/辆,可全部租出;“十一”黄金周期间,日租金每增加15元/辆,则多一辆车未能租出;公司平均每日的各项支出为1440元.设公司每日租出x辆车,日收益为y元.(日收益=日租金总收入﹣平均每日各项支出)(1)求每辆车的日租金(用含x的代数式表示);(2)要使公司日收益最大,每日应租出多少辆?(3)每日租出多少辆车时,公司的日收益既不盈利也不亏损?16.用代数式表示如图图形阴影部分的面积.17.如图,已知正方形的边长为2,分别以正方形两个对角顶点为圆心,以边长为半径作两段圆弧,求阴影部分的面积.(结果用π表示)18.求各图中的阴影面积(单位:cm)19.某中学七年级A班有40人,某次活动中分为四组,第一组有a人,第二组比第一组的一半多6人,第三组的人数等于前两组人数的和.用含a的式子表示:(1)第二组的人数;(2)第三组的人数;(3)第一、二、三组的总人数;(4)第四组的人数.20.四人做传数游戏,甲任报一个数给乙,乙把这个数加1传给丙,丙再把所得的数乘以2后传给丁,丁把所听到的数减1报出答案.(1)如果甲所报的数为x,请把丁最后所报的答案用代数式表示出来,(2)若甲报的数为9,则丁的答案是多少?(3)若丁报出的答案是15,则甲传给乙的数是多少?21.某工厂第一车间有x人,第二车间比第一车间人数的少30人,如果从第二车间调出10人到第一车间,那么:(1)两个车间共有多少人?(2)调动后,第一车间的人数比第二车间多多少人?22.如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.(1)图②中的大正方形的边长为;阴影部分的正方形的边长为;(2)请用两种方式表示图②中阴影部分的面积;(3)观察图②,(m+n)2、(m﹣n)2、mn这三个代数式之间有何数量关系?若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.23.如图,大正方形的边长为a,小正方形的边长为2,求阴影部分的面积.24.康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:甲地(元/台)乙地(元/台)A地600500B地400800从A地运往甲地x台,总费用多少元?(用含x的代数式表示)25.求出图中阴影部分的面积.26.用字母表示下列图①,②中阴影部分的面积.27.如图,阳光中学新修了一个运动场,运动场的两端为半圆形,中间区域为足球场,外面铺设有塑胶环形跑道,四条跑道的宽均为1米.(1)用含a、b的代数式表示塑胶环形跑道的总面积;(2)若a=50米,b=20米,每铺1平方米塑胶需120元,求四条跑道铺设塑胶共花费多少元?(π=3)28.将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b,AD=30.(1)当a=8,b=3时,长方形ABCD的面积.(2)S1﹣S2的值(用含a,b的式子表示).29.某种T形零件尺寸如图所示(左右宽度相同)求:(1)阴影部分的周长是多少?(用含有x,y的代数式表示)(2)阴影部分的面积是多少?(用含有x,y的代数式表示)(3)当x=3,y=2时,计算阴影部分的面积?30.小王购买了一条经济适用房,地面结构如图所示(单位:m2)(1)用含x,y的式子表示地面总面积;(2)准备在地面铺设地砖,铺1m2地砖的平均费用为80元,当x=4,y=1.5时,求铺地砖的总费用为多少元?31.如图,长方形ABCD的长为a,宽为b,分别以A,B为圆心,以AD,BC 为半径作两个圆.(1)用代数式表示阴影部分的周长和面积;(2)当a=8,b=3时,求阴影部分的周长和面积.32.2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.①请用含a、b的式子表示该截面面积;②当a=2cm,b=3cm时,求这个火箭模型的截面的面积.33.某校大礼堂第一排有a个座位,后面每一排都比前一排多2个座位.(1)求第n排的座位数.(2)若该礼堂一共有20排座位,且第一排的座位数也是20,计算一下该礼堂能容纳多少人?34.根据如图的数值转换器,当输入的x,y满足时,请列式并求出输出的结果.35.历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)(f可用其它字母,但不同的字母表示不同的多项式)形式来表示,例如f(x)=x2+3x﹣5,把x=某数时多项式的值用f(某数)来表示.例如x=﹣1时多项式x2+3x﹣5的值记为f(﹣1)=(﹣1)2+3×(﹣1)﹣5=﹣7.已知g(x)=﹣2x2﹣3x+1,h(x)=ax3+2x2﹣x﹣12.(1)求g(﹣2)值;(2)若h()=﹣11,求g(a)的值.36.已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为﹣1.(1)求c的值;(2)已知当x=1时,该代数式的值为﹣1,试求a+b的值;(3)已知当x=3时,该代数式的值为9,试求当x=﹣3时该代数式的值.37.求值:(1)当|x+2|+|y﹣1|=0时,求代数式﹣3(x+2y)2﹣2(y﹣x)2的值.(2)x和y互为相反数,m与n互为倒数,|a|=1,求a2﹣(x+y+mn)a+(x+y)2006+(﹣mn)2007的值.38.“*”是规定的一种运算法则:a*b=a2﹣2b.(1)求2*3的值为(2)若(﹣3)*x=7,求x的值;(3)若2*(4*x)=2+x,求x的值.39.已知,求(x+y)2005+(ab)2004﹣3a的值.40.如图是某市设计的长方形休闲广场,两端是两个半圆形的花坛,中间是一个直径为长方形宽度一半的圆形喷水池,(1)用图中所标字母表示广场空地(图中阴影部分)的面积.(2)若休闲广场的长为80米,宽为40米,求广场空地的面积(计算结果保留π)七年级第四章代数式及代数式求值(4.1-4.3)参考答案一.选择题(共1小题)1.A;二.填空题(共2小题)2.(2);3.9x;y=x+8;三.解答题(共37小题)4.3n+12;5.;6.;7.;8.;9.;10.;11.;12.;13.;14.16;45;15.;16.;17.;18.;19.;20.;21.;22.m+n;m﹣n;23.;24.;25.;26.;27.;28.690;29.;30.;31.;32.;33.;34.;35.;36.;37.;38.﹣2;39.;40.;1 / 1。
