江科附中2016-2017学年高一上学期期中数学试卷
江西省景德镇市第一中学20162017学年高一上学期期中考

2016-2017学年度高一上学期期中考试高一(17)班数学试卷一、选择题(每题5分,共60分)1、已知集合{}2|220,A x x ax a R =++=∈,{}2|320,B x x x a a R =++=∈,{}2A B =且A B I =,则()()I I C A C B =( )A.1{5,}2-B.1{5,,2}2-C.{5,2}-D.1{,2}2二、已知函数()f x ()x R ∈知足()2()f x f x -=-,若函数1x y x+=与()y f x =图象的交点为11(,)x y 22(,)(,)m m x y x y 则1()mi i i x y =+=∑( )A. 0B. mC. 2mD. 4m 3、设函数211log (2)1()21x x x f x x -+-<⎧=⎨≥⎩ 则2(2)(log 12)f f -+=( )A. 3B. 6C. 9D. 12 4、若是函数21()(2)(8)1(0,0)2f x m x n x m n =-+-+≥≥在区间1[,2]2上单调递减,那么mn的最大值为( )A. 16B. 18C. 25D.8125、已知()f x 是偶函数且在[0,]+∞上是减函数,若(lg )(2)f x f >,则x 的取值范围是( )A.1(,1)100B.1(0,)(1,)100+∞C.1(,100)100D.(0,1)(100,)+∞六、已知0w >,函数()in()4f x S wx π=+在(,)2ππ单调递减,则w 的取值范围是( )A. 15[,]24 B. 13[,]24 C. 1(0,]2D. (0,2]7、若sin 2α=sin()βα-=且[,]4παπ∈,3[,]2πβπ∈,则αβ+的值是( )A.74π B. 94π C. 54π或74π D. 54π或94π 八、在ABC 中,角A B C 、、所对边的长别离为a b c 、、,若2222a b c +=,则Cos C 的最小值为( )C.12D.12-九、已知等差数列{}n a 的通项是12n a n =-,前n 项和为n S ,则数列{}n Sn的前11项和为( )A. -45B. -50C. -55D. -6610、设等差数列{}n a 的前n 项和为n S ,若344(1)2016(1)1a a -+-=,320132013(1)2016(1)1a a -+-=-,则下列结论正确的是( )A.2016201342016,S a a =->B.2016201342016,S a a =>C.2016201342016,S a a =-<D.2016201342016,S a a =<11、设函数()y f x =的概念域为D ,若对于任意的12,x x D ∈,当122x x a +=时,恒有12()()2f x f x b +=,则称(,)a b 为函数()y f x =图象的对称中心,研究函数3()sin 1f x x x =++的某一个对称中心,并利用对称中心的上述概念,可取得(2016)(2015)(2015)(2014)(2014)(2015)(2016)f f f f f f f -+-+-+-++++=( )A. 0B. 2016C. 4032D. 40331二、已知函数()f x 是概念在R 上的奇函数,当0x ≥时,222()(23)f x x a x a a =-+--,若对于任意x R ∈,都有(2)()f x f x -≤,则实数a 的取值范围是( )A. 11[,]66-B. [C. 11[,]33- D. [二、填空题(每题5分,共20分)13、在等差数列{}n a 中,25a =,621a =,记数列1{}n a 的前n 项和为n S ,若2115n n mS S +-≤对n N *∈恒成立,则正整数m 的最小值为14、已知a b c 、、别离为ABC 三个内角A B C 、、所对边,2a =,且(2)(sin sin )()sin b A B c b C +-=-,则ABC 的面积的最大值为1五、若是对一切正实数x y 、,都成立不等式29cos sin 4y x a x y-≥-,则实数a 的取值范围是 1六、111(1)(1)(1)121231232012---=+++++++三、解答题(共70分)17、(10分)已知集合{}{}2|(1)0,,|230M x x x a a R N x x x =--<∈=--≤,若M N N =,求实数a 的取值范围1八、(12分)已知函数()423,x x f x a a R =+⋅+∈(1)4a =-时且[0,2]x ∈,求函数的值域(2)若关于x 的方程()0f x =在(0,)+∞有两个不同实根,求实数a 的取值范围1九、(12分)已知ABC 中,角A B C 、、所对边别离为a b c 、、,且sin b B =(1)求角A 的大小(2)若4a =c -的最大值20、(12分)已知函数2()Sin(2)Sin(2)2Cos 1,33f x x x x x R ππ=++-+-∈(1)求函数()f x 的最小正周期(2)求函数()f x 在区间[,]44ππ-上的最大值和最小值2一、(12分)设等差数列{}n a 的前n 项和为n S ,且424S S =,221n n a a =+ (1)求数列{}n a 的通项公式(2)设数列{}n b 的前n 项和为n T ,且12n n na T λ++=(λ为常数)令2n n C b = ()n N *∈,求数列{}n C 的前n 项和n R22、(12分)已知数列{}n a 知足112a =且21n n n a a a +=- ()n N *∈ (1)证明:112nn a a +≤≤ ()n N *∈ (2)设数列{}2n a 的前n 项和为n S ,证明:112(2)2(1)n S n n n ≤≤++ ()n N *∈。
江科附中2020年高一期中考试数学试卷

对于任意给定的自然数 n0 ,则 f (ai )(i 1, 2, 3, , m) 的所有可能的值的集合为
;若 n0 2020,则
n2020 的值为
;
江科附中 2020 年高一上学期期中考试数学试卷
试卷第 2页,总 4页
三、解答题(共 70 分)
17.(10 分)已知全集U R ,集合 A {y | y 3 x2 , x R且x 0},集合 B 是函数 y log7 (x 2)
A.109
B.1010
C.10109
D.10110
5.为了得到函数 y ln( x 2) 的图象,只需把函数 y ln x 的图象上所有的点(
)
e
A. 向左平移 2 个单位长度,再向上平移 1 个单位长度
B.向右平移 2 个单位长度,再向上平移 1 个单位长度
C.向左平移 2 个单位长度,再向下平移 1 个单位长度
D.向右平移 2 个单位长度,再向下平移 1 个单位长度
6.函数 f x loga 6 ax 在0, 2上为减函数,则 a 的取值范围是( )
A. (0,1)
B. 1,3
C. 1,3
D.3,
7.已知 a
1 65
,b
1 6
0.2
,c
log 3
7
2 5 ,则(
)
A. a b c
B. b a c
江科附中 2020 年高一上学期期中考试数学试卷
试卷第 1页,总 4页
A
B
C
D
9.设
f
(x)
是连续的偶函数,且当
x
0
时
f
(x)
是单调函数,则满足
f
江苏省天一中学2016-2017学年高一上学期期中考试数学试题(原卷版)
( )过点 .
( )直线在 轴上的截距为 .
19.求经过M(-1,2),且满足下列条件的直线方程
(1)与直线2x+y+5=0平行;
(2)与直线2x+y+5=0垂直.
20.圆心在直线 ,且与直线 相切于点 的圆的标准方程为__________.
21.直线l经过点P(5,5),且和圆C:x2+y2=25相交,截得的弦长为4 ,求l的方程.
A. B.
C. D.
6.直线2x-y+4=0同时过第象限
A.一,二,三B.二,三,四
C.一,二,四D.一,三,四
7.若三点A(3,1),B(-2,b),C(8,11)在同一直线上,则实数b等于
A.2B.3
C.9D. -9
8.以 为端点的线段的垂直平分线的方程是
A. B.
C. D.
9.两个球 半径之比为1∶3,那么两个球的表面积之比为( )
C.(-2,0)
D. (0,-2)
3.已知 , ,则直线 与直线 的位置关系是()
A.平行B.相交或异面C.异面D.平行或异面
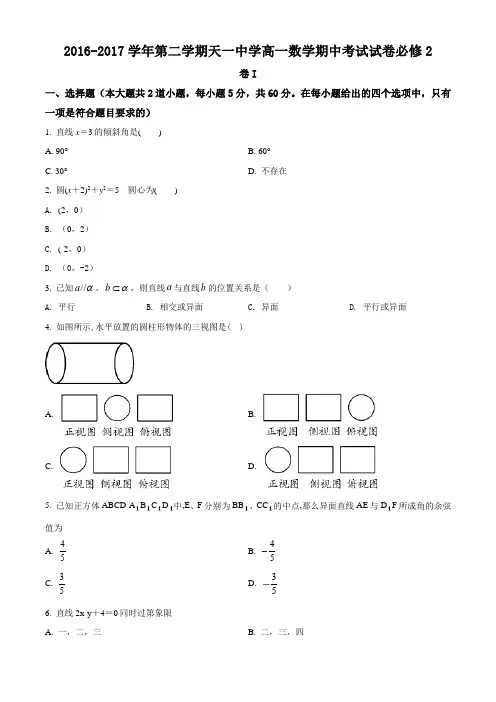
4.如图所示,水平放置的圆柱形物体的三视图是( )
A. B.
C. D.
5.已知正方体ABCD-A B C D 中,E、F分别为BB 、CC 的中点,那么异面直线AE与D F所成角的余弦值为
2Hale Waihona Puke .如图,在正方体 中,(1)求证:直线BD与平面 平行;
(2)求证:面 面
2016-2017学年第二学期天一中学高一数学期中考试试卷必修2
卷I
一、选择题(本大题共2道小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
江西省九江市2016-2017学年高一下学期期中数学试卷Word版含解析

江西省九江市2016-2017学年高一下学期期中数学试卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣2,﹣1,0,1},B={x|﹣2≤x<1},则A∩B=()A.{﹣1,0} B.{﹣1,0,1} C.{﹣2,﹣1,0} D.{﹣2,﹣1,1}2.设函数f(x)=,则f等于()A.﹣1 B.1 C.﹣5 D.53.函数y=sin2x是()A.最小正周期为2π的偶函数 B.最小正周期为2π的奇函数C.最小正周期为π的偶函数D.最小正周期为π的奇函数4.已知log b a c,则()A.a<b<c B.c<a<b C.b<a<c D.b<c<a5.函数f(x)=2x﹣1+x﹣5的零点所在的区间为()A.(0,1)B.(1,2)C.(2,3)D.(3,4)6.要得到函数y=sin(x﹣)的图象,只需将函数y=sinx的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位7.在数列{a n}中,a1=1,a n+1=a n+2,S n为{a n}的前n项和,若S n=100,则n等于()A.7 B.8 C.9 D.108.设a,b∈R,且a>b,则下列结论中正确的是()A.>l B.<C.|a|>|b| D.a3>b39.下列表达式中,正确的是()A.sin(α+β)=cosαsinβ+sinαcosβB.cos(α+β)=cosαcosβ+sinαsinβC.sin(α﹣β)=cosαsinβ﹣sinαcosβ D.cos(α﹣β)=cosαcosβ﹣sinαsinβ10.函数f (x )=3sin (ωx+φ)的部分图象如图,则f (x )的单调递增区间为( )A .(k π﹣,k π﹣),k ∈ZB .(2k π﹣,2k π﹣),k ∈ZC .(2k ﹣,2k ﹣),k ∈ZD .(k ﹣,k ﹣),k ∈Z11.已知等比数列{a n }中,a n =2×3n ﹣1,则由此数列的偶数项所组成的新数列的前n 项和S n 的值为( )A .3n ﹣1B .3(3n ﹣1)C .D .12.菱形ABCD 边长为2,∠BAD=120°,点E ,F 分别别在BC ,CD 上,=λ, =μ,若•=1,•=﹣,则λ+μ=( )A .B .C .D .二、填空题:本大题共4小题,每小题5分,共20分.13.log 64+log 69﹣8= .14.不等式≥0的解集是 .15.函数y=sinx ﹣cosx 的最大值为 .16.设x >0,y >0,若log 23是log 2x 与log 2y 的等差中项,则+的最小值为 .三、解答题:本大题共6个题,共70分.解答应写出文字说明、证明过程或演算步骤.17.向量=(4,﹣3),=(2x ,y ),=(x+,2),已知∥,⊥,求x ,y 的值.18.已知函数f (x )=的定义域是集合A ,函数g (x )=ln (x ﹣a )的定义域是集合B .(1)求集合A 、B ;(2)若C={x|2<1},求A∩C. 19.已知函数f (x )=b•a x (其中a ,b 为正实数且a≠1)的图象经过点A (1,27),B (﹣1,3)(1)试求a 、b 的值;(2)若不等式a x +b x ≥m 在x ∈等于( )A.﹣1 B.1 C.﹣5 D.5【考点】函数的值.【分析】根据分段函数的表达式,利用代入法进行求解即可.【解答】解:f(3)=32﹣3﹣5=9﹣3﹣5=1,f(1)=1﹣2=﹣1,即f=f(1)=﹣1,故选:A3.函数y=sin2x是()A.最小正周期为2π的偶函数 B.最小正周期为2π的奇函数C.最小正周期为π的偶函数D.最小正周期为π的奇函数【考点】三角函数的周期性及其求法;正弦函数的奇偶性.【分析】根据三角函数的周期公式算出最小正周期T=π,结合正弦函数的奇偶性即可得到本题答案.【解答】解:∵函数y=sin2x中ω=2∴最小正周期为T==π又∵y=sin2x满足f(﹣x)=﹣f(x)∴函数y=sin2x是奇函数因此,函数y=sin2x是最小正周期为π的奇函数故选:D4.已知log b a c,则()A.a<b<c B.c<a<b C.b<a<c D.b<c<a【考点】对数值大小的比较.【分析】直接利用对数函数的单调性结合已知得答案.【解答】解:∵函数y=是减函数,∴由log b a c,得c<a<b.故选:B.5.函数f(x)=2x﹣1+x﹣5的零点所在的区间为()A.(0,1)B.(1,2)C.(2,3)D.(3,4)【考点】函数零点的判定定理.【分析】根据零点的判定定理,对选项逐一验证即可.【解答】解:∵f(0)f(1)=()(1+1﹣5)>0,排除A.f(1)f(2)=(1+1﹣5)(2+2﹣5)>0,排除Bf(2)f(3)=(2+2﹣5)(4+3﹣5)<0,一定有零点故选C.6.要得到函数y=sin(x﹣)的图象,只需将函数y=sinx的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【考点】函数y=Asin(ωx+φ)的图象变换.【分析】由条件利用y=Asin(ωx+φ)的图象变换规律,得出结论.【解答】解:将函数y=sinx的图象向右平移个单位,可得函数y=sin(x﹣)的图象,故选:B.7.在数列{a n}中,a1=1,a n+1=a n+2,S n为{a n}的前n项和,若S n=100,则n等于()A.7 B.8 C.9 D.10【考点】数列的求和.【分析】由已知可得数列{a n}是首项为1,公差为2的等差数列,求出其前n项和后得答案.【解答】解:由a1=1,a n+1=a n+2,得数列{a n}是首项为1,公差为2的等差数列,则,由S n=100,得n=10.故选:D.8.设a,b∈R,且a>b,则下列结论中正确的是()A.>l B.<C.|a|>|b| D.a3>b3【考点】不等式的基本性质.【分析】对于A,B,C,举反例即可判断,对于D,根据幂函数的性质即可判断.【解答】解:对于A,若a=1,b=﹣1,则<1,故A不成立,对于B,若a=1,b=﹣1,则>,故B不成立,对于C,若a=1,b=﹣1,则|a|=|b|,故C不成立,对于D,对于幂函数y=x3为增函数,故a3>b3,故D成立,故选:D.9.下列表达式中,正确的是()A.sin(α+β)=cosαsinβ+sinαcosβB.cos(α+β)=cosαcosβ+sinαsinβC.sin(α﹣β)=cosαsinβ﹣sinαcosβ D.cos(α﹣β)=cosαcosβ﹣sinαsinβ【考点】两角和与差的余弦函数.【分析】由条件根据根据两角和差的正弦、余弦公式,得出结论.【解答】解:根据两角和差的正弦、余弦公式可得,sin(α+β)=cosαsinβ+sinαcosβ成立,而cos(α+β)=cosαcosβ+sinαsinβ、sin(α﹣β)=cosαsinβ﹣sinαcosβ、cos(α﹣β)=cosαcosβ﹣sinαsinβ都不正确,故选:A.10.函数f(x)=3sin(ωx+φ)的部分图象如图,则f(x)的单调递增区间为()A.(kπ﹣,kπ﹣),k∈Z B.(2kπ﹣,2kπ﹣),k∈ZC.(2k﹣,2k﹣),k∈Z D.(k﹣,k﹣),k∈Z【考点】正弦函数的图象.【分析】由周期求出ω,由五点法作图求出φ的值,再利用正弦函数的单调性,求得f(x)的增区间.【解答】解:根据函数f(x)=3sin(ωx+φ)的部分图象,可得•=,求得ω=π.再根据五点法作图可得π•+φ=π,求得φ=,∴(x )=3sin (πx+).令2k π﹣≤πx+≤2k π+,求得 2k ﹣≤x≤2k﹣,故函数的增区间为2k ﹣,2k ﹣),k ∈Z ,故选:C .11.已知等比数列{a n }中,a n =2×3n ﹣1,则由此数列的偶数项所组成的新数列的前n 项和S n 的值为( )A .3n ﹣1B .3(3n ﹣1)C .D . 【考点】等比数列的前n 项和.【分析】求出等比数列{a n }中的第二项和第四项,求得新数列的公比,由等比数列的求和公式,即可得到所求.【解答】解:等比数列{a n }中,a n =2×3n ﹣1,即有a 2=6,a 4=54,则新数列的公比为9,即有S n ==.故选:D .12.菱形ABCD 边长为2,∠BAD=120°,点E ,F 分别别在BC ,CD 上,=λ, =μ,若•=1, •=﹣,则λ+μ=( )A .B .C .D . 【考点】平面向量的基本定理及其意义.【分析】利用两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义由若•=1,求得4λ+4μ﹣2λμ=3 ①;再由•=﹣,得﹣2λ﹣2μ+2λμ=﹣②,结合①②求得λ+μ的值. 【解答】解:由题意可得•==+++=2×2×cos120°++=﹣2+4μ+4λ+λμ×2×2×cos120°=4λ+4μ﹣2λμ﹣2=1,∴4λ+4μ﹣2λμ=3 ①.•=﹣•(﹣)=(1﹣λ)=(1﹣λ)•(1﹣μ)═(1﹣λ)(1﹣μ)×2×2×cos120°=(1﹣λ﹣μ+λμ)(﹣2)=﹣,即﹣2λ﹣2μ+2λμ=﹣②,由①②求得λ+μ=,故选:C.二、填空题:本大题共4小题,每小题5分,共20分.13.log64+log69﹣8= ﹣2 .【考点】对数的运算性质.【分析】利用对数的运算法则及有理数指数幂的运算法则即可求得.【解答】解:原式=log6(4×9)﹣=2﹣22=﹣2.故答案为:﹣2.14.不等式≥0的解集是.【考点】其他不等式的解法.【分析】解不等式转化为不等式组,解出即可.【解答】解:原不等式可化为:或,解得:﹣≤x<,故答案为:.15.函数y=sinx﹣cosx的最大值为 2 .【考点】两角和与差的正弦函数.【分析】变形可得y=2(cos sinx﹣sin cosx)=2sin(x﹣),易得最值.【解答】解:化简可得y=sinx﹣cosx=2(sinx﹣cosx)=2(cos sinx﹣sin cosx)=2sin(x﹣)∴当sin(x﹣)=1时,原函数取最大值2故答案为:216.设x>0,y>0,若log23是log2x与log2y的等差中项,则+的最小值为.【考点】基本不等式;对数的运算性质.【分析】由已知结合等差中项的概念求得xy=9,再利用不等式的性质求得+的最小值.【解答】解:∵log23是log2x与log2y的等差中项,∴log2x+log2y=2log23=log29,则log2xy=log29,∴xy=9.则+.故答案为:.三、解答题:本大题共6个题,共70分.解答应写出文字说明、证明过程或演算步骤.17.向量=(4,﹣3),=(2x,y),=(x+,2),已知∥,⊥,求x,y的值.【考点】平面向量共线(平行)的坐标表示;平面向量数量积的运算.【分析】由已知向量的坐标,结合向量共线与垂直的坐标表示列关于x,y的方程组,求解方程组得答案.【解答】解: =(4,﹣3),=(2x,y),=(x+,2),由已知a∥b,a⊥c,可得,解得:x=6,y=﹣9.18.已知函数f(x)=的定义域是集合A,函数g(x)=ln(x﹣a)的定义域是集合B.(1)求集合A、B;(2)若C={x|2<1},求A∩C.【考点】交集及其运算;函数的定义域及其求法.【分析】根据函数的定义域的求法,求出集合A,B,C,再根据交集的定义即可求出.【解答】解:(1)因为(1+x)(2﹣x)≥0所以﹣1≤x≤2,集合A={x|﹣1≤x≤2};…因为x﹣a>0,所以x>a,集合B={x|x>a}…(2)因为,所以x2﹣2x﹣3<0解得:{x|﹣1<x<3},…则A∩C={x|﹣1<x≤2}.…19.已知函数f(x)=b•a x(其中a,b为正实数且a≠1)的图象经过点A(1,27),B(﹣1,3)(1)试求a、b的值;(2)若不等式a x+b x≥m在x∈﹣98,化简可得到纯收入关于使用时间n的函数解析式,然后构造不等式,解不等式即可得到n的取值范围.(2)由(1)中的纯收入关于使用时间n的函数解析式,我们对两种方案分析进行分析比较,易得哪种方案更合算.【解答】解:(1)由题设知每年的费用是以12为首项,4为公差的等差数列.设纯收入与年数的关系为f(n),则f(n)=50n﹣﹣98=40n﹣2n2﹣98,由f(n)>0,得10﹣又∵n∈N*,∴3≤n≤17.即从第3年开始获利.(2)①年平均收入为40﹣2×14=12,当且仅当n=7时,年平均获利最大,为12万元/年.此时,总收益为12×7+26=110(万元).②f(n)=﹣2(n﹣10)2+102,∵当n=10时,f(n)max=102(万元).此时,总收益为102+8=110(万元).由于这两种方案总收入都为110万元,而方案①只需7年、而方案②需要10年,故方案①更合算.。
江西省赣州市2016-2017学年高一下学期期中联考数学试卷Word版含解析

江西省赣州市2016-2017学年高一下学期期中联考数学试卷一、选择题(共12小题,每小题5分,满分60分)1.计算:cos210°=()A.B.C.D.2.如图,四边形ABCD中, =,则相等的向量是()A.与B.与C.与D.与3.已知角α的终边经过点P(﹣b,4)且cosα=﹣,则b的值等于()A.3 B.﹣3 C.±3 D.54.扇形的半径是6cm,圆心角为15°,则扇形面积是()A.B.3πcm2C.πcm2D.5.在△ABC中,点P为BC边上一点,且=2,,则λ=()A.B.C.D.6.若函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.7.如图是函数y=Asin(ωx+φ)的图象的一段,它的解析式为()A.B.C.D.8.△ABC的外接圆的圆心为O,半径为2,且,则向量在方向上的投影为()A.B.3 C.D.﹣39.把函数f(x)=cos(2x+)的图象沿x轴向左平移m个单位(m>0),所得函数为奇函数,则m的最小值是()A.B. C.D.10.如图,已知△ABC中,AB=AC=4,∠BAC=,点D是BC的中点,若向量=+m,且点M在△ACD的内部(不含边界),则的取值范围是()A.(﹣2,4)B.(﹣2,6)C.(0,4)D.(0,6)11.如图,设点A是单位圆上的一定点,动点P由点A出发在圆上按逆时针方向旋转一周,点P旋转过的弧为l,弦AP为d则函数d=f(l)的图象是()A.B.C.D.12.设向量与的夹角为θ,定义与的“向量积”:是一个向量,它的模,若,则=()A.B.2 C. D.4二、填空题:本大题共4小题,每小题5分,共20分.13.已知,且,则tanφ=______.14.设向量,是夹角为的单位向量,若=+2,则||=______.15.已知f(x)=sin(ω>0),f()=f(),且f(x)在区间上有最小值,无最大值,则ω=______.16.函数f(x)=3sin(2x﹣)的图象为C,则以下结论中正确的是______.(写出所有正确结论的编号).①图象C关于直线x=对称;②图象C关于点对称;③函数f(x)在区间(﹣,)内是增函数;④由y=3sin2x的图象向右平移个单位长度可以得到图象C.三、解答题:本大题共6小题,共70分.(解答应写出必要的文字说明、证明过程及演算步骤.)17.已知向量.(1)若,求k的值;(2)若,求m的值.18.已知f(α)=(1)化简f(α);(2)若f(α)=,且0<α<,求sinα+cosα的值.19.已知向量=(cosα,sinα),=(cosβ,sinβ),=(﹣1,0)(1)求向量的长度的最大值;(2)设α=,β∈(0,π),且⊥(+),求β的值.20.已知函数f(x)=sin(2x﹣)(1)画出函数f(x)在区间[0,π]的简图(要求列表);(2)求函数f(x)的单调递减区间.21.已知函数f(x)=sin(2ωx﹣)+b,且函数的对称中心到对称轴的最小距离为,当x∈[0,]时,f(x)的最大值为1(1)求函数f(x)的解析式(2)若f(x)﹣3≤m≤f(x)+3在x∈[0,]上恒成立,求m的取值范围.22.已知平面向量=(﹣,1),=(,),=﹣+m, =cos2x+sinx,f(x)=•,x∈R.(1)当m=2时,求y=f(x)的取值范围;(2)设g(x)=f(x)﹣m2+2m+5,是否存在实数m,使得y=g(x)有最大值2,若存在,求出所有满足条件的m值,若不存在,说明理由.江西省赣州市2016-2017学年高一下学期期中联考数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分) 1.计算:cos210°=( )A .B .C .D .【考点】运用诱导公式化简求值.【分析】把所求式子中的角210°变为180°+30°,利用诱导公式cos=﹣cos α及特殊角的三角函数值化简,即可求出原式的值. 【解答】解:cos210°=cos=﹣cos30°=﹣.故选B2.如图,四边形ABCD 中,=,则相等的向量是( )A .与B .与C .与D .与 【考点】相等向量与相反向量.【分析】四边形ABCD 中, =,四边形ABCD 是平行四边形,利用平行四边形的性质和向量相等即可得出.【解答】解:∵四边形ABCD 中, =,∴四边形ABCD 是平行四边形,∴. 故选D .3.已知角α的终边经过点P (﹣b ,4)且cos α=﹣,则b 的值等于( ) A .3 B .﹣3 C .±3 D .5 【考点】任意角的三角函数的定义.【分析】根据三角函数的定义建立方程关系即可.【解答】解:∵角α的终边经过点P (﹣b ,4)且cos α=﹣,∴cos α==﹣,则b >0,平方得,即b2=9,解得b=3或b=﹣3(舍),故选:A4.扇形的半径是6cm,圆心角为15°,则扇形面积是()A.B.3πcm2C.πcm2D.【考点】扇形面积公式.【分析】根据扇形的面积公式S=解答该题.【解答】解:∵扇形的半径为6cm,圆心角为60°,∴S==cm.故选:D.5.在△ABC中,点P为BC边上一点,且=2,,则λ=()A.B.C.D.【考点】平面向量的基本定理及其意义.【分析】根据题意画出图形,结合图形利用平面向量的线性运算,即可得出λ的值.【解答】解:如图所示,△ABC中, =2,∴==(﹣);∴=+=+(﹣)=+,又,∴λ=.故选:D.6.若函数y=3cos(2x+φ)的图象关于点(,0)中心对称,那么|φ|的最小值为()A.B.C.D.【考点】余弦函数的图象.【分析】由题意可得3cos(+φ)=0, +φ=kπ+,即φ=kπ﹣,k∈Z,由此可得|φ|的最小值.【解答】解:∵函数y=3cos(2x+φ)的图象关于点(,0)中心对称,故3cos(+φ)=0,∴+φ=kπ+,即φ=kπ﹣,k∈Z,∴|φ|的最小值为,故选:A.7.如图是函数y=Asin(ωx+φ)的图象的一段,它的解析式为()A.B.C.D.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】通过函数的图象,求出A,求出周期,得到ω,函数经过(),求出φ,得到函数的解析式.【解答】解:由题意与函数的图象可知:A=,T=2×()=π,∴ω=2,因为函数图象经过,所以==,所以.解得φ=,所以函数的解析式为:.故选D.8.△ABC的外接圆的圆心为O,半径为2,且,则向量在方向上的投影为()A.B.3 C.D.﹣3【考点】平面向量数量积的含义与物理意义.【分析】由题意画出图形,借助与图形利用向量在方向上的投影的定义即可求解.【解答】解:由题意因为△ABC的外接圆的圆心为O,半径为2,且,对于⇔,所以可以得到图形为:因为,所以四边形ABOC为平行四边形,又由于,所以三角形OAB为正三角形且边长为2,所以四边形ABOC为边长为2且角ABO为60°的菱形,所以向量在方向上的投影为: =故选:A9.把函数f(x)=cos(2x+)的图象沿x轴向左平移m个单位(m>0),所得函数为奇函数,则m的最小值是()A.B. C.D.【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用函数y=Asin(ωx+φ)的图象变换可得f(x+m)=cos(2x﹣2m+),利用诱导公式﹣2m+=kπ+,(k∈Z),f(x+m)为奇函数,当k=﹣1时,m取最小值.【解答】解:函数f(x)=cos(2x+)的图象沿x轴向左平移m个单位,f(x+m)=cos(2x+2m+),函数为奇函数,∴2m+=kπ+,(k∈Z),故当k=0时,m的最小值,故答案选:D.10.如图,已知△ABC中,AB=AC=4,∠BAC=,点D是BC的中点,若向量=+m,且点M在△ACD的内部(不含边界),则的取值范围是()A.(﹣2,4)B.(﹣2,6)C.(0,4)D.(0,6)【考点】平面向量数量积的运算.【分析】在AB上取点P使得AP==1,以AP,AC为邻边方向作平行四边形,根据M的位置判断m的取值范围,用表示出,代入数量积运算得出关于m的函数,求出该函数的值域即可.【解答】解:在AB上取点P使得AP=,过P作PN∥AC交AD于Q,交BC于N,分别作AB的平行线NF,EQ.则M在线段NQ上(不含端点),∵AB=AC=4,D为BC的中点,∴AD平分∠BAC.∴AE=AP=AB=1,,∴NP=3,∴AF=3.∵=+m,∴<m<.∵==﹣,又=0,∴=(+m)•(﹣)=﹣+m2=16m2﹣3,∵<m<,∴﹣2<16m2﹣3<6.故选B.11.如图,设点A是单位圆上的一定点,动点P由点A出发在圆上按逆时针方向旋转一周,点P旋转过的弧为l,弦AP为d则函数d=f(l)的图象是()A.B.C.D.【考点】扇形面积公式;弧长公式.【分析】取AP的中点为D,设∠DOA=θ,在直角三角形求出d的表达式,根据弧长公式求出l的表达式,再用l表示d,根据解析式选出答案.【解答】解:取AP的中点为D,设∠DOA=θ,则d=2sinθ,l=2θR=2θ,∴θ=∴d=2sin,根据正弦函数的图象知,C中的图象符合解析式.故选C.12.设向量与的夹角为θ,定义与的“向量积”:是一个向量,它的模,若,则=()A.B.2 C. D.4【考点】平面向量的综合题.【分析】设的夹角为θ,由向量的数量积公式先求出cosθ==﹣,从而得到sinθ=,由此能求出.【解答】解:设的夹角为θ,则cosθ==﹣,∴sinθ=,∴=2×2×=2.故选B.二、填空题:本大题共4小题,每小题5分,共20分.13.已知,且,则tanφ= ﹣.【考点】同角三角函数基本关系的运用.【分析】先利用诱导公式化简原式求得sinφ,进而利用同角三角函数的基本关系求得cosφ的值,则tanφ的值可得.【解答】解:,∴sinφ=﹣<0,∵,∴﹣<φ<0,∴cosφ==,∴tanφ==﹣,故答案为:﹣.14.设向量,是夹角为的单位向量,若=+2,则||= .【考点】平面向量数量积的运算.【分析】计算,开方即可得出||.【解答】解:,.=3.∴||=.故答案为.15.已知f(x)=sin(ω>0),f()=f(),且f(x)在区间上有最小值,无最大值,则ω= .【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】根据f ()=f (),且f (x )在区间上有最小值,无最大值,确定最小值时的x值,然后确定ω的表达式,进而推出ω的值.【解答】解:如图所示,∵f (x )=sin ,且f ()=f (),又f (x )在区间内只有最小值、无最大值, ∴f (x )在处取得最小值.∴ω+=2k π﹣(k ∈Z ).∴ω=8k ﹣(k ∈Z ).∵ω>0,∴当k=1时,ω=8﹣=;当k=2时,ω=16﹣=,此时在区间内已存在最大值.故ω=.故答案为:16.函数f (x )=3sin (2x ﹣)的图象为C ,则以下结论中正确的是 ②③ . (写出所有正确结论的编号).①图象C 关于直线x=对称;②图象C 关于点对称;③函数f (x )在区间(﹣,)内是增函数;④由y=3sin2x 的图象向右平移个单位长度可以得到图象C .【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用正弦函数f(x)=3sin(2x﹣)的性质,对①②③④四个选项逐一判断即可.【解答】解:∵f(x)=3sin(2x﹣),①:由2x﹣=kπ+(k∈Z)得:x=+(k∈Z),∴f(x)=3sin(2x﹣)的对称轴方程为:x=+(k∈Z),当k=0时,x=,k=﹣1时,x=﹣,∴图象C关于直线x=对称是错误的,即①错误;②:∵f()=3sin(2×﹣)=0,∴图象C关于点(,0)对称,即②正确;③:由2kπ﹣≤2x﹣≤2kπ+得:kπ﹣≤x≤kπ+(k∈Z),∴f(x)=3sin(2x﹣)的增区间为[kπ﹣,kπ+](k∈Z),当k=0时,[﹣,]为其一个增区间,故③正确;④:将y=3sin2x的图象向右平移个单位长度可以得到y=3sin2(x﹣)=3sin(2x﹣)≠3sin(2x﹣)=f(x),故④错误.综上所述,②③正确.故答案为:②③.三、解答题:本大题共6小题,共70分.(解答应写出必要的文字说明、证明过程及演算步骤.)17.已知向量.(1)若,求k的值;(2)若,求m的值.【考点】平面向量数量积的运算;平面向量共线(平行)的坐标表示;数量积判断两个平面向量的垂直关系.【分析】(1)根据所给的向量的坐标,表示出已知平行的向量的坐标,根据两个向量平行的条件,写出关于k的等式,解方程即可.(2)根据所给的向量,表示出要证明垂直的两个向量的坐标,根据两个向量垂直,得到数量积等于0,得到关于m的等式,解方程即可.【解答】解:(1)∵,∴3,.∵,∴﹣9(1+2k)=﹣2+3k,∴k=﹣.(2)∵m,由,得1×(m﹣2)﹣2×(﹣2m﹣3)=0,∴m=﹣.18.已知f(α)=(1)化简f(α);(2)若f(α)=,且0<α<,求sinα+cosα的值.【考点】三角函数的化简求值.【分析】(1)直接利用诱导公式化简表达式,求解即可.(2)判断正弦函数与余弦函数的范围,利用同角三角函数基本关系式化简求解即可.【解答】解:(1)f(α)==﹣=sinαcosα.(2)f(α)=,且0<α<,sinα>0,cosα>0,sinα+cosα>0.可得:sinαcosα=,2sinαcosα=.1+2sinαcosα=.∴sinα+cosα=.19.已知向量=(cosα,sinα),=(cosβ,sinβ),=(﹣1,0)(1)求向量的长度的最大值;(2)设α=,β∈(0,π),且⊥(+),求β的值.【考点】三角函数中的恒等变换应用;平面向量数量积的运算.【分析】(1)根据向量的坐标运算模长公式及向量的坐标表示,再由余弦函数的值域即可求得最大值;(2)运用向量垂直的条件,结合向量的数量积的坐标表示,以及同角的平方关系,即可求得cosβ的值,根据β∈(0,π),即可求得β的值.【解答】解:(1)=(cosβ﹣1,sinβ),∴丨丨===,∴当cosβ=﹣1,丨丨取最大值,最大值为2,向量的长度的最大值2;(2)α=,⊥(+),∴•+•=0,cosαcosβ﹣sinαsinβ﹣cosα=0,(cosβ+sinβ)=,sinβ+cosβ=1,∵sin2β+cos2β=1,解得:cosβ=0或1,∵β∈(0,π),β=.20.已知函数f(x)=sin(2x﹣)(1)画出函数f(x)在区间[0,π]的简图(要求列表);(2)求函数f(x)的单调递减区间.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】(1)利用用五点法做函数y=Asin(ωx+φ)的图象的方法,作出f(x)在区间[0,π]的简图.(2)利用正弦函数的减区间,求得函数f(x)的单调递减区间.【解答】解:(1)对于函数f(x)=sin(2x﹣),∵x∈[0,π],可得2x﹣∈[﹣,],(2)令2kπ+≤2x﹣≤2kπ+,求得kπ+≤x≤kπ+,可得函数f(x)的单调递减区间为[kπ+,kπ+],k∈Z.21.已知函数f(x)=sin(2ωx﹣)+b,且函数的对称中心到对称轴的最小距离为,当x∈[0,]时,f(x)的最大值为1(1)求函数f(x)的解析式(2)若f(x)﹣3≤m≤f(x)+3在x∈[0,]上恒成立,求m的取值范围.【考点】正弦函数的图象;正弦函数的定义域和值域.【分析】(1)根据函数的性质求出ω和b,即可求函数f(x)的解析式(2)分别求出f(x)﹣3和f(x)+3的取值范围,结合恒成立问题即可得到结论.【解答】解:(1)∵函数的对称中心到对称轴的最小距离为,∴=,即周期T=π,即||=π,解得ω=1或ω=﹣1,若ω=1,则f(x)=sin(2x﹣)+b,当x∈[0,]时,2x﹣∈[﹣,],∴当2x﹣=,时,函数f(x)取得最大值为f(x)=+b=+b=+b=1,即b=﹣,此时;若ω=﹣1,则f(x)=sin(﹣2x﹣)+b,当x∈[0,]时,﹣2x﹣∈[﹣π,﹣],∴当﹣2x﹣=0时,函数f(x)取得最大值为f(x)=0+b=1,即b=1,此时,综上或.(2)若,由(1)知,函数f (x )的最大值为1,最小值为f (x )=﹣+1=﹣﹣=﹣﹣=﹣2,即﹣2≤f (x )≤1,则﹣5≤f (x )﹣3≤﹣2,1≤f (x )+3≤4,∵f (x )﹣3≤m ≤f (x )+3在x ∈[0,]上恒成立,∴﹣2≤m ≤1;若.由(1)知,函数f (x )的最大值为1,最小值为f (x )=(﹣1)+1=1﹣,即1﹣≤f (x )≤1,则﹣2﹣≤f (x )﹣3≤﹣2,4﹣≤f (x )+3≤4,∵f (x )﹣3≤m ≤f (x )+3在x ∈[0,]上恒成立,∴﹣2≤m ≤4﹣.22.已知平面向量=(﹣,1),=(,),=﹣+m , =cos 2x +sinx ,f (x )=•,x ∈R .(1)当m=2时,求y=f (x )的取值范围;(2)设g (x )=f (x )﹣m 2+2m+5,是否存在实数m ,使得y=g (x )有最大值2,若存在,求出所有满足条件的m 值,若不存在,说明理由.【考点】平面向量数量积的运算;两角和与差的正弦函数;正弦函数的定义域和值域.【分析】(1)当m=2时,求出和的坐标,可得函数y=f (x )=•=2﹣(sinx ﹣1)2,再利用二次函数的性质求得函数的值域.(2)根据和的坐标,求得函数y=f (x )=•=cos 2x+msinx ,可得g (x )的解析式.令sinx=t ,则﹣1≤t ≤1,g (x )=h (t )=﹣t 2+mt ﹣m 2+2m+6,函数h (t )的对称轴为 t=,再分当<0时和当m ≥0时两种情况,分别利用二次函数的单调性以及g (x )有最大值2,求得m 的值,从而得出结论.【解答】解:(1)当m=2时, =﹣+2=(﹣+1, +),=cos 2x +sinx =(sinx ﹣cos 2x , sinx+cos 2x ),函数y=f (x )=•=(﹣+1)•(sinx ﹣cos 2x )+(+)•(sinx+cos 2x )=cos 2x+2sinx=1﹣sin 2x+2sinx=2﹣(sinx ﹣1)2,故当sinx=1时,函数y 取得最大值为2,当sinx=﹣1时,函数y 取得最小值为﹣2, 故函数的值域为[﹣2,2].(2)∵=﹣+m =(﹣+, +),=cos2x+sinx=(sinx﹣cos2x, sinx+cos2x ),函数y=f(x)=•=(﹣+)•(sinx﹣cos2x )+(+)•(sinx+cos2x )=cos2x+msinx,∴g(x)=f(x)﹣m2+2m+5=cos2x+msinx﹣m2+2m+5=1﹣sin2x+msinx﹣m2+2m+5=﹣sin2x+msinx﹣m2+2m+6.令sinx=t,则﹣1≤t≤1,g(x)=h(t)=﹣t2+mt﹣m2+2m+6,函数h(t)的对称轴为 t=,当<0时,h(t)的最大值为h(1)=﹣1+m﹣m2+2m+6=2,求得m=.当m≥0时,h(t)的最大值为h(﹣1)=﹣1﹣m﹣m2+2m+6=2,求得m=.综上可得,存在实数m=或m=,使得y=g(x)有最大值2.。
【精编】2016-2017年浙江省杭州市西湖高中高一(上)数学期中试卷带解析答案

2016-2017学年浙江省杭州市西湖高中高一(上)期中数学试卷一、选择题(共8小题,每题5分,共40分)1.(5分)已知全集U={0,1,2,3,4},M={0,1,2},N={2,3},则M∩(∁N)=()UA.{2,3,4}B.{2}C.{3}D.{0,1}2.(5分)在同一坐标系中,函数y=2﹣x与y=log2x的图象是()A.B.C.D.3.(5分)已知a=0.72.1,b=0.72.5.c=2.10.7,则这三个数的大小关系为()A.b<a<c B.a<b<c C.c<a<b D.c<b<a4.(5分)如果函数f(x)=x2+(1﹣a)x+3在区间[1,4]上是单调函数,那么实数a的取值范围是()A.a≥9或a≤3 B.a≥7或a≤3 C.a>9或a<3 D.3≤a≤95.(5分)已知函数f(x)=为自然对数的底数,则f[f(e)]=()A.0 B.1 C.2 D.eln 26.(5分)设lg2=a,lg3=b,则log125=()A.B.C.D.7.(5分)已知f(x)为奇函数,且在(0,+∞)上是递增的,若f(﹣3)=0,则xf(x)>0的解集是()A.{x|﹣3<x<0或x>3}B.{ x|x<﹣3或0<x<3}C.{ x|x<﹣3或x>3}D.{ x|﹣3<x<0或0<x<3}8.(5分)函数f(x)=log 2(2x)的最小值为()A.0 B.C.D.二、填空题(共36分,第9—12题每题6分,第13-15每题4分)9.(6分)函数f(x)=的定义域是;值域是.10.(6分)函数f(x)=log(﹣x2+4x﹣1),则当x=时,f(x)有最(填大或小)值.11.(6分)函数f(x)=a x﹣1+1的图象恒过点;若对数函数g(x)=log b x 的图象经过点(3,4),则b=.12.(6分)函数y=log0.3(﹣x2+4x)的单调递增区间是;单调递减区间是.13.(4分)已知函数f(x)=的定义域是R,则实数m的取值范围是.14.(4分)已知函数f(x)=是(﹣∞,+∞)上的减函数,那么a的取值范围为.15.(4分)设有限集合A={a1,a2,..,a n},则a1+a2+…+a n叫做集合A的和,记作S A,若集合P={x|x=2n﹣1,n∈N*,n≤4},集合P的含有3个元素的全体子集分别记为P1,P2,…,P k,则P1+P2+…+P k=.三、解答题:本大题共5题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(1)计算:﹣(﹣)0++;(2)计算.17.(15分)已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.(1)求A∩B、(∁U A)∪(∁U B);(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.18.(15分)定义在R上的函数f(x),f(0)≠0,f(1)=2,当x>0,f(x)>1,且对任意a,b∈R,有f(a+b)=f(a)•f(b).(1)求证:对任意x∈R,都有f(x)>0;(2)判断f(x)在R上的单调性,并用定义证明;(3)求不等式f(3﹣2x)>4的解集.19.(15分)设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.(1)求f(x)的最小值g(a)的解析式;(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R 均成立,若存在,求出m的值;若不存在,请说明理由.20.(15分)函数f(x)=log a(3﹣ax)(a>0,a≠1)(1)当a=3时,求函数f(x)的定义域;(2)若g(x)=f(x)﹣log a(3+ax),请判定g(x)的奇偶性;(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.2016-2017学年浙江省杭州市西湖高中高一(上)期中数学试卷参考答案与试题解析一、选择题(共8小题,每题5分,共40分)1.(5分)已知全集U={0,1,2,3,4},M={0,1,2},N={2,3},则M∩(∁N)=()UA.{2,3,4}B.{2}C.{3}D.{0,1}【解答】解:全集U={0,1,2,3,4},M={0,1,2},N={2,3},∴∁U N={0,1,4},∴M∩(∁U N)={0,1}.故选:D.2.(5分)在同一坐标系中,函数y=2﹣x与y=log2x的图象是()A.B.C.D.【解答】解:∵函数y=2﹣x=是减函数,它的图象位于x轴上方,y=log2x是增函数,它的图象位于y轴右侧,观察四个选项,只有A符合条件,故选:A.3.(5分)已知a=0.72.1,b=0.72.5.c=2.10.7,则这三个数的大小关系为()A.b<a<c B.a<b<c C.c<a<b D.c<b<a【解答】解:根据指数函数的性质可得:函数y=0.7x的底数小于1,是减函数,∵2.1<2.5,∴0.72.1>0.72.5,即a>b.又∵c=2.10.7>2.10=1,a=0.72.1<0.70=1,∴c<a,所以:b<a<c,故选:A.4.(5分)如果函数f(x)=x2+(1﹣a)x+3在区间[1,4]上是单调函数,那么实数a的取值范围是()A.a≥9或a≤3 B.a≥7或a≤3 C.a>9或a<3 D.3≤a≤9【解答】解:由题意知,函数f(x)=x2+(1﹣a)x+3的对称轴x=﹣,开口朝上f(x)在区间[1,4]上单调函数,∴﹣≤1 或﹣≥4,∴a≥9或a≤3,故选:A.5.(5分)已知函数f(x)=为自然对数的底数,则f[f(e)]=()A.0 B.1 C.2 D.eln 2【解答】解:函数f(x)=为自然对数的底数,则f[f(e)]=f(lne)=f(1)=2.故选:C.6.(5分)设lg2=a,lg3=b,则log125=()A.B.C.D.【解答】解:∵lg2=a,lg3=b,则log125==.故选:A.7.(5分)已知f(x)为奇函数,且在(0,+∞)上是递增的,若f(﹣3)=0,则xf(x)>0的解集是()A.{x|﹣3<x<0或x>3}B.{ x|x<﹣3或0<x<3}C.{ x|x<﹣3或x>3}D.{ x|﹣3<x<0或0<x<3}【解答】解:∵y=f(x)在(0,+∞)上单调递增,且f(﹣3)=﹣f(3)=0,∴当x∈(0,3)时,f(x)<0,此时xf(x)<0当x∈(3,+∞)时,f(x)>0,此时xf(x)>0又∵y=f(x)为奇函数,∴y=f(x)在(﹣∞,0)上单调递增,且f(﹣3)=0,∴当x∈(﹣∞,﹣3)时,f(x)<0,此时xf(x)>0当x∈(﹣3,0)时,f(x)>0,此时xf(x)<0综上xf(x)>0的解集为(﹣∞,﹣3)∪(3,+∞)故选:C.8.(5分)函数f(x)=log 2(2x)的最小值为()A.0 B.C.D.【解答】解:由条件可知函数的定义域为(0,+∞),则f(x)=log 2(2x)=log2x•()=log2x•(2+2log2x),设t=log2x,则函数等价为y=t(1+t)=t2+t=(t+)2﹣,故当t=﹣时,函数取得最小值﹣,故选:C.二、填空题(共36分,第9—12题每题6分,第13-15每题4分)9.(6分)函数f(x)=的定义域是(﹣∞,2)∪(2,+∞);值域是(﹣∞,3)∪(3,+∞).【解答】解:由题意:分母不能为0,即x﹣2≠0,解得:x≠2,∴函数的定义域为(﹣∞,2)∪(2,+∞);函数f(x)=化简可得:f(x)==3+∵≠0∴f(x)≠3∴函数的值域为(﹣∞,3)∪(3,+∞).故答案为:(﹣∞,2)∪(2,+∞);(﹣∞,3)∪(3,+∞).10.(6分)函数f(x)=log(﹣x2+4x﹣1),则当x=2时,f(x)有最小(填大或小)值﹣1.【解答】解:令t=﹣x2+4x﹣1,t=﹣x2+4x﹣1=﹣(x﹣2)2+3≤3,∴f(x)=log(﹣x2+4x﹣1)≥﹣1,此时x=2,故答案为:2;小;﹣111.(6分)函数f(x)=a x﹣1+1的图象恒过点(1,2);若对数函数g(x)=log b x的图象经过点(3,4),则b=.【解答】解:函数f(x)=a x﹣1+1,当x=1,f(1)=2;∵对数函数g(x)=log b x的图象经过点(3,4),∴g(3)=log b3=4,∴b=,故答案为:12.(6分)函数y=log0.3(﹣x2+4x)的单调递增区间是[2,4);单调递减区间是(0,2] .【解答】解:令t=﹣x2+4x>0,求得0<x<4,可得函数的定义域为(0,4),y=log0.3t,本题即求函数t在定义域内的单调区间.再利用二次函数的性值可得,t在定义域(0,4)内的减区间为[2,4),故函数y的增区间为[2,4);t在定义域(0,4)内的增区间为(0,2],故函数y的减区间为(0,2],故答案为:[2,4);(0,2].13.(4分)已知函数f(x)=的定义域是R,则实数m的取值范围是[0,8] .【解答】解:∵f(x)=的定义域为R,∴mx2+mx+2≥0在R上恒成立,①当m=0时,有2>0在R上恒成立,故符合条件;②当m≠0时,由,解得0<m≤8,综上,实数m的取值范围是[0,8].故答案为:[0,8].14.(4分)已知函数f(x)=是(﹣∞,+∞)上的减函数,那么a的取值范围为(﹣,1] .【解答】解:由题意得:,解得:﹣<a≤1,故答案为:(﹣,1].15.(4分)设有限集合A={a1,a2,..,a n},则a1+a2+…+a n叫做集合A的和,记作S A,若集合P={x|x=2n﹣1,n∈N*,n≤4},集合P的含有3个元素的全体子集分别记为P1,P2,…,P k,则P1+P2+…+P k=48.【解答】解:由题意:集合P={x|x=2n﹣1,n∈N*,n≤4},那么:集合P={1,3,5,7},集合P的含有3个元素的全体子集为{1,3,5},{1,3,7},{1,5,7},{3,5,7},由新定义可得:P1=9,P2=11,P3=13,P4=15则P1+P2+P3+P4=48.故答案为:48.三、解答题:本大题共5题,共74分.解答应写出文字说明、证明过程或演算步骤.16.(14分)(1)计算:﹣(﹣)0++;(2)计算.【解答】解:(1)原式==0.4﹣1﹣1+23+0.5=2.5﹣1+8+0.5=10.…(6分)(2)原式====.…(12分)17.(15分)已知全集U=R,集合A={x|x<﹣4,或x>2},B={x|﹣1≤2x﹣1﹣2≤6}.(1)求A∩B、(∁U A)∪(∁U B);(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.【解答】解:(1)∵﹣1≤2x﹣1﹣2≤6,∴1≤2x﹣1≤8,∴1≤2x﹣1≤8,∴1≤x≤4.∴B={x|1≤x≤4}.…(2分)又∵A={x|x<﹣4,或x>2},∴A∩B={x|2<x≤4},…(4分)(C U A)∪(C U B)=C U(A∩B)={x|x≤2,或x>4}…(6分)(2)∵集合M={x|2k﹣1≤x≤2k+1}是集合A={x|x<﹣4,或x>2}的子集∴2k﹣1>2或2k+1<﹣4,…(10分)∴或.即实数k的取值范围为.…(12分)18.(15分)定义在R上的函数f(x),f(0)≠0,f(1)=2,当x>0,f(x)>1,且对任意a,b∈R,有f(a+b)=f(a)•f(b).(1)求证:对任意x∈R,都有f(x)>0;(2)判断f(x)在R上的单调性,并用定义证明;(3)求不等式f(3﹣2x)>4的解集.【解答】解:(1)证明:令a=b=0,则f(0)=f(0)•f(0),又f(0)≠0,∴f(0)=1,当x<0时,﹣x>0,∴f(﹣x)>1,∵f(0)=f(x)•f(﹣x)=1,∴f(x)=,∵f(﹣x)>1,∴0<<1,即0<f(x)<1,又当x>0,f(x)>1;且f(0)=1,所以对任意x∈R,都有f(x)>0.(2)f(x)在R上是增函数,证明如下:设x1<x2,则f(x2)=f(x2﹣x1+x1)=f(x2﹣x1)f(x1),∵x2﹣x1>0,∴f(x2﹣x1)>1,又f(x1)>0,∴f(x2﹣x1)f(x1)>f(x1),即f(x2)>f(x1),∴f(x)在R上是增函数.(3)∵f(2)=f(1)•f(1)=4,∴f(3﹣2x)>4⇔f(3﹣2x)>f(2),∵f(x)在R上是增函数,∴3﹣2x>2,解得x<.∴不等式f(3﹣2x)>4的解集为(﹣∞,).19.(15分)设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.(1)求f(x)的最小值g(a)的解析式;(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R 均成立,若存在,求出m的值;若不存在,请说明理由.【解答】解:(1)对称轴x=﹣a①当﹣a≤0⇒a≥0时,f(x)在[0,2]上是增函数,x=0时有最小值f(0)=﹣a﹣1…(1分)②当﹣a≥2⇒a≤﹣2时,f(x)在[0,2]上是减函数,x=2时有最小值f(2)=3a+3…(1分)③当0<﹣a<2⇒﹣2<a<0时,f(x)在[0,2]上是不单调,x=﹣a时有最小值f(﹣a)=﹣a2﹣a﹣1…(2分)∴…(2分)(2)存在,由题知g(a)在是增函数,在是减函数∴时,,…(2分)g(a)﹣m≤0恒成立⇒g(a)max≤m,∴…(2分),∵m为整数,∴m的最小值为0…(1分)20.(15分)函数f(x)=log a(3﹣ax)(a>0,a≠1)(1)当a=3时,求函数f(x)的定义域;(2)若g(x)=f(x)﹣log a(3+ax),请判定g(x)的奇偶性;(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.【解答】解:(1)由题意:f(x)=log3(3﹣3x),∴3﹣3x>0,即x<1,…(2分)所以函数f(x)的定义域为(﹣∞,1).…(3分)(2)易知g(x)=log a(3﹣ax)﹣log a(3+ax),∵3﹣ax>0,且3+ax>0,∴,关于原点对称,…(4分)又∵g(x)=log a(3﹣ax)﹣log a(3+ax)=,∴g(﹣x)==﹣=﹣g(x),…(5分)∴g(x)为奇函数.…(6分)(3)令u=3﹣ax,∵a>0,a≠1,∴u=3﹣ax在[2,3]上单调递减,…(7分)又∵函数f(x)在[2,3]递增,∴0<a<1,…(8分)又∵函数f(x)在[2,3]的最大值为1,∴f(3)=1,…(9分)即f(3)=log a(3﹣3a)=1,∴.…(10分)赠送初中数学几何模型【模型三】双垂型:图形特征:60°运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
江西省南昌市八一中学、洪都中学、麻丘中学等六校高一
2016~2017学年度第一学期高一数学期中联考试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分.共4开,考试时间120分钟,考生作答时将答案答在答题卡上,在本试卷上答题无效.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求。
)1、下列各式中,正确的个数是①{0}φ=;②{0}φ⊆;③{0}φ∈;④0={0};⑤0{0}∈;⑥{1}{1,2,3}∈;⑦{1,2}{1,2,3}⊆;⑧{,}{,}a b b a ⊆ A.1个B.2个C.3个D.4个2、设全集U 是实数集R ,{|||2},{|13}M x x N x x =≥=<<,则图中阴影部分所表示的集合是A.{|21}x x -<< B .{|22}x x -<< C .{|12}x x <<D .{|2}x x <3、下列各组函数中,表示同一函数的是A.2()1,()1x f x x g x x=-=- B.2()||,()()f x x g x x ==C.33(),()f x x g x x ==D.2()2,()4f x x g x x ==4、函数()2562x x f x x -+=-的定义域是A .{x |2<x <3}B .{x |x <2或x >3}C .{x |x ≤2或x ≥3} D.{x |x <2或x ≥3} 5、下列四个函数中,在区间(0,)+∞上单调递增的函数是 A.()3f x x =-+ B. 2()(1)f x x =+C.()|1|f x x =--D.1()f x x=6、设2()f x x bx c =++,且(1)(3)f f -=,则A .(1)(1)f c f >>-B .(1)(1)f c f <<-C .(1)(1)f f c >->D .(1)(1)f f c <-< 7、已知映射:,f A B A B R →== ,对应法则2:2f x y x x →=-+,对于实数k B ∈在A 中没有原象,则k 的取值范围是MUNA .1k >B .1k ≥C .1k <D .2k ≤8、已知函数()f x 在R 上是奇函数,且(4)()f x f x +=,当()0,2x ∈时,2()2f x x =,则(7)f =( )A.18B.2C.1D.-29、已知函数()f x =221,1,,1x x x ax x ⎧+<⎪⎨+≥⎪⎩若((0))4f f a =,则函数()f x 的值域( ) A .[1,)-+∞ B .()1,+∞ C .()3,+∞ D .9[,)4-+∞ 10、设a =0.60.6,b =0.61.5,c =1.50.6,则a 、b 、c 的大小关系是A .a b c <<B .a c b <<C .b a c <<D .b c a << 11、设偶函数()f x 满足3()8(0)f x x x =-≥,则{|(2)0}x f x ->=( )A.{|24}x x x <->或B. {|04}x x x <>或C. {|06}x x x <>或D. {|22}x x x <->或 12、某工厂2015年生产某产品2万件,计划从2016年开始每年比上一年增产20%,从哪一年开始 这家工厂生产这种产品的年产量超过6万件(已知lg 2=0.3010,lg 3=0.4771)( )A .2019年B .2020年C .2021年D .2022年第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13、已知集合{(,)|46},{(,)|4},A x y x y B x y x y =+==-=⋂则A B=_______________; 14、已知2(1)2,(1)f x x x f x +=+-=则 ;15、如图,幂函数αx y =在第一象限的图象,比较1,,,,,04321αααα的大小 ;16、若一系列函数的解析式相同,值域相同,但其定义域 不同,则称这一系列函数为“同族函数”,则解析式为2y x =, 值域为{1,2}的“同族函数”共有 个。
高一数学上学期期中习题
内蒙古北方重工业集团有限公司第三中学2016-2017学年高一数学上学期期中试题第一部分一.选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知{}4,3,2,1=U ,{}4,3,1=A ,{}4,3,2=B ,那么=)(B A C U ( ) A .{}2,1 B .{}4,3,2,1 C .φD .{}φ 2. 满足条件{1,2}{1,2,3,4,5}B =的所有集合B 的个数为( )A .2B .3C .4D .8 3. 定义在实数集R 上的函数()y f x =满足121212()()0()f x f x x x x x ->≠-,若()51f =-,(7)0f =,那么(3)f -的值可以为( )A 、-5B 、5C 、0D 、-1 4. 下列函数中,满足()()()f xy f x f y =+的单调递增函数是( )A.()12xf x ⎛⎫= ⎪⎝⎭B.()2xf x =C.()12log f x x = D. ()2log f x x =5. 函数3)1(log 2)(+++=x x f a x,()01a a >≠且恒过定点( )A .)3,0(B .)4,0(C .)27,1(- D . )4,1(-6. 已知函数()()()33,0log ,0x x f x x x ⎧≤⎪=⎨>⎪⎩,则12f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦( )A.1-3D.127. 0.760.76,0.7,log 6的大小顺序是( ) A. 60.70.70.7log 66<<B. 60.70.70.76log 6<< C. 0.760.7log 660.7<< D.60.70.7log 60.76<<8. 已知函数⎪⎩⎪⎨⎧≤+->-=1,2,1,11)(x a x x x x f 在R 上满足:对任意21x x ≠,都有)()(21x f x f ≠,则实数a 的取值范围是( )A. ),2[+∞B.]2,(--∞C. ]2,(-∞D.),2[+∞-9. 设R x ∈,定义符号函数x sgn =000,1,0,1<=>⎪⎩⎪⎨⎧-x x x ,则( )A 、x x x sgn =B 、x x x sgn =C 、x x x sgn =D 、x x x sgn =10. 函数ln ||||x x y x =的图象可能是( ) xy1-1Oxy1-1Oxy1-1Oxy1-1OA B C D11. 已知函数12)(-=xx f ,21)(x x g -=,构造函数)(x F ,定义如下:当)(|)(|x g x f ≥时,|)(|)(x f x F =,当)(|)(|x g x f <时,)()(x g x F -=,那么)(x F ( ) A .有最小值0,无最大值 B .有最小值1-,无最大值 C .有最大值1,无最小值 D .无最小值,也无最大值 12.已知定义域为R 的函数()f x 是奇函数,当0x ≥时,()22f x x a a =--,且对R x ∈,恒有)()2(x f x f <-,则实数a 的取值范围为( )A.⎪⎭⎫ ⎝⎛-21,21 B.⎥⎦⎤⎢⎣⎡-21,21 C.⎪⎪⎭⎫ ⎝⎛-22,22 D.⎥⎦⎤⎢⎣⎡-22,22 第二部分二、填空题:本题共有4小题,每小题5分, 共20分. 13.函数xx y -++=211的定义域为 . 14. 若函数||)(a x x f +=的图像关于y 轴对称,则()f x 的单调减区间为 .15.某食品的保鲜时间y (单位:小时)与储存温度x (单位:C )满足函数关系bkx ey +=( 718.2=e 为自然对数的底数,k 、b 为常数)。
2016--2017学年度上学期高一期中考试数学试卷
安义中学2016-2017学年度上学期高一年级期中考试数 学 试 卷一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的.本大题共12小题,每小题5分,共60分.)1.全集为实数集R ,M ={}{}),则(<,M C x x N x x R 122=≤≤-∩N =( ) A .{}2-<x xB .{}12<<x x -C .{}1<x xD .{}12<x x ≤-2.下列图形中,可以表示以M={x |0≤x ≤1}为定义域,以N={y |0≤y ≤1}为值域的函数的图象是 ( )A B C D3.设f ,g 都是由集合A 到A 的映射,其对应法则如下表(从上到下);x 1 2 3 4 x 1 2 3 4f(x) 3421g(x) 4321则f [g (1)]的值为( ) A .1 B .2 C .3 D .44.函数y =a x -2-1(a >0且a ≠0)图象必经过点( )A .(0,1)B .(1,1)C .(2,0)D .(2,2)5.若函数y=f(x)的图像与y=1nx 的图像关于y=x 对称,则f (1)=( )A .1B .eC .e 2D .1n(e -1)6.函数f (x )=4x 2-m x +5在区间[-2,+∞]上是增函数,在区间(-∞,2)上是减函数,则f (1)等于( ) A .-7 B .1 C .-16 D .25 7.若a=20.5,b=log π3,c=1n 31,则( ) A .b >c >aB .b >a >cC .a >b >cD .c >a >b8.f (x )=⎪⎩⎪⎨⎧=00002< > x x x x π,则f {f [f (-3)]}等于( )A .0B .πC .9D .π29.已知函数f (x )=等于,则,若)()(111a f b a f xxg-=+-( ) A .bB .-bC .b 1D .-b110.已知f (x )={)1(1)1(413≥+-x x og x a x a a <)(是(-∞,+∞)上的减函数,那么a 的取值范围是( )A .[3171,)B .(0,31) C .(71,1) D .(31,1) 11.若函数f (x )为偶函数,且在)[∞+,0上是增函数,又f (-3)=0,则不等式(x -2)f (x )<0的解集为( )A .(-∞,-3)∪(2,3)B .(-3,2)∪(3,+∞)C .(-3,3)D .(2,3)12.对于实数m ,n 定义运算“⊕”:m ⊕n =⎪⎩⎪⎨⎧-≤-+-nm mn n nm mn m > 2212,设f (x )=(2x -1)⊕(x -1),且关于x 的方程f (x )=a 恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3 的取值范围是( )A .(-321,0) B .(-161,0) C .(0,321) D .(0,161) 二、填空题:(本大题共4小题,每小题5分,满分20分)13.函数f (x )=1n x +2x -6的零点在区间(a ,a+1),a ∈Z 内,则a = . 14.A 若{}20172017201b ab a a a b a ++=⎭⎬⎫⎩⎨⎧,则,,,,的值为 .15.函数f (x )=)32(1313-2++-x g xx 的定义域为 .16.给出下列五个命题:①函数y =f (x ),x ∈R 的图象与直线x=a 可能有两个不同的交点; ②函数y=log 2x 2与函数y=2log 2x 是相等函数;③对于指函数y=2x 与冥函数y =x 2,总存在x 0,当x >x 0时,有2x >x 2成立; ④对于函数y =f (x ),x ∈[a ,b ],若有f (a )×f (b )<0,则f (x )在(a ,b )内有零点; ⑤已知x 1是方程x +1g x =5的根,x 2是方程x +10x =5的根,则x 1+x 2=5. 其中正确的序号是三、解答题(本大题共6小题,共70分) 17.(本小题满分10分) 计算下列各式的值:(1)31021)278()53()412( -+-- (2)++1001lg 25.6log 5.2In 3log 122++e18.(本小题满分12分)已知集合A={}{}4)2(log 362<,或+=-≤≥x x B x x x . (1)求B C A R ⋂;(2)已知{}B C R a a x a x C ⊆∈+=,若<<)(12,求实数a 的取值范围.19.(本小题满分12分) 设函数,则:244)(+=x xx f (1)证明:1)1()(=-+x f x f ;(2)计算:)20152014()20153()20152()20151(f f f f +⋯+++.20.(本小题满分12分)已知函数12)(2-+-=a ax x x f 在区间[0,1]上有最小值-2,求a 的值.21.(本小题满分12分)据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本y (万元)可以看成月产量x(吨)的二次函数. 当月产量为10吨时,月总成本成为20万元;当月产量为15吨时,月总成本最低为17.5万元.(1)写出月总成本y (万元)关于月产量x (吨)的函数有关系; (2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润,最大利润多少?22.(本小题满分12分) 已知函数).23()11(1)(,恒过定点且>, ≠+=-a a ax f a x(1)求实数a ;(2)在(1)的条件下,将函数f(x)的图象向下平移1个单位,再向左平移a 个单位后得到函数g(x),设函数g(x )的反函数为h(x ),求h(x )的解析式;(3)对于定义在[1,9]的函数y =h(x ),若在其定义域内,不等式[h(x )+2]2≤h (x 2)+m +2恒成立,求m 的取值范围.。
高一数学上学期期中试题17
江西省赣州市厚德外国语学校2016-2017学年高一数学上学期期中试题注:全卷总分150分,考试时间120分钟,请按要求作答。
一、选择题。
本题共12个小题,每小题5分,共60分。
在每题列出的四个选项中,只有一项是最符合题目要求的。
1.下列表示错误的是 ( )A .{a }∈{a ,b }B .{a ,b }⊆{b ,a }C .{-1,1}⊆{-1,0,1}D .∅⊆{-1,1}2. 设集合M ={x |-3<x <2},N ={x |1≤x ≤3},则M ∩N =( )A .[2,3]B .[1,2]C .(2,3]D .[1,2)3.函数y =x -1+lg(2-x )的定义域是( )A .(1,2)B .[1,4]C .[1,2)D .(1,2] 4. 函数()521-+=-x x f x 的零点所在区间为()A .(0,1)B .(1,2)C .(2,3)D .(3,4) 5.三个数23.0-=a ,3.0log 2=b,3.02=c 之间的大小关系是( )A .a b c << B .b c a << C .b a c << D .a c b <<6.若f (x )=-x 2+2(a -1)x +2在(-∞,4]上单调递增,则实数a 的取值范围是( )A .a ≥-3B .a ≤-3C .a ≤5D .a ≥57. 要得到y =3×(13)x 的图象,只需将函数y =(13)x的图象( )A .向左平移3个单位B .向右平移3个单位C .向左平移1个单位D .向右平移1个单位8.函数)10(2)(1≠>+=-a a a x f x 且的图象恒过定点()A .(1,3)B .(0,1)C .(1,1)D .(0,3) 9.在下列四图中,二次函数y =ax 2+bx 与指数函数y =(ba)x的图象只可为( ) 10.若实数a 、b 、c 满足c b a643==,则下列等式成立的是( )11.已知定义在R 上函数⎩⎨⎧≥<+-=1log 14)13(f(x)x xx a x a a 对任意21x x ≠都有0)]()()[(2121<--x f x f x x ,那么a 的取值范围是( )A.(0,1)B.(0,31) C.[71,31) D.[71,1)12.设()f x 满足(-)=()f x f x -,且在[1,1]-上是增函数,且(1)1f -=-,若函数2()21f x t at ≤-+对所有的[1,1]x ∈-,当[1,1]a ∈-时都成立,则t 的取值范围是( )A .1122t -≤≤ B .22t -≤≤ C . 12t ≥或或0t = D .2t ≥或2t ≤-或0t = 或12t ≤-二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上) 13. 幂函数f (x)的图象过点(4,2),则f (16)的值为________. 14.化简()()4433log 3log 9log 2log 8++= ________.15.设g (x )=⎩⎪⎨⎪⎧e x,x ≤0,ln x ,x >0,则g (g (12))=________.16.已知0<a <1,则方程a x=|log a x |的实根个数是________.三、解答题(本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分) 计算下列各式的值: (1)2175.003101.016)87(064.0++---;(2)3log 3335258log 932log 2log 2-+-. 18. (本小题满分12分)已知集合A={x |a -1<x <2a +1},B={x |0<x <1},若A∩B=φ,求实数a 的取值范围.19.(本小题满分12分)二次函数f (x )满足f (x +1)-f (x )=2x 且f (0)=1. (1)求f (x )的解析式;(2)当x ∈[-1,1]时,不等式f (x )>2x +m 恒成立,求实数m 的取值范围. 20.(本小题满分12分)解关于x 的不等式:()10282≠>≥-a a a ax x 且21. (本小题满分12分)正在建设中的郑州地铁一号线,将有效缓解市内东西方向交通的压力. 根据测算,如果一列车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次;每天来回次数是每次拖挂车厢节数的一次函数,每节车厢单向一次最多能载客110人,试问每次应拖挂多少节车厢才能使该列车每天营运人数最多?并求出每天最多的营运人数.(注:营运人数指列车运送的人数) . 22. (本小题满分12分)设函数2()log ()x x f x a b =-,且(1)1f =,2(2)log 12f =.(1)求a b ,的值;(2)当[12]x ∈,时,求()f x 的最大值.2016—2017学年第一学期厚德外国语学校期中考试高一数学学科答题卷二、填空题:(每小题5分,共20分)13、 4 14、 6 15、 16、 2三、解答题:(本大题共6小题,共70分.解答题应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分) 计算下列各式的值:(1)(2).18. (本小题满分12分)已知集合A={x |a -1<x <2a +1},B={x |0<x <1},若A ∩B=φ,求实数a 的取值范围.解:依题意可知,①当∅=⋂∅=B A A 时,,有121+≥-a a ,解得2-≤a②19.(本小题满分12分)二次函数f (x )满足f (x +1)-f (x )=2x且f (0)=1. (1)求f (x )的解析式;(2)当x ∈[-1,1]时,不等式f (x )>2x +m 恒成立,求实数m 取值范围. 解:(1)依题意可设)0()(2≠++=a c bx ax x f ,座位号1 2 3 4 5 6 7 8 9 10 11 12 ADCCBDDACBCD2175.003101.016)87(064.0++---⎩⎨⎧≥-+<-⎩⎨⎧≤++<-∅=⋂∅≠11a 121012121a a a a a B A A 或,可知时,由当则有 ⎩⎨⎧=++=-+==xb a ax x f x fc f 22)()1(1)0(根据待定系数可得⎩⎨⎧=+=022b a a 解得⎩⎨⎧-==11b a所以1)(2+-=x x x f20.(本小题满分12分)解关于x 的不等式:()10282≠>≥-a a a a x x 且21. (本小题满分12分)正在建设中的郑州地铁一号线,将有效缓解市内东西方向交通的压力. 根据测算,如果一列车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次;每天来回次数是每次拖挂车厢节数的一次函数,每节车厢单向一次最多能载客110人,试问每次应拖挂多少节车厢才能使该列车每天营运人数最多?并求出每天最多的营运人数.(注:营运人数指列车运送的人数) .解;设每次拖挂车厢节数为x 节,每天来回次数为y 次, 每天营运人数为z 人, 依题意可设)0(≠+=k b kx y,则根据条件得答:每次拖挂6节车厢可以使列车运营人数最多,最多为15840人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择题(每小题5分,共60分)
1.已知集合,,,}2{}3,2,1{}4,3,2,1{===B A U 则=B C A U
A.}2{
B.}3,2{
C.}3{
D.}3,1{
2.若函数x x f 21)(-=,则)(x f 的定义域为
A .),0[+∞ B.),1[+∞ C.]0,(-∞ D.]1,(-∞
3.已知函数⎩⎨⎧≤->=3
,33,log )(2x x x x x f ,则))1((-f f 的值为 A .1- B .0 C .1 D .2 4.设5.12=a ,5.1log 21=b ,5.1)
21
(=c ,则c b a ,,的大小关系
A .b c a >>
B .b a c >>
C .c b a >>
D .c a b >>
5.下列从集合A 到集合B 的对应关系中,既是映射关系又是函数关系的是
6.已知指数函数0(3)(2>+=-a a x f x 且)1≠a 的图像恒过定点P ,则定点P 的坐标是
A .(2,3)
B .(2,4)
C .(3,3)
D .(3,4)
7.已知函数)(x f 是定义域为R 的奇函数,当0<x 时,x x x f -=2)(,那么当0>x 时,
)(x f 的解析式是
A .x x x f -=2-)(
B .x x x f +=2
)(
C .x x x f -=2)(
D .x x x f +-=2)(
8.已知)(x f 是定义在),0(+∞上的单调增函数,若)2()(x f x f ->,则x 的范围是 A.),1(+∞ B . ),(1-∞ C .)(2,0 D .)(2,1
9.已知函数⎩
⎨⎧≥<-+=1,ln 1,2)1()(x x x a x a x f 的值域为R ,则实数a 范围是 A.]1,1[- B .]1,1(- C .),1[+∞ D .),(1-∞
10.函数)(x f |
|2x =的定义域为],[b a ,值域为]4,1[,a 变动时,方程)(a g b =表示的图形可以是
11.已知函数x x x f +-=22
1)(在定义域内存在区间[m,n]上的值域为[3m,3n],则m+n 的值是 A .-2 B .-3 C .-4 D .-5 12.设函数⎩⎨⎧>-≤=-0),
1(0,3)(x x f x x f x ,则方程2)(+=x x f 实根的个数是 A .2 B .3 C .4 D .4个以上
二.填空题(每小题5分,共20分)
13.已知2
1
a )0(4>=a ,则=a 2log ______________ 14.已知函数22
1)(x
x x f +=,那么=++++)31()21()3()2()1(f f f f f _________ 15.设2a =3b
m =,且111=+b
a ,则=m _________ 16.函数⎪⎩⎪⎨⎧<+-≥=111
,log )(21x x x x x f ,则满足方程)(log )]([21m f m f f =的m 的取值范围是___________
三.解答题
17.(本小题满分10分)
化简或求值
(1)03121-2-3
13278-4122)()((+⨯ (2)14lg 2lg 5lg 2lg 2lg 22+-+⋅+
18. (本小题满分12分) 已知函数1
21)(+-=x a x f (I )确定a 的值,使)(x f 为奇函数;
(II )当)(x f 为奇函数时,求)(x f 的值域。
19. (本小题满分12分)
已知集合}01|{},105|{},61|{>+=<<=<≤=ax x C x x B x x A
(I )求B A C B A R )(,;
(II )若A C A = ,求实数a 的取值范围。
20.(本小题满分12分)
已知幂函数12)33()(++-=m x
m m x f 为偶函数,)10]()([log )(≠>-=a a ax x f x g a 且
(I )求)(x f 的解析式;
(II )若)(x g 在区间)3,2(上为增函数,求实数a 的取值范围。
21. (本小题满分12分)
已知二次函数)(x f 满足不等式25)(-<x x f 的解集是(1,2),且)(x f 图像过点(-1,-1)
记函数⎩
⎨⎧≤->=0),(0|,log |)(2x x f x x x g , (I )求)(x f 的解析式,并画出)(x g 的图像;
(II )求关于x 的方程02)(5)(22=+-x g x g 不同
的根的个数。
22. (本小题满分12分) 函数)(111)(2R a x x x a x f ∈-+++-=
(I )设x x t -++=11,求t 的取值范围,并把)(x f 表示为t 的函数)(t ϕ; (II )记)(x f 的最大值为)(a g ,求)(a g 的表达式。
