初一证明题
初一几何证明典型例题

初一几何证明典型例题1、已知:AB=4,AC=2,D是BC中点,AD是整数,求AD解:延长AD到E,使AD=DE∵D是BC中点∴BD=DC 在△ACD和△BDE中AD=DE∠BDE=∠ADCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE∵AB=4即4-2<2AD<4+21<AD<3∴AD=2ADBC2、已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2ABCDEF21证明:连接BF和EF∵BC=ED,CF=DF,∠BCF=∠EDF∴△BCF≌△EDF (S、A、S)∴ BF=EF,∠CBF=∠DEF连接BE在△BEF中,BF=EF∴∠EBF=∠BEF。
∵ ∠ABC=∠AED。
∴ ∠ABE=∠AEB。
∴ AB=AE。
在△ABF和△AEF中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴△ABF≌△AEF。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE,EF//AB,求证:EF=ACBACDF21E 过C作CG∥EF交AD的延长线于点GCG∥EF,可得,∠EFD=CGDDE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGDEF=CG∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC 为等腰三角形,AC=CG又 EF=CG∴EF=ACA4、已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD =∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠AB C=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF ∵CE⊥AB ∴∠CEB=∠CEF =90 ∵EB=EF,CE=CE,∴△CEB≌△CEF ∴∠B=∠CFE ∵∠B +∠D=180,∠CFE+∠CFA=180 ∴∠D=∠CFA ∵AC平分∠BAD ∴∠DAC=∠FAC ∵AC=AC ∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
七年级数学典型几何证明50题
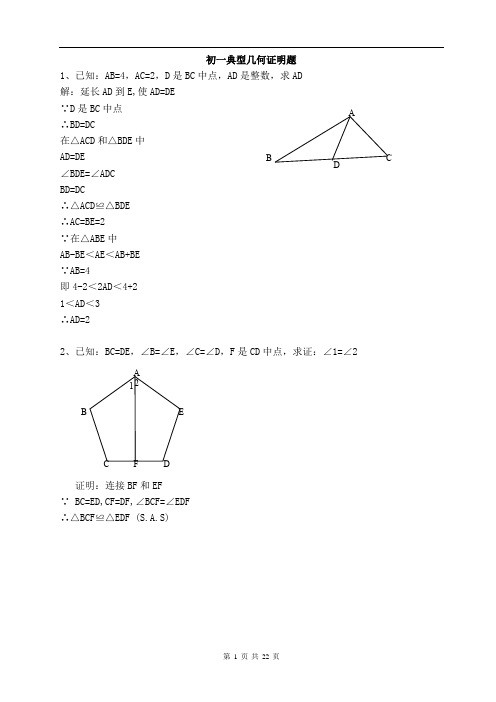
初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
初一数学证明题汇集

(一) 证明题练习1.如图,已知AC AB , EF BC,AD BC, 1 写出推理过程;2.如图,BD>^ ABC的角平分线,DE//CB交AB于点E,/A=45°,Z BD(=60°,求△ BDE各内角的度数.3.如图,四边形ABCDK E是AD中点, 且CE交BA延长线于点F, CE= EF.(1) 试说明:CD/ AB(2) 若BEL CF试说明:CF平分/ BCD4.如图,四边形ABC呼,AC交BD于点0,则有这样的结论:AC+BD>AB+CD尔能说出理由吗5女口图,AB=EB BC=BF ABE CBF .EF和AC相等吗为什么6. 如图,AD // BC , AD平分/ EAC你能确定/ B与/ C的数量关系吗请说明理由E7. 如图,已知D为仏ABC边BC延长线上一点,DF丄AB于F交AC于E, / A=35°/ D=42 ,求/ ACD的度数8. 如图,点E、F在正方形ABCD勺边BG CD上,且BE二CF试判断AEBF的关系,并说明理由9. 如图AB=AC CDL AB于D, BE!AC于E, BE与CD相交于点O(1) 求证AD=AE(2) 连接OA BC试判断直线OA BC的关系并说明理由.v1.0可编辑可修改2(二)解方程组练习 (1)J ;(3)3x 2y 4 2x 3y 7x 2 2(y 1)2(x 2) y 2 4(三)化简求解题练习1.先化简,再求值:(x 5y)( x 5y) ( x 5y)2,其中X二一1 y=1x=-2.先化简再求值:(x 1)(x 1) 3(x 1)(x 3) 2(x 2)2其中3先化简,再求值:(a 2)(a 2) a(1 a);其中a 5。
2。
七年级证明题及答案

七年级证明题及答案【篇一:七年级数学证明题专练】p> xxx年级xx班级姓名:_______________班级:_______________考号:_______________一、简答题(每空?分,共?分)1、如图,已知∠b =∠c,∠1 =∠2,可推得ab∥cd。
理由如下:=∠2(已知),且∠1 =∠cgd(__________________________)∴∠2 =∠cgd (等量代换)∴ce∥bf(_______________________________)∴∠ =∠bfd(__________________________)又∵∠b =∠c(已知)∴∠bfd =∠b()∴ab∥cd(________________________________)2、说理过程填空(每空1分,共5分)已知:∠bcf=∠b+∠f。
试说明:ab//ef理由:经过点c作cd//ab∴∠bcd=∠b()∵∠bcf=∠b+∠f(已知)∴∠()=∠f()∴cd//ef()∴ab//ef()3、如图,ab∥cd,bn、dn分别平分∠abm、∠mdc,试问∠bmd与∠bnd之间的数量关系如何?证明你的结论.5、如图,已知be∥df,∠b=∠d,则ad与bc平行吗?试说明理由.(8分)二、填空题(每空?分,共?分)6、在等腰rt△abc中。
ac=bc,以斜边ab为一边作等边△abd.使点c、d在ab的同侧,再以cd为一边作等边△cde,使得c、e在ad 的异侧,若ae=1,则cd的长为。
三、选择题(每空?分,共?分)7、如图所示,ab=bc=cd=de=1,ab⊥bc、ac⊥cd,ad⊥de,则ae等于()a.1 b. c.d.28、园丁住宅小区有一块草坪如图所示.已知ab=3m,bc=4m,cd=12m,da=13m,且ab⊥bc,这块草坪的面积是( ) a.24m b.36m c.48m d.72m22229、2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形。
七年级数学典型几何证明50题

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)ADBCA BC DEF 21∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角) ∴△EFD≌△CGD EF =CG ∠CGD=∠EFD 又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB≌△CEF∴∠B=∠CFE∵∠B+∠D=180°,∠CFE+∠CFA=180°∴∠D=∠CFA∵AC平分∠BAD∴∠DAC=∠FAC∵AC=AC∴△ADC≌△AFC(SAS)∴AD=AF∴AE=AF+FE=AD+BE6、如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
初一下册几何证明题 -回复

1. 证明垂直平分线上的任意一点到线段的两个端点的距离相等。
答案:垂直平分线是指将线段垂直平分的线段,根据垂直平分线的定义,可以得出两个三角形的两边相等,故两点到端点的距离也相等。
2. 证明等腰三角形的底边上的两个角相等。
答案:等腰三角形定义为两个底边边长相等的三角形,由于底边相等,根据三角形内角的和为180度,可得两个角相等。
3. 证明平行线与横切线之间的对应角相等。
答案:根据平行线的性质,平行线之间的对应角相等,同时,横切线与平行线相交,所以横切线上的角与平行线之间的对应角也相等。
4. 证明等腰梯形的非平行边上的两个角相等。
答案:等腰梯形的定义为有两个非平行边相等的梯形,根据等腰梯形的性质,它的两个非平行边上的角相等。
5. 证明从圆心到圆上任意一点的线段长度相等。
答案:从圆心到圆上任意一点的线段长度相等,这是由于圆的所有点到圆心的距离都相等的性质。
6. 证明三角形内角和等于180度。
答案:三角形内角和等于180度是由三角形的内角和定理所决定的,即任何三角形的内角和等于180度。
7. 证明同角的弧所对的圆心角相等。
答案:同角的弧所对的圆心角相等是由圆的性质决定的,圆心角的度数恰好等于所对弧的度数。
8. 证明同弧所对的圆心角相等。
答案:同弧所对的圆心角相等,这是圆的性质之一,不论弧所对的两个角是否位于同一圆上,它们的度数恰好相等。
9. 证明直角三角形的斜边上的角是直角。
答案:直角三角形的定义为有一个角是直角(90度)的三角形,直角三角形的斜边上的角一定是直角。
10. 证明等腰梯形的对角线相等。
答案:等腰梯形的对角线相等是由等腰梯形的性质所决定的,它的两个对角线互相平分,并且相互垂直,所以对角线相等。
初一数学几何证明题答案

初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点 ∴BD=DC在△ACD 和△BDE 中 AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23、4、 证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDFBC DF ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
已知:∠1=∠2,CD=DE ,EFP 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-ABBA CDF2 1 EA在AC 上取点E , 使AE =AB 。
∵AE =AB AP =AP ∠EAP =∠BAE ,∴△EAP ≌△BAP ∴PE =PB 。
PC <EC +PE∴PC <(AC -AE )+PB ∴PC -PB <AC -AB 。
8. 已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 证明:在AC 上取一点D ,使得角DBC=角C ∵∠ABC=3∠C∴∠ABD=∠ABC-∠DBC=3∠C-∠C=2∠C ; ∵∠ADB=∠C+∠DBC=2∠C; ∴AB=AD∴AC – AB =AC-AD=CD=BD在等腰三角形ABD 中,AE 是角BAD 的角平分线, ∴AE 垂直BD∵BE ⊥AE∴点E 一定在直线BD 上,在等腰三角形ABD 中,AB=AD ,AE 垂直BD ∴点E 也是BD 的中点 ∴BD=2BE ∵BD=CD=AC-AB ∴AC-AB=2BE9. 如图,在△ABC 中,BD =DC ,∠1=∠2,求证:AD ⊥BC .P DACB解:延长AD 至BC于点E,∵BD=DC ∴△BDC是等腰三角形∴∠DBC=∠DCB又∵∠1=∠2 ∴∠DBC+∠1=∠DCB+∠2即∠ABC=∠ACB∴△ABC是等腰三角形∴AB=AC在△ABD和△ACD中AB=AC∠1=∠2BD=DC∴△ABD和△ACD是全等三角形(边角边)∴∠BAD=∠CAD∴AE是△ABC的中垂线∴AE⊥BC∴AD⊥BC10. 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA证明:∵OM平分∠POQ∴∠POM=∠QOM∵MA⊥OP,MB⊥OQ∴∠MAO =∠MBO =90 ∵OM =OM∴△AOM ≌△BOM (AAS ) ∴OA =OB ∵ON =ON∴△AON ≌△BON (SAS ) ∴∠OAB=∠OBA ,∠ONA=∠ONB ∵∠ONA+∠ONB =180 ∴∠ONA =∠ONB =90 ∴OM ⊥AB11. 如图,已知AD ∥BC ,∠PAB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB . 证明:在AB 上取F ,使AF =AD ,连接EF ∵AE 平分∠DAB ∴∠DAE=∠FAE 在⊿ADE 和⊿AFE 中AD =AF ∠DAE=∠FAE AE = AE∴⊿ADE ≌⊿AFE (SAS ) ∴∠ADE=∠AFE∵AB 如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立若成立PEDCBA{{请给予证明;若不成立请说明理由.(1)证:∵DE ⊥AC 于E ,BF ⊥AC 于F , ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD , ∴Rt △DEC ≌Rt △BFA (HL ) ∴DE=BF .在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF∴△DEM ≌△BFM(AAS) ∴MB=MD ,ME=MF(2) 证:∵DE ⊥AC 于E ,BF ⊥AC 于F , ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD , ∴Rt △DEC ≌Rt △BFA (HL ) ∴DE=BF .在△DEM 和△BFM 中 ∠DEM=∠BFM ∠DME=∠BMF DE=BF{{∴△DEM≌△BFM(AAS)∴MB=MD,ME=MF13如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.证:∵∠CEB=∠CAB=90°∠ADB=∠CDE在△ABD中,∠ABD = 180°-∠CAB-∠ADB 在△CED中,∠DCE = 180°-∠CEB-∠CDE ∴∠ABD =∠DCE在△ABD和△ACF中∠DAB=∠CAFAB=AC∠ABD =∠DCF∴△ABD≌△ACF(ASA)∴BD=CF∵BD是∠ABC的平分线∴∠FBE =∠CBE在△FBE和△CBE中∠FBE =∠CBEBE=BE∠BEF =∠BEC∴△FBE≌△CBE(ASA)∴CE=FE CF=2CE∴BD=2CEFEDC BA{ {14. 如图:DF=CE,AD=BC,∠D=∠C。
初一几何难题-练习题(含答案)
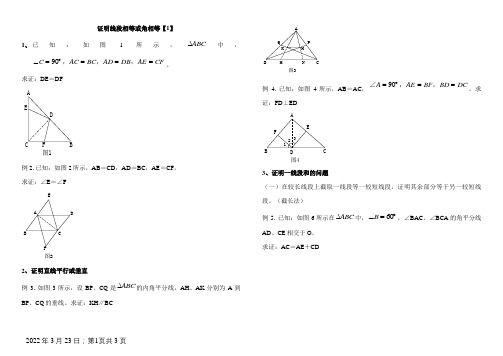
(一)在较长线段上截取一线段等一较短线段,证明其余部分等于另一较短线段。(截长法)
例5.已知:如图6所示在 中, ,∠BAC、∠BCA的角平分线AD、CE相交于O。
求证:AC=AE+CD
(二)延长一较短线段,使延长部分等于另一较短线段,则两较短线段成为一条线段,证明该线段等于较长线段。(补短法)
2.已知:如图12所示,在 中, ,CD是∠C的平分线。
求证:BC=AC+AD
3.已知:如图13所示,过 的顶点A,在∠A内任引一射线,过B、C作此射线的垂线BP和CQ。设M为BC的中点。求证:MP=MQ
4. 中, 于D,求证:
例6.已知:如图7所示,正方形ABCD中,F在DC上,E在BC上, 。
求证:EF=BE+DF
4、中考题:
如图8所示,已知 为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连结CE、DE。
求证:EC=ED
证明几何不等式:
例题:已知:如图9所示, 。
求证:
【实战模拟】
1.已知:如图11所示, 中, ,D是AB上一点,DE⊥CD于D,交BC于E,且有 。求证:
证明线段相等或角相等【1】
1、已知:如图1所示, 中, 。
求证:Dபைடு நூலகம்=DF
例2.已知:如图2所示,AB=CD,AD=BC,AE=CF。
求证:∠E=∠F
2、证明直线平行或垂直
例3.如图3所示,设BP、CQ是 的内角平分线,AH、AK分别为A到BP、CQ的垂线。求证:KH∥BC
例4.已知:如图4所示,AB=AC, 。求证:FD⊥ED
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图,四边形ABCD 中,∠A =∠C =90°,BE 平分∠ABC ,DF 平分∠ADC ,试问BE 与DF 平行吗?为什么?
2、如图,△ABC 中,∠A=36°,∠ABC=40°,BE 平分∠ABC ,∠E=18。
试证明CE 平分∠ACD.
3、已知:如图∠1=∠2,∠C=∠D ,那么∠A=∠F 吗?试说明理由
4、如图AB ∥CD ∠1=∠2,∠3=∠4,试说明AD ∥BE ;
5、已知AB ∥CD ,直线a 交AB 、CD 分别于点E 、F ,点M 在EF 上,P 是直线CD 上的一个动点,(点P 不与F 重合)
(1)当点P 在射线FC 上移动时,∠FMP+∠FPM=∠AEF 成立吗?请说明理由。
(2)当点P 在射线FD 上移动时,∠FMP+∠FPM 与∠AEF 有什么关系?并说明你的理由。
H
G
2
1
F
E
D
C
B
A
6、如图,E 、F 分别是AB 、CD 上一点,D ∠=∠2,
1∠与C ∠互余, AF EC ⊥.试说明CD AB //
7、如图,已知ABC ∆,AD BC ⊥于D ,E 为AB 上一点,EF BC ⊥于F ,//DG BA 交CA 于G .求证12∠=∠.
8、如图5-29,已知:AB //CD ,求证:∠B +∠D +∠BED =360︒(至少用三种方法)
E
A
B
C
D
9、如图,已知AB ∥CD ,∠1:∠2:∠3=1:2:3,求证:BA 平分∠
EBF
10、已知,如图,AB ∥CD ∥GH ,EG 平分∠BEF ,FG 平分∠EFD,求证:∠EGF=90°
11.如图,AD ∥BC ,∠B=∠D ,求证:AB ∥CD 。
1
A
E 2 3
F C D
D
G A E B H C
F
1 2
3 4 D
C
A
12.如图CD ⊥AB ,EF ⊥AB ,∠1=∠2,求证:∠AGD=∠ACB 。
13. 已知∠1=∠2,∠1=∠3,求证:CD ∥OB 。
14. 如图,已知∠1=∠2,∠C=∠CDO ,求证:CD ∥OP 。
15. 已知∠1=∠2,∠2=∠3,求证:CD ∥EB 。
16. 如图∠1=∠2,求证:∠3=∠4。
B D E
/F
C A
2G
3B D
/
P C A
O
2
3B D /P
C O 2B
D
E /
C O 2
3B D /C A
23
4
17. 已知∠A=∠E ,FG ∥DE ,求证:∠CFG=∠B 。
18.已知,如图,∠1=∠2,∠2+∠3=1800,求证:a ∥b ,c ∥d 。
19.如图,AC ∥DE ,DC ∥EF ,CD 平分∠BCA ,求证:EF 平分∠BED 。
20、已知,如图,∠1=450,∠2=1450,∠3=450,∠4=1350,求证:l 1∥l 2,l 3∥l 5,l 2∥l 4。
21、如图,∠1=∠2,∠3=∠4,∠E=900,求证:AB ∥CD 。
B
D
E F
C
A G 2
1
3a c d
b A B C D F
E 21
l l l 3
412
34
5
l 21
A B C D 34E
22、如图,∠A=2∠B ,∠D=2∠C ,求证:AB ∥CD 。
23、如图,EF ∥GH ,AB 、AD 、CB 、CD 是∠EAC 、∠FAC 、∠GCA 、∠HCA 的平分线,求证:∠BAD=∠B=∠C=∠D 。
24、已知,如图,B 、E 、C 在同一直线上,∠A=∠DEC ,∠D=∠BEA ,∠A+∠D=900,求证:AE ⊥DE ,AB ∥CD 。
25、如图,已知,BE 平分∠ABC ,∠CBF=∠CFB=650,∠EDF=500,,求证:BC ∥AE 。
26、已知,∠D=900,∠1=∠2,EF ⊥CD ,求证:∠3=∠B 。
27、如图,AB ∥CD ,∠1=∠2,∠B=∠3,AC ∥DE ,求证:AD ∥BC 。
B
C D O
A B C D F E
A
G H
B
C D E A B C D
E
A 21
B C D
F
3E A 2
1B
C
D 3
E
A
28.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2
29.如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、
∠BCD,且点E在AD上。
求证:BC=AB+DC。
30.已知:AB=CD,∠A=∠D,求证:∠B=∠C.
31.如图:DF=CE,AD=BC,∠D=∠C。
求证:△AED≌△BFC。
32.如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。
求证:AM是△
ABC的中线。
33.AB=AC,DB=DC,F是AD的延长线上的一点。
求证:BF=CF
34.如图:AB=CD,AE=DF,CE=FB。
求证:AF=DE。
35.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证: AE=AF。
36.如图,在四边形ABCD中,E是AC上的一点,∠1=∠2,∠3=∠4,求证: ∠5=∠6.
37.如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
38.如图(13)△ABC≌△EDC。
求证:BE=AD。
39.如图:AD=BC,DE⊥AC于E,BF⊥AC于F,DE=BF。
求证:(1)AF=CE,(2)AB ∥CD。
40.如图,已知P点是∠AOB平分线上一点,PC
⊥OA,PD⊥OB,垂足为C、D,(1)∠PCD=∠PDC吗?为什么?(2)OP是CD的垂直平分线吗?为什么?
41.如图,AD为△ABC的高,∠B=2∠C用轴对称图形证明:CD=AB+BD。
42.如图,P是∠BAC平分线AD上一点,P与A不重合,AC>AB。
求证:PC-PB<AC-AB。
43.如图,四边形ABCD中,AD∥BC,AB=AD,
(1)观察∠ABD与∠CBD,你能得到什么结论?
(2)试说明你得到的结论.
44.如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
45.如图,点G在CA的延长线上,AF=AG,∠ADC=∠GEC.求
证:AD平分∠BAC.
46.已知:,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC 上的点,且满足EA=CF.求证:DE=DF.
47.如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足分别为C,D. (1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?
48.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
49.如图,在等腰△ABC中,AB=AC,AD是BC边上的高,点E、F分别是边AB、AC 上的点,且EF∥BC.
(1)试说明△AEF是等腰三角形;
(2)试比较DE与DF的大小关系,并说明理由.
50..如图,△ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.给出下列四个条件:①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)上述四个条件中,哪两个条件可判定△ABC是等腰三角形;
(2)选择第(1)小题中的一种情形,证明△ABC是等腰三角形。
